Current Source Topologies for Photovoltaic Applications: An Overview

Abstract

Current source topologies have several advantages compared to conventional voltage systems. Their inherent voltage-boosting function, intrinsic short-circuit protection, no electrolytic capacitor, direct-current control, continuous input current, and high reliability make them exceptional candidates for power generation systems, particularly for photovoltaic applications. This study provides an overview of the current source topologies for multi-stage photovoltaic grid-connected systems by comparing the number of components, performance, power-decoupling techniques, efficiency, and frequency operation. The overview reveals gain, performance, energy quality and lifetime improvements, thereby providing current source systems as an attractive alternative for renewable applications.

1. Introduction

Today, renewable energy is a favorable solution for providing green energy to address global power issues [1]. Photovoltaic (PV) power generation systems are trending technologies owing to their efficiency, projection, suitability, practicality, and use [2]. The PV systems are divided into two principal groups [3]: standalone systems, which operate independently, and interconnected systems, which operate in parallel with the electric utility grid [4].

The interconnected systems are classified based on the number of stages in power processing, use of transformer, transformerless configurations (to provide galvanic isolation between panel terminals and AC line), and type of commutation used. Thus, topologies that depend on the number of stages in energy processing are divided into single- and multistage systems, as shown in Figure 1.

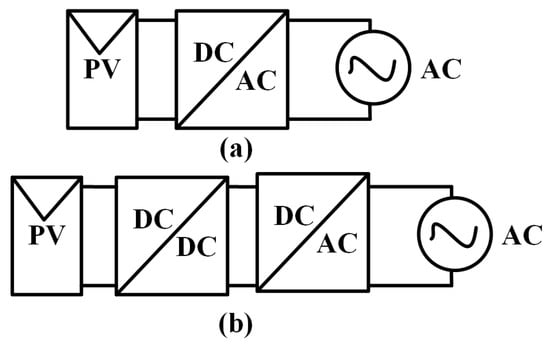
Figure 1. Types of PV inverters: (a) single stage, (b) multi stage [5].

The boosting voltage level, processing of the maximum power point tracking (MPPT), and injected voltage waveform are included in the system capabilities shown in Figure 1. It should be noted that the key to using a single stage is to avoid a bulky transformer to reduce the size, weight, and power losses [6]. However, these inverters have drawbacks, such as low DC voltage range, poor power quality, and reduced power-processing capability.

In contrast, multi-stage inverters (Figure 1b) have galvanic isolation between the PV source and the grid to avoid common ground problems, protect power semiconductor devices, and boost the input voltage [7]. In addition, to interconnect DC and AC components, the system must inject an AC component with proper voltage magnitude, frequency, and phase into the grid network. This can generate more power losses owing to the saturation of magnetic cores [8] and thus needs compliance with international standards to ensure the correct interconnection. Table 1 lists some of these standards [9].

Table 1. Standards of PV-interconnected systems.

Parameters	IEEE 1547	IEC 61727
Formation	USA	United Kingdom
THD	<5%	5%
Power Factor	-	0.9
DC injection	Less than 0.5% of rated output current	Less than 1% of rated output current
Nominal Power	This standard covers distributed resources as large 10 MVA	10 kW or smaller PV systems connected to a low voltage utility grid
Voltage ranger for normal operation	88–110%	85–110%

Voltage and current-fed converters are part of the applied power topologies from Figure 1b [10,11,12,13,14]; among the two, the voltage ones are widely used systems because of their simple design and control. However, current source topologies provide numerous attractive features [15], such as inherent short-circuit capability, no electrolytic capacitor, step-up voltage capability, and continuous input current, which renders them as an interesting alternative not only for PV systems, but also for all DC-AC long lifetime applications.

In this context, this study provides an overview of the current source topologies for PV grid-connected systems by comparing the number of components, efficiency, complexity, reliability, and frequency operation with their conventional counterparts. The overview reveals the reliability, short-circuit protection, input current, voltage boosting, THD, and grid-integration improvements, thus providing current source systems as an attractive alternative for renewable applications.

The remainder of this study is organized as follows. Section 2 presents a comparison of the DC-DC stage between the non-resonant, quasi-resonant, and resonant converters. Section 3 presents some differences between the two principal DC-AC inverters: voltage and current inverters; additionally, it presents part of the principal characteristics of the latter. Finally, Section 4 presents the summary and concluding remarks.

2. DC-DC Power Converters

2.1. Non-Resonant DC-DC Power Converters

The system described in Figure 1b can be detailed into the five stages as shown in Figure 2.

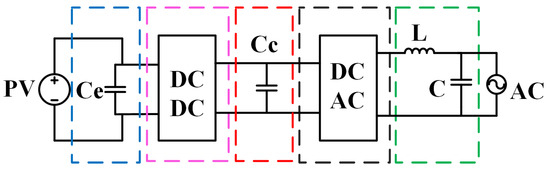
Figure 2. Conventional scheme used for multi-stage PV-connected applications.

Based on the conventional scheme shown in Figure 2, the first stage ($C_e$) allows a low-frequency ripple. The second stage increases the voltage level of the PV according to the inverter specifications. The third and fourth stages represent the decoupling capacitor ($C_c$) and inverter, which must fulfill the following functions: (1) to shape the current into a sinusoidal waveform, and (2) if the PV array voltage is lower than the grid voltage, the PV array voltage must be boosted with an additional element. Finally, the fifth stage filters the sinusoidal signal.

In single-phase PV-connected applications, $C_c$ has critical importance because it must store the necessary energy to buffer the inherent time-varying double-line frequency ripple from the AC port [16]. Therefore, the decoupling component commonly used is an electrolytic capacitor, which reduces the lifetime of the system but is necessary to conserve energy. This point is critical because the application is generally used for power decoupling, a bulky and low reliable electrolytic capacitor, which considerably reduces the lifetime of the application [17].

For PV applications in the DC-DC stage, the pulse width modulated (PWM) converters are among the most applied topologies. One example is the boost converter [18,19]. This topology has advantages, such as low cost, low number of elements, and relative simplicity of design and implementation, which renders them suitable for the PV applications. However, issues, such as hard switching, severe reverse recovery in the output diode, limited efficiency, low power density, and low voltage gain, render it a viable option for low-power applications.

Other topologies used are the conventional and active flyback converters [20,21], whose particular characteristics in low-power applications are the well-coupled transformer, simplicity and low cost. However, issues, such as the high-voltage stress, reverse recovery loss, discontinuous input current (such as buck and buck-boost), large air gap for high power applications, and leakage inductance energy loss, do not render them a strong candidate for PV applications.

Similar to a flyback, the forward converter exhibits a high step-up voltage for low power applications [22]. Nevertheless, the energy is not transferred in a whole switching period, which not only increases the peak current, but also decreases the efficiency of the converter. Alternatively, Ćuk and SEPIC converters have a continuous input current [23,24], a characteristic that is fundamental for maximum renewable source energy extraction [25]. However, the Ćuk converter has an inverted output voltage, whereas SEPIC presents several constraints that need to be considered during its design.

From the above characteristics, Table 2 lists a comparison between DC-DC PWM voltage source and current source converters (VSC and CSC respectively).

Table 2. Characteristics of DC-DC PWM converters.

Ref.	CSC	VSC	Power Rating (W)	Decoupling Capacitor (μF)	Switching Frequency (kHz)	Efficiency (%)	Switches and Diodes
[26]		🗸	300	1500	9.6	89	3 + 2 Diode
[27]		🗸	250	5000	65	94	5
[28]	🗸		5000	80	50.4	95	8 + 1 Diode
[29]	🗸		200	14.4	100	91.2	2 + 6 Diode
[30]		🗸	200	5600	100	95.7	2 + 2 Diode
[31]		🗸	250	11,000	70	95.11	4 + 2 Diode
[32]	🗸		500	70	20	85.3	4 + 3 Diode
[33]	🗸		135	10	50	80	-
[34]		🗸	120	250	70	92.4	1 + 4 Diode
[35]	🗸		250	47	50	95.4	1 + 5 Diode
[36]	🗸		60	1000	20	94.76	2 + 5 Diode
[37]	🗸		340	220	50	96.5	1 + 5 Diode
[38]	🗸		100	100	50	94.2	1 + 3 Diode
[39]	🗸		200	100	50	95	1 + 6 Diode

Table 2 summarizes that PWM topologies for PV applications are required to be designed at low switching frequencies to avoid high power losses. In this context, the trend of increasing the switching frequency to demand an optimal weight, size, cost, and power density is not completely in agreement with PWM converters. However, topologies with continuous input current, such as SEPIC, Ćuk, and Zeta converters, are preferred for maximum renewable source energy extraction. On the other hand, for low power levels in which galvanic isolation is required, flyback, forward and push-pull converters are still popular.

A different category of DC-DC converters exists, where the switching frequency can be chosen to be as high as several hundred kilohertz, particularly for certain applications where high power density is of primary concern. These DC-DC converters are quasi-resonant.

2.2. Quasi-Resonant DC-DC Power Converters

In contrast with PWM topologies, for a quasi-resonant converter, the zero voltage switching and zero current switching techniques (ZCS and ZVS) are performed by applying an $LC$ resonant array across the switch [40], where the injected energy is exchanged between the inductor and capacitor in a periodic sinusoidal form. Therefore, the current or voltage waveform of the semiconductor is forced to oscillate almost into a sinusoidal waveform, thus creating switching conditions at zero current or voltage during turn-on and turn-off instances; hence, semiconductor turn-off power losses are reduced.

Another characteristic of quasi-resonant converters is high-frequency operation without an increase in power loss. This characteristic reduces the reactive components of the topology and increases the power density of the system with less switching-voltage stress and noise [41].

The $LC$ tank can be used as a lossless waveform device, where the resonance condition always appears at the turn-on instance. For this arrangement, if an ideal switch $Q_1$ is implemented in the M- or L-type configuration (Figure 3a), and an anti-parallel diode $D_1$ is added, the voltage across $C_r$ is clamped by $D_1$ to positive, with the resonant switch operating in a half-wave mode (Figure 3b). However, if $D_1$ is implemented in series with $Q_1$, the resonant switch operates in the full-wave mode (Figure 3c).

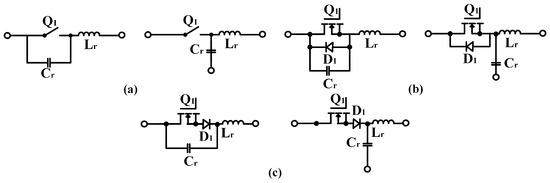
Figure 3. Voltage mode resonant switches: (a) m-type, l-type configurations, (b) half-wave mode, and (c) full-wave mode.

As shown in Figure 3, when the resonant switch is turned on, the voltage can saturate before the current gradually increases in approximately a sinusoidal manner. Because of the resonance between $L_r$ and $C_r$, the current through $Q_1$ tends to oscillate to a negative value, aiming for $Q_1$ to have a natural commutation, and the turn-off state is determined by the resonant frequency ($f_r$), which cannot be freely varied. A common topology obtained by applying a resonant switch is the boost converter [42,43,44] (Figure 4a). This topology can be analyzed as a constant current ($I_1$) that feeds a voltage load $V_2$ (Figure 4b). By adding $L_r$ and $C_r$ through $Q_1$, the quasi-resonant topology performs ZVS (Figure 4c).

Figure 4. Boost converter: (left) common structure, (middle) steady-state equivalent circuit, and (right) ZVS quasi-resonant converter.

The converter shown in Figure 4c has four operating modes. For the first mode (Figure 5a), $Q_1$ and $D_1$ are off and $I_1$ flows into $C_r$, thus linearly increasing its voltage ($V_{Cr}$). The second mode (Figure 5b) describes the resonance state when $D_1$ is conducted by driving a portion of $I_1$ to $V_2$. In this mode, the voltage across the inductor ($V_{Lr}$) and the current across $C_r$ ($i_{Cr}$) are the differences between $V_{Cr}$-$V_2$ and $I_1$-$i_{Lr}$, respectively. In the third mode (Figure 5c), $L_r$ is discharged and its time is determined when $i_{Lr}$ reaches zero. Finally, in the fourth mode (Figure 5d), $I_1$ flows through $Q_1$ and remains constant until $Q_1$ turns off.

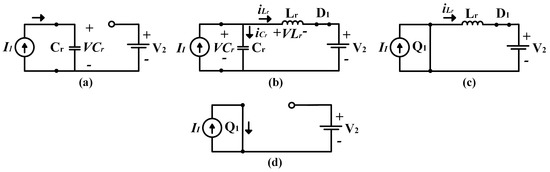
Figure 5. Operation modes: (a) charging of $C_r$, (b) resonant mode, (c) discharging of $C_r$, and (d) freewheeling mode.

The quasi-resonant buck converter [45,46] (Figure 6a) is another topology whose switching period consists of four operating modes. In the first mode (Figure 6b), $Q_1$ is turned on, which allows the inductor $L_r$ to be charged with input current $I_I$. The second mode is the resonance condition performed by the series $L_r$,$C_r$ array (Figure 6c). During this time, the input current increases its value, diode $D_1$ is off, and the difference between $I_I$ and $I_2$ flows across $C_r$ ($I_{Cr}$), which causes a sinusoidal increment of $V_{Cr}$. In the third mode (Figure 6d), $Q_1$ is turned off, which generates $C_r$ to be discharged and causes the energy stored in $C_r$ to flow directly to the load until $V_{Cr}$ decreases linearly to zero. Finally, in the fourth mode (Figure 6e), the output current flows, which causes $D_1$ to conduct concluding the switching cycle of the converter.

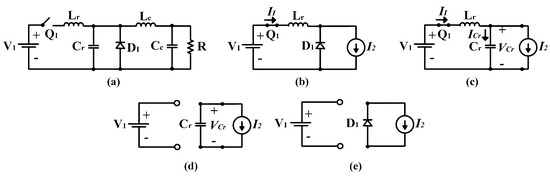
Figure 6. Topology and operation modes: (a) quasi-resonant buck converter, (b) charging of $L_r$, (c) resonant mode, (d) discharging of $L_r$, and (e) freewheeling mode.

Similar to the quasi-resonant boost and buck converter, the common quasi-resonant buck–boost topology (Figure 7a) tends to reduce power losses, thereby providing a robust system with an excellent transient response and noise immunity by applying a ZCS condition [47,48]. Therefore, the new quasi-resonant buck-boost topologies develop an arrangement with a reduced capacitor size, whose inverter is generally composed of two interleaved converters with a smaller number of components for its implementation.

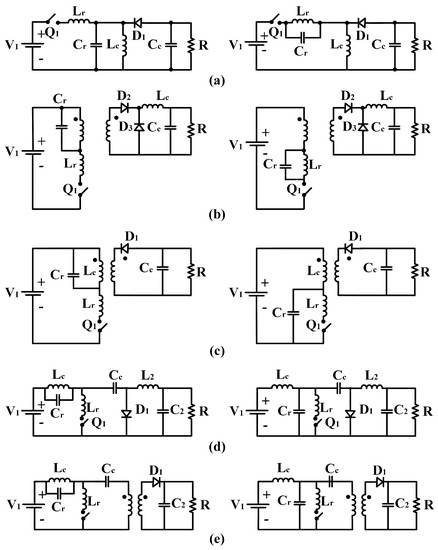
Figure 7. Quasi-resonant topologies: (a) buck–boost, (b) forward, (c) flyback, (d) Ćuk, and (e) SEPIC.

Other quasi-resonant topologies are based on the forward (Figure 7b), flyback (Figure 7c), Ćuk (Figure 7d), and SEPIC (Figure 7e) converters [49,50,51,52,53,54]. These topologies eliminate most of the issues encountered in PWM systems because of their fast response for the dynamic PV system, soft-switching operation, reduction in voltage stress, high voltage gain, and high power density. However, some quasi-resonant topologies still have poor cross-regulation, are limited to discontinuous conduction mode (DCM), have a challenging electromagnetic interference (EMI) filter design, require a high output capacitance, and present high input current ripple. The major causes of losses are switch turn-off and diode reverse recovery, which is a significant disadvantage for many of these converters.

Table 3 lists a general summary of some quasi-resonant topologies reported in the literature.

Table 3. Characteristics of DC-DC quasi-resonant power converters.

Ref.	CSC	VSC	Power Rating (W)	Decoupling Capacitor (μF)	Switching Frequency (kHz)	Efficiency (%)
[55]	🗸		500	4.9	100	94
[56]	🗸		140	10	150	93
[57]		🗸	400	100	61.6	98.4
[58]	🗸		175	25	250	96.5
[59]		🗸	500	75	-	96.2
[60]	🗸		200	50	88	96.2
[61]		🗸	250	-	100	93.2

Quasi-resonant DC-DC converters offer to PV-connected applications, operating at high switching frequency, high voltage gain, low input ripple, low transformer turn ratio, and low current stress on switches to reduce the size of the magnetic components and increase power density. Full-bridge, half-bridge, and push–pull converters are the most utilized topologies [62], which achieve soft commutations and reduce the negative impacts of high ripple current, providing high efficiency over a considerable range of power ratings.

2.3. Resonant DC-DC Power Converters

Resonant power converters are suitable for medium- to high-power applications and have numerous benefits compared to the conventional PWM converters, such as low EMI, low switching losses, low volume and weight, high operating frequency, and low reverse-recovery losses [63]. These resonant converters can be divided into two categories: voltage-fed DC-DC resonant converters (VFRC), which have fewer components, higher efficiency, and higher frequency operation; and current-fed DC-DC resonant converters (CFRC), which do not present a pulsating input current but require a large inductor to feed the inverter.

One VFRC that applies a series LLC resonant tank, which achieves ZVS operation of the primary switches and ZCS operation of the rectifier diodes, is presented in [64]. However, the hold-up time presents an unfavorable effect on the efficiency because the DC/DC conversion stage should cover a wide range of input voltages. Similarly, full- and half-bridge resonant converters can run over an extensive input voltage capacity and a considerable load range while keeping excellent efficiency [65,66,67].

Another VFRC is the LLCC series-parallel resonant converter [68,69], which uses a full-bridge inverter connected to a half-bridge rectifier and transformer. This converter operates at a high frequency, which allows for a considerable decrease in the size of its magnetic elements. Furthermore, it presents the ZVS and ZCS in MOSFETs and diodes.

In contrast to the VFRC, the CFRC uses parallel resonant tanks and unidirectional switches that apply IGBTs, BJTs, or an array of MOSFET in series with a diode. These converters present ZVS, and in comparison, with other resonant converters, use only two choke inductors instead of the push–pull current source inverter, and only two grounded switches instead of the full bridge. One of these topologies that can be applied in an interconnected PV system is the current source parallel resonant converter (CSPRC) [70], wherein the AC load can be connected in parallel with a resonant capacitor. If the quality factor (Q) of the resonant tank is higher and the switching frequency is close to the resonant frequency, the output voltage applied to the load is almost sinusoidal. The topology is shown in Figure 8.

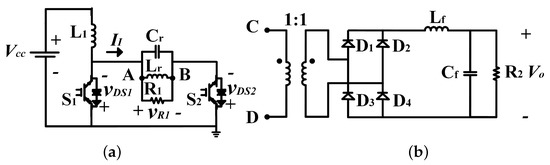
Figure 8. Resonant converter. (a) CSPRC, (b) adding transformer and rectifier.

The circuit in Figure 8 is comprised of four stages: The first stage consists of a DC input current source ($I_I$) forming by the DC input source ($V_{cc}$) and the choke inductor ($L_1$). The second stage consists of a parallel resonant tank ($C_r$, $L_r$, $R_1$) which converts the square-wave voltage ($v_{DS1}$ and $v_{DS2}$) into a sinusoidal output voltage ($v_{R1}$) and $R_1$, $R_2$ represents the DC power; also, the magnetic isolation is derived by $L_r$, where A and B are coupled to C and D. The third stage consists of a full-wave rectifier ($D_1$, $D_2$, and $D_3$, $D_4$), where the input power is in phase with the input voltage and contains only the fundamental component of the square-wave input current. Finally, the fourth stage consists of the decoupling elements ($L_f$ and $C_f$).

The CSPRC, compared to conventional non-resonant topologies, provides a continuous input current with a very low AC ripple, does not present stability problems, and due to the use of the parallel resonant tank, presents a natural array with transformers, which is desirable for PV-connected applications. However, the resonant tank and the components used need to be carefully selected since these parameters affect directly the overlapped signals in the two bidirectional two-quadrant switches ($S_1$ and $S_2$). Therefore, slightly overlapping gate-to-source voltages should be used.

Similar to the CSPRC, the current-fed push–pull converter is another topology that is suitable for PV-connected applications, owing to its small ripple of both an input current and output voltage with fewer components. In comparison with the voltage-fed push–pull converter, only an input inductor to obtain a small ripple of the input current and an output capacitor to obtain a small ripple of the output voltage is necessary [71]. As the primary side voltage is higher than the input source voltage, the copper loss and leakage of the transformer are reduced.

In contrast, the performance of the traditional current-fed push–pull converter is affected by issues, such as voltage spikes of switches, high-voltage stress, reverse recovery, and low power conversion. As the duty cycle needs to be 50%, the operating range of the input voltage is relatively narrow. However, applying a voltage-doubler rectifier in combination with resonant techniques enables achieving soft-switching techniques and removes the reverse-recovery problem, thereby providing a topology with a higher voltage conversion ratio and efficiency.

A focused work in a current-fed push–pull converter was presented in [72], which presented a topology (Figure 9) to decrease the switching losses and turn ratio of the transformer by applying soft switching of the primary switches ($S_1$, $S_2$) and a voltage doubler of the secondary side.

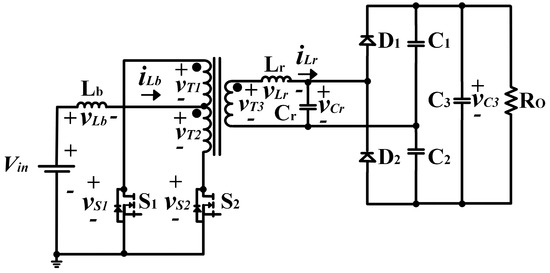
Figure 9. Push–pull converter.

The topology in Figure 9 comprises switches $S_1$ and $S_2$, a current source ($L_b$), a voltage-doubler diode ($D_1$, $D_2$), an $LC$ resonant tank ($L_r$, $C_r$), and a transformer, whose primary side voltages ($v_{T1}$, $v_{T2}$) are the sum of the input voltage ($v_{in}$) and $v_{Lb}$. This topology reduces the switching losses by applying ZVS and ZCS and presents continuous input current, high voltage gain, fewer components, natural isolation arrangement, and high efficiency, which results in a proper topology for PV-connected applications.

Similar to the current-fed push–pull converter, the high step-up current-fed converter decreases switching losses by applying ZVS and ZCS [73]. In addition, the arrangement in the transformer reduces the weight and volume, has a higher voltage gain with a lower transformer turn ratio, and reduces the complexity in the control stage by applying only two switches [74].

An example of a high step-up current-fed converter is presented in [75], which presents a new ZVS current-fed isolated push–pull converter, where all switches are in the on-state under ZVS and ZCS, and the off-state under almost ZVS. Moreover, the topology absorbs the voltage across its main switch, thus exhibiting high efficiency and high gain voltage. The circuit is illustrated in Figure 10.

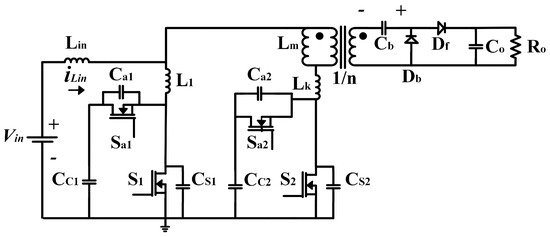
Figure 10. High step-up current-fed converter.

In Figure 10, $S_1$, $S_2$ are the main switches and CS1, CS2 represent their snubber capacitors; $L_k$, $L_m$ are the leakage and magnetizing inductances, respectively; $S_{a1}$, $S_{a2}$ are the auxiliary switches; $C_{c1}$, $C_{c2}$ are the clamp capacitors; $C_b$ is the blocking capacitor; $D_b$, $D_f$ is the secondary-side transformer diode; and $C_o$ is the output capacitor.

A main feature of the circuit shown in Figure 10 is its ability to absorb the leakage inductance energy and clamp the voltage stress across the switches, thereby reducing the switching losses and improving the power density. In addition, it presents a high-voltage gain, high efficiency, and low input current ripple, which renders the topology suitable for high-power applications with low input and high output voltages, such as PV systems.

Based on the above description, Table 4 lists some characteristics offered by the DC-DC resonant converters, Table 5 lists comparison indices for VSC and CSC used in PV-connected applications, and Table 6 lists some features and drawbacks offered for current-fed topologies.

Table 4. Characteristics of DC-DC resonant power converters.

Ref.	Topology	Power Rating (kW)	Decoupling Capacitor (μF)	Switching Frequency (kHz)	Efficiency (%)
[68]	LLC	0.250	200	140	98
[71]	Push-pull	1.5	560	70	95.5
[72]	Current-fed push-pull	0.25	-	100	96.6
[75]	Current-fed converter	0.4	22	100	92.3
[76]	Interleaved resonant converter	1.2	1100	70	-
[77]	LLC	2	1000	120	97.7
[78]	LLCC	0.167	-	268.5	96
[79]	Current-fed multi resonant inverter	0.15	2.2	365	97.2
[80]	Current-fed multi resonant	0.15	0.224	255	95.4
[81]	Current-fed multi resonant	0.15	16	255	95.2
[82]	The parallel current-fed resonant converter	1	220	135	93.3

Table 5. Comparison indices between DC-DC CSC and VSC.

Comparison Indices	VSC	CSC
Input current	Discontinuous	Continuous
DC power supply	Voltage source	Current source
DC side energy storage	Capacitor	Inductor
Dynamic performance	High	Low
Converter structure	Complex	Simple
Application	Industry	High-power
Current ripple	High	Low
Size	Small	Bulky
Leakage inductance	Large	Reduced

Table 6. Features and drawbacks of current-fed topologies [83,84,85,86].

Reference	Features	Drawbacks
[87]	All the switches are unidirectional; thus, lower cost and high efficiency can be acquired Low number of passive components is needed	The gain is not constant All the switches are unidirectional; thus, they can only be used at unity power factor The developed MPPT algorithm is complicated
[88]	Low value of energy storage inductance Single-stage boost conversion High efficiency Leakage current reduction Small DC inductance	High efficiency compared with other current fed inverter The frequency is limited by the unidirectional switch Its application is restricted to single-phase transformerless PV systems Unidirectional switches are necessary to the inverter
[89,90]	Continuous input current	The gain in the positive half-cycle is different to the negative half-cycle, so a DC current injection is expected High number of passive components

3. MPPT for DC-DC Power Converters

As MPPT is an essential capability for PV power generation systems, classifying the different algorithms reported in the literature is essential to determine their performance. Thus, ref. [91] classified MPPT methods for PV systems into three categories: offline, online, and hybrid. The offline method uses the physical values of the PV system to generate control signals, the online method requires instantaneous values of the output voltage, and the hybrid method requires a separate algorithmic loop.

From this classification, the classical algorithms used in some PWM converters are perturb and observe (PO) [92], fractional open-circuit voltage [93], fractional short-circuit current [94], and incremental conductance [95]. However, in contrast to conventional PWM converters that are modulated by the variation in duty cycle, the quasi-resonant and resonant converters must be controlled with frequency modulation [96].

Frequency-based MPPT algorithms increase the system complexity owing to the voltage maximum power point (MPP) variation, which requires a DC-DC converter that allows variations in its effective input resistance. Hence, as the resonant converters have to work very close to the resonance condition, the switching and resonant frequencies must to be close. This can affect the interval of variation in switching frequency and the values of the resonant components, which can drastically reduce the number of topologies that can be applied.

In addition, the literature reports some applications of tracking the MPP for PV systems by applying fuzzy logic controllers [97], neural networks [98], evolutionary algorithms [99], and hybrid methods [100]. Thus, it exhibits a faster converging speed, good performance and efficiency, fewer oscillations, and no convergence from the MPP under varying weather conditions. For these conditions, particularly for partial shading conditions (PSC), the literature summarizes some strategies based on PSC into four categories.

• Hardware and control methods based on array reconfiguration.
• Control method based on artificial intelligence algorithms.
• Improved direct control methods based on perturbation self-optimization.
• Some MPPT methods based on partial shading detection schemes.

From the previous overview, Table 7 lists the MPPT algorithms classified based on the topology to be implemented.

Table 7. MPPT algorithms for PV-connected applications.

Ref.	Approach	Method	Topology
[101]		Perturbe	Boost
[102]		and	Boost
[103]		observe	Boost
[104]	Classical algorithms	Open circuit voltage	DC-DC PWM
[105]		Short circuit current	DC-DC PWM
[106]		Incremental	Ćuk
[107]		conductance	Flyback
[64]		Frequency modulated	LLC resonant converter
[108]	Frequency modulated algorithms	Center point iteration (CPI) method	LLC resonant converter
[109]		Frequency modulated P & O	LCLC resonant converter
[110]		Hybrid frequency modulated algorithm	LLC resonant converter
[111] [112]		Hardware and control methods based on array reconfiguration	Switching matrix Switching matrix
[113]	Algorithms based on partial shading conditions	Control method based on artificial intelligence algorithms	Boost
[114]		Improved direct control methods based on perturbation self-optimization	SEPIC
[115]			Boost
[116]		Some MPPT methods based on other principles	Boost

4. DC-AC Inverter

For PV-connected applications, the DC-AC inverters can be classified into self- and line-commutated inverters [117]. The self-commutated inverter transfers the current and controls the turn-on and turn-off conditions by applying both an H-bridge arrangement and a PWM technique. In contrast, the grid network dictates the commutation process for the line-commutated inverter, thus controlling the turn-on and turn-off conditions using an additional circuit.

Self-commuted inverters are classified into the following two types: first, voltage source inverters (VSIs), which can be designed by an input parallel-capacitor with a discontinuous input current ($I_{VSI}$) (Figure 11a); and second, current source inverters (CSIs), which can be designed by a bulky series inductor, where its input side is fed with a constant DC source with the same polarity, thus aiming that the $I_{CSI}$ is continuous (Figure 11b).

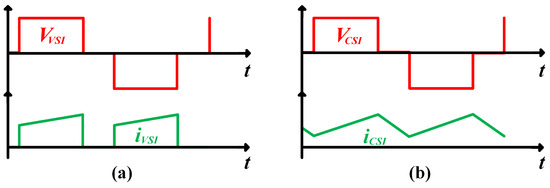
Figure 11. Voltage and current representation over one switching period at the entrance of the inverter: (a) VSI and (b) CSI.

From Figure 11 the CSI can apply the $LC$ or $LCL$ filter, as compared to the VSI, which has the diagonals switched with a certain dead time and generally uses an $LC$ filter. However, for a single-phase multistage PV-connected system, the pulsating energy manifests itself as a current or voltage ripple for a CSI or VSI, respectively, which generates problems related to the filtering stage, size of passive elements, power losses, quality of the power signal, and performance.

In this regard, for an interconnected single-phase system, a low power ripple will cause a DC-link current or voltage ripple for the inverter because the grid voltage and current are defined as

$$\begin{array}{cc}\hfill v\left(t\right)=& Vcos\left(\omega t\right)\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill i\left(t\right)=& Icos(\omega t+\varphi )\hfill \end{array}$$

(2)

where V and I are the voltage and current supplied by the inverter; $\omega$ is the angular frequency (AC); and $\varphi$ is the offset angle between V and I. Thus, the instantaneous power flow is

$$\begin{array}{cc}\hfill p\left(t\right)=& v\left(t\right)·i\left(t\right)=\frac{1}{2}VIcos\left(\varphi \right)+\frac{1}{2}VIcos(2\omega t+\varphi )\hfill \end{array}$$

(3)

Equation (3) shows the instantaneous power flow considering the time intervals at which the power varies at twice the line frequency. This oscillating ripple degrades the performance of MPPT, and affects the extraction efficiency in single phase PV inverters [118], thereby causing the decoupling DC component to have a high energy density. Thus, in several cases, the use of an electrolytic capacitor is required [119]. Nevertheless, as described above, these capacitors have several disadvantages, which reduce the lifetime of the system [120], thus rendering them undesirable for application.

4.1. The Typical Voltage Source Inverter

The conventional VSI [121] is composed of a power-decoupling component ($C_f$), a current source ($I_{in}$), four bidirectional voltage switches ($S_1$–$S_4$), an output $LC$ filter ($LC$), three parasitic resistances $r_1$, $r_2$, and $r_3$, and a switch to interconnect the inverter with the utility grid (Figure 12). The averaged mathematical model of the VSI was defined by applying Kirchhoff’s voltage and current laws, as shown in Equation (4).

$$\begin{array}{cc}\hfill {\dot{i}}_{ac}+r_2{i}_{ac}+v& =U{V}_{dc}\hfill \end{array}$$

(4a)

$$\begin{array}{cc}\hfill \dot{v}+\frac{1}{r_3}v-i_{ac}& =0\hfill \end{array}$$

(4b)

where u is the duty cycle with values between $[-1,1]$. Considering that the VSI is decoupled with the DC/DC converter, the direct current bus ($I_{in}$) is constant.

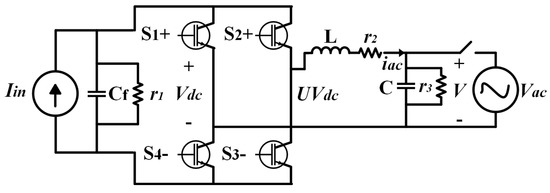
Figure 12. Typical VSI.

The VSI can operate in the voltage control mode (VCM), also known as grid-forming, and the current control mode (CCM), known as grid-following, where both modes can be applied to an interconnected system [122]. However, CCM is used commonly because it exhibits s better suppression of the current ripple and energy control, thus providing a higher power factor. In addition, the polarity of the input current on the DC side determines the direction of the average power flowing through the inverter; however, the VSI is not entirely compatible with low-power single-phase applications because the input voltage is typically lower than the peak voltage of the grid network.

4.2. Typical Current Source Inverter

The common CSI [123] (Figure 13) is composed of a DC voltage source ($V_{in}$), an inductor ($L_d$) that absorbs the voltage harmonics produced by the CSI, four unidirectional switches ($S_1$, $S_2$, and $S_3$, $S_4$), and an output $LC$ filter (C and L) with parasitic resistances $r_1$, $r_2$, and $r_3$. The mathematical model is given by Equation (5). In this case, the complexity of the model concerning the VSI is evident because there is a non-linear model, that is, there are products of state variables with the control signal. This type of model is known as a bilinear system [124,125].

$$\begin{array}{cc}\hfill {\dot{i}}_d+r_d{i}_d+u{V}_c& =V_{in}\hfill \end{array}$$

(5a)

$$\begin{array}{cc}\hfill {\dot{v}}_c+\frac{1}{r_2}{v}_c+i_L-u{i}_d& =0\hfill \end{array}$$

(5b)

$$\begin{array}{cc}\hfill {\dot{i}}_L+r_3{i}_L-v_c& =-v_{ac}\hfill \end{array}$$

(5c)

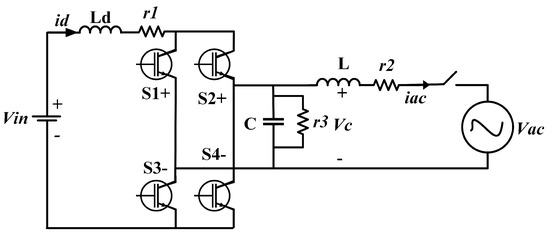
Figure 13. Typical CSI.

In Figure 13, power decoupling is realized by applying a DC-link inductor, which retains the input current through the inverter instead of the electrolytic capacitor in a VSI. In addition, the CSI draws a continuous input current, which makes it suitable for renewable applications. This current generates an AC waveform, where $L_d$ is charged during the shoot-through periods and discharged during normal conduction.

Additionally, the CSI can operate without the need of a previous DC-DC converter while the input voltage is under the peak value of the grid voltage. However, the input current ripple of the inductor increases as a result of the switching frequency and inductance values, and the control is more complex compared to the VSI because the control variable appears in both the inductor-current and capacitor-voltage equations.

Based on previous characteristics, the literature shows important contrasts between VSI and CSI. Some of these characteristics are listed in Table 8.

Table 8. Differences between VSI and CSI [117,118,119,120,121,122,123,124,125,126].

Issue	VSI	CSI
Power source	An input DC voltage source with insignificant impedance	High input impedance from a changeable current
Dependency on load	Amplitude in terms of the output voltage is independent of the load. Additionally, the load determines the waveform and magnitude of the output current	Amplitude of the output current is independent of the load. Additionally, the load determines the waveform and magnitude of the output voltage
Power loss	Low conduction losses and high switching losses	High conduction losses and low switching losses
Power decoupling	Constant input voltage is maintained, and its decoupling energy device (capacitor) is efficient, cheap, and small	Presents a continuous input current, its decoupling energy device (inductor) presents higher reliability than VSI. Nevertheless, its inductor adds more power losses, cost, and is bulky
Advantages	Fewer components and high-efficiency operation	High frequency operation, continuous input current, does not need a filter stage to avoid the ripple current being reflected on the PV system, short-circuit protection provided by the current source, and a load voltage with low total harmonic distortion
Disadvantages	Low reliability, and frequency operation. Additionally, as the input current is discontinuous, need an additional filter stage	Need a large and bulky inductor to feed the current inverter, presents less efficiency and the control stage is more complex

According to Table 8, the CSI presents important characteristics that make it a good alternative for renewable applications than the commonly used VSI. Therefore, there is a need to study the feasibility of these systems with the aim of determining the main characteristics and drawbacks that they offer to PV-connected applications. Some of these studies are described below.

4.3. Inverter Topologies Fed by a Current Source

According to the literature, the use of CSI can potentially eliminate the decoupling electrolytic capacitor used by the VSI, thereby resulting in numerous benefits [127]. One study focused on this issue is presented in [128], which offers a power-decoupling circuit viewed as a controlled voltage source in series with a DC inductor. The topology is shown in Figure 14.

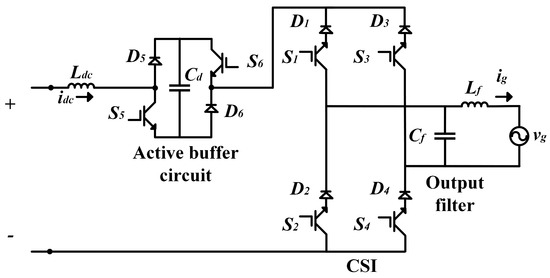
Figure 14. Single-phase current source converter.

The topology in Figure 14 comprises an active buffer circuit that consists of four power semiconductor devices ($S_5$, $S_6$, and $D_5$, $D_6$) and an active buffer capacitor ($C_d$) that absorbs the power pulsation with a twice-line frequency. The switching modes of the circuits are presented in Table 9.

Table 9. Switching modes in the current source converter.

	${\mathit{S}}_5$	${\mathit{S}}_6$
Mode 1	0	1
Mode 2	0	0
Mode 3	1	0
Mode 4	1	1

As per Table 9, in Modes 1 and 3, $C_d$ is disconnected from the main circuit and buffer, and works as a freewheeling path. In Mode 2, $C_d$ is charged by absorbing the excess energy provided by the utility grid. Finally, in Mode 4, $C_d$ is discharged, and the insufficient energy required by the load is supplemented.

This type of topology presents a possibility to replace the original electrolytic capacitor with a film capacitor with a low rated voltage, which can extend the lifetime and reduce the size and weight of the system.

Another advantage of CSI is the possibility to reduce the input current ripple [129]. The study involving it explains the performance of a CSI with six voltage bidirectional switches comprised of three upper ($S_{au}$, $S_{bu}$, and $S_{cu}$) and three lower switches ($S_{al}$, $S_{bl}$, and $S_{cl}$), as shown in Figure 15.

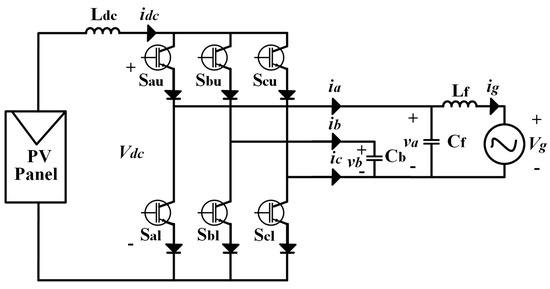
Figure 15. CSI with six voltage bidirectional switches.

The circuit in Figure 15 implements a current source ($L_{dc}$) whose size depends on the switching frequency. The voltage of section b ($v_{dc}$) is connected to the grid by $C_b$ and the inverter is interconnected through an $LC$ filter, which comprises $C_f$ and $L_f$. The work in Figure 15 is presented to have a low-frequency ripple by comparing the link ($i_{dc}$) and a reference current, as well as a component of the grid current calculated from the reactive power, which ensures that among the currents $i_a$, $i_b$, and $i_c$, $i_b$ can achieve a continuous power flow. However, one critical issue in this type of topology is the performance and power oscillation on the DC link, which results in a bulky inductor, whose main drawbacks are low power density and dynamic response degradation. Thus, an effort focused on proposing solutions to the aforementioned problems is reported in [130], whose main contribution is an active power filter (APF) to compensate for power ripple.

This work is shown in Figure 16, and presents an auxiliary circuit (APF) as a novel power decoupling by applying the typical H-bridge CSI, and an active voltage regulator (AVR) connected to the grid voltage (vg) through the $LC$ filter ($C_{ac}$ and $L_{ac}$).

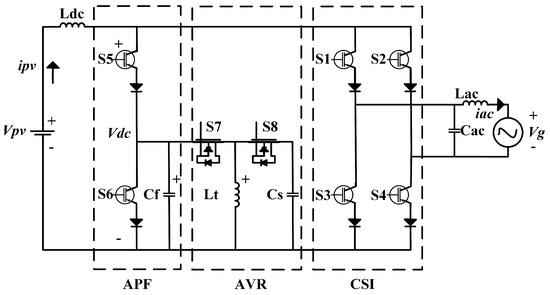
Figure 16. Power decoupling circuit for CSI.

As shown in Figure 16, the APF circuit has one phase leg connected to the CSI and an auxiliary DC source ($C_f$). In addition, a bidirectional buck–boost converter comprises the AVR (in discontinuous current mode), with an energy transfer inductor ($L_t$) and an energy storage capacitor ($C_s$), performing an optimal power density, aiming for an important size reduction in the passive components.

However, according to the literature, the use of a CSI negatively impacts the inverter efficiency because presents high conduction losses due to its high levels of current during its control stage [131]. In this regard, a study focused on passivity-based control (PBC) was conducted [132]. This proposal maintained an output voltage with fast dynamic response, continuous-time domain, negligible sensitivity, guaranteed stability, good load regulation, no performance limitation, and low THD.

As mentioned earlier, the decoupling energy of a CSI compared to that of a VSI provides an attractive option for a longer lifetime, owing to the elimination of the electrolytic capacitor. Ref. [133] is a focused study on this issue, which introduces a different energy management by applying six bidirectional switches, excluding the $LC$ filter at the output inverter. The electrolytic capacitor is replaced by managing the decoupling energy with the component $C_c$, which is connected on the AC side to absorb the AC fluctuation, thereby allowing a smaller capacitor. The topology and switching modes are illustrated in Figure 17.

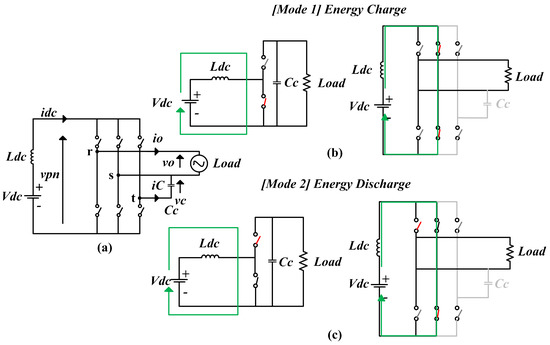
Figure 17. Topologies: (a) structure of the single-phase current source inverter with power decoupling function, (b) boost technique of conventional circuit, (c) boost technique of the presented circuit.

The topology in Figure 17a comprises a direct input voltage ($V_{dc}$) and current source ($L_{dc}$), six bidirectional switches and a film capacitor ($C_c$); because $L_{dc}$ works as a filter inductance, an $LC$ output filter is not required. The principle of voltage boost can be explained by the commutations of the switches. Thus, as shown in Figure 17b, the DC voltage is increased by storing energy in $L_{dc}$ (Mode 1) and discharging it through the upper arm (Mode 2). By contrast, in Figure 17c, the AC voltage is raised directly by $L_{dc}$ (Mode 1) and discharged to the load (Mode 2), thus allowing a no longer step-up boost circuit. Finally, by controlling the capacitor current ($i_c$), power flows to offset the $2\omega$ component in the output power. Consequently, the input power becomes constant and does not fluctuate.

However, as mentioned earlier, the recognized issue of the leakage current in an interconnected PV system depends extremely on the value of the parasitic capacitance between the PV panel and the ground [134].

As shown in Figure 18, the potential differences produced by the switching states on the inverter inject leakage current on the DC and AC sides, which causes grid current distortion, losses in the PV system, electromagnetic interference (EMI), and harmonics injected into the utility grid. Consequently, consideration of the appearance of leakage current during the design of a PV-connected application becomes critical because the leakage current cannot be totally eliminated, but can be reduced.

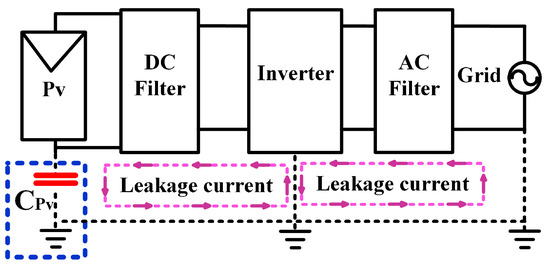
Figure 18. Simplified common-mode leakage current.

A precise focused study to reduce the leakage current is presented in [135], which presents a novel CSI with AC-side clamping (Figure 19).

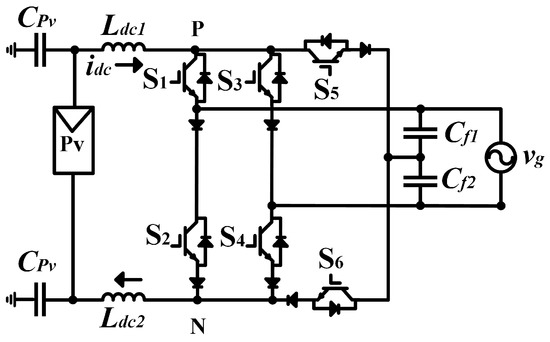
Figure 19. CSI with AC-side clamping [135].

The circuit in Figure 19 comprises two DC-side inductors ($L_{dc1}$ and $L_{dc2}$), six insulated-gate bipolar transistors ($S_1$, $S_2$, $S_3$, and $S_4$, $S_5$, and $S_6$), and two AC-side filter capacitors ($C_{f1}$ and $C_{f2}$). $v_g$ represents the AC-side voltage, and $C_{Pv}$ represents the parasitic capacitance between the PV system and the ground. This circuit reduces the leakage current and suppresses the switching-frequency common-mode voltage when the positive and negative DC-side buses (P and N, respectively) are clamped at the midpoint of the AC-side filter capacitors during the freewheeling period (when $S_5$ and $S_6$ are turned on, respectively).

As described below, there are some important issues to be considered when choosing the type of inverter to be implemented; these include power decoupling, number of switches, THD, and leakage current. In this regard, Table 10 shows some inverters presented for PV-connected applications, considering the work presented in [136].

Table 10. Single-stage inverters for PV-connected applications.

Ref.	Type	Power Rating (kW)	Switches	Decoupling Component
[128]	CSI	-	6	Bulky inductor
[129]	CSI	3	6	Bulky inductor
[130]	H-bridge CSI	3	6	Bulky inductor
[133]	CSI	3	6	Bulky inductor
[135]	CSI with AC-side clamping	3	6	Bulky inductor
[137]	Buck-boost	3	4	Electrolytic capacitor
[138]	Boost	3	4	Electrolytic capacitor
[139]	Buck-boost	3	4	Electrolytic capacitor

According to Table 10, CSI is a good candidate for grid-interconnected systems because it does not require the use of electrolytic capacitors, which are essential for the lifetime of an application. In addition, with an active damping control or by applying an additional switch, it is possible to reduce the harmonic content, minimize losses, and attenuate the excitation of the LC filter. However, the limited acceptance of a bulky inductor and the need to use (sometimes) more power semiconductor devices are some of the issues that CSI must improve with the aim of consolidating itself for this application.

4.4. Control of Inverters

Control of the VSI and CSI can be classified into (a) grid forming and (b) grid following. Grid forming is responsible for fixing the voltage and frequency at the output, and grid following is responsible for injecting active and reactive power into the electrical network, as shown in Figure 20.

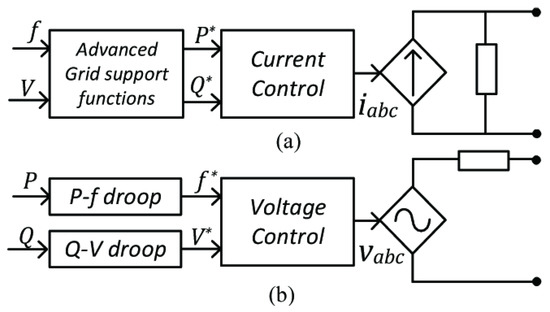
Figure 20. Inverter controllers: (a) grid-following control with grid support functions; and (b) grid-forming droop control [122].

Grid-following inverters rely primarily on measuring the point of the connection voltage to be synchronized with the grid [140,141,142]. Apart from sensing the point of connection voltage, its phase angle and frequency are extracted using a phase-locked loop, which is subsequently used by a current controller [143,144,145,146].

However, grid-forming inverters exploit droop control for grid synchronization [147,148,149] and regulate the point of connection voltage as the frequency and magnitude of this voltage are provided by active and reactive power control loops, which operate primarily based on droop control [150,151].

Currently, most commercial PV inverters operate as grid-following sources that regulate their power output by measuring the angle of the grid voltage by applying a phase-locked loop [152]. Therefore, they simply follow the angle or frequency of the grid and do not actively control their frequency outputs. In contrast, a grid-forming source actively controls its frequency and is used extensively in microgrid setups.

5. Summary and Conclusions

Some main features offered for the current source topologies are listed below.

For current source DC-DC converters, they are as follows:

• Reliable auto short-circuit protection.
• A constant and continuous input current.
• A simple gate-drive circuit without requirement of isolation or optical couplers.
• A reduced leakage inductance.
• Inherent voltage boosting capability.
• A filter stage is not required to prevent the ripple current from being reflected in the PV system.
• Simple converter structure.
• Low switch count, low switching dv/dt.
• Controllable current at its output terminals.
• Smooth DC-output current.

For current source inverters, they are as follows:

• Better sinusoidal output voltage.
• Low THD.
• A reduced leakage current.
• High reliability and long lifetime owing to the use of a bulky inductor as a power-decoupling component instead of an electrolytic capacitor.
• A small filter is required on the AC side.
• Excellent grid-integration performance, such as sinusoidal current/voltage and fully controlled power factor.
• Inherent current-limiting capability.
• The DC-link inductor provides natural protection against short-circuit faults.
• Lower voltage stresses.
• Direct-current control capability, where AC current is controlled in magnitude and phase.Less switching loss.
• Avoids shoot-through damage.
• Lower operation and maintenance cost.

The advantages described above could be translated into a considerable increase in the reliability and lifetime of the system, thereby increasing the interest in these topologies that, according to the literature, represent the minority part of the systems studied for renewable energy applications. In this regard, the viability that the current-fed topologies present compared to that of the voltage-fed topologies, has to be considered and more research will be necessary to determine the real opportunities and limitations that these topologies can offer to the application.