Abstract
Recently, studies on secure database outsourcing have been highlighted for the cloud computing environment. A few secure Top-k query processing algorithms have been proposed in the encrypted database. However, the previous algorithms can support either security or efficiency. Therefore, we propose a new Top-k query processing algorithm using a homomorphic cryptosystem, which can support both security and efficiency. For security, we propose new secure and efficient protocols based on arithmetic operations. To obtain a high level of efficiency, we also propose a parallel Top-k query processing algorithm using an encrypted random value pool. Through our performance analysis, the proposed Top-k algorithms present about 1.5∼7.1 times better performance with regard to a query processing time, compared with the existing algorithms.
1. Introduction
With the increasing popularity of cloud computing, there has been growing interest in outsourcing databases. Cloud computing provides a service that allows internet-connected users to use virtual computing resources such as storage, computation, and network [1,2,3,4,5]. Generally, three requirements are considered for outsourcing databases in cloud computing. First, it is essential to provide data privacy because the data owner’s database contains the sensitive information of clients [6,7]. Second, the query and the query result must be protected because these information can contain and infer the sensitive information of the query issuer [8,9]. Finally, data access patterns must be protected because an attacker can infer sensitive information by analyzing the data access patterns [10,11,12]. Therefore, secure query processing over an encrypted database has been researched to protect the original data, queries, and access patterns. Previous strategies modify plaintexts to their substituted data, and outsource them to a cloud [13,14,15,16,17,18]. However, these previous strategies cannot completely protect both data and queries because they are weak to various attacks. To tackle this problem, recent strategies encrypt the original data and outsource them to the cloud [19,20,21,22,23,24,25]. That is, a data owner encrypts the database before he/she outsources the original data to a cloud. The cloud can process the query that is issued from a user. The user can obtain the results from the cloud. Figure 1 shows an encrypted database outsourcing model.
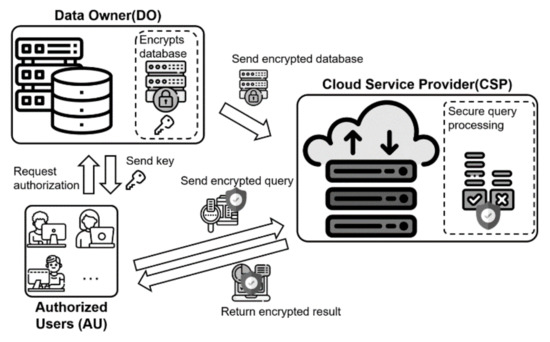
Figure 1.
Encrypted database outsourcing model.
Top-k query processing algorithms are used for various applications such as location-based service, e-commerce, and web search engine [26]. First, H-I. Kim et al.’s algorithm [27] proposed Top-k query processing algorithms based on the Paillier cryptosystem. However, while processing the Top-k query processing algorithms, the algorithm needs a high computational cost because it uses secure protocols based on binary operations. Second, H-J. Kim et al.’s algorithm [28] proposed Top-k query processing algorithms using Yao’s garbled circuit. By using Yao’s garbled circuit, the algorithm uses a secure protocol to check whether or not a node includes a point without binary bit operations for ciphertext. However, since Yao’s garbled circuit [29,30] is based on a hardware-based Boolean circuit, the algorithm still requires repetitive bit operations, thus causing a high computation cost. Both algorithms have a critical problem in that they need a high computational cost for Top-k query processing. To the best of our knowledge, there is no conventional Top-k query processing algorithm that is suitable for parallel processing. To tackle this problem, we propose a new Top-k query processing algorithm using new secure protocols based on arithmetic operations over encrypted database in cloud computing. In terms of efficiency, our algorithm uses both new secure protocols and a data filtering technique using kd-tree [31]. The proposed secure protocols optimize the procedure of comparison by using arithmetic operations, rather than employing binary bit operations, which require a high computation cost. Moreover, to improve the efficiency, we propose a parallel Top-k query processing algorithm using a thread pool. In addition, while hiding data access patterns, our algorithm support security for both original data and user query by using the Paillier cryptosystem [32] and secure two-party computation [33,34,35]. To prove the security of our algorithm, we provide the formal security proofs of both the proposed secure protocols and Top-k query processing algorithms. Through the performance analysis, we prove that our Top-k query processing algorithms outperform the existing ones. The contributions of our paper are as follows:
- We present an architecture for outsourcing both the encrypted data and index.
- We propose new secure protocols based on arithmetic operations (e.g., ASC, ASRO, and ASPE) to protect original data, user query, and access patterns.
- We propose a new Top-k query processing algorithm that can support both security and efficiency.
- We propose a new parallel Top-k query processing algorithm using a random value pool to improve the efficiency of Top-k query processing.
- We also present the comprehensive performance analysis of our algorithms with a synthetic and real dataset.
We organize the rest of the paper as follows. In Section 2, we describe the Paillier cryptosystem, adversarial attack model, and related work. In Section 3, we present the two-party computation structure and new secure protocols. In Section 4, we describe a a new Top-k query processing algorithm. In Section 5, we describe a parallel Top-k algorithm. In Section 6, we present the security proof of our Top-k algorithms. In Section 7, we describe the performance analysis of our Top-k algorithms. Finally, we conclude this paper.
2. Background and Related Work
2.1. Background
Paillier cryptosystem.The Paillier cryptosystem [32] is an additive homomorphic and probabilistic asymmetric encryption scheme for public key cryptography. The public key for encryption is represented by (N, g), where N is a multiplication of the large prime integer p and q, and g is a circular integer in . Here, denotes an integer domain ranging from zero to . The secret key for decryption is represented by (p, q). Let E(·) represent the encryption function and D(·) represent the decryption function. The Paillier cryptosystem includes the following characteristic.
- Homomorphic addition: The multiplication of two ciphertexts E() and E() generates the ciphertext of the sum of their plaintexts and (Equation (1)).
- Homomorphic multiplication: The th power of ciphertext E() generates the ciphertext of the multiplication of and (Equation (2)).
- Semantic security: Encryptions of the same plaintexts generate different ciphertexts in the same public key (Equation (3)).
Adversarial attack model. In the outsourcing database environment, two attack models can be considered: a semi-honest attack model and a malicious attack model [36,37]. In the semi-honest (or honest-but-curious) attack model, the cloud performs its own protocol honestly, but attempts to obtain sensitive data about the data owner and the authorized user. To protect a semi-honest attack, original data should be encrypted before outsourcing. A malicious attack model tries to achieve the original data or disable service. To protect the original data under the malicious attack, a service provider concentrates on distinguishing attacks and restoring the damaged formal procedure. Since we concentrate on protecting sensitive data in an outsourced environment, we propose secure query processing under the semi-honest attack model. A secure protocol for the semi-honest attack model is defined as follows [36,37].
Definition 1.
Assuming is the input parameters of cloud , is the execution image of for the protocol ρ. If the simulating execution image is indistinguishable from , the protocol ρ is a secure protocol under the semi-honest attack model.
2.2. Related Work
The existing privacy-preserving Top-k query processing algorithms are as follows. First, J. Vaidya et al. [38] proposed a privacy-preserving Top-k query processing algorithm using Fagin’s scheme [39], in which the data are vertically partitioned. If each party reports the scored data being ordered based on the local score until there are at least k common data in the output of all of the parties, the union of the reported data includes Top-k results. The algorithm determines the actual Top-k results by identifying an approximate cutoff score separating the k-th data item from those below it. The algorithm has an advantage in that it does not reveal the score of an individual datum by using a secure comparison technique. However, in terms of query privacy, an attacker can infer the preference of a user because the cutoff score is easily estimated by using a binary search over the range of values. According to data privacy, because the algorithm does not encrypt the partitioned data, the attacker can obtain the original data under the semi-honest attack model. In addition, data access patterns are not protected because the identification of the Top-k result is disclosed.
Second, M. Burkhart et al. [40] proposed a Top-k query processing algorithm that utilizes hash tables and a secret sharing technique. The algorithm aggregates the distributed key-value data by using Shamir’s secret sharing technique, and finds the k number of key-value pairs with the largest aggregated values as the Top-k result. To reduce computation time, the algorithm uses fixed-length hash tables for avoiding expensive key comparison operations. However, the algorithm cannot guarantee the accurate result because the aggregated results are probabilistic, in that the algorithm performs a binary search for estimating the intermediate threshold separating the k-th item from the (k+1)-th item. Moreover, an attacker can infer the preference of a user because a threshold is easily estimated by using binary search over the range of values. The algorithm cannot conceal data access patterns because the index of a hash table related to the Top-k results is revealed.
Third, Y. Zheng et al. [41] proposed a privacy-preserving Top-k query processing algorithm over vertically distributed data sources. To support data privacy, the service provider () divides the data owner’s database into data sources () for each attribute. The generates the encryption keys and determines the positive weight values for the scoring function , where is a data record and . Then, the distributes the encryption keys to each and sends the corresponding weight to via a secure channel. For supporting the Top-k query, each outsources its data to the cloud. Because both and are private information, encrypts the product of and before outsourcing them to the cloud. However, in the semi-honest attack model, an attacker can achieve the sensitive data from data sources because a data owner transmits data records and weights to the data sources in plaintext. Therefore, the algorithm does not protect data, query, and access pattern.
Fourthly, H-I. Kim et al. [27] proposed a privacy-preserving Top-k query processing algorithm (STop) grounded using both an encrypted kd-tree index and the Paillier cryptosystem [31]. The Paillier cryptosystem can provide homomorphic operation and protect a chosen-plaintext attack or a chosen-ciphertext one, so that the cloud can obtain the Top-k query result without decrypting both a user’s query and original data. The algorithm also proposed a secure protocol based on binary bit operations that can access all leaf nodes without the exposure of data access patterns. The algorithm can protect the user’s query, sensitive data, and data access patterns. However, because the secure protocol consists of binary bit operations for ciphertext, it is necessary to perform a binary bit operation as many times as the data size. The repetitive binary bit operations cause high computation cost.
Finally, H-J. Kim et al. [28] proposed a privacy-preserving Top-k query processing algorithm (STop) using Yao’s garbled circuit [29,30]. Yao’s garbled circuit is a secure protocol that enables two-party secure computation in which two semi-honest parties can jointly calculate a function over private inputs by using a Boolean circuit. By using Yao’s garbled circuit, the algorithm uses a secure protocol to check whether or not a node includes a point without binary bit operations for ciphertext. The algorithm can present more efficiently than STop while providing the same level of privacy as STop. However, since Yao’s garbled circuit is based on a hardware-based Boolean circuit, the algorithm still requires repetitive bit operations, thus causing a high computation cost.
Table 1 summarize the existing studies based on the characteristics. We describe their comparison with regard to three major characteristics, i.e., hiding access patterns, computation overhead, and security risk. First, H-I. Kim et al.’s work [27] and H-J. Kim et al.’s work [28] can protect data access patterns, while J. Vaidya and C. Clifton’s work [38], M. Burkhart and X. Dimitropoulos’s work [40], and Y. Zheng et al.’s work [41] cannot protect it. Second, J. Vaidya and C. Clifton’s work [38] and M. Burkhart and X. Dimitropoulos’s work [40] require low computational overhead because they do not use any encryption scheme, while H-I. Kim et al.’s work [27] and H-J. Kim et al.’s work [28] need high computational overhead due to the use of the Paillier cryptosystem [32]. Finally, H-I. Kim et al.’s work [27] and H-J. Kim et al.’s work [28] have low risk with regard to security because they protect sensitive data, uses’s query, and data access patterns, while J. Vaidya and C. Clifton’s work [38], M. Burkhart and X. Dimitropoulos’s work [40], and Y. Zheng et al.’s work [41] have high security risk because they only protect sensitive data.

Table 1.
Comparison of the existing studies.
3. Overall System Architecture
3.1. System Architecture
Since we adopt the semi-honest attack model [36,37], we consider the cloud as insider adversaries. Under the semi-honest adversarial model, the cloud follows the procedure of protocol, but can attempt to achieve the additional information not allowed to the cloud. Therefore, earlier studies [13,16] are performed under the semi-honest attack model. Meanwhile, a secure protocol is a communication protocol that is an agreed sequence of actions performed by two or more communicating entities (e.g., cloud A and cloud B) in order to accomplish some mutually desirable goal [34,35]. It makes use of cryptographic techniques, allowing the communicating entities to achieve a security goal. For example, the entities encrypt the information or permutate the sequence of data by using the random value for data protection. A protocol can be proven to be secure under the semi-honest adversarial model by using Definition 1 in Section 2.
The system is organized according to four components: Cloud A(), Cloud B(), data owner (), and authorized user (). The possesses the original database (T) of a set of records [27]. A record (1 ≤ i ≤ n) is composed of m columns, where m denotes the number of data dimensions, and the j-th columns of is represented by (1 ≤ j ≤ m). The divides T by using the kd-tree [27] to provide the indexing on T. If we retrieve the tree structure in a hierarchical manner, the access pattern can be disclosed. Therefore, we only consider the leaf nodes of the kd-tree, and all the leaf nodes are retrieved once during the query processing step. Hence, a node denotes a leaf node. Let h denote the level of the constructed kd-tree, and F denotes the fanout of each leaf node. A node is denoted by (1 ≤ z ≤ ), where is the number of leaf nodes. The region data of is shown as the upper bound and the lower bound (1 ≤ z ≤ , 1 ≤ j ≤ m). Each node retains the identifiers () of the data located inside the node region. To preserve the data privacy, the encrypts T attribute-wise using the public key () of the Paillier cryptosystem [32] before outsourcing the database to the cloud. Therefore, the make encrypt for 1 and 1 . The also encrypts the region data of all nodes of the kd-tree, so as to support efficient query processing. Especially, and of each node are encrypted attribute-wise, such that and are created with 1 and 1 . Figure 2 presents the example of the encrypted kd-tree when the number of data items is 20 and the level of the kd-tree is 3. The encrypted kd-tree consists of four regions (leaf nodes), i.e., , and . For example, the lower bound and upper bound of are <E(0), E(0)> and <E(6), E(5)>, respectively. Additionally, includes five data items, i.e., E() = <E(2), E(1)>, E() = <E(1), E(2)>, E() = <E(2), E(3)>, E() = <E(4), E(4)>, and E() = <E(5), E(3)>.
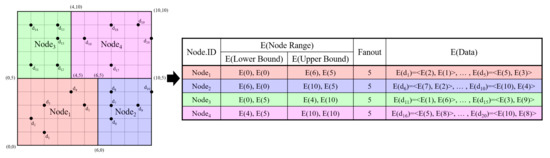
Figure 2.
Example of the encrypted kd-tree.
We consider that and are non-colluding and semi-honest clouds. Thus, they correctly follow the procedure of protocols. To support Top-k query processing over the encrypted database, a secure multi-party computation (SMC) is required between and . To establish the structure of SMC, the outsources both the encrypted data and its encrypted index to the with , while the sends to the . The encrypted index includes the region data of each node in ciphertext and the ids of the data located inside the node, in plaintext. The also sends to s to authorize them to encrypt a Top-k query. When issuing a query, an first creates E() by encrypting a query q attribute-wise for . and process the query and return its result to the .
3.2. Secure Protocol
Since the proposed Top-k query processing algorithm is constructed using several secure protocols, we use four secure protocols from the literature [19,27,28], such as Secure Multiplication (SM) [19], Secure Bit-Not (SBN) [27], Secure Compare (CMP-S) [27,28], and Secure Minimum from Set of n values (SMS) [27,28]. In addition, we newly suggest secure protocols: Advanced Secure Compare (ASC), Advanced Secure Range Overlapping (ASRO), and Advanced Secure Point Enclosure (ASPE). By using arithmetic operations, the proposed secure protocols improve the existing comparison protocols that employ binary bit comparison [19] and garbled circuit comparison [29,30]. Therefore, the proposed secure protocols require a low computation cost.
Advanced Secure Compare (ASC) protocol. The ASC protocol compares two encryption values securely and returns whether the first value is greater than another or not. For two encryption values E(u) and E(v), the ASC protocol returns E(1) if ; otherwise it returns E(0). The procedure of the ASC protocol is described in Algorithm 1. First, selects two random numbers and their encryption values, <, E()>, <, E()>, from the random value pool (line 1). Second, computes and by using the Paillier cryptosystem (lines 2∼3). Third, randomly selects one of two functions, : and : . The chosen function cannot expose to . Then, sends data to , according to the chosen function. If : is chosen, transmits <E(), E()> to . If : is chosen, transmits <E(), E()> to . Fourth, receives a pair of encryption <E(), E()> from (line 9). decrypts E() and E(). Because does not know the sequence of data received from , cannot determine whether <, > is <,> or <,>. If is less than or equal to , sends E() = E(1) to . Otherwise, sends E() = E(0) to (lines 10∼16). Finally, receives E() from . If : is selected, returns E(). Otherwise, returns SBN(E()) because sends <E(), E()>, which is the reverse order of the original pair <E(), E()> (lines 18∼21). The procedure of the ASC protocol is presented in Algorithm 1.
For example, compares E(u) = E(5), E(v) = E(10) by using the ASC protocol. First, picks the random value = 3, = 2 in the random value pool. calculates E() = . Second, selects one of two functions, and . If we assume that chooses , the sequence of data is <E(), E()>. Therefore, transmits <E(32), E(17)> to . Third, sets <> to <32, 17> by decrypting <E(32), E(17)>. Because is greater than , is set to 0. encrypts and sends E() = E(0) to . Finally, receives E() = E(0) from . Because selects , returns SBN(E()) = E(1).
Advanced Secure Range Overlapping (ASRO) protocol. The ASRO protocol determines whether two encrypted ranges are overlapped or not. A region is denoted by the lower bound (lb) and the upper bound (ub). Figure 3 presents the overlapping and the non-overlapping between two regions (i.e., and ) in the ASRO protocol. The and are overlapped if or for all dimensions. For two encrypted range values E() and E(), the ASRO protocol returns E(1) if and are overlapped; otherwise it returns E(0).
| Algorithm 1 ASC Protocol. |
Input: Output: if , return E(1), otherwise, return E(0) : 01. pick two pairs <, E()> and <, E()> in random value pool 02. E() ← 03. E() ← 04. randomly selected or 05. if is selected then 06. Transmit <E(), E()> to 07. else if is selected then 08. Transmit <E(), E()> to 09. receive E(), E() // cannot know any information from . 10. D(E()) 11. D(E()) 12. if 13. E() ← E(1) 14. else 15. E() ← E(0) 16. Transmit to 17. receive 18. if is selected, then 19. return E() 20. else 21. return SBN(E()) |
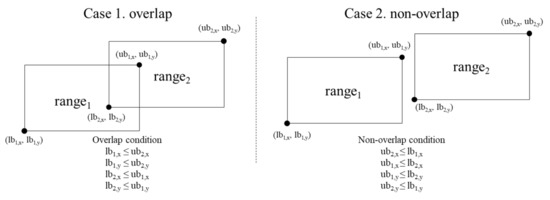
Figure 3.
Overlapping and non-overlapping between two regions in the ASRO protocol.
First, initializes E() as E(1) (line 1). Second, for all dimensions, performs ASC(E(), E()), where of dimensions, and stores the result of the ASC protocol into E(). The ASC protocol is used to check whether the lower bound of is less than the upper bound of for each dimension. Then, performs SM(E(), E()) [19] and stores its result into E() (lines 2∼4). Third, for all dimensions, performs ASC(E(), E()) and stores its result into E(). The ASC protocol is used to check whether the lower bound of is less than the upper bound of for each dimension. Then, performs SM(E(), E()) and stores its result into E() (lines 5∼7). The SM protocol is used to determine whether the point is included into a range for all dimensions. Finally, return E() as the result of the ASRO protocol. The procedure of the ASRO protocol is presented in Algorithm 2.
| Algorithm 2 ASRO Protocol. |
Input: E(), E() (range consists of <> , m is the number of dimension) Output: if and is overlapped, return E(1), otherwise, return E(0) : 01. E() ← E(1) 02. for 03. E() ← ASC(E(), E()) 04. E() ← SM(E(), E()) 05. for 06. E() ← ASC(E(), E()) 07. E() ← SM(E(), E()) 08. return E() |
For example, in Figure 4, checks the overlap between E() and E() by using the ASRO protocol. First, sets E() as E(1). Second, for the x-axis, calculates ASC(E(), E()) = ASC(E(1), E(5)) = E(1) and stores its result into E(). calculates SM(E(), E()) = SM(E(1), E(1)) = E(1) and stores it into E(). For the y-axis, calculates ASC(E(), E()) = ASC(E(1), E(5)) = E(1) and stores it into E(). calculates SM(E(), E()) = SM(E(1), E(1)) = E(1) and stores it into E(). Third, for the x-axis, calculates ASC(E(), E()) = ASC(E(2), E(4)) = E(1) and stores it into E(). calculates SM(E(), E()) = SM(E(1), E(1)) = E(1) and stores it in E(). For the y-axis, calculates ASC(E(), E()) = ASC(E(3), E(4)) = E(1) and stores it into E(). calculates SM(E(), E()) = SM(E(1), E(1)) = E(1) and stores it into E(). Finally, returns E() = E(1) as the result of the ASRO protocol.
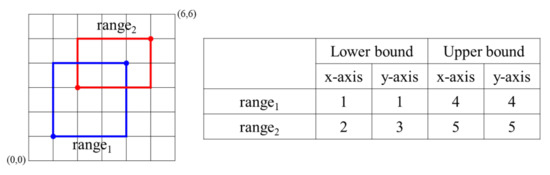
Figure 4.
Overlapping between E() and E(.
Advanced Secure Point Enclosure (ASPE) protocol. The ASPE protocol determines whether a point is included in the given range or not. A point p is included in a range if for all dimensions. When an encrypted point value E(p) and an encrypted range E(range) are given, the ASPE protocol returns E(1) if the range includes the point(p); otherwise, it returns E(0). First, assigns E(1) to E() (line 1). Second, for each dimension i, executes E() = ASC(E(), E()) and E() = SM(E(), E()) (lines 2∼4). The ASC protocol is used to check whether p is less than the upper bound of the range for each dimension. The SM protocol is used to determine whether the point is included into a range for all dimensions. Third, for each dimension i, performs E() = ASC(E(), E()), and E() = SM(E(),E()) (lines 5∼7). Finally, returns E() (line 8). We skip the example of the ASPE protocol because the process of the ASPE protocol is identical to that of the ASRO protocol, except that the input is a point, not a range. The procedure of the ASPE protocol is presented in Algorithm 3.
| Algorithm 3 ASPE Protocol. |
Input: E(p), E(range) (range consists of <> , m is the number of dimension) Output: if range includes p, return E(1), otherwise, return E(0) : 01. E() ← E(1) 02. for 03. E() ← ASC(E(p), E()) 04. E() ← SM(E(), E()) 05. E() ← ASC(E(), E(p)) 06. E() ← SM(E(), E()) 07. return E() |
4. Privacy-Preserving Top- Query Processing Algorithm
In this section, we suggest a privacy-preserving Top-k query processing algorithm that uses new secure protocols, such as the ASC, ASRO, and ASPE protocols mentioned in Section 3. The proposed Top-k query processing algorithm retrieves k data items that have the highest score for a scoring function over the encrypted database. The algorithm is organized in three phases; node data search phase, Top-k retrieval phase, and Top-k result refinement phase.
4.1. Node Data Search Phase
While hiding the data access patterns, securely extracts all the data items from a node containing the highest score. The procedure of the node data search phase is presented in Algorithm 4. First, for the extraction of data items related to the query, securely calculates a max point () = <>, where is the highest score for dimension j() (lines 1∼4). To calculate , adds E() and E() for , where m is the number of dimensions. means the largest absolute value among the coefficients. is determined according to the sign of the coefficients for the ith dimension. If is greater than hint, is positive and so is set to E(). Otherwise, is set to E(0). By finding the node including , can extract the data items that have the possibility of the highest score.
Second, finds a node including mp by executing E() = ASPE(E(), E()) for , where means the total number of the leaf nodes in the kd-tree (lines 5∼6). The result of the ASPE protocol for all leaf nodes, i.e., E(), is <E(), E(), …, E()>. Because our Top-k query processing algorithm utilizes the ASPE protocol, it can achieve a better performance than the existing algorithms [27,28]. In contrast, the existing algorithms cause a large computational overhead because they perform an iterative operation as many times as the bit length of data. Third, make E() by shuffling E() using a random permutation function . Then, sends E() to (lines 7∼8).
Fourthly, by decrypting E(), counts how many has 1 (i.e., c) (lines 9∼10). Fifthly, generates c number of node groups () (line 11). assigns a node with = 1 into a different group among c node groups. evenly assigns the remaining nodes with = 0 into c node groups (lines 12∼14). Then, randomly shuffles the ids of the nodes in each node group and sends to the shuffled , i.e., (line 15).
Fifthly, obtains by deshuffling using (line 17∼18). Finally, for all the data items of each node for each , performs E() = E() × SM(E(), E()) where , in the selected , and (lines 19∼25). Here, z means the id of the jth nodes of and w means where is the number of data items extracted from encrypted leaf nodes of the kd-tree. E() is the result of the ASPE protocol corresponding to . By repeating these steps with an updated , returns <E(), E(), …, E()>. Consequently, all the data items in a node, including mp, are securely obtained without exposing the data access patterns [10,11].
| Algorithm 4 Node data search phase. |
Input: <E(), E(), …, E() | >, E()=<E(), E(), …, E() | means coefficient of score function and >, <E(), E(), …, E() | is the maximum data domain of i dimension >, E() // hint means the largest of the absolute values among coefficients Output: <E(), E(), …, E()> // all candidates inside nodes being related to a query : 01. for 02. E() ← E()×E() 03. E() ← ASC(E(), E()) 04. E() ← SM(E(), E(0)) × SM(SBN(E()), E()) 05. for // where h means the level of the kd-tree 06. E() ← ASPE(E(), E()) 07. E() ←(E()) // shuffle the order of array E() = <E(), E(), …, E()> 08. send E() to : 09. ← D(E()) 10. the number of ’1’ in 11. generate c number of Node Group such that = <, , …, > 12. for 13. assign into a node with = 1 and nodes with = 0 14. shuffle the ids of nodes in 15. send = <, , …, > to : 16. 0 // is # of data items extracted from the encrypted leaf nodes of kd-tree 17. for 18. shuffle node ids using for each // = <, , …, > 19. for 20. for // in the selected 21. id of jth nodes of 22. for //: # of data items in each nodes 23. for 24. if (s 1) 25. E() ← E(0) where // E() = <E(), E(), …, E()> 26. E() ← E()×SM(, E()) 27. 28. send <E(), E(), …, E()> |
Figure 5 presents an example of the node data search phase. The example reuses the same data items in Figure 2. First, executes the ASPE protocol between E() and E() for . sets the result of the ASPE protocol as E() and transmits the result to . In Figure 5, for , performs the ASPE protocol between E() = E() = <E(0), E(0)>, E() = <E(6), E(5)> and E() = <E(10), E(10)>, and sets the result of the ASPE protocol, i.e., E(0), as E(). obtains the result of the ASPE protocol as <, E(0)>, <, E(0)>, <, E(0)>, <, E(1)>.
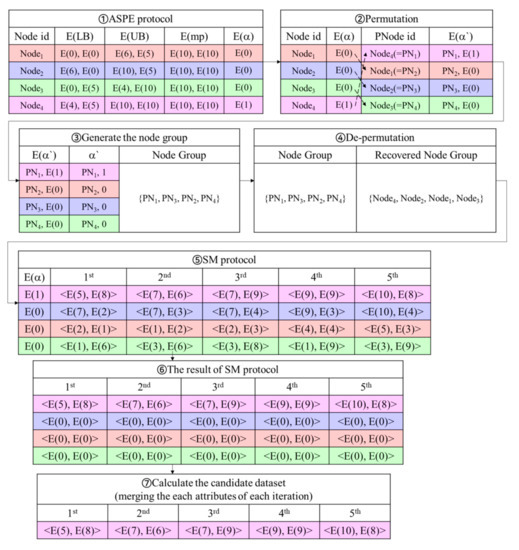
Figure 5.
Example in node data search phase.
Second, permutates the order of <, E()>, <, E()>, …, <, E()> and assigns new ids based on the shuffled order of nodes, so that conceals the original node ids from . To recover the original node ids, stores the pairs of <the original id, the new id>. For example, in Figure 5, the original order of <, E(0)>, <, E(0)>, <, E(0)>, <, E(1)> is permutated to <, E(1)>, <, E(0)>, <, E(0)>, <, E(0)>. Then, converts , , , and into , , , and , respectively. The permutated order is <, E(1)>, <, E(0)>, <, E(0)>, <, E(0)>. Then, sends the permutated order to .
Third, obtains the permutated order and decrypts it. In Figure 5, obtains <, E(1)>, <, E(0)>, <, E(0)>, <, E(0)>, and gets <, 1>, <, 0>, <, 0>, <, 0> by decrypting it. To create node groups, counts how many 1s are in the order. Each node group has one core node whose equals to 1, where . Nodes whose equals to 0, where , are uniformly designated in the node groups. Additionally, transmits the node groups to . For example, counts how many 1s are in the order of <, 1>, <, 0>, <, 0>, <, 0>, and generates a node group with the core node (). The nodes <, 0>, <, 0>, and <, 0> are designated in the node group. transmits the node group, i.e., , , , , to .
Fourth, recovers the original node ids by using the pairs of <the original id, the new id>. In Figure 5, using <>, <>, <>, <>; gains as the original node ids. Fifth, executes the SM protocol between the encrypted data item in a node group and E(). executes SM(E(1), E()), SM(E(0), E()), SM(E(0), E()), and SM(E(0), E()). The results of the SM protocol are E(), E(0), E(0), E(0), and stores E() in the candidate set by merging the results. Sixth, for each node group, the algorithm performs the steps 5∼7 as many times as the # of data items. In Figure 5, by merging the results, obtains E(), E(), E(), E(), E().
4.2. Top-k Retrieval Phase
From the candidates obtained in the previous phase, the algorithm retrieves k number of data items with the highest score. The procedure of the Top-k retrieval phase is as follows. First, calculates the score by using a score function that is represented by the encrypted coefficients(). Second, finds the maximum score, i.e., , among the calculated score. An attacker cannot distinguish which data item has because of the Paillier cryptosystem [32]. Third, to mark the encrypted data item with , subtracts from the score. If the result of subtraction equals E(0), the data items have the maximum score. Because E(0) is unchanged by the homomorphic multiplication in the Paillier cryptosystem, the algorithm securely obtains Top-k. Fourth, the algorithm also executes the homomorphic multiplication of the result by a random value, so as to conceal the original data. To hide the data access patterns, the algorithm permutates the order of the result. Finally, the algorithm finds a data item with the highest score and replays the above process until k number of results are searched. The pseudo code of the Top-k retrieval phase is presented in Algorithm 5. First, using a score function (SF), securely computes the score E() between E() and E() for (lines 1∼2). Second, executes SMAX to obtain the maximum value E() among E() for (lines 3∼4). Third, computes E() = E() × E(, for . calculates E() = , where means a random value for . obtains E() by permutating E() and transmits E() to (lines 5∼9). Fourthly, after decrypting E(), stores E() = E(1) if E() = 0 for . Otherwise, sets E() = E(0). sends E(U) = <E(), E(), …, E()> to (lines 10∼13). Fifthly, obtains E(V) by shuffling E(U) using . Then, does SM(E(), E()) to obtain E() where and (lines 14∼17). Sixthly, sets E() with the highest score to E(0) by computing Equation (4) (lines 18∼19). Because the highest score is set to E(0) and the other scores are unchanged, the algorithm can obtain the Top-k result while preventing the same result from being selected more than twice.
Finally, by calculating E() = for and , can securely extract the data item corresponding to the E() (lines 20∼21). This procedure is replayed k times to search the Top-k result.
Figure 6 presents an example of the Top-k retrieval phase. The example reuses the data items in Figure 2. The permutated function is bypassed. First, computes the score by using a score function (SF), and stores the result in E() for (①). In Figure 6, executes SF(E() = <E(), E()>, E(coef) = <E(), E()>) = SF(<E(5), E(8)>, <E(3), E(2)>) = E(31), and stores it into E(). Second, the highest score is calculated by using the SMAX. stores SMAX(E(), E(), E(), E(), E()) = SMAX(E(31), E(38), E(39), E(45), E(46)) = E(46) in E() (②). Third, to gain the encrypted data item with the highest score, stores E(-) in E() for (③). If is the same as , E() is set to E(0). For E(), stores E(46-46) = E(0) into E(). Fourth, executes the homomorphic multiplication of E() by a random value to prevent the leakage of sensitive data(④). For E(), when a random value = 2, stores E(15×2) = E(30) into E(). Fifth, for , if E() is E(0), sets E() to E(1); otherwise, sets E() to E(0) (⑤). Sixth, obtains Top-k by doing the SM protocol between E() and E() for and summing the result of the SM protocol up (⑥~⑦). In Figure 6, for the x-axis, performs SM(E( = 0), E( = 5)), SM(E( = 0), E( = 8)), SM(E( = 0), E( = 7)), SM(E( = 0), E( = 9)), and SM (E( = 1), E( = 10)). For the y-axis, performs SM(E( = 0), E( = 8)), SM(E( = 0), E( = 7)), SM(E( = 0), E( = 9)), SM(E( = 0), E( = 9)), and SM (E( = 1), E( = 8)). sums E(0), E(0), E(0), E(0), and E(10) for the x-axis while summing E(0), E(0), E(0), E(0), and E(8) for the y-axis. Thus, gains <E(10), E(8)> as the Top-k result. Seventh, using Equation (4), stores the score of the searched Top-k result into E(0) so that can avoid selecting the same Top-k data for the next time. In Figure 6, stores SM(E(0), E(1))× SM(E(46), E(0)) = E(0) into E(). Finally, replays the previous procedure until the Top-k data is searched (②~⑧).
| Algorithm 5 Top-k retrieval phase. |
Input: <E(), E(), …, E() | = >, E(), k // means coefficient of score function and k means the number of Top-k Output: <E(), E(), …, E()> // temporary Top-k results : 01. for 02. E() ← SF(E(), E()) // SF is a score function for Top-k 03. for 04. E() ← SMAX(E(), E(), …, E()) 05. for 06. E() ← E()×E() 07. E() ← // means random value for i 08. E() ←() // =<, , …, > 09. send E()=<E(), E(), …, E()> to : 10. for 11. if D() = 0 then E() ← E(1) 12. else E() ← E(0) 13. send E(U)=<E(), E(), …, E()> to : 14. E(V) ←(U) // E(V)=<E(), E(), …, E()> 15. for 16. for // m means 17. E() ← SM(E(), E()) // E()=<E(), E(), …,E()> 18. if 19. E() ← SM(E(), E(0))×SM(SBN(E()), E()) 20. for 21. E() ← // E()=<E(), E(), …, E()> 22. E() ← E() ∪ E() 23. Return E()=<E(), E(), …, E()> |
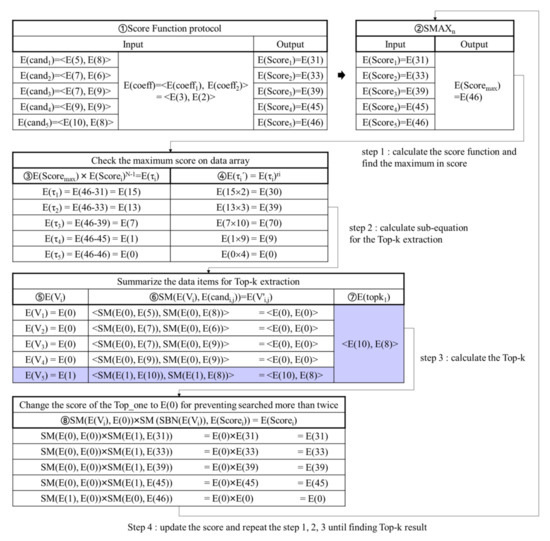
Figure 6.
Example of Top-k retrieval phase.
4.3. Top-k Result Refinement Phase
The Top-k result refinement confirms the correctness of the current Top-k result. Especially, the neighboring nodes must be searched to obtain data items with the higher score than the criteria. Therefore, we calculate the max point of ith node ( = <>, where is the highest score for dimension j()), such that the is a point in the ith node whose score is the highest for the given query (). If the coefficient for the jth dimension is positive, stores the upper bound value of the ith node into . Otherwise, stores the lower bound value of the ith node into . If the score of is greater than the criteria, extracts the data items from the ith node. Finally, after searching all the nodes, recalculates the final Top-k result in the same way as Algorithm 5. The process of the Top-k result refinement phase is presented in Algorithm 6. First, calculates E() = SF(E(), E()) to gain the minimum score between the Top-k result and the query (line 1). Second, for each node, executes SM(E(), E())×SM(SBN(E()), E()) for and , and stores the result into E() (lines 2∼4). E() is the value computed by the ASC protocol for the jth dimension in the node data search phase. securely obtains the max point of the ith node, i.e., E(). Fourthly, calculates the highest score between the query and E() by using the score function (SF), i.e., E() (line 5). To prevent the same node from being selected more than twice, securely computes E() = SM(E(), E(0))×SM(SBN(E()), E()), where E() is the value returned by the ASPE protocol, and sets E() to E(0), where the node has already been retrieved in the node data search phase (line 6). By performing E() = ASC(E(criteria), E()), sets E() to E(1) for the ith node if E(criteria) is less than E(). Otherwise, sets E() to E(0) (line 7). Fifthly, securely obtains the data items stored in nodes with E() = E(1) and generates E() by merging them with E() (lines 8∼9). Then, executes the Top-k retrieval phase based on E() to calculate the final Top-k result E() for (line 10). Sixthly, to hide the Top-k result from , calculates E() = E() × E() for and using a random value . Then, transmits E() to and to (lines 18∼22). Seventhly, decrypts E() and transmits the decrypted value to (lines 23∼26). Finally, gains the plaintexts of the Top-k result by calculating - (lines 27∼29). As a result, can reduce the computation overhead without using decryption operations.
| Algorithm 6 Top-k result refinement phase. |
Input: <E(), E(), …, E() | >, <E(), E(), …, E()>, E(), k // means coefficient of score function and k means the number of Top-k Output:=<, , …, > // final Top-k results : 01. E(criteria) = SF(E(), E()) 02. for 03. for 04. E()←SM(E(), E())×SM(SBN(E()), E()) // E() is value returned by ASPE protocol in line 6 of Algorithm 4 05. E() ← SF(E(), E()) 06. E() ← SM(E(), E(0))× SM(SBN(E()), E()) // E() is value returned by ASPE protocol in line 6 of Algorithm 4 07. E() ← ASC(E(criteria), E()) 08. E() ← perform 7 ∼ 27 lines of Algorithm 4 with <E(), E(), …, E()>, E() = <E(), E(), …, E()> 09. E() ← E()∪<E(), E(), …, E()> 10. E() ← perform Algorithm 5 with E(), E() and k 11. for 12. for 13. pick up the random value // =<, , …, > 14. E() ← E()×E() // E()=<E(), E(), …, E()> and E()=<E(), E(), …,E()> 15. send <E(), E(), …, E() > to and <, , …, > to // means authorized user : 16. for 17. for 18. ← D(E()) // = <, , …,> 19. send <, , …, > to : 20. for 21. for 22. ← - // = <, , …, > |
Figure 7 presents an example of the Top-k result refinement phase. First, calculates the max point of the ith node ()(①). For , performs = <E(), E()> = <SM(E(0), E(0))×SM(E(1), E(6)), SM(E(0), E(0))×SM(E(1), E(5))> = <E(6), E(5)>. calculates the same operation for , , and . Second, calculates the highest score in the ith node() (②). For the highest score of , performs E() = SM(E(3), E(6))×SM(E(2), E(5)) = E(28). computes the highest scores for , , and . Third, to prevent the same node from being selected more than twice, sets E() to E(0) because has been already searched in the node data search phase (③). For , performs E() = SM(E(1), E(0))×SM(E(0), E(50)) = E(0). Fourth, for node expansion, checks whether the ith node needs to be searched by performing the ASC protocol between E(criteria) and E() for (④). For , performs E() = ASC(E(criteria), E()) = ASC(E(38), E(40)) = E(1), where E(criteria) equals E(38). Fifth, extracts all the data items in the expansion node() by using the node data search phase (⑤). Finally, obtains the final Top-k results by performing the Top-k retrieval phase in Figure 7 (⑥).
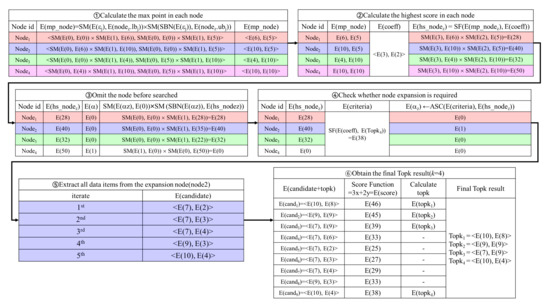
Figure 7.
Example of Top-k result refinement phase.
5. Privacy-Preserving Parallel Top- Query Processing Algorithm
In this section, we propose a privacy-preserving parallel Top-k query processing algorithm, which is the expansion of the proposed Top-k query processing algorithm mentioned in Section 4, so that it can be efficiently executed in a multi-core environment. The proposed parallel Top-k query processing algorithm consists of three phases; the parallel node data search phase, parallel Top-k retrieval phase, and parallel Top-k result refinement phase.
5.1. Parallel Node Data Search Phase
obtains all the data items from a node having a max point() in a parallel way. To expand the node data search phase in Section 4.1 to a multi-core environment, we utilize a thread pool where tasks can be executed simultaneously. The procedure of the parallel node data search phase is presented in Algorithm 7. First, computes in the same way as Algorithm 4 (lines 1∼4). Second, creates a thread pool based on queue (line 5). If a thread is able to process in the thread pool, assigns a task to a thread in a First-In-First-Out manner. Third, for the ith node where , allocates to the thread pool the task of the ASPE protocol (Algorithm 3 in Section 3), i.e., Proc_ASPE(E(), E(), E()). The result of the ASPE protocol is set in E() = E(), E(), …, E() (lines 6∼7). Fourthly, creates E() by permutating E() using a random function and transmits E() to (lines 8∼9). Fifthly, performs the lines 9∼15 in Algorithm 4 to determine which node is selected (line 10). Sixthly, to recover the original node ids from the shuffled node ids, obtains node groups () with the original node ids by performing the lines 16∼18 in Algorithm 4 (line 11). Seventhly, gets access to one data item in each node for each and allocates to the thread pool the task of Extract_candidate (lines 12∼17). The procedure of Extract_candidate securely obtains the candidate data items of the node, which includes . For this, performs E()←E()×SM(E(), E()), where , z = id of jth nodes of , , and . Here, , in the selected , and = the number of data items extracted from the encrypted leaf nodes of kd-tree. Finally, merges all candidate data items obtained in a parallel way (line 18).
| Algorithm 7 Parallel node data search phase. |
Input: <E(), E(), …, E() | >, E()=<E(), E(), …, E() | means coefficient of score function and >, <E(), E(), …, E() | is the maximum data domain of i dimension >, E() // hint means the largest of the absolute values among coefficients Output: <E(), E(), …, E()> // all candidates inside nodes being related to a query : 01. for 02. E() ← E()×E() 03. E() ← ASC(E(), E()) 04. E() ← SM(E(), E(0)) × SM(SBN(E()), E()) 05. generate thread_pool // create a thread and wait in the pool until a task is given 06. for 07. call thread_pool_push(Proc_ASPE(E(), E(), E())) // assign the task to an available thread 08. E() ←(E()) // shuffle the order of array E() = <E(), E(), …, E()> 09. send E() to : 10. perform line 9∼15 in Algorithm 4 : 11. perform line 16∼18 in Algorithm 4 12. for 13. for // in the selected 14. id of jth nodes of 15. for //: the number of data items in each nodes 16. call thread_pool_push(Extract_candidate(E(), E(), m, s, , E())) 17. 18. return <E(), E(), …, E()> procedure 1. Proc_ASPE(E(), E()) Begin Procedure 01. E() ← ASPE(E(), E()) 02. return E() End Procedure end procedure procedure 2. Extract_candidate(E() = <E(), E(), …, E()>, E()) Begin Procedure 01. for 02. if (s 1) 03. E() ← E(0) where // E() = <E(), E(), …,E()> 04. E() ← E()×SM(, E()) 05. return E() = <E(), E(), …, E()> End Procedure end procedure |
5.2. Parallel Top-k Retrieval Phase
retrieves k number of data items with the highest score in a parallel way. The process of the parallel Top-k retrieval phase is presented in Algorithm 8. First, to calculate the scores of the candidates in a parallel way, allocates to the thread pool the task of the score function, i.e., Proc_SF(E(), E(), E()) for . The result of the Proc_SF is set to E() = E(), E(), …, E() (lines 1∼2). Second, executes SMAX to search the maximum E() among E() for (lines 3∼4). Third, to determine the data items with the highest score in a parallel way, allocates to the thread pool the task of Mark_Top_one. The procedure of Mark_Top_one securely sets the data item with the highest score to E(0). For this, performs E() ← (E()×E()) for , where r means a random number and N is created in the Paillier cryptosystem (lines 5∼6). Fourthly, gains E() by permutating E() = < E(), E(), …, E()> using a random function and sends E() to (lines 7∼8). Fifthly, after decrypting E(), performs lines 10∼13 in Algorithm 4 to mark which data item contains the highest score (line 9). That is, stores E() into E(1) if E() = 0 for . Otherwise sets E() to E(0). Sixthly, obtains E(V) by recovering E(U) = <E(), E(), …, E()> using (line 10). Seventhly, to prune out the data items except the data item with the highest score (Top-one) in a parallel way, allocates to the thread pool the task of Pruneout_From_Top2. The procedure of Pruneout_From_Top2 securely sets the data items except Top-one to E(0) by performing Prunout_From_Top2(E(), E(), E(), E()) for and . The result of the Prunout_From_Top2 is stored in both E() = E(), E(), …, E() and E() = E(), E(), …, E() (lines 11∼12). Eighthly, to obtain the Top-one in a parallel way, allocates the task of Find_Top_one to the thread pool. The procedure of Find_Top_one securely merges all the data items. For this, Find_Top_one performs a secure additive operation, i.e., E() ← E()×E() for , , and . The result of the Find_Top_one is stored into E() = <E(), E(), …, E()> (lines 13∼14). Finally, obtains the Top-k result by merging all the Top_one for k rounds by repeating lines 4∼15 in Algorithm 8 (lines 15∼16).
5.3. Parallel Top-k Result Refinement Phase
determines whether or not the Top-k result obtained in the parallel Top-k retrieval phase is sufficient or not, in a parallel way. If not sufficient, performs both the parallel node data search phase and the parallel Top-k retrieval phase again. The process of the parallel Top-k result refinement phase is presented in Algorithm 9. First, calculates E(criteria) = SF(E(), E()) to gain the minimum score between the Top-k result and the query (line 1). Second, to determine the neighboring nodes that need to be searched to acquire data items with a higher score than E(criteria) in a parallel way, allocates the task of check_node_expansion to the thread pool (lines 2∼5). To find the max point of each node, performs E()←SM(E(), E())×SM(SBN(E()), E()) for and . Here, E() is obtained by the ASC protocol in line 3 of Algorithm 6. If the coefficient for the jth dimension is positive, E() is set to E(0). Otherwise, E() is set to E(1). To calculate the highest score of each node, performs E() ← SF(E(), E()) for the ith node. To find nodes whose highest score is greater than the criteria, performs E() ← ASC(E(criteria), E()) for the ith node. If E() is E(1), the ith node needs to be expanded for the parallel Top-k result refinement. Third, calculates the final Top-k result in ciphertext by including the additional Top-k result obtained by performing Algorithm 8 (line 6). Fourthly, to hide the Top-k result from , calculates E() = E() × E() for and , utilizing a random value . Then, transmits to and to (lines 7∼11). Fifthly, decrypts E() and transmits them to (lines 12∼15). Finally, gains the plaintext of the Top-k result by calculating - (lines 16∼18). As a result, can reduce the computation overhead without using decryption operations.
| Algorithm 8 Parallel Top-k retrieval phase. |
Input: <E(), E(), …, E() | = >, E(), k // means coefficient of score function and k means the number of Top-k Output: <E(), E(), …, E()> // temporary Top-k results : 01. for 02. call thread_pool_push(Proc_SF(E(), E(), E())) 03. for 04. E() ← SMAX(E(), E(), …, E()) 05. for 06. call thread_pool_push(Mark_Top_one(E(), E(), E())) 07. E() ←() // =<, , …, > 08. send E()=<E(), E(), …, E()> to : 09. perform line 10∼13 in Algorithm 5 : 10. E(V) ←(U) // E(V) = <E(), E(), …, E()> 11. for 12. call thread_pool_push(Pruneout_From_Top2(E(), E(), E(), E())) 13. for 14. call thread_pool_push(Find_Top_one(E(), , E())) 15. E() ← E() ∪ E() 16. return E() = <E(), E(), …, E()> procedure 3. Proc_SF(E(), E()) Begin Procedure 01. E() ← SF(E(), E()) 02. return E() End Procedure end procedure procedure 4. Mark_Top_one(E(), E()) Begin Procedure 01. E() ← E()×E() 02. E() ← // r means random value 03. return E() End Procedure end procedure procedure 5. Pruneout_From_Top2(E(), E(), E()) Begin Procedure 01. for // m = dimension 02. E() ← SM(E(), E()) 03. if s < k // k = topk and s is from 1 to k 04. E() ← SM(E(), E(0))×SM(SBN(E()), E()) 05. return E(), E() End Procedure end procedure procedure 6. Find_Top_one(E(), , E()) Begin Procedure 01. for // = candidates 02. E() ← E()×E() // s = index of loop from 1 to k, k = topk 03. return E() End Procedure end procedure |
| Algorithm 9 Parallel Top-k result refinement phase. |
Input: <E(), E(), …, E() | >, <E(), E(), …, E()>, E(), k // means coefficient of score function and k means the number of Top-k Output: = <, , …, > // final Top-k results : 01. E(criteria) = SF(E(), E()) 02. for 03. call thread_pool_push(check_node_expansion(E(), E(), E(), E(), E(criteria), m), E()) 04. E() ← perform 7 ∼ 27 lines of Algorithm 6 with <E(), E(), …, E()>, E() = <E(), E(), …, E()> 05. E() ← E()∪<E(), E(), …, E()> 06. E() ← perform Algorithm 8 with E(), E() and k 07. for 08. for 09. pick up the random value // = <, , …, > 10. E() ← E()×E() // E()=<E(), E(), …, E()> and E() = <E(), E(), …,E()> 11. send <E(), E(), …, E() > to and <, , …, > to : 12. for 13. for 14. ← D(E()) // = <, , …,> 15. send <, , …, > to : 16. for 17. for 18. ← - // = <, , …, > procedure 7. Check_node_expansion(E() = <E(),E(), …, E()>, E(), E(), E(), E(criteria), m = dimension) Begin Procedure 01. for 02. E()←SM(E(), E())×SM(SBN(E()), E()) // E() is value returned by ASPE protocol in Algorithm 6 03. E() ← SF(E(), E()) 04. E() ← SM(E(), E(0))× SM(SBN(E()), E()) // E() is value returned by ASPE protocol in Algorithm 6 05. E() ← ASC(E(criteria), E()) 06. return E() End Procedure end procedure |
6. Security Proof
6.1. Security Proof of the Secure Protocols
In this section, we present the security proof of the ASC and the ASPE protocols proposed in Section 3. To prove that the proposed protocols are secure under the semi-honest model, we present that the simulated images of the proposed protocols are computationally indistinct from their actual execution images. Security proof of the ASC protocol: We describe the security proof of the ASC protocol by analyzing the security of the execution images of and . First, the execution image on the side, i.e., , is shown in Equation (5). Here, and are the encrypted data given from (line 9 of Algorithm 1), , and , and are acquired by decrypting E() and E(). is the result computed by the ASC protocol utilizing and on the side.
For example, we assume that is the simulated execution image utilizing the ASC protocol on the side. Here, E() and E() are the non-deterministic numbers chosen in , and and are the indistinct numbers that are added by random value. is the result of the ASC protocol utilizing and on the side. Because the ASC protocol is executed based on the Paillier cryptosystem, it can support semantic security. Therefore, E() and E() are computationally indistinct from and . is indistinct from and because is computed by multiplying two indistinct numbers in , and . Therefore, we say that is computationally indistinct from . Because can check only the result (e.g., ) of the comparison between the non-deterministic numbers (e.g., and ), cannot obtain the original data while performing the ASC protocol. Furthermore, the execution image of is , such that E() from can be considered as the result of the ASC protocol. Assume that the simulated image of is , where E() is randomly made from . Thus, E() is computationally indistinct from E(). Based on the above analysis, there is no information leakage, both at the and sides. Thus, we can conclude that the proposed ASC protocol is secure under the semi-honest adversarial model. Security proof of the ASPE protocol: We describe the security proof of the ASPE protocol by analyzing the security of the execution images of the side and the side. First, the execution image on the side, i.e., , is shown in Equation (6). Here, means the execution image of the ASC protocol and means the execution image of the SM protocol.
In the security proof of the ASC protocol, we have already proven the security of the ASC protocol on the side. Additionally, Y. Elmehdwi et al.’s work [19] proved the security of the SM protocol on the side. Because the ASPE protocol is composed of the ASC protocol and the SM protocol, the ASPE protocol is secure on the side, based on composition theory [42]. On the other hand, the execution image of is , which can be considered as the result of the ASC protocol and the SM protocol. In the security proof of the ASC protocol, we already proved the indistinguishability of the ASC protocol on the side. Additionally, Y. Elmehdwi et al.’s work proved the security of the SM protocol on the side [19]. Because the ASPE protocol consists of the ASC protocol and the SM protocol, the ASPE protocol is secure on the side, based on composition theory [42]. Based on the above analysis, there is no information leakage, both at the and the side. Thus, we can conclude that the proposed ASPE protocol is secure under the semi-honest attack model.
6.2. Security Proof of the Proposed Top-k Query Processing Algorithm
We prove that the proposed Top-k query processing algorithm on the encrypted database is secure against the semi-honest adversarial model. The proposed Top-k query processing algorithm in the encrpyted database is composed of the node data search phase (Algorithm 4), the Top-k retrieval phase (Algorithm 5), and the Top-k result refinement phase (Algorithm 6). To prove that the proposed Top-k query processing algorithm is secure under the semi-honest adversarial model, security analysis is executed by each phase. First, because the node data search phase is composed of the ASPE protocol, which has been proven to be secure, Algorithm 4 is secure under the semi-honest adversarial model by composition theory [42]. Second, the Top-k retrieval phase is secure in the side, because performs the score function, and the SMAX and SM protocols have been proven to be secure in previous studies [27,28]. Even if decrypts the received data from in the Top-k retrieval phase, cannot obtain the original data. The reason for this that the data given from is changed by raising the original data to the power of a random integer and performing a permutation function. Thus, based on the composition theory [42], Algorithm 5 is secure under the semi-honest adversarial model. Lastly, the images made by the Top-k result refinement phase are the same as those made by Algorithms 4 and 5. Thus, the Top-k result refinement phase (Algorithm 6) is secure against the semi-honest adversarial model. Because all the phases of the proposed Top-k algorithm are secure, the proposed Top-k algorithm on the encrypted database is proven to be secure against the semi-honest adversarial model.
7. Performance Analysis
7.1. Performance Evaluation of the Proposed Top-k Query Processing Algorithm in a Single-Core Environment
In the performance analysis, we compare the proposed privacy-preserving Top-k query processing algorithm with H-I. Kim et. al.’s work [27] (STop) and H-J. Kim et. al.’s work [28] (STop). For performance analysis, three algorithms were programmed by using C++ language under CPU: an Intel(R) Xeon(R) E5-2630 v4 @ 2.20GHz, RAM: 64 GB (16 GB × 4AE) DDR3 UDIMM 1600 MHz and OS: Linux Ubuntu 18.04.2. We compare three algorithms regarding algorithm processing time by changing # of data, # of k, the level of the kd-tree, and the # of the data dimension. For performance experiments, we randomly make 100,000 data points with six dimensions. The domain of the data ranges from 0 to 2. Table 2 presents the parameters for performance evaluation in a single-core environment.

Table 2.
Parameters for performance evaluation in a multi-core environment.
Figure 8 presents the performances of STop, STop, and the proposed algorithm regarding the height of kd-tree(h). The number of data items(n) is computed as , where is the number of leaf nodes in the kd-tree. Based on n, it is crucial to select the proper height(h) of the kd-tree. In Figure 8, three algorithms present the best performance when h = 10. The performance of STop is greatly influenced by h because STop utilizes secure protocols using encrypted binary operations, which need a high computational cost. Whereas, the proposed algorithm is relatively less influenced by h than STop because it utilizes secure protocols using arithmetic operations that need low computational cost. Therefore, we set h to 10 in our experiment.
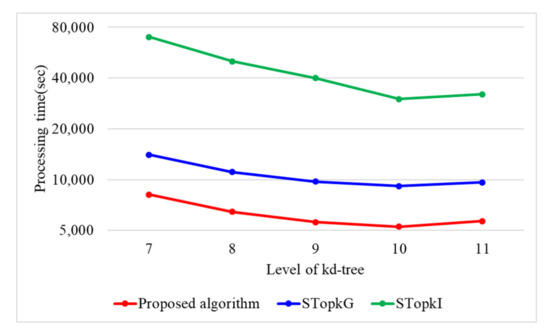
Figure 8.
Processing time with varying levels of kd-tree.
When the encryption key size is 1024 bit, Figure 9 presents the processing time with a varying number of data items. When the number of data items is 20 k, 40 k, 60 k, 80 k, and 100 k, the proposed algorithm requires 2383, 4453, 5287, 6836, and 8447 s, respectively. STop requires 4082, 7653, 9156, 11,895, and 14,799 s, while STop requires 23,124, 28,015, 32,280, 38,636, and 46,989 s when the number of data items is 20 k, 40 k, 60 k, 80 k, and 100 k. Therefore, the proposed algorithm presents 1.7 and 6.6 times better performance than STop and STop, respectively, because the proposed algorithm uses secure protocols based on arithmetic operations. STop and STop use secure protocols based on binary operations. The binary operations have the disadvantage of having to perform more iterations compared to the arithmetic operations.
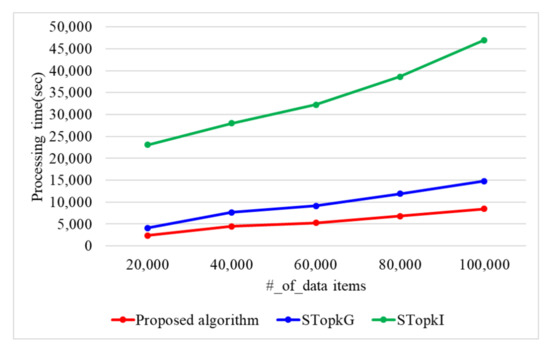
Figure 9.
Processing time with a varying number of data items.
Figure 10 presents the processing time with a varying number of k when the encryption key size is 1024 bit and n is 60 k. When the number of k is 5, 10, 15, and 20, the proposed algorithm requires 4749, 5287, 7693, and 8856 s. STop requires 8297, 9156, 13,232, and 15,043 s, while STop requires 22,288, 32,380, 76,076, and 97,021 s. The proposed algorithm presents 1.7 and 7.9 times better performance than STop and STop, respectively, because the proposed algorithm uses secure protocols based on arithmetic operations. As k increases, the number of data items searched increases in the Top-k result refinement phase. Because the proposed algorithm utilizes the ASC protocol, it presents better performance than both STop and STop. STop presents a better performance than STop because it utilizes Yao’s garbled circuit.
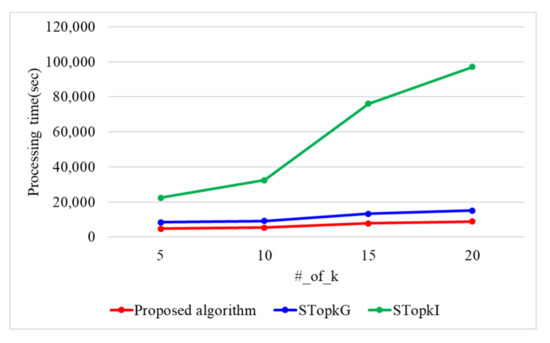
Figure 10.
Processing time with a varying number of k.
When n is 100 k, Figure 11 presents the processing time with a varying key size. When the key size is 512 and 1024, the proposed algorithm requires 2041 and 8486 s, respectively. STop requires 4367 and 14,847 s, while STop requires 13,500 and 46,989 s. Because the proposed algorithm utilizes secure protocols using arithmetic operations, the proposed algorithm outperforms STop and STop by 1.9 and 6.0 times. STop and STop use secure protocols based on binary operations, which have the disadvantage of having to perform more iterations compared to arithmetic operations.
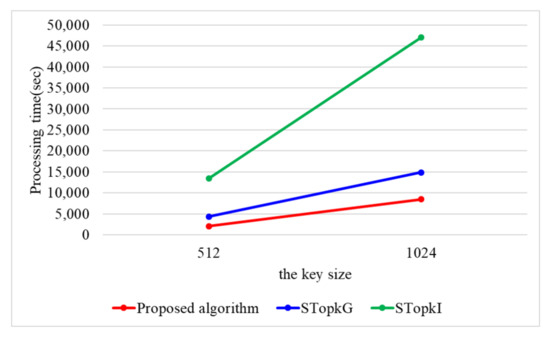
Figure 11.
Processing time with a varying key size.
7.2. Performance Evaluation of the Proposed Top-k Query Processing Algorithm in a Multi-Core Environment
For performance evaluation in a multi-core environment, we compare the proposed parallel Top-k query processing algorithm with the parallel version of existing works. For this, we make parallel STop (PSTop) and STop (PSTop) so that H-I. Kim et. al.’s work [27] and H-J. Kim et. al.’s work [28] can operate in a multi-core environment, respectively. For performance analysis, three algorithms were programmed by using C++ language under CPU: Intel(R) Xeon(R) E5-2630 v4 @ 2.20 GHz, RAM: 64 GB (16 GB×4AE) DDR3 UDIMM 1600MHz and OS: Linux Ubuntu 18.04.2. We compare the proposed parallel algorithm with both PSTop and PSTop, regarding the algorithm processing time by changing the # of data(n), # of k, and # of threads. For our experiments, we randomly make 100,000 data points with six dimensions. The domain of the data ranges from 0 to . Table 3 describes the parameters for performance analysis in a multi-core environment.

Table 3.
Parameters for performance evaluation in multi-core environment.
Figure 12 presents the processing time with a varying number of threads when n is 100k and the number of k is 10. When # of threads is 2, 4, 6, 8, and 10, the proposed parallel algorithm requires 4451, 2547, 1871, 1552, and 1291 s, respectively. PSTop requires 7621, 4304, 3154, 2575, and 2115 s while PSTop requires 23,765, 13,293, 9520, 7671, and 6294 s when the number of threads is 2, 4, 6, 8, and 10. Therefore, the proposed parallel algorithm presents 1.6 and 5 times better performance than PSTop and PSTop, respectively. This is because the proposed parallel algorithm utilizes secure protocols using arithmetic operations. On the contrary, both PSTop and PSTop use a secure protocol based on binary operations, which have the disadvantage of performing more iterations compared to the arithmetic operations.
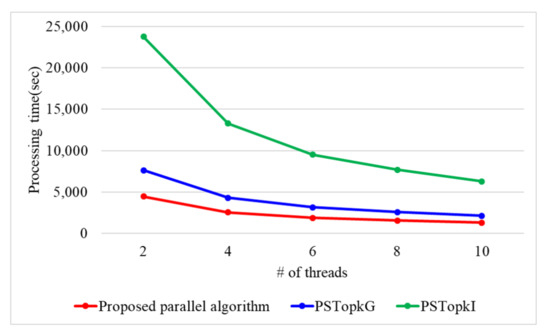
Figure 12.
Processing time with a varying number of threads.
When the number of k is 10 and the number of threads is 10, Figure 13 presents the processing time with varying n. When n is 20 k, 40 k, 60 k, 80 k, and 100 k, the proposed algorithm requires 433, 762, 808, 1041, and 1301 s, respectively. SPTop requires 642, 1192, 1337, 1711, and 2127 s, while PSTop requires 3193, 3994, 4344, 5254, and 6272 s. Thus, the proposed parallel algorithm presents 1.5 and 5.5 times better performance than PSTop and PSTop, respectively. This is because the proposed algorithm utilizes secure protocols using arithmetic operations. On the contrary, PSTop and PSTop use a secure protocol based on binary operations that require more iterations.
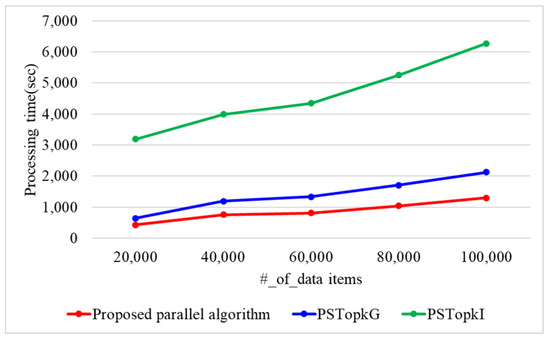
Figure 13.
Processing time with a varying number of data items in 10 thread.
Figure 14 presents the processing time with a varying number of k when the number of threads is 10 and n is 60 k. When the number of k is 5, 10, 15, and 20, the proposed parallel algorithm requires 681, 845, 1401, and 1664 s. PSTop requires 1165, 1392, 2148, and 2466 s, while PSTop requires 3000, 4472, 10,235, and 13,042 s. Therefore, the proposed parallel algorithm presents 1.5 and 6.2 times better performance than PSTop and PSTop, respectively, As k increases, the number of data items searched increases in the Top-k result refinement phase. Because the proposed parallel algorithm utilizes the ASC protocol, it presents a better performance than both PSTop and PSTop. PSTop presents a better performance than PSTop because it uses Yao’s garbled circuit.
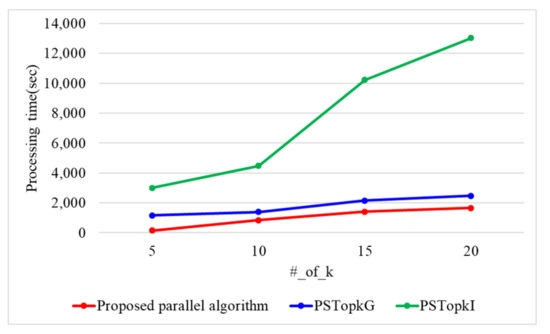
Figure 14.
Processing time with a varying number of k in 10 thread.
Table 4 presents the parameters for our performance analysis using a real dataset. We utilize a chess dataset [43] made by a chess endgame database for a white king and rook against a black king. The chess dataset intends to categorize the optimal depth of win for white. We compare the proposed parallel algorithm with both PSTop and PSTop, regarding the query processing time by varying the number of k, the level of the kd-tree, and the number of threads.

Table 4.
Parameters for performance evaluation for real dataset.
In order to select the optimal level of kd-tree, we conduct the performance evaluation of three algorithms regarding the level of kd-tree. Figure 15 presents the processing time with a varying level of kd-tree when the number of threads is 10 and the number of k is 10. When the level of kd-tree ranges from 5 to 12, the proposed parallel algorithm requires 639, 524, 425, 354, 305, 267, 289, and 312 s. PSTop requires 1122, 916, 749, 631, 546, 453, 498, and 539 s, while PSTop requires 4282, 3497, 2771, 2259, 1929, 1625, 1745, and 1931 s. Three algorithms present the best performance in the case of h = 10. Thus, for our experiment, we use h as 10.
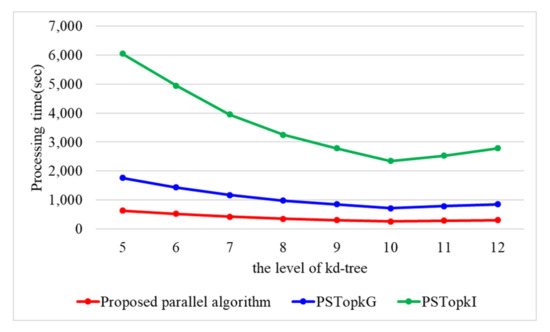
Figure 15.
Processing time with a varying level of kd-tree in real dataset.
When the number of threads is 10, Figure 16 presents the processing time with a varying number of k. When the number of k is 5, 10, 15, and 20, the proposed parallel algorithm requires 147, 266, 407, and 505 s. PSTop requires 316, 453, 769, and 933 s, while PSTop requires 1028, 1625, 3003, and 3758 s. The proposed parallel algorithm outperforms PSTop and PSTop by 1.8 and 6.9 times. As k increases, the number of data items searched increases in the Top-k result refinement phase. Because the proposed parallel algorithm utilizes the ASC protocol using the arithmetic operation, it presents a better performance than both PSTop and PSTop. Because PSTop uses Yao’s garbled circuit, it presents a better performance than PSTop.
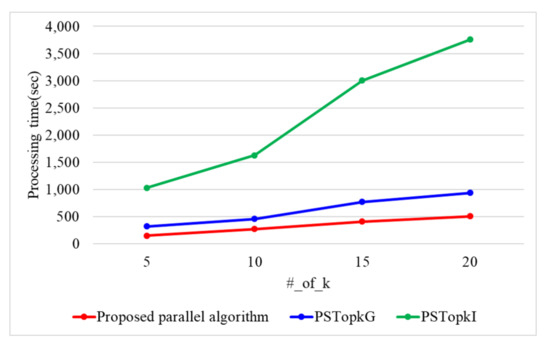
Figure 16.
Processing time with a varying number of k in real dataset.
When the number of k is 10, Figure 17 presents the processing time with a varying number of threads. When the number of threads is 2, 4, 6, 8, and 10, the proposed parallel algorithm requires 718, 443, 349, 299, and 266 s. PSTop requires 1280, 753, 597, 503, and 452 s, while PSTop requires 6122, 3396, 2461, 1976, and 1629 s. Because the proposed parallel algorithm utilizes secure protocols using arithmetic operations, it outperforms PSTop and PSTop by 1.7 and 7.1 times. On the contrary, PSTop and PSTop use secure protocol based on binary operations which have to perform more iterations compared to the arithmetic operations.
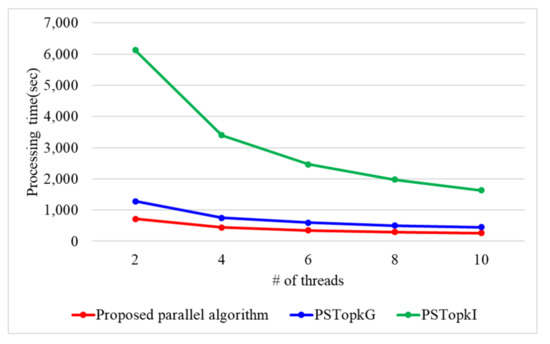
Figure 17.
Processing time with a varying number of threads in real dataset.
8. Discussion
Impact of new secure protocols with low computation cost: A secure protocol is essential for secure query processing in a multi-party computation environment. We need to streamline the process of secure protocols because we aim for secure query processing by utilizing the Paillier cryptosystem, which uses a large amount of computing resources. First, H-I. Kim et al.’s work [27] used secure protocols, such as SCMP, SPE, SMAX, and SMAX for Top-k query processing. By utilizing the Paillier cryptosystem, H-I. Kim et al.’s work [27] can hide sensitive data and user’s query. It utilizes arithmetic operations to hide the sensitive data, and a permutation technique to hide data access patterns. However, the weakness of H-I. Kim et. al.’s work [27] is that it requires an extremely high computational cost because the SCMP, SPE, SMAX, and SMAX protocols utilize binary operations. For example, when we execute the SMAX protocol between E(11) and E(15), clouds convert an encrypted decimal into an encrypted binary array: E(11) = {E(0), E(1), E(0), E(1), E(1), E(15) = {E(0), E(1), E(1), E(1), E(1). After that, clouds execute the SMAX protocol between E(11) = {E(0), E(1), E(0), E(1), E(1) and E(15) = {E(0), E(1), E(1), E(1), E(1). Consequently, the SMAX protocol needs a high computation cost since it executes binary operations as many times as its bit length. Due to the same reason, the SCMP, SPE, and SMAX protocols require high computation costs. Second, H-J. Kim et al.’s work [44] and Y. Kim et al.’s work [45] proposed secure protocols such as GSCMP and GSPE, which are utilized for index searching to perform kNN and kNN classification based on Yao’s garbled circuit. However, since both GSCMP and GSPE utilize the binary array as input, they need high computation expense due to the same reason as the SMAX protocol. On the contrary, the proposed algorithm uses the new ASC and ASPE protocols, which calculate one Paillier arithmetic operation. The reason for this is that they utilize an encrypted decimal as input, rather than an binary array. Consequently, the new ASC and ASPE protocols need low computation cost.
Impact of a random value pool for parallel processing: In the proposed system architecture, we utilize multi-party computation for the parallel Top-k query processing algorithm. Thus, we must prevent from the leakage of sensitive data while performing secure protocols. For this, generates a random integer r from and encrypts r by utilizing the Paillier cryptosystem. Then, performs the addition of both the encrypted random integer E(r) and the encrypted plaintext E(m) by computing E() = E(m) × E(r). Because is independent from m, cannot achieve sensitive data for decryption. However, calculating homomorphic addition and homomorphic multiplication to protect sensitive data results in poor performance, since modular and exponential operations in homomorphic addition and homomorphic multiplication require higher computing resources than other encrypted operations. In Table 5, regarding the Secure Multiplication protocol, H.-I. Kim et al.’s work [27] and H.-J. Kim et al.’s work [28] need three times the encryption: two encryptions for random integers at and one encryption for the multiplication at . On the contrary, the proposed algorithm needs one encryption for the multiplication at because it picks up the random integers from the encrypted random value pool at . With regard to the Secure Compare protocol, H-I. Kim et al.’s work [27] and H.-J. Kim et al.’s work [28] need times encryption, where D is a data domain. On the contrary, the proposed algorithm needs one encryption for the comparison at utilizing the random value pool. Thus, the proposed algorithm can save the computational cost for encryption by utilizing the random value pool.

Table 5.
Comparison of the number of encryption according to encrypted random value pool.
Impact of time complexity: To prove that the proposed algorithm is more efficient than the existing algorithms, we analyze the time complexity of both the proposed algorithm and existing ones (H.-I. Kim et al. [27] and H.-J. Kim et al. [28]). Because the number of data, the number dimension, the number of bit length, and the number of Top-k affect the efficiency of the Top-k query processing algorithm, we describe the time complexity in terms of them. Table 6 shows the average time complexity and the worst time complexity for the proposed algorithm and the existing ones [27,28]. The worst time complexity occurs in the case of a query to expand other kd-tree nodes in the Top-k result refinement phase. The average time complexity is measured by considering all queries that require or do not require the expansion of other kd-tree nodes in the Top-k result refinement phase. In the average time complexity, the proposed algorithms show lower time complexity than the existing algorithms. This is because the proposed algorithm uses the secure protocol based on decimal arithmetic operation, rather than using one based on binary operation. In the worst time complexity, the proposed algorithm shows lower time complexity than the existing algorithms. The reason is the same as the average time complexity.

Table 6.
Time complexity for proposed algorithm and existing algorithm.
9. Conclusions and Future Work
In this paper, we proposed a new Top-k query processing algorithm to support both security and efficiency in cloud computing. For security, we propose new secure and efficient protocols based on the arithmetic operations ASC, ASRO, and ASPE. To reduce the query processing time, we propose a privacy-preserving parallel Top-k query processing algorithm by utilizing a random value pool. In addition, we proved that the proposed algorithm is secure against the semi-honest adversarial model. From our performance analysis, the proposed algorithm outperformed the existing algorithms by 1.7∼6.6 times, since it uses new secure protocols with a streamlined process. In addition, when the number of threads ranges from 2 to 10, the proposed parallel algorithm outperforms the existing algorithms by 1.5∼7.1 times, since it uses not only new secure protocols, but also the random value pool. For future work, we plan to use the proposed secure protocols for various privacy-preserving data mining algorithms.
Author Contributions
Conceptualization, H.-J.K.; methodology, H.-J.K.; software, H.-J.K.; validation, H.-J.K., Y.-K.K., H.-J.L., J.-W.C.; formal analysis, H.-J.K., Y.-K.K., H.-J.L., J.-W.C.; investigation, H.-J.K., Y.-K.K., H.-J.L., J.-W.C.; resources, H.-J.K., Y.-K.K., H.-J.L., J.-W.C.; data curation, H.-J.K.; writing—original draft preparation, H.-J.K.; writing—review and editing, H.-J.K., Y.-K.K., H.-J.L., J.-W.C.; visualization, H.-J.K.; supervision, Y.-K.K., J.-W.C.; project administration, J.-W.C.; funding acquisition, J.-W.C., All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Korean government (MSIT) No. 2019R1I1A3A01058375. This paper was funded by Jeonbuk National University in 2020.
Acknowledgments
This work was supported by a National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. 2019R1I1A3A01058375). This paper was supported by research funds of Jeonbuk National University in 2020.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hayes, B. Cloud computing. Commun. ACM 2008, 51, 9–11. [Google Scholar] [CrossRef]
- Qian, L.; Luo, Z.; Du, Y.; Guo, L. Cloud computing: An overview. In Proceedings of the IEEE International Conference on Cloud Computing, Bangalore, India, 21–25 September 2009; pp. 626–631. [Google Scholar]
- Grolinger, K.; Higashino, W.A.; Tiwari, A.; Capretz, M.A. Data management in cloud environments: NoSQL and NewSQL data stores. J. Cloud Comput. Adv. Syst. Appl. 2013, 2, 1–24. [Google Scholar] [CrossRef]
- Zhao, L.; Sakr, S.; Liu, A.; Bouguettaya, A. Cloud Data Management; Springer: Berlin/Heidelberg, Germany, 2014; 189p. [Google Scholar]
- Agrawal, D.; Das, S.; Abbadi, A.E. Data management in the cloud: Challenges and opportunities. In Synthesis Lectures on Data Management; Springer: Nature/Cham, Switzerland, 2012; Volume 4, 138p. [Google Scholar]
- Sun, Y.; Zhang, J.; Xiong, Y.; Zhu, G. Data security and privacy in cloud computing. Int. J. Distrib. Sens. Netw. 2014, 10, 190903. [Google Scholar] [CrossRef]
- Sharma, Y.; Gupta, H.; Khatri, S.K. A security model for the enhancement of data privacy in cloud computing. In Proceedings of the 2019 Amity International Conference on Artificial Intelligence (AICAI), Dubai, United Arab Emirates, 4–6 February 2019; pp. 898–902. [Google Scholar]
- Garigipati, N.; Krishna, R.V. A study on data security and query privacy in cloud. In Proceedings of the 2019 3rd International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 23–25 April 2019; pp. 337–341. [Google Scholar]
- Cao, N.; Yang, Z.; Wang, C.; Ren, K.; Lou, W. Privacy-preserving query over encrypted graph-structured data in cloud computing. In Proceedings of the 2011 31st International Conference on Distributed Computing Systems, Minneapolis, MN, USA, 20–24 June 2011; pp. 393–402. [Google Scholar]
- Islam, M.S.; Kuzu, M.; Kantarcioglu, M. Access pattern disclosure on searchable encryption: Ramification, attack and mitigation. In Proceedings of the 19th Annual Network and Distributed System Security Symposium, San Diego, CA, USA, 5–8 February 2012; p. 12. [Google Scholar]
- Williams, P.; Sion, R.; Carbunar, B. Building castles out of mud: Practical access pattern privacy and correctness on untrusted storage. In Proceedings of the 15th ACM Conference on Computer and Communications Security, Alexandria, VI, USA, 27–31 August 2008; pp. 139–148. [Google Scholar]
- Cui, S.; Belguith, S.; Zhang, M.; Asghar, M.R.; Russello, G. Preserving access pattern privacy in sgx-assisted encrypted search. In Proceedings of the 2018 27th International Conference on Computer Communication and Networks (ICCCN), Hangzhou, China, 30 July–2 August 2018; pp. 1–9. [Google Scholar]
- Yiu, M.L.; Ghinita, G.; Jensen, C.S.; Kalnis, P. Enabling search services on outsourced private spatial data. VLDB J. 2010, 19, 363–384. [Google Scholar] [CrossRef]
- Boldyreva, A.; Chenette, N.; Lee, Y.; Oneill, A. Order-preserving symmetric encryption. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cologne, Germany, 26–30 April 2009; pp. 224–241. [Google Scholar]
- Boldyreva, A.; Chenette, N.; O’Neill, A. Order-preserving encryption revisited: Improved security analysis and alternative solutions. In Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2011; pp. 578–595. [Google Scholar]
- Qi, Y.; Atallah, M.J. Efficient privacy-preserving k-nearest neighbor search. In Proceedings of the 28th International Conference on Distributed Computing Systems, Beijing, China, 17–20 June 2008; pp. 311–319. [Google Scholar]
- Shaneck, M.; Kim, Y.; Kumar, V. Privacy preserving nearest neighbor search. In Machine Learning in Cyber Trust; Springer: Berlin/Heidelberg, Germany, 2009; pp. 247–276. [Google Scholar]
- Vaidya, J.; Clifton, C. Privacy-preserving top-k queries. In Proceedings of the 21st International Conference on Data Engineering (ICDE’05), Tokyo, Japan, 5–8 April 2005; pp. 545–546. [Google Scholar]
- Elmehdwi, Y.; Samanthula, B.K.; Jiang, W. Secure k-nearest neighbor query over encrypted data in outsourced environments. In Proceedings of the 2014 IEEE 30th International Conference on Data Engineering, Chicago, IL, USA, 31 March–4 April 2014; pp. 664–675. [Google Scholar]
- Kim, H.J.; Kim, H.I.; Chang, J.W. A privacy-preserving kNN classification algorithm using Yao’s garbled circuit on cloud computing. In Proceedings of the 2017 IEEE 10th International Conference on Cloud Computing (CLOUD), Honolulu, HI, USA, 25–30 June 2017; pp. 766–769. [Google Scholar]
- Zhou, L.; Zhu, Y.; Castiglione, A. Efficient k-NN query over encrypted data in cloud with limited key-disclosure and offline data owner. Comput. Secur. 2017, 69, 84–96. [Google Scholar] [CrossRef]
- Kim, H.I.; Kim, H.J.; Chang, J.W. A secure kNN query processing algorithm using homomorphic encryption on outsourced database. Data Knowl. Eng. 2019, 123, 101602. [Google Scholar] [CrossRef]
- Sun, X.; Wang, X.; Xia, Z.; Fu, Z.; Li, T. Dynamic multi-keyword top-k ranked search over encrypted cloud data. Int. J. Secur. Its Appl. 2014, 8, 319–332. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, S.; Xia, Z. A distributed privacy-preserving data aggregation scheme for smart grid with fine-grained access control. J. Inf. Secur. Appl. 2022, 66, 103118. [Google Scholar] [CrossRef]
- Hozhabr, M.; Asghari, P.; Javadi, H.H.S. Dynamic secure multi-keyword ranked search over encrypted cloud data. J. Inf. Secur. Appl. 2021, 61, 102902. [Google Scholar] [CrossRef]
- Ilyas, I.F.; Beskales, G.; Soliman, M.A. A survey of top-k query processing techniques in relational database systems. ACM Comput. Surv. 2008, 40, 1–58. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.I.; Kim, H.J.; Chang, J.W. A privacy-preserving top-k query processing algorithm in the cloud computing. In Proceedings of the International Conference on the Economics of Grids, Clouds, Systems, and Services, Athens, Greece, 20–22 September 2016; pp. 277–292. [Google Scholar]
- Kim, H.J.; Chang, J.W. A new Top-k query processing algorithm to guarantee confidentiality of data and user queries on outsourced databases. Int. J. Syst. Assur. Eng. Manag. 2019, 10, 898–904. [Google Scholar] [CrossRef]
- Yao, A.C.C. How to generate and exchange secrets. In Proceedings of the 27th Annual Symposium on Foundations of Computer Science, Toronto, ON, Canada, 27–28 October 1986; pp. 162–167. [Google Scholar]
- Lindell, Y.; Pinkas, B. A proof of security of Yao’s protocol for two-party computation. J. Cryptol. 2009, 22, 161–188. [Google Scholar] [CrossRef]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Prague, Czech Republic, 2–6 May 1999; pp. 223–238. [Google Scholar]
- Lindell, Y. Secure multiparty computation for privacy preserving data mining. In Encyclopedia of Data Warehousing and Mining; IGI Global: Hershey, PA, USA, 2005; pp. 1005–1009. [Google Scholar]
- Hazay, C.; Lindell, Y. Efficient Secure Two-Party Protocols: Techniques and Constructions; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Cramer, R.; Damgård, I.B. Secure Multiparty Computation; Cambridge University Press: Cambridige, UK, 2015. [Google Scholar]
- Hazay, C.; Lindell, Y. A note on the relation between the definitions of security for semi-honest and malicious adversaries. Available online: https://eprint.iacr.org/2010/551.pdf (accessed on 6 September 2022).
- Veugen, T.; Blom, F.; de Hoogh, S.J.; Erkin, Z. Secure comparison protocols in the semi-honest model. IEEE J. Sel. Top. Signal Process. 2015, 9, 1217–1228. [Google Scholar] [CrossRef]
- Vaidya, J.; Clifton, C.W. Privacy-preserving kth element score over vertically partitioned data. IEEE Trans. Knowl. Data Eng. 2008, 21, 253–258. [Google Scholar] [CrossRef]
- Fagin, R. Combining fuzzy information from multiple systems. J. Comput. Syst. Sci. 1999, 58, 83–99. [Google Scholar] [CrossRef]
- Burkhart, M.; Dimitropoulos, X. Fast privacy-preserving top-k queries using secret sharing. In Proceedings of 19th International Conference on Computer Communications and Networks, Zurich, Switzerland, 2–5 August 2010; pp. 1–7. [Google Scholar]
- Zheng, Y.; Lu, R.; Yang, X.; Shao, J. Achieving efficient and privacy-preserving top-k query over vertically distributed data sources. In Proceedings of the ICC 2019-2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Goldreich, O. Foundations of Cryptography: Volume 2, Basic Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Chess (King-Rookvs.King) DataSet. Available online: http://archive.ics.uci.edu/ml/datasets/Chess+%28King-Rook+vs.+King%29 (accessed on 7 July 2022).
- Kim, H.J.; Lee, H.; Kim, Y.K.; Chang, J.W. Privacy-preserving kNN query processing algorithms via secure two-party computation over encrypted database in cloud computing. J. Supercomput. 2022, 78, 9245–9284. [Google Scholar] [CrossRef]
- Kim, Y.K.; Kim, H.J.; Lee, H.; Chang, J.W. Privacy-preserving parallel kNN classification algorithm using index-based filtering in cloud computing. PLoS ONE 2022, 17, e0267908. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).