A Solar Radiation Forecast Platform Spanning over the Edge-Cloud Continuum
Abstract
:1. Introduction
- Investigation on the real-life feasibility of determining cloud type based on several sources such as multispectral information extracted from weather satellites (e.g., GOES, Meteosat); and
- A new method based on statistics and machine learning to forecast solar irradiance for a given site based on historical correlation between cloudy pixel value and measured irradiance (performed a priori by a nearby solar monitoring station).
2. Related Work
2.1. Solar Irradiance Prediction Solutions
2.2. Cloud Dynamics
2.3. Cloud Type Inference
2.4. Solar Irradiance Prediction
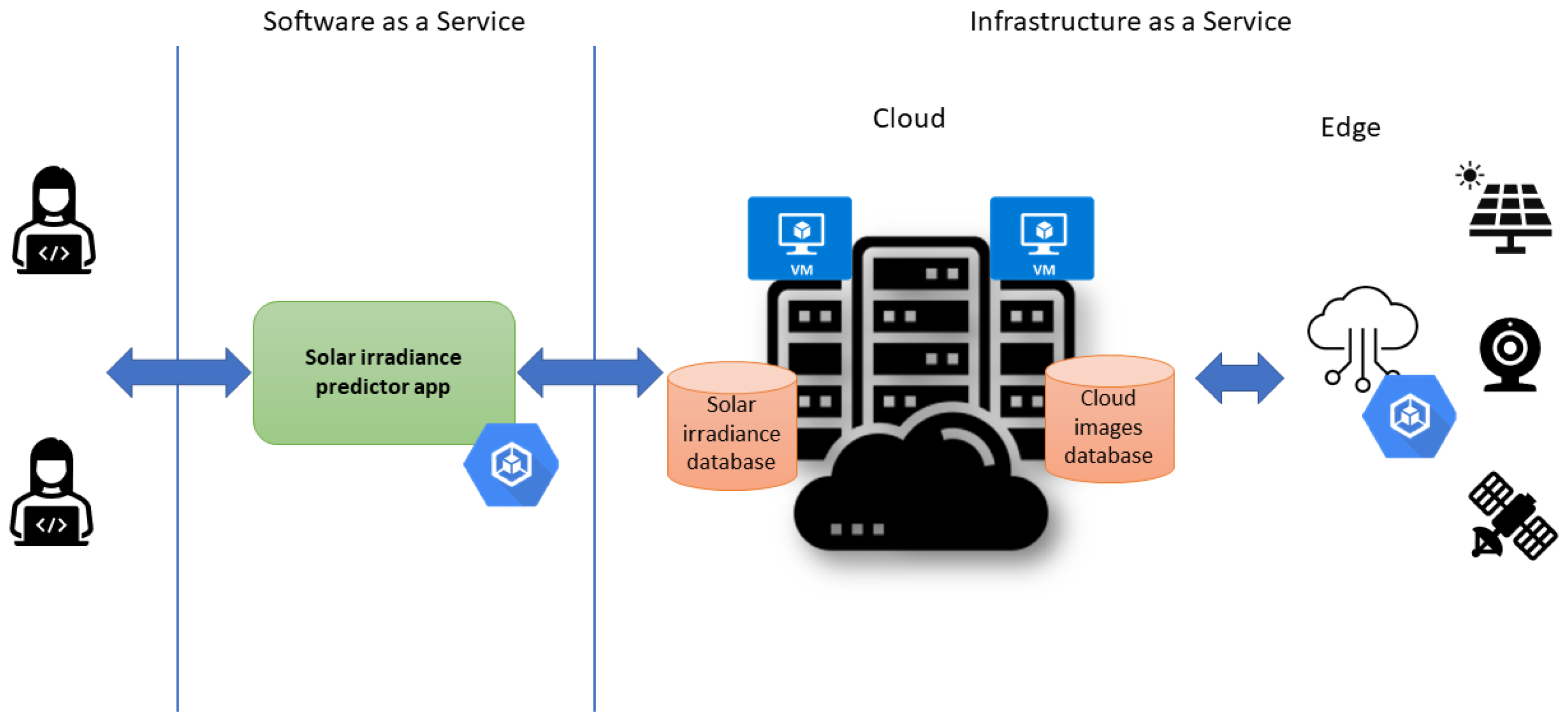
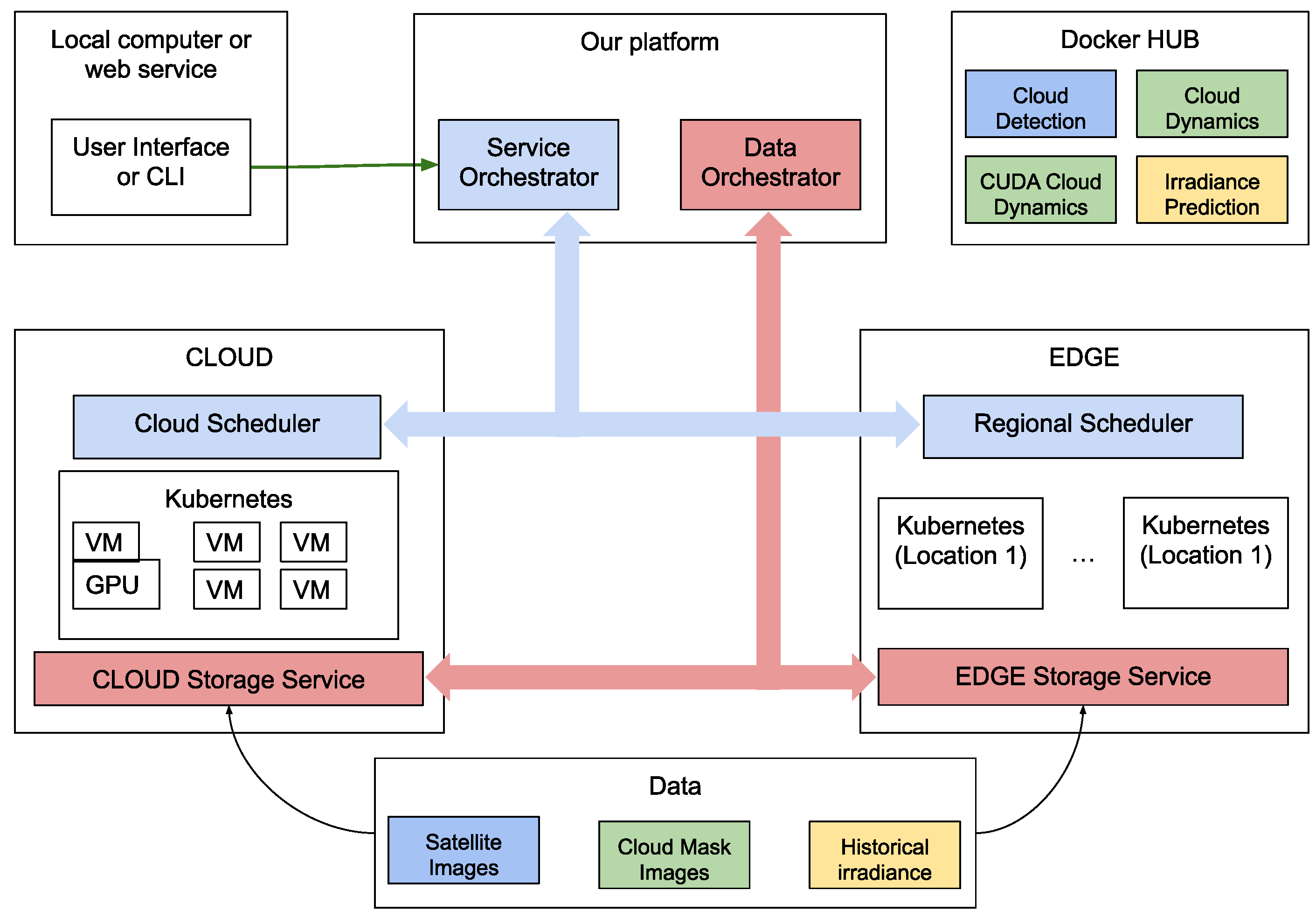
3. Proposed Architecture
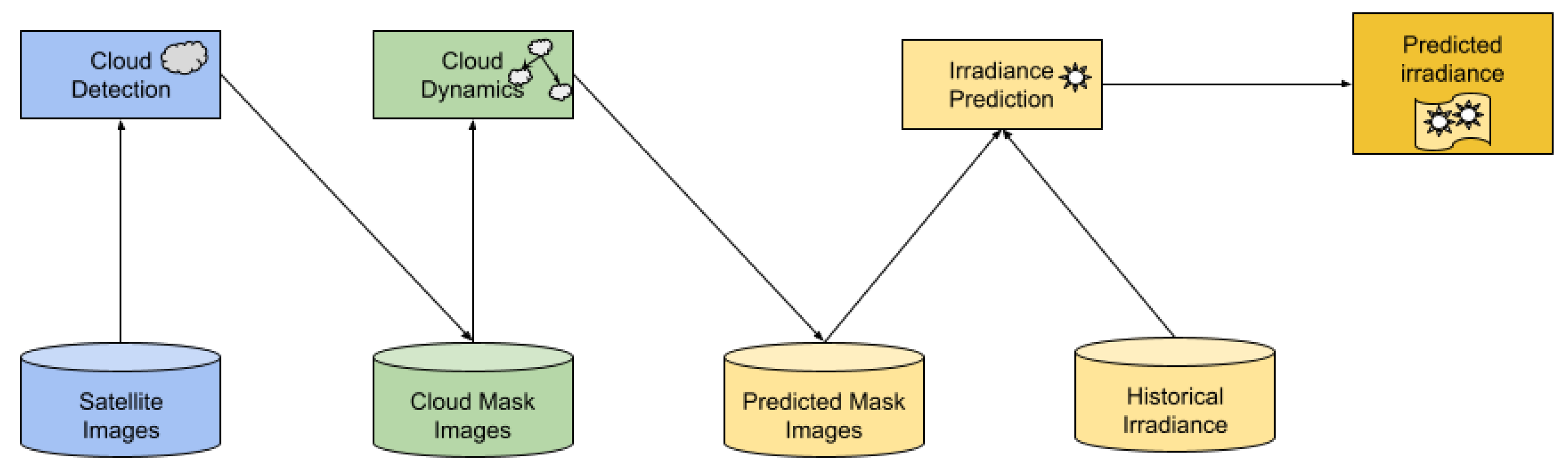
3.1. Example Workflow
3.2. Datasets
- Imagery from NOAA Goes satellite. The color composite images from this geostationary satellite include North America and are captured at 30 intervals. The dynamics module was tested on 1920 × 1080 pixel images from 2017 onward.
- Imagery from Sentinel 2. The orbiting satellites provide imagery in 13 reflectivity bands (see Table 2) at 10, 20, and 60 m spatial resolutions. We used imagery that captured western Romania, which includes the city of Timisoara where the solar platform providing our irradiance data is installed. Images were retrieved for the years 2020 and 2021. Sentinel images are squares with a width of 10,980 pixels.
- Irradiance from a solar platform. The West University of Timisoara (UVT) has a solar radiation station that measures irradiance among other metrics. We retrieved GI and DI in days where Sentinel imagery was also available.
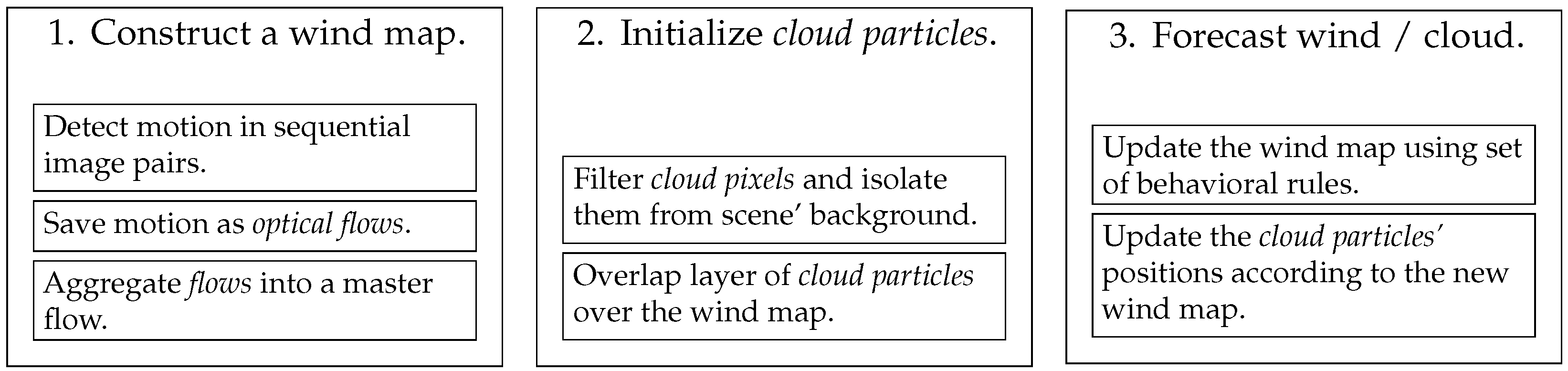
3.3. Cloud Dynamics Module
3.4. Cloud Detection Module
3.5. Irradiance Prediction Module
4. Results
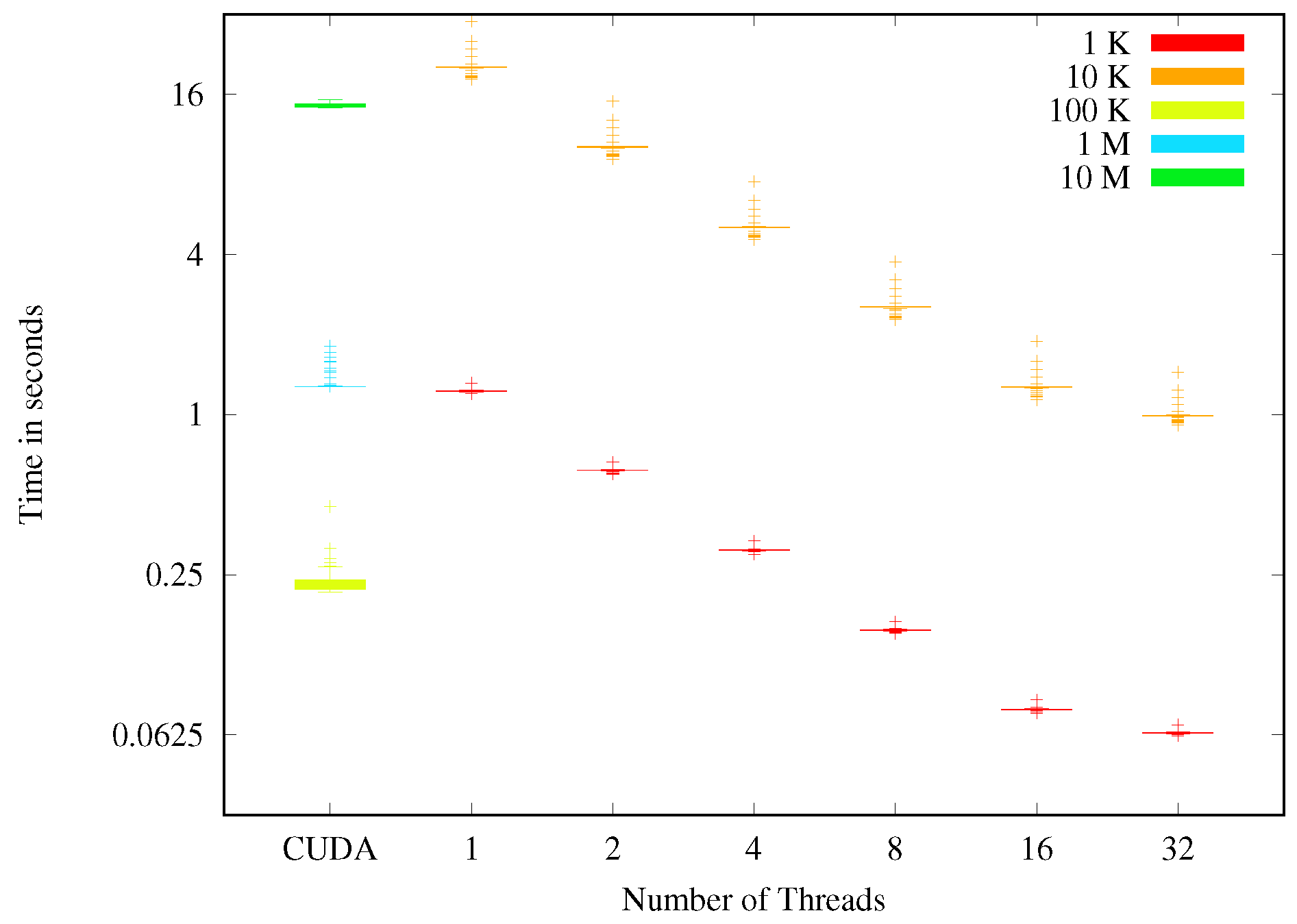
4.1. Scalability and Accuracy of the Cloud Dynamics Module
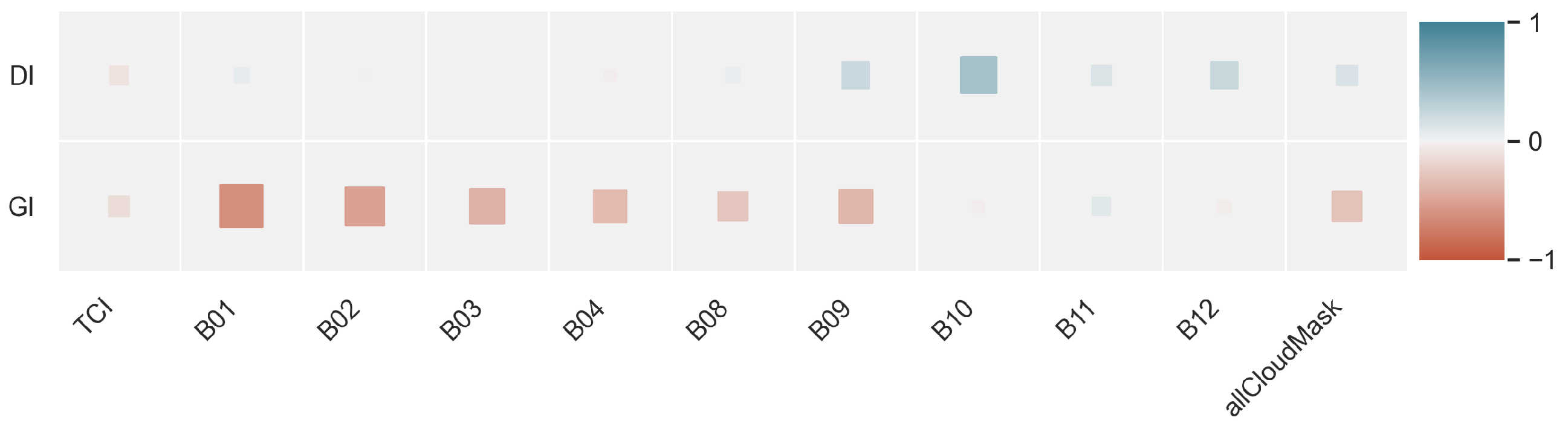
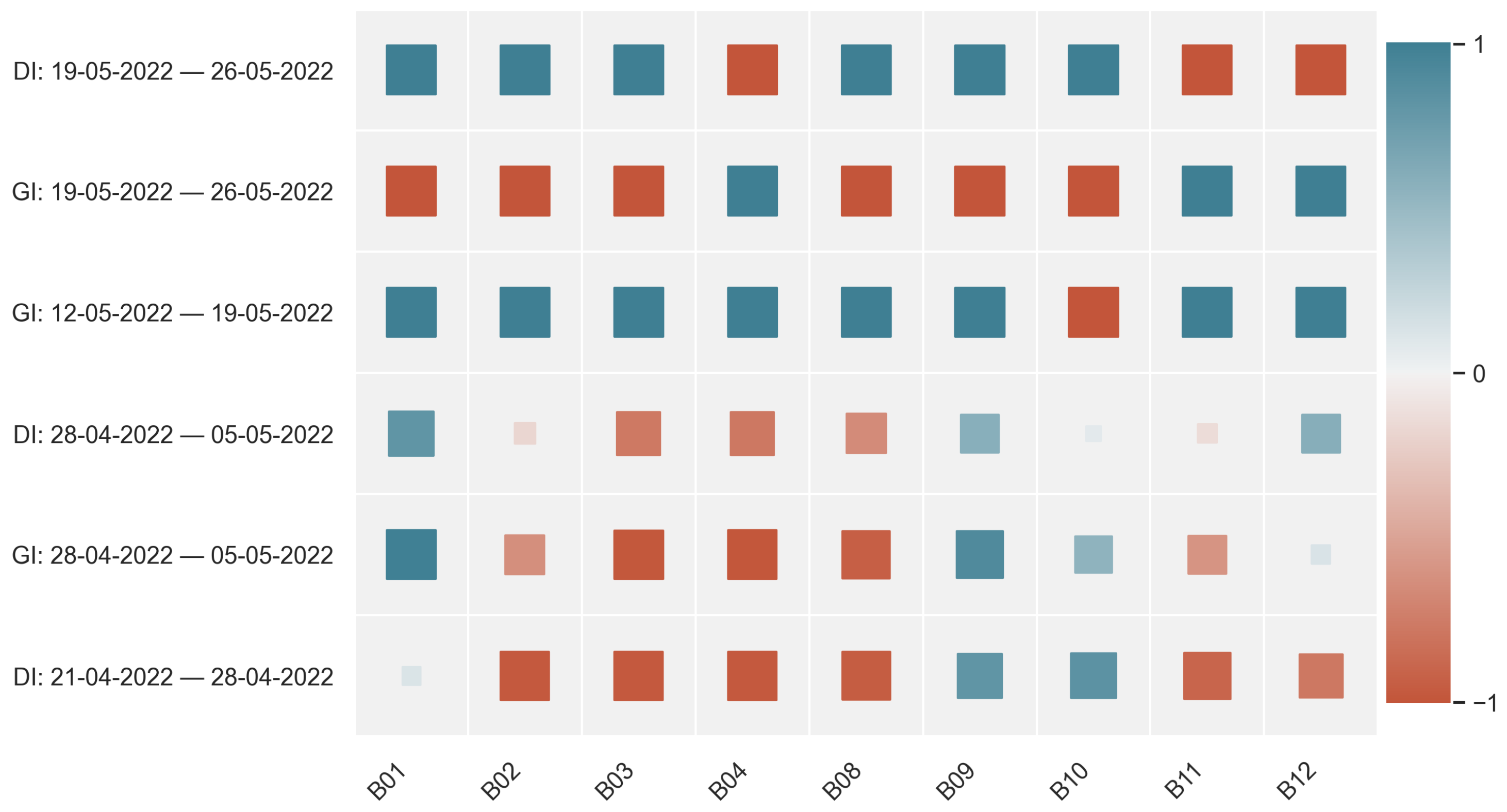
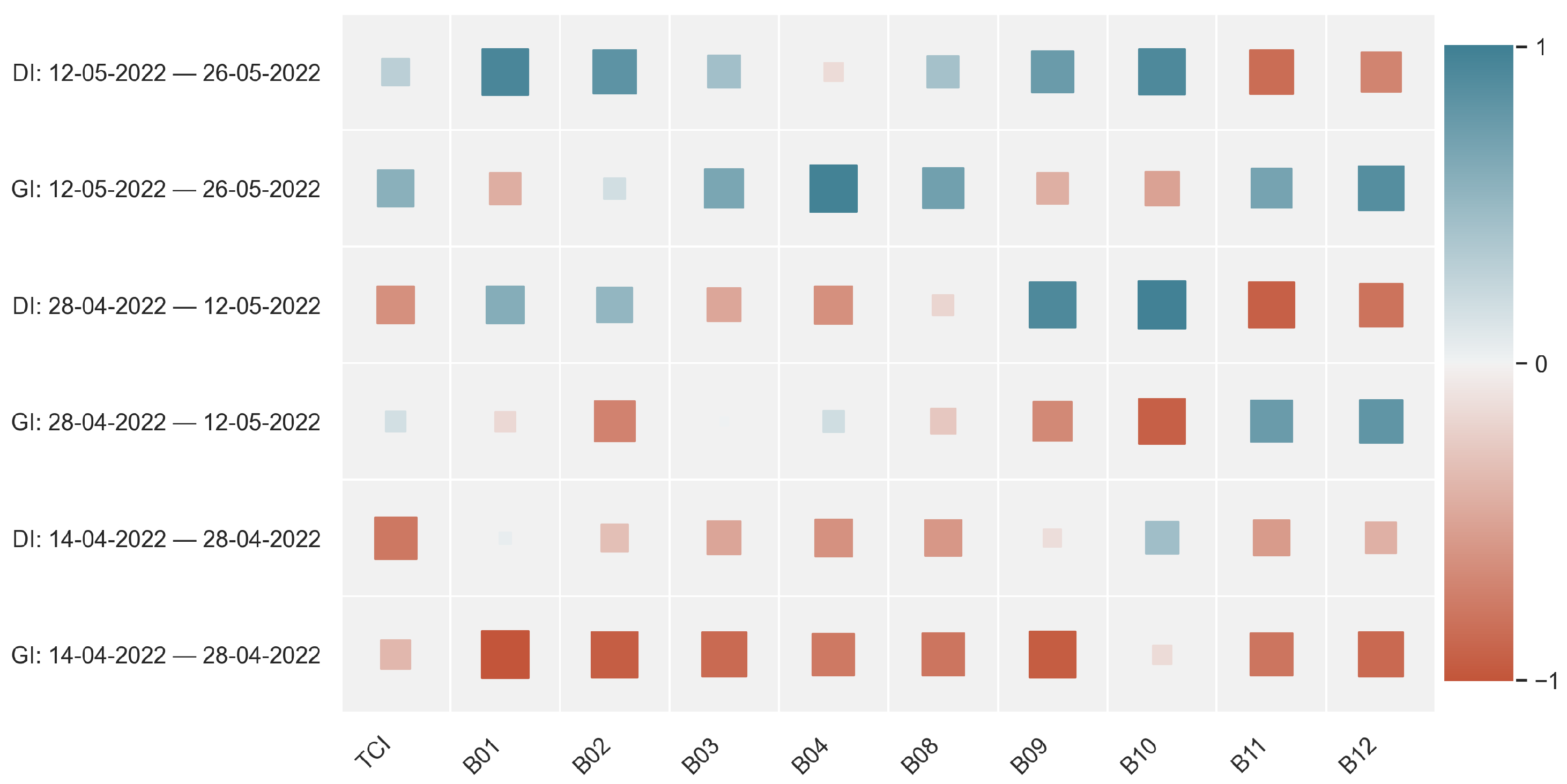
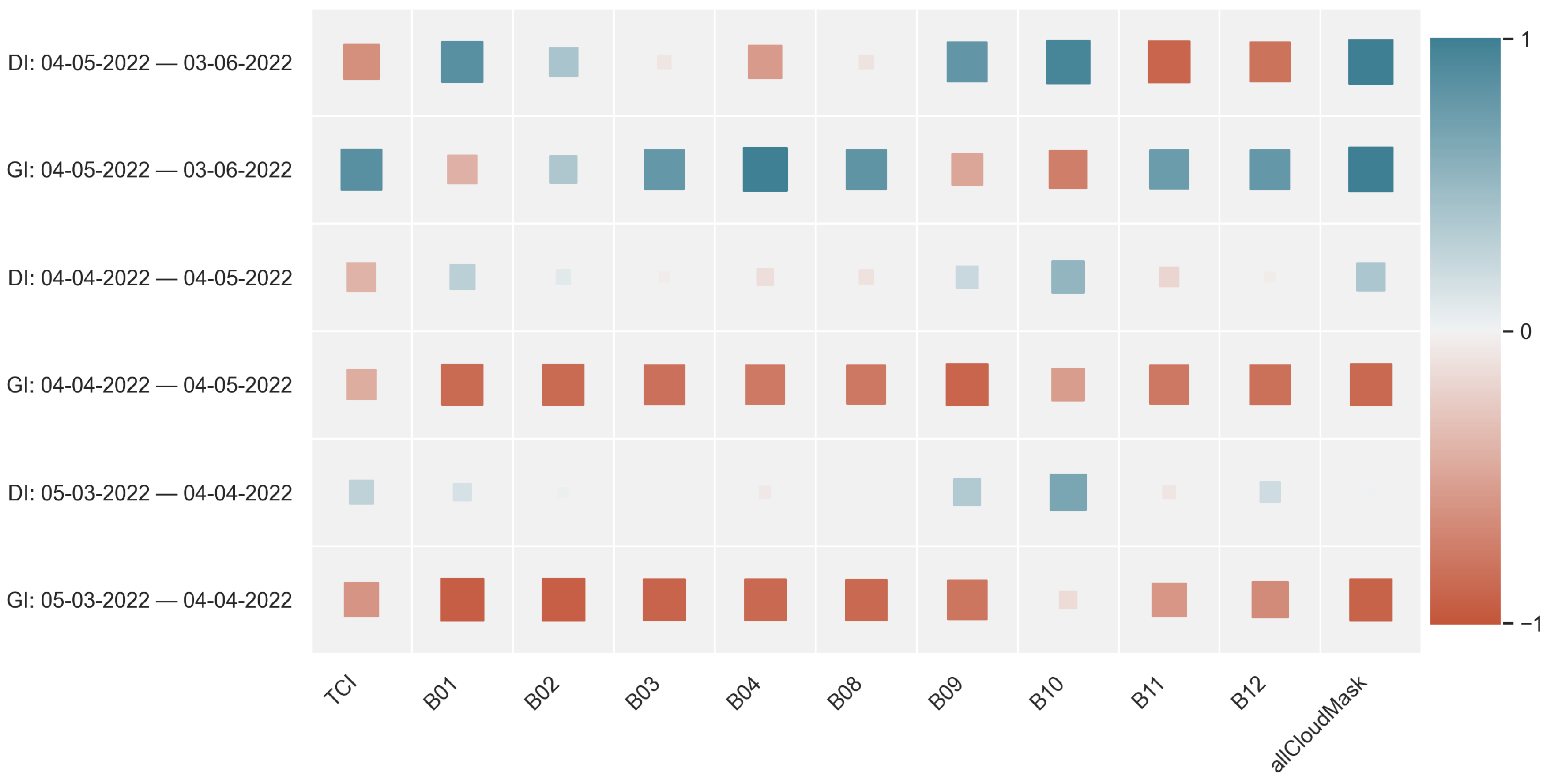
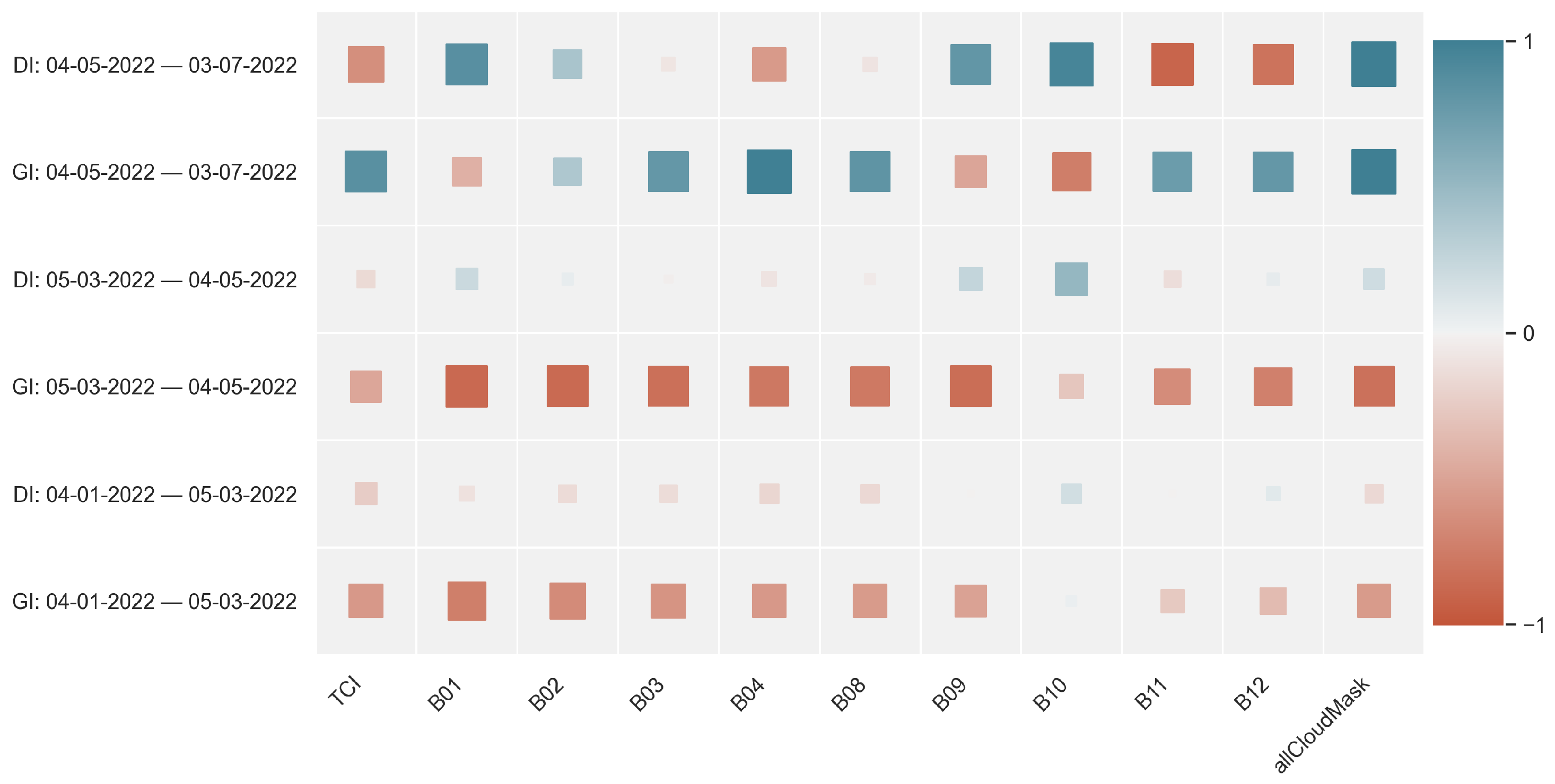
4.2. Correlation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DAG | Direct Acyclic Graph |
| DAM | Day Ahead Market |
| EO | Earth Observation |
| IoT | Internet of Things |
| NWP | Numerical Weather Prediction |
| ML | Machine Learning |
| PV | Photovoltaic |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Square Error |
| NOAA | National Oceanic and Atmospheric Administration |
| IR | Infrared |
| NIR | Near Infrared |
| VIS | Visible |
| GOES | Geostationary Operational Environmental Satellite |
| CUDA | Compute Unified Device Architecture |
| CPU | Computing Processing Unit |
| GPU | Graphics Processing Unit |
| GI | Global Irradiance |
| DI | Diffuse Irradiance |
| TCI | True Color Image |
| WV | Water Vapor |
| SIC | Snow-Ice-Cloud |
| UVt | West University of Timisoara |
References
- The International Energy Agency. Available online: https://www.iea.org/reports/solar-pv (accessed on 15 November 2021).
- Fara, L.; Diaconu, L.; Craciunescu, D.; Fara, S. Forecasting of Energy Production for Photovoltaic Systems Based on ARIMA and ANN Advanced Models. Int. J. Photoenergy 2021, 2021, 677488. [Google Scholar] [CrossRef]
- Fabbri, A.; Roman, T.; Abbad, J.; Quezada, V. Assessment of the cost associated with wind generation prediction errors in a liberalized electricity market. IEEE Trans. Power Syst. 2005, 20, 1440–1446. [Google Scholar] [CrossRef]
- Clouds and Solar Radiation-Remote Sensing of the Ocean and Atmosphere Atmosphere. Available online: https://marine.rutgers.edu/dmcs/ms552/f2008/solar_cloud.pdf (accessed on 15 November 2021).
- Valk, P.; Feijt, A.; Roozekrans, H.; Roebeling, H.; Rosema, A. Operationalisation of an Algorithm for the Automatic Detection and Characterisation of Clouds in METEOSAT Imagery; Technical Report; BCRS Report 1998: USP-2: NRSP-2: NUSP; Beleidscommissie Remote Sensing (BCRS): Delft, The Netherlands, 1998. [Google Scholar]
- Zamo, M.; Mestre, O.; Arbogast, P.; Pannekoucke, O. A benchmark of statistical regression methods for short-term forecasting of photovoltaic electricity production, part I: Deterministic forecast of hourly production. Solar Energy 2014, 105, 792–803. [Google Scholar] [CrossRef]
- IEA. Regional Solar Power Forecasting; Technical Report, IEA. 2020. Available online: https://iea-pvps.org/key-topics/regional-solar-power-forecasting-2020/ (accessed on 15 November 2021).
- Kleissl, J. Solar Energy Forecasting and Resource Assessment; Academic Press: Boston, MA, USA, 2013. [Google Scholar] [CrossRef]
- Validation of short and medium term operational solar radiation forecasts in the US. Solar Energy 2010, 84, 2161–2172. [CrossRef]
- Oana, L.; Frincu, M. Benchmarking the WRF Model on Bluegene/P, Cluster, and Cloud Platforms and Accelerating Model Setup Through Parallel Genetic Algorithms. In Proceedings of the 2017 16th International Symposium on Parallel and Distributed Computing (ISPDC), Innsbruck, Austria, 3–6 July 2017; pp. 78–84. [Google Scholar] [CrossRef]
- Spataru, A.; Tranca, L.C.; Penteliuc, M.E.; Frincu, M. Parallel Cloud Movement Forecasting based on a Modified Boids Flocking Algorithm. In Proceedings of the 2021 20th International Symposium on Parallel and Distributed Computing (ISPDC), Cluj-Napoca, Romania, 28–30 July 2021; pp. 89–96. [Google Scholar] [CrossRef]
- Penteliuc, M.E.; Frincu, M. Short Term Cloud Motion Forecast based on Boid’s Algorithm for use in PV Output Prediction. In Proceedings of the 2021 IEEE/PES Innovative Smart Grid Technologies Europe (iSGT Europe, Espoo, Finland, 18–21 October 2021. [Google Scholar]
- Penteliuc, M.; Frincu, M. Prediction of Cloud Movement from Satellite Images Using Neural Networks. In Proceedings of the 2019 21st International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC), Timisoara, Romania, 4–7 September 2019; pp. 222–229. [Google Scholar] [CrossRef]
- SolCast. 2019. Available online: https://solcast.com (accessed on 27 November 2021).
- Solar Forecasting Accuracy Improves by 33% through AI Machine Learning. 2019. Available online: https://www.solarpowerportal.co.uk/news/solar_forecasting_accuracy_improves_by_33_through_ai_machine_learning (accessed on 27 November 2021).
- Meniscus Solar Map—Solar Irradiance Predictions for the Next 2 1/2 Hours. Available online: www.meniscus.co.uk/solutions-built-using-meniscus-analytics-platforms/map-solar-predicts-solar-irradiance/ (accessed on 27 November 2021).
- Hamill, T.M.; Nehrkorn, T. A short-term cloud forecast scheme using cross correlations. Weather. Forecast. 1993, 8, 401–411. [Google Scholar] [CrossRef]
- Panofsky, H.A.; Brier, G.W. Some Applications of Statistics to Meteorology; Mineral Industries Extension Services, College of Mineral Industries: State College, PA, USA, 1958. [Google Scholar]
- Farnebäck, G. Two-Frame Motion Estimation Based on Polynomial Expansion. Image Analysis; Bigun, J., Gustavsson, T., Eds.; Springer: Berlin Heidelberg: Berlin/Heidelberg, Germany, 2003; pp. 363–370. [Google Scholar] [CrossRef] [Green Version]
- Chow, C.W.; Belongie, S.; Kleissl, J. Cloud motion and stability estimation for intra-hour solar forecasting. Solar Energy 2015, 115, 645–655. [Google Scholar] [CrossRef]
- Espinosa-Gavira, M.J.; Agüera-Pérez, A.; Palomares-Salas, J.C.; de-la Rosa, J.J.G.; Sierra-Fernández, J.M.; Florencias-Oliveros, O. Cloud motion estimation from small-scale irradiance sensor networks: General analysis and proposal of a new method. Solar Energy 2020, 202, 276–293. [Google Scholar] [CrossRef]
- Bosch, J.; Kleissl, J. Cloud motion vectors from a network of ground sensors in a solar power plant. Solar Energy 2013, 95, 13–20. [Google Scholar] [CrossRef]
- Escrig, H.; Batlles, F.; Alonso, J.; Baena, F.; Bosch, J.; Salbidegoitia, I.; Burgaleta, J. Cloud detection, classification and motion estimation using geostationary satellite imagery for cloud cover forecast. Energy 2013, 55, 853–859. [Google Scholar] [CrossRef]
- Jamaly, M.; Kleissl, J. Spatiotemporal interpolation and forecast of irradiance data using Kriging. Solar Energy 2017, 158, 407–423. [Google Scholar] [CrossRef]
- Martínez-Chico, M.; Batlles, F.; Bosch, J. Cloud classification in a mediterranean location using radiation data and sky images. Energy 2011, 36, 4055–4062. [Google Scholar] [CrossRef]
- Goodwin, N.; Collett, L.; Denham, R.; Flood, N.; Tindall, D. Cloud and cloud shadow screening across Queensland, Australia: An automated method for Landsat TM/ETM + time series. Remote. Sens. Environ. 2013, 134, 50–65. [Google Scholar] [CrossRef]
- Miller, S.D.; Rogers, M.A.; Haynes, J.M.; Sengupta, M.; Heidinger, A.K. Short-term solar irradiance forecasting via satellite/model coupling. Solar Energy 2018, 168, 102–117. [Google Scholar] [CrossRef]
- Cheng, H.Y.; Yu, C.C. Multi-model solar irradiance prediction based on automatic cloud classification. Energy 2015, 91, 579–587. [Google Scholar] [CrossRef]
- Mecikalski, J.; Minnis, P.; Palikonda, R. Use of satellite derived cloud properties to quantify growing cumulus beneath cirrus clouds. Atmos. Res. 2013, 120–121, 192–201. [Google Scholar] [CrossRef]
- Kim, K.H.; Baltazar, J.C.; Haberl, J.S. Evaluation of Meteorological Base Models for Estimating Hourly Global Solar Radiation in Texas. Energy Procedia 2014, 57, 1189–1198. [Google Scholar] [CrossRef]
- Muneer, T.; Gul, M. Evaluation of sunshine and cloud cover based models for generating solar radiation data. Energy Convers. Manag. 2000, 41, 461–482. [Google Scholar] [CrossRef]
- Huang, J. ASHRAE Research Project 1477-RP Development of 3012 Typical Year Weather Files for International Locations; Final Report; White Box Technologies: Salt Lake City, UT, USA, 2011. [Google Scholar]
- Martin, L.; Zarzalejo, L.F.; Polo, J.; Navarro, A.; Marchante, R.; Cony, M. Prediction of global solar irradiance based on time series analysis: Application to solar thermal power plants energy production planning. Solar Energy 2010, 84, 1772–1781. [Google Scholar] [CrossRef]
- Fu, C.L.; Cheng, H.Y. Predicting solar irradiance with all-sky image features via regression. Solar Energy 2013, 97, 537–550. [Google Scholar] [CrossRef]
- Cheng, H.Y.; Yu, C.C.; Lin, S.J. Bi-model short-term solar irradiance prediction using support vector regressors. Energy 2014, 70, 121–127. [Google Scholar] [CrossRef]
- Alzahrani, A.; Shamsi, P.; Dagli, C.; Ferdowsi, M. Solar Irradiance Forecasting Using Deep Neural Networks. Procedia Comput. Sci. 2017, 114, 304–313. [Google Scholar] [CrossRef]
- Burns, B.; Grant, B.; Oppenheimer, D.; Brewer, E.; Wilkes, J. Borg, Omega, and Kubernetes. Queue 2016, 14, 10:70–10:93. [Google Scholar] [CrossRef]
- Böhm, S.; Wirtz, G. Profiling Lightweight Container Platforms: MicroK8s and K3s in Comparison to Kubernetes. In ZEUS; Distributed Systems Group, University of Bamberg: Bamberg, Germany, 2021; pp. 65–73. [Google Scholar]
- Reynolds, C.W. Flocks, Herds and Schools: A Distributed Behavioral Model. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH’87, Anaheim, CA, USA, 27–31 July 1987; Association for Computing Machinery: New York, NY, USA, 1987; pp. 25–34. [Google Scholar] [CrossRef]
- Chapter 2 Cloud Type Identification by Satellites. In Analysis and Use of Meteorological Satellite Images. 2002. Available online: http://rammb.cira.colostate.edu/wmovl/VRL/Texts/SATELLITE_METEOROLOGY/CHAPTER-2.PDF (accessed on 27 November 2021).
- Wooster, M.J.; Roberts, G.; Freeborn, P.H.; Xu, W.; Govaerts, Y.; Beeby, R.; He, J.; Lattanzio, A.; Fisher, D.; Mullen, R. LSA SAF Meteosat FRP products—Part 1: Algorithms, product contents, and analysis. Atmos. Chem. Phys. 2015, 15, 13217–13239. [Google Scholar] [CrossRef]
- ABI Bands Quick Information Guides. Available online: https://www.goes-r.gov/mission/ABI-bands-quick-info.html (accessed on 27 November 2021).
- Menzel, P. Chapter 6 Clouds. In Applications with Meteorological Satellites; WMO Library: Genève, Switzerland, 2001. [Google Scholar]
- Menzel, W. Remote Sensing Applications with Meteorological Satellites, NOAA Satellite and Information Service; University of Wisconsin: Madison, WI, USA, 2006. [Google Scholar]
- Oreopoulos, L.; Wilson, M.J.; Várnai, T. Implementation on Landsat Data of a Simple Cloud-Mask Algorithm Developed for MODIS Land Bands. IEEE Geosci. Remote. Sens. Lett. 2011, 8, 597–601. [Google Scholar] [CrossRef] [Green Version]
- Ai, Y.; Li, J.; Shi, W.; Schmit, T.J.; Cao, C.; Li, W. Deep convective cloud characterizations from both broadband imager and hyperspectral infrared sounder measurements. J. Geophys. Res. Atmos. 2017, 122, 1700–1712. [Google Scholar] [CrossRef]
- Lee, Y.; Kummerow, C.D.; Zupanski, M. A simplified method for the detection of convection using high-resolution imagery from GOES-16. Atmos. Meas. Tech. 2021, 14, 3755–3771. [Google Scholar] [CrossRef]
- EUMeTrain: Fog and Stratus. Available online: http://www.eumetrain.org/satmanu/CMs/FgStr/navmenu.php (accessed on 27 November 2021).
- Nielsen, A.H.; Iosifidis, A.; Karstoft, H. IrradianceNet: Spatiotemporal deep learning model for satellite-derived solar irradiance short-term forecasting. Sol. Energy 2021, 228, 659–669. [Google Scholar] [CrossRef]
- Husselmann, A.; Hawick, K. Simulating Species Interactions and Complex Emergence in Multiple Flocks of Boids with GPUS. In Proceedings of the IASTED International Conference on Parallel and Distributed Computing and Systems, Innsbruck, Austria, 15–17 February 2011. [Google Scholar] [CrossRef]
- Li, X.; Ma, L.; Chen, P.; Xu, H.; Xing, Q.; Yan, J.; Lu, S.; Fan, H.; Yang, L.; Cheng, Y. Probabilistic solar irradiance forecasting based on XGBoost. In Proceedings of the ICPE 2021-The 2nd International Conference on Power Engineering, Nanning, China, 9–11 December 2021; pp. 1087–1095. [Google Scholar] [CrossRef]
- Ramirez-Vergara, J.; Bosman, L.B.; Leon-Salas, W.D.; Wollega, E. Ambient temperature and solar irradiance forecasting prediction horizon sensitivity analysis. Mach. Learn. Appl. 2021, 6, 100128. [Google Scholar] [CrossRef]


| Parameter | Description |
|---|---|
| dtype | type satellite data to be used for prediction |
| frames | number of frames-ahead to be predicted |
| boids | number of boid-objects to be used for the simulation of cloud movement |
| Sentinel | Meteosat | NOAA | |||
|---|---|---|---|---|---|
| Band | Resolution | Wavelength | Purpose | SEVIRI | GOES-R |
| 1 | 60 m | 443 nm | Aerosol detection | n/a | n/a |
| 2 | 10 m | 490 nm | Color Blue | n/a | Band 1 |
| 3 | 10 m | 560 nm | Color Green | n/a | n/a |
| 4 | 10 m | 665 nm | Color Red | Band 1 VIS0.6 | Band 2 |
| 5 | 20 m | 705 nm | Vegetation | n/a | n/a |
| 6 | 20 m | 740 nm | Vegetation | n/a | n/a |
| 7 | 20 m | 783 nm | Vegetation | Band 2 VIS0.8 | n/a |
| 8 | 10 m | 842 nm | Near Infrared | Band 2 VIS0.8 | Band 3 |
| 8A | 20 m | 865 nm | Vegetation | n/a | Band 3 |
| 9 | 60 m | 945 nm | Water Vapor | n/a | n/a |
| 10 | 60 m | 1375 nm | Cirrus Cloud | n/a | Band 4 |
| 11 | 20 m | 1610 nm | Snow-Ice-Cloud | Band 3 NIR1.6 | Band 5 |
| 12 | 20 m | 2190 nm | Snow-Ice-Cloud | n/a | Band 6 |
| Date | GI | DI | TCI | B01 | B02 | B03 | B04 | B08 | B09 | B10 | B11 | B12 | mask1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 April 2022 | 517 | 312 | 189 | 3783 | 3749 | 3548 | 3645 | 4120 | 2740 | 1932 | 3162 | 2679 | - |
| 4 April 2022 | 651 | 270 | 188 | 3725 | 3438 | 3336 | 3625 | 4169 | 3001 | 1078 | 4786 | 4221 | - |
| 6 April 2022 | 785 | 83 | 255 | 2893 | 3847 | 4098 | 4778 | 4917 | 1873 | 1013 | 4467 | 3007 | 4917 |
| 9 April 2022 | 337 | 324 | 255 | 8261 | 7866 | 7344 | 7937 | 8232 | 5618 | 1628 | 6243 | 5220 | 8232 |
| 11 April 2022 | 940 | 222 | 79 | 2529 | 2515 | 2286 | 2108 | 2098 | 1347 | 1014 | 1719 | 1422 | 2098 |
| 14 April 2022 | 849 | 118 | 255 | 2870 | 3915 | 3973 | 4611 | 5042 | 2252 | 1029 | 4585 | 3631 | 5042 |
| 16 April 2022 | 452 | 399 | 234 | 5216 | 4651 | 4182 | 4279 | 4860 | 2971 | 1033 | 4697 | 3978 | - |
| 19 April 2022 | 198 | 184 | 255 | 6587 | 6725 | 6314 | 6902 | 7452 | 5179 | 1273 | 7096 | 6187 | 7452 |
| 21 April 2022 | 854 | 433 | 128 | 2955 | 2882 | 2705 | 2797 | 3257 | 2123 | 1460 | 2389 | 2000 | - |
| 24 April 2022 | 832 | 298 | 216 | 2916 | 3489 | 3594 | 4022 | 4544 | 1897 | 1031 | 4311 | 3444 | - |
| 26 April 2022 | 821 | 125 | 255 | 2947 | 3833 | 4102 | 4673 | 5070 | 1903 | 1023 | 4616 | 3314 | 5070 |
| 29 April 2022 | 976 | 165 | 186 | 4223 | 3725 | 3561 | 3610 | 4405 | 2554 | 1022 | 4335 | 3737 | - |
| 1 May 2022 | 874 | 110 | 255 | 2997 | 3762 | 4058 | 4636 | 5005 | 2091 | 1021 | 4473 | 3385 | 5005 |
| 4 May 2022 | 882 | 140 | 255 | 2935 | 3885 | 4133 | 4766 | 5252 | 1829 | 1015 | 5027 | 4021 | - |
| 6 May 2022 | 687 | 494 | 191 | 4113 | 3881 | 3700 | 3669 | 4817 | 3353 | 2467 | 3182 | 2853 | - |
| 14 May 2022 | 1013 | 249 | 255 | 3180 | 4542 | 4907 | 5545 | 6088 | 1942 | 1017 | 5538 | 4300 | 6088 |
| 16 May 2022 | 845 | 172 | 245 | 3023 | 3677 | 3792 | 4443 | 4954 | 1905 | 1046 | 4813 | 3347 | - |
| 19 May 2022 | 940 | 98 | 255 | 3012 | 4134 | 4505 | 5155 | 5516 | 2605 | 1019 | 5252 | 4069 | 5516 |
| 21 May 2022 | 857 | 453 | 255 | 5237 | 4986 | 4727 | 4753 | 5764 | 4041 | 2324 | 2927 | 2711 | - |
| Coefficient | MAE | RMSE | |
|---|---|---|---|
| TCI | 0.03644642678338772 | 242.42154794617383 | 274.7408497562563 |
| B01 | 0.0820348043032918 | 230.80298574638536 | 262.10447565483634 |
| B02 | −0.21622423375748578 | 226.0133833016301 | 266.59864257524436 |
| B03 | 0.16484461491503566 | 258.6680008229855 | 289.54645358512585 |
| B04 | 0.18979026867512105 | 242.25312734146155 | 278.8299007436962 |
| B08 | −0.004685782814821238 | 263.14349948394886 | 297.98935481964486 |
| B09 | 0.1666511708442644 | 213.59486036305327 | 243.97853837735866 |
| B10 | −0.014280286109260798 | 206.04134647422316 | 243.33683919725743 |
| B11 | −0.09136205237619488 | 213.875380476756 | 253.2442376883533 |
| B12 | −0.015120462726200268 | 275.1958711048938 | 311.08537403125933 |
| mask1 | −0.03157307096771955 | 261.67319967290194 | 317.8092308395099 |
| Coefficient | MAE | RMSE | |
|---|---|---|---|
| TCI | −0.0994881915821475 | 109.1422687328849 | 139.87949383832782 |
| B01 | −0.04660898451208051 | 91.47501179095161 | 125.09773057981627 |
| B02 | −0.006483852227510134 | 87.28399557078228 | 112.28440557826498 |
| B03 | −0.03451064554614436 | 90.44762037974252 | 107.51985827433974 |
| B04 | −0.019033305619853502 | 81.80569395778589 | 101.4159979735758 |
| B08 | −0.024606201009772732 | 75.72686996307678 | 97.97877522070938 |
| B09 | −0.11615994107608651 | 100.78955376918246 | 134.09884693197583 |
| B10 | 0.017187645831838072 | 81.23618926107555 | 114.61636948767924 |
| B11 | −0.05413538201239265 | 96.29763294968915 | 126.01369289709537 |
| B12 | 0.03296695291836593 | 82.92904576107716 | 108.01263505006585 |
| mask1 | −0.04226888637819548 | 66.96540604389577 | 91.83241938981622 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frincu, M.; Penteliuc, M.; Spataru, A. A Solar Radiation Forecast Platform Spanning over the Edge-Cloud Continuum. Electronics 2022, 11, 2756. https://doi.org/10.3390/electronics11172756
Frincu M, Penteliuc M, Spataru A. A Solar Radiation Forecast Platform Spanning over the Edge-Cloud Continuum. Electronics. 2022; 11(17):2756. https://doi.org/10.3390/electronics11172756
Chicago/Turabian StyleFrincu, Marc, Marius Penteliuc, and Adrian Spataru. 2022. "A Solar Radiation Forecast Platform Spanning over the Edge-Cloud Continuum" Electronics 11, no. 17: 2756. https://doi.org/10.3390/electronics11172756
APA StyleFrincu, M., Penteliuc, M., & Spataru, A. (2022). A Solar Radiation Forecast Platform Spanning over the Edge-Cloud Continuum. Electronics, 11(17), 2756. https://doi.org/10.3390/electronics11172756







