Real-Time Drift-Driving Control for an Autonomous Vehicle: Learning from Nonlinear Model Predictive Control via a Deep Neural Network
Abstract
1. Introduction
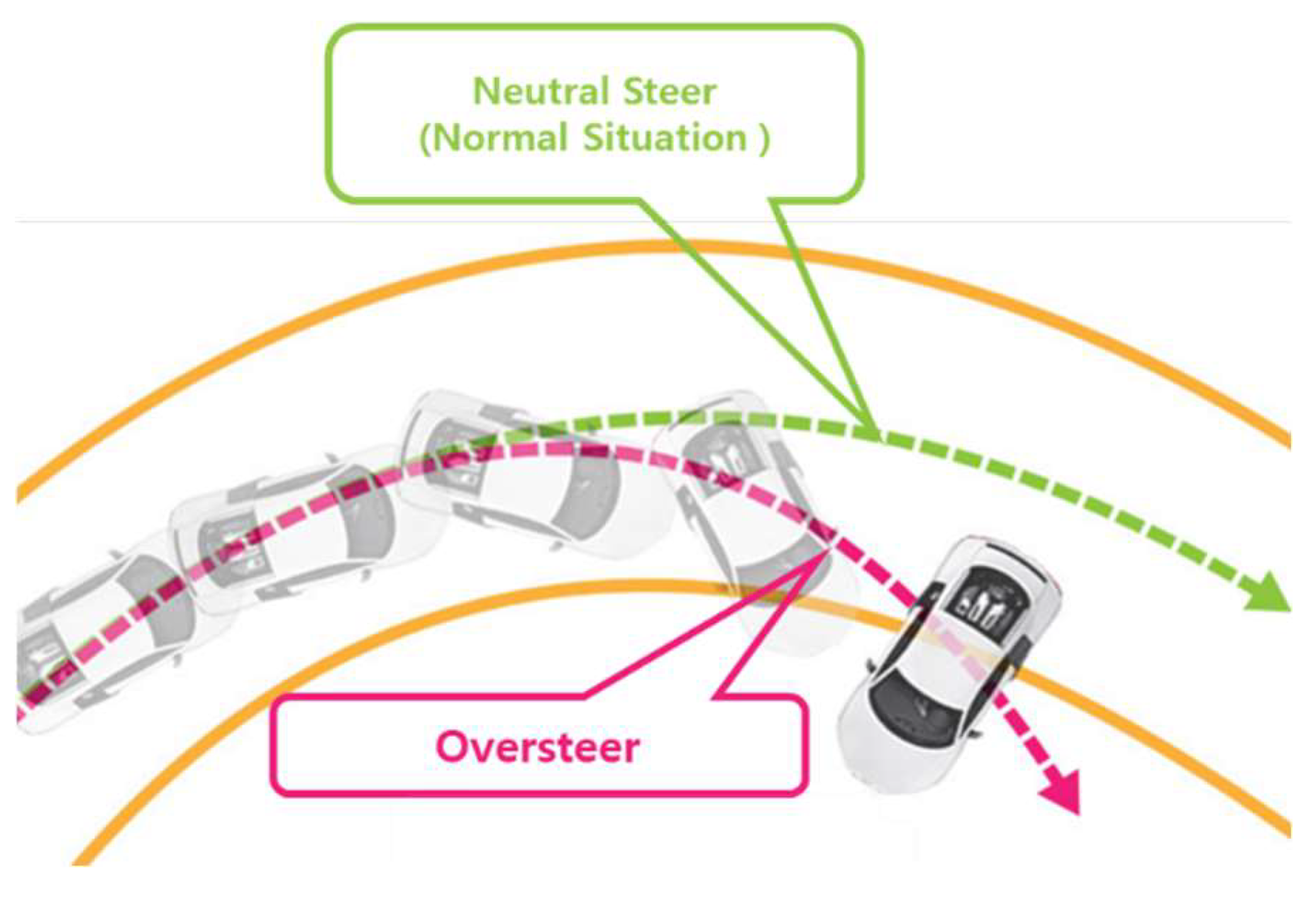
2. Vehicle Dynamics Analysis
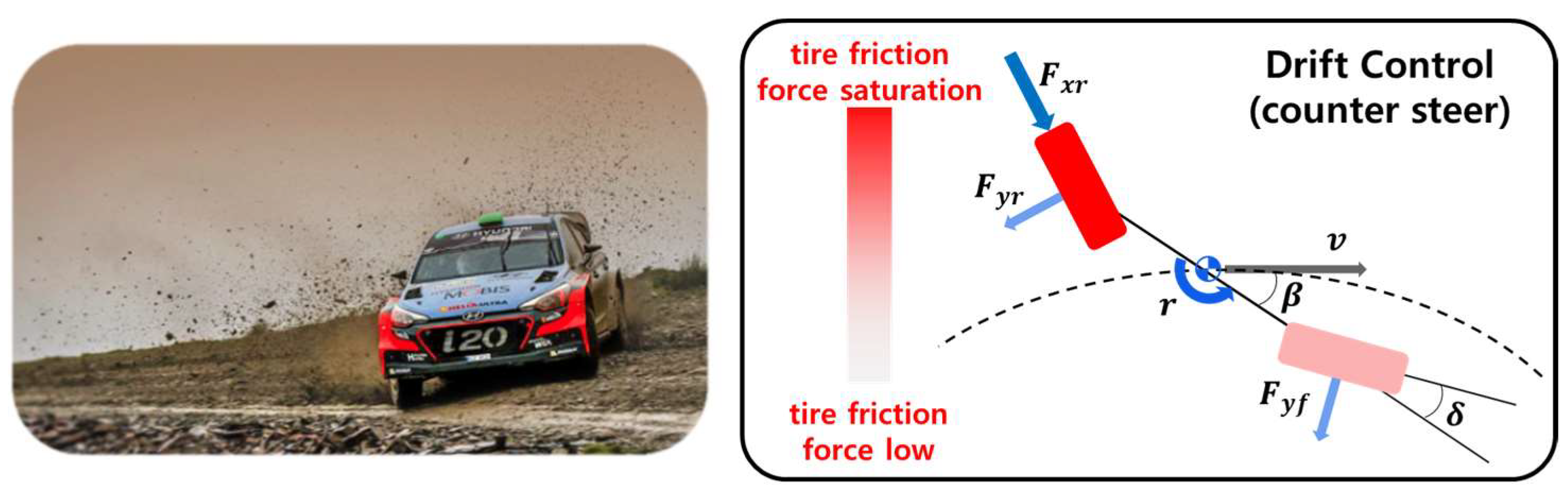
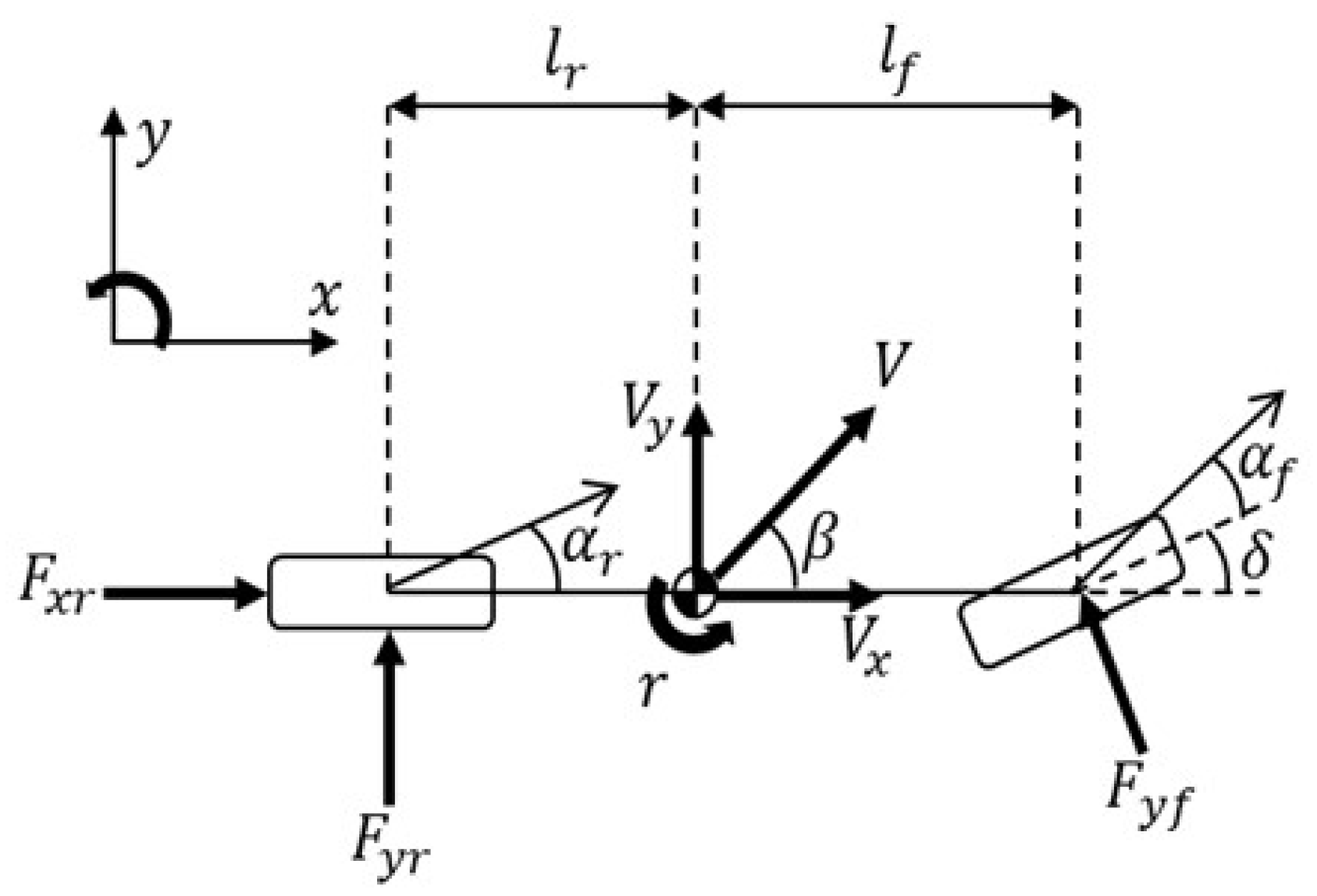
2.1. Three-Degrees-of-Freedom Bicycle Model
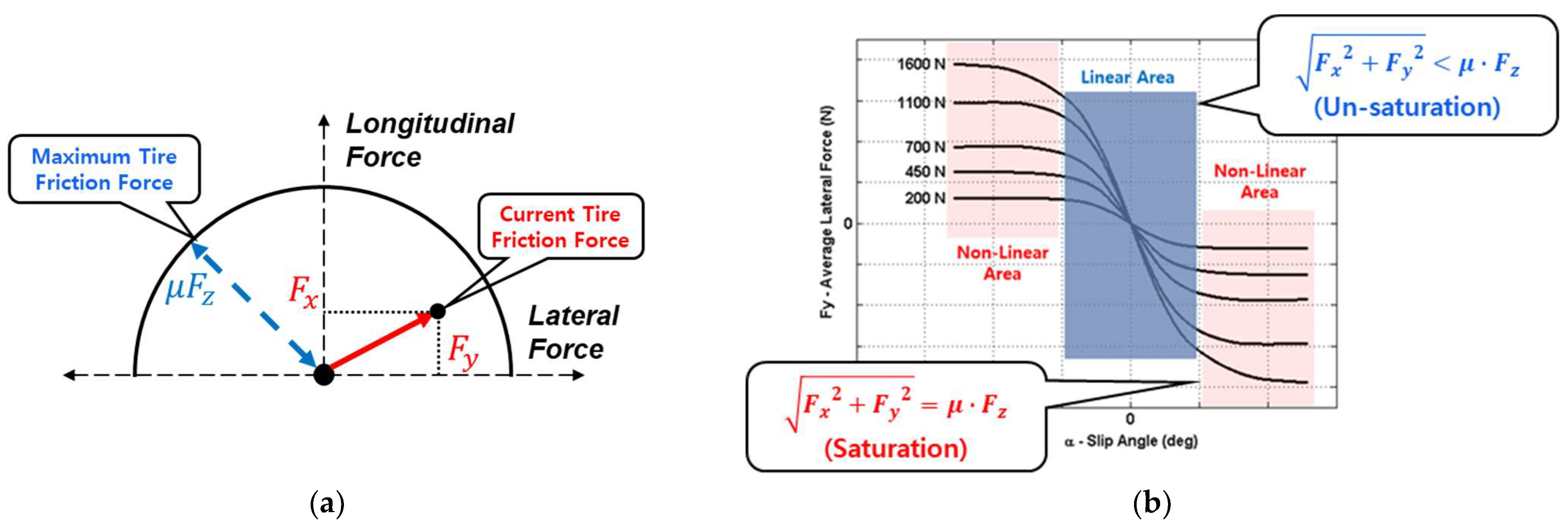
2.2. Brush Tire Model
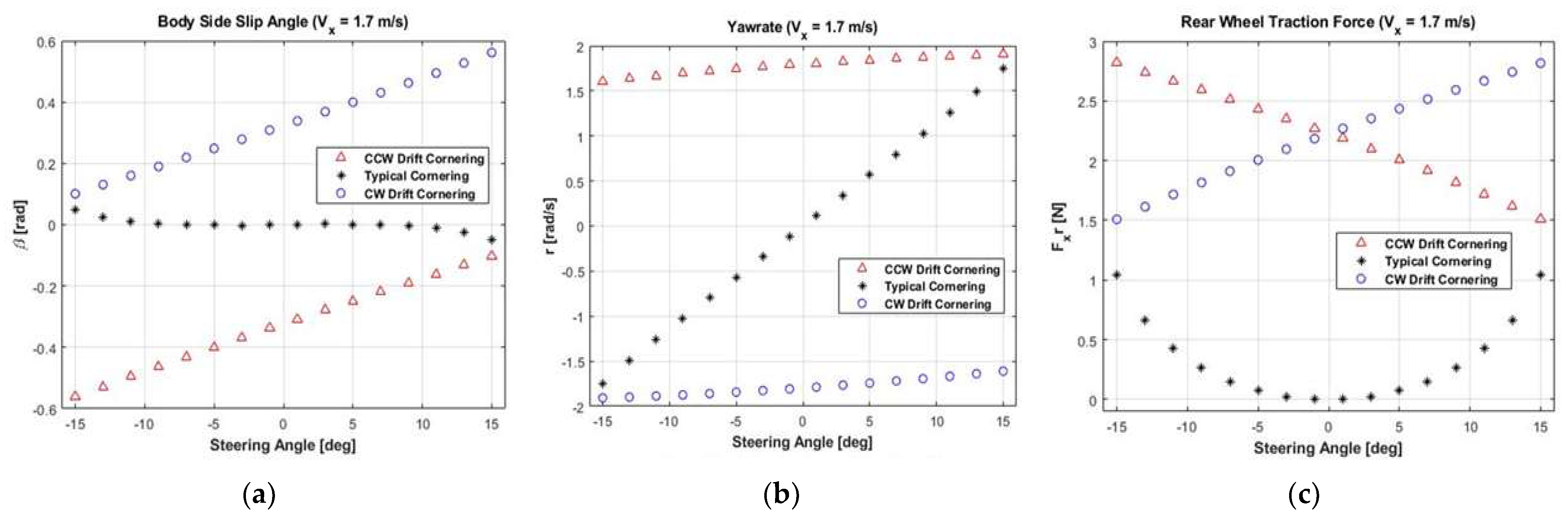
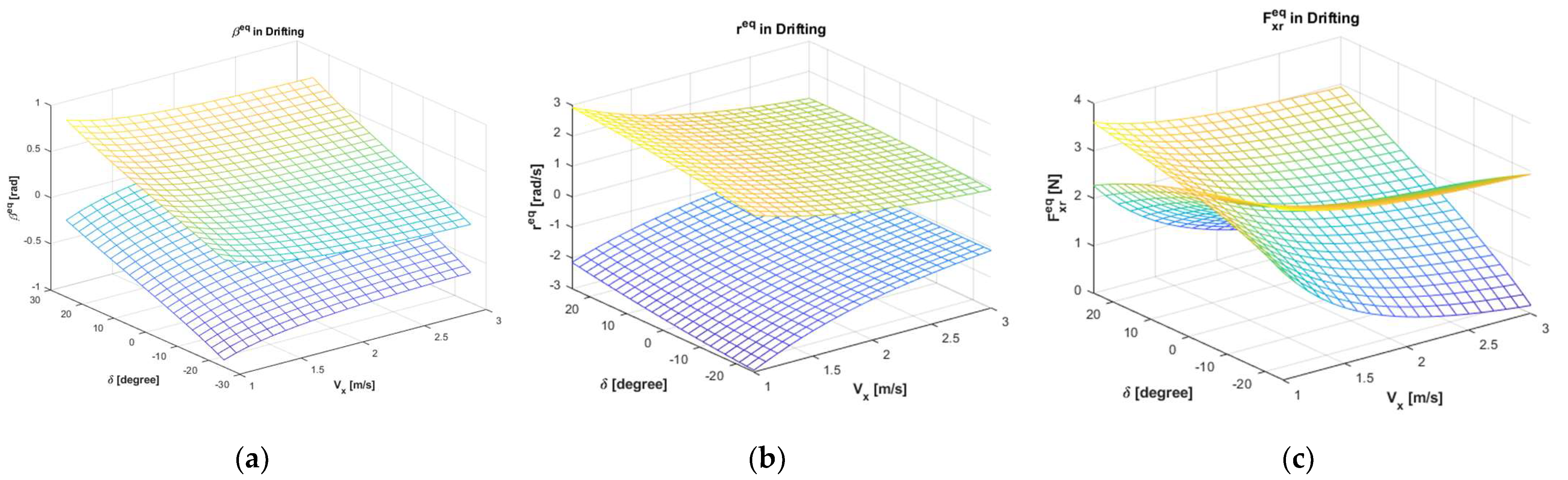
2.3. Drift Equilibrium State Analysis
3. Design of the Nonlinear Model Predictive Controller
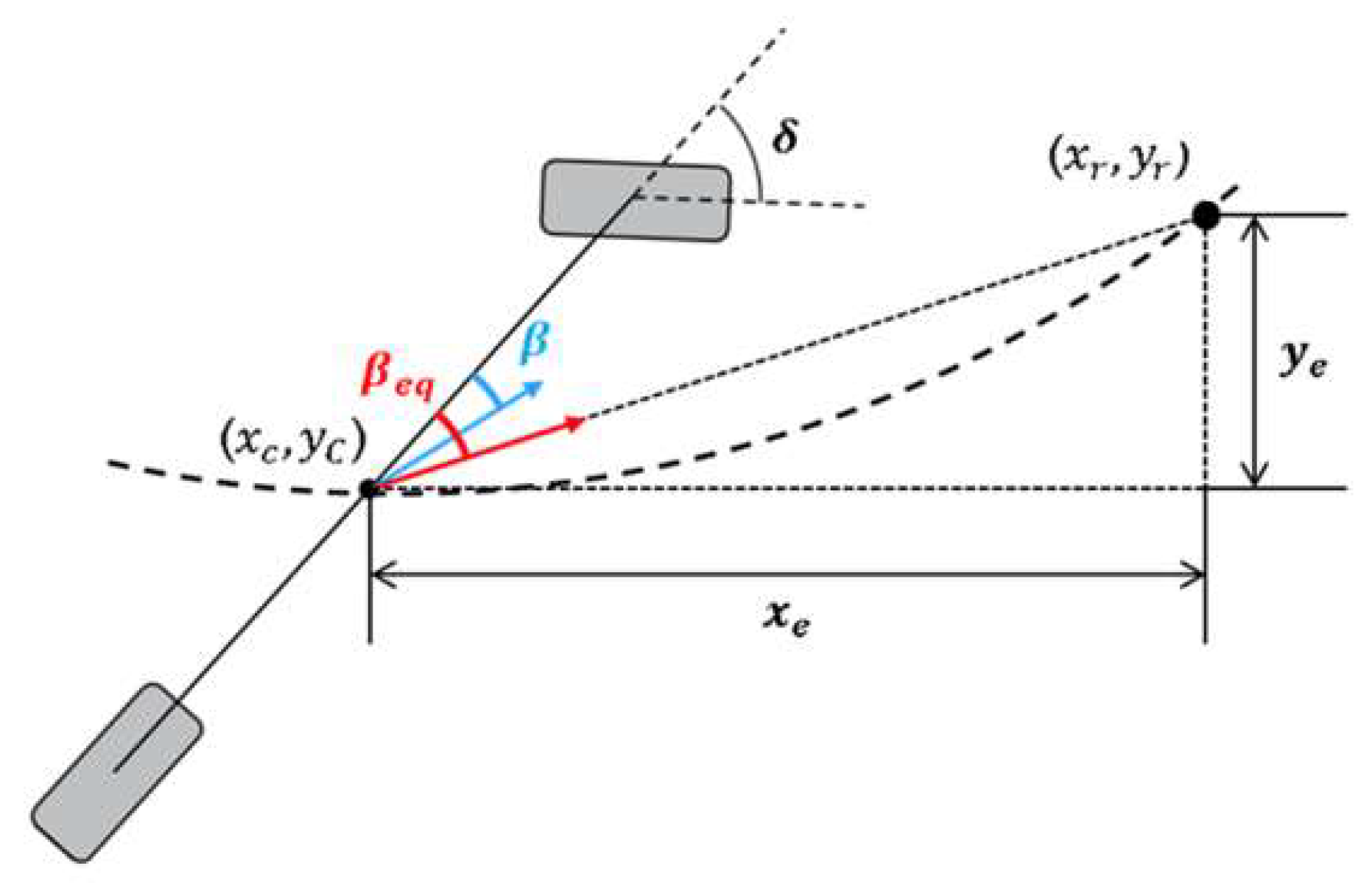
3.1. Vehicle State Prediction Model
3.2. Nonlinear Model Predictive Controller Cost Function
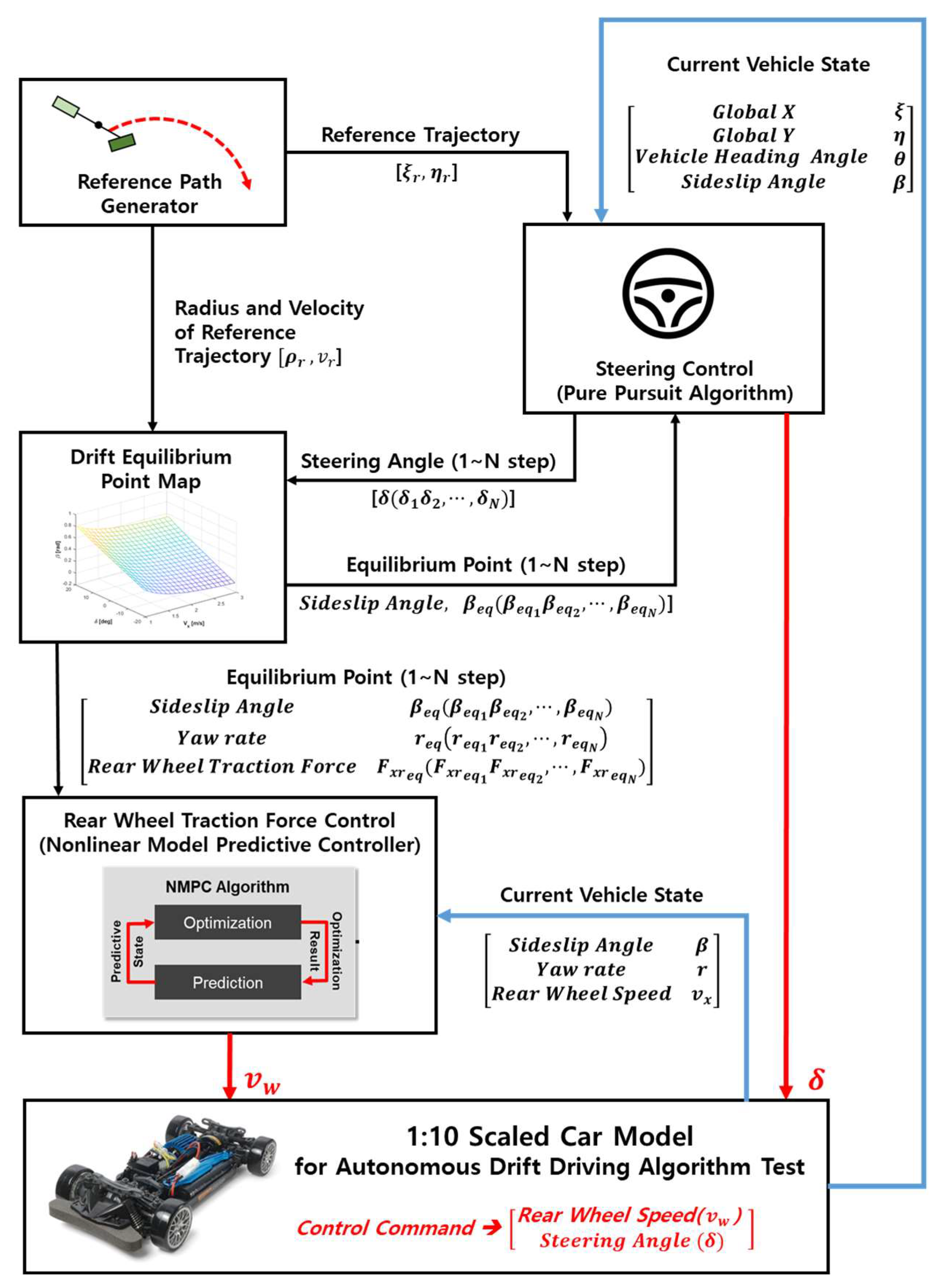
3.3. Nonlinear Model Predictive Controller System for Drift Driving
4. Drift-Driving Test of the Nonlinear Model Predictive Controller
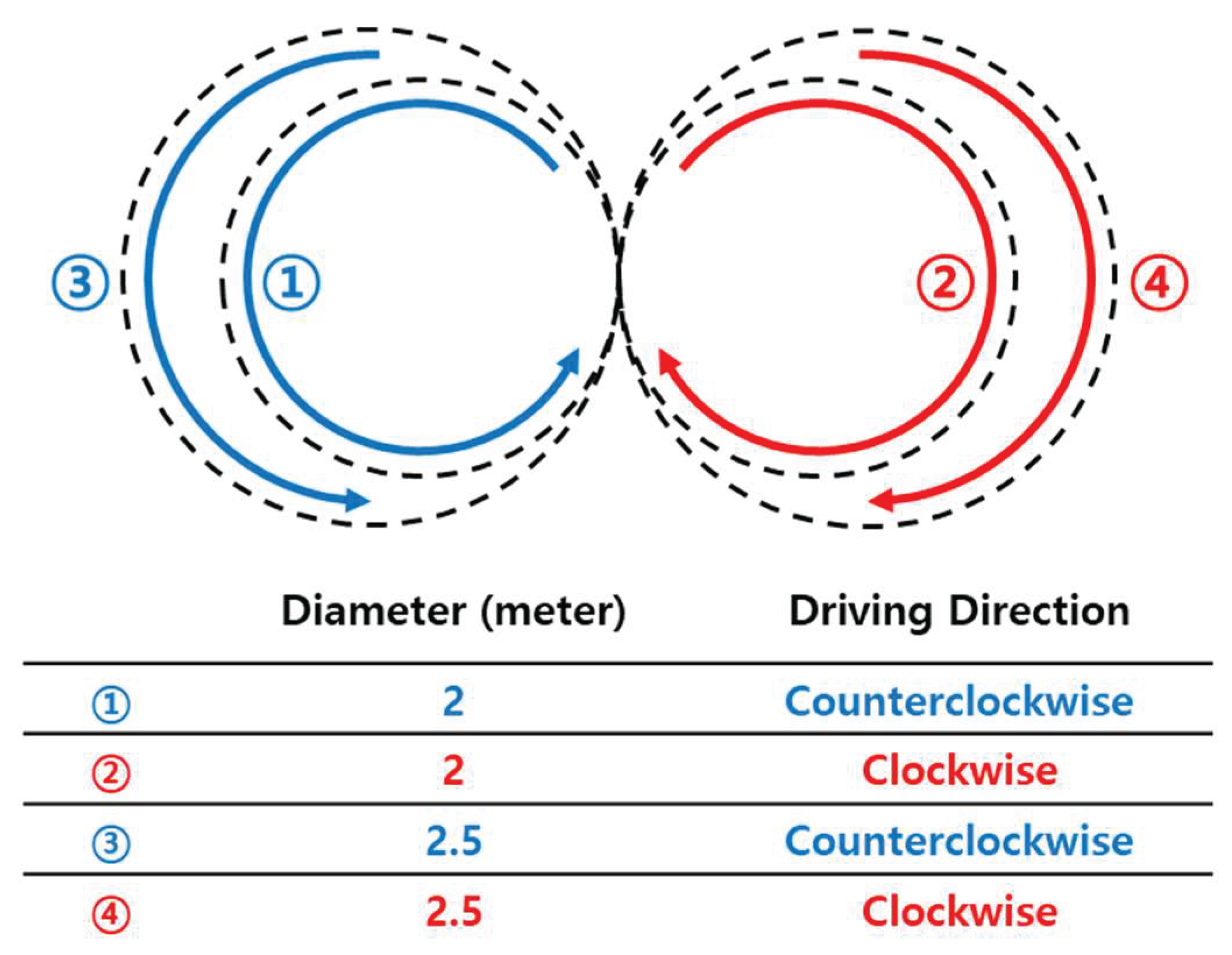
4.1. Test Scenario
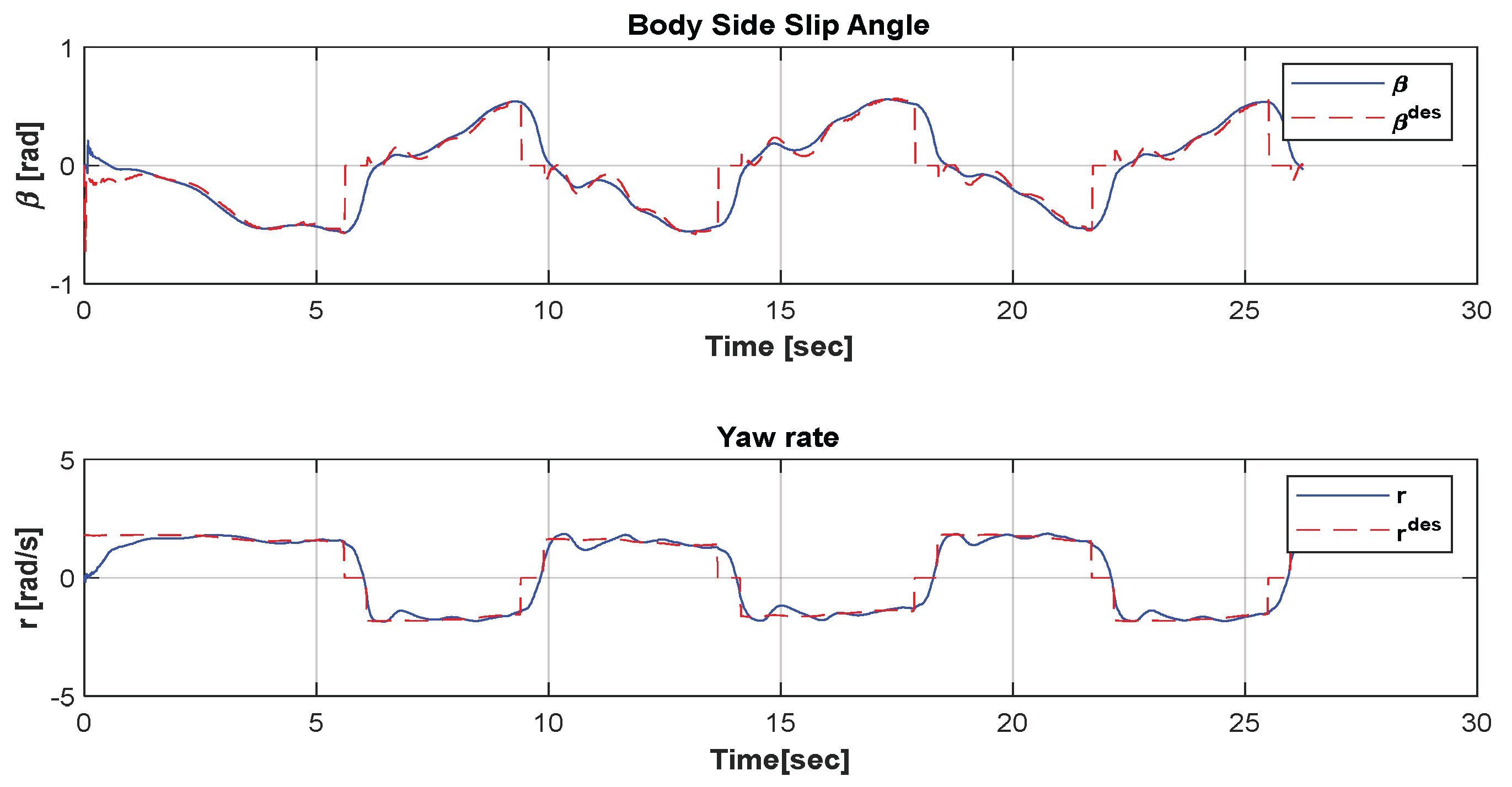
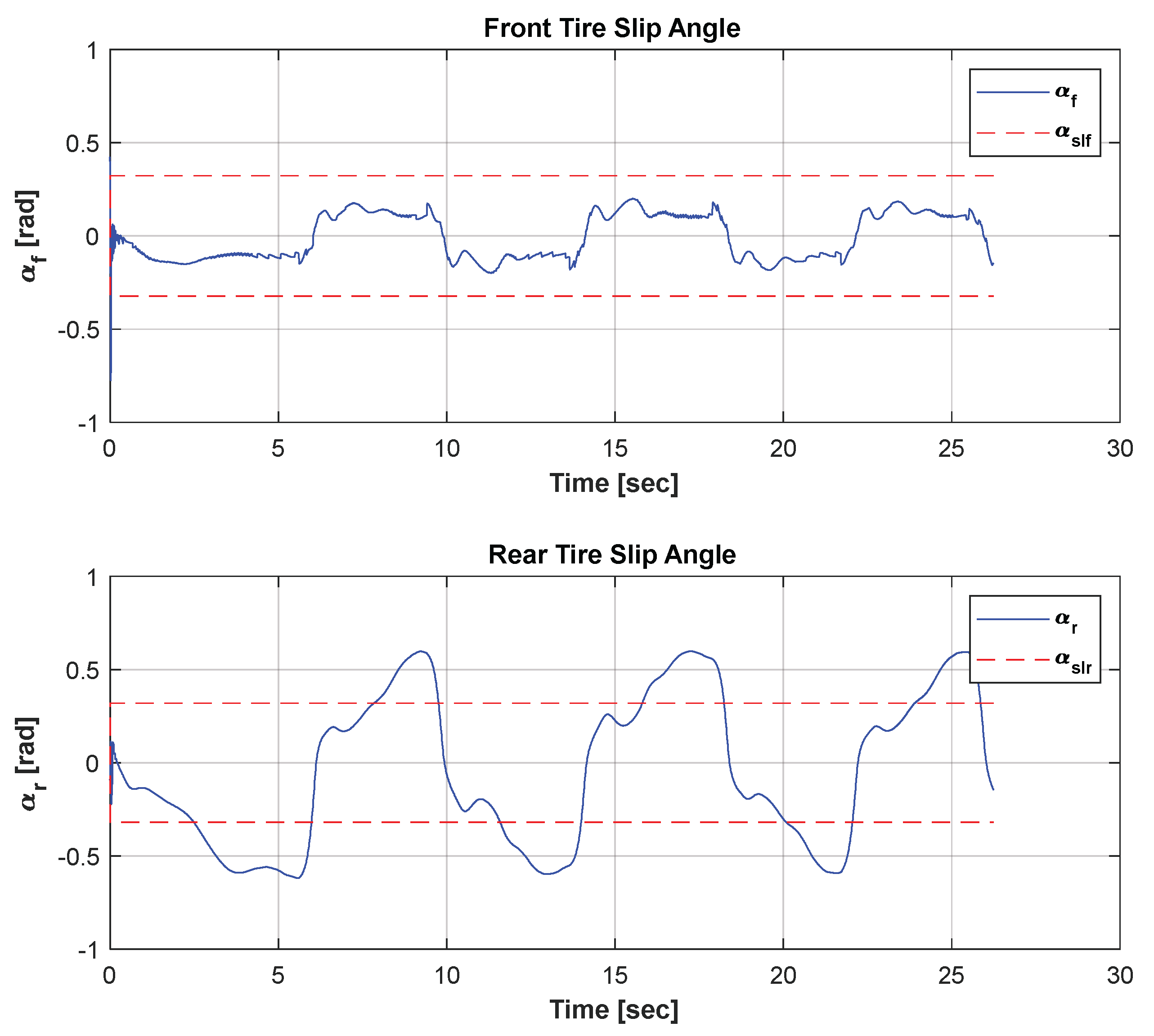
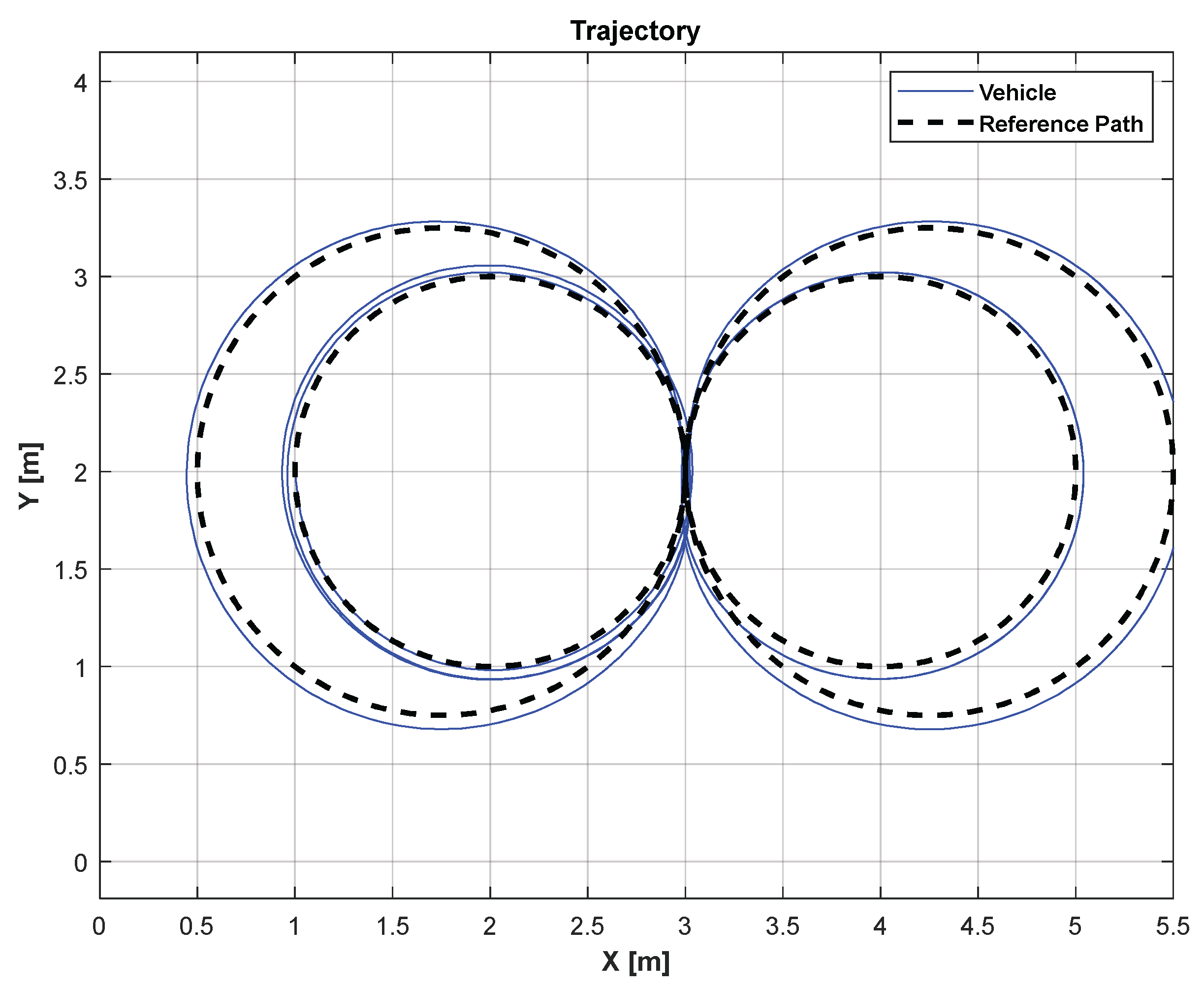
4.2. Drift Test Results
5. Design of the Neural Network Drift Controller
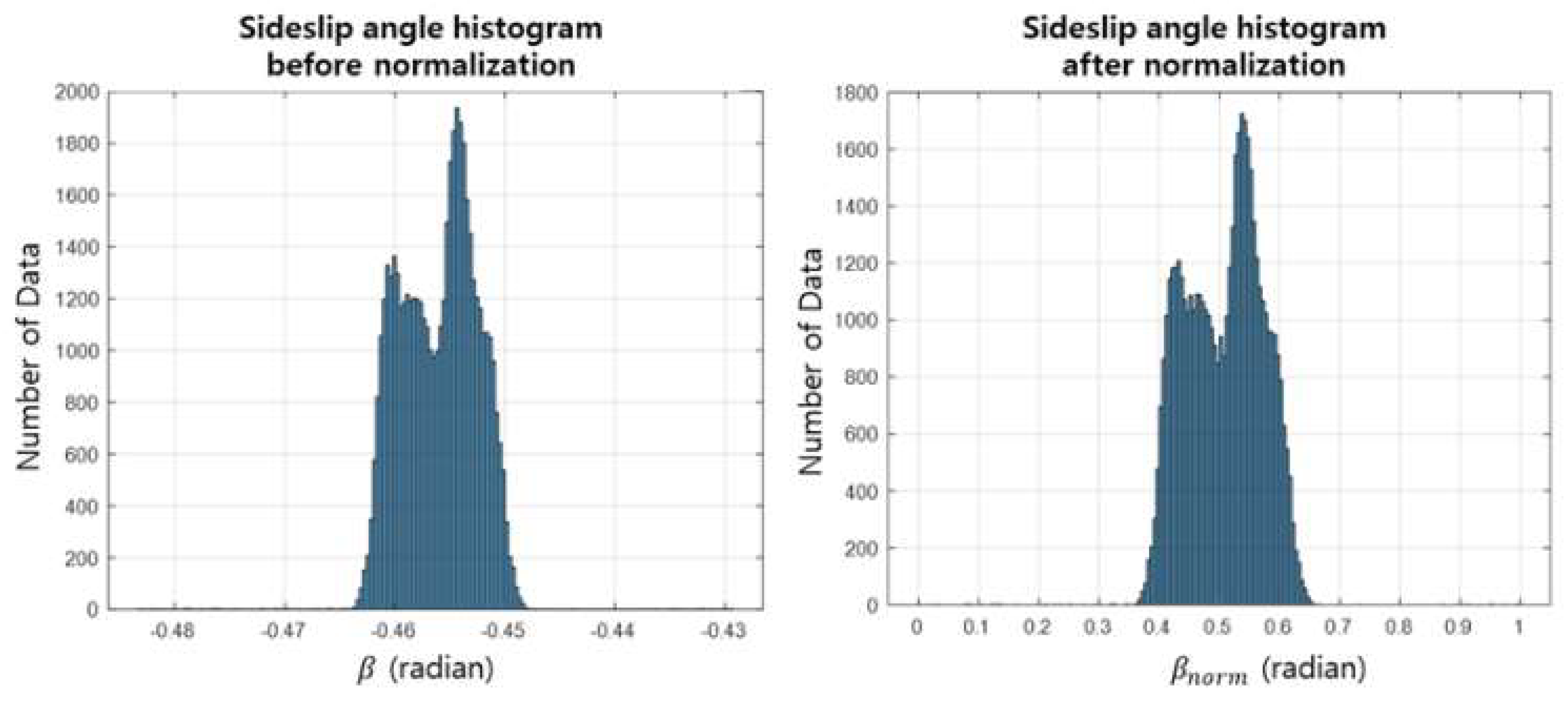
5.1. Training Data Preprocess
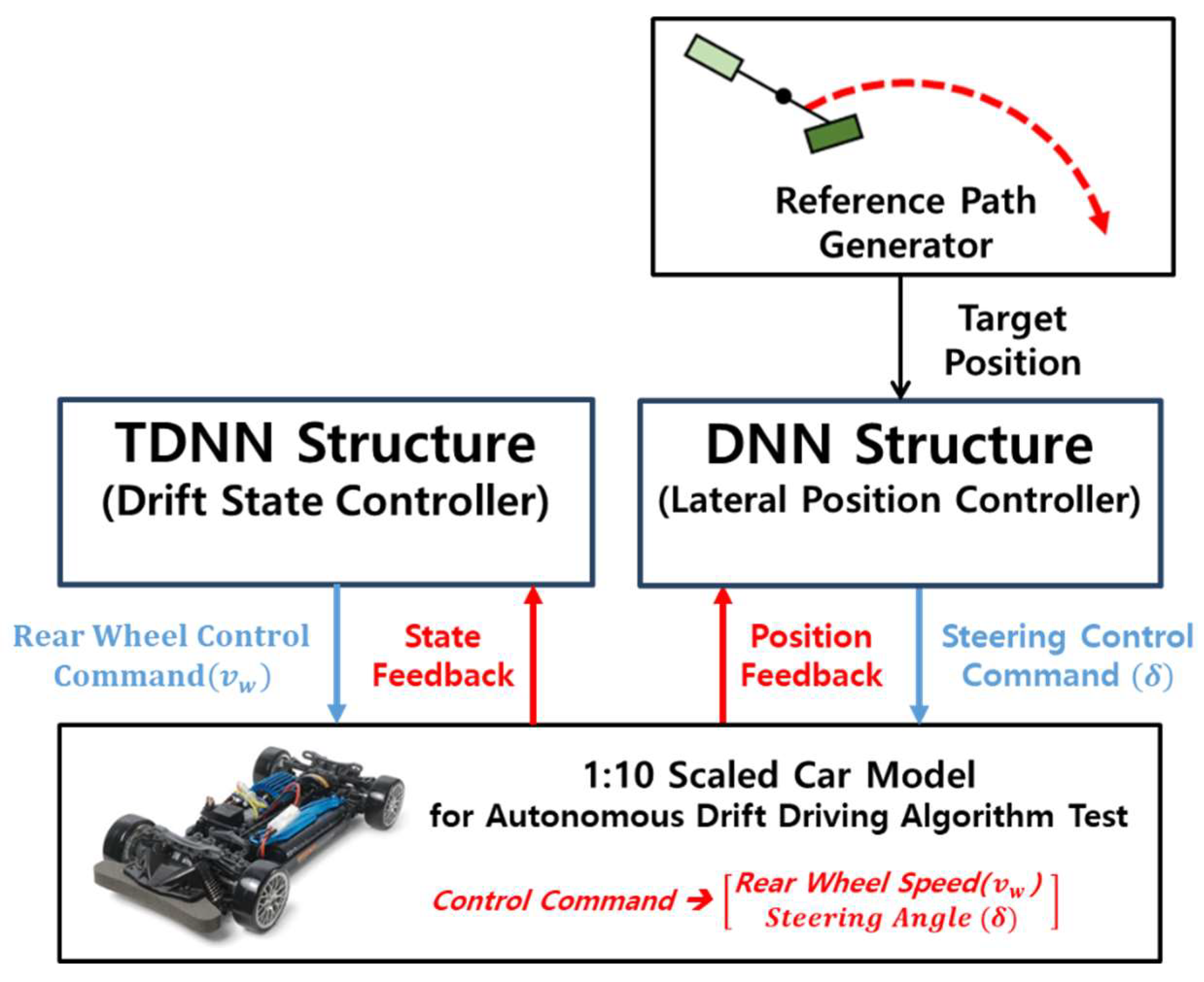
5.2. Neural-Network-Based Controller Architecture
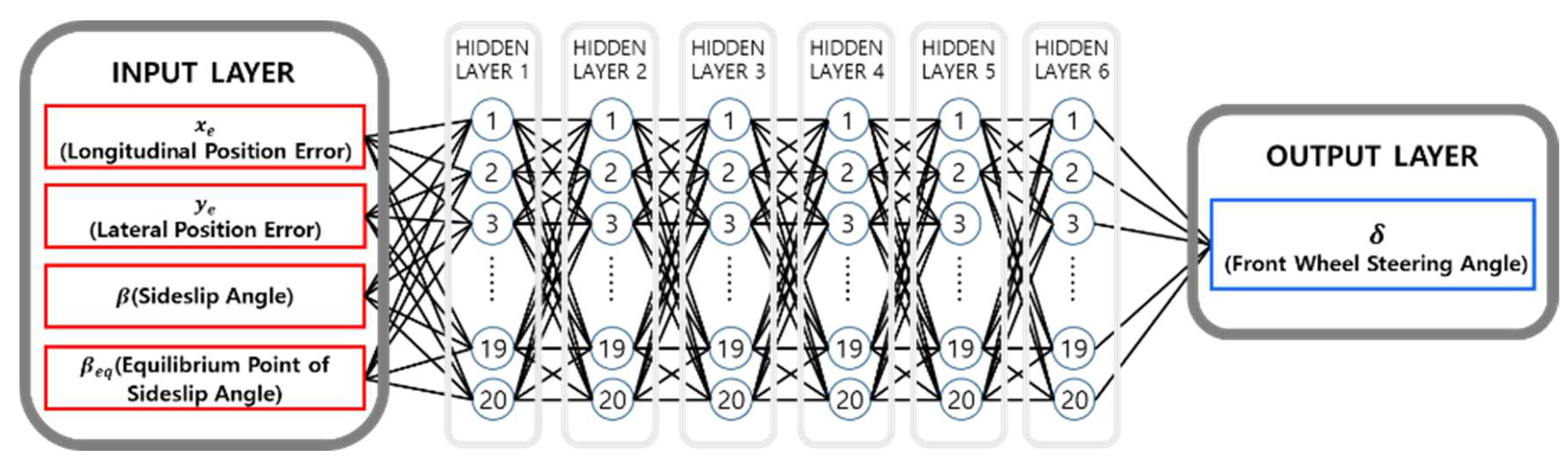
5.2.1. Deep Neural-Network-Based Controller for Steering Control
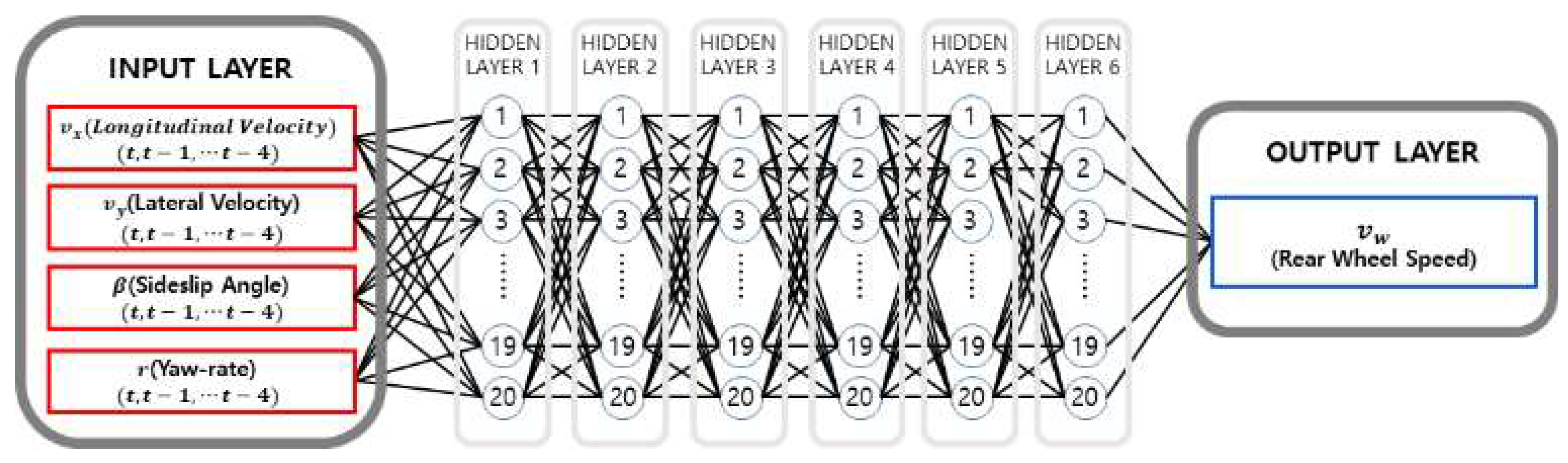
5.2.2. Time Delay Neural-Network-Based Controller for Drift State Control
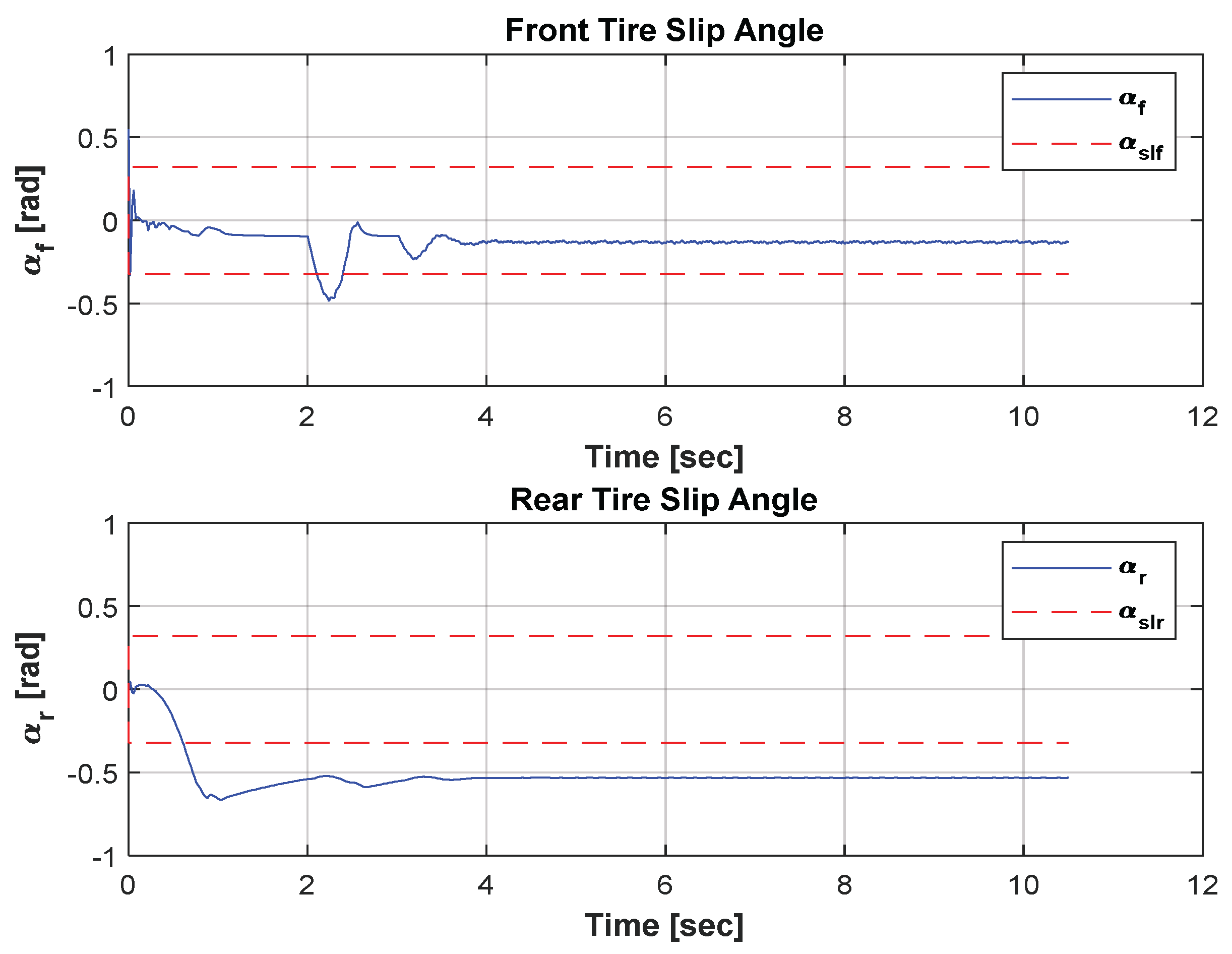
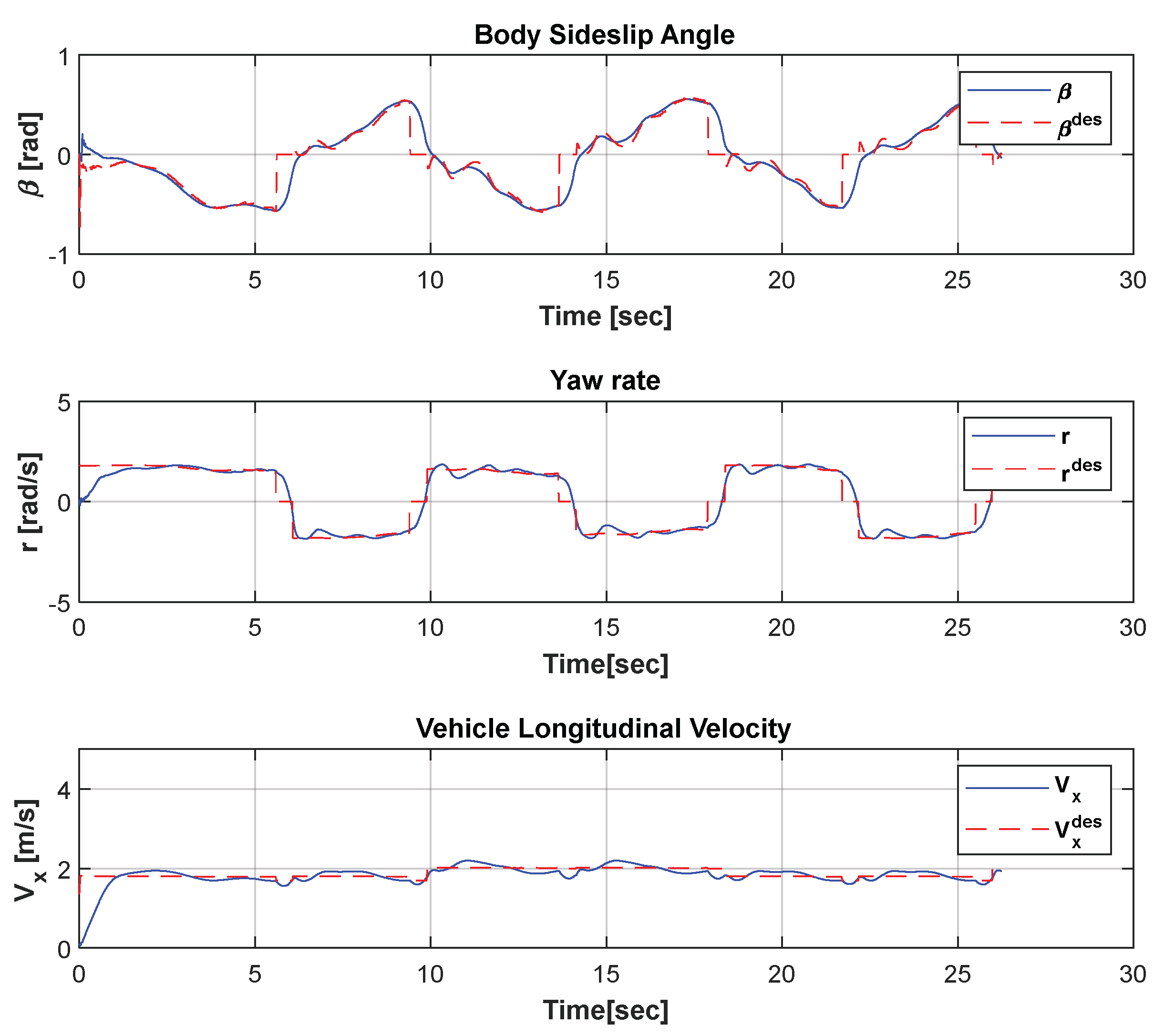
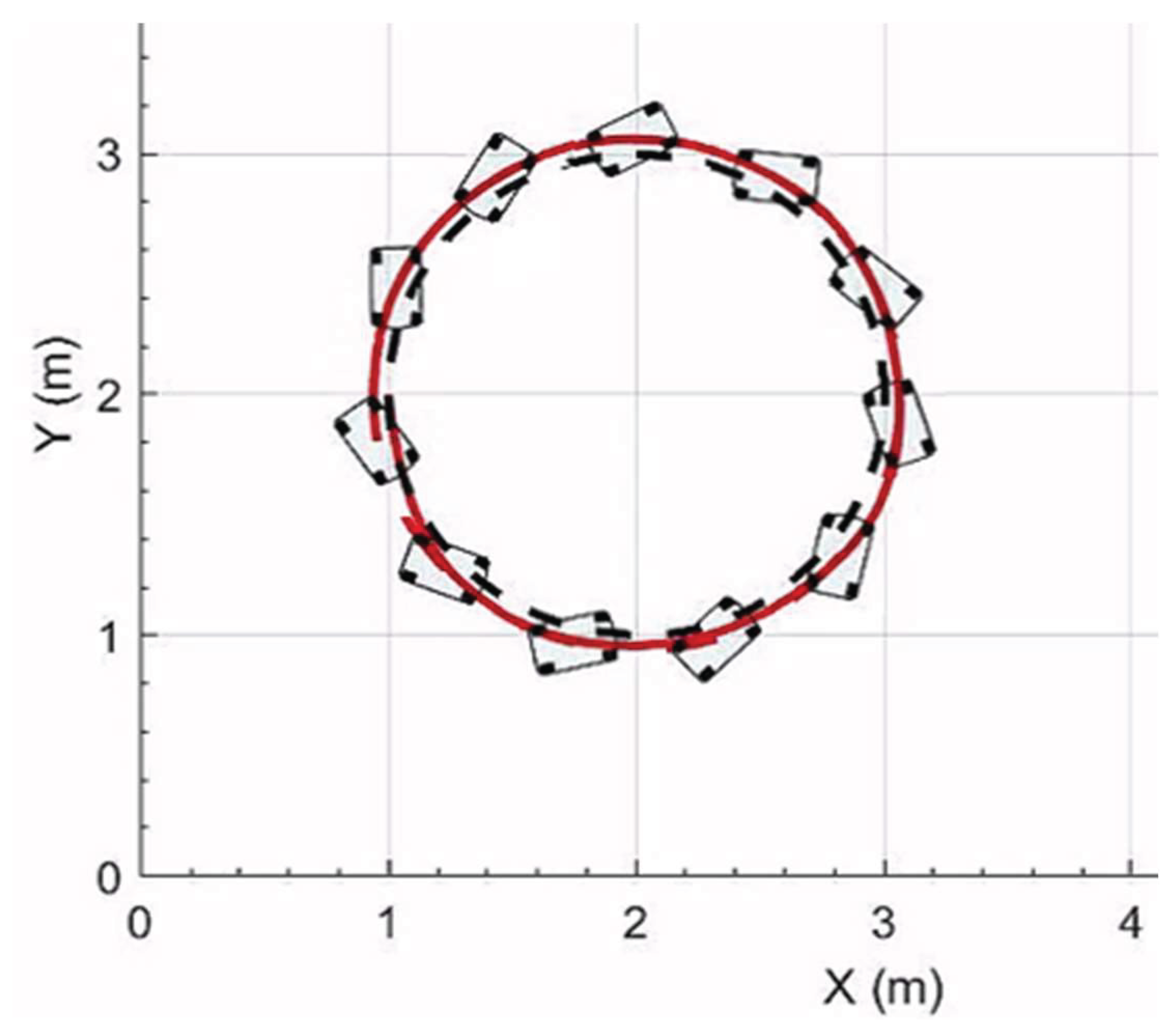
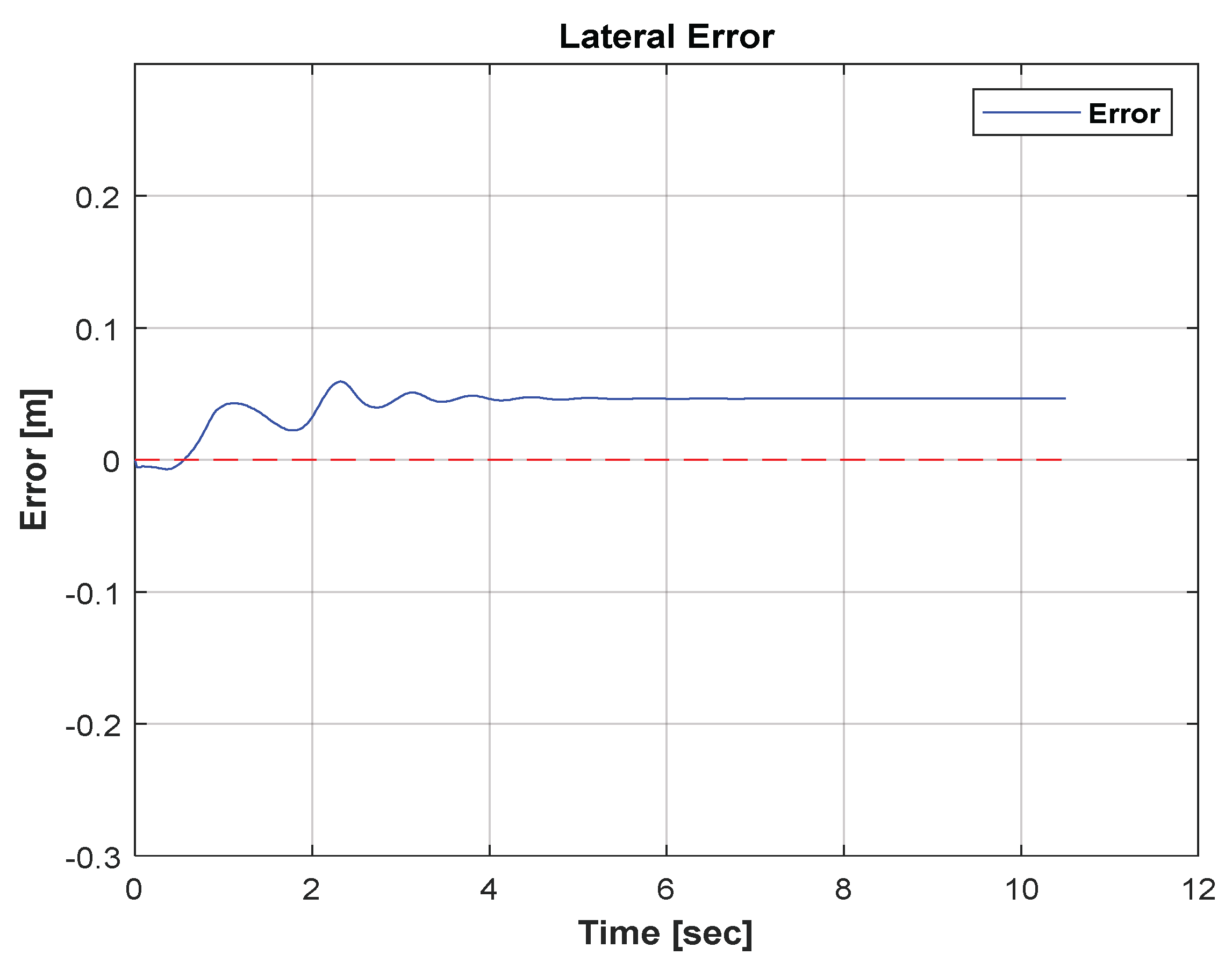
6. Simulation Results of the Neural Network Drift Controller
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, F.; Gonzales, J.; Li, S.E.; Borelli, F.; Li, K. Drift Control for Cornering Maneuver of Autonomous Vehicle. Mechatronics 2018, 54, 164–174. [Google Scholar] [CrossRef]
- Hindiyeh, R.Y. Dynamics and Control of Drifting in Automobiles. Ph.D. Thesis, Department of Mechanical Engineering, Stanford University, Stanford, CA, USA, 2013. [Google Scholar]
- Goh, J.Y.; Goel, T.; Gerdes, J.C. Towards Automated Vehicle Control Beyond the Stability Limits: Drifting Along a General Path. J. Dyn. Syst. Meas. Control 2020, 142, 02004. [Google Scholar] [CrossRef]
- Park, M.; Kang, Y. Experimental Verification of a Drift Controller for Autonomous Vehicle Tracking: A Circular Trajectory Using LQR Method. Int. J. Control Autom. Syst. 2021, 19, 404–416. [Google Scholar] [CrossRef]
- Kim, M.; Lee, T.; Kang, Y. Experimental Verification of the Power Slide Driving Technique for Control Strategy of Autonomous Race Cars. Int. J. Precis. Eng. Manuf. 2020, 21, 377–386. [Google Scholar] [CrossRef]
- Cai, P.; Mei, X.; Tai, L.; Sun, Y.; Liu, M. High-Speed Autonomous Drifting with Deep Reinforcement Learning. IEEE Robot. Autom. Lett. 2020, 5, 1247–1254. [Google Scholar] [CrossRef]
- Guo, H.; Tan, Z.; Liu, J.; Chen, H. MPC-based Steady-state Drift Control under Extreme Condition. In Proceedings of the 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 4708–4721. [Google Scholar]
- Xu, D.; Han, Y.; Ge, C.; Qu, L.; Zhang, R.; Wang, G. A Model Predictive Control Method for Vehicle Drifting Motions with Measurable Errors. World Electr. Veh. J. 2022, 13, 54. [Google Scholar] [CrossRef]
- Hristozov, A. The Role of Artificial Intelligence in Autonomous Vehicles. Available online: https://www.embedded.com/the-role-of-artificial-intelligence-in-autonomous-vehicles/ (accessed on 15 July 2020).
- Hristozov, A. Artificial Intelligence Algorithms and Challenges for Autonomous Vehicles. Available online: https://www.embedded.com/artificial-intelligence-algorithms-and-challenges-for-autonomous-vehicles/ (accessed on 3 August 2020).
- Huang, M.; Gao, W.; Wang, Y.; Jiang, Z. Data-Driven Shared Steering Control of Semi-Autonomous Vehicles. IEEE Trans. Hum.-Mach. Syst. 2019, 49, 350–361. [Google Scholar] [CrossRef]
- Zribi, A.; Chtourou, M.; Djemel, M. A New PID Neural Network Controller Design for Nonlinear Processes. J. Circuits Syst. Comput. 2018, 27, 1850065. [Google Scholar] [CrossRef]
- Chertovskikh, P.; Seredkin, A.; Godyzov, O.; Styuf, A.; Pashkevich, M.; Tokarev, M. An Adaptive PID Controller with an Online Auto-tuning by a Pretrained Neural Network. J. Phys. Conf. Ser. 2019, 1359, 15–22. [Google Scholar] [CrossRef]
- Yaadav, A.; Gaur, P. AI-based Adaptive Control and Design of Autopilot System for Nonlinear UAV. Indian Acad. Sci. 2014, 39, 765–783. [Google Scholar] [CrossRef]
- Jhang, X.; Bujarbaruah, M.; Borrelli, F. Safe and Near-Optimal Policy Learning for Model Predictive Control Using Primal-Dual Neural Networks. In Proceedings of the IEEE American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 354–359. [Google Scholar]
- Rankovic, V.; Radulovic, J.; Grufovic, N.; Divac, D. Neural Network Model Predictive Control of Nonlinear Systems Using Genetic Algorithms. Int. J. Comput. Commun. Control 2012, 7, 540–549. [Google Scholar] [CrossRef]
- Shi, T.; Wang, P.; Chan, C.; Zou, C. A Data Driven Method of Optimizing Feedforward Compensator for Autonomous Vehicle. IEEE Intell. Veh. Symp. 2019, 1901, 2012–2017. [Google Scholar]
- Vasikaninová, A.; Bakošová, M. Neural Network Predictive Control of a Chemical Reactor. Acta Chim. Slovaca 2009, 2, 21–36. [Google Scholar]
- Zhang, Z.; Wu, Z.; Rincon, D.; Christofides, P. Real-Time Optimization and Control of Nonlinear Processes Using Machine Learning. Mathematics 2019, 7, 890. [Google Scholar] [CrossRef]
- Wong, W.; Chee, E.; Li, J.; Wang, X. Recurrent Neural Network-Based Model Predictive Control for Continuous Pharmaceutical Manufacturing. Mathematics 2018, 6, 242. [Google Scholar] [CrossRef]
- Ramdane, H. Adaptive Neural Network Model Predictive Control. Int. J. Innov. Comput. Inf. Control 2013, 9, 1245–1257. [Google Scholar]
- Limon, D.; Calliess, J.; Maciejowski, J.M. Learning-based Nonlinear Model Predictive Control. IFAC-PapersOnLine 2017, 50, 7769–7776. [Google Scholar] [CrossRef]
- Afram, A.; Sharifi, F.J.; Fung, A.S.; Raahemifar, K. Artificial Neural Network (ANN) Based Model Predictive Control (MPC) and Optimization of HVAC systems: A state of the Art Review and Case Study of a Residential HVAC System. Energy Build. 2017, 141, 96–113. [Google Scholar] [CrossRef]
- Gonzalez, L.P.; Sanchez, S.S.; Guzuman, J.G.; Boada, M.J.L.; Boada, B.L. Simultaneous Estimation of Vehicle Roll and Sideslip Angles through a Deep Learning Approach. Sensors 2020, 20, 3679. [Google Scholar] [CrossRef]
- Mohamed, I.; Rovetta, S.; Do, T.; Dragicević, T.; Diab, A. A Neural Network Based Model Predictive Control of Three-Phase Inverter with an Output LC Filter. IEEE Access 2019, 7, 124737–124749. [Google Scholar] [CrossRef]
- Peng, H.; Song, N.; Li, F.; Tang, S. A Mechanistic-Based Data-Driven Approach for General Friction Modeling in Complex Mechanical System. ASME J. Appl. Mech. 2022, 89, 071005. [Google Scholar] [CrossRef]
- Peng, H.; Song, N.; Kan, Z. Data-Driven Model Order Reduction with Proper Symplectic Decomposition for Flexible Multibody System. Nonlinear Dyn. 2022, 107, 173–203. [Google Scholar] [CrossRef]
- Kang, B.; Lucia, S. Learning-based Approximation of Robust Nonlinear Predictive Control with State Estimation Applied to a Towing Kite. In Proceedings of the 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 16–22. [Google Scholar]
- Lee, T.; Kang, Y. Performance Analysis of Deep Neural Network Controller for Autonomous Driving Learning from a Nonlinear Model Predictive Control Method. Electronics 2021, 10, 767. [Google Scholar] [CrossRef]
- Winkler, D.A.; Le, T.C. Performance of Deep and Shallow Neural Networks, the Universal Approximation Theorem, Activity Cliffs, and QSAR. Mol. Inform. 2017, 36, 1–2. [Google Scholar]
- Lucia, S.; Karg, B. A Deep Learning-based Approach to Robust Nonlinear Model Predictive Control. IFAC-PapersOnLine 2018, 51, 511–516. [Google Scholar] [CrossRef]
| Symbol | Meaning | Unit |
|---|---|---|
| Front tire lateral force | N | |
| Rear tire lateral force | N | |
| Vehicle velocity | m/s | |
| Rear-wheel velocity | m/s | |
| Longitudinal velocity | m/s | |
| Tire slip angle | rad | |
| Front tire slip angle | rad | |
| Rear tire slip angle | rad | |
| Friction coefficient | - | |
| Friction coefficient of tire skids | - | |
| Yaw rate | rad/s | |
| Steering angle | rad | |
| Sideslip angle | rad | |
| Vehicle mass | kg | |
| Distance from the center of gravity (CG) to the front axle | M | |
| Distance from CG to the rear axle | M | |
| Yaw moment of inertia | N·m/rad2 | |
| Rear tire longitudinal slip angle | - | |
| Tire slip ratio | - |
| Mean and Standard Deviation | Normalization Variables | ||||
|---|---|---|---|---|---|
| Min | Max | ||||
| Input Data | * | −0.0307 | 0.1819 | −0.2697 | 0.2674 |
| † | 0.0080 | 0.2070 | −0.2688 | 0.2695 | |
| −0.4278 | 0.1314 | −0.5625 | −0.3534 | ||
| o | −0.4969 | 0.1213 | −0.6379 | −0.2630 | |
| Output Data | −0.1742 | 0.1216 | −0.3876 | 0.0651 | |
| Mean and Standard Deviation | Normalization Variables | ||||
|---|---|---|---|---|---|
| Min | Max | ||||
| Input Data | −0.0307 | 0.1819 | −0.2697 | 0.2674 | |
| 0.0080 | 0.2070 | −0.2688 | 0.2695 | ||
| −0.4278 | 0.1314 | −0.5625 | −0.3534 | ||
| −0.4969 | 0.1213 | 0.6379 | 0.2630 | ||
| Output Data | * | −0.1742 | 0.1216 | −0.3876 | 0.0651 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, T.; Seo, D.; Lee, J.; Kang, Y. Real-Time Drift-Driving Control for an Autonomous Vehicle: Learning from Nonlinear Model Predictive Control via a Deep Neural Network. Electronics 2022, 11, 2651. https://doi.org/10.3390/electronics11172651
Lee T, Seo D, Lee J, Kang Y. Real-Time Drift-Driving Control for an Autonomous Vehicle: Learning from Nonlinear Model Predictive Control via a Deep Neural Network. Electronics. 2022; 11(17):2651. https://doi.org/10.3390/electronics11172651
Chicago/Turabian StyleLee, Taekgyu, Dongyoon Seo, Jinyoung Lee, and Yeonsik Kang. 2022. "Real-Time Drift-Driving Control for an Autonomous Vehicle: Learning from Nonlinear Model Predictive Control via a Deep Neural Network" Electronics 11, no. 17: 2651. https://doi.org/10.3390/electronics11172651
APA StyleLee, T., Seo, D., Lee, J., & Kang, Y. (2022). Real-Time Drift-Driving Control for an Autonomous Vehicle: Learning from Nonlinear Model Predictive Control via a Deep Neural Network. Electronics, 11(17), 2651. https://doi.org/10.3390/electronics11172651






