Abstract
Least squares regression (LSR) is an effective method that has been widely used for subspace clustering. Under the conditions of independent subspaces and noise-free data, coefficient matrices can satisfy enforced block diagonal (EBD) structures and achieve good clustering results. More importantly, LSR produces closed solutions that are easier to solve. However, solutions with block diagonal properties that have been solved using LSR are sensitive to noise or corruption as they are fragile and easily destroyed. Moreover, when using actual datasets, these structures cannot always guarantee satisfactory clustering results. Considering that block diagonal representation has excellent clustering performance, the idea of block diagonal constraints has been introduced into LSR and a new subspace clustering method, which is named block diagonal least squares regression (BDLSR), has been proposed. By using a block diagonal regularizer, BDLSR can effectively reinforce the fragile block diagonal structures of the obtained matrices and improve the clustering performance. Our experiments using several real datasets illustrated that BDLSR produced a higher clustering performance compared to other algorithms.
1. Introduction
High-dimensional data are increasingly common in everyday life, which has greatly affected the methods that are used for data analysis and processing. Performing clustering analyses on high-dimensional data has become one of the hot spots in current research. It is usually assumed that high-dimensional data are distributed within a joint subspace, which is composed of multiple low-dimensional subspaces. This supposition has become the premise of the study of subspace clustering [1].
Over the last several decades, researchers have proposed many useful approaches for solving clustering problems [2,3,4,5,6,7]. Among these methods, spectral-type subspace clustering has become the most popular for use in subspace algorithms because of its outstanding clustering effects when processing high-dimensional data. The spectral-type method mainly utilizes local or global information from data samples to construct affinity matrices. In general, the representation matrices greatly affect the performance of spectral-type subspace clustering. In recent years, a vast number of different methods have been proposed in the attempt to find better representation matrices. Two typical representative methods in linear spectral-type clustering are sparse subspace clustering (SSC) [2,8] and low-rank representation (LRR) [3,9], which are based on linear representation. They emphasize sparseness and low rank when solving coefficient matrices.
Initially, SSC used the L0 norm to represent the sparsity of the matrices. When considering that the optimization of the L0 norm is NP-hard, the L0 norm was finally replaced by the L1 norm. SSC pursues the sparse representation by minimizing the L1 norm of coefficient matrices, which can better classify data. However, the obtained matrices are too sparse and miss the important correlation structures of the data. Thus, SSC leads to unsatisfactory clustering results for highly correlated data. To make up for the shortcomings of SSC, LRR employs the nuclear norm to search for low-rank representations with the goal of better analyzing the relevant data. By describing global structures, LRR improves the clustering performance of highly correlated data. However, the coefficient matrices that are obtained using the LRR model may not be sparse enough. To this end, many improved methods have been proposed.
Luo et al. [10] made use of the prior of sparsity and low rank and then presented a multi-subspace representation (MSR) model. Zhuang et al. [11] improved the MSR model by adding non-negative constraints to the coefficient matrices and then proposed a non-negative low-rank sparse representation (NNLRS) model. Both the MSR and NNLRS models ensure that coefficient matrices have both sparsity and grouping effects by using a combination of sparsity and low rank. To explore local and global structures, Zheng et al. [12] incorporated local constraints into LRR and presented a locally constrained low-rank representation (LRR-LC) model. Chen et al. [13] developed another new model by adding symmetric constraints to the LRR so that highly correlated data in the subspaces had consistent representation. To better reveal the essential structures of subspaces, Lu et al. [14] utilized the F norm to constrain the coefficient matrices and proposed the use of least squares regression (LSR) for subspace clustering. This method demonstrated that enforced block diagonal (EBD) conditions were helpful for block diagonalization, i.e., under EBD conditions, the structures of the obtained coefficient matrices are block diagonal. In the meantime, LSR encouraged the grouping effect by clustering highly correlated data together. It has been theoretically proven that LSR tends to shrink the coefficients of related data and is robust to noise. More importantly, the objective function of LSR produces closed solutions, which are easy to solve and reduce the time complexity of the algorithm. Generally, under the independent subspace assumption, the models that use the L1 norm, nuclear norm or F norm as regularization terms can satisfy EBD conditions. This can help them to learn affinity matrices with block diagonal properties.
Assuming that the data samples are not contaminated or damaged and that the subspaces are independent of each other, the above methods can obtain coefficient matrices with block diagonal structures. However, the structures that are obtained using these methods are unstable because the required assumptions are often not established. When a fragile block diagonal structure is broken, it causes the clustering performance to decline to a great extent. For this reason, many subspace algorithms have been proposed that extend the idea of block diagonal structures. Zhang et al. [15] introduced an effective structure into LRR and proposed a recognition method to distinguish block diagonal low-rank representation (BDLRR), which learned distinguished data representations while shrinking non-block diagonal parts and highlighting block diagonal representations to improve the clustering effects. Feng et al. [16] devised two new subspace clustering methods, which were based on a graph Laplace constraint. Using the above methods, block diagonal coefficient matrices can be precisely constructed. However, their optimization processes are inefficient because each updating cycle contains an iterative projection. Hence, the hard constraints of the coefficient matrices are difficult to satisfy precisely. To settle this matter, Lu et al. [17] used block diagonal regularization to add constraints into the solutions and then put forward a block diagonal representation (BDR) model. These constraints, which were more flexible than direct hard constraints, could help the BDR model to easily obtain solutions with block diagonal properties. Therefore, the regularization was called a soft constraint. This block diagonal regularization caused BDR to be non-convex, but it could be solved via simple and valid means. This model imposed block diagonal structures on the coefficient matrices, which was more likely to lead to accurate clustering results. Due to the good performance of the k-diagonal block within subspace clustering, numerous corresponding extended algorithms [18,19,20] have been proposed.
Under the conditions of independent subspaces and noise-free data, LSR can obtain coefficient matrices that have block diagonal properties, which usually produce exact clustering results. However, the coefficient matrices that are obtained using the LSR method are sensitive to noise or corruption. In real environments, data samples are often contaminated by noise. In this case, the fragile block diagonal structures can become damaged. When the block diagonal structures are violated, the LSR method does not necessarily lead to satisfactory clustering results.
Inspired by the BDR method, we constructed a novel block diagonal least squares regression (BDLSR) subspace clustering method by combining LSR and BDR. Considering that the LSR method meets EBD conditions and has a grouping effect, we directly pursued block diagonal matrices on the basis of LSR. The block diagonal regularizer was a soft constraint that encouraged the block diagonalization of the coefficient matrices and could improve the accuracy of the clustering. However, the appearance of the block diagonal regularizer resulted in the non-convexity of BDLSR. Fortunately, the alternating minimization method could be used to solve the objective function. Meanwhile, the convergence of the objective function could also be proven. Our experimental results from using several public datasets indicated that BDLSR was more effective.
The rest of the paper is organized as follows. The least squares regression model and the block diagonal regularizer are briefly reviewed in Section 2. The BDLSR model is proposed, optimized and discussed explicitly in Section 3. In Section 4, the experimental effectiveness of BDLSR is demonstrated using three datasets. Finally, the conclusions are summarized.
2. Notations and Preliminaries
2.1. Notations
Many notations were used in this study, which are shown in Table 1.

Table 1.
The notations that were used in this study.
2.2. Least Squares Regression
In real data, most data have strong correlations. However, SSC enforces solutions to be sparse and LRR causes the solutions to have low-rank representation; therefore, these methods still cannot obtain the intrinsic structures of the data very well. To better explore these correlations, Lu et al. [14] obtained coefficient matrices using the F norm constraint and proposed a least squares regression (LSR) subspace algorithm. LSR has a grouping effect, which makes it helpful for the better clustering of highly correlated data.
In a given data matrix Y, the data samples are from multiple independent linear subspaces. To determine the clustering number of the subspaces, the data samples need to be divided into their respective subspaces. Ideally, the data are clean. By solving the following optimization problems, LSR can solve the coefficient matrix Z:
where, denotes the F norm of Z, which is defined as . Note that the constraint in the above model can help to avoid trivial solutions. In other words, each data sample is only represented by itself and then the case of Z being the identity matrix can be avoided.
When the data contain noise, a noise term is added to enhance the robustness of the model. The extended function of LSR is shown below:
where is a regularization parameter, which is used to balance the two terms within the above objective function. Note that LSR produces analytical solutions, which are easy to solve. Due to these advantages, LSR has attracted the attention of a growing number of researchers.
2.3. The Block Diagonal Regularizer
Existing studies [2,3,14] have shown that block diagonal structures can better reveal the essential attributes of subspaces. Ideally, under the assumption of independent subspaces and noise-free data, the obtained coefficient matrix Z has a k-block diagonal structure, where k represents the number of blocks or subspaces. Then, Z can be expressed as follows:
Here, each block represents a subspace, the size of blocks represents the dimensions of the subspaces and the data within the same block belong to the same subspace.
However, due to noise in the data, the assumption of independent subspaces is usually incorrect. Hence, the solutions of the model are always far from the k-block diagonal structure. To obtain the above structure, a block diagonal regularizer was proposed in [17]:
where satisfies the constraints of and and is an affinity matrix, denotes the k-block diagonal regularizer (which is defined as the sum of the smallest k eigenvalues of ) and denotes the corresponding Laplacian matrix (which is defined as , where B1 represents the product of matrix B and vector 1). Here, denotes the i-th eigenvalue of when arranged in decreasing order. Due to , is positive semidefinite and for all values of i. More precisely, B has a k-block diagonal when (and only when):
The term in Equation (2) is a soft constraint, which does not directly require exact solutions with block diagonal structures. However, the number of blocks can be controlled and correct clustering results can still be obtained. Hence, the regularizer is more flexible and produces accurate clustering results more easily than hard constraints [16].
3. Subspace Clustering Using BDLSR
In this section, our BDLSR method, which is a combination of least squares regression and block diagonal representation, is proposed for subspace clustering. Then, the objective function of the BDLSR model is presented and the optimization process is described. Finally, the convergence of the BDLSR model is proven.
3.1. The Proposed Model
In theory, under the independent subspace assumption, LSR can obtain coefficient matrices that have block diagonal attributes. In other words, when the similarity between classes is zero and the similarity within classes is more than zero, perfect data clustering can usually be achieved. However, in real environments, the block diagonal structures of the solutions can be easily broken by data noise or corruptions. Considering the advantages of block diagonal representation, we integrated it into the objective function of LSR to obtain solutions with strengthened block diagonal structures, which required the matrices to be simultaneously non-negative and symmetric. Then, we proposed the BDLSR method for subspace clustering. The objective function of BDLSR for handling noisy data was as follows (where and Y is a data matrix):
where the coefficient matrix B is non-negative and symmetric and its diagonal elements are all zero. The above conditions had to be satisfied to use a block diagonal regularizer. However, the conditions limited the representation capability of B. To alleviate this issue, we needed to relax the restrictions on B. Thus, we introduced an intermediary term Z into the above formula. The new model was rewritten equivalently as follows (where ):
where and are the balance parameters. When was sufficiently large, Equation (4) was equivalent to Equation (3). The new added item was strongly convex for updating Z and B; thus, it was easy to solve closed-form solutions and perform convergence analyses. Then, we could alternatively optimize the variables Z, V and B.
3.2. The Optimization of BDLSR
Next, we solved the minimization problem of the BDLSR model in Equation (4). Because of the block diagonal regularizer, it was observed that Equation (4) was non-convex. The key to solving this issue was the non-convex term . Fortunately, we could utilize the related theorem in [17,21] to reformulate . The theorem in [17] was presented as follows.
We let . Then:
where .
Then, could be reformulated as a convex problem:
Due to being defined as , Equation (4) was equivalent to the following problem:
The above problem involved three variables, which could be obtained by alternating the minimization. Then, we decomposed the problem into three subproblems and developed the update steps separately.
By fixing the variables B and V, we could update Z using:
Note that Equation (6) was a convex program. By setting the partial derivative of Z to 0, we could obtain its closed-form solution. The solution was:
Similarly, by fixing the variables B and Z, we could update V using:
According to Equation (8), we could obtain the solution for V as follows:
where consists of k eigenvectors, which are associated with the k smallest eigenvalues of .
Then, we could solve B. By fixing the variables Z and V, we could update B using:
By converting Equation (10), the following function was obtained:
According to the proposition in [17], we could obtain the closed-form solution of B:
where:
The complete optimization procedure for the BDLSR model for subspace clustering is summarized in Algorithm 1.
| Algorithm 1 The optimization process for solving Equation (5). |
| Input: Data matrix Y, , . |
| Initialize:. |
| while not converge do |
| 1: Update by solving (6). |
| 2: Update by solving (8). |
| 3: Update by solving (11). |
| 4: m = m + 1. |
| end while |
| Output:. |
3.3. Discussion
To solve Equation (4), we developed an iterative update algorithm, which is shown in this section. For a given data matrix, we could settle the proposed BDLSR problem by using representation matrices Z and B, which could be obtained using Algorithm 1. Then, we used Z and B to construct the affinity matrices, e.g., or . Finally, we performed spectral-type subspace clustering on the constructed affinity matrices.
We noted that the BDLSR algorithm contained three parameters, which could be utilized to balance the different terms in Equation (4). We could first run BDR for the suitable and values or run LSR for the suitable and values. After that, we could search the last remaining parameter to achieve the highest clustering accuracy.
Note that the number of subspaces had to be known to construct the affinity matrices. Considering this requirement is required for all spectral-type subspace algorithms, the number always had to be known. Our proposed BDLSR algorithm used the block diagonal structure and its clustering effectiveness was shown in the following experiments.
3.4. Convergence Analysis
Because of the block diagonal regularizer, the objective function in Equation (4) was non-convex. Fortunately, Equation (4) could be solved by alternating the minimization and its solution could be proven to converge to the global optimum. The alternating minimization method is summarized in Algorithm 1. Now, we explain the convergence of Algorithm 1 theoretically.
To guarantee the convergence of BDLSR, the sequence that was generated by Algorithm 1 needed to be proven to have at least one limit point. In addition, any limit point of was a stationary point of Equation (5). Now, with regard to Algorithm 1, we detail the convergence analysis by referring to [17].
The objective function of Equation (5) was denoted as , where m represents the m-th iteration. We let and . The indicator functions of and were denoted as and , respectively.
First, according to the update process of in Equation (6), we obtained:
Note that is -strongly convex with regard to Z. We obtain
Then, due to the optimality of in Equation (8), we obtained:
Next, according to the update process of in Equation (11), we obtained:
Note that was strongly -convex with regard to B. We obtained:
By combining and simplifying (13)–(15), we obtained:
Hence, monotonically decreased and was upper bounded. This implied that and were bounded. Additionally, implied that and were bounded.
Since and were positive semidefinite, we obtained . Thus, . Then, by summing Equation (16) over m = 0, 1, 2, …, we obtained:
This implied:
and
Using Equation (18) and the update process of in Equation (8), we obtained:
Then, since , and were bounded, a point and a subsequence existed such that , and . Then, according to Equations (17)–(19), we obtained , and . On the other hand, by considering the optimality of in Equation (8), in Equation (6) and in Equation (10), we obtained:
By letting in Equation (20), we obtained:
Thus, was a stationary point of Equation (5).
4. Experiments
4.1. Experimental Settings
4.1.1. Data
To evaluate the BDLSR model, we performed experiments using different datasets: Hopkins 155 [22], ORL [23] and Extended Yale B [17].
The Hopkins 155 dataset contains 156 different sequences, which were extracted from moving objects. Some samples from the Hopkins 155 dataset are shown in Figure 1.

Figure 1.
Samples from the Hopkins 155 dataset.
The ORL dataset, which was created by Cambridge University, contains 400 facial photos of 40 subjects with a dark uniform background under different conditions for time, light and facial expression. We resized each photo to 32 × 32. Some samples from the ORL dataset are shown in Figure 2.

Figure 2.
Samples from the ORL dataset.
The Extended Yale B dataset is composed of images of 38 individuals and can be used for facial recognition. The dataset contains 2414 images, with 64 photos of each individual under different conditions and angles. We resized each photo to 32 × 32. Some samples from the Extended Yale B dataset are shown in Figure 3.

Figure 3.
Samples from the Extended Yale B dataset.
4.1.2. Baseline
We chose representative subspace clustering algorithms for comparison to verify the effectiveness of BDLSR, including SSC [8], LRR [9], LSR [14] and BDR-B(BDR-Z) [17]. These algorithms are spectral-type algorithms and construct affinity matrices by applying coefficient matrices to achieve the final results.
SSC (sparse subspace clustering) is based on sparse representation, which ensures the sparsity of the coefficient matrices by minimizing the L1 norm. LRR (low-rank representation) is a typical subspace algorithm that searches for low-rank representations of coefficient matrices using the nuclear norm. LSR (least squares regression) is an easy-to-solve clustering subspace algorithm that uses the F norm to constrain coefficients so that there is a grouping effect between the coefficients. BDR (block diagonal representation) is a novel spectral clustering subspace algorithm that uses a block diagonal regularizer, which provides two methods for solving coefficient matrices: BDR-B and BDR-Z.
In this paper, we chose AC and NMI [24] as the evaluation criteria to quantitatively evaluate BDLSR. AC was used to evaluate the accuracy of the clustering and NMI was used to evaluate the correlations between the clustering results and the real results. The larger the AC and NMI values, the better the clustering results.
We supposed that and were the ground truth label and the obtained label of a data sample , respectively, to define AC is as follows (where n is the number of data samples):
where the delta function = 1 when (and only when) a = b.
We supposed that the two clustering results were D and D’ to define NMI as follows:
where and represent the entropy and the mutual information of the clustering results, respectively.
All algorithms were implemented using the MATLAB2016a program on Windows 10.
4.2. Experimental Results
Here, we discuss the clustering effects of BDLSR during our experiments using the Hopkins 155, ORL and Extended Yale B datasets. The comparison algorithms in our experiments were SSC, LRR, LSR and BDR-B (BDR-Z). The code was provided by the original authors to ensure the accuracy of the algorithms. The parameters were adjusted to the optimal values, according to the settings in the original papers.
In our experiments, the specific parameter adjustment process was as follows. We first determined the initial value ranges of the parameters and , according to the parameter settings in the BDR algorithm. Then, we used the parameter values of and that were provided in [17] as the initial values to try for another parameter and determined the value range of this parameter according to the changes in the clustering results. Finally, the grid search method was used for an exhaustive search of the value ranges of the three determined parameters and the values of the parameters were selected when the BDLSR algorithm produced the best performance. In this paper, , and were selected for Hopkins 155, , and were selected for ORL and , and were selected for Extended Yale B.
The Hopkins 155 dataset contains 156 motion sequences, which are classified into groups of two and three motions. In this experiment, we used the mean and median values of AC to evaluate the different algorithms. We adopted two settings to construct data matrices: 2F-dimensional and 4k-dimensional data points. Table 2 and Table 3 show the AC values of each algorithm using the Hopkins 155 dataset. The partial comparative data in Table 1 and Table 2 originated from [17]. In the experiment, we set , , for 2F-dimensional data and , , for 4k-dimensional data. Using the selected parameter settings, BDLSR could perform well in most cases. From Table 2 and Table 3, it can be seen that the AC value of BDLSR was higher than those of the other algorithms under the two different settings, except for the three motions in Table 2. These results showed that BDLSR had some advantages over other representative clustering algorithms when using the Hopkins 155 dataset.

Table 2.
The accuracy (%) when using the Hopkins 155 dataset with 2F-dimensional data.

Table 3.
The accuracy (%) when using the Hopkins 155 dataset with 4k-dimensional data.
The ORL dataset includes 40 subjects, with 10 photos of each. We selected the first k (10, 20, 30, 40) subjects of the dataset for the face clustering experiments. The comparison results from using the ORL dataset are shown in Table 4. We set different parameters for the different numbers of subjects in the experiments. For instance, we set for 40 subjects. From Table 4, it can be seen that BDLSR improved the AC value from 74.75% to 81.00% and the NMI value from 87.53% to 88.68% when using BDLSR-Z. This showed that BDLSR produced the best clustering results out of all of the algorithms for 10, 20, 30 and 40 subjects.

Table 4.
The results from the different algorithms when using the ORL dataset (%).
The Extended Yale B dataset includes 2414 photos of 38 individuals. We selected the first k (3, 5, 8, 10) individuals of the dataset to compare the AC and NMI values of the different algorithms. The comparison results from using the Extended Yale B dataset are shown in Table 5. We set for 10 subjects in these experiments. From Table 5, it can be seen that BDLSR improved the AC value from 93.59% to 94.06% and the NMI value from 89.82% to 90.10% when using BDLSR-B. This showed that BDLSR achieved better results than the other algorithms for 3, 5, 8 and 10 subjects.

Table 5.
The results from the different algorithms when using the Extended Yale B dataset (%).
From the results, it can be seen that the BDR algorithm produced good clustering results. However, the proposed BDLSR algorithm had higher AC and NMI values than the BDR algorithm. This demonstrated that the combination of LSR and BDR could enhance the grouping effect on related data and improve the clustering results.
4.3. Parameter Analysis
The BDLSR algorithm mainly involved three parameters and . Now, we further discuss the effects of the parameter settings on the performance of BDLSR. Considering that BDLSR mainly used block diagonal regularization and least squares regression to improve the clustering effect, we mainly discuss the influence of the parameters and on the AC and NMI values. Then, we present the clustering results that were achieved by fixing and setting different values for and .
Figure 4 displays the AC values when using the Hopkins 155 dataset with different parameter settings. For 2F dimensional data, = 0.09 and . For 4k dimensional data, = 0.07 and . For both settings, . By taking the results of all motions in the Hopkins 155 dataset as the example, we could observe the changes in the AC values that were caused by the BDLSR-B method for 2F-dimensional data and those that were caused by the BDLSR-Z method for 4k-dimensional data. From Figure 4, it can be seen that the AC values fluctuated very little with the changes to α and . When , and , , the clustering effect was the best.
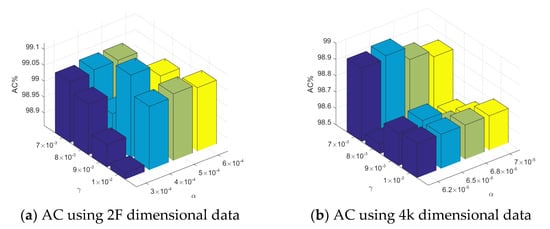
Figure 4.
The AC values when using the Hopkins 155 dataset with 2F- and 4k-dimensional data.
Figure 5 displays the AC and NMI values when using the ORL dataset with different parameter settings. We set = 0.07, and . To observe the changes in the AC and NMI values that were caused by the BDLSR-Z method, we took 40 individuals from the ORL dataset as the example. From Figure 5, it can be seen that the AC values changed significantly and the NMI values changed slightly within a certain value range. When and , BDLSR-Z produced the best clustering effect.
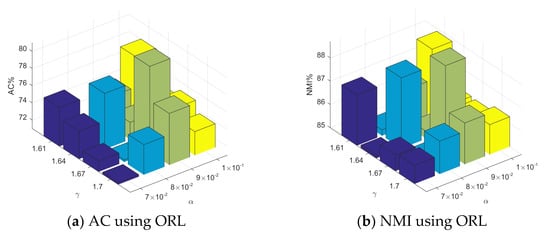
Figure 5.
The AC and NMI values when using the ORL dataset.
Figure 6 displays the AC and NMI values when using the Extended Yale B dataset with different parameter settings, where λ = 50, and . To observe the changes in the AC and NMI values that were caused by the BDLSR-B method, we took 5 individuals from the Extended Yale B dataset as the example. From Figure 6, it can be seen that the AC and NMI values were relatively stable. On the whole, changes in the parameters had little impact on the clustering effect.
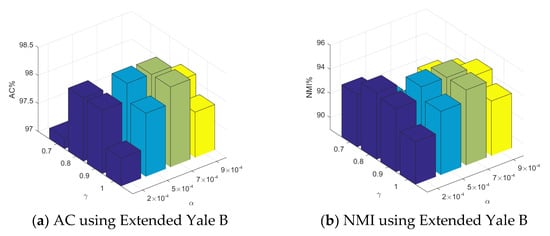
Figure 6.
The AC and NMI values when using the Extended Yale B dataset.
4.4. Ablation Studies
In this section, we reveal the influences of various parameters on the clustering results of the algorithm using ablation studies. Specifically, the original parameter settings remained unchanged when using the three standard datasets, then , and were set to perform the ablation studies. The comparison results are shown in Table 6, Table 7, Table 8 and Table 9.

Table 6.
A comparison of the accuracy (%) results when using the Hopkins 155 dataset with 2F-dimensional data in the ablation studies.

Table 7.
A comparison of the accuracy (%) results when using the Hopkins 155 dataset with 4k-dimensional data in the ablation studies.

Table 8.
A comparison of the results from the different algorithms when using the ORL dataset (%).

Table 9.
A comparison of the results from the different algorithms when using the Extended Yale B dataset in the ablatio studies (%).
From the comparative data in Table 6, Table 7, Table 8 and Table 9, it can be seen that after the ablation studies, the clustering effects when using the three standard datasets decreased significantly (except the three motions in the Hopkins 155 dataset with 2F-dimensional data). Our experimental results showed that each component of the objective function of the BDLSR algorithm played an effective role. This also showed that the combination of block diagonal structures and LSR could effectively improve the performance of subspace clustering.
5. Conclusions
In this work, to obtain the advantages of both the LSR and BDR algorithms, block diagonal structures were introduced into an LSR algorithm. Then, the BDLSR method was proposed for subspace clustering. The algorithm made use of a regularization item to enhance the fragile block diagonal structures that were obtained using LSR and could produce better clustering results and demonstrate a strong competitiveness. After that, we settled the objective function using the alternating minimization method. In addition, we also theoretically proved the convergence of this algorithm and verified its effectiveness using three standard datasets. Our experimental results showed that the BDLSR method achieved the best clustering results compared to other algorithms in almost all cases when using the three standard datasets. However, the algorithm also had some shortcomings: it involved more parameters (three parameters), which needed more time to be adjusted; additionally, the clustering results from a certain dataset were not the best out of the compared algorithms. To solve these shortcomings, in our future work, we will explore the concept of parameter reduction and how to set the minimum number of parameters while ensuring the best clustering accuracy so as to obtain a clustering algorithm with an even better performance.
Author Contributions
Conceptualization, methodology and software, L.F. and G.L.; writing—original draft preparation, L.F.; writing—review and editing, G.L.; validation, T.L.; data curation, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by projects from the National Natural Science Foundation of China (grant number: 61976005), the Science Research Project from Anhui Polytechnic University (grant number: Xjky2022155) and the Industry Collaborative Innovation Fund from Anhui Polytechnic University and Jiujiang District (grant number: 2021cyxtb4).
Institutional Review Board Statement
The study did not require ethical approval.
Informed Consent Statement
Not applicable.
Data Availability Statement
The study did not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LSR | Least squares regression |
| EBD | Enforced block diagonal |
| BDLSR | Block diagonal least squares regression |
| SSC | Sparse subspace clustering |
| LRR | Low-rank representation |
| MSR | Multi-subspace representation |
| NNLRS | Non-negative low-rank sparse representation |
| LRR-LC | Locally constrained low-rank representation |
| BDR | Block diagonal representation |
References
- Parsons, L.; Haque, E.; Liu, H. Subspace clustering for high dimensional data: A review. ACM SIGKDD Explor. Newsl. 2004, 6, 90–105. [Google Scholar] [CrossRef]
- Elhamifar, E.; Vidal, R. Sparse subspace clustering. In Proceedings of the 2009 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009; pp. 2790–2797. [Google Scholar]
- Liu, G.; Lin, Z.; Yu, Y. Robust subspace segmentation by low-rank representation. In Proceedings of the 27th International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010; pp. 663–670. [Google Scholar]
- Yang, C.; Liu, T.; Lu, G.; Wang, Z. Improved nonnegative matrix factorization algorithm for sparse graph regularization. In Data Science, Proceedings of the International Conference of Pioneering Computer Scientists, Engineers and Educators (ICPCSEE 2021), Taiyuan, China, 17–20 September 2021; Springer: Singapore, 2021; Volume 1451, pp. 221–232. [Google Scholar]
- Qian, C.; Brechon, T.; Xu, Z. Clustering in pursuit of temporal correlation for human motion segmentation. Multimed. Tools Appl. 2018, 77, 19615–19631. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Yang, Y.; Liu, B.; Fujita, H. A study of graph-based system for multiview clustering. Knowl.-Based Syst. 2019, 163, 1009–1019. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, S.; Zheng, F.; Cen, Y. Graph-regularized least squares regression for multiview subspace clustering. Knowl.-Based Syst. 2020, 194, 105482. [Google Scholar] [CrossRef]
- Elhamifar, E.; Vidal, R. Sparse Subspace Clustering: Algorithm, Theory, and Applications. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2765–2781. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust recovery of subspace structures by low-rank representation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 171–184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luo, D.; Nie, F.; Ding, C.; Huang, H. Multisubspace representation and discovery. In Machine Learning and Knowledge Discovery in Databases; Springer: Berlin/Heidelberg, Germany, 2011; pp. 405–420. [Google Scholar]
- Zhuang, L.; Gao, H.; Lin, Z.; Ma, Y.; Zhang, X.; Yu, N. Nonnegative low rank and sparse graph for semisupervised learning. In Proceedings of the 2012 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 2328–2335. [Google Scholar]
- Zheng, Y.; Zhang, X.; Yang, S.; Jiao, L. Low-rank representation with local constraint for graph construction. Neurocomputing 2013, 122, 398–405. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y. Subspace Clustering by Exploiting a Low-Rank Representation with a Symmetric Constraint. Available online: http://arxiv.org/pdf/1403.2330v2.pdf (accessed on 23 April 2015).
- Lu, C.; Min, H.; Zhao, Z.; Zhu, L.; Huang, D.; Yan, S. Robust and efficient subspace segmentation via least squares regression. In Computer Vision—ECCV 2012, Proceedings of the 2012 Computer Vision European Conference on Computer Vision (ECCV), Florence, Italy, 7–13 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 347–360. [Google Scholar]
- Zhang, Z.; Xu, Y.; Shao, L.; Yang, J. Discriminative block-diagonal representation learning for image recognition. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3111–3125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feng, J.; Lin, Z.; Xu, H.; Yan, S. Robust subspace segmentation with block-diagonal prior. In Proceedings of the 2014 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 3818–3825. [Google Scholar]
- Lu, C.; Feng, J.; Lin, Z.; Mei, T.; Yan, S. Subspace clustering by block diagonal representation. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 487–501. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.; Guo, X.; Liu, G.; Wang, J. Implicit block diagonal low rank representation. IEEE Trans. Image Process. 2018, 27, 477–489. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Wang, Y.; Sun, J.; Ji, Z. Structured block diagonal representation for subspace clustering. Appl. Intell. 2020, 50, 2523–2536. [Google Scholar] [CrossRef]
- Wang, L.; Huang, J.; Yin, M.; Cai, R.; Hao, Z. Block diagonal representation learning for robust subspace clustering. Inf. Sci. 2020, 526, 54–67. [Google Scholar] [CrossRef]
- Dattorro, J. Convex Optimization & Euclidean Distance Geometry 2016. p. 515. Available online: http://meboo.Convexoptimization.com/Meboo.html (accessed on 1 March 2021).
- Tron, R.; Vidal, R. A benchmark for the comparison of 3-D motion segmentation algorithms. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Samaria, F.; Harter, A. Parameterisation of a stochastic model for human face identification. In Proceedings of the 1994 IEEE Workshop on Applications of Computer Vision, Sarasota, FL, USA, 5–7 December 1994; pp. 138–142. [Google Scholar]
- Cai, D.; He, X.; Wang, X.; Bao, H. Locality preserving nonnegative matrix factorization. In Proceedings of the 21st International Joint Conference on Artificial Intelligence, Pasadena, CA, USA, 11–17 July 2009; pp. 1010–1015. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).