Abstract
Aiming at the difficulty in detecting defects of key equipment of transmission lines in small samples and complex environments, and the problems of low accuracy and unreliability in one-time detection using traditional deep learning-based methods, an image detection scheme combining optimized deep convolutional neural networks and Kalman filtering is proposed. The convolutional neural network architecture is based on Faster Region-based Convolutional Neural Networks (R-CNNs). First, the model backbone network is constructed by MobileNet, which effectively reduces the computational cost. Secondly, a soft nonmaximum suppression algorithm is integrated to solve the occlusion problem of target parts, and the context-aware ROI pooling layer replaces the original pooling layer, maintaining the original structure of small-sized components. Finally, the detection results are corrected twice by Kalman filtering to further improve the detection accuracy and reliability. The experimental results show that this method can realize the accurate detection of components in complex transmission line equipment, the mean Average Precision (mAP) reaches 91.10%, which is 11.05% higher than the original model, and the detection time of each picture is only 0.05 s. Compared with other detection algorithms under the same conditions, the comprehensive performance of the proposed method can be improved by 20%.
1. Introduction
The transmission line is one of the main components of power grid operation, and it is also the terminal facility of the power transmission system. Ensuring its normal operation is the premise of the safe operation of the power grid [1]. Most of the transmission lines are laid in the complex external environment, and are easily affected by natural or human factors to cause failure, which seriously affects the safe operation and normal power supply of the distribution network. Insulators and fittings are the key components on the transmission line. Once a fault occurs, it will directly affect the continuity of the power supply and seriously endanger the operation safety of the power grid [2,3]. Therefore, how to take effective means to monitor and detect transmission line components is of great significance. The detection of components on traditional distribution lines mainly relies on manual operations, which is not only time-consuming, labor-intensive, and inefficient, but also easily causes certain damage to the structure of line components. With the rapid development of nondestructive testing technology, manual inspection has gradually transformed into a noncontact detection method based on image processing, marking that the defect detection of key equipment in transmission lines is gradually moving toward an intelligent stage [4,5,6,7,8].
Among them, the image processing technology based on deep learning is widely used in the defect detection of transmission line equipment due to its accuracy and efficiency [9]. Reference [10] used deep learning to complete the localization of insulator infrared images. Reference [11] used deep learning to complete the defect identification of power distribution equipment, and used radio-frequency identification (RFID) instructions to complete the trinity association of tower coordinates, related equipment pictures, and physical ID. Tao et al. used the deep learning You Only Look Once (YOLO) algorithm to locate and identify insulator defects [12]. In [13], a network model based on target detection Faster Region-based Convolutional Neural Networks (R-CNNs) + Feature Pyramid Networks (FPNs) was proposed to classify the defects of components such as anti-vibration hammers and pressure equalizing rings of overhead lines. Reference [14] proposed a lightweight network for the detection of insulators. Reference [15] used a single shot multibox detector (SSD) convolutional neural network to accurately locate and detect the defect position of the transmission line insulator. Reference [16] proposed an improved Faster R-CNN algorithm to identify defects in key components of transmission lines. Zhao et al. completed insulator infrared detection using deep convolution feature maps [17]. However, most of the above target detection frameworks, such as Faster R-CNN [18] and SSD [19], have a good effect on parts with obvious defect shapes and larger sizes, but for small equipment’s subtle faults (cracks, wear, etc.), the detection accuracy is greatly reduced. Therefore, traditional deep learning models have great limitations and are difficult to adapt to the requirements of transmission line equipment defect detection tasks.
At the same time, due to the large amount of transmission line equipment, the collected image data usually contain a lot of noise, which leads to the positioning deviation of the detection model, and the detection accuracy is greatly reduced [20]. In recent years, the method based on the Kalman filter has been widely used in various research, which can correct the detection results and obtain the estimated value or correction value of the research object [21]. Reference [22] constructed a new fuzzy logic algorithm based on the Kalman filter, which can effectively eliminate the influence of noise and also has strong robustness to modeling errors. Liu et al. implemented the correction of the geometric parameters of the catenary through the Kalman filter. The experimental results showed that the method can effectively improve the detection accuracy of the model [23]. The above research has effectively improved the accuracy of the detection results through the correction method, but the dataset of transmission line equipment in my country is usually not open to the public, the limited image dataset is even extremely unbalanced, and the detection model is prone to the risk of overfitting.
In summary, this paper proposes a defect detection scheme for key equipment of transmission lines in complex environments. First, for the small sample environment, this paper adopts data augmentation to expand the sample, and secondly proposes an improved Faster R-CNN framework, using MobileNet [24], the soft Non-Maximum Suppression (soft-NMS) algorithm [25], and the Context-Aware Region of Interest (CAROI) pooling layer [26], respectively, to replace the Visual Geometry Group-16 (VGG-16) benchmark network [27], NMS algorithm [28], and Region-of-Interest (ROI) pooling layer [29] in the initial framework to achieve a small-scale defect identification of transmission line components. Finally, according to the complex noise environment in the image, the detection results are corrected by Kalman filtering, which effectively improves the detection accuracy and robustness of the model in this paper.
The main innovations are as follows:
- This paper uses a more lightweight network. The feature extraction network VGG-16 of Faster R-CNN is replaced by a lightweight MobileNet network, which greatly reduces redundant computation.
- In this paper, the soft-NMS algorithm is used to replace the original NMS algorithm to improve the detection accuracy, and CAROI is used to replace the original ROI pooling layer to maintain the original structure of small-sized components to improve the detection accuracy.
Finally, this paper uses Kalman filtering to correct the detection results and uses Kalman filtering to eliminate the complex noise environment in the image.
2. System Overview
In order to solve the problems of high difficulty and complex environment in the detection of subtle component defects in current transmission lines, this paper optimizes its network architecture based on the original Faster R-CNN model, and combines image sample enhancement and secondary correction of positioning results. The scheme obtains the final transmission line equipment defect detection system. The overall framework of the system is shown in Figure 1.
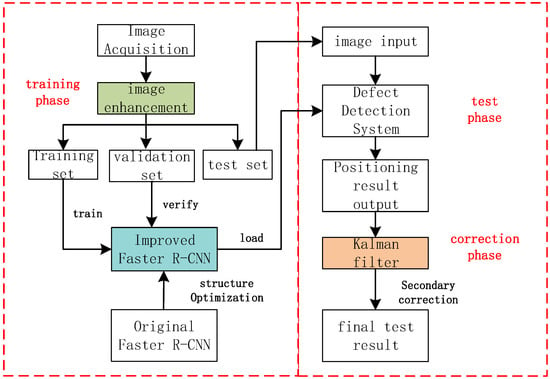
Figure 1.
Overall framework of defect detection system for key components of transmission lines.
The whole detection system is divided into three parts: model training, model testing, and model detection result correction. First, the collected pictures of key components of transmission lines are obtained by the image enhancement method to obtain enough training samples, and are then divided into the training set, verification set, and test set according to a certain proportion. The training set and validation set samples are used to train and verify the defect detection model of power transmission line parts, wherein the model is obtained by optimizing the original Faster R-CNN detection network structure to adapt to the defect detection of small parts. Next, the trained optimization model is loaded into the defect detection system, and images of power transmission line components to be detected are selected from the test set samples and input to the system to obtain preliminary detection results. Finally, according to the preliminary defect localization effect of the model, a secondary localization correction scheme is proposed, and a Kalman filter is used to optimize and adjust the defect prediction position, which further improves the localization accuracy and generalization performance of the model, and meets the defect detection requirements of key components of transmission lines.
3. Faster R-CNN Framework Improvement
Figure 2 shows the overall framework of the improved Faster R-CNN. In order to distinguish it from the original Faster R-CNN, the red cylinder in the figure highlights the optimization module of the improved network. First, in the original Faster R-CNN framework, MobileNet is used instead of VGG-16 to build the base convolutional layer to reduce the network computation. Then, after the Region Proposal Network (RPN), the soft-NMS algorithm is used to solve the target part occlusion problem. Finally, the initial ROI pooling layer is replaced by a CAROI pooling layer to maintain the original structure of small defective parts. The optimization framework is mainly introduced in detail from three modules below.
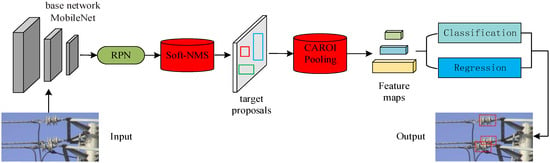
Figure 2.
The overall framework of the improved Faster R-CNN.
3.1. Basic Network
The base network of Faster RCNN adopts VGG-16 [30]. However, experiments have shown that almost 80% of the time of all models is spent on the basic network, and a lightweight basic network can greatly improve the detection speed of the entire algorithm. As an efficient network, the MobileNet architecture decomposes the convolution into 3 × 3 depthwise convolution and 1 × 1 pointwise convolution, which effectively reduces the computational cost and the number of parameters. As shown in the comparison results of MobileNet and VGG-16 in ImageNet shown in Table 1, the accuracy of MobileNet is close to VGG-16, but 32 times smaller than VGG-16, and the computational parameters are 27 times less. This paper replaces the base network VGG-16 in Faster R-CNN with MobileNet. MobileNet introduces both a width multiplier and a resolution multiplier to achieve a balance between resources and accuracy. Width multipliers reduce the size of the network, while resolution multipliers change the input size of the image, reducing the internal representation of each layer. As this paper only uses convolutional layers from the MobileNet architecture, it is not necessary to fix the size of the input image.

Table 1.
Comparison results of MobileNet and VGG-16 on ImageNet.
The deep separable convolution layer is composed of deep convolution and point convolution. The deep convolution applies a single filter to each input channel, and the point convolution applies a 1 × 1 convolution for a linear combination output. In addition, MobileNet adopts batch normalization processing and the relu nonlinear activation function. The computational complexity is only proportional to the square of the output feature mapping channel and the convolution kernel size, so it is easy to control the complexity of the model.
3.2. RPN Network
RPN first generates a set of anchor boxes at the center of the sliding window in the convolutional feature map, and the size of the anchor boxes is related to the sliding window and aspect ratio. In order to balance the recall rate and processing speed, this paper adopts anchor boxes with sizes of 128, 256, and 512 and three aspect ratios of 1:1, 1:2, and 2:1. A total of 9 kinds of anchor boxes are generated in the sliding window. For a feature map of input size 14 × 14, 1764 anchor boxes are generated.
After the RPN processes each anchor box, it will obtain two output results. The first is the objective score, meaning the probability that the anchor is the target. The second is the bounding box regression score, which is used to adjust the anchors to fit the object. As the anchors usually overlap, the same object will inevitably generate multiple redundant bounding boxes. Using nonmaximum suppression (NMS) can eliminate redundant windows and find the best detection position. In most advanced object detection, including Faster R-CNN, the NMS algorithm is used to remove redundant candidate boxes [31]. Traditional NMS directly deletes all boxes whose IOU value exceeds a predefined threshold. However, due to the complexity of the actual detection environment, the threshold of the NMS algorithm is difficult to determine, and positive candidate boxes may be removed unexpectedly. This paper adopts soft-NMS to solve the threshold problem. Soft-NMS does not completely suppress the neighbors of a successful candidate but computes the overlap level of the neighbors and the winning candidate score for partial suppression.
Figure 3 shows an example of the detection results of NMS (left) and soft-NMS (right). It can be clearly seen that due to the overlap of the two devices on the transmission line, NMS detects only one target, while soft-NMS can keep the two devices separately.

Figure 3.
Detection results with (a) NMS and (b) soft-NMS.
3.3. Context-Aware ROI Pooling
As shown in Figure 4, in the two-stage object detection algorithms Fast R-CNN and Faster R-CNN, a ROI pooling layer is adopted to resize the proposal box to a fixed size [32]. The ROI pooling layer uses max pooling to convert features within any valid region of interest into a small feature map with a fixed h × w spatial extent. ROI max-pooling works by dividing the h × w proposal into a grid of H × W sub-windows of approximate (h/H) × (w/W) size, and then max-pooling the values in each sub-window into the corresponding output grid cells. If the suggestion box is smaller than the size of H × W, the suggestion box needs to be enlarged to the size of H × W by adding the copy value. Therefore, ROI pooling avoids double-computing the size of the proposal box, which significantly speeds up training and testing [33]. Because this method of adding duplicate values has a greater impact on the small proposal box, and the small defect target is mostly located by the small proposal box, it may destroy the original structure of the small defect target. In addition, adding replicated values leads to an incorrect representation of forward propagation in gradient descent computations, and increases the accumulation of errors in backpropagation. Therefore, the use of ROI pooling will reduce the detection performance of small defect targets. In this paper, CAROI pooling is used to adjust the size of the proposal box without destroying the original structure of the small defect target, which can also improve the performance of small defect detection [34]. As shown in Figure 5, in CAROI, if the size of the proposal box is larger than the fixed size, the maximum pooling is used to reduce the size of the proposal box. If it is smaller than the fixed size, deconvolution is used to expand the proposal box to the fixed size. As shown in Equation (1):

Figure 4.
ROI pooling principle.
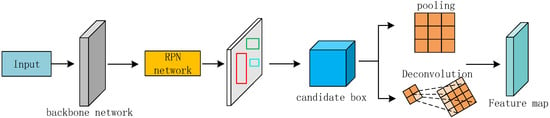
Figure 5.
CAROI pooling principle.
For example, in Equation (1), yk is the fixed size of the output feature map, Fk is the input suggestion box, and hk is the kernel of the deconvolution. The size of the kernel is equal to the ratio of the output feature map to the input suggestion box. In addition, if one of the width or height of the suggested box is higher than the fixed value, the other is smaller than the fixed value. CAROI will use deconvolution to first expand the size of the proposal box, and then use max pooling to reduce the proposal box to a fixed size. Therefore, after using CAROI pooling, the proposals would have been resized to a fixed size while still extracting discriminative features from small proposals.
4. Kalman Filter Correction
Traditional denoising methods are roughly divided into spatial pixel feature denoising algorithms and transform domain denoising algorithms. Spatial pixel feature denoising includes median filtering, Gaussian filtering, and other denoising methods that directly process pixels. The transform domain denoising algorithm aims to transform the signal, filter the noise, and then transform it to the space–time domain. Most papers are now optimizing pixel processing functions or optimizing threshold functions in transform domain denoising algorithms. In [35], Luisier et al. proposed a general approach (PURE-LET) to design and optimize a broad class of transform-domain thresholding algorithms for denoising images contaminated by mixed Poisson–Gaussian noise. In [36], Sun et al. proposed a bilateral spectrum weighted total variation (BSWTV) to optimize regularization in image denoising. In [37], Foi et al. proposed an algorithm to fully automatically estimate model parameters given a single noisy image to optimize the pixel feature denoising process.
After using the optimized Faster R-CNN model to detect the transmission line components, the defect localization results can be obtained. On this basis, the secondary correction of the results can further improve the detection effect. In statistics and control theory, the Kalman filter, as a recursive predictive filtering algorithm, is widely used and powerful: it provides an efficient and computable method to estimate the past and current state of a signal. It is even possible to estimate the future state, and to be able to update and process the data collected in the field in real time, which is more accurate than estimation based on a single measurement, even if the exact nature of the model is not known [38]. Therefore, this paper uses the Kalman filter to correct the detection results of the model.
The Kalman filter utilizes the equation of state of a linear system, which can be viewed as a projection of state variables on a linear space generated by observations [39,40]. Its principal Equation is as follows:
Among them, k represents the state index, represents the current estimated value, Kk is the Kalman gain, Zk is the system measurement value, and is the estimator at the previous moment. The predicted value is updated by the state measurement value at time k, and the update method is based on the minimum mean square error; finally, the best estimated value is obtained.
Kalman filtering is mainly implemented through three steps: modeling, measurement update and measurement update, and iteration. Among them, the modeling is shown in Equation (3). In the Equation, uk represents the control signal, its value is 0, wk−1 is the noise function, xk is the signal, A and B are the matrix coefficients, and k represents the state index.
The observed value is shown in Equation (4), where ZK represents the measured value in state k; VK is a noise function, which usually obeys a Gaussian distribution; H is a coefficient matrix:
The time update and measurement update mainly consist of 5 equations, and the 2 equations in the time update stage are shown in Equations (5) and (6). Among them, is the prior evaluation, is the prior error covariance, and Q is the system noise. Two priors will be used in the measurement update state equation.
The three equations in the measurement update phase are shown in Equations (7)–(9). Among them, R represents the loop, Kk represents the Kalman gain at time k, and is the estimated value of the system at time k.
The iterative process first needs to estimate the initial state; set the initial values of A, B, R, H, and other parameters; calculate and through Equations (5) and (6); bring it into the above Equations (7) and (8); obtain the estimated value of X1; update the error covariance matrix PI through Equation (9); recalculate the and PI obtained in the measurement update stage as the initial value of the time update, to realize the iteration.
In the actual transmission line system, the dimensions of each component are manufactured according to the unified national standards, their positional relationship is always relatively fixed, and the aspect ratio is also a constant. In the Kalman modeling process, through this feature, the relative coordinates of small parts can be predicted based on the positions of some large-sized parts, which is equivalent to xk in Kalman filtering. In the process of locating the defects of the key components of the actual transmission line, the initial prediction result is obtained through the improved Faster R-CNN and used as an observation value, which is equivalent to ZK in the Kalman filter, and then the five equations of the Kalman filter are used continuously. For iteration, each iteration process is the correction process of the Kalman filter algorithm, and finally, the optimal one is evaluated, and a set of optimal defect positions is output to further improve the defect detection performance.
5. Experimental Results and Analysis
5.1. Experimental Environment
Table 2 shows the software and hardware environment of this paper. The experiments are based on the deep learning open-source frameworks Tensorflow and Keras, and are programmed in Python language.

Table 2.
Experimental environment.
5.2. Dataset Processing
In practical application scenarios, due to the limitation of acquisition conditions, the defect detection of transmission line components faces the problems of difficulties in collecting complete defective samples and low detection accuracy, and deep learning algorithms require a large number of datasets as support. In view of the insufficient number of fault samples, in order to train a defect detection model with good performance, an image enhancement method is adopted in this paper. The purpose of image enhancement is to improve the sensitivity of the model to defect images, obtain enough samples for deep training of the model, effectively reduce the risk of overfitting, and thus improve the generalization ability of the defect detection model. The image enhancement method performs extended processing such as brightening, adding noise, translation, and affine to the captured original image. The enhancement results are shown in Figure 6.

Figure 6.
Image enhancement results.
5.3. Model Training Parameter Settings
In the experiment, first, the enhanced image is randomly divided into the training set, test set, and verification set. The training set accounts for 80%, and the test set and verification set account for 10%. During model training, the weights of each batch of normalization layers are frozen to shorten the training time and avoid over fitting. The RPN network and classifier are trained in turn. The Adam algorithm [41] is used to optimize the loss function of bounding box regression. The balance parameter λ in the loss function is set to 0.5, the initial learning rate of the RPN and the classifier is set to 0.002, the momentum value is set to 0.8, and the batch size Batch_Size is set to 32. When the total number of iterations reaches 80%, the learning rate is adjusted to 0.0002, and a total of 2000 training iterations are performed.
5.4. Evaluation Indicators
In order to test the detection effect of the trained model, this paper evaluates its performance in various aspects through Precision (P), Recall (R), mean Average-Precision (mAP), Intersection over Union (IOU), and Detection time. The calculation of P and R is shown in Equations (10) and (11). In the Equation: True Positive (TP) is the number of correct samples that are identified as positive samples; False Positive (FP) is the number of negative samples that are wrongly identified as positive samples; False Negative (FN) is the number of positive samples that are wrongly identified as negative samples. The average precision Average-Precision (AP) is the area enclosed by the precision-recall (P-R) curve, and the AP value represents the recognition accuracy of a single category, which is calculated as shown in Equation (12). mAP represents the overall recognition accuracy of all categories, and the relationship between it and the AP value is shown in Equation (13). The calculation of IOU is shown in Equation (14), where S is the overlapping area between the predicted frame and the actual frame, and S is the total area occupied by the predicted frame and the actual frame. T is the time required for the model to detect a picture, which is used to evaluate the detection speed of the algorithm.
5.5. Display of Experimental Results
In this experiment, the proposed improved algorithm is used to perform preliminary detection on several key components of the transmission line, and on this basis, the detection results are corrected by the Kalman filter. Figure 7 shows the representative defect detection results of different types of components, of which the left side is the preliminary detection result of the improved model, and the right side is the defect location result corrected by the Kalman filter. According to the test results, it can be clearly seen that the improved model can effectively locate and identify defects of larger parts, but the defect detection accuracy of some fine parts has decreased. After Kalman filtering, the defect detection of small parts can also reach the same accuracy as large-scale defects. Based on the comprehensive analysis of the above experimental results, the improved algorithm designed in this paper combined with the Kalman filter correction has a good effect on the defect image detection of key components of transmission lines.


Figure 7.
Defect detection results; (a) insulator, (b) wire clip and (c) hardware. Among them, the left side is the preliminary detection result, and the right side is the corrected result.
5.6. Comparison and Analysis of Experimental Results of Different Algorithms
In order to further verify the superiority of the method proposed in this paper, comparative experiments were conducted with YOLO, SSD, MS-CNN, original Faster R-CNN, and improved Faster R-CNN on the same dataset. In the experiment, mAP, IOU, and detection time were used to evaluate the performance of each method. The comparison of detection results of different methods is shown in Table 3. It can be seen from the table that the accuracy of the improved Faster R-CNN model + Kalman filter proposed in this paper is improved by 11.05% and 4.94%, respectively, compared with the original Faster R-CNN and the improved Faster R-CNN. In terms of detection efficiency, the method takes 0.12 s to process an image, which is slightly slower than other single-stage detection algorithms. The original Faster R-CNN takes 2 s, which is longer than the MobileNet, but with higher accuracy. The MobileNet architecture significantly improves the processing speed of this method, but the accuracy is slightly low. There is no absolute advantage to comprehensively compare the two, and MS-CNN has a higher detection accuracy; however, its detection time is longer. The YOLO model only needs 0.04 s to detect a single image, but the accuracy is lower than other methods. From comprehensive analysis of the comparison results of the six methods in the table under the same test samples, the improved Faster R-CNN + Kalman filter proposed in this paper has the best comprehensive performance, has significant advantages in the defect detection effect, and can meet the needs of transmission line defect detection.

Table 3.
Performance comparison of different detection methods.
In order to verify the robustness of the model, binary noise is used in this chapter, and the image pixels are randomly set to zero through different probabilities to analyze the adaptability of the model under different noise disturbances. The results are shown in Table 4. It can be seen from the results that the model can maintain a high accuracy under noise disturbance. At the same time, with the increase in the number of defective samples, the accuracy rate is gradually improved, so in order to increase the number of defective samples in the training set, the recognition accuracy rate can be improved.

Table 4.
Model recognition rates under different noise probabilities.
In order to verify the effectiveness of the noise reduction method in this paper, this paper compares the Kalman filter with various common noise reduction methods. The results are shown in Table 5. From the results we can know that the method in this paper is more accurate than other methods, but the detection time shows no big difference.

Table 5.
Comparison of different denoising methods.
6. Conclusions
In this paper, the problem of fault detection of transmission line equipment is studied in depth, and a fault detection method based on a deep convolutional neural network and Kalman filter is proposed. In order to improve the detection accuracy and model robustness in complex environments such as large-scale changes and target occlusion, this paper first uses the lightweight MobileNet to build the backbone network of the Faster R-CNN framework, which improves the model detection speed; secondly, after the RPN network, the soft-NMS algorithm is used to solve the problem of redundant candidate boxes; finally, CAROI pooling is used to adjust the candidate boxes to the specified size without ignoring important context information. In addition, this paper also proposes a Kalman filter correction scheme to further improve the model detection accuracy. The method is evaluated and compared with other detection algorithms on the same dataset. The experimental results show that the method is slightly inferior to the single-stage detection algorithm in processing speed, but it has achieved good results in detection accuracy and has the best overall performance. In addition, the framework can be easily extended and applied to defect identification in other environmental backgrounds, which has certain reference value.
Author Contributions
Data curation, B.W.; Formal analysis, J.W.; Funding acquisition, F.D.; Investigation, B.W.; Methodology, J.W., F.D. and B.W.; Project administration, F.D.; Resources, B.W.; Software, J.W.; Supervision, F.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of China (51767006), Natural Science Foundation of Jiangxi Province (20202ACBL214021, 20202BAB202005), Key Research and Development Plan of Jiangxi Province (20202BBGL73098), and Science and Technology Project of Education Department of Jiangxi Province (GJJ190311, GJJ180308).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, H. National Quality Infrastructure Supports Smart Grid Construction in China-Taking the State Grid as an Example. IOP Conf. Ser. Earth Environ. Sci. 2020, 531, 012011. [Google Scholar] [CrossRef]
- Devices Create Smarter Grids with Accurate Line Fault Detection; Transmission & Distribution World: Overland Park, KS, USA, 2019.
- Wang, S.; Zhou, Z.; Zhao, W. Semantic Segmentation and Defect Detection of Aerial Insulators of Transmission Lines. J. Phys. Conf. Ser. 2022, 2185, 012086. [Google Scholar] [CrossRef]
- Li, Y.; Song, Y.; Yang, Z.; Xie, X. Use of line laser scanning thermography for the defect detection and evaluation of composite material. Sci. Eng. Compos. Mater. 2022, 29, 74–83. [Google Scholar] [CrossRef]
- Yücel, M.K.; Legg, M.; Kappatos, V.; Gan, T.-H. An ultrasonic guided wave approach for the inspection of overhead transmission line cables. Appl. Acoust. 2017, 122, 23–34. [Google Scholar] [CrossRef]
- Zhang, Q.; Chang, X.; Meng, Z.; Li, Y. Equipment detection and recognition in electric power room based on faster R-CNN. Procedia Comput. Sci. 2021, 183, 324–330. [Google Scholar] [CrossRef]
- Liu, X.; Lin, Y.; Jiang, H.; Miao, X.; Chen, J. Slippage fault diagnosis of dampers for transmission lines based on faster R-CNN and distance constraint. Electr. Power Syst. Res. 2021, 199, 107449. [Google Scholar] [CrossRef]
- Rodriguez, F.M., Jr.; Bastos, G.B.; Seruffo, M.C.R.; Costa, F.A.R.; Figueiredo, K.; de Melo, H., Jr. Analysis of migration to the Brazilian free energy market based on statistical methods and artificial neural networks. SBIC 2021, 1–8. [Google Scholar] [CrossRef]
- Zhou, J.H.; Liu, Z.Y.; Chen, G. Intelligent Inspection of the High-Speed Train Bogie Flaw Based on Eddy Current. Appl. Mech. Mater. 2015, 3785, 738–739. [Google Scholar] [CrossRef]
- Huang, H.; Huang, Y.; Mu, X.; Wang, X. Research on Recognition and Location Method of Insulator in Infrared Image Based on Deep Learning. J. Phys. Conf. Ser. 2021, 2087, 012090. [Google Scholar] [CrossRef]
- Wang, W.; Wei, J.; Zhu, Y.; Zhou, S. Power distribution equipment and defect identification technology based on deep learning. J. Phys. Conf. Ser. 2021, 2030, 012075. [Google Scholar] [CrossRef]
- Tao, W.; Wang, W.; Yue, L.; Xie, B.; Yin, W.; Wang, H. Insulator Defect Detection Method for Lightweight YOLOV3. Comput. Eng. 2019, 45, 275–280. [Google Scholar]
- Alahyari, A.; Hinneck, A.; Tariverdi, R.; Pozo, D. Segmentation and Defect Classification of the Power Line Insulators: A Deep Learning-based Approach. arXiv 2020, arXiv:2009.10163. [Google Scholar]
- Lan, Y.; Xu, W. Insulator defect detection algorithm based on a lightweight network. J. Phys. Conf. Ser. 2022, 2181, 012007. [Google Scholar] [CrossRef]
- Qi, Y.; Du, L.; Zhao, Z.; Cui, Y.; Si, W. Insulator Detection Based on SSD with the Default Box Adaptively Selection. Comput. Sci. Appl. Eng. 2018, 110, 1–4. [Google Scholar] [CrossRef]
- Ni, H.; Wang, M.; Zhao, L. An improved Faster R-CNN for defect recognition of key components of transmission line. Math. Biosci. Eng. 2021, 18, 4679–4695. [Google Scholar] [CrossRef]
- Zhao, Z.; Fan, X.; Xu, G.; Zhang, L.; Qi, Y.; Zhang, K. Aggregating Deep Convolutional Feature Maps for Insulator Detection in Infrared Images. IEEE Access 2017, 5, 21831–21839. [Google Scholar] [CrossRef]
- Zhou, Y.; Wen, S.; Wang, D.; Mu, J.; Irampaye, R. Object Detection in Autonomous Driving Scenarios Based on an Improved Faster-RCNN. Appl. Sci. 2021, 11, 11630. [Google Scholar] [CrossRef]
- Lv, L.; Tan, Y. Detection of cabinet in equipment floor based on AlexNet and SSD model. J. Eng. 2019, 2019, 605–608. [Google Scholar] [CrossRef]
- Gao, S.; Kang, G.; Yu, L.; Zhang, D.; Wei, X.; Zhan, D. Adaptive Deep Learning for High-Speed Railway Catenary Swivel Clevis Defects Detection. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1299–1310. [Google Scholar] [CrossRef]
- Zhu, J.; Chang, X.; Zhang, X.; Su, Y.; Long, X. A Novel Method for the Reconstruction of Road Profiles from Measured Vehicle Responses Based on the Kalman Filter Method. Comput. Model. Eng. Sci. 2022, 130, 1719–1735. [Google Scholar] [CrossRef]
- Ren, K.; Zhang, D.; Mohammed, S.; Calvi, A. A Kalman filtering fuzzy logic algorithm for recognition of lane departure. J. Intell. Fuzzy Syst. 2021, 41, 4855–4862. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, W.; Han, Z. A high-precision detection approach for catenary geometry parameters of electrical railway. IEEE Trans. Instrum. Meas. 2017, 66, 1798–1808. [Google Scholar] [CrossRef]
- Li, Y.; Huang, H.; Xie, Q.; Yao, L.; Chen, Q. Research on a Surface Defect Detection Algorithm Based on MobileNet-SSD. Appl. Sci. 2018, 8, 1678. [Google Scholar] [CrossRef] [Green Version]
- Bodla, N.; Singh, B.; Chellappa, R.; Davis, L.S. Soft-NMS—Improving Object Detection with One Line of Code. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Yao, L.; Sheng, Q.Z.; Qin, Y.; Wang, X.; Shemshadi, A.; He, Q. Context-aware Point-of-Interest Recommendation Using Tensor Factorization with Social Regularization. In Proceedings of the International ACM Sigir Conference, Santiago, Chile, 9–13 August 2015; ACM: New York, NY, USA, 2015. [Google Scholar]
- Xie, X.; Xiao, H.; Quan, L.; Shi, G. Visualization and Pruning of SSD with the base network VGG16. In Proceedings of the 2017 International Conference, Paris, France, 21–25 May 2017; ACM: New York, NY, USA, 2017. [Google Scholar]
- Shi, M.; Ouyang, P.; Yin, S.; Liu, L.; Wei, S. A Fast and Power-Efficient Hardware Architecture for Non-Maximum Suppression. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 1870–1874. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Deng, W. Anchor Generation Optimization and Region of Interest Assignment for Vehicle Detection. Sensors 2019, 19, 1089. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tun, N.L.; Gavrilov, A.; Tun, N.M.; Trieu, D.M.; Aung, H. Remote Sensing Data Classification Using a Hybrid Pre-Trained VGG16 CNN-SVM Classifier. In Proceedings of the 2021 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus), Moscow, Russia, 26–29 January 2021. [Google Scholar]
- Zhao, W.; Yan, H.; Shao, X. Object detection based on improved non-maximum suppression algorithm. Appl. Soft Comput. 2019, 81, 105478. [Google Scholar]
- Wang, K.; Liu, M.Z. Object Recognition at Night Scene Based on DCGAN and Faster R-CNN. IEEE Access 2020, 8, 193168–193182. [Google Scholar] [CrossRef]
- Yan, C.; Chen, W.; Chen, P.C.Y.; Kendrick, A.S.; Wu, X. A new two-stage object detection network without RoI-Pooling. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018. [Google Scholar]
- Hu, X.; Xu, X.; Xiao, Y.; Chen, H. SINet: A Scale-insensitive Convolutional Neural Network for Fast Vehicle Detection. IEEE Trans. Intell. Transp. Syst. 2018, 3, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Luisier, F.; Blu, T.; Unser, M. Image Denoising in Mixed Poisson–Gaussian Noise. IEEE Trans. Image Process. 2011, 20, 696–708. [Google Scholar] [CrossRef] [Green Version]
- Sun, K.; Simon, S. Bilateral Spectrum Weighted Total Variation for Real-World Super-Resolution and Image Denoising. arXiv 2021, arXiv:2106.00768. [Google Scholar]
- Foi, A.; Trimeche, M.; Katkovnik, V.; Egiazarian, K. Practical Poissonian-Gaussian Noise Modeling and Fitting for Single-Image Raw-Data. IEEE Trans. Image Process. 2008, 17, 1737–1754. [Google Scholar] [CrossRef] [Green Version]
- An, Y.; Wang, X.; Chu, R.; Yue, B.; Wu, L.; Cui, J.; Qu, Z. Event classification for natural gas pipeline safety monitoring based on long short-term memory network and Adam algorithm. Struct. Health Monit. 2019, 19, 1151–1159. [Google Scholar] [CrossRef]
- Fraser, C.T.; Ulrich, S. Adaptive extended Kalman filtering strategies for spacecraft formation relative navigation. Acta Astronaut. 2021, 178, 700–721. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, R.; Li, S.; Qi, S. Temperature Sensor Denoising Algorithm Based on Curve Fitting and Compound Kalman Filtering. Sensors 2020, 20, 1959. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kohli, H.; Agarwal, J.; Kumar, M. An Improved Method for Text Detection using Adam Optimization Algorithm. Glob. Transit. Proc. 2022, 3, 230–234. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).