A Link Prediction Algorithm Based on GAN

Abstract

Link prediction, as an important research direction in complicated network analysis, has broad application prospects. However, traditional link prediction algorithms are generally designed by the sparse expression of the adjacency matrix, which is computationally expensive and inefficient, being also unable to run on large-scale networks and to preserve their higher order structural features. To fill this gap, we propose a GAN (generative adversarial network)-based link prediction algorithm. The algorithm layers the network graph, preserving the local features and higher-level structural features of the original network graph, and uses a generative adversarial model to recursively and backwardly obtain the low-dimensional vector form of the vertices in each layer of the network graph as the initialization of the network graph in the previous layer. It then obtains the low-dimensional vector form of all the vertices in the original network graph for link prediction, and the problem of local minima that can be generated by random initialization is solved. The experimental results show that our method is superior to many state-of-the-art algorithms.

1. Overview

With the rapid development of the Internet, complex networks in various fields [1] have become increasingly large. In these complex networks, all vertices represent objects that may or may not be linked to each other. The links between objects in the complex networks are frequently unknown, and their structure can change during the process of network development. Link prediction in the network is useful to explain the reasons for the formation of links and network structure at the micro-level. Through the known data information of nodes and links in the network, link prediction is required to predict the missing data in the network, the data that may appear in the future, and the erroneous data information. Essentially, link prediction is the most basic problem in the field of information science, and its purpose is to predict whether there is a link between two nodes. With the deepening of network scientific research, link prediction from the perspective of network structure has received more and more attention, and link prediction has become a bridge between network science and information science. Thus, link predictions in complex networks [2] include both the detection of cryptic associations and the assessment of the potential links that may be generated in the future.

In the real world, there is a wide range of application scenarios, especially in social networks [3], which can judge whether there is a certain connection between two people, suggesting potential friends for users. In an e-commerce network, the users can also be recommended to other users through the link prediction method. In biological networks, link prediction can guide experiments on proteins [4]. In citation networks, link prediction can predict future collaborations between authors [5]. In addition, link prediction technology can also perform label classification, and predict what type of unlabeled nodes belong together based on node similarity [6]. Known links in networks usually represent only a small number of the existing associations between all network vertices. The discovery of unknown links requires significant manpower and material resources when only data collection and experiments are involved. Therefore, it is of great importance to study and develop link prediction algorithms.

The traditional link prediction algorithms are known to be less efficient, and they cannot describe high-order network structure characteristics well. In this paper, an antagonistic hierarchical network was generated to develop a self-learning algorithm for link prediction. The algorithm stratifies the network graph and recursively and retrospectively provides low-dimensional vector representations of vertices in each layer of the network graph by using the generative adversarial model. These data are then used by the algorithm for the initialization of the network graph in the previous layer, which enables it to obtain the low-dimensional vector representations of all vertices in the original network graph and to make the final link prediction.

2. Related Work

At present, the traditional link prediction algorithms are mainly based on likelihood analysis and similarity-based analysis methods [7].

(1)

The link prediction algorithm is based on likelihood analysis. This type of algorithm starts from likelihood analysis and can guide different algorithmic frameworks. The link prediction performance of this type of algorithm is superior, but the algorithm complexity of this type of algorithm is higher than that of other types. Clauset et al. proposed a technique for inferring hierarchies from network data through which missing links in the network can be predicted, and then proposed the hierarchical structure model (HSM) [8], which exhibited better predictive performance for networks with obvious hierarchies. Pan et al. calculated the probability of the network according to the predefined Hamiltonian amount of structure, and scored the unobserved links by adding the link to the network conditional probability. In terms of finding missing links and detecting spurious links, through simulation experiments on seven real networks, it was proved that the algorithm had high accuracy [9] Despite the accuracy of the likelihood analysis method, its framework is more complex, the computational complexity is high, and it is not suitable for large-scale networks.

(2)

The similarity-based link prediction algorithm estimates associations between vertices based on their similarities. Therefore, the most important issue for this algorithm is the correct determination of similarity level among all network vertices. Similarity-based link prediction is divided into the following two categories:

(1)

Link prediction method based on similarity of vertex attributes. [7]. Most of these link prediction methods are used in complex networks composed with labeled vertices, such as social networks. Using the information from the labels, it is possible to estimate vertex similarity. A greater similarity between the attributes of two vertices indicates a higher probability of connection between them.

(2)

Link prediction method based on network structure similarity [7]. Most of these link prediction methods are used in complex networks where it is difficult to obtain vertex attribute information. These methods mainly utilize the local information similarity index, path similarity index, and random walk similarity index. The local information similarity indices mainly include the common neighbors (CN) index [6], the preferential attachment (PA) index [6], and the Adamic–Adar (AA) index [6]. Path-based similarity indexes mainly include the local path(LP) index [6] and the Katz index [6]. Random walk similarity index mainly includes SimRank index [10], average commuting time index [11], and Cos+ index [11].

The traditional link prediction algorithm is generally designed according to the sparse representation of the adjacent matrix, for which the calculation cost is high, efficiency is low, and the high-order structural characteristics of the network diagram cannot be retained. Therefore, it cannot be run on large-scale networks.

In recent years, with the development of network representation learning (NRL), the network representation learning-based link prediction algorithm has achieved good results [12]. Responding to the proximity of vertices in the network, the algorithm self-trains to obtain the low-dimensional representation vector of vertices, thus calculating the probability of associations between vertices. It can keep the network structure robust, reduce the calculation cost, and improve the calculation efficiency.

In 2014, Perozzi et al. proposed DeepWalk [13] algorithm, which generated node sequences by constructing random paths of nodes in complex networks. It processed the node sequences using Skip-Gram and the Hierarchical Softmax [14] model, obtaining vector representation of vertices. In 2015, Tang et al. proposed the LINE [15] algorithm, which was improved on the basis of DeepWalk. LINE learned vertex representation by explicitly modeling first-order and second-order proximity, instead of capturing network structure by random walk. In 2016, Grover et al. proposed the Node2vec [16] algorithm, which was also an improvement of DeepWalk. In the process of random walk, an offset parameter is set, and the search mode of the model is controlled by the size adjustment the offset parameter, which is biased towards width-first search [17] or depth-first search [18]. In 2018, Wang et al. proposed the GraphGAN [19] algorithm, which is represented by the low-dimensional vector of the vertex in the network graph of generative confrontation network learning.

The network representation learning algorithms mentioned above have two common problems. (1) They only pay attention to the local characteristics of the network graph, ignoring their high-order structural characteristics; (2) in the absence of prior knowledge, vector representation is usually initialized with random numbers, and there is a risk of convergence to a poor local minimum.

The algorithm in this paper layers the original network graph according to its first-order proximity and second-order proximity. In each hierarchical process, vertices with higher first-order proximity and second-order proximity in the upper-level subnetwork graph are merged to form a smaller subnetwork graph. In this way, not only are the local characteristics of the original network graph preserved, but the higher-order adjacency of the original network graph is reduced in the process of scale reduction, which simplifies and more effectively preserves the higher-order adjacency of the network graph. In this algorithm, the vector representation learned from the smaller subnetwork graph is taken as the initial vector representation of its upper subnetwork graph, which enables avoidance of the risk of local minima caused by random initialization.

3. Algorithm Description

3.1. Algorithm Definition Description

This paper mainly uses the following five definitions:

(1) Complex network: Let $G=(V,E)$ be a given network graph, where $v=\{v_1,v_2,\cdots \cdots ,v_v\}$ denotes a vertex set, which represents data objects, and $E={\left\{e_{ij}\right\}}_{i,j=1}^V$ denotes an edge set of the network. For a given vertex $v_c$, let $N(v_c)$ be the vertex directly connected with the vertex $v_c$ (that is, the direct neighbor of $v_c$).

(2) Generative countermeasure network (GAN): The generative countermeasure network consists of a generator and a discriminator, both of which are a complete neural network. Through the game between the generator and the discriminator, new data similar to real data can be generated according to the original data set.

First, when a real data distribution is entered, the generator mimics the real dataset, generates approximately realistic data, and inputs it to the discriminator with the real dataset. The discriminator identifies the input data according to its knowledge, assigns as correct a label as possible to it, compares it with the real label, updates itself according to the comparison result, and gives feedback to the generator at the same time. The generator then updates itself based on the feedback from the discriminator. This cycle continues until the generator and discriminator reach a fit, and the generator can simulate data that are nearly identical to the real data.

(3) First-order proximity [19]: The first-order proximity in the network represents the local similarity between two vertices. For two vertices $u$ and $v$, if there are edges $(u,v)$ between them, then vertices $u$ and $v$ have first-order proximity.

(4) Second-order proximity [19]: The second-order proximity between a pair of vertices in a network is the similarity between their neighborhood network structures. If two vertices $u$ and $v$ have the same neighbor node, then vertices $u$ and $v$ have second-order proximity.

(5) Third-order proximity (high order proximity): High-order proximity between pairs of vertices in a network is the similarity between global network structures. Taking third-order proximity as an example, vertices $u$ and $v$ have third-order proximity if they are connected to two vertices with second-order proximity, respectively.

3.2. Basic Algorithm Index

This paper mainly applies the following three indexes:

(1) AA index: The number of a node’s neighbors in the complex network is called the degree of the node. The AA index gives a weight to each common neighbor of two nodes according to the degree information of the common neighbors of two nodes. AA indicators are defined as:

$$S_{x,y}={\displaystyle \sum _{z\in N(x)\cap N(y)}\frac{1}{\lg k(z)}}$$

(1)

where $N(x)$ is a neighbor of node $x$, and $k(x)=|n(x)|$ is the degree of node $x$. The weight of each common neighbor is equal to the diameter of the degree.

(2) Local path index (LP): LP index considers the common neighbors with path lengths of 2 and 3 between two vertices, and uses the number information of different paths between vertices to represent the similarity between them. LP index is defined as:

$$S_{x,y}=A_{x,y}^2+\alpha A_{x,y}^3$$

(2)

where $\alpha$ is an adjustable parameter to control the proportion of third-order paths, $A$ is an adjacency matrix, and $A_{x,y}^n$ represents the number of paths of length $n$ between vertices $x$ and $y$.

(3) Katz index: Katz index considers the common neighbors of all path lengths between two vertices on the basis of LP index, and gives greater weight to the common neighbors with smaller path lengths, which is defined as:

$$S_{x,y}=\beta A_{x,y}+{\beta }^2{A}_{x,y}^2+{\beta }^3{A}_{x,y}^3+\cdots$$

(3)

where β is a weight attenuation factor, and the value of β is less than the reciprocal of the maximum eigenvalue of the adjacency matrix.

3.3. Algorithm Framework

The algorithm framework of this paper is shown in Figure 1.

The algorithm is mainly divided into three parts:

(1) Hierarchical processing of network graph. As shown in ① and ② in Figure 1, the network graph layering algorithm (Netlay) is used to recursively fold the edges and merge the vertices of the original network graph $G_0$ to form a multi-layer sub-network graph $G_0$ to $G_n$ with a progressively smaller scale (the three-layer structure is taken as an example in Figure 1, $n=2$).

(2) Obtaining the low-dimensional vector representation of vertices in the network graph. As shown in ③~⑦ in Figure 1, firstly, the smallest subnetwork graph $G_n$ is preprocessed by Node2vec [16] algorithm to generate $\mathrm{init}{E}_{G_n}$. Then $E_{G_n}$ is represented by the low-dimensional vector of the subnetwork graph $G_n$ generated by the generative countermeasure network embedGAN. Then, $E_{G_n}$ is taken as the initial vector representation $\mathrm{init}{E}_{G_{n01}}$ of the upper subnetwork graph $G_{n01}$, and is input into the embedGAN model to generate the low-dimensional vector representation $E_{G_{n01}}$ of subnetwork graph $G_{n01}$. According to this method, backtracking is carried out until the low-dimensional vector representation $E_{G_0}$ of the original network graph $G_0$ is obtained.

(3) As shown in ⑧ in Figure 1, according to the low-dimensional vector representation $E_{G_0}$ of vertices obtained by training, the similarity between vertices is calculated to predict whether there is an edge between two nodes.

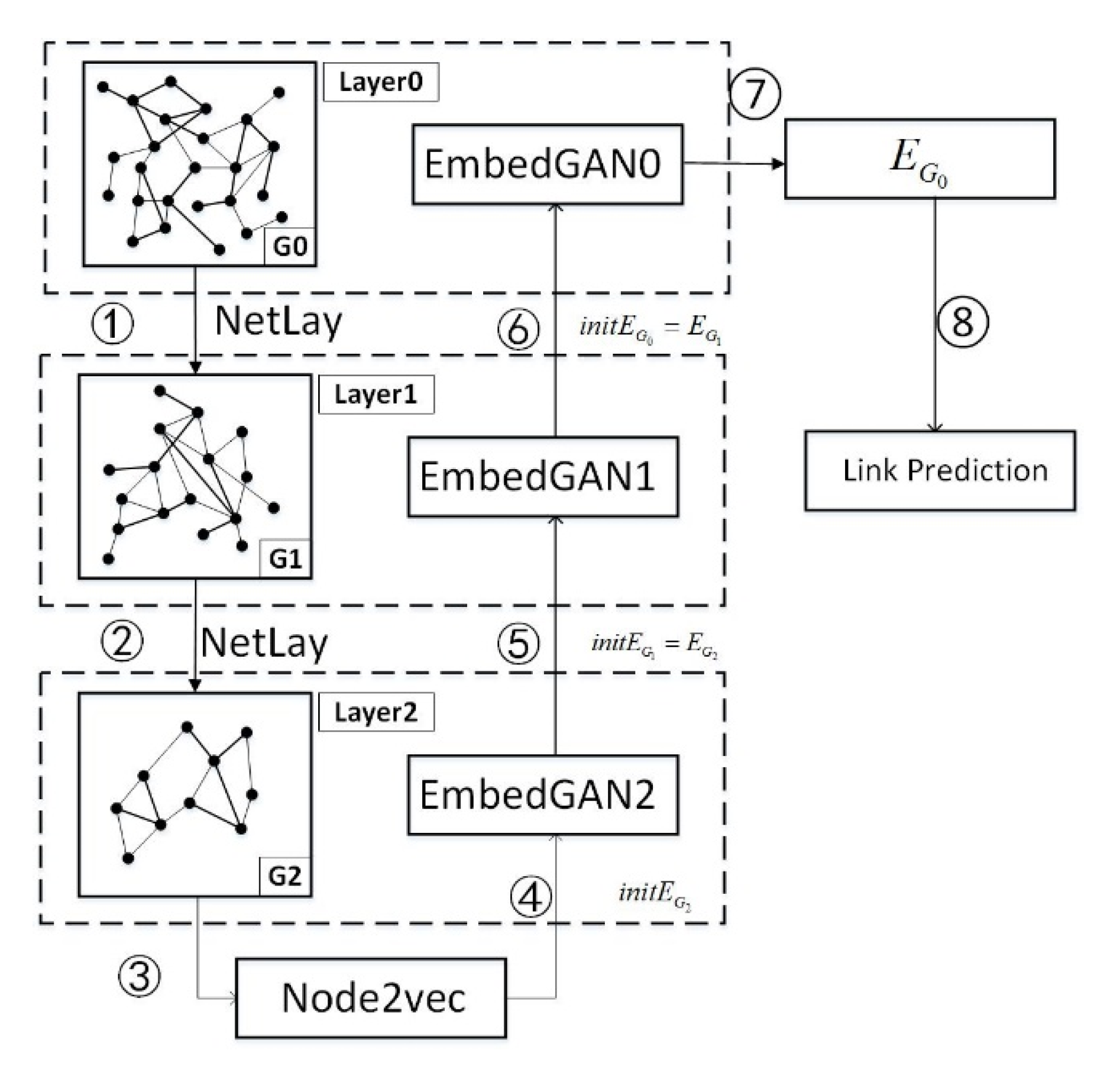
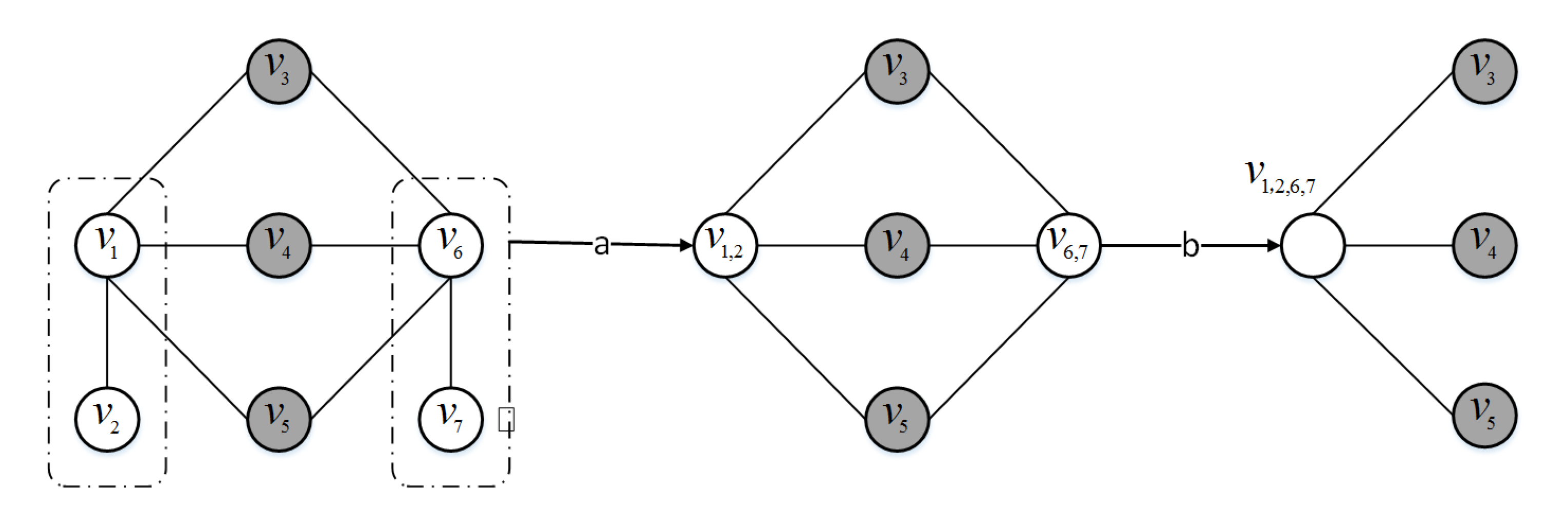
3.4. Hierarchical Network Graph

In this paper, the original network graph $G$ was layered using the network graph layering algorithm, and a series of subnetwork graphs $G_0, G_1, \cdots , G_n$ with smaller scale were generated, where $G_0=G$.

The hierarchical network algorithm includes two key parts: edge folding and vertex merging.

Edge Folding. Edge folding can effectively preserve the first-order adjacency between vertices. As shown in Figure 2, vertex $v_2$ is connected with vertex $v_1$, and neither of them exist in any closed loop, which means that vertex $v_2$ and vertex $v_1$ have first-order proximity. The algorithm performs edge folding on vertices with first-order proximity in network graph. As shown in process a of Figure 2, the edges $(v_1,v_2)$ are folded, and the vertex $v_1$ and the vertex $v_2$ are merged into one vertex $v_{1,2}$. Vertices with first-order adjacency in the network graph can be merged using the edge folding method, and the merged subnetwork graph sufficiently preserves the first-order adjacency between vertices in the original network graph.

Vertex merging. In the real-world network graph, a large number of vertices cannot be merged by the edge folding algorithm, because there may be a large number of common neighbors among these vertices; that is, they may have high second-order adjacency. In this paper, vertex merging method was used to merge these vertices with higher second-order adjacency, which can effectively reduce the scale of network graph and preserve the second-order adjacency between vertices in the original network graph. As shown in process b of Figure 2, in the network diagram, vertices $v_{1,2}$ and $v_{6,7}$ had common neighbors $v_3$, $v_4$, and $v_5$, and they had high second-order proximity, so they could be merged into one vertex $v_{1,2,6,7}$ by using vertex merging method.

Hierarchical network graph algorithm NetLay. The hierarchical network graph algorithm folds the edges of each layer of network graph first, and then merges the vertices up until the generation of the sub-network that is smaller than specific threshold (the threshold set in this paper is the number of vertices that is less than half of their total number in the original network graph). The hierarchical network graph algorithm is shown in Algorithm 1:

Algorithm 1: Network graph layering algorithm NetLay.

Input: Network graph $G=(V,E)$. Output: A subnetwork diagram that scales down layer by layer $G_0, G_1, \cdots , G_n$. 1. n = 0 2. $G_0$ = G 3. while $\left|V_n\right|>threshold$: 4.   $G_n$ = Edge Collapsing  ($G_n$) 5.   $G_{n+1}$ = Vertex Merging  ($G_n$) 6.    n = n + 1 7. return $G_0, G_1, \cdots , G_n$

Because the edge folding algorithm retained the original graph first-order proximity and the vertex merging algorithm retained the original graph second-order proximity, the layered network graph had similar structural characteristics with the original network graph. The layered networks also preserved the local structure of original graph, but their scale was much reduced when compared to the original graph, which made them able to easily map low-dimensional vector space.

In Figure 3, $v_3$ and $v_4$ have third-order proximity in the left network diagram, and it can also be seen from the figure that $v_3$ and $v_4$ have high structural similarity. According to the above hierarchical network algorithm, edge folding and vertex merging were performed on the left network graph to obtain the right subnetwork graph. It can be seen that since $v_1$ and $v_2$ were merged into one vertex $v_{1,2}$, the third-order adjacency between $v_3$ and $v_4$ was reduced to the second-order adjacency, and the similar structural characteristics were still retained.

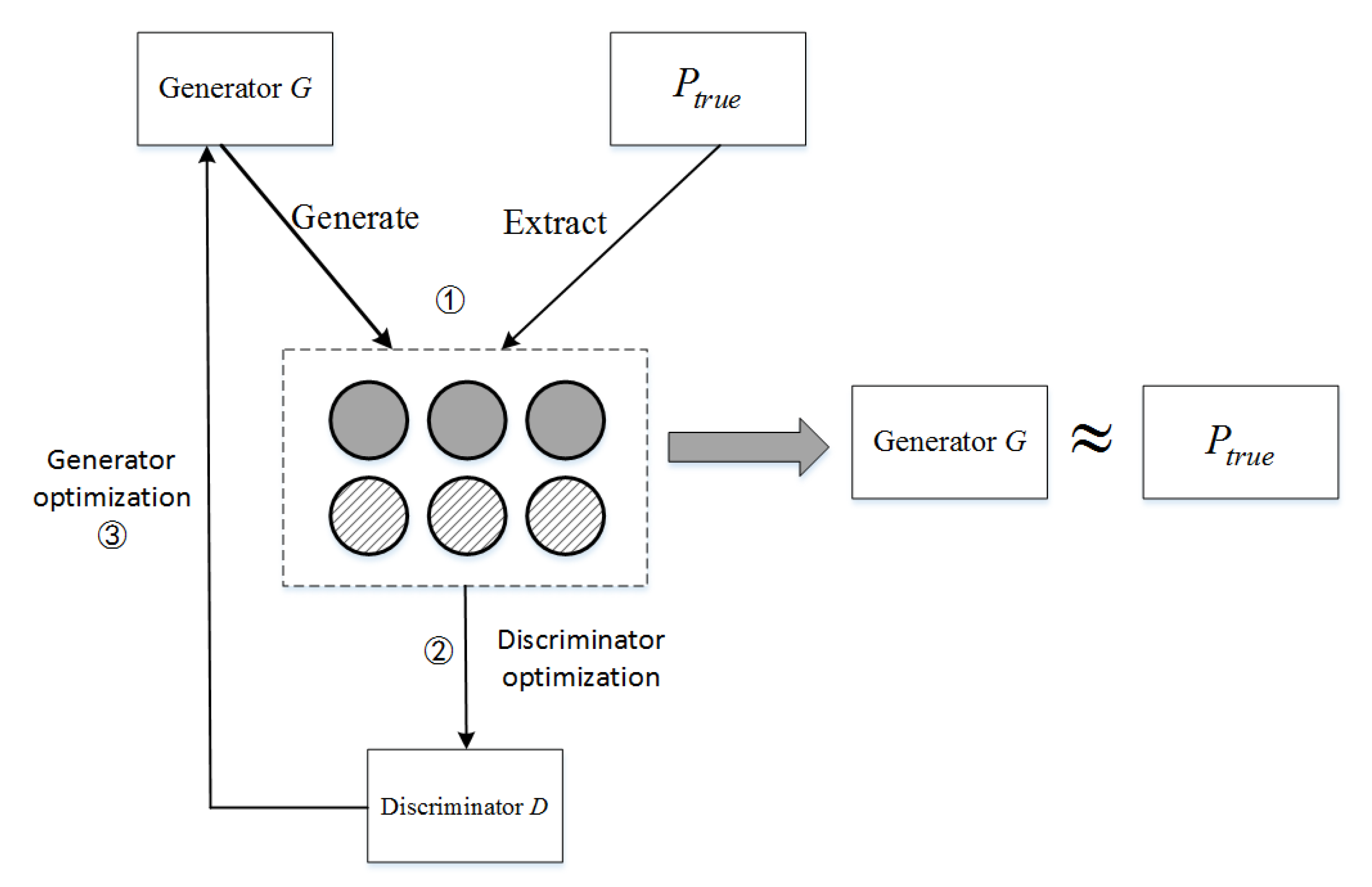
3.5. EmbedGAN Network Framework

After layering the network, the network graph of each layer was recursively processed with the generative countermeasure network embedGAN. The embedGAN frame consists of a generator $G(v|v_c;{\theta }_G)$ and discriminator $G(v|v_c;{\theta }_D)$.

For a given vertex $v_c$, the conditional probability $p_{ture}(v|v_c)$ represents the true connectivity distribution of the vertex $v_c$. The generator G extracts nodes by random walk with deviation [20], and sets two offset coefficients to control random walk, trying to generate a real direct neighbor $v$ that is as similar to $v_c$ as possible, so as to fit the real connectivity distribution $p_{ture}(v|v_c)$ of $v_c$. The discriminator distinguishes as closely as possible whether these vertices are actually connected with $v_c$ or whether they are generated by generator. The generator and the discriminator are similar to playing a max–min game about the cost function $V(G,D)$, and the optimal parameters of the generator and the discriminator are determined by alternately maximizing and minimizing the cost function $V(G,D)$, as shown in Formula (4). In this competition, the generator and the discriminator make progress together until the discriminator cannot distinguish the distribution generated by the generator from the real connectivity distribution.

$$\begin{array}{l}{\min }_{{\theta }_G}{\max }_{{\theta }_D}V(G,D)=\\ {\displaystyle \sum _{c=1}^V(E_{v-p_{\mathrm{tuk}}\left({\cdot |}_c\right)}\left[\mathrm{lb}D\left(v,v_c;{\theta }_D\right)\right]+}\\ E_{~G\left(\cdot \mid v_c:{\theta }_G\right)}\left[\mathrm{lb}\left(1-D\left(v,v_c;{\theta }_D\right)\right)\right])\end{array}$$

(4)

Discriminator optimization. In this paper, the discriminator $G(v|v_c;{\theta }_D)$ is defined as the sigmoid function of the inner product represented by the low-dimensional vector of two input vertices, as shown in Formula (5):

$$D\left(v,v_c\right)=\sigma \left(d_v^{\mathrm{T}}{d}_{vc}\right)=\frac{1}{1+\exp \left(-d_v^{\mathrm{T}}{d}_{vc}\right)}$$

(5)

where $d_v$ and $d_{vc}$ are low-dimensional vector representations corresponding to vertices $v$ and $v_c$ in the low-dimensional vector representation matrix of the discriminator. When the inputs are negative samples generated by the generator and real positive samples, the discriminator calculates the probability of edge between source node $v_c$ and neighbor node $v$ according to sigmoid function, assigns labels to all positive and negative samples, and compares them with real labels. According to the comparison results, the gradient descent method is used to update the low-dimensional vector representations $d_v$ and $d_{vc}$ of vertices $v$ and $v_c$ to maximize the probability that the discriminator assigns correct labels to positive and negative samples.

In the process of random gradient descent, the learning rate set by the algorithm decreases with the increase in iteration times. When the gradient is large, the learning rate is relatively large, which makes the solution faster. When the gradient decreases slowly, the learning rate also decreases, which makes the gradient decreasing process more stable, as shown in Formula (6):

$${\nabla }_{{\theta }_D}V(G,D)=\{\begin{array}{l}{\nabla }_{{\theta }_D}\mathrm{lb}D\left(v,v_c\right)\hspace{1em}v~p_{\mathrm{true}}\hfill \\ {\nabla }_{{\theta }_D}\left(1-1\mathrm{b}D\left(v,v_c\right)\right)\hspace{1em}v~G\hfill \end{array}$$

(6)

Generator optimization. The generator samples as many negative samples as possible that are close to the true connectivity distribution to minimize the probability that the discriminator correctly assigns labels to positive and negative samples. Since the generator’s sampling is discrete, the gradient of $V(G,D)$ with respect to ${\theta }_G$ is calculated as shown in Formula (7). According to the feedback information of the discriminator, the generator uses gradient descent method to update the low-dimensional vector representation matrix of the generator.

$$\begin{array}{l}{\nabla }_{{\theta }_G}V(G,D)={\nabla }_{{\theta }_G}{\displaystyle \sum _{c=1}^V{E}_{v-G\left(\mid v_c\right)}}\left[\mathrm{lb}\left(1-D\left(v,v_c\right)\right)\right]=\\ {\displaystyle \sum _{c=1}^V{\displaystyle \sum _{i=1}^N{\nabla }_{{\theta }_G}}}G\left(v_i\mid v_c\right)\mathrm{lb}\left(1-D\left(v_p{v}_c\right)\right)=\\ {\displaystyle \sum _{c=1}^V{E}_{mG\left(\cdot \mid v_c\right)}}\left[{\nabla }_{{\theta }_G}\mathrm{lb}G\left(v\mid v_c\right)\mathrm{lb}\left(1-D\left(v,v_c\right)\right)\right]=\\ {\displaystyle \sum _{c=1}^V{\displaystyle \sum _{i=1}^{N}G}}\left(v_i\mid v_c\right){\nabla }_{{\theta }_G}\mathrm{lb}G\left(v_i\mid v_c\right)\mathrm{lb}\left(1-D\left(v_b,v_c\right)\right)\end{array}$$

(7)

Generator sampling method. The generator uses a biased random walk with step size $l$ to sample the negative samples. If the source node is $v_c$, the current node is $v$, and the previous hop node is $t$, then the next hop node $x$ needs to be determined. Define $N(v)$ as the set of direct neighbors of vertex $v$ (that is all vertices directly connected with $v$ in the graph), and the transition probability between $v$ and its neighbor $v_i\in N(v)$ is defined as shown in Formula (8):

$$p_v\left(v_i\mid v\right)=\frac{\exp \left(g_{v_i}^{\mathrm{T}}{g}_v\right)}{{\displaystyle \sum _{v_j\in N(v)}\exp }\left(g_{v_j}^{\mathrm{T}}{g}_v\right)}$$

(8)

where $g_{v_i}$ and $g_v$ are k-dimensional vector representations of vertices $v_i$ and $v$ relative to the generator.

At each step, the transition probability $p_v(v_i|v)$ between the current node $v$ and its neighbor nodes is calculated according to Formula (8). Then the transition probability $p_v(v_i|v)$ is weighted by the deviation coefficient $\alpha$ of random walk, and the nonstandard transition probability $w_v(v_i|v)=\alpha (t,v_i)\cdot p_v(v_i|v)$ is obtained. According to the nonstandard transition probability, the next hop node of random walk is extracted.

$\alpha (t,v_i)$ is set as shown in Formula (9):

$$\alpha \left(t,v_i\right)=\{\begin{array}{l}\frac{1}{p},d_{t{v}_i}=0\hfill \\ 1,d_{t{v}_i}=1\hfill \\ \frac{1}{q},d_{t{v}_i}=2\hfill \end{array}$$

(9)

where $d_{t{v}_i}$ represents shortest path distance between node $t$ and $v_i$, and parameters $p$ and $q$ control the speed of the neighborhood away from source node $v_c$ in the process of travel, so that the form of travel can be converted between width-first search and depth-first search.

Parameter $p$ controls the probability of backtracking forward. As shown in Figure 4, when the parameter $p$ is set to a higher value (greater than $max(q,1)$), the probability of the next hop node retraversing vertices is reduced. Conversely, when $p$ is set to a lower value (less than $min(q,1)$), the probability of backtracking forward to vertex $t$ increases.

Parameter $q$ is responsible for controlling whether the next hop node is close to the previous hop node $t$. As shown in Figure 4, when the parameter $q>1$, the random walk is similar to the width-first search and tends to visit the vertices connected to the previous hop node $t$. When the parameter $q<1$, the random walk is similar to the depth-first search and tends to visit vertices far from the node t of the previous hop.

The random walk can be controlled by changing the size of parameters $p$ and $q$. In this way, the extracted nodes are not always far away from the given source node $v_c$, and the sampling efficiency is thus improved.

When the non-standard metastatic probability $w_v(v_i,v)$ is obtained, one node is selected as the next hop node $x$ using the alias method [21]. When the step of the swing reaches the length of the set, the current node $v$ is extracted as a negative sample vertex. The sampling policy of the generator is shown in Algorithm 2.

Algorithm 2: Builder sampling strategy

Input. Network graph G = (V, E), the vector of the vertices in the figure represents ${\left\{g_i\right\}}_{i\in v}$, step information d between the steps of the steps, the deviation parameters p and q, the source node $v_c$. Output. Pat out node $v_{g,e}$. 1. $t=v_c,v=v_c$ 2. for j in range(l): 3.  for $v_i$ in $N(v)$: 4.      calculate relevance probability $p_v(v_i|v)$ according to Equation (5) 5.     if $d_{t{v}_i}=0$: 6.       ${\mathrm{w}}_{\mathrm{v}}\left({\mathrm{v}}_{\mathrm{i}}|\mathrm{v}\right)=\frac{1}{\mathrm{p}}\cdot {\mathrm{p}}_{\mathrm{v}}\left({\mathrm{v}}_{\mathrm{i}}\mid \mathrm{v}\right)$ 7.     elif ${\mathrm{d}}_{{\mathrm{tv}}_i}=2$: 8.       ${\mathrm{w}}_{\mathrm{v}}\left({\mathrm{v}}_{\mathrm{i}}\mid \mathrm{v}\right)=\frac{1}{\mathrm{q}}\cdot {\mathrm{p}}_{\mathrm{v}}\left({\mathrm{v}}_{\mathrm{i}}\mid \mathrm{v}\right)$ 9.     else: 10.       ${\mathrm{w}}_{\mathrm{v}}\left({\mathrm{v}}_{\mathrm{i}}\mid \mathrm{v}\right)={\mathrm{p}}_{\mathrm{v}}\left({\mathrm{v}}_{\mathrm{i}}\mathrm{v}\right)$ 11. select $x$ with Alias Method 12. $\mathrm{t}=\mathrm{v},\mathrm{v}=\mathrm{x}$ 13. ${\mathrm{v}}_{\mathrm{gen}}=\mathrm{x}$ 14. return ${\mathrm{v}}_{\mathrm{gen}}$

Path from source node $v_c$ to extracted vertex $v_{gen}$ is $P_{v_c\to v_{\mathrm{gen}}}=\left(v_{r_0}, v_{r_1}, \cdots , v_{r_m}\right)$, where $v_{r_0}=v_c$ and $v_{r_m}=v_{gen}$, then connectivity $G(v|v_c;{\theta }_G)$ is defined as shown in Formula (10):

$$G\left(v\mid v_c\right)\left({\displaystyle \prod _{j=1}^{m}p}\left(v_{r_j}\mid v_{r_{j-1}}\right)\right)$$

(10)

EmbedGAN Algorithm. The embedGAN algorithm framework is shown in Figure 5. The embedGAN algorithm model takes the input vector as the initial vector representation matrix of the generator and discriminator. In each iteration, the generator generates a certain number of negative samples for each source node, extracts the same number of positive samples and gives them to the discriminator for training, marked by ① in Figure 5. The discriminator assigns labels to positive and negative samples according to its low-dimensional vector representation, and compares them with real labels to get errors. Then it uses the random gradient descent method to update its low-dimensional vector representation to minimize the error, as shown in ② in Figure 5. The discriminator transmits the error information to the generator, and the generator updates its low-dimensional vector representation according to the error information fed back by the discriminator. The generator and the discriminator constantly update their low-dimensional vector representation in confrontation until the discriminator cannot distinguish positive and negative samples, and the low-dimensional vector representation of the generator is the low-dimensional vector representation of the vertex of the final output network graph, as shown in ③ in Figure 5.

The generative countermeasure network embedGAN is used to generate a low-dimensional vector representation algorithm of vertices in the network graph, as shown in Algorithm 3.

Algorithm 3: EmbedGAN Algorithm

Input The network graph $G=(V,E)$, the initial vector of the vertex in the graph represents ${\left\{g_i\right\}}_{i\in v}$, the step size $l$, the deviation parameters $p$ and $q$, and the distance information between vertices $d$. Output The low-dimensional vector of the vertices in the network graph $G$ represents $E_G$. 1. pre-train $\mathrm{G}\left(\mathrm{v}\mid {\mathrm{v}}_{\mathrm{c}};{\theta }_{\mathrm{G}}\right)$ and $\mathrm{D}\left(\mathrm{v},{\mathrm{v}}_{\mathrm{c}};{\theta }_{\mathrm{D}}\right)$ 2. while embed GAN no converge: 3.    for G-steps: 4.     $\mathrm{G}\left(\mathrm{v}\mid {\mathrm{v}}_{\mathrm{c}};{\theta }_{\mathrm{G}}\right)$ generates $\mathrm{s}$ vertices for each vertex ${\mathrm{v}}_{\mathrm{c}}$ according to Algorithm 2 5.      update ${\theta }_{\mathrm{G}}$ according to Equations $(7)$, $(8)$ and $(10)$ 6.      update ${\left\{g_i\right\}}_{i\in v}$ 7.    for D-steps: 8. sample $t$ positive vertices from ground truth and $t$ negative vertices from $\mathrm{G}\left(\mathrm{v}\mid {\mathrm{v}}_{\mathrm{c}};{\theta }_{\mathrm{G}}\right)$ for each vertex ${\mathrm{v}}_{\mathrm{c}}$ 9. update ${\theta }_{\mathrm{D}}$ according to Equations $(5)$ and $(6)$ 10. update ${\left\{{\mathrm{d}}_{\mathrm{i}}\right\}}_{\mathrm{i}\in \mathrm{V}}$ 11. return ${\left\{g_i\right\}}_{i\in V},{\left\{d_i\right\}}_{i\in V}$

3.6. GAHNRL Algorithm

The process of the GAHNRL algorithm in this paper is as follows:

(1) According to the network graph layering algorithm in Algorithm 1, the original network graph $G$ is layered to generate a series of subnetwork graphs $G_0, G_1, \cdots , G_n$ with reduced scale layer by layer, where $G_0=G$.

(2) The smallest subnetwork graph $G_n$ is processed using Node2vec algorithm, and generate the initial vector representation of vertices in this layer subnetwork graph.

(3) Starting from $G_n$, the initial vector representation of each layer of subnetwork graph and vertex in the graph is recursively input into the generative countermeasure network for training.

(4) The algorithm learns to obtain low-dimensional vector representation of vertices in $G_n$ using embedGAN algorithm in Algorithm 3, taking the learned low-dimensional vector representation as initial vector representation of the upper layer subnetwork graph $G_{n-1}$, recursively carrying out backtracking learning until learning the initial network graph $G_0$, and finally obtaining low-dimensional vector representation $E_{G_0}$ of all vertices.

(5) According to the similarity between vertices calculated by $E_{G_0}$, the algorithm predicts whether there is an edge between two nodes.

GAHNRL algorithm framework is shown in Algorithm 4.

Algorithm 4: GAHNRL Algorithm

Input The network graph $G=(V,E)$, the step size $l$, the deviation parameters $p$ and $q$, and the distance information between vertices $d$. Output The low-dimensional vector of the vertices in the network graph $G$ represents $E_G$. 1.$G_0=G$ 2. for $\mathrm{j}$ in range ($1,\mathrm{n}$): 3.  $G_j=NetLay\left(G_{j-1}\right)$ 4.  ${\mathrm{initE}}_{G_n}=\mathrm{Node}2\mathrm{vec}\left(G_n\right)$ 5.  ${\mathrm{E}}_{{\mathrm{G}}_{\mathrm{n}}}=$ EmbedGAN ($G_n$,${\mathrm{initE}}_{G_n}$) 6. for $i=n-1$ to 0: 7.  ${\mathrm{initE}}_{G_n}={\mathrm{E}}_{{\mathrm{G}}_{i+1}}$ 8.  ${\mathrm{E}}_{{\mathrm{G}}_{\mathrm{n}}}=$ EmbedGAN (${\mathrm{G}}_{\mathrm{n}}$,${\mathrm{initE}}_{G_n}$) 9. return ${\mathrm{E}}_{{\mathrm{G}}_{}}$

4. Experiments

4.1. Experimental Dataset

In this paper, four open-source representative real network datasets in different fields are selected, including social network Facebook [22], Wiki-Vote [23], cooperative network CA-GrQc [24], and cellular metabolic network Metabolic [25]. The weight and direction of each edge are ignored in the four datasets, and the detailed information is shown in

Table 1. Network dataset information.

Dataset	N	E
Wiki-Vote	7115	103,689
Facebook	4039	88,234
GA-GrQc	5242	28,980
Metabolic	2349	11,693

, where N represents the number of nodes and E represents the number of edges.

4.2. Evaluation Criterion

In this paper, 10% of the edges randomly selected from original network graph were added to the test set as positive samples, 90% were used as the training set, and the edges randomly generated with the same number of positive samples as the test set were added to the test set as negative samples.

In this paper, precision and AUC were used to evaluate the performance of the algorithm, which are the two most commonly used evaluation indexes in link prediction tasks.

Precision is the proportion of $L$ predicted edges in test set that accurately predict whether there is a link. If there are $L$ positive samples and $L$ negative samples in the test set, the probability that there may be links between vertex pairs in each sample is calculated according to the algorithm and arranged in descending order. If there are $m$ positive samples among the first $L$ samples, then precision is defined as $m/L$.

AUC is the probability that a positive sample and a negative sample are randomly selected from the test set; that is, the positive sample score is higher than the negative sample score. In $n$ independent repeated experiments, there are $n_1$ positive sample scores higher than negative sample scores, and $n_2$ positive sample scores equal to negative sample scores, so AUC is defined as:

$$\mathrm{AUC}=\frac{n_1+0.5\times n_2}{n}$$

(11)

4.3. Experimental Setup

In the algorithm of this paper, the step length $l$ was set to 10, and experiments were carried out on four datasets for different parameters $p$ and $q$. The accuracy of the Metabolic dataset is shown in

Table 2. Experimental results for different parameters.

Parameter	p = 0.5	p = 1.0	p = 1.5
q = 0.5	0.872	0.922	0.919
q = 1.0	0.898	0.927	0.931
q = 1.5	0.909	0.918	0.907

, the Facebook dataset in

Table 3. Experimental results for different parameter settings on Facebook dataset.

Parameter	p = 0.5	p = 1.0	p = 1.5
q = 0.5	0.889	0.929	0.930
q = 1.0	0.919	0.936	0.942
q = 1.5	0.911	0.933	0.910

, the Wiki-Vote dataset in

Table 4. Experimental results for different parameter settings on Wiki-Vote dataset.

Parameter	p =0.5	p =1.0	p = 1.5
q = 0.5	0.841	0.865	0.887
q = 1.0	0.872	0.891	0.903
q = 1.5	0.855	0.887	0.862

, and the CA-GrQc dataset in

Table 5. Experimental results for different parameter settings on CA-GrQc dataset.

Parameter	p = 0.5	p = 1.0	p = 1.5
q = 0.5	0.871	0.868	0.881
q = 1.0	0.878	0.898	0.896
q = 1.5	0.884	0.918	0.863

. From Table 2, Table 3 and Table 4, it can be seen that when parameter $p$ was set to 1.5 and parameter $q$ was set to 1, the experimental effect was the best (see bold face) on three datasets. On the CA-GrQc dataset, when parameter $p$ was set to 1 and parameter $q$ was set to 1, the experimental effect was best, but when parameter $p$ was set to 1.5 and parameter $q$ was set to 1, the experimental effect was not significantly different from the best result; thus, this paper set parameter $p$ to 1.5 and parameter $q$ to 1 for all datasets.

4.4. Result Analysis

In order to prove the stability and accuracy of the experiment, 10 repeated experiments were carried out in this paper, and the average of the 10 experimental results was taken as final result. This section introduces the comparison of link prediction accuracy and AUC between three traditional algorithms and four network representation learning algorithms under the same conditions. The accuracy is shown in

Table 6. Comparison results of different algorithms: accuracy.

Algorithm	Facebook	Facebook	Facebook	Facebook
LP	0.891	0.891	0.891	0.891
Katz	0.610	0.610	0.610	0.610
AA	0.968	0.968	0.968	0.968
LINE	0.897	0.897	0.897	0.897
DeepWalk	0.908	0.908	0.908	0.908
Node2vec	0.912	0.912	0.912	0.912
GraphGan	0.932	0.932	0.932	0.932
GAHNRL	0.942	0.942	0.942	0.942

, and AUC is shown in

Table 7. Comparison results of different algorithms: AUC.

Algorithm	Facebook	Facebook	Facebook	Facebook
LP	0.9546	0.9546	0.9546	0.9546
Katz	0.6098	0.6098	0.6098	0.6098
AA	0.9780	0.9780	0.9780	0.9780
LINE	0.9050	0.9050	0.9050	0.9050
DeepWalk	0.9610	0.9610	0.9610	0.9610
Node2vec	0.9682	0.9682	0.9682	0.9682
GraphGan	0.9705	0.9705	0.9705	0.9705
GAHNRL	0.9814	0.9814	0.9814	0.9814

(the first two optimal values are highlighted in bold).

In Table 6 and Table 7, traditional algorithms include LP, Katz, and AA, and network representation learning algorithms include LINE, DeepWalk, Node2vec, and GraphGAN.

It can be seen from Table 6 and Table 7 that:

(1) The accuracy and AUC of the GAHNRL algorithm in this paper were better than those of the four network representation learning algorithms and the traditional Katz algorithm on four datasets.

(2) Compared with the traditional LP algorithm, the accuracy and AUC value of this algorithm on the other three datasets excluding the Wiki-Vote dataset were superior.

(3) Compared with the traditional AA algorithm, the accuracy and AUC value of this algorithm on the GA-GrQc dataset and metaphysical dataset were better than the AA algorithm, and the AUC value on the Facebook dataset was better than that of the AA algorithm.

Traditional algorithms express the adjacency matrix of network vertices in the form of one-hot, which has high computational cost and cannot maintain the high-order structural characteristics of a network graph. When the number of samples in the training set is reduced, the traditional algorithm cannot maintain the stability of the algorithm, and accuracy is obviously reduced. However, the algorithm in this paper processes the network graph hierarchically, and better preserves the high-order structural characteristics of the original network graph, so it has better stability when the training set samples are few. The accuracy changes in the algorithm in this paper and the traditional algorithms when the number of samples decreases are shown in Figure 6.

The experiment was divided into training sets according to 10~90%, and the accuracy changes under different training set ratios were tested respectively. By observing Figure 6, it can be seen that the AA algorithm was superior to GAHNRL when the training set ratio was 40~90% in the Facebook dataset, and was superior to the Wiki-Vote dataset when the network scale was small and the known trainable edges were sufficient. However, when the training set ratio was 10~30%, the known edges available for training in the network decreased. The accuracy of the AA algorithm was obvious, as shown in Figure 7. AA algorithm uses one-hot format, which takes up more memory, while the GAHNRL algorithm uses low-dimensional vector to represent adjacency matrix, so the memory occupancy rate is smaller than that of the AA algorithm. On the whole, the GAHNRL algorithm has less fluctuation and better performance.

5. Conclusions

Link prediction is an important research direction for complex network analysis, and shows strong application prospects. However, traditional link prediction algorithms are generally designed based on the sparse representation of adjacency matrices, which have high computational cost and low efficiency, cannot effectively preserve high-order structural features of network graphs, and cannot run on large-scale networks. To address these issues, we propose a GAN (generative adversarial network)-based link prediction algorithm. The algorithm retains the local characteristics and high-order structural characteristics of the original network graph, and applies the generative adversarial network model to network representation learning to achieve better results. The obtained vector representation is used as the initial vector representation of the upper-layer network graph to be iteratively solved to solve the problem of local minima that may be generated by random initialization. The experimental results show that the performance of this algorithm is more stable compared with LP, Katz, and other algorithms. In the next step, the algorithm optimization for heteregenous and dynamic networks should be carried out, adding tags and node-attribute information to broaden the algorithm’s application scenarios.