Asynchronous and Decoupled HIL Simulation of a DC Nanogrid
Abstract
:1. Introduction
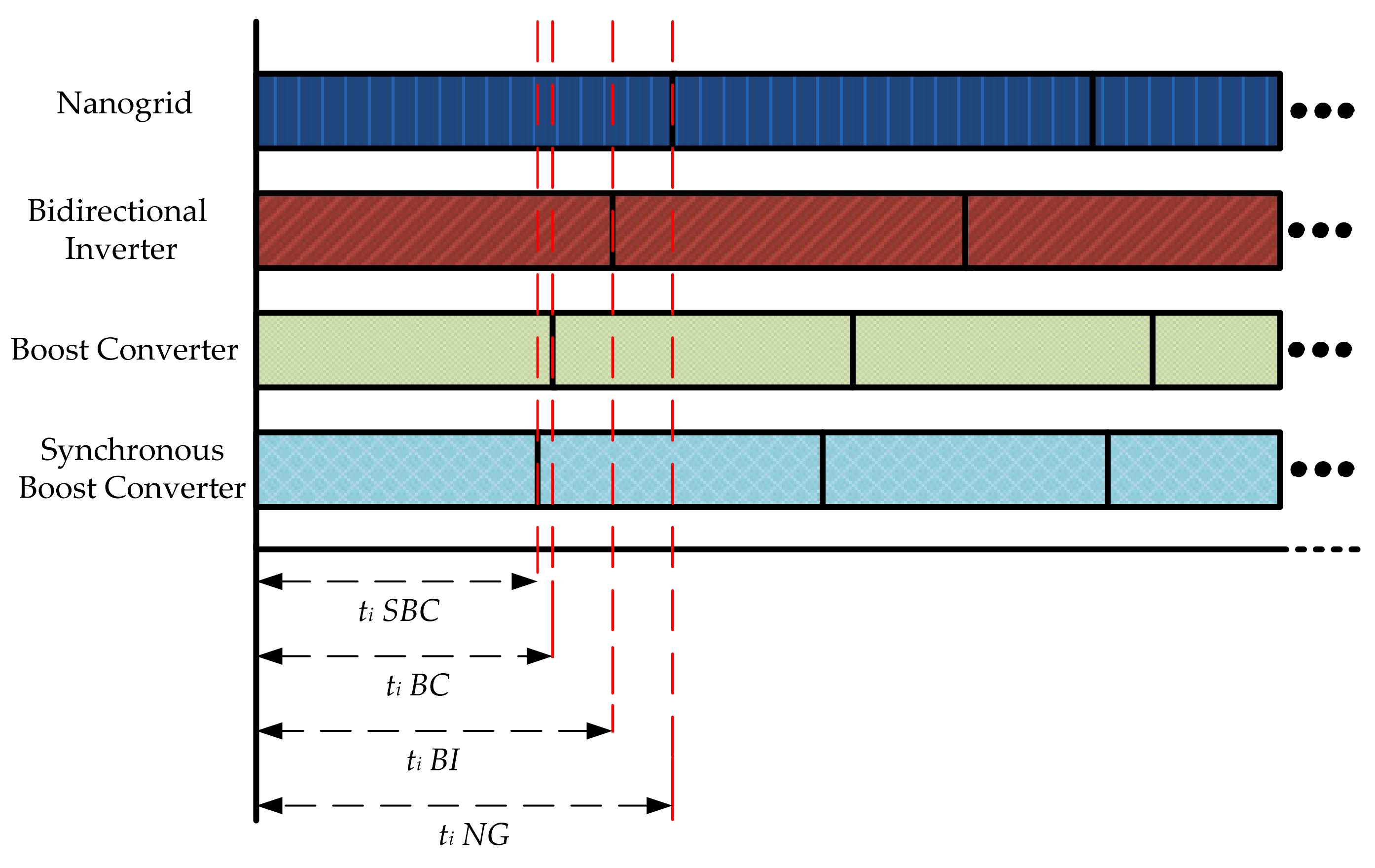
2. Proposed HIL Simulation for NG
3. Methodology
3.1. DC Nanogrid Topology
3.2. DC Nanogrid Model
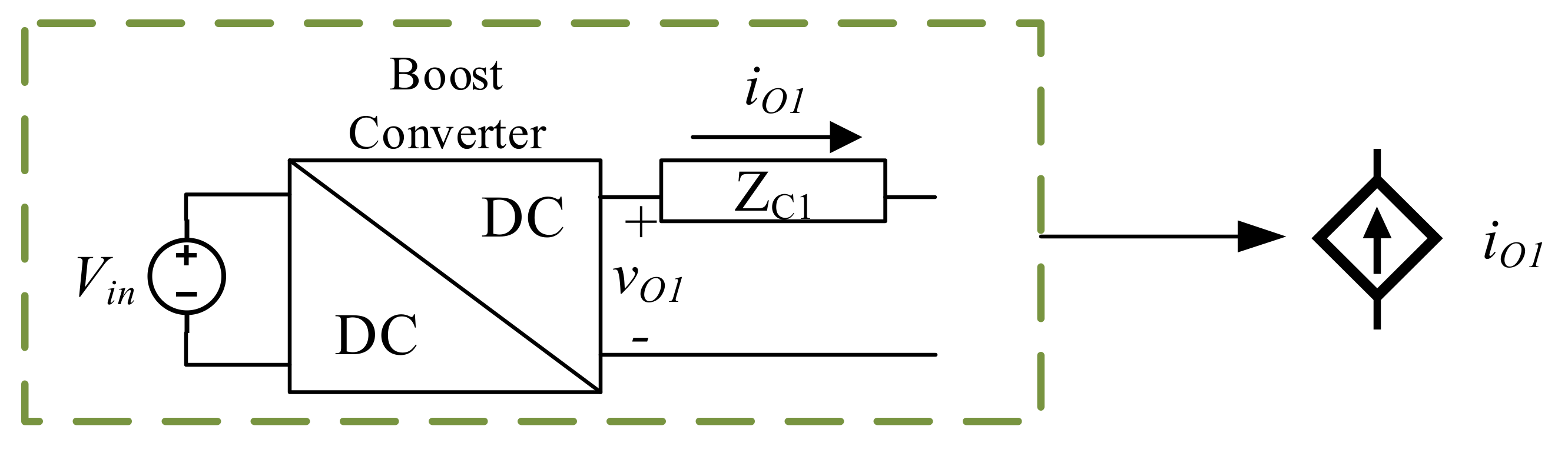
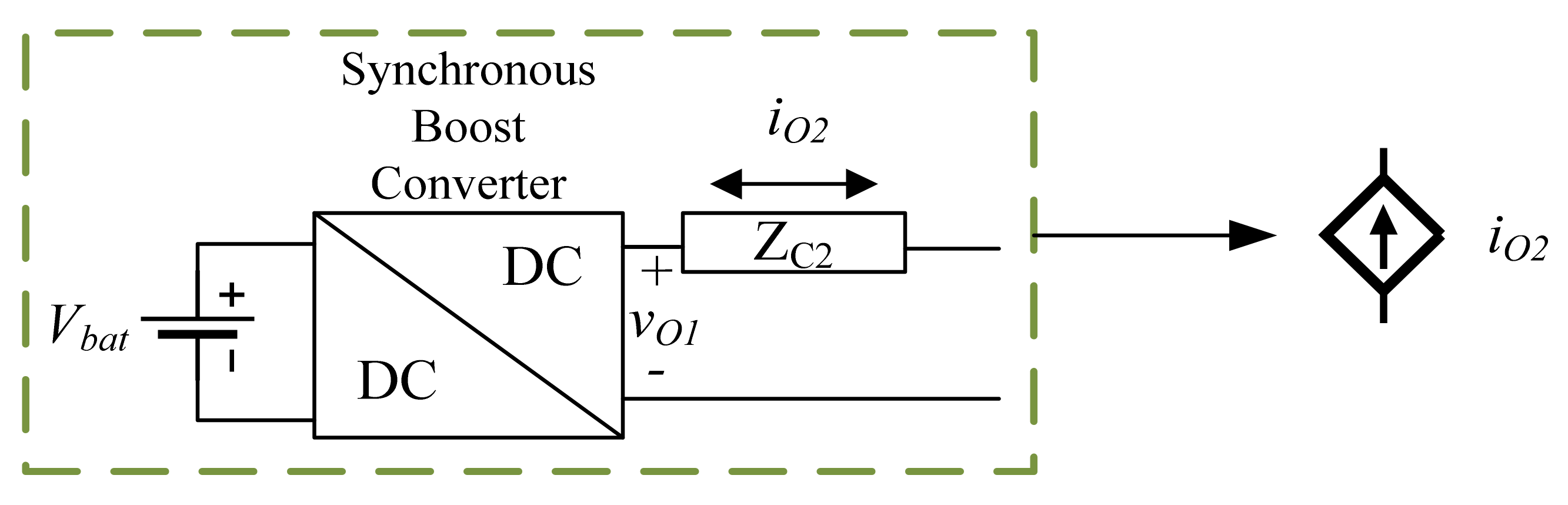
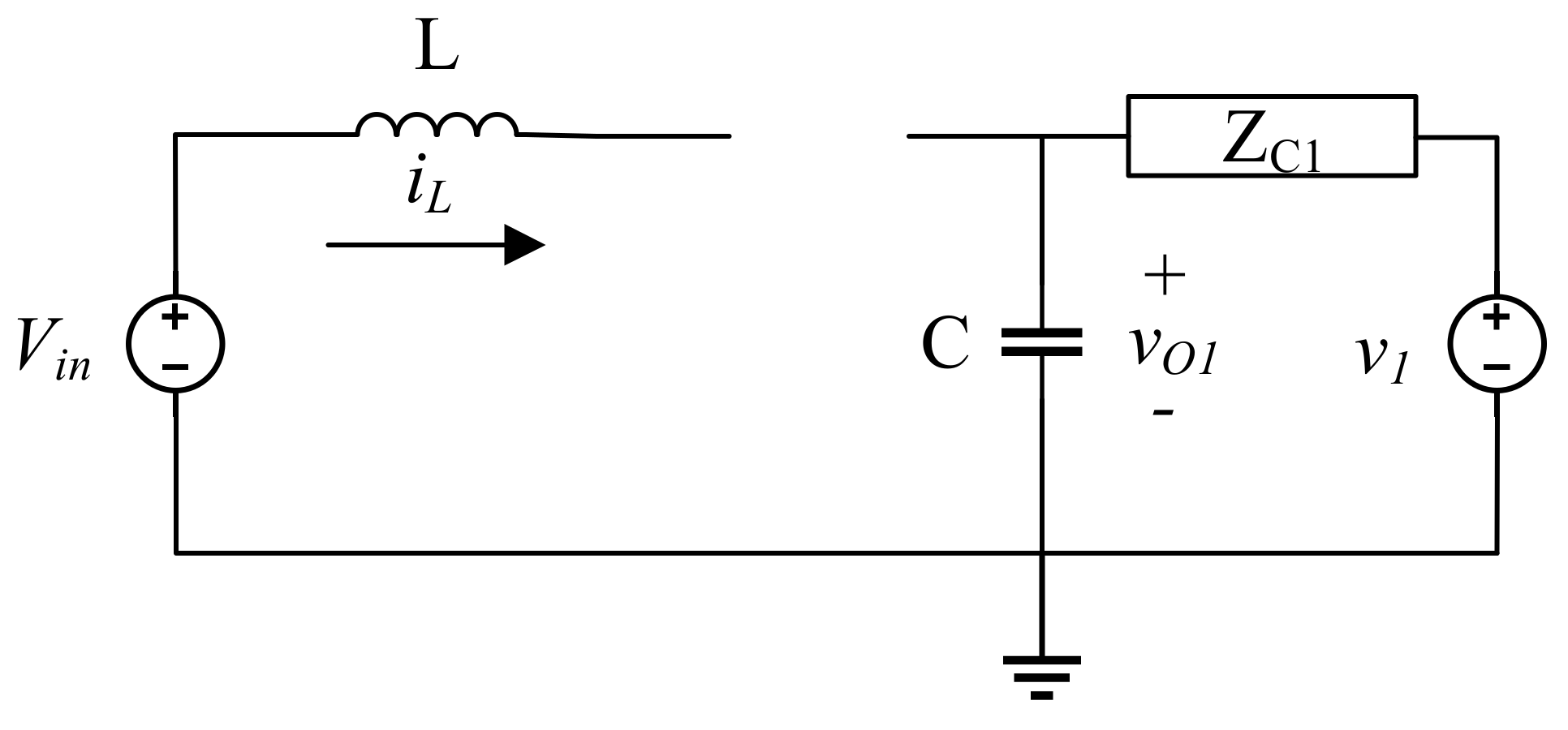
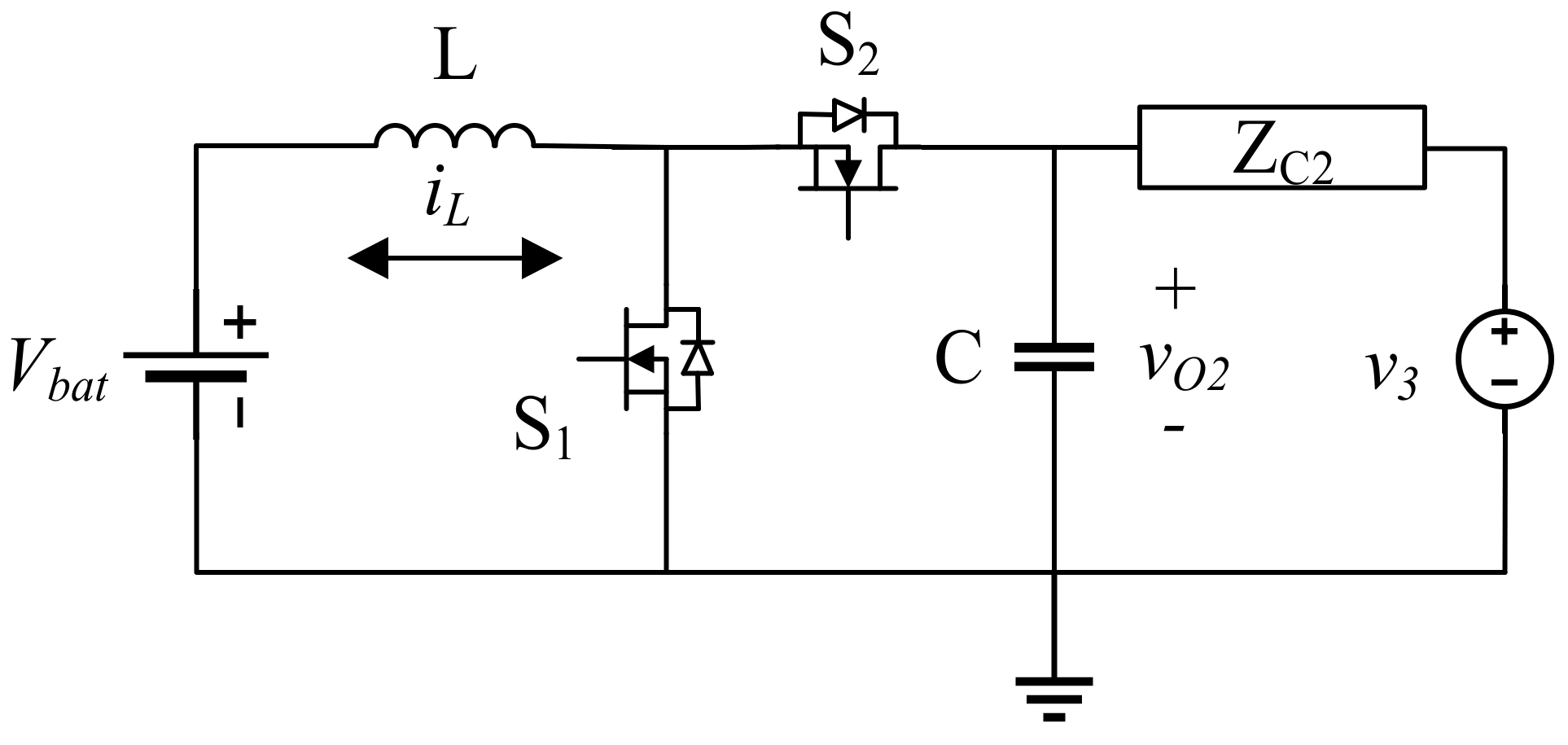
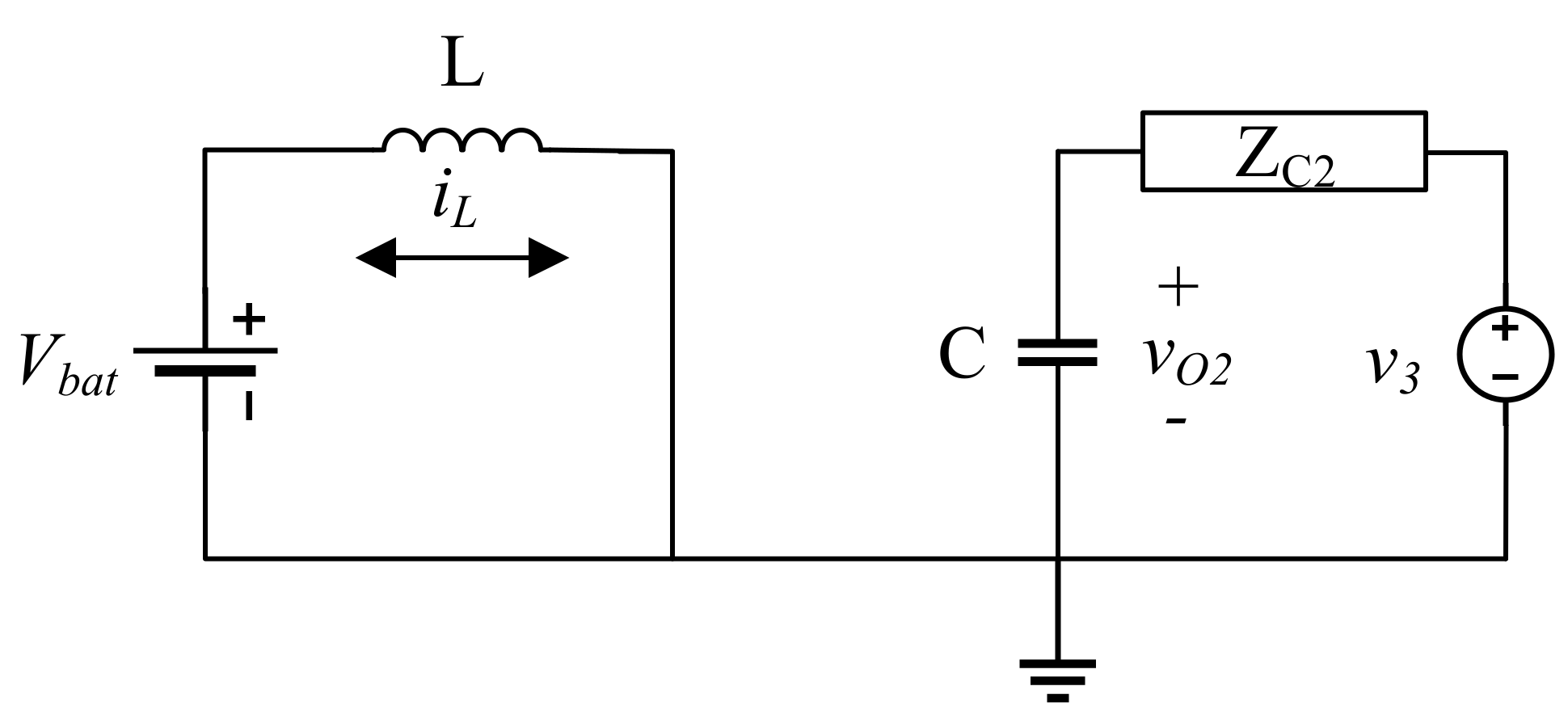
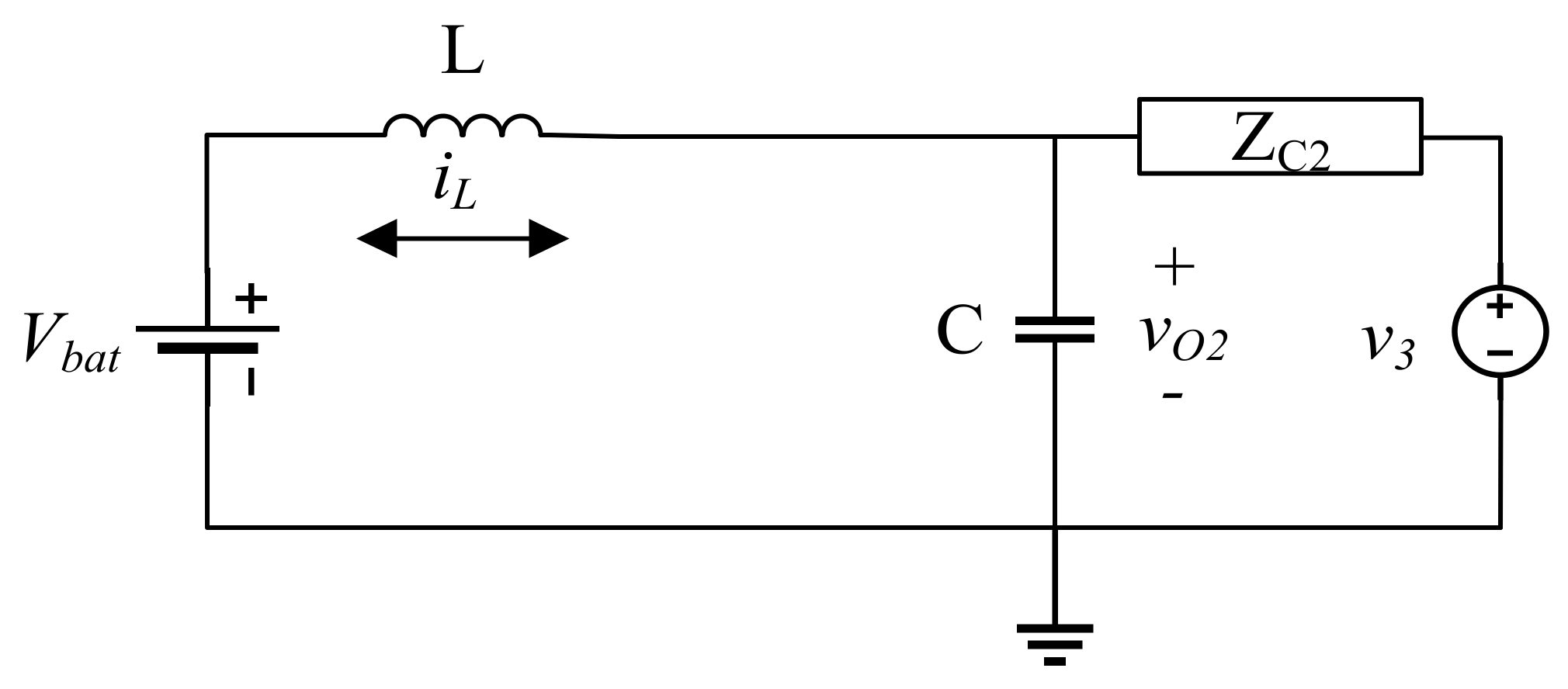
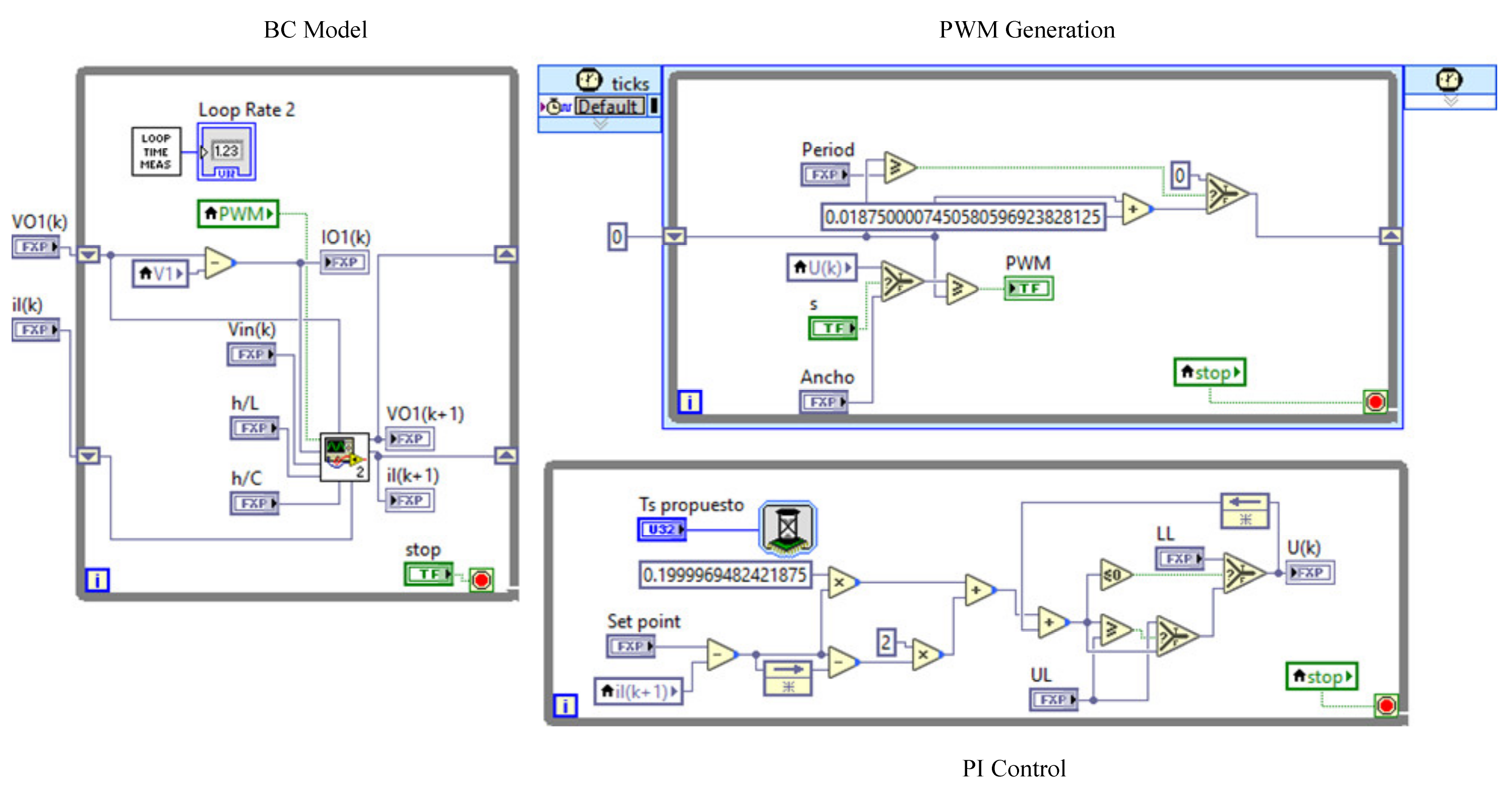
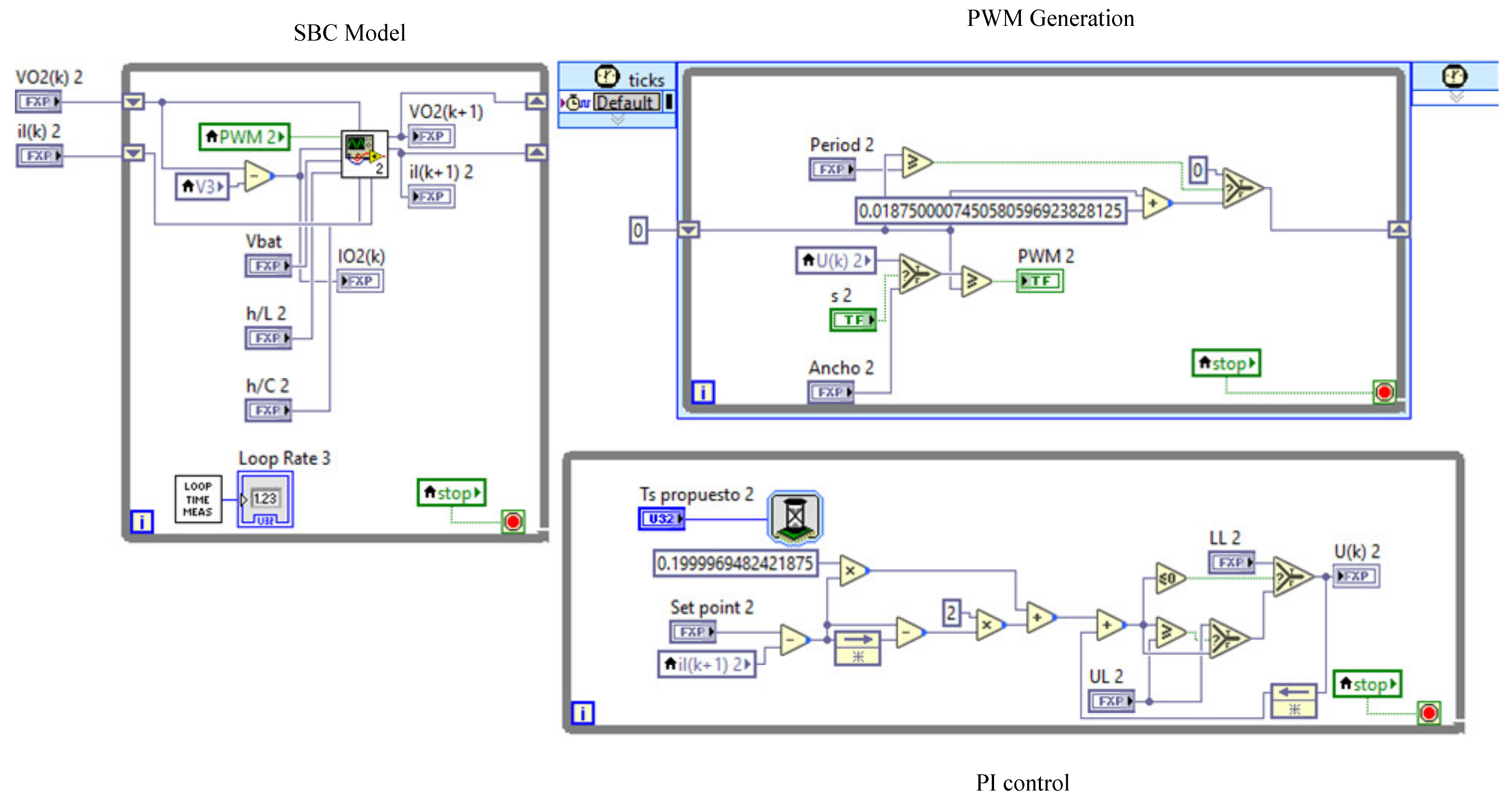
3.3. Power Converter Models
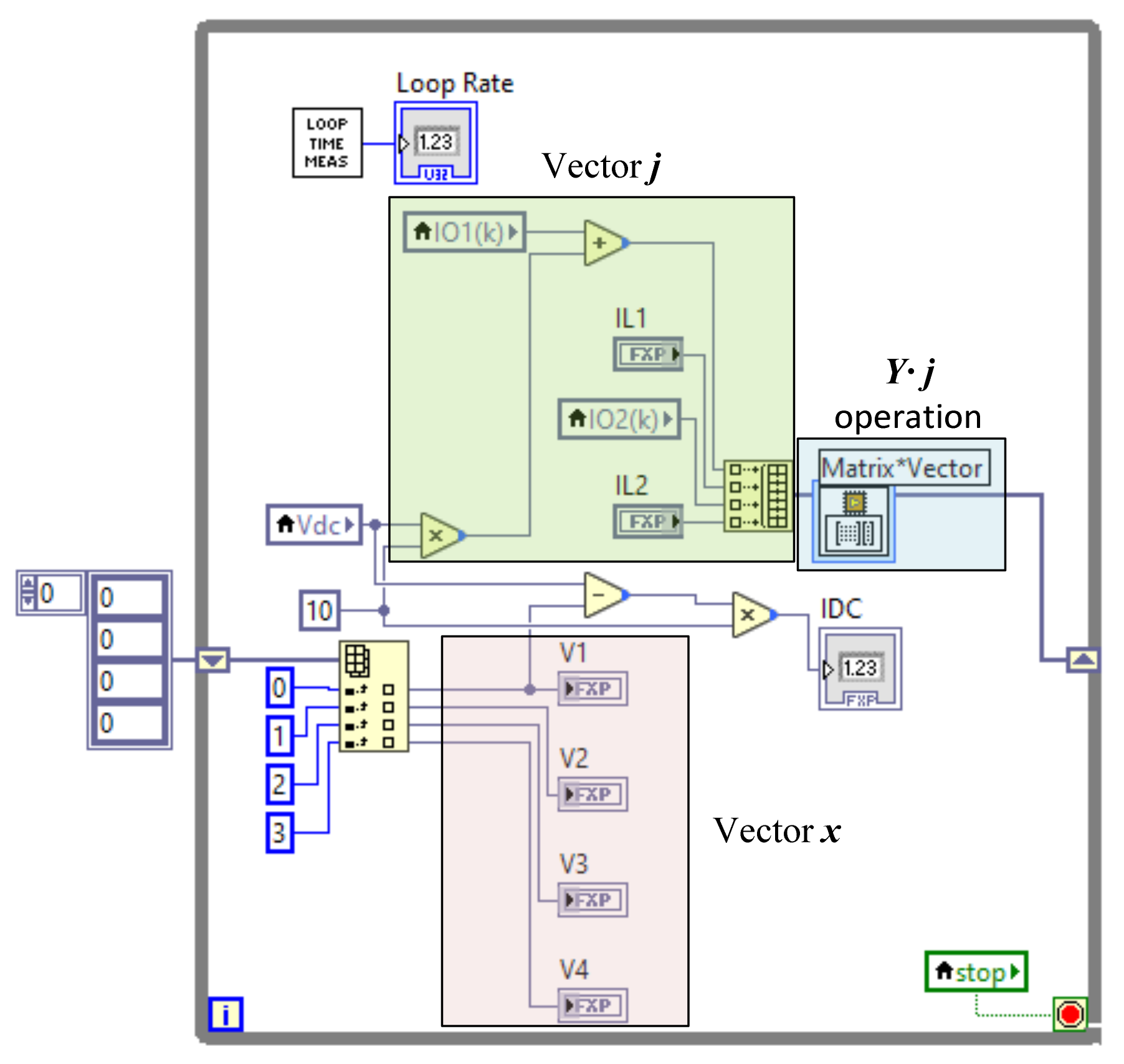
3.4. FPGA Implementation
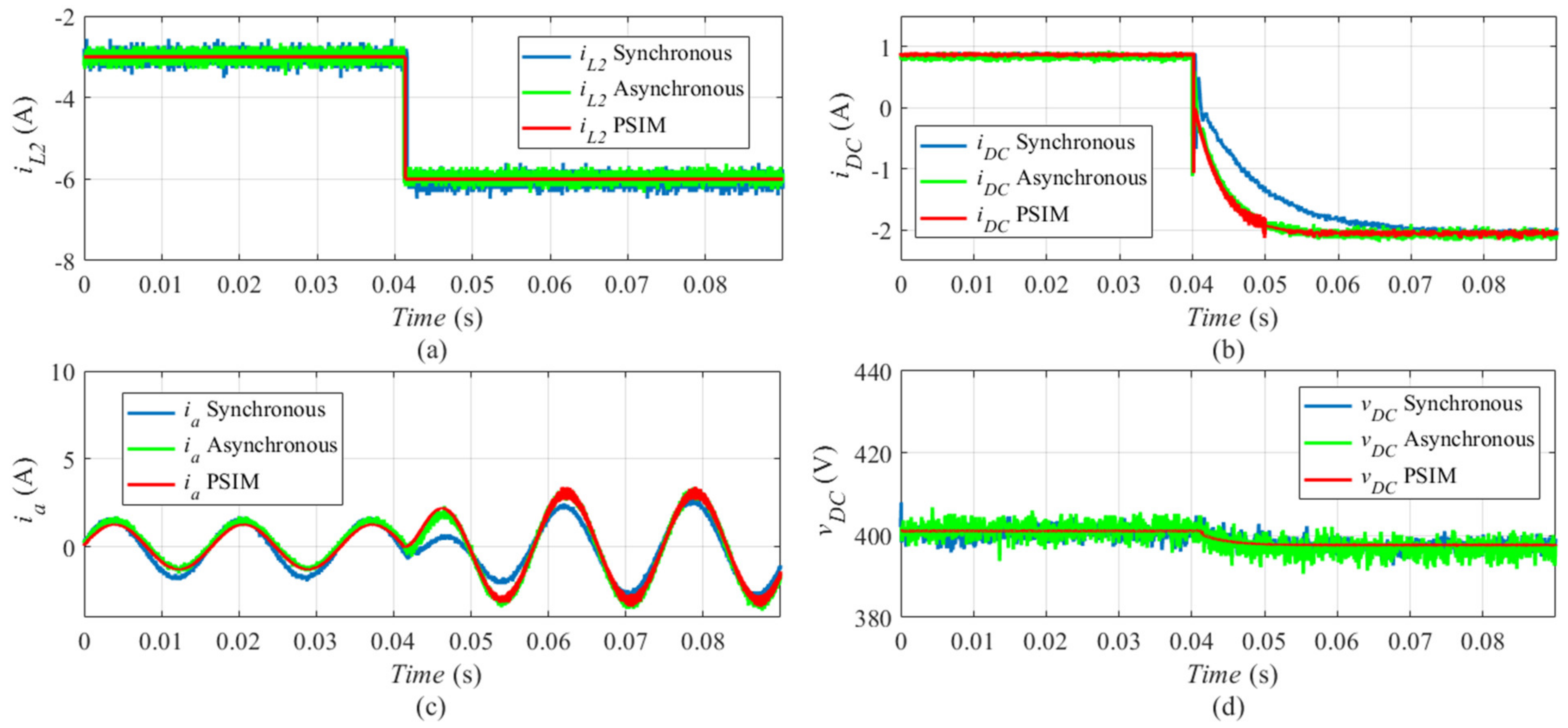
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| DG | Distributed generation |
| NG | Nanogrid |
| AC | Alternate current |
| DC | Direct current |
| RES | Renewable energy system |
| MG | Microgrids |
| HIL | Hardware In the Loop |
| FPGA | Field Programmable Gate Array |
| DSP | Digital Signal Processor |
| ti | Integration Time |
| NAM | Nodal Analysis Method |
| SS | State Spaces |
| BC | Boost converter |
| Vin | Input voltage of the BC |
| SBC | Synchrounous Boost Converter |
| Vbat | Battery Voltage connected to SBC |
| BI | Bidirectional Power inverter |
| iLx | Load current x |
| iL | Inductor current of the BC and SBC |
| iOx | DC/DC converter output current |
| vOx | DC/DC converter output voltage |
| ZCx | Impedance between the NG and the DC/DC converter |
| ZLx | Impedance between the NG nodes |
| vxn | The phase ‘x’ inverter voltage |
| vX | The phase ‘X’ grid voltage |
| ix | The phase ‘x’ inverter current |
References
- Yerasimou, Y.; Kynigos, M.; Efthymiou, V.; Georghiou, G.E. Design of a Smart Nanogrid for Increasing Energy Efficiency of Buildings. Energies 2021, 14, 3683. [Google Scholar] [CrossRef]
- Burmester, D.; Rayudu, R.; Seah, W.; Akinyele, D. A review of nanogrid topologies and technologies. Renew. Sustain. Energy Rev. 2017, 67, 760–775. [Google Scholar] [CrossRef]
- Goikoetxea, A.; Canales, J.M.; Sanchez, R.; Zumeta, P. DC versus AC in residential buildings: Efficiency comparison. In Proceedings of the Eurocon, Zagreb, Croatia, 1–4 July 2013. [Google Scholar]
- Xum, J.; Wang, K. FPGA-Based Sub-Microsecond-Level Real-Time Simulation for Microgrids With a Network-Decoupled Algorithm. IEEE Trans. Power Deliv. 2020, 35, 987–998. [Google Scholar]
- Etemadi, A.H.; Davison, E.J.; Iravani, R. A Decentralized Robust Control Strategy for Multi-DER Microgrids—Part II: Performance Evaluation. IEEE Trans. Power Deliv. 2012, 27, 1854–1861. [Google Scholar] [CrossRef]
- Jeon, J.; Kim, J.; Kim, H.; Kim, S.; Cho, C.; Kim, J.; Ahn, J.; Nam, K. Development of Hardware In-the-Loop Simulation System for Testing Operation and Control Functions of Microgrid. IEEE Trans. Ind. Electron. 2010, 25, 2919–2929. [Google Scholar] [CrossRef]
- Wang, J.; Song, Y.; Wendong, J.G.; Monti, A. Development of a Universal Platform for Hardware In-the-Loop Testing of Microgrids. IEEE Trans. Ind. Inf. 2014, 10, 2154–2165. [Google Scholar] [CrossRef]
- Xia, Y.; Wei, W.; Peng, Y.; Yang, P.; Yu, M. Decentralized Coordination Control for Parallel Bidirectional Power Converters in a Grid-Connected DC Microgrid. IEEE Trans. Smart Grid 2018, 9, 6850–6861. [Google Scholar] [CrossRef]
- Yang, P.; Xia, Y.; Yu, M.; Wei, W.; Peng, Y. A Decentralized Coordination Control Method for Parallel Bidirectional Power Converters in a Hybrid AC–DC Microgrid. IEEE Trans. Ind. Electron. 2018, 65, 6217–6228. [Google Scholar] [CrossRef]
- Yoo, C.; Choi, W.; Chung, I.; Won, D.; Hong, S.; Jang, B. Hardware-in-the-loop simulation of DC microgrid with Multi-Agent System for emergency demand response. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Huang, Z.; Dinavahi, V. An Efficient Hierarchical Zonal Method for Large-Scale Circuit Simulation and Its Real-Time Application on More Electric Aircraft Microgrid. IEEE Trans. Ind. Electron. 2019, 66, 5778–5786. [Google Scholar] [CrossRef]
- Huang, Z.; Dinavahi, V. A fast and stable method for modeling generalized nonlinearities in power electronic circuit simulation. IEEE Trans. Power Electron. 2019, 34, 3124–3138. [Google Scholar] [CrossRef]
- Li, P.; Wang, Z.; Wang, C.; Fu, X.; Yu, H.; Wang, L. Synchronizations mechanism and interfaces design of multi-FPGA-based real-time simulator for microgrids. IET Gener. Transm. Distrib. 2017, 11, 3088–3096. [Google Scholar] [CrossRef]
- Milton, M.; Benigni, A.; Monti, A. Real-Time Multi-FPGA Simulation of Energy Conversion Systems. IEEE Trans. Energy Conv. 2019, 34, 2198–2208. [Google Scholar] [CrossRef]
- Swift, G.W.; Chatzivasileiadis, S.; Tschudi, W.; Glover, S.; Starke, M.; Wang, J.; Yue, M.; Hammerstrom, D.; Backhaus, S. DC Microgrids Scoping Study—Estimate of Technical and Economic Benefits. Los Alamos National Laboratory. Available online: https://www.energy.gov/oe/downloads/dc-microgrids-scoping-study-estimate-technical-and-economic-benefits-march-2015 (accessed on 10 January 2022).
- Estrada, L.; Vazquez, N.; Vaquero, J.; Hernandez, C.; Arau, J.; Huerta, H. Finite Control Set—Model Predictive Control Based on Sliding Mode For Bidirectional Power Inverter. IEEE Trans. Energy Conv. 2021, 36, 2814–2824. [Google Scholar] [CrossRef]
- Estrada, L.; Vázquez, N.; Vaquero, J.; de Castro, Á.; Arau, J. Real-Time Hardware in the Loop Simulation Methodology for Power Converters Using LabVIEW FPGA. Energies 2020, 13, 373. [Google Scholar] [CrossRef] [Green Version]
- Kazimierczuk, M.K. Pulse-Width Modulated DC–DC Power Converters; John Wiley and Sons: Dayton, OH, USA, 2008. [Google Scholar]










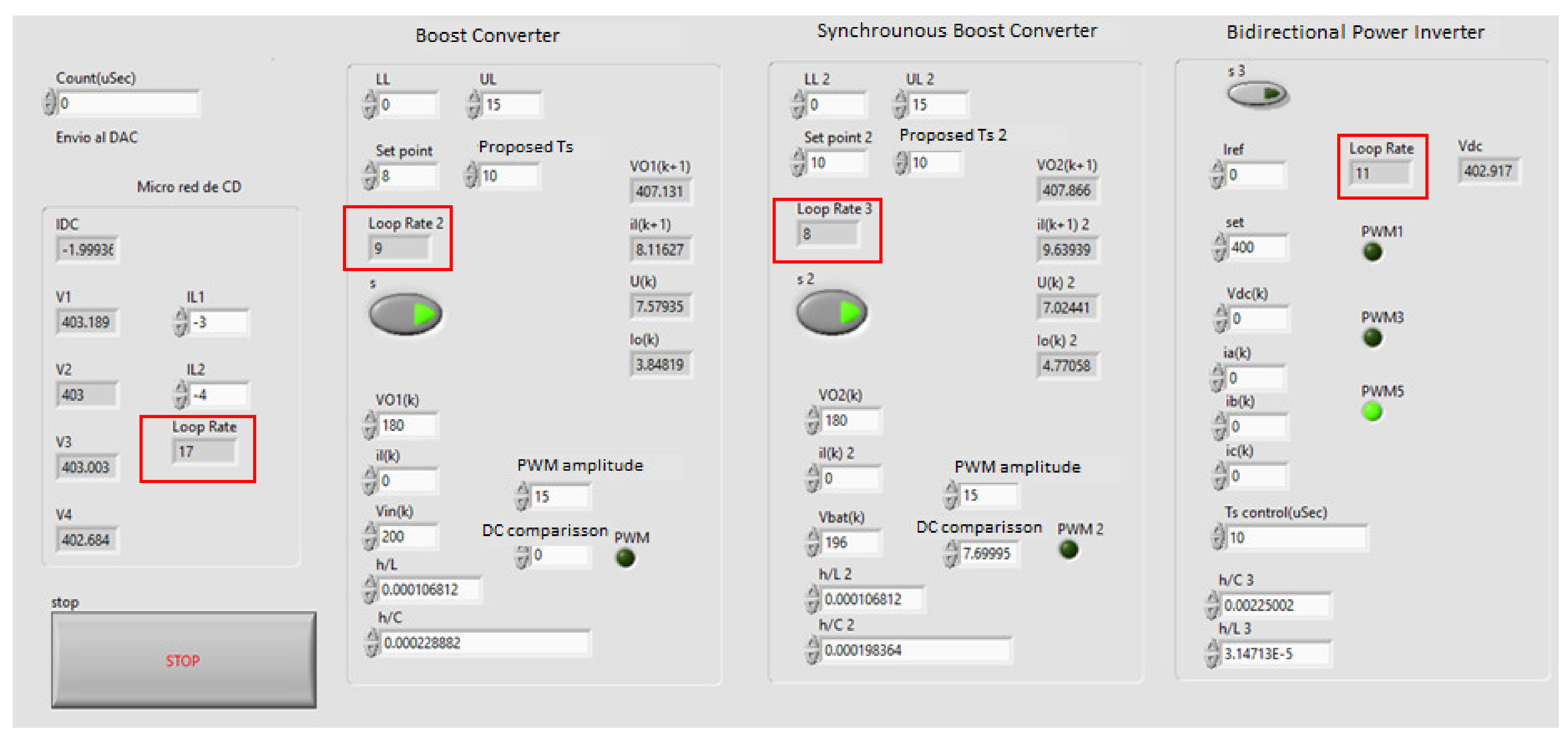


| Element | Clock Cycles | Time |
|---|---|---|
| NG | 17 | 425 ns |
| BC | 9 | 225 ns |
| SBC | 8 | 200 ns |
| BI | 11 | 275 ns |
| Parameter | Value | Unit |
|---|---|---|
| DC Bus | 400 | V |
| Line Impedance | 0.1 | Ω |
| Load Power | 4 | kW |
| Parameter | Value | Unit |
|---|---|---|
| Output Power | 4 | kW |
| Output Voltage | 420 | V |
| Input Voltage | 200 | V |
| Efficiency | 85 | % |
| Inductor Current Ripple | 5 | % of IDC |
| Output Voltage Ripple | 1 | % of Vo |
| Parameter | Value | Unit |
|---|---|---|
| Output Power | 4 | kW |
| Output Voltage | 420 | V |
| Input Voltage | 196 | V |
| Efficiency | 85 | % |
| Inductor Current Ripple | 5 | % of IDC |
| Output Voltage Ripple | 1 | % of Vo |
| Parameter | Value | Unit |
|---|---|---|
| Inductor | 2 | mH |
| Capacitor | 1 | mF |
| Signal | MAE PSIM vs. HIL Asynchronous | MAE PSIM vs. HIL Synchronous | Unit |
|---|---|---|---|
| iO1 | 0.122 | 0.216 | A |
| ia | 0.080 | 0.194 | A |
| iDC | 0.047 | 0.140 | A |
| vDC | 1.40 | 1.00 | V |
| Signal | MAE PSIM vs. HIL Asynchronous | MAE PSIM vs. HIL Synchronous | Unit |
|---|---|---|---|
| iO2 | 0.132 | 0.175 | A |
| ia | 0.169 | 0.697 | A |
| iDC | 0.129 | 0.231 | A |
| vDC | 1.45 | 1.11 | V |
| Signal | MAE PSIM vs. HIL Asynchronous | MAE PSIM vs. HIL Synchronous | Unit |
|---|---|---|---|
| iL2 | 0.115 | 0.143 | A |
| ia | 0.186 | 0.435 | A |
| iDC | 0.055 | 0.154 | A |
| vDC | 1.45 | 1.10 | V |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Estrada, L.; Vaquero, J.; Rodríguez-Lorente, A.; Arau, J.; de Castro, A.; Sanchez, A.; Vazquez, N. Asynchronous and Decoupled HIL Simulation of a DC Nanogrid. Electronics 2022, 11, 2045. https://doi.org/10.3390/electronics11132045
Estrada L, Vaquero J, Rodríguez-Lorente A, Arau J, de Castro A, Sanchez A, Vazquez N. Asynchronous and Decoupled HIL Simulation of a DC Nanogrid. Electronics. 2022; 11(13):2045. https://doi.org/10.3390/electronics11132045
Chicago/Turabian StyleEstrada, Leonel, Joaquín Vaquero, Alba Rodríguez-Lorente, Jaime Arau, Angel de Castro, Alberto Sanchez, and Nimrod Vazquez. 2022. "Asynchronous and Decoupled HIL Simulation of a DC Nanogrid" Electronics 11, no. 13: 2045. https://doi.org/10.3390/electronics11132045
APA StyleEstrada, L., Vaquero, J., Rodríguez-Lorente, A., Arau, J., de Castro, A., Sanchez, A., & Vazquez, N. (2022). Asynchronous and Decoupled HIL Simulation of a DC Nanogrid. Electronics, 11(13), 2045. https://doi.org/10.3390/electronics11132045








