A Watermarking Optimization Method Based on Matrix Decomposition and DWT for Multi-Size Images
Abstract
1. Introduction
- (1)
- The algorithm of watermarking can be adapted to multi-size host images and obtain better invisibility and robustness.
- (2)
- To the best of our knowledge, this is the first time that DWT, HMD, SVD, PSO, Arnold transform and logistic mapping combinations are applied to an image watermarking technique.
- (3)
2. Related Work
3. Materials and Methods
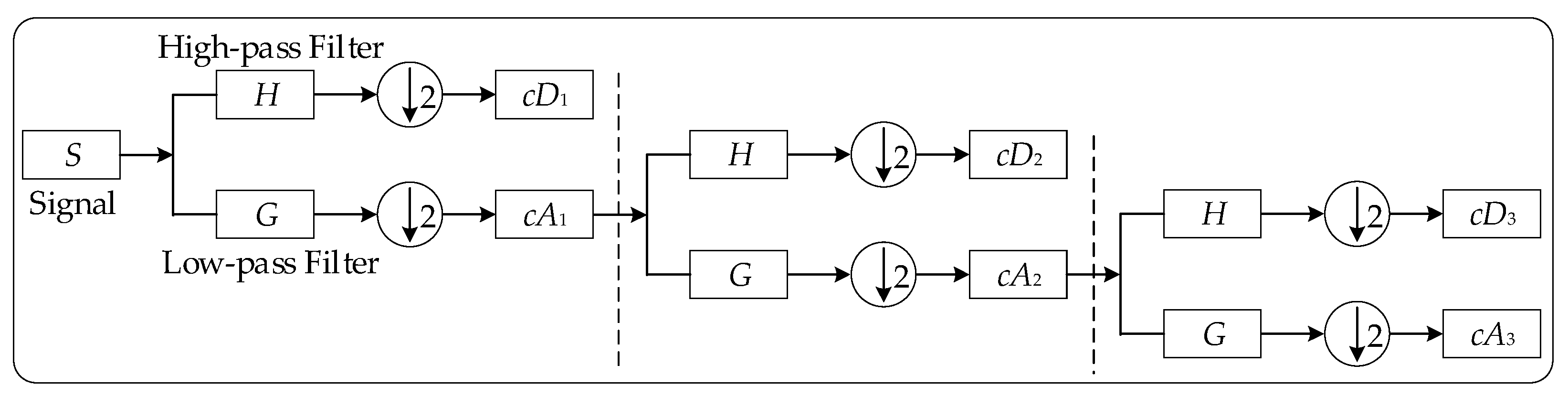
3.1. Discrete Wavelet Transform (DWT)
3.2. Matrix Decomposition
3.2.1. Hessenberg Matrix Decomposition
3.2.2. SVD Decomposition
3.3. Watermarking Encryption
3.3.1. Arnold Transform
3.3.2. Logistic Mapping
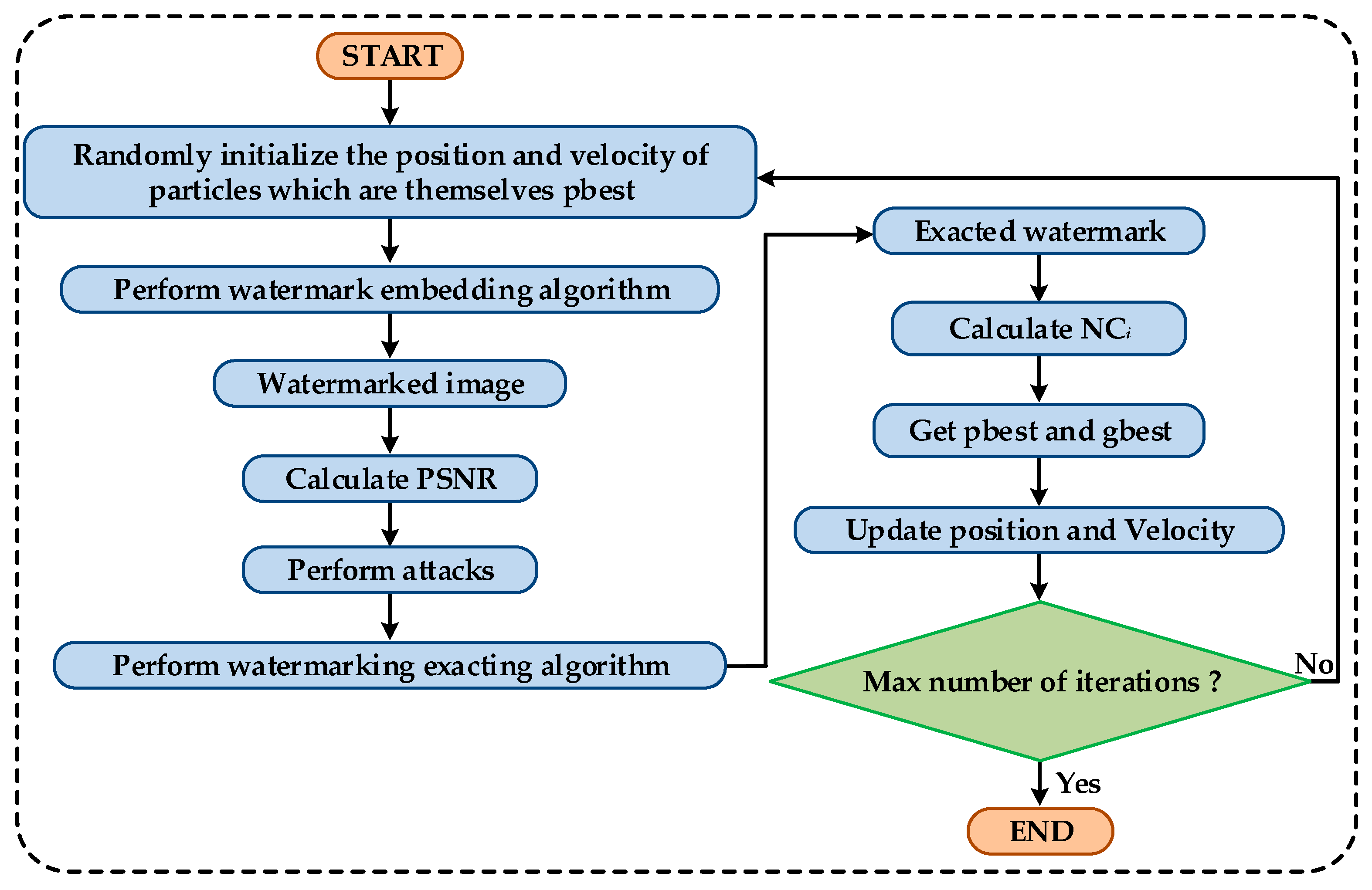
3.4. Particle Swarm Optimization Algorithm
4. Proposed Scheme
4.1. Scaling Factor
| Algorithm 1: Using PSO to calculate the best α |
| Input: Number of particles, N = 50, Weights, W = 0.5, Learning factor, C1 = 2, C2 = 2, Maximum number of iterations, T = 100. 1. Randomly initialize the position and velocity of each particle 2. Set and 3. 4. While iter < = T Implement Algorithm 1 using α Perform attacks tests Implement Algorithm 2 Calculate PSNRs using Equation (13), NCs using Equation (14), fitness value using Equation (15) Update and Update the position and velocity of each particle using Equations (10) and (11) end 5. Output: α. |
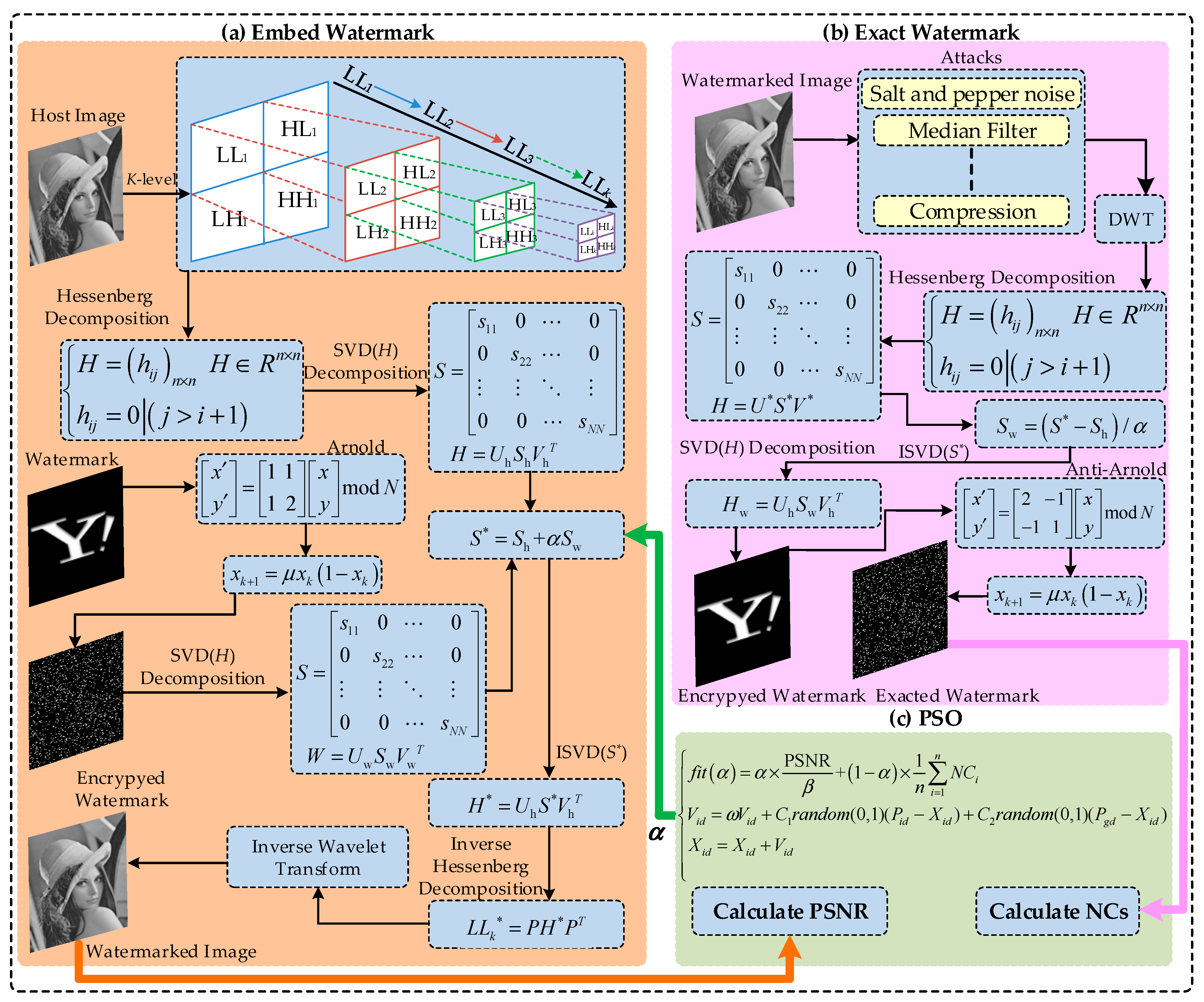
4.2. Watermark Embedding Algorithm
| Algorithm 2: Embedding algorithm |
| Input: Host image; watermark image; calculated by PSO. 1. Perform K-level DWT on the host image to obtain , 2. Perform HMD on , using Equation (4) to obtain H 3. Perform SVD on H using Equation (6) to obtain 4. Encrypt watermark using Equations (7) and (9) to obtain 5. Perform SVD on using Equation (6) to obtain 6. Using to embed watermark, 7. Calculate the new Hessenberg matrix 8. Calculate new low-frequency sub-band 9. Using IDWT to obtain the watermarked image Output: watermarked. |
4.3. Watermark Exacting Algorithm
| Algorithm 3: Exacting algorithm |
| Input: Watermarked image. 1. Perform K-level DWT on watermarked to obtain 2. Perform HMD on to obtain 3. Perform SVD on using Equation (6) to obtain 4. Using to exact into , 5. Calculate the watermark using in step 5 of Algorithm 2, 6. Decrypt Output: exacted watermark image. |
5. Results and Comparisons
5.1. Simulation Results
5.1.1. Invisibility Analysis
5.1.2. Robustness Analysis
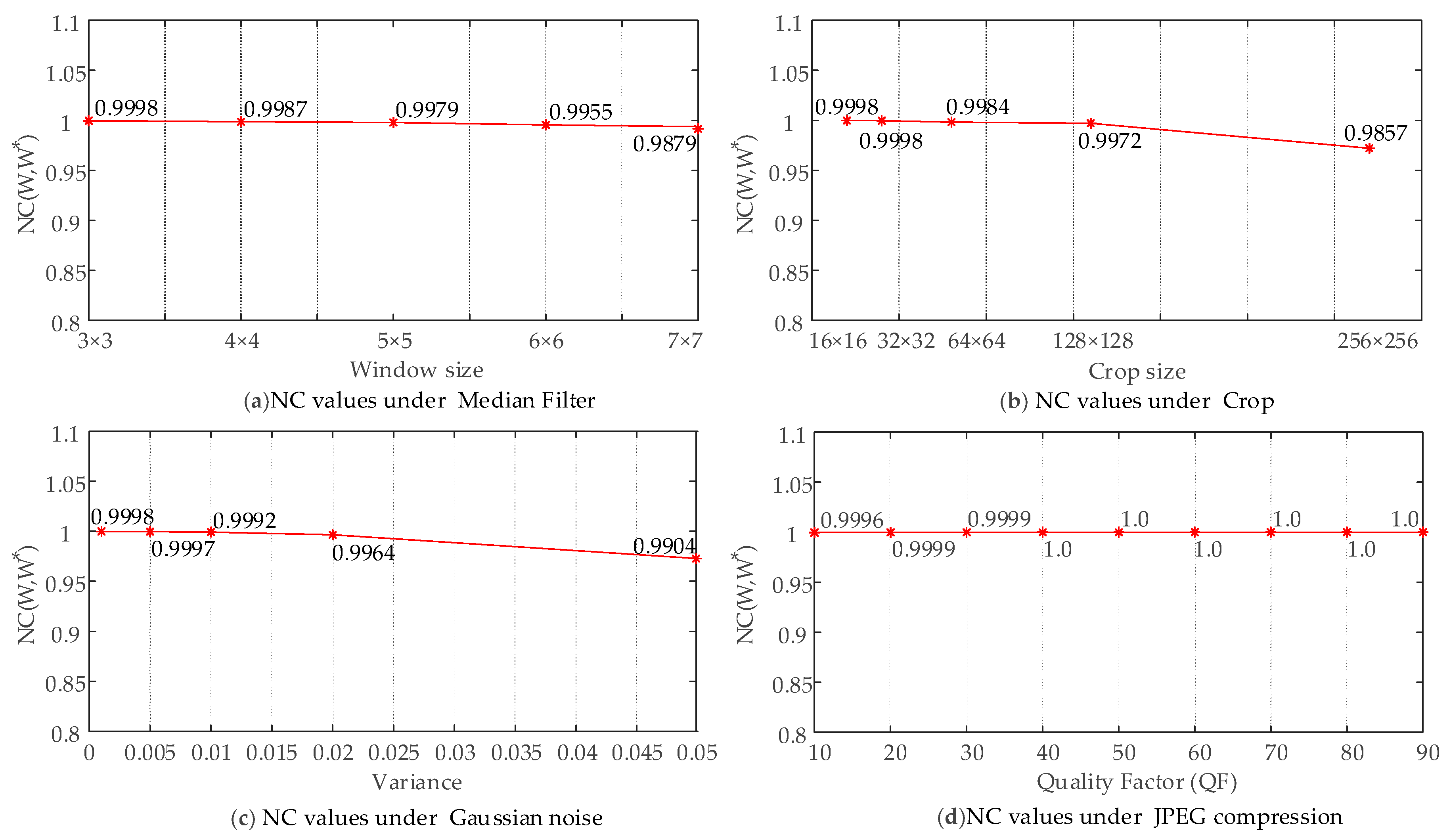
5.1.3. Analysis of Attack Test Results
5.2. Algorithm Comparisons
5.2.1. Invisibility Comparison
5.2.2. Robustness Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nikolaidis, A.; Pitas, I. Asymptotically optimal detection for additive watermarking in the DCT and DWT domains. IEEE Trans. Image Process 2003, 12, 563–571. [Google Scholar] [CrossRef] [PubMed]
- Kwitt, R.; Meerwald, P.; Uhl, A. Lightweight detection of additive watermarking in the DWT-Domain. IEEE Trans. Image Process 2011, 20, 474–484. [Google Scholar] [CrossRef] [PubMed]
- Nezhadarya, E.; Wang, Z.J.; Ward, R.K. Robust image watermarking based on multiscale gradient direction quantization. IEEE Trans. Inf. Forensic Secur. 2011, 6, 1200–1213. [Google Scholar] [CrossRef]
- Urvoy, M.; Goudia, D.; Autrusseau, F. Perceptual DFT watermarking with improved detection and robustness to geometrical distortions. IEEE Trans. Inf. Forensic Secur. 2014, 9, 1108–1119. [Google Scholar] [CrossRef]
- Solachidis, V.; Pitas, L. Circularly symmetric watermark embedding in 2-D DFT domain. IEEE Trans. Image Process 2001, 10, 1741–1753. [Google Scholar] [CrossRef]
- Shabir, A.P.; Javaid, A.S.; Nazir, A.L.; Ghulam, M.B. Robust and blind watermarking technique in DCT domain using inter-block coefficient differencing. Digit. Signal Process 2016, 53, 11–24. [Google Scholar] [CrossRef]
- Lei, B.Y.; Soon, I.Y.; Li, Z. Blind and robust audio watermarking scheme based on SVD–DCT. Signal Process. 2011, 91, 1973–1984. [Google Scholar] [CrossRef]
- Moosazadeh, M.; Ekbatanifard, G. A new DCT-based robust image watermarking method using teaching-learning-based optimization. J. Inf. Secur. Appl. 2019, 47, 28–38. [Google Scholar] [CrossRef]
- Ferad, E.; Muhammad, N.K. A robust image watermarking technique with an optimal DCT-psychovisual threshold. IEEE Access 2018, 6, 20464–20480. [Google Scholar] [CrossRef]
- Liu, R.Z.; Tan, T.N. An SVD-Based watermarking scheme for protecting rightful ownership. IEEE Trans. Multimed. 2002, 4, 121–128. [Google Scholar] [CrossRef]
- Fan, M.Q.; Wang, H.X.; Li, S.K. Restudy on SVD-based watermarking scheme. Appl. Math. Comput. 2008, 203, 926–930. [Google Scholar] [CrossRef]
- Anand, A.; Singh, A.K. Dual watermarking for security of COVID-19 patient record. IEEE Trans. Depend. Secur. 2022. [Google Scholar] [CrossRef]
- Lai, C.C.; Tsai, C.C. Digital image watermarking using discrete wavelet transform and singular value decomposition. IEEE Trans. Instrum. Meas. 2010, 59, 3060–3063. [Google Scholar] [CrossRef]
- Ali, M.; Ahn, C.W. An optimized watermarking technique based on self-adaptive DE in DWT–SVD transform domain. Signal Process. 2014, 94, 545–556. [Google Scholar] [CrossRef]
- Fares, K.; Khaldi, A.; Redouane, K.; Salah, E. DCT & DWT based watermarking scheme for medical information security. Biomed. Signal Process. 2021, 66, 102403. [Google Scholar] [CrossRef]
- Zermi, N.; Khaldi, A.; Redouane, K.; Fares, K.; Salah, E. A DWT-SVD based robust digital watermarking for medical image security. Forensic Sci. Int. 2021, 320, 110691. [Google Scholar] [CrossRef]
- Nasir, N.H.; Shabir, A.P.; Nazir, A.L.; Javaid, A.S.; Mohammad, E.; Khan, M. Dual watermarking framework for privacy protection and content authentication of multimedia. Future Gener. Comp. Syst. 2018, 94, 654–673. [Google Scholar] [CrossRef]
- Wang, B.W.; Zhao, P. An adaptive image watermarking method combining SVD and Wang-Landau sampling in DWT domain. Mathematics 2020, 8, 691. [Google Scholar] [CrossRef]
- Jane, O.; Elbaşi, E.; İlk, H.G. Hybrid non-blind watermarking based on DWT and SVD. Appl. Res. Technol. 2014, 12, 750–761. [Google Scholar] [CrossRef][Green Version]
- Zhou, X.; Zhang, H.; Wang, C.Y. A robust image watermarking technique based on DWT, APDCBT, and SVD. Symmetry 2018, 10, 77. [Google Scholar] [CrossRef]
- Zhang, L.N.; Wei, D.Y. Dual DCT-DWT-SVD digital watermarking algorithm based on particle swarm optimization. Multimed. Tools Appl. 2019, 78, 28003–28023. [Google Scholar] [CrossRef]
- Singh, R.; Ashok, A. An optimized robust watermarking technique using CKGSA in frequency domain. J. Inf. Secur. Appl. 2021, 58, 102734. [Google Scholar] [CrossRef]
- Alshoura, W.H.; Zainol, Z.; Teh, J.S.; Alawida, M. An FPP-resistant SVD-based image watermarking scheme based on chaotic control. Alex. Eng. J. 2022, 61, 5713–5734. [Google Scholar] [CrossRef]
- Manuel, C.H.; Antonio, C.H.; Francisco, J.G. Improving DFT-based image watermarking using particle swarm optimization algorithm. Mathematics 2021, 9, 1795. [Google Scholar] [CrossRef]
- Adnan, M.C.; Syed, M.A.; Zahid, M. A novel optimized semi-blind scheme for color image watermarking. IEEE Access 2020, 8, 169525–169547. [Google Scholar] [CrossRef]
- Falgun, T.; Vinay, K.S. An adaptive, secure and imperceptive image watermarking using swarm intelligence, arnold transform, SVD and DWT. Multimed. Tools Appl. 2021, 80, 12275–12292. [Google Scholar] [CrossRef]
- Balasamy, K.; Ramakrishnan, S. An intelligent reversible watermarking system for authenticating medical images using wavelet and PSO. Clust. Comput. 2019, 22, 4431–4442. [Google Scholar] [CrossRef]
- Mona, M.S.; Aboul, E.H.; Hoda, M.O. An adaptive watermarking approach based on weighted quantum particle swarm optimization. Neural Comput. Appl. 2016, 27, 469–481. [Google Scholar] [CrossRef]
- Abdelhakim, A.M.; Saleh, H.I.; Nassar, A.M. A quality guaranteed robust image watermarking optimization with artificial bee colony. Expert Syst. Appl. 2017, 72, 317–326. [Google Scholar] [CrossRef]
- Gao, H.; Chen, Q. A robust and secure image watermarking scheme using SURF and improved artificial bee colony algorithm in DWT domain. Optik 2021, 242, 166954. [Google Scholar] [CrossRef]
- Zheng, Q.M.; Liu, N.; Wang, F.H. An adaptive embedding strength watermarking algorithm based on shearlets’ capture directional features. Mathematics 2020, 8, 1377. [Google Scholar] [CrossRef]
- Su, Q.T.; Chen, B.J. A novel blind color image watermarking using upper Hessenberg matrix. AEU-Int. J. Electron. Commun. 2017, 78, 64–71. [Google Scholar] [CrossRef]
- Vali, M.H.; Aghagolzadeh, A.; Baleghi, Y. Optimized watermarking technique using self-adaptive differential evolution based on redundant discrete wavelet transform and singular value decomposition. Expert Syst. Appl. 2018, 114, 296–312. [Google Scholar] [CrossRef]
- Alshoura, W.H.; Zainol, Z.; Teh, J.S.; Alawida, M. A new chaotic image watermarking scheme based on SVD and IWT. IEEE Access 2020, 8, 43391–43406. [Google Scholar] [CrossRef]
- Reem, A.; Hanaa, A.A. Securing color video when transmitting through communication channels using DT-CWT-Based watermarking. Electronics 2022, 11, 1849. [Google Scholar] [CrossRef]
- Alzahrani, A. Enhanced invisibility and robustness of digital image watermarking based on DWT-SVD. Appl Bionics Biomech. 2022, 2022, 5271600. [Google Scholar] [CrossRef] [PubMed]
- Stephane, G.M. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Varad, A.P.; Rutvik, P.; Ashwin, K.; Kishor, M.B.; Vipin, M.K. Digital image noise estimation using DWT coefficients. IEEE Trans. Image Process 2021, 30, 1962–1972. [Google Scholar] [CrossRef]
- Hasan, N.; Islam, M.S.; Chen, W.Y.; Kabir, M.A.; AL-Ahmadi, S. Encryption based image watermarking algorithm in 2DWT-DCT domains. Sensors 2021, 21, 5540. [Google Scholar] [CrossRef]





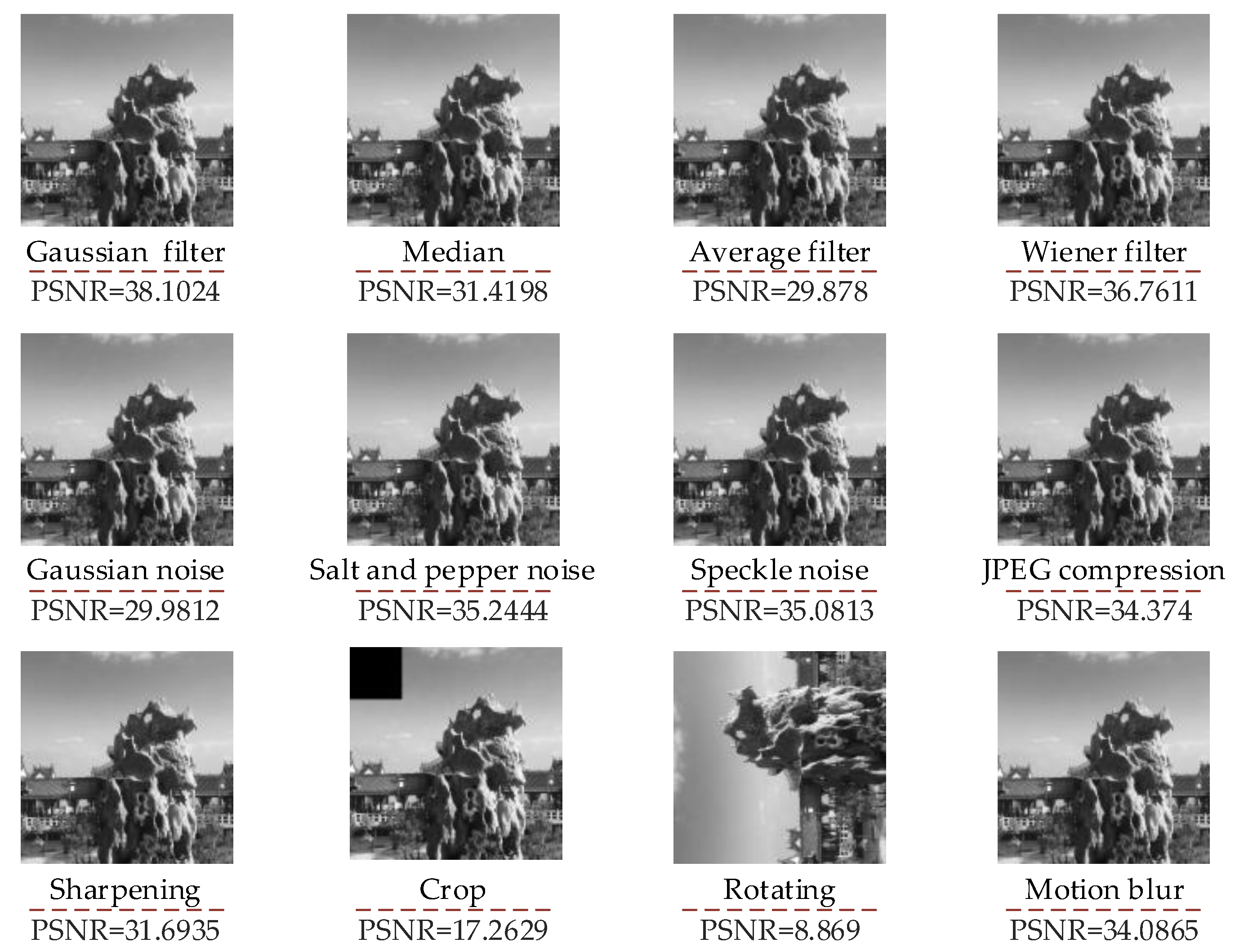

| Attacks | Parameters |
|---|---|
| Gaussian filter | 5 × 5 |
| Median filter | 3 × 3 |
| Average filter | 3 × 3 |
| Wiener filter | 3 × 3 |
| Gaussian noise | Variance = 0.01 |
| Salt and pepper noise | Density = 0.01 |
| Speckle noise | Variance = 0.01 |
| JPEG compression | Quality factor (QF) = 50 |
| Sharpening | 0.7 |
| Crop | Left 12% |
| Rotate | 90° |
| Motion blur | Theta = 4, Len = 7 |
| Attacks. | Girl | Park | Man | Lena | Goldhill | Baboon | House | Woman | Pepper |
|---|---|---|---|---|---|---|---|---|---|
| No | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Gaussian filter | 0.9999 | 0.9999 | 0.9998 | 0.9999 | 0.9999 | 0.9999 | 0.9996 | 0.9997 | 0.9996 |
| Median filter | 0.9999 | 0.9985 | 0.9999 | 0.9999 | 0.9997 | 0.9999 | 0.9993 | 0.9999 | 0.9998 |
| Average filter | 0.9999 | 0.9986 | 0.9999 | 0.9999 | 0.9998 | 0.9999 | 0.9966 | 0.9961 | 0.9958 |
| Wiener filter | 0.9997 | 0.9987 | 0.9996 | 0.9994 | 0.9993 | 0.9994 | 0.9988 | 0.9984 | 0.9987 |
| Gaussian noise | 0.9999 | 0.9998 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 |
| Salt and pepper noise | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9998 | 0.9999 | 0.9999 |
| Speckle noise | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 |
| JPEG | 0.9999 | 0.9999 | 0.9999 | 0.9998 | 0.9998 | 0.9996 | 0.9992 | 0.999 | 0.9995 |
| Crop | 0.9949 | 0.9946 | 0.9923 | 0.9917 | 0.9935 | 0.9919 | 0.9931 | 0.9909 | 0.9852 |
| Sharpening | 0.9996 | 0.9988 | 0.9997 | 0.9981 | 0.9988 | 0.9981 | 0.9977 | 0.9968 | 0.9967 |
| Rotating | 0.9995 | 0.9998 | 0.9996 | 0.9989 | 0.9984 | 0.9982 | 0.9983 | 0.998 | 0.9978 |
| Motion blur | 0.9987 | 0.9986 | 0.9997 | 0.9967 | 0.9969 | 0.9961 | 0.9874 | 0.9899 | 0.9862 |
| Attacks | Parameters | Host Image Size | ||
|---|---|---|---|---|
| 1024 × 1024 | 512 × 512 | 256 × 256 | ||
| Median Filter | 3 × 3 | 0.9994 | 0.9999 | 0.9985 |
| 5 × 5 | 0.9985 | 0.9978 | 0.9939 | |
| 7 × 7 | 0.9967 | 0.9879 | 0.9882 | |
| Gaussian Noise | 0.001 | 0.9995 | 0.9998 | 0.9993 |
| 0.005 | 0.9990 | 0.9997 | 0.9896 | |
| 0.01 | 0.9984 | 0.9992 | 0.9842 | |
| JPEG | 20 | 0.9995 | 0.9993 | 0.9992 |
| 50 | 0.9997 | 1 | 0.9996 | |
| 70 | 1 | 1 | 0.9999 | |
| Crop | Left6% | 0.9995 | 0.9982 | 0.9875 |
| Left 12% | 0.9964 | 0.9970 | 0.9828 | |
| Left 25% | 0.9871 | 0.9865 | 0.9738 | |
| Images | [19] | [21] | [26] | Proposed |
|---|---|---|---|---|
| Lena | 43.8934 | 44.5125 | 43.9583 | 48.8785 |
| Woman | 43.9624 | 44.5182 | 43.9501 | 49.5695 |
| Goldhill | 43.9619 | 43.9023 | 43.9687 | 48.9170 |
| House | 43.8264 | 44.3835 | 43.9876 | 49.5075 |
| Attacks | [19] | [21] | [26] | Proposed |
|---|---|---|---|---|
| Filter | 25.8663 | 28.8229 | 27.6937 | 35.4073 |
| Salt and pepper noise | 28.9628 | 25.3931 | 29.828 | 35.9293 |
| JPEG (Q = 10) compression | 27.2172 | 33.8331 | 30.2218 | 37.1349 |
| Crop 1/4 left up | 11.4584 | 11.7034 | 11.6027 | 11.7954 |
| Sharpening | 28.7682 | 20.1304 | 31.0584 | 34.859 |
| Rotating 45° | 10.1527 | 10.4813 | 10.3741 | 10.5114 |
| Attacks | [19] | [21] | [26] | Proposed |
|---|---|---|---|---|
| Gaussian filter | 0.9786 | 0.9998 | 0.9377 | 0.9999 |
| Median | 0.9328 | 0.9980 | 0.9872 | 0.9983 |
| Average filter | 0.9784 | 0.9969 | 0.9369 | 0.9976 |
| Wiener filter | 0.8933 | 0.9981 | 0.9903 | 0.9989 |
| Gaussian noise | 0.9546 | 0.9711 | 0.9913 | 0.9999 |
| Salt and pepper noise | 0.9921 | 0.9881 | 0.9948 | 0.9999 |
| Speckle noise | 0.9917 | 0.9782 | 0.9955 | 0.9999 |
| JPEG(Q = 10) compression | 0.9949 | 0.9997 | 0.9982 | 0.9996 |
| Crop 1/4 left up | 0.6999 | 0.9702 | 0.9492 | 0.9865 |
| Sharpening | 0.8637 | 0.9617 | 0.9923 | 0.9964 |
| Rotating 45° | 0.7010 | 0.9805 | 0.9026 | 0.9509 |
| Motion blur | 0.9032 | 0.9969 | 0.9921 | 0.9967 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Ji, H. A Watermarking Optimization Method Based on Matrix Decomposition and DWT for Multi-Size Images. Electronics 2022, 11, 2027. https://doi.org/10.3390/electronics11132027
Wang L, Ji H. A Watermarking Optimization Method Based on Matrix Decomposition and DWT for Multi-Size Images. Electronics. 2022; 11(13):2027. https://doi.org/10.3390/electronics11132027
Chicago/Turabian StyleWang, Lei, and Huichao Ji. 2022. "A Watermarking Optimization Method Based on Matrix Decomposition and DWT for Multi-Size Images" Electronics 11, no. 13: 2027. https://doi.org/10.3390/electronics11132027
APA StyleWang, L., & Ji, H. (2022). A Watermarking Optimization Method Based on Matrix Decomposition and DWT for Multi-Size Images. Electronics, 11(13), 2027. https://doi.org/10.3390/electronics11132027






