A Watermarking Optimization Method Based on Matrix Decomposition and DWT for Multi-Size Images

Abstract

Image watermarking is a key technology for copyright protection, and how to better balance the invisibility and robustness of algorithms is a challenge. To tackle this challenge, a watermarking optimization method based on matrix decomposition and discrete wavelet transform (DWT) for multi-size images is proposed. The DWT, Hessenberg matrix decomposition (HMD), singular value decomposition (SVD), particle swarm optimization (PSO), Arnold transform and logistic mapping are combined for the first time to achieve an image watermarking optimization algorithm. The multi-level decomposition of DWT is used to be adapted to multi-size host images, the Arnold transform, logistic mapping, HMD and SVD are used to enhance the security and robustness, and the PSO optimized scaling factor to balance invisibility and robustness. The simulation results of the proposed method show that the PSNRs are higher than 44.9 dB without attacks and the NCs are higher than 0.98 under various attacks. Compared with the existing works, the proposed method shows high robustness against various attacks, such as noise, filtering and JPEG compression and in particular, the NC values are at least 0.44% higher than that in noise attacks.

1. Introduction

Digital watermarking technology, as a widely used protection technology, has been applied to protect many areas of multimedia copyrights. The watermarking algorithm should have good invisibility and robustness, thus protecting the watermark from various attacks. Currently, image watermarking algorithms are mainly performed in the transform domain, such as discrete wavelet transform (DWT) [1,2,3] and discrete Fourier transform (DFT) [4,5], as well as discrete cosine transform (DCT) [6,7,8,9] and these are the most commonly used watermarking algorithms. Matrix decomposition is also used in watermarking algorithms due to its higher stability [10,11,12]. Watermarking algorithms of singular value decomposition (SVD) decomposition combined with DWT or DCT [13,14,15,16] are one of the widely used methods in image watermarking algorithms.

Digital watermarking is to embed certain information (watermark) that proves copyright into the protected object (host image). Among them, watermarks are pre-designed author information or company logos with fixed sizes, while the host image is more diverse in size. Image watermarking techniques for the watermark and fixed-size host images are usually discussed by scholars. Lai et al. [13] directly embedded the watermark into the singular values of the intermediate frequency band, which was obtained from the DWT decomposition of the host image. The simulation results showed that the method is resistant to various image processing attacks. However, the algorithm required that the size ratio of the host image to the watermark must be 2:1. Advith et al. [14] discussed the color image watermarking algorithm using DWT combined with DFT and SVD. However, the host image and the watermark must be equal in size. Hurrah et al. [17] proposed a double-blind watermarking framework based on DWT, DCT, the Arnold transform, and a new encryption algorithm for the protection of multimedia images. However, the ratio of the host image to the watermarked image in this algorithm must be 4:1. Wang et al. [18] proposed an adaptive image watermarking method based on wavelet transform, SVD, and Wang-Landau sampling method. The effectiveness and significance of the method are shown by the simulation results, although the ratio of the host image to the watermark must be 3:1.

The size of the host image is required to be fixed in these algorithms, which have achieved results in the terms of robustness and invisibility. The algorithm for watermark adaptation to multi-size host images still needs to be further investigated. The workload will be increased to some extent if the ratio of the host image to the watermark has to be changed. A method is proposed to adaptively select the level of decomposition for the host image by using the multi-scale property of DWT. The watermark is embedded in the host image, whose level of DWT is due to the ratio between the host image and the watermark.

The obvious diagonal traces are discovered in the extracted watermark under the attacks, which is due to the SVD used in the algorithms [19,20]. Moreover, the false positive problem (FPP) is easily found in the watermarking methods that used SVD [21,22,23]. Zhang et al. [21] introduced generalized Arnold transform in the algorithm to solve the diagonal problem and FPP problem due to SVD. In this paper, we perform the Arnold transform as well as logistic mapping to above the issue caused by SVD. The watermark image is encrypted by the dual-encryption. In the process, the matrix $U$ and $V^T$ of the watermark are protected by keys of the encryption. Thus, attackers could only extract a noise-like watermark with counterfeit $U$ and $V^T$. Moreover, to further ensure the stability of the watermarking algorithm, the Hessenberg matrix decomposition (HMD) is applied to the singular values of the low-frequency sub-bands of the host image after DWT.

In addition, the scaling factor is used to control the embedding strength of the algorithm. The larger the scaling factor, the better the robustness and the weaker the invisibility, and vice versa [4,8,22]. To balance the invisibility and robustness of watermarking algorithms, many evolutionary and population intelligence optimization algorithms are used to solve the scaling factor of the watermarking algorithm. For example, particle swarm optimization (PSO) algorithms [21,24,25,26,27,28], and artificial bee colony optimization algorithms [29,30,31] have been used to optimize the scaling factor. The scaling factor is optimized by using the PSO on account of the advantages of low computational complexity and fast convergence.

A watermarking optimization method based on matrix decomposition and DWT for multi-size images is proposed. The host image is decomposed into four sub-bands by multi-level DWT, HMD and SVD are applied to the low-frequency band. The watermark image is encrypted by the Arnold transform and logistic mapping, and then the singular value of the encrypted watermark is modified by the scaling factor to embed the low-frequency band of the host image. In addition, the scaling factor is optimized by PSO. The main contributions of this paper are as follows:

(1)

The algorithm of watermarking can be adapted to multi-size host images and obtain better invisibility and robustness.

(2)

To the best of our knowledge, this is the first time that DWT, HMD, SVD, PSO, Arnold transform and logistic mapping combinations are applied to an image watermarking technique.

(3)

The invisibility and robustness of the proposed method are better than the existing works of [19,21,26], particularly the NC values, which are at least 0.44% higher than that of existing works in noise attacks.

The rest of the paper is organized as follows. Section 2 introduces a related work. Section 3 introduces the concepts of DWT, matrix decomposition, PSO algorithm, the Arnold transform, and logistic mapping. Section 4 details the multi-size image watermarking algorithm with dual encryption of DWT and matrix decomposition, the simulation results and performance comparison are given in Section 5, and conclusions are given in Section 6.

2. Related Work

Image watermarking algorithms are a hot research topic in image copyright protection technology. The various methods are used by scholars to improve the invisibility and robustness of the algorithms, such as the combination of DWT, DCT, SVD and so on. The research works on image watermarking techniques in recent years are introduced.

In 2017, Su et al. [32] proposed a blind color image watermarking scheme using HMD and Arnold transform.

In 2018, Vali et al. [33] presented a new blind image watermarking technique based on redundant DWT and SVD.

In 2019, Zhang et al. [21] proposed a DWT-DCT domain image watermarking algorithm based on PSO, the watermark image is encrypted by the generalized Arnold transform.

In 2020, Alshoura et al. [34] proposed a new watermarking scheme using a chaotic map based on SVD to overcome the FPP issue.

In 2021, Reem et al. [35] proposed a color video watermarking system based on SVD and dual-tree complex wavelet transform.

In 2021, Falgun et al. [26] proposed an improved DWT-SVD watermarking algorithm by using Arnold transform and PSO. The PSNRs for invisibility and the NCs for robustness are greater than 40 and 0.9, respectively.

In 2022, Alzahrani [36] proposed a digital watermark algorithm using DWT-SVD that analyzes various types of watermark attacks. The PSNRs for invisibility and the NCs for robustness are greater than 40 and 0.85, respectively.

3. Materials and Methods

3.1. Discrete Wavelet Transform (DWT)

The wavelet transform is a localized analysis of time (spatial) frequency, which can automatically adapt to the demands of analysis of the time-frequency signal and focus on any details of the signal. The low and high frequencies of the signal are performed time and frequency subdivision by wavelet transform through telescoping translation operation, respectively.

One must assume that $\psi (t)$ is a fundamental wavelet or mother wavelet function. All wavelets are obtained by scaling and shifting the mother wavelet. The factors of scaling and translation are set to a and b, respectively. The following family of wavelet functions can be obtained by Equation (1).

$$\phi (t)=\frac{1}{\sqrt{\left|a\right|}}\psi (\frac{t-b}{a}), \begin{array}{cc}& \end{array} a\ne 0$$

(1)

In continuous wavelet transform, calculating wavelet coefficients at every possible scale is an amount of work, and it generates a lot of data. The values $a=2^m,b=n{2}^m,\begin{array}{c}\end{array}m,n\in Z$ are used to discretize function $\phi (t)$; the 1-D DWT of the signal $f(k)$ is shown in the following Equation (2):

$$DWT(m,n)=2^{-\frac{m}{2}}{\displaystyle \sum _{k=-\infty }^{\infty }f(k){\phi }^{\ast }(2^{-m}k-n)}$$

(2)

where ${\phi }^{\ast }$ is the complex conjugate of $\phi (t)$.

As the scale and positions are chosen based on the power of two, the analysis becomes much more efficient and just as accurate. This is the DWT based on the multi-resolution analysis that is proposed by Mallat in 1989 [37]. The signal is obtained by using the wavelet expansion coefficients through a filter bank, which contains a high-pass filter and a low-pass filter [27,37,38], as shown in Figure 1. The high-frequency coefficient and low-frequency coefficient of the signal are output by the high-pass filter $H$ and low-pass filter $G$, respectively. The $c{A}_i$ is the approximate component and $c{D}_i$ is the detail component [39].

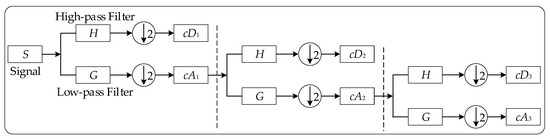
Figure 1. Three level decomposition of 1-D signal.

Many different wavelet bases (Morlet, Daubechies, Haar) are used for wavelet decomposition and reconstruction of images. The Haar wavelet is a basis function used for the decomposition of the host image into diverse sub-bands in this paper. The Haar wavelet is defined as Equation (3) [38].

$$\psi (t)=\left\{\begin{array}{cc}1\hfill & 0\le t<\frac{1}{2}\\ -1\hfill & \frac{1}{2}\le t<1\\ 0\hfill & other\end{array}\right.,$$

(3)

Haar wavelet can quickly solve features of multi-size images using integral calculations, due to its lower complexity than the others. It is suitable as a wavelet basis function for intelligent optimized watermarking algorithms.

Since the images in this paper are digital images, which are in the form of a 2-D matrix, the 2-D DWT is used to process such types of images. First, 1-D DWT is performed on the image by rows, and then 1-D DWT is performed on the obtained result by column, and vice versa. Therefore, Figure 2 is decomposed by the two-dimensional DWT, the four sub-bands are LH1, HL1, HH1 and LL1, respectively, and then the secondary decomposition is performed on LL1, which is decomposed into four sub-bands LL2, HL2, LH2, and HH2.

Figure 2. The decomposition process of 2-D DWT. (a) Original image, (b) one-level decomposition image; (c) two-level decomposition image.

3.2. Matrix Decomposition

Matrix decomposition refers to the decomposition of a matrix into the product of several matrices by some algorithm based on certain principles. In this paper, HMD and SVD decomposition are used to improve the stability and robustness of the watermarking algorithm.

3.2.1. Hessenberg Matrix Decomposition

The proposed uses HMD [32] to decompose the images, and the HMD is a special square matrix with the following equation:

$$I=PH{P}^T,$$

(4)

where I is the general matrix corresponding to the image; P is the orthogonal matrix. The H is the upper Hessenberg matrix.

$$\left\{\begin{array}{l}H={(h_{ij})}_{n\times n}\in R^{n\times n}\\ h_{ij}=0(j>i+1)\end{array}\right.,$$

(5)

3.2.2. SVD Decomposition

SVD [10,11,12,13] is a mathematical analysis method for an image I of size $N\times N$, that can be expressed as follows:

$$I=US{V}^T,$$

(6)

where U and V are two orthogonal matrices and S are a singular value matrix whose diagonal elements are the singular values of the image matrix I.

SVD has extremely important applications in image transformation, especially in digital watermarking. The singular values of an image characterize the distribution of the matrix data. The stability of the singular values is good and, in general, the singular values do not change significantly when the image is processed. In addition, SVD is a scaled invariant and there is no limit to the size of the image matrix. However, false positives are common in image watermarking algorithms using SVD.

To avoid the occurrence of false positives, this paper uses the Arnold transform combined with logistic mapping to double encrypt the watermarked image in the watermarked image pre-processing.

3.3. Watermarking Encryption

3.3.1. Arnold Transform

The Arnold transform [26] was proposed by the famous Russian mathematician Vladimir Arnold, known as the cat face transforms. The basic principle is to represent the matrix of a digital image as a binary function, which is encrypted by replacing the pixel coordinates of the original digital image with their positions. The process is as follows:

$$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{l}1\hspace{0.33em}\hspace{0.33em}1\\ 1\hspace{0.33em}\hspace{0.33em}2\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]\mathrm{mod}N,$$

(7)

where N is the number of image dimensions and $(x\hspace{0.33em},y)$ is the coordinate of a point in the digital image, $(x\hspace{0.33em},y)\in \left\{1\hspace{0.33em},2\hspace{0.33em},\cdots \hspace{0.33em}N-1\right\}$; $(x^{\prime }\hspace{0.33em},y^{\prime })$ is the transformed coordinate $(x^{\prime }\hspace{0.33em},y^{\prime })\in \left\{1\hspace{0.33em},2\hspace{0.33em},\cdots \hspace{0.33em}N-1\right\}$.

The inverse transformation formula of Arnold transform can be written as follows.

$$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{l}2\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}-1\\ -1\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}1\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]\mathrm{mod}N,$$

(8)

3.3.2. Logistic Mapping

Logistic mapping [33] is encrypted through a logistic chaotic sequence, where only the chaotic coefficients and the initial value (key) are set and the watermarked image is brought to a chaotic state by iteration. This is achieved through the following equation:

$$x_{k+1}=\mu x_k(1-x_k)$$

(9)

where the chaos coefficient $\mu \in [0,4]\hspace{0.33em},x_k\in (0,1)$. The logistic mapping reaches a chaotic state when $3.56995<\mu \le 4$.

The algorithm is very sensitive to the number of Arnold permutations, logistic chaos coefficients, initial values, and other keys. If one or two of the keys are incorrect, the algorithm will fail to decrypt. The encryption algorithm in this paper can effectively ensure the security of the whole watermarking algorithm, as shown in Figure 3. In the process, $U$ and $V^T$ of the watermark image are protected by keys of the encryption. Thus, attackers could only extract a noise-like watermark with counterfeit $U$ and $V^T$.

Figure 3. Duel-encrypted watermarked image. (a) Original watermark, (b) Arnold encrypted image, (c) logistic mapped image; (d) decrypted image.

3.4. Particle Swarm Optimization Algorithm

PSO [21,29], also known as particle swarm optimization algorithm or bird flock foraging algorithm, is a new evolutionary algorithm developed by J. Kennedy and R. C. Eberhart et al. The particle swarm algorithm has simpler rules than the genetic algorithm and finds the global optimum by following the current searched optimum.

The scaling factor has an important impact on the watermarking algorithm, which is used to balance the invisibility and robustness of the algorithm. In this paper, we introduce PSO to optimize the scaling factor of the algorithm. The flow chart of PSO is shown in Figure 4. In addition, PSO updates the velocity vector of each individual using the Equations (10) and (11).

$$V_{id}=\omega V_{id}+C_{1}rand(0,1)(P_{id}-X_{id}) +C_{2}rand(0,1)(P_{gd}-X_{id}),$$

(10)

$$X_{id}=X_{id}+V_{id},$$

(11)

where $\omega \in [0,1]$ is the weighting factor, $C_1,C_2\in [0,4]$ is the acceleration constant, denotes the $P_{id}$ individual optimal solution, and $P_{gd}$ denotes the global optimal solution.

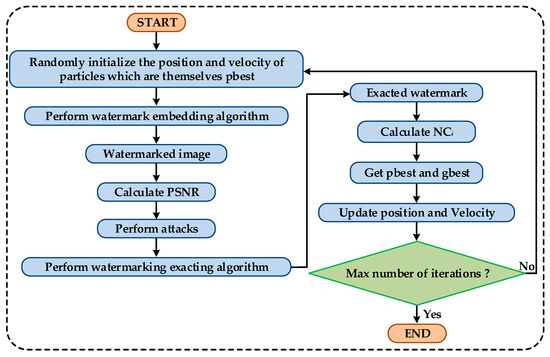
Figure 4. The flow chart of PSO.

4. Proposed Scheme

This part introduces the proposed algorithm. Section 4.1 presents how to find the optimal scaling factor by PSO in the proposed algorithm. Section 4.2 and Section 4.3 introduce the watermarking embedding and extracting scheme.

4.1. Scaling Factor

Usually, PSNR and NC values are used as the evaluation index of the algorithm [21]. PSNR calculates the peak signal-to-noise ratio between the watermarked image and the original image, and NC calculates the correlation coefficient between the extracted watermarked image and the original watermarked image.

$$\mathrm{MSE}=\frac{1}{M\times N}{\displaystyle \sum _{i=0}^{M-1}{\displaystyle \sum _{j=0}^{N-1}{[I(i,j)-I_w(i,j)]}^2}},$$

(12)

where $I(i,j)$ is the original image; $I_w(i,j)$ is the watermarked image.

$$\mathrm{PSNR}=10\log 10(\frac{{255}^2}{\mathrm{MSE}}),$$

(13)

$$\mathrm{NC}=\frac{{\displaystyle \sum _{i=0}^{M-1}{\displaystyle \sum _{j=0}^{N-1}W(i,j)\tilde{W}(i,j)}}}{\sqrt{{\displaystyle \sum _{i=0}^{M-1}{\displaystyle \sum _{j=0}^{N-1}{W}^2(i,j)}}}\sqrt{{\displaystyle \sum _{i=0}^{M-1}{\displaystyle \sum _{j=0}^{N-1}{\tilde{W}}^2(i,j)}}}},$$

(14)

where $W(i,j)$ is the watermarked image and $\tilde{W}(i,j)$ is the watermarked image extracted from one of the attacks.

As shown in Figure 5, the scaling factor is proportional to the NC value and inversely proportional to the PSNR value. As is well known, the larger the NC value, the stronger the robustness, and the smaller the PSNR value, the weaker the invisibility. This paper optimized the scaling factor value through the NC values and PSNR values.

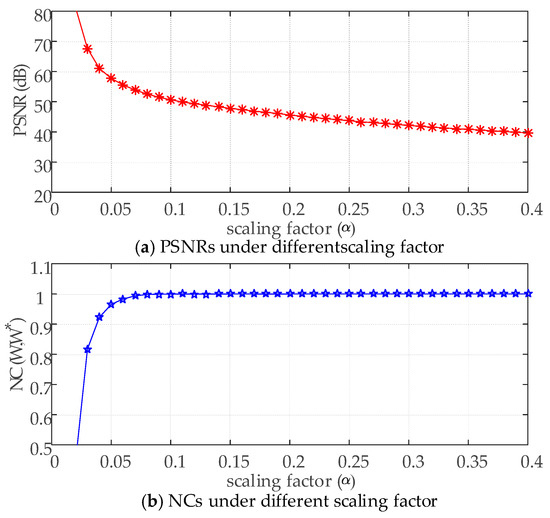
Figure 5. PSNRs and NCs under different scaling factors.

We defined the fitness function by applying NC and PSNR to maximize the robustness and invisibility of the algorithm.

$$fit(\alpha )=\alpha \cdot \frac{\mathrm{PSNR}}{\beta }+(1-\alpha )\frac{1}{n}{\displaystyle \sum _{i=1}^n{\mathrm{NC}}_i},$$

(15)

where $\alpha$ is the scaling factor, $\beta$ is a constant to adjust the size of the PSNR, which is taken as 37 dB in this paper, and $n$ indicates the total number of attacks.

The pseudo-code for the PSO algorithm is shown in Algorithm 1.

Algorithm 1: Using PSO to calculate the best α

Input: Number of particles, N = 50, Weights, W = 0.5, Learning factor, C1 = 2, C2 = 2, Maximum number of iterations, T = 100.     1. Randomly initialize the position and velocity of each particle     2. Set $pbest$ and $gbest$     3. $\alpha =gbest$     4. While iter < = T             Implement Algorithm 1 using α             Perform attacks tests             Implement Algorithm 2             Calculate PSNRs using Equation (13), NCs using Equation (14), fitness value using Equation (15)             Update $pbest$ and $gbest$             Update the position and velocity of each particle using Equations (10) and (11) end     5. $\alpha =gbest$ Output: α.

4.2. Watermark Embedding Algorithm

In the embedding algorithm, the host image and the watermark image both are grayscale images. The host image is N × N, the watermarked image is M × M. Here, the dimensions of M and N satisfy the equation $M/N=2^k,k=1,2,3,4$. In the algorithm, the host image is decomposed into four sub-bands by multi-level DWT; the HMD and SVD are applied to the low-frequency band. The watermark image is encrypted by the Arnold transform and logistic mapping, then the singular value of the encrypted watermark is modified by the scaling factor to embed the low-frequency band of the host image. The process is shown in Figure 6. Existing algorithms require a pre-set ratio of the host image to the watermarked image, which cannot be changed arbitrarily. In this paper, the proposed algorithm applies to many sizes of host images with the help of a multi-level transform of DWT. The pseudo-code for the embedding process of the watermark is shown in Algorithm 2.

Algorithm 2: Embedding algorithm

Input: Host image; watermark image; $\alpha$ calculated by PSO.     1. Perform K-level DWT on the host image to obtain $L{L}_k$, $k=lb\left(N/M\right)$     2. Perform HMD on $L{L}_k$, using Equation (4) to obtain H     3. Perform SVD on H using Equation (6) to obtain $S_{\mathrm{h}}$     4. Encrypt watermark using Equations (7) and (9) to obtain $\tilde{W}$     5. Perform SVD on $\tilde{W}$ using Equation (6) to obtain $U_w\hspace{0.33em},S_w\hspace{0.33em},\hspace{0.33em}{V}_w$     6. Using $\alpha$ to embed watermark, $S^{\ast }=S_{\mathrm{h}}+\alpha S_{\mathrm{w}}$     7. Calculate the new Hessenberg matrix     8. Calculate new low-frequency sub-band     9. Using IDWT to obtain the watermarked image Output: watermarked.

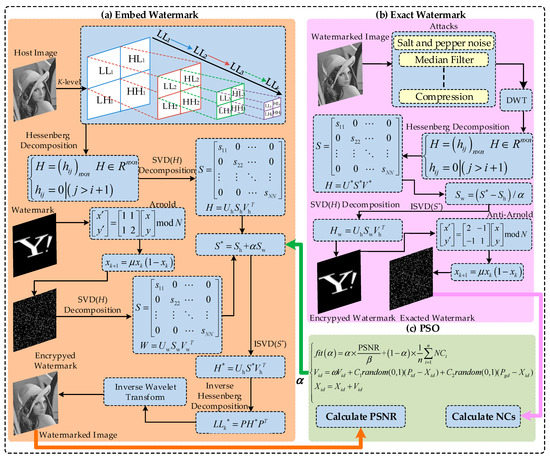
Figure 6. Embedding and extraction process of proposed.

4.3. Watermark Exacting Algorithm

The watermarking extracting process is shown in Figure 6b. It is the inverse of the embedding algorithm and the pseudo-code is shown in Algorithm 3.

Algorithm 3: Exacting algorithm

Input: Watermarked image.     1. Perform K-level DWT on watermarked to obtain $L{L}^{\ast }{}_k$     2. Perform HMD on $L{L}^{\ast }{}_k$ to obtain $H^{\ast }$     3. Perform SVD on $H^{\ast }$ using Equation (6) to obtain $S^{\ast }$     4. Using $\alpha$ to exact $S$ into $S^{\ast }$, $S=(S^{\ast }-S_{\mathrm{h}})/\alpha$     5. Calculate the watermark using $U_w\hspace{0.33em}\mathrm{and}\hspace{0.33em}{V}_w$ in step 5 of Algorithm 2, $\tilde{W}=U_{w}S{V}_w{}^T$     6. Decrypt $\tilde{W}$ Output: exacted watermark image.

5. Results and Comparisons

We conducted some simulations to evaluate the invisibility and robustness of the algorithm. The simulations are performed on a laptop with Intel Core i5 CPU and 16 GB memory, the MATLAB version 9.5 (R2018b) of MathWorks is employed for the modeling and optimization. The images used for the tests are shown in Figure 7, which includes nine standard grayscale host images of different sizes and one binary watermarked image. The image Park is taken by the author, the image Logo is a watermark and the rest are standard MATLAB images.

Figure 7. The host image and watermark image.

The PSNR is a quality evaluation index used in the watermark algorithm. The bigger the PSNR value, the higher quality of the watermarked image. The robustness of the watermarking algorithm mainly examines whether the watermark could be extracted accurately after attacks. The bigger the NC value, the closer it is to the original watermarked image.

5.1. Simulation Results

5.1.1. Invisibility Analysis

Using Algorithm 2, different host images are selected and a fixed size watermarked image is embedded into the host image, and the invisibility of the algorithm is measured using PSNR. The simulation results are shown in Figure 8. The proposed use of the PSNR value to measure the invisibility of the watermarking algorithm. A general watermarking algorithm PSNR value of more than 30 dB can indicate that the watermark is transparent and invisible in the human eye visual system. The PSNR values of the algorithms in this paper are over 44.9 dB without attacks, and it is obvious that the algorithms in this paper meet the requirements of watermark invisibility.

Figure 8. The simulation results of invisibility.

5.1.2. Robustness Analysis

The robustness of the watermarking algorithm is usually measured by calculating the NCs value of the extracted watermark and the original watermark after the attack on the image containing the watermark. The larger the NC value, the stronger the ability of the algorithm to resist the attack; the better the robustness. In this paper, we choose different attacks, such as filtering and cropping, and the attack parameters are shown in Table 1.

Table 1. Parameters of attacks.

Attacks	Parameters
Gaussian filter	5 × 5
Median filter	3 × 3
Average filter	3 × 3
Wiener filter	3 × 3
Gaussian noise	Variance = 0.01
Salt and pepper noise	Density = 0.01
Speckle noise	Variance = 0.01
JPEG compression	Quality factor (QF) = 50
Sharpening	0.7
Crop	Left 12%
Rotate	90°
Motion blur	Theta = 4, Len = 7

A 1024 × 1024 grayscale image of Park is selected as the host image, and the watermark in Figure 7 is embedded into the host image for the attack test. The watermarked image after being attacked is shown in Figure 9. Figure 10 gives the watermark extracted from the watermarked Park image after the attack. From Figure 10, it can be observed that even though the watermarked image extracted in the motion blur attack has been degraded, it is still possible to extract a relatively clear watermark.

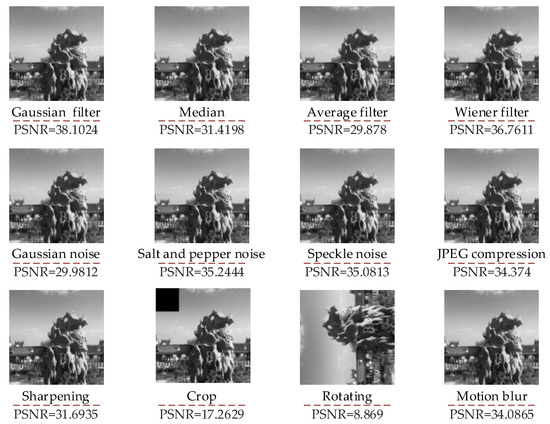
Figure 9. Watermarked images under various attacks.

Figure 10. Extracted watermark under various attacks.

Various attacks are performed on the watermarked image, then the NCs of the extracted watermark and the original watermark are calculated by Equation (13) so that the robustness of the watermarking algorithm can be evaluated objectively. The computational results are shown in Table 2. The larger the ratio of the host image to the watermark, the larger the NC value of the extracted watermark after being attacked and vice versa. In particular, when the host image size is 1024 × 1024, the NC values are greater than 0.995, except for crop attack and motion blur, whose Nc values are higher than 0.98. The commendable robustness is shown in general by testing the attacks on different watermarked images.

Table 2. NC values after various attacks.

Attacks.	Girl	Park	Man	Lena	Goldhill	Baboon	House	Woman	Pepper
No	1	1	1	1	1	1	1	1	1
Gaussian filter	0.9999	0.9999	0.9998	0.9999	0.9999	0.9999	0.9996	0.9997	0.9996
Median filter	0.9999	0.9985	0.9999	0.9999	0.9997	0.9999	0.9993	0.9999	0.9998
Average filter	0.9999	0.9986	0.9999	0.9999	0.9998	0.9999	0.9966	0.9961	0.9958
Wiener filter	0.9997	0.9987	0.9996	0.9994	0.9993	0.9994	0.9988	0.9984	0.9987
Gaussian noise	0.9999	0.9998	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999
Salt and pepper noise	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9998	0.9999	0.9999
Speckle noise	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999	0.9999
JPEG	0.9999	0.9999	0.9999	0.9998	0.9998	0.9996	0.9992	0.999	0.9995
Crop	0.9949	0.9946	0.9923	0.9917	0.9935	0.9919	0.9931	0.9909	0.9852
Sharpening	0.9996	0.9988	0.9997	0.9981	0.9988	0.9981	0.9977	0.9968	0.9967
Rotating	0.9995	0.9998	0.9996	0.9989	0.9984	0.9982	0.9983	0.998	0.9978
Motion blur	0.9987	0.9986	0.9997	0.9967	0.9969	0.9961	0.9874	0.9899	0.9862

5.1.3. Analysis of Attack Test Results

We further analyze the robustness of the algorithm by varying the intensity of the attack test. The host image in the analysis is a Lena image of size 512 × 512.

Firstly, the filtering attack is performed on the image containing the watermark, as shown in Figure 11a. The median filtering is performed on the image containing the watermark, and the filtering window sizes are 3 × 3, 4 × 4, 5 × 5, 6 × 6, and 7 × 7. Although the NC values of the watermark gradually decrease as the filtering window increases, the simulation results show that the NC values are still not lower than 0.99.

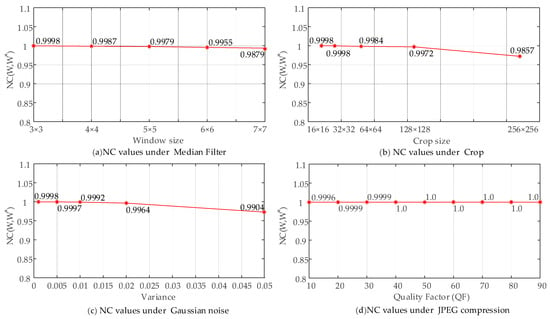
Figure 11. NC values under attacks with different parameters.

As shown in Figure 11b, the watermarked images are tested by cropping, and the cropping sizes are 16 × 16 pixels, 32 × 32 pixels, 64 × 64 pixels, 128 × 128 pixels, and 256 × 256 pixels in the upper left corner, respectively. The simulation results show that the visual quality of the extracted watermark decreases as the cropping size increases. Even so, when the cropping size is 256 × 256, which is equivalent to 1/4 of the clipped image, the NC values of the extracted watermark are not less than 0.98, indicating that the algorithm in this paper can resist the cropping attack well.

In Figure 11c, the Gaussian noise attack is performed on the image containing the watermark, and when the noise intensity is 0.01, the NC values of the extracted watermark is 0.9998, and the watermark information is not corrupted at all. When the noise intensity increases to 0.05, the watermark information is corrupted to some extent, but the watermark information can still be accurately identified with an NC value of 0.9731, which shows better robustness.

In Figure 11d, the NC values of the watermark gradually increase as the QF of JPEG compression increases. When the QF is taken as 10, the NC values of the extracted watermark are not less than 0.99, which indicates that the algorithm in this paper can resist JPEG compression attacks well.

For the NC values under different attacks as shown in Table 3, the NC values are not less than 0.98, except for the attack of cropping 25% of the image, which has an NC value of 0.9738. The commendable robustness is reflected in the simulation results.

Table 3. NC values after different attacks.

Attacks	Parameters	Host Image Size
		1024 × 1024	512 × 512	256 × 256
Median Filter	3 × 3	0.9994	0.9999	0.9985
	5 × 5	0.9985	0.9978	0.9939
	7 × 7	0.9967	0.9879	0.9882
Gaussian Noise	0.001	0.9995	0.9998	0.9993
	0.005	0.9990	0.9997	0.9896
	0.01	0.9984	0.9992	0.9842
JPEG	20	0.9995	0.9993	0.9992
	50	0.9997	1	0.9996
	70	1	1	0.9999
Crop	Left6%	0.9995	0.9982	0.9875
	Left 12%	0.9964	0.9970	0.9828
	Left 25%	0.9871	0.9865	0.9738

5.2. Algorithm Comparisons

In this section, the invisibility and robustness of the algorithm are analyzed by comparing the proposed method with the existing optimization algorithms [19,21,26], when the size of the host image and watermark are 512 × 512 and 128 × 128, respectively. The simulation conditions of the literature [21] and the proposed method are the same; thus, the results can be compared directly. The watermark is embedded into the Lena image using the algorithm of [19,26], respectively. The PSNRs of the watermarked image and the original image are calculated as shown in Table 4. The attack test is performed on the watermarked image, and the PSNRs of the degraded image and the NCs of extracted watermark are obtained, as shown in Table 5 and Table 6.

Table 4. The comparison of the invisibility based on PSNR values without attack.

Images	[19]	[21]	[26]	Proposed
Lena	43.8934	44.5125	43.9583	48.8785
Woman	43.9624	44.5182	43.9501	49.5695
Goldhill	43.9619	43.9023	43.9687	48.9170
House	43.8264	44.3835	43.9876	49.5075

Table 5. PSNR values of different algorithms under attacks.

Attacks	[19]	[21]	[26]	Proposed
Filter	25.8663	28.8229	27.6937	35.4073
Salt and pepper noise	28.9628	25.3931	29.828	35.9293
JPEG (Q = 10) compression	27.2172	33.8331	30.2218	37.1349
Crop 1/4 left up	11.4584	11.7034	11.6027	11.7954
Sharpening	28.7682	20.1304	31.0584	34.859
Rotating 45°	10.1527	10.4813	10.3741	10.5114

Table 6. NC values of different algorithms under attacks.

Attacks	[19]	[21]	[26]	Proposed
Gaussian filter	0.9786	0.9998	0.9377	0.9999
Median	0.9328	0.9980	0.9872	0.9983
Average filter	0.9784	0.9969	0.9369	0.9976
Wiener filter	0.8933	0.9981	0.9903	0.9989
Gaussian noise	0.9546	0.9711	0.9913	0.9999
Salt and pepper noise	0.9921	0.9881	0.9948	0.9999
Speckle noise	0.9917	0.9782	0.9955	0.9999
JPEG(Q = 10) compression	0.9949	0.9997	0.9982	0.9996
Crop 1/4 left up	0.6999	0.9702	0.9492	0.9865
Sharpening	0.8637	0.9617	0.9923	0.9964
Rotating 45°	0.7010	0.9805	0.9026	0.9509
Motion blur	0.9032	0.9969	0.9921	0.9967

5.2.1. Invisibility Comparison

PSNR is one of the main criteria to measure the image quality, and the larger the PSNR value between two images, the more similar the two images are. Firstly, we compare the PSNRs of the proposed algorithm and the algorithm [19,21,26] in the absence of attacks. The results are shown in Table 4.

The invisibility of the proposed algorithm under various attacks is compared with the existing algorithms [19,21,26] in Table 5. The host image uses the Lena image of size 512 × 512 and the watermarked image uses size 128 × 128.

5.2.2. Robustness Comparison

The robustness is compared with the existing algorithms as shown in Table 6; the NC values of the watermarks extracted by the proposed method are better than the existing algorithms [19,21,26] under different attacks. The NC values of the proposed are 4.53%, 2.88% and 0.86% higher in Gaussian noise, the NC values of the proposed are 0.78%, 1.18% and 0.51% higher in salt and pepper noise and the NC values of the proposed are 0.81%, 2.17% and 0.44% higher in speckle noise. According to the analysis of the above results, the robustness of the proposed optimization method is better under different noise attack conditions.

6. Conclusions

In this paper, a watermarking optimization method based on matrix decomposition and DWT for multi-size images is proposed. The DWT, HMD, SVD, PSO, Arnold transform and logistic mapping are combined to achieve watermark protection. The watermark is embedded into multi-size host images using the method in this paper; PSNRs are higher than 44.9 dB without attacks and the NCs are higher than 0.98 under various attacks. Compared with the existing works, the proposed method shows preferable robustness under various attacks, particularly the NC values of the proposed method, which are 4.53%, 2.88% and 0.86% higher than the studies [19,21,26] in Gaussian noise attack, with the analogous advantage in salt and pepper and speckle noise attack. Therefore, the robustness and invisibility of the watermarking algorithm are enhanced by using the proposed method. In the future, our research will focus on further extending the algorithm to watermarked images capable of adapting to color host images of arbitrary size.