Research on the Life Prediction Method of Meters Based on a Nonlinear Wiener Process
Abstract
:1. Introduction
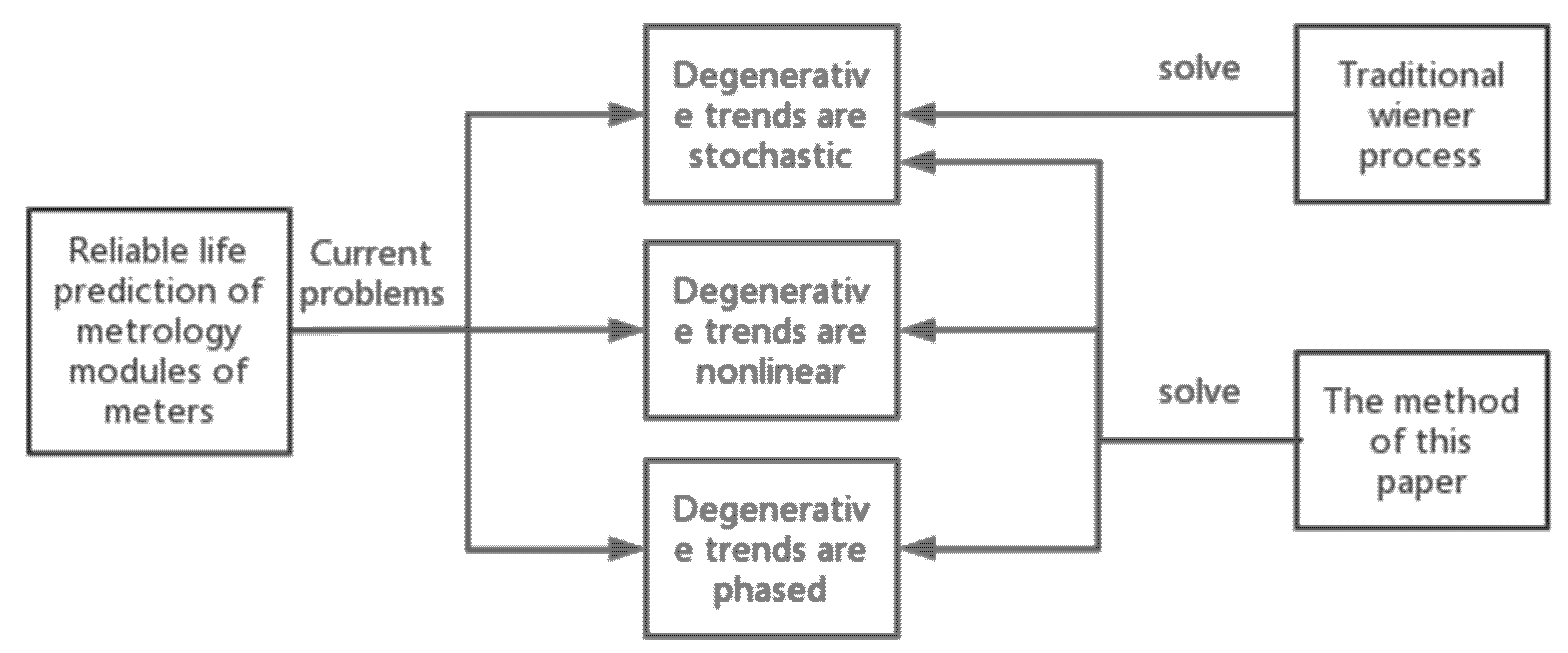
2. Related Work
2.1. Comparison with Traditional Wiener Process Methods
- a.
- The modeling does not take into account the nonlinear degradation trend in the modeling object. Since complex electronic products contain a variety of modules, the final degradation trend of the electronic product should theoretically be a combination of the degradation trends of each module. However, in the actual operation [10], within a certain time range, each module degradation starts to accelerate at different time points and degradation speed, so it may cause the randomness and nonlinearity of the final degradation trend of the electronic product.
- b.
- The model did not take into account whether the modeling object has stage characteristics. For example, capacitors [11], light-emitting [12] diodes, and other electronic products have stage changes in their degradation process, so it is necessary to consider how to deal with the stage characteristics of the degradation trend in the modeling process for the meter that contains these components.
2.2. Application of the Wiener Process Method
3. Problem Formulation and Methodology
3.1. Data Modeling Based on Wiener Process
- a.
- For any t > 0, the data must obey the normal distribution ;
- b.
- The data must have independent smooth increments.
3.2. Estimation of Winner Process Parameters
3.3. Linearization of the Nonlinear Model
- a.
- The Wiener model is established in segments and the data are assumed to be fixed as a whole.
- b.
- The performance degradation trajectory is obtained, and the fitting equation is calculated.
- c.
- The coefficients of the time scale transformation function are estimated by using the coefficients of the fitting equation. The time scale change model is used to transform time t, and the nonlinear degradation process is transformed into a linear degradation process.
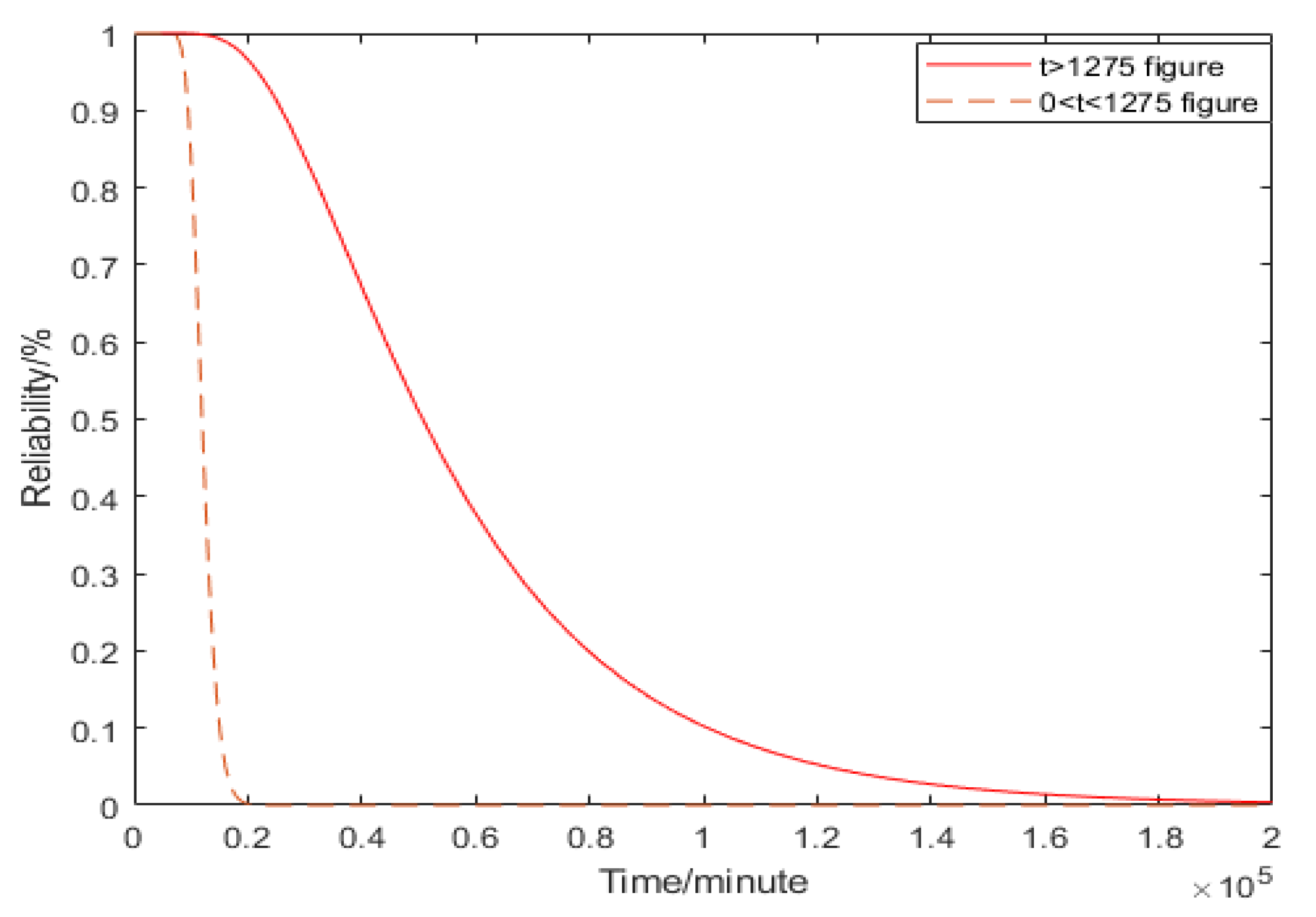
3.4. Reliability Life Prediction Model of a Meter Based on Nonlinear Data
4. Analysis of Results
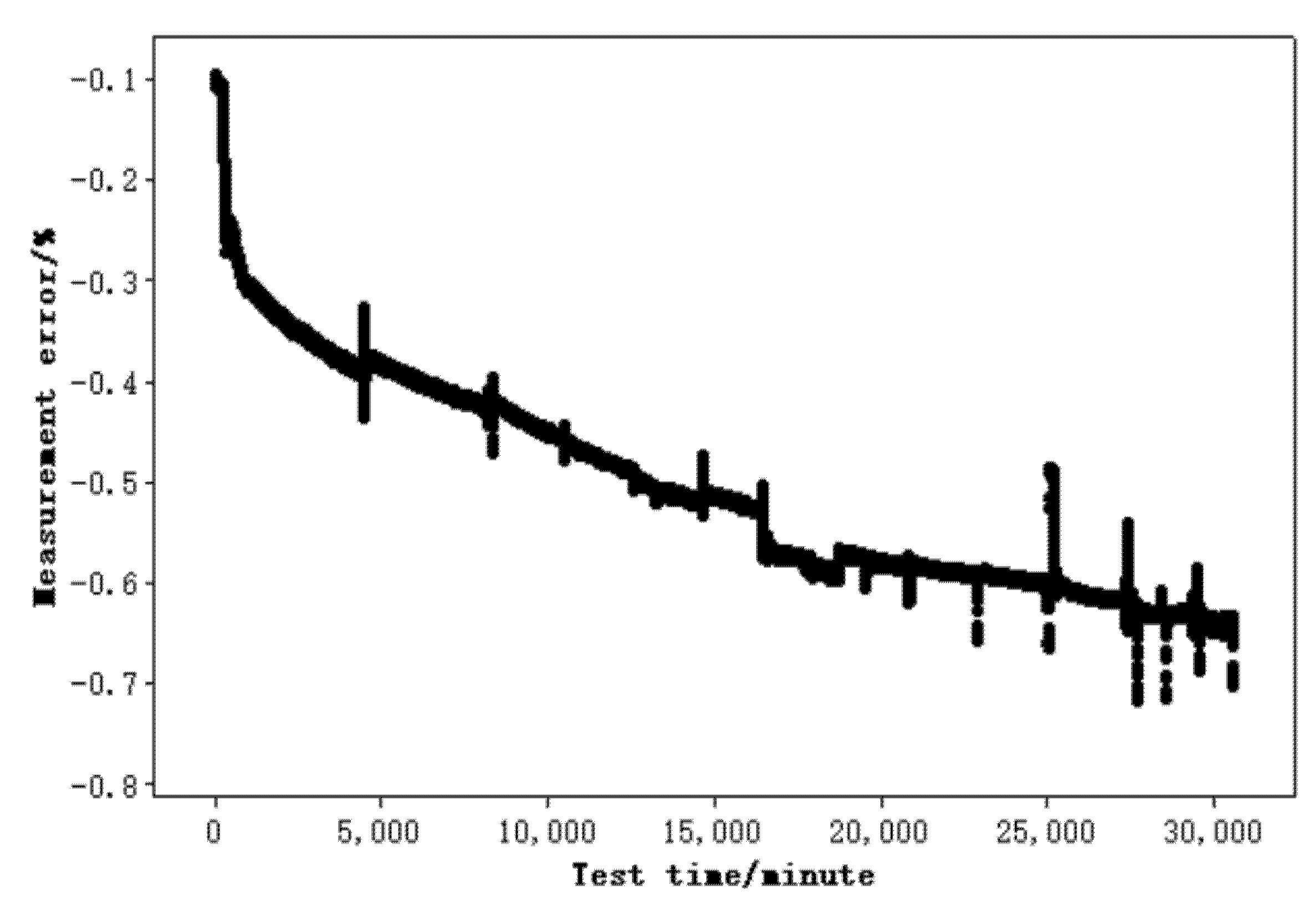
4.1. Experimental Design
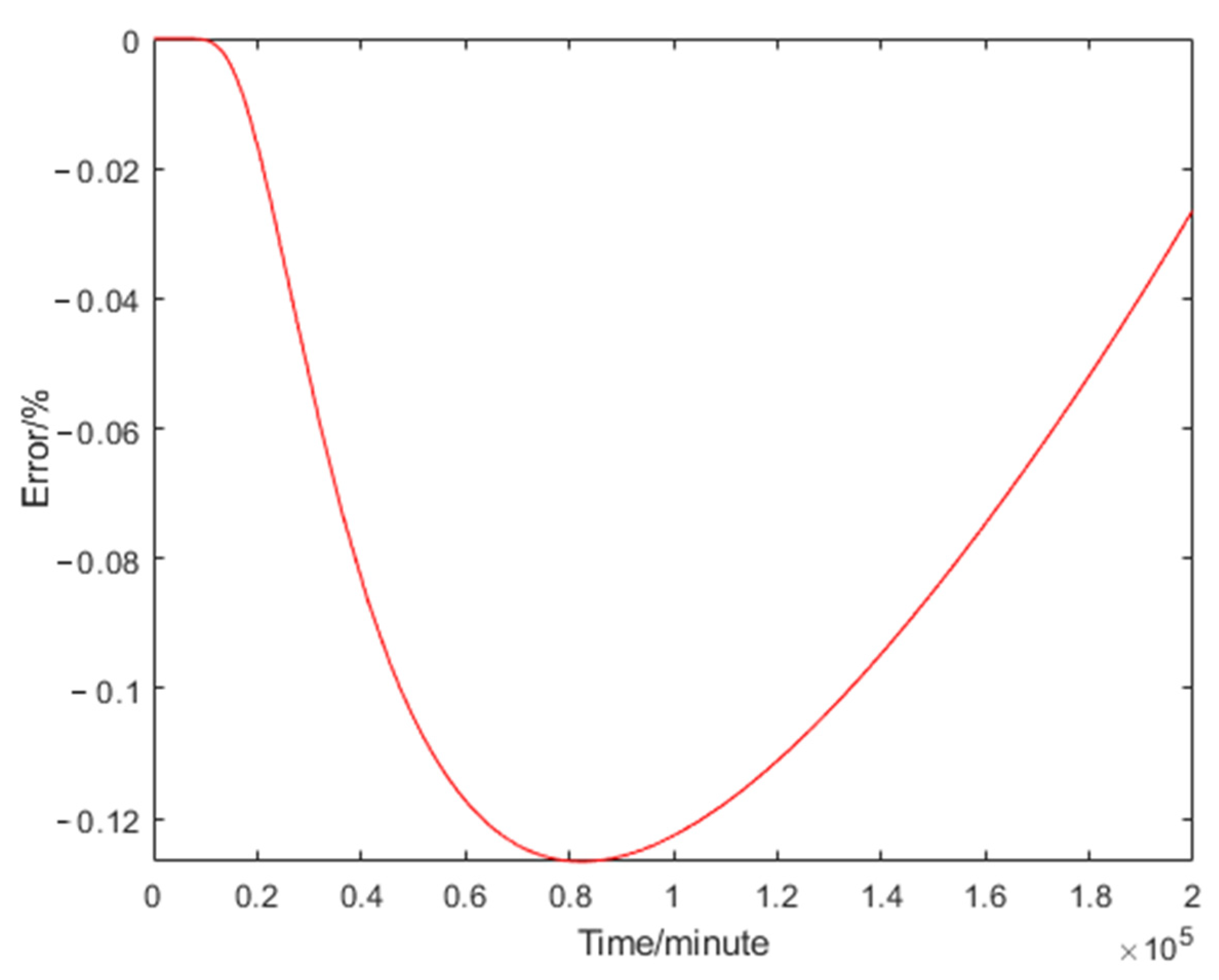
4.2. Comparison with Traditional Models
4.3. Field data Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jaiswal, D.M.; Thakre, M.P. Modeling & Designing of Smart Energy Meter for Smart Grid Applications. Glob. Transit. Proc. 2022, 3, 311–316. [Google Scholar]
- Zhang, X.; Yang, J.; Kong, X. A literature review on planning and analysis of multi-stress accelerated life test for reliability assessment. Recent Pat. Eng. 2021, 15, 12–21. [Google Scholar] [CrossRef]
- Li, Q.; Yan, C.; Chen, G.; Wang, H.; Li, H.; Wu, L. Remaining Useful Life prediction of rolling bearings based on risk assessment and degradation state coefficient. ISA Trans. 2022. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Zhao, Z.; Ren, J.; Zhai, Z.; Wang, S.; Chen, X. A transferable lithium-ion battery remaining useful life prediction method from cycle-consistency of degradation trend. J. Power Sources 2022, 521, 230975. [Google Scholar] [CrossRef]
- Al-Bossly, A. Bayesian Statistics Application on Reliability Prediction and Analysis. J. Stat. Appl. Probab. 2020, 9, 19–34. [Google Scholar]
- Ma, L.; Meng, Z.; Teng, Z.; Qiu, W. A reliability evaluation framework for smart meters based on AGG-ARIMA and PFR. Meas. Sci. Technol. 2022, 33, 045006. [Google Scholar] [CrossRef]
- Yang, H.; Wang, P.; An, Y.; Shi, C.; Sun, X.; Wang, K.; Zhang, X.; Wei, T.; Ma, Y. Remaining useful life prediction based on denoising technique and deep neural network for lithium-ion capacitors. eTransportation 2020, 5, 100078. [Google Scholar] [CrossRef]
- Song, K.; Cui, L. A common random effect induced bivariate gamma degradation process with application to remaining useful life prediction. Reliab. Eng. Syst. Saf. 2022, 219, 108200. [Google Scholar] [CrossRef]
- Yan, W.; Kong, W.; Liu, W.; Xiong, Y.; Zhang, J. Reliability assessment of photovoltaic modules with initial degradation random characteristics. Acta Energ. Sol. Sin. 2022, 43, 152. [Google Scholar]
- Dong, X.; Dai, Y.; Wang, Q.; Chen, Z.; Du, Y.; Wang, P.; Qi, J. Reliability Modeling Methods Using Field Operation Data of Smart Electricity Meters Based on Wiener Process. In Proceedings of the 2020 Global Reliability and Prognostics and Health Management (PHM-Shanghai), Shanghai, China, 16–18 October 2020. [Google Scholar]
- Kurzweil, P. Josef Schottenbauer, and Christian Schell. Past, present and future of electrochemical capacitors: Pseudocapacitance, aging mechanisms and service life estimation. J. Energy Storage 2021, 35, 102311. [Google Scholar] [CrossRef]
- Ibrahim, M.S.; Fan, J.; Yung, W.; Jing, Z.; Fan, X.; Driel, W.; Zhang, G. System level reliability assessment for high power light-emitting diode lamp based on a Bayesian network method. Measurement 2021, 176, 109191. [Google Scholar] [CrossRef]
- Fuli, Y.; Ke, Z.; Renmin, G. Reliability prediction method of smart meter based on Hadoop platform and published parameter estimation. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020. [Google Scholar]
- Gao, H.; Cui, L.; Dong, Q. Reliability modeling for a two-phase degradation system with a change point based on a Wiener process. Reliab. Eng. Syst. Saf. 2020, 193, 106601. [Google Scholar] [CrossRef]
- Wang, X.; Hu, C.; Ren, Z.; Xiong, W. Performance degradation modeling and remaining useful life prediction for aero-engine based on nonlinear Wiener process. Acta Aeronaut. Et Astronaut. Sin. 2020, 41, 11. [Google Scholar]
- Sun, F.; Li, H.; Cheng, Y.; Liao, H. Reliability analysis for a system experiencing dependent degradation processes and random shocks based on a nonlinear Wiener process model. Reliab. Eng. Syst. Saf. 2021, 215, 107906. [Google Scholar] [CrossRef]
- Ge, R.; Zhai, Q.; Wang, H.; Huang, Y. Wiener degradation models with scale-mixture normal distributed measurement errors for RUL prediction. Mech. Syst. Signal Process. 2022, 173, 109029. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, S.; Wei, K.; Zuo, H.; Du, R.; Shu, X. A novel based-performance degradation Wiener process model for real-time reliability evaluation of lithium-ion battery. J. Energy Storage 2022, 50, 104313. [Google Scholar] [CrossRef]
- Yan, B.; Ma, X.; Huang, G.; Zhao, Y. Two-stage physics-based Wiener process models for online RUL prediction in field vibration data. Mech. Syst. Signal Process. 2021, 152, 107378. [Google Scholar] [CrossRef]
- Liao, G.; Yin, H.; Chen, M.; Lin, Z. Remaining useful life prediction for multi-phase deteriorating process based on Wiener process. Reliab. Eng. Syst. Saf. 2021, 207, 10736. [Google Scholar] [CrossRef]
- Bian, L.; Wang, G.; Liu, P. Reliability analysis for multi-component systems with interdependent competing failure processes. Appl. Math. Model. 2021, 94, 446–459. [Google Scholar] [CrossRef]
- Chen, Z. Common fault Analysis and Countermeasures of key Components of intelligent electricity meter. J. Phys. Conf. Ser. 2020, 1654, 012055. [Google Scholar] [CrossRef]
- Si, X.; Li, T.; Zhang, J.; Lei, Y. Nonlinear degradation modeling and prognostics: A Box-Cox transformation perspective. Reliab. Eng. Syst. Saf. 2022, 217, 108120. [Google Scholar] [CrossRef]
- Zhang, H. Two-stage nonlinear Wiener process degradation modeling and reliability analysis. Syst. Eng. Electron. Technol. 2020, 42, 6. [Google Scholar]
- Lin, J.; Liao, G.; Chen, M.; Yin, H. Two-phase degradation modeling and remaining useful life prediction using nonlinear wiener process. Comput. Ind. Eng. 2021, 160, 107533. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Meter test voltage | Rated voltage of meter |
| Meter test current | Rated current of meter |
| Power factor | 1 |
| Temperature of environmental test chamber | 85 ℃ |
| Humidity of environmental test chamber | 95% |
| Number of test days | 30 |
| Number of test tables | 30 |
| Test Time/Minute | Measurement Error/% | |||
|---|---|---|---|---|
| Sample 1 | Sample 2 | … | Sample 30 | |
| 0 | −0.1013 | −0.0917 | … | −0.0870 |
| 10,000 | −0.4557 | −0.4848 | … | −0.4840 |
| … | … | … | … | … |
| 32,736 | −0.6912 | −0.7218 | … | −0.7315 |
| Parameter | ||||
|---|---|---|---|---|
| Value | ||||
| Parameter | ||||
| Value |
| Relative Error of the Unprocessed Model/% | Relative Error of the Nonlinear Model/% |
|---|---|
| 10.273 | 6.956 |
| −10.377 | −5.722 |
| −11.696 | −8.637 |
| 7.079 | 3.834 |
| 8.510 | 5.358 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Zhong, C.; Peng, X.; Zhou, S.; Zhou, J.; Zhang, Z. Research on the Life Prediction Method of Meters Based on a Nonlinear Wiener Process. Electronics 2022, 11, 2026. https://doi.org/10.3390/electronics11132026
Chen J, Zhong C, Peng X, Zhou S, Zhou J, Zhang Z. Research on the Life Prediction Method of Meters Based on a Nonlinear Wiener Process. Electronics. 2022; 11(13):2026. https://doi.org/10.3390/electronics11132026
Chicago/Turabian StyleChen, Jiayan, Chaochun Zhong, Xiaoxiao Peng, Shaoyuan Zhou, Juan Zhou, and Zhenyu Zhang. 2022. "Research on the Life Prediction Method of Meters Based on a Nonlinear Wiener Process" Electronics 11, no. 13: 2026. https://doi.org/10.3390/electronics11132026
APA StyleChen, J., Zhong, C., Peng, X., Zhou, S., Zhou, J., & Zhang, Z. (2022). Research on the Life Prediction Method of Meters Based on a Nonlinear Wiener Process. Electronics, 11(13), 2026. https://doi.org/10.3390/electronics11132026






