Abstract
In cognitive radio networks, wireless nodes adapt to the surrounding radio environment and utilize the spectrum of licensed users. The cognitive radio environment is dynamic, and wireless channels are accessible by both legitimate and illegitimate users. Therefore, maintaining the security of cognitive radio networks is a challenging task, which must be addressed thoroughly. Further, with the recent exponential surge in wireless nodes and associated high data rate requirements, energy consumption is also growing at an unprecedented rate. Hence, energy efficiency becomes an important metric that must be considered in the design of future wireless networks. Accordingly, by considering the great ecological and economic benefits of green wireless networks, this work focus on energy-efficient resource allocation in secure cognitive radio networks. Since physical-layer security is an emerging technique that improves the security of communication devices, in this paper, an ergodic secure energy efficiency problem for a cognitive radio network is formulated with a primary user, a secondary user, and an eavesdropper. As the formulated problem is non-convex, a concave lower bound is applied to transform the original non-convex problem into a convex one. Further, by adopting the fractional programming and dual decomposition techniques, optimal power allocation strategies are obtained with the aim of maximizing the ergodic secure energy efficiency of the secondary user with constraints on the average interference power and average transmit power. Numerical examples are used to demonstrate the effectiveness of the proposed algorithm.
1. Introduction
Cognitive radio is a promising technique that utilizes unused spectrum bands and improves the network’s spectral efficiency (SE). Apart from spectral efficiency, energy efficiency (EE) is another important design criterion that should be considered for future green wireless networks [1]. The unprecedented increase of mobile devices and the escalating high data rate requirements have contributed to the sharp growth of energy consumption and greenhouse gas emission. It is reported that 2% to 10% of the global energy consumption and 2% of the greenhouse gas are generated by information and communication technologies [2]. Accordingly, green cognitive radio is an attractive technology that can improve both the spectral efficiency and energy efficiency of a wireless network simultaneously. In such a green cognitive radio spectrum-sharing system, a secondary user (SU) coexists with the primary user (PU) and transmits information in the same spectrum bands of the PU in an energy-efficient way on the condition that the interference caused to the PU by the SU is tolerable within specific margins [3].
However, due to the dynamic nature of a cognitive radio environment, security is also an important issue that has been attracting growing attention [4]. There may exist malicious users that may (i) illegitimately access the PU bands or change the radio environment, resulting in the inability of the legitimate SU to use PU bands, or (ii) intercept confidential information transmitted by the legitimate SU. Traditionally, cryptographic techniques through data encryption at the application layer have been applied to guarantee that confidential information is reliably transmitted. However, cryptographic techniques have significant implementation complexity, which significantly increases the overhead of networks and decreases the efficiency of the communication system [5]. This high implementation complexity consumes too much energy, which contradicts the vision of green communication. In this regard, security at the physical layer can improve the security of green cognitive radio, which is based on the physical-layer characteristics of the wireless channels and, hence, has reduced the implementation complexity. Recently, work on physical-layer security in cognitive radio has made considerable progress. In [6], the authors provide an information-theoretic perspective of the physical-layer security of a secondary user in a multiple-input single-output cognitive radio channel. Next, in [7], the authors show that the secrecy capacity (SC) of the secondary user is limited by the channel state information (CSI). In order to overcome this limit, multiple-input multiple-output techniques and cooperative relaying techniques have been exploited. For example, in [8], the authors study the achievable rates of the multi-antenna or multiple-input multiple-output secrecy channel with multiple single/multi-antenna eavesdroppers and show that the maximum achievable secrecy rate is obtained by maximizing the minimum difference between the channel mutual information of the secrecy user and those of the eavesdroppers. Similarly, ref. [9] studies the secure multiple-antenna transmission over slow fading channels and maximizes the secrecy throughput by designing beamforming and power allocation between the information signal and the artificial noise of the SU. The authors in [10] investigate the physical-layer security of cognitive radio transmissions in the presence of multiple eavesdroppers and proposes the multi-user scheduling scheme with the primary quality of service (QoS) constraint. However, in this work, the authors did not consider user fairness in the multi-user scheduling for improving the cognitive radio security against eavesdropping attacks. Further, in [11], the authors derive the secrecy outage probability and study the diversity performance of a multi-user multi-eavesdropper cognitive radio system in the presence of coordinated and uncoordinated eavesdroppers with a primary QoS constraint. However, here, the authors study the physical-layer security of cognitive transmissions by ignoring the security of the primary network. Some other works include [12], where the authors examine secure ergodic resource allocation problems in an orthogonal frequency division multiple-access-based relay-assisted underlay cognitive radio network in the presence of passive eavesdroppers where the objective is to maximize the secrecy rate, and [13], where the authors analyze multi-objective resource allocation for secure communication in cognitive radio. In the latter, the trade-off among total transmit power, energy harvesting efficiency, and interference power was reported, while it was shown that the secrecy could be significantly improved by using multi-input multi-output techniques or cooperative relaying techniques.
In addition to the security requirements, energy efficiency is also a vital issue in cognitive radio networks because of the high energy requirement of modern wireless networks, which has both economic and ecological implications. The following discussion elaborates on a few pieces of literature that study energy efficiency in cognitive radio networks. The authors in [14] proposed an energy-efficient joint pilot and data power allocation scheme with a max–min fair energy efficiency guarantee in an uplink massive multiple-input multiple-output cognitive radio network. In [15], an energy-efficient resource allocation scheme for orthogonal frequency division multiple-access-based cognitive radio networks is proposed under the constraints of the system power budget, primary users’ interference, secondary users’ rate requirements, fairness, and channel uncertainty. A fast power allocation algorithm and an efficient heuristic sub-channel allocation algorithm are given that yield a good trade-off between energy efficiency and computational complexity. Similarly, ref. [16] investigated energy-efficient transmissions for multiple-input multiple-output cognitive radio networks and optimized the time allocations and beamforming vectors to minimize the energy consumption of the SU, and [17] studied the cooperative sensing scheduling by considering both sensing performance and energy efficiency under a practical scenario where both PU channels and SUs have heterogeneous characteristics. Next, the energy-efficient resource allocation in an orthogonal frequency division multiple-access-based cognitive radio network is investigated in [18] under the constraints of the transmission power budget of the cognitive radio system, interference threshold of primary users, and traffic demands of secondary users, and a fast barrier method is developed to speed up the computation of the Newton step, while [19] studies the energy efficiency of cognitive relay networks, where a cognitive capacity harvesting network architecture was proposed, and a spectrum- and energy-efficient relay station placement strategy was developed. In [20], the authors study the energy-efficient resource allocation in heterogeneous cognitive radio networks with femtocells. The resource allocation problem is formulated as a three-stage Stackelberg game, and an iteration algorithm is given to obtain the Stackelberg equilibrium solution for the energy-efficient resource allocation. However, the authors only considered perfect channel state information scenarios in this work and did not consider uncertainties in the channel parameters. Similarly, in [21], the authors designed sensing-access strategies to maximize the energy efficiency of multi-channel cognitive radio networks using sequential channel sensing. The design problem is formulated as a stochastic sequential decision-making problem and was solved by dynamic programming. In [22], the authors studied the energy efficiency of full-duplex cognitive radio. Using discrete-time embedded Markov-chain modeling, the effect of the frequency of sensing is analyzed on the energy efficiency, throughput, and probability of collision for a target false alarm and miss detection levels. By using sleeping times in the sensing mechanism, the system performance was analyzed in different average power consumption distributions for the transmitting and sensing operations of the cognitive device. The performance of full-duplex cognitive radio was compared with a conventional half-duplex cognitive radio, and the results verified that even under poor channel conditions, the full-duplex cognitive radio can achieve a higher level of energy efficiency without compromising its throughput. Finally, in [23], the authors proposed an energy-efficient power allocation scheme by taking into consideration the various types of probabilities associated with the sensing process as performance parameters. Based on these probabilities, the authors proposed a new method to utilize PU carriers. The trade-off between the sensing quality and the achievable sum rate while using PU sub-carriers was used for allocating the optimal transmit power. Regarding the energy efficiency issue in traditional secure wireless communication networks [24,25,26,27,28], there are many challenges for energy efficiency maximization in secure green cognitive radio networks. In particular, in a secure green cognitive radio, the interference by the SU to the PU must be considered while maintaining the quality of service at the PU. Recently, energy-efficient secure communication in cognitive radio networks has been investigated in several research articles. In [29], the authors studied a secure energy efficiency maximization problem for a guaranteed minimum secrecy capacity of an SU under a peak interference power constraint and an average/peak transmit power constraint. In [30], the authors obtained the maximum secrecy energy efficiency of an underlay cognitive relay network in the presence of an eavesdropper over a multi-antenna relay. Similarly, in [31], the authors investigated a secure energy efficiency optimization problem in a multiple-input single-output underlay cognitive radio network in the presence of an unauthorized energy harvesting energy receiver. However, these works consider only the perfect channel state information scenario. To our best knowledge, the secure energy efficiency maximization problem has not been studied in secure cognitive radio from the perspective of green communications.
In this paper, unlike the above-mentioned works, an ergodic secure energy efficiency maximization problem is considered for a secure cognitive radio network, where the SU and PU coexist in the presence of an eavesdropper and fading channel, subject to the average interference power constraint identified as the metric for protecting the quality of service of the PU and the average transmit power constraint that limits the SU transmit power. An iterative algorithm is proposed to find the optimal power allocation policy for the designed framework based on dual-decomposition.
The remainder of the paper is organized as follows. Section 2 presents the system model. The ergodic secure energy efficiency maximization problem subject to the AIP and ATP constraints is presented in Section 3. Section 4 presents a model extension for robust power allocation. Section 5 presents the simulation results. Section 6 gives the concluding remarks.
2. System Model
In this section, we first expatiate the network model, followed by the transmission model. Lastly, we describe power constraints necessary for secondary user transmission and to protect the primary user from interference generated by the secondary user.
2.1. Network Model
Figure 1 shows an underlay cognitive radio model, which consists of a single PU and SU pair. The SU opportunistically accesses the spectrum unused by the PU if and only if the engendered interference is not traded off with the performance of the PU. There is a passive eavesdropper (ED) in the wire-tap link. The secure green cognitive radio system operates on a spectrum sharing program, where the SU-Tx intends to send a confidential message to the SU-Rx on the same narrow-band as the PU-Tx. At the same time, the eavesdropper tries to eavesdrop and intercept the information sent by the SU-Tx. The passive eavesdropper attempts to intercept the SU’s information without modifying it or misleading the SU, and also, the SU does not receive any feedback or trust any feedback from the passive eavesdropper. All the terminals have one antenna.
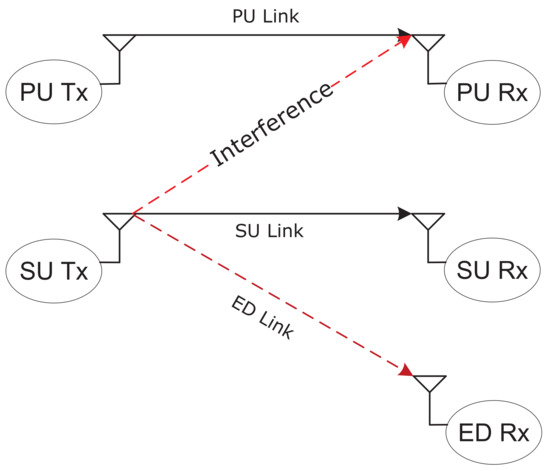
Figure 1.
An illustration of the considered CR model.
All the links between the SU-Tx and PU-Rx (interference link), Su-Tx-SU-Rx (SU-link), and SU-Tx and ED-Rx (ED-link) are block faded with independent and identically distributed (i.i.d) channel power gains with continuous probability density functions. The block fading additive white Gaussian noise channels are the general class of block-interference channels as described in [32]. It happens that, in several wireless communication conditions, variations in the propagation environment take place on a very slow time scale with respect to the signaling rate. The channel coefficient stays constant during each transmission block, but probably changes from one block to a new block [33]. Blocks can be assumed as separated either in time (e.g., in a time division multiple access system as in [34]), as separated in frequency (e.g., in a multi-carrier system as in [35]), or as separated both in frequency and time (e.g., in a slow frequency–time hopping system as in [36].
This paper considers a point-to-point flat fading channel. A wireless channel is thought to be flat fading if its gain is constant and it has a linear phase response over a bandwidth that is greater than the bandwidth of the transmitted signal [37]. The flat fading channel can cause a decrease in the signal-to-noise ratio (SNR) [38]. The flat fading channels are also known as amplitude-varying channels or narrow-band channels as the signal is narrow with respect to the channel bandwidth [39]. This channel model is also well fitted to the case of a multi-carrier system with B parallel sub-channels, possibly located at non-adjacent carrier frequencies [40].
It is assumed that the interference at the SU-Rx and the eavesdropper from the PU-Tx are circularly symmetric complex Gaussian. This model for the interference is a worst-case model and was used in [41]. Thus, the interference and the noise at the SU-Rx and the eavesdropper are circularly symmetric complex additive white Gaussian noise with variance and , respectively.
The secondary user is assumed to have perfect knowledge of instant channel state information (CSI) for all fading states. The interference channel state information from the SU transmitter to the PU receiver can be obtained at the SU transmitter through cooperation with the PU. For the ED link, the statistical channel state information is available at the legitimate transmitter, which is generic and extensively adopted in the literature (see [21,22,23]). In practice, this corresponds to the scenario where the eavesdropper was a legacy user previously, but now identified as an eavesdropper since the SU-Tx wants to transmit some confidential message to the SU-Rx and keeps it a secret from the eavesdropper. In this work, nodes are static for simplicity, and the focus is more on the energy efficiency aspects of cognitive radio networks. Note that for readability, key notations are depicted in Table 1.

Table 1.
Key notations.
2.2. Transmission Model
In this paper, the objective is to find the optimal cognitive power that maximizes the energy efficiency for a given channel realization and with respect to power and interference constraints. The energy efficiency can be calculated as ratio of spectral efficiency and total consumed power. The total consumed power is the sum of transmit power and circuit power . The circuit power includes the consumption of analog-to-digital converters, filters, mixers, amplifiers, etc. The circuit’s output power plays an important part in determining the optimal power for maximizing the EE. Indeed, if , the power that optimizes the EE tends to zero, and the problem is addressed immediately. The rest of the study assumes that , implying that the optimal power is not zero.
Let , , and represent the channel coefficients of the links from SU-Tx to PU-Rx, SU-Tx to SU-Rx, and SU-Tx to ED-Rx, respectively. The channels may follow any distribution, e.g., Rayleigh, Nakagami, Rician, etc. For simulation and numerical results, we adopted a Rayleigh fading distribution. All channels are block fading and experience independent and identical Rayleigh fading. Let , , represent instantaneous channel power gains for the channel from the SU transmitter to the PU receiver, the channel from the SU transmitter to the SU receiver, and the channel from the secondary user transmitter to the eavesdropper, respectively. Here, denotes the fading index for all related channels. Given the transmission power at the secondary transmitter is , the received signals at the SU-Rx and ED-Rx are given as
respectively. Here, represents the transmitted symbol from the SU-Tx. and are independent complex additive white Gaussian noise (AWGN) with zero mean and and variances.
The capacity of the channel between the SU-Tx and SU-Rx, considering the unit bandwidth, is given by
where . Similarly, the capacity of the channel between the SU-Tx and ED-Rx for the unit bandwidth is
where . The secrecy rate or secrecy capacity (SC) of the secondary user is given by
where denotes .
2.3. Power Constraints
There are two types of power constraints with respect to secondary user communication, namely peak transmit power (PTP) and average transmit power (ATP) constraints. The PTP constraint is due to the non-linearity of power amplifiers, while the ATP constraint’s aim is to satisfy the long-term power budget of the SU. The ATP/PTP constraints can be written as
where, is the transmit power of the SU in fading state . and represent the maximum PTP and the maximum ATP of the SU, respectively. is the expectation operator. To protect the primary user from interference generated by secondary user transmission, an interference power constraint must be imposed on the secondary user. It is shown in [42] that the average interference power (AIP) constraint can better shield the primary user from secondary user transmission. Hence the AIP constraint is considered here on the secondary user and can be written as
where denotes the maximum tolerable AIP. Note that this work uses only the ATP and AIP constraints.
3. Ergodic Secure EE Maximization under Average Transmit Power and Average Interference Power Constraints
In this section, the ergodic secure energy efficiency maximization problem is studied under the AIP and ATP constraints. The corresponding ergodic secrecy capacity (SC) maximization problem is also simulated and investigated to present a benchmark. The energy-efficient optimal power allocation strategy for the ergodic secure EE maximization and the optimal power allocation strategy for the ergodic SC maximization are proposed.
3.1. Problem Formulation and Transformation
According to [43], a source can reliably transmit data to a destination with a non-zero rate when the desired receiver has better channel conditions than the eavesdropper. As presented in [5], the SC of the SU is the difference between the capacity of the secondary link and that of the wire-tap link, denoted by and given as
where and . Here, is an indicator function for whether the SU transmits information or not in fading state . For , , and for . As discussed in [12], the ergodic SC is the long-term average SC. Thus, the ergodic secure EE maximization can be formulated as problem P1 and can be given as
where denotes the ergodic EE function of . and represent the amplifier coefficient and the constant circuit power consumption of the SU-Tx, respectively.
Lemma 1.
When is non-zero, is non-convex with respect to .
Proof.
This can be shown by taking the second-order derivative of with respect to , i.e.,
As the second-order derivative of is the summation of concave plus convex terms, hence the optimization problem is non-convex. □
Now, the optimization problem P1 is non-convex in nature due to (i) the fractional form of the objective function in (9a) and () being a mixed binary integer non-linear programming problem [44]. There is no standard technique to solve such an optimization problem. Therefore, to determine the optimal resource allocation policies, the original optimization problem needs to be transformed into an analytically tractable form. First, apply the change of variable to by putting as follows:
Using , problem can be equivalently written as
The new constraints after the change of variable are given below:
Furthermore, use the successive convex approximation approach to transform the problem P1a into a tractable one by maximizing a lower-bound of the achievable sum rate in the following:
where and . Using , problem P1a can be rewritten as
The lower bound relationship is always valid if the coefficients are chosen as follows [45]:
Similarly,
The lower bound becomes tight with equality when the coefficients are selected as specified above.
3.2. Optimal Power Allocation
Because of the fractional form, the objective function in P1b is still non-convex. By utilizing the properties of non-linear fractional programming, which is useful to deal with the concave-over-convex fractional function in an iterative manner, the objective function can be transformed in subtractive form. Let denote the set . According to Dinkelbach’s method [46], problem P1b can be equivalent to a parameter optimization problem, denoted by P2, given as
where is a non-negative parameter. It is seen that can be regarded as the cost factor of the power consumption.
Remark 1.
When η approaches zero, it implies that the cost for power resource utilization is negligible, and the power allocation policy bears resemblance to an ergodic secure capacity maximization problem. However, when the values of η increase, the network utility stresses the importance of the power resource for the design of power allocation in cognitive radio networks. No transmission will be the best strategy to maximize the EE when .
Let and denote the EE optimal transmit power of the SU in terms of maximizing the ergodic secure EE and the optimal of P2, respectively. The EE optimal power allocation strategy can be obtained by using Theorem 1, given as follows.
Theorem 1.
The EE optimal power allocation, , achieves the maximum ergodic secure EE if and only if
Proof.
Let and denote the EE optimal solution of and the corresponding maximum ergodic secure EE. Then,
Accordingly,
Now, according to Equations (27), the maximum of is zero and is achieved when the EE optimal power is adopted and the maximum ergodic secure EE is obtained. □
Now, for a given , the Lagrange duality method can be applied to solve problem P2. The Lagrangian function of P2 can be given as
where and denote the non-negative dual variables. Then, the Lagrange dual function of P2 can be given as
where .
The problem is decomposed and solved via two iterative steps: the first step is related to a subproblem for finding the solutions of the power control, and the second step involves a master dual problem for updating the Lagrangian multipliers. Thus, by taking the partial derivative of with respect to and equating the result to zero, the optimal can be obtained. In the master problem, for the obtained in the sub-problem, the Lagrangian multipliers and are updated using the sub-gradient method [44]. The proposed iterative algorithm is summarized in Algorithm 1.
| Algorithm 1. Iterative ergodic secure EE maximization algorithm. |
|
4. Limitations of Proposed Scheme and Model Extension for Robust Power Allocation
In this work, nodes are static for simplicity, and the focus is more on the energy efficiency aspects of cognitive radio networks. However, the mobility of the wireless nodes and the distance between nodes also affects the performance of cognitive radio networks. The mobility of nodes and distance are interrelated. When the mobile nodes move, the mutual distance between the primary user and cognitive users changes dynamically [47]. As a result of this, the channel between them is time-varying. Therefore, even if at a particular time, the cognitive radio user detects the presence of the PU accurately, this situation might change after the movement of the PU or cognitive radio user [48]. If spectrum sensing algorithms are aware of these topological changes, then it would protect primary users from interference. Mobility also affects other network characteristics such as network connectivity [49], routing [50], capacity [51], coverage [52], etc. Mobility also plays a critical role in latency.
Mobility is also an intrinsic feature to support distinct kinds of wireless services in cognitive radio networks. The IEEE 802.22 Working Group has recently adopted an amendment for the operation of portable devices [53]. Allowing node mobility in cognitive radio networks will introduce numerous challenges, making it necessary to revisit the current system design and protocols, such as mechanisms for spectrum sensing, interference management, and routing. Despite its importance, however, mobility is still largely unexplored in the context of dynamic spectrum access. Therefore, the mobility of nodes affects the performance of cognitive radio networks in a big way.
Here, we assume that channels are flat fading. However, frequency-selective fading would provide an extra facet for optimization (e.g., more power can be transmitted opportunistically at frequencies where the secondary–primary channel has higher attenuation). To report the result of sensing, one or more reporting channels are needed. The reporting channel uses a different band from that used for sensing. In this work, we are assuming that sensing results are transmitted using the PU’s spectrum when the absence of the PU is confirmed. Here, the potential interference to the PU is controllable, and hence, we can meet the PU’s outage probability requirements. However, because of the misdetection probability of the PU, this method still generates interference to the primary user, and therefore, we need a specific reporting channel design. The reporting channel design can be explored in a future extension of this research.
In this work, we assumed that all the channel state information (CSI) is perfectly known at all transceivers. The CSI for the secondary link can be obtained by the classic channel training, estimation, and feedback mechanisms. However, obtaining the CSI of the link from the secondary transceiver to the primary receiver and eavesdropper link is a challenging task as this CSI knowledge requires the primary user and eavesdropper to cooperate. If there is no cooperation of the users, then there is the possibility of interference in the primary communication link. Therefore, timely and accurate knowledge of the CSI requires considerable resource overhead. In the next part of this section, we extend our proposed framework to the non-perfect CSI scenario.
In practice, perfect CSI is challenging to obtain due to the inherently time-varying nature of wireless channels, delay, noise, and limited bandwidth in feedback channels and other factors. This section considers a more practical scenario where cognitive radio users do not have perfect CSI knowledge [54] and proposes a robust resource allocation policy. The proposed design framework can be easily extended to accommodate this scenario by replacing the channels with the following:
where , , and are the estimated channels and , , and are the channel estimation errors. The proposed power allocation schemes obtained under imperfect CSI are beneficial in practical settings and give insight into the impact of channel uncertainty on the system performance. At the same time, the EE in the presence of perfect CSI of the transmission and interference links serves as a baseline to compare the performances attained under the assumption of imperfect CSI.
5. Numerical Results
This section presents simulation results to demonstrate the SU’s achievable maximum ergodic secure EE with the proposed EE optimal power allocation strategies under the ATP and AIP constraints. The achievable maximum ergodic secure EE is compared with that achieved with the optimal power allocation strategies for the ergodic SC maximization (SCM). The values of and are W and , while and were set as and 1, respectively. The maximum number of iterations for inner and outer loops is 10. The maximum tolerance value is along with as the positive step sizes.
Figure 2 illustrates the convergence of the proposed iterative power allocation algorithm. The values of the ATP and AIP were set as mW and mW, respectively. It can be observed that the obtained ergodic secure EE and SC of the proposed algorithms monotonically increase with the number of iterations, and the number of iterations required for convergence is less than four. The quick convergence, however, comes at the expense of a lower ergodic secondary secrecy sum rate (weaker performance). This is due to the algorithm skipping over certain possible solutions that would satisfy the requirements and yield a greater sum rate. As a result, the designer may always strike a balance between the problem’s complexity and the performance of the secondary network.
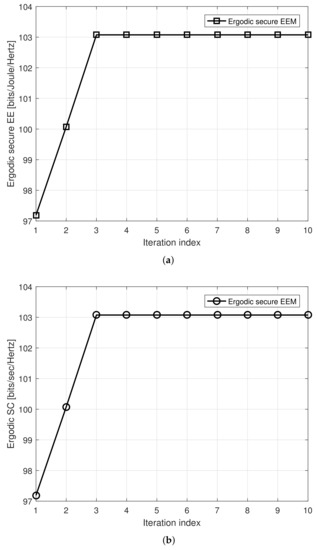
Figure 2.
Convergence behavior of iterative algorithms. (a) EE versus number of iterations, (b) SE versus number of iterations.
Figure 3 shows the performance comparison of the proposed energy efficiency maximization (EEM) algorithm with that of the SCM. The AIP constraint was set as W. Several interesting observations are noted from this figure. It can be seen that the average ergodic secure EE of the SU achieved by both algorithms is identical for W. However, when W, the maximum ergodic secure EE of the proposed EEM algorithm is better than that of the SCM. This indicates that the power allocation strategy for the ergodic SCM is not “optimal” with respect to the ergodic secure EE maximization. On the other hand, the SCM algorithm outperforms the proposed EEM algorithm in terms of the average ergodic SC for W. This is because the SU user utilizes the maximum power to enhance the ergodic SC without being concerned about the ergodic secure EE. Thus, the trade-off between the achievable ergodic secure EE and the ergodic SC of the SU can be understood from Figure 3. Moreover, we can also observe that EEM has an average ergodic EE gain of over 21% over SCM when W.
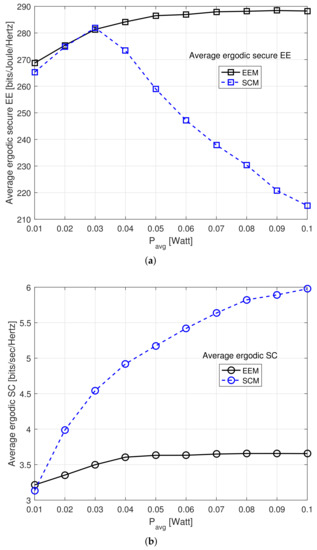
Figure 3.
Average ergodic secure EE and SC of SU versus . (a) Average ergodic secure EE of SU versus , (b) Average ergodic SC of SU versus .
Figure 4 shows the ergodic EE and SC of the SU versus the ATP for the ergodic secure EEM algorithm. The AIP constraint was set as W. It is seen that the average ergodic EE and SC of the SU achieved for the ergodic EEM algorithm improve with increasing AIP values. A higher AIP value indicates that the PU receiver can tolerate higher interference power from the SU. Thus, the SU uses more power to improve ergodic secure EE and ergodic SC. In the case of non-cognitive transmission, the positive value of secrecy can be obtained when the secondary channel is strictly more robust than the eavesdropper channel. However, for cognitive transmission, the interference temperature limits the capacity regardless of transmit power.
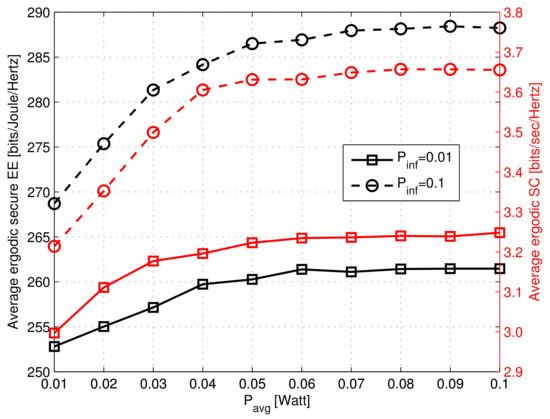
Figure 4.
Average ergodic secure EE and SC of SU versus .
Figure 5 shows the average ergodic EE and SC performance of the SU for different AIP. The average ergodic EE and SC increase with increasing and become constant after W. When ATP increases from W to W, the average ergodic EE and SC achieved for the proposed algorithm also increase. This can be explained by the fact that a higher ATP can provide more flexibility to the transmit power of the SU. As given in [42], the AIP constraint is superior in terms of achievable ergodic and outage capacity for secondary users and the PU. The same can be seen here, and the simulation results confirmed that the SU’s various capacity limits also increase with increasing AIP constraints. This is due to interference diversity, where a limit on randomized average interference power over the different fading states increases the PU’s and SU’s capacity. Hence, the AIP constraint results in larger capacities for both the SU and PU. As shown in Figure 4, the EE of the SU also increases with the ATP and AIP, which agree with the analytical results obtained in Section 3. Here, it is assumed that perfect CSI is available for the PU interference channel at each fading state. The discussion of the AIP presented in this paper can be extended for the more general case where only statistical knowledge is available.
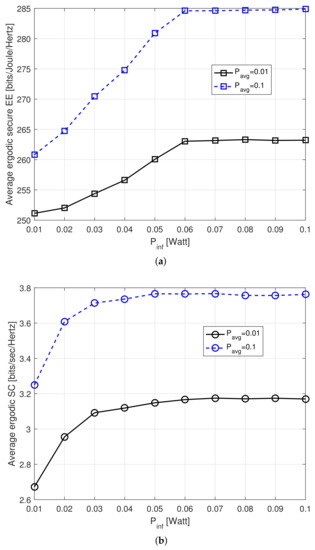
Figure 5.
Average ergodic secure EE and SC of SU versus . (a) Average ergodic secure EE of SU versus , (b) Average ergodic secure EE and SC of SU versus .
Finally, Figure 6 shows how the proposed EEM algorithm compares to the EEM algorithm in a network without an eavesdropper in terms of average ergodic EE and SC performance. Here, the value . In both cases, the value of the average EE and average SC for the SU increases with increasing . As seen earlier, the higher AIP value indicates that the PU receiver can tolerate higher interference power from the SU. Thus, the SU user uses more power to improve ergodic secure EE and ergodic SC. The average EE becomes constant after in both cases, and the average capacity becomes constant after . As expected, the average EE and average capacity values are quite higher when there is no eavesdropper. This is because the presence of the eavesdropper causes several channel impairments, and hence, the average EE and SE of the network decrease. Here, we can see that EEM without the eavesdropper has an average secure EE gain of around 16% over secure EEM.
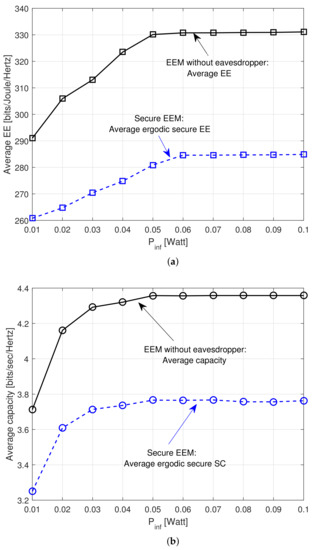
Figure 6.
Average ergodic secure EE and SC of SU versus average capacity of the network without eavesdropper. (a) Average ergodic secure EE of SU versus , (b) Average ergodic secure EE and SC of SU versus .
6. Discussion and Conclusions
6.1. Discussion
In this work, we investigated the issue of eavesdropping in underlay cognitive radio networks where the eavesdropper reduces the secrecy capacity of the secondary link. To gain an insight into the convoluted effects that system parameters such as the transmission power and interference power have on the underlay network’s performance, we exclusively focused on characterizing various key aspects that may have potential impacts on secure underlay CRNs. We examined the spectrum sharing cognitive radio (CR) systems where either a peak or an average power constraint and average interference power constraint are assumed and found the power that maximizes the EE despite its non-convexity. An algorithm for energy efficiency maximization was proposed, and it was seen that the running time of the algorithm is fast and the algorithm converges quickly. We also highlight the discrepancy in performances between adopting the EE criterion and adopting the SE criterion. It was seen that the maximum ergodic secure EE of the SU achieved for the ergodic secure EE maximization is not less than that achieved for the ergodic SC maximization, irrespective of the ATP constraint or the PTP constraint. This indicates that the power allocation strategy for the ergodic SC maximization is not “optimal” with respect to the ergodic secure EE maximization, while the proposed EE optimal power allocation strategies can guarantee that the SU achieves the maximum ergodic secure EE. It was seen that the ergodic SC of the SU achieved for the ergodic SC maximization is larger than that obtained for the ergodic secure EE maximization, irrespective of the ATP constraint or the PTP constraint. In other words, the SU cannot be guaranteed to achieve the maximum ergodic secure EE and the maximum ergodic SC simultaneously. If the SU wants to achieve the maximum ergodic secure EE, the achievable ergodic SC of the SU may decrease and vice versa. It was seen that the ergodic secure EE of the SU first increases with the looser ATP constraint and then decreases with the looser ATP constraint when the optimal power allocation strategies for the ergodic SC maximization are used, while the ergodic SC of the SU always increases with the looser ATP constraint. This shows that there exists a trade-off between the ergodic secure EE and ergodic SC of the SU. It is interesting to note that the ergodic secure EE achieved for the ergodic EE maximization is the same as that achieved for the ergodic SC maximization when the ATP constraint is very tight compared with the AIP constraint. The reason is that only the ATP constraint is active when the ATP/PTP constraint is very tight.
6.2. Conclusions
In this paper, physical-layer security from an energy efficiency perspective was studied in a green CR network with a spectrum sharing paradigm. The ergodic secure energy-efficient maximization problem was formulated under the AIP and ATP constraints. Using fractional programming techniques and the Lagrange duality method, the EE optimal power allocation strategies were designed to maximize the ergodic secure EE of the SU. An iterative power allocation algorithm was proposed to solve the ergodic secure EE maximization problem. The optimal power allocation strategies for maximizing the ergodic SC of the SU were also proposed. With the help of simulations, the achievable maximum ergodic secure EE of the SU with the proposed EE optimal power allocation strategy was demonstrated.
Author Contributions
R.Y. simulated the proposed method and analyzed the results and wrote the paper; K.S. proposed the problem and helped in designing the system model and the problem formulation; A.K. assisted in polishing the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SE | Spectral efficiency |
| EE | Energy efficiency |
| SC | Secrecy capacity |
| SU | Secondary user |
| PU | Primary user |
| CSI | Channel state information |
| QoS | Quality of service |
| PU-Tx | Primary user transmitter |
| SU-Tx | Secondary user transmitter |
| PTP | Peak transmit power |
| ATP | Peak transmit power |
| AIP | Average interference power |
| SCM | Secrecy capacity maximization |
| EEM | Secrecy capacity maximization |
| SNR | Signal-to-noise ratio |
References
- Tragos, E.Z.; Zeadally, S.; Fragkiadakis, A.G.; Siris, V.A. Spectrum assignment in cognitive radio networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2013, 15, 1108–1135. [Google Scholar] [CrossRef]
- Feng, D.; Jiang, C.; Lim, G.; Cimini, L.J.; Feng, G.; Li, G.Y. A survey of energy-efficient wireless communications. IEEE Commun. Surv. Tutor. 2013, 15, 167–178. [Google Scholar] [CrossRef]
- Huang, X.; Han, T.; Ansari, N. On green-energy-powered cognitive radio networks. IEEE Commun. Surv. Tutor. 2015, 17, 827–842. [Google Scholar] [CrossRef]
- Zou, Y.; Zhu, J.; Wang, X.; Hanzo, L. A survey on wireless security: Technical challenges, recent advances, and future trends. Proc. IEEE 2016, 104, 1727–1765. [Google Scholar] [CrossRef]
- Sharma, R.K.; Rawat, D.B. Advances on security threats and countermeasures for cognitive radio networks: A survey. IEEE Commun. Surv. Tutor. 2015, 17, 1023–1043. [Google Scholar] [CrossRef]
- Pei, Y.; Liang, Y.C.; Zhang, L.; Teh, K.C.; Li, K.H. Secure communication over MISO cognitive radio channels. IEEE Trans. Wirel. Commun. 2010, 9, 1494–1502. [Google Scholar] [CrossRef]
- Pei, Y.; Liang, Y.C.; Teh, K.C.; Li, K.H. Secure communication in multiantenna cognitive radio networks with imperfect channel state information. IEEE Trans. Signal Process. 2011, 59, 1683–1693. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, R.; Liang, Y.C.; Xin, Y.; Cui, S. On the relationship between the multi-antenna secrecy communications and cognitive radio communications. IEEE Trans. Commun. 2010, 58, 1877–1886. [Google Scholar] [CrossRef]
- Wang, C.; Wang, H.M. On the secrecy throughput maximization for MISO cognitive radio network in slow fading channels. IEEE Trans. Inf. Forensics Secur. 2014, 9, 1814–1827. [Google Scholar] [CrossRef]
- Zou, Y.; Wang, X.; Shen, W. Physical-layer security with multiuser scheduling in cognitive radio networks. IEEE Trans. Commun. 2013, 61, 5103–5113. [Google Scholar] [CrossRef]
- Zou, Y.; Li, X.; Liang, Y.C. Secrecy outage and diversity analysis of cognitive radio systems. IEEE J. Sel. Areas Commun. 2014, 32, 2222–2236. [Google Scholar] [CrossRef]
- Mokari, N.; Parsaeefard, S.; Saeedi, H.; Azmi, P.; Hossain, E. Secure robust ergodic uplink resource allocation in relay-assisted cognitive radio networks. IEEE Trans. Signal Process. 2015, 63, 291–304. [Google Scholar] [CrossRef]
- Ng, D.W.K.; Lo, E.S.; Schober, R. Multiobjective resource allocation for secure communication in cognitive radio networks with wireless information and power transfer. IEEE Trans. Veh. Technol. 2016, 65, 3166–3184. [Google Scholar] [CrossRef]
- Cui, M.; Hu, B.J.; Tang, J.; Wang, Y. Energy-efficient joint power allocation in uplink massive MIMO cognitive radio networks with imperfect CSI. IEEE Access 2017, 5, 27611–27621. [Google Scholar] [CrossRef]
- Wang, S.; Shi, W.; Wang, C. Energy-efficient resource management in OFDM-based cognitive radio networks under channel uncertainty. IEEE Trans. Commun. 2015, 63, 3092–3102. [Google Scholar] [CrossRef]
- Fu, L.; Zhang, Y.J.A.; Huang, J. Energy efficient transmissions in MIMO cognitive radio networks. IEEE J. Sel. Areas Commun. 2013, 31, 2420–2431. [Google Scholar]
- Sun, X.; Tsang, D.H.K. Energy-efficient cooperative sensing scheduling for multi-band cognitive radio networks. IEEE Trans. Wirel. Commun. 2013, 12, 4943–4955. [Google Scholar] [CrossRef][Green Version]
- Wang, S.; Ge, M.; Zhao, W. Energy-efficient resource allocation for OFDM-based cognitive radio networks. IEEE Trans. Commun. 2013, 61, 3181–3191. [Google Scholar] [CrossRef]
- Yue, H.; Pan, M.; Fang, Y.; Glisic, S. Spectrum and energy efficient relay station placement in cognitive radio networks. IEEE J. Sel. Areas Commun. 2013, 31, 883–893. [Google Scholar] [CrossRef]
- Xie, R.; Yu, F.R.; Ji, H.; Li, Y. Energy-efficient resource allocation for heterogeneous cognitive radio networks with femtocells. IEEE Trans. Wirel. Commun. 2012, 11, 3910–3920. [Google Scholar]
- Pei, Y.; Liang, Y.C.; Teh, K.C.; Li, K.H. Energy-efficient design of sequential channel sensing in cognitive radio networks: Optimal sensing strategy, power allocation, and sensing order. IEEE J. Sel. Areas Commun. 2011, 29, 1648–1659. [Google Scholar] [CrossRef]
- Bayat, A.; Aïssa, S. Full-duplex cognitive radio with asynchronous energy-efficient sensing. IEEE Trans. Wirel. Commun. 2018, 17, 1066–1080. [Google Scholar] [CrossRef]
- Yadav, R.; Kumar, A.; Singh, K. Green power allocation for cognitive radio networks with spectrum sensing. IEEJ Trans. Electr. Electron. Eng. 2019, 14, 403–410. [Google Scholar] [CrossRef]
- Zappone, A.; Lin, P.H.; Jorswieck, E.A. Energy-efficient secure communications in MISO-SE systems. In Proceedings of the Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2–5 November 2014; IEEE: Piscataway, NJ, USA; pp. 1001–1005. [Google Scholar]
- Kwon, T.; Wong, V.W.S.; Schober, R. Secure MISO cognitive radio system with perfect and imperfect CSI. In Proceedings of the IEEE Global Communications Conference, Anaheim, CA, USA, 3–7 December 2012; IEEE: Piscataway, NJ, USA; pp. 1236–1241. [Google Scholar]
- Wang, D.; Bai, B.; Chen, W.; Han, Z. Achieving high energy efficiency and physical-layer security in AF relaying. IEEE Trans. Wirel. Commun. 2016, 15, 740–752. [Google Scholar] [CrossRef]
- El-Halabi, M.; Liu, T.; Georghiades, C.N. Secrecy capacity per unit cost. IEEE J. Sel. Areas Commun. 2013, 31, 1909–1920. [Google Scholar] [CrossRef]
- Ng, D.W.K.; Lo, E.S.; Schober, R. Energy-Efficient resource allocation for secure OFDMA systems. IEEE Trans. Veh. Technol. 2012, 61, 2572–2585. [Google Scholar] [CrossRef]
- Zhou, F.; Wang, Y.; Qin, D.; Wang, Y.; Wu, Y. Secure EE maximisation in green CR: Guaranteed SC. IET Commun. 2017, 11, 2507–2513. [Google Scholar] [CrossRef]
- Ouyang, J.; Zhu, W.P.; Massicotte, D.; Lin, M. Energy efficient optimization for physical layer security in cognitive relay networks. In Proceedings of the IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; IEEE: Piscataway, NJ, USA; pp. 1–6. [Google Scholar]
- Zhang, M.; Cumanan, K.; Burr, A. Secure energy efficiency optimization for MISO cognitive radio network with energy harvesting. In Proceedings of the IEEE International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 11–13 October 2017; IEEE: Piscataway, NJ, USA; pp. 1–6. [Google Scholar]
- Kaplan, G.; Shamai, S. Error probabilities for the blockfading Gaussian channel. Arch. Elek. Ubertragung 1995, 49, 192–205. [Google Scholar]
- McEliece, R.; Stark, W. Channels with block interference. IEEE Trans. Inform. Theory 1984, 30, 44–53. [Google Scholar] [CrossRef]
- Ozarow, L.; Shamai, S.; Wyner, A.D. Information theoretic considerations for cellular mobile radio. IEEE Trans. Veh. Technol. 1994, 43, 359–378. [Google Scholar] [CrossRef]
- Agarwal, M.; Guo, D.; Honig, M.L. Limited-Rate Channel State Feedback for Multicarrier Block Fading Channels. IEEE Trans. Inform. Theory 2010, 56, 6116–6132. [Google Scholar] [CrossRef][Green Version]
- Caire, G.; Knopp, R.; Humblet, P. System capacity of F-TDMA cellular systems. IEEE Trans. Commun. 1998, 46, 1649–1661. [Google Scholar] [CrossRef]
- Haykin, S.; Moher, M. Modern Wireless Communications, 1st ed.; Prentice Hall: Hoboken, NJ, USA, 2005. [Google Scholar]
- Bertoni, H. Radio Propagation for Modern Wireless Systems, 1st ed.; Prentice Hall: Hoboken, NJ, USA, 2000. [Google Scholar]
- Paulraj, A.; Nabar, R.; Gore, D. Introduction to Space-Time Wireless Communications, 1st ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Rappaport, T.S. Wireless Communications: Principles and Practice, 2nd ed.; Pearson: London, UK, 2002. [Google Scholar]
- Wang, D.; Bai, B.; Chen, W.; Han, Z. Energy efficient secure communication over decode-and-forward relay channels. IEEE Trans. Commun. 2015, 63, 892–905. [Google Scholar] [CrossRef]
- Zhang, R. On peak versus average interference power constraints for protecting primary users in cognitive radio networks. IEEE Trans. Wirel. Commun. 2009, 8, 1128–1138. [Google Scholar] [CrossRef]
- Liu, R.; Trappe, W. Securing Wireless Communications at the Physical Layer, 1st ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Singh, K.; Gupta, A.; Ratnarajah, T. QoS-driven resource allocation and EE-balancing for multiuser two-way amplify-and-forward relay networks. IEEE Trans. Wirel. Commun. 2017, 16, 3189–3204. [Google Scholar] [CrossRef]
- Dinkelbach, W. On fractional programming. Manag. Sci. 1967, 13, 492–498. [Google Scholar] [CrossRef]
- Min, A.W.; Shin, K.G. Impact of mobility on spectrum sensing in cognitive radio networks. In Proceedings of the ACM Workshop on Cognitive Radio Networks, Beijing, China, 13–18 September 2009; ACM: New York, NY, USA; pp. 3–18. [Google Scholar]
- Cacciapuoti, A.S.; Akyildiz, I.F.; Paura, L. Primary-user mobility impact on spectrum sensing in Cognitive Radio networks. In Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, Toronto, ON, Canada, 11–14 September 2011; IEEE: Piscataway, NJ, USA; pp. 451–456. [Google Scholar]
- Sama, P.; Wicker, S.B. On the Behaviour of Communication Links of a Node in a Multi-Hop Mobile Environment. In Proceedings of the 5th ACM International Symposium on Mobile Ad Hoc Networking and Computing, Tokyo, Japan, 24–26 May 2004; ACM: New York, NY, USA; pp. 145–156. [Google Scholar]
- Luo, J.; Hubaux, J.P. Joint Mobility and Routing for Lifetime Elongation in Wireless Sensor Networks. In Proceedings of the IEEE 24th Annual Joint Conference of the IEEE Computer and Communications Societies, Miami, FL, USA, 13–17 March 2005; IEEE: Piscataway, NJ, USA; pp. 1735–1746. [Google Scholar]
- Grossglauser, M.; Tse, D.N.C. Mobility Increases the Capacity of Ad Hoc Wireless Networks. IEEE/ACM Trans. Netw. 2002, 10, 477–486. [Google Scholar] [CrossRef]
- Liu, B.; Brass, P.; Dousse, O.; Nain, P.; Towsley, D. Mobility Improves Coverage of Sensor Networks. In Proceedings of the 6th ACM International Symposium on Mobile Ad Hoc networking and Computing, Urbana-Champaign, IL, USA, 25–27 May 2005; ACM: New York, NY, USA; pp. 300–308. [Google Scholar]
- Tawil, V.; Caldwell, W.; Reede, I.; Kiernan, T.; Stevenson, C.R. IEEE 802.22-09/0029r0; DRAFT 802.22a (amendment) PAR; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar]
- Masmoudi, R.; Belmega, E.V.; Fijalkow, I. Impact of imperfect CSI on resource allocation in cognitive radio channels. In Proceedings of the IEEE 13th International Conference on Wireless and Mobile Computing, Networking and Communications, Rome, Italy, 9–11 October 2017; IEEE: Piscataway, NJ, USA; pp. 293–299. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).