Bacterial Evolutionary Algorithm-Trained Interpolative Fuzzy System for Mobile Robot Navigation
Abstract
:1. Introduction
2. Related Works
3. Problem Statement
4. Proposed Method
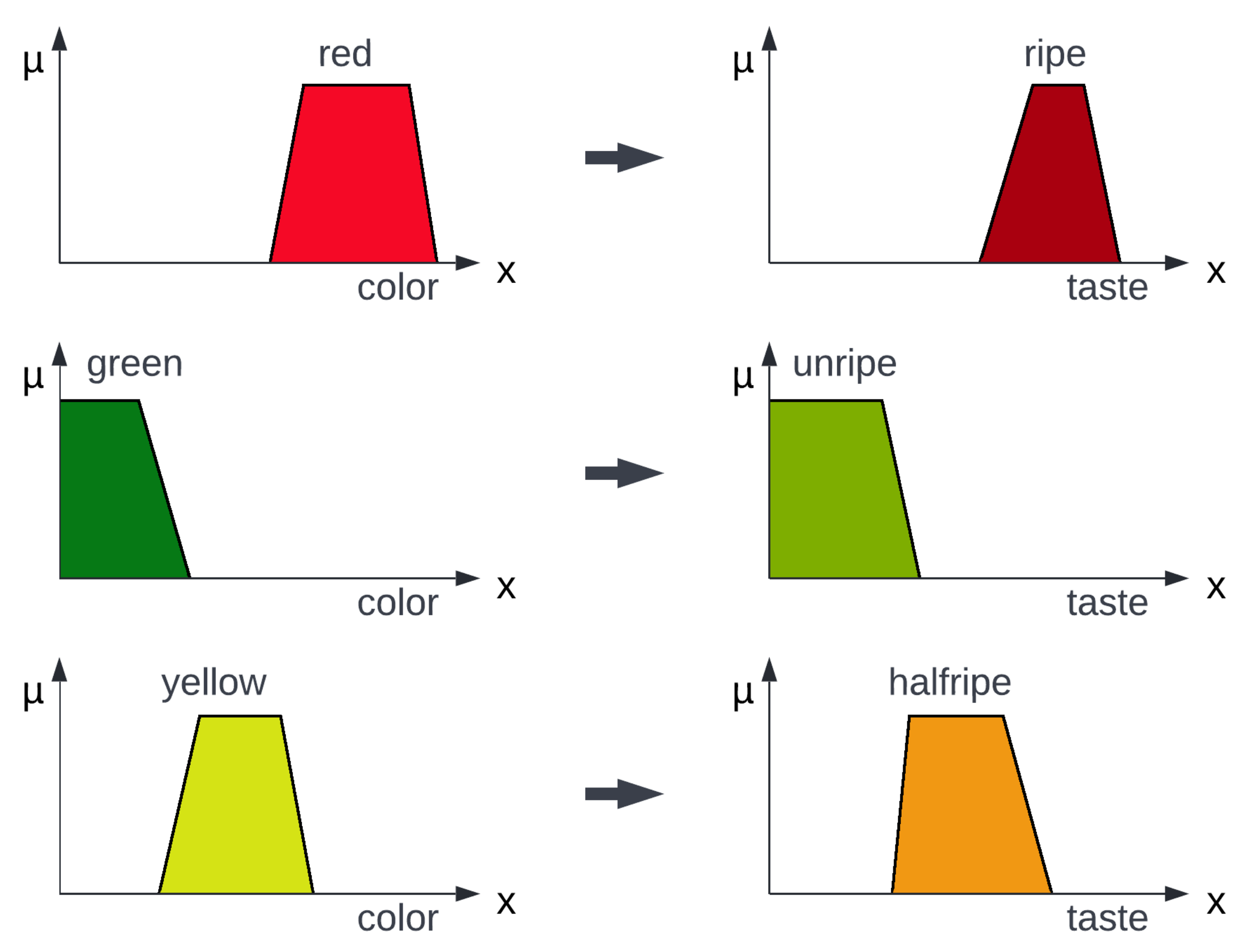
4.1. Interpolative Fuzzy Systems
4.2. Application of Interpolative Fuzzy Systems for Controlling a Mobile Robot
- The robot has not yet left only those objects that are within the angular ranges 0°–90° or 270°–359°, so only within these ranges is the distance measured;
- The dependence on the position of the objects is described by a cosine function because it takes its maximum value at 0°, and 0 at 90° and 270°, and takes non-negative values in the ranges given in the context;
- Object distances are included in the denominator because the smaller the distances, the greater the risk.
4.3. Bacterial Evolutionary Algorithms
4.3.1. The Bacterial Mutation
4.3.2. Gene Transfer
4.4. Application of Bacterial Evolutionary Algorithms for Training Interpolative Fuzzy Systems
4.4.1. The Structure of the Algorithm
- Ten individuals in the population;
- Ten generations;
- Five clones for each mutation. The operation is performed for each gene one by one;
- Twenty infections in gene transfers. Each gene transfer involves the transfer of one gene;
- Randomly generated initial population.
4.4.2. The Cost Function
- If the robot hits the obstacle, the cost will be very high. This is the worst-case scenario, because safety is the highest priority for drivers on the roads. If the robot did not hit the wall, it will stop randomly;
- The distance from the wall after stopping is penalized. This prevents the robot from becoming stuck near an object. Keeping an appropriate distance does not require much effort to ensure the robot’s safety. It is acceptable to be bold, and it is fine as long as the robot does not hit the wall;
- The duration of the simulation is penalized in such a way that the longer the robot takes to move toward the wall, the slower it moves. Slow motion is not beneficial if the path is clear. As long as the robot does not hit the wall, or as long as there are no obstacles nearby, the faster it goes, the better.
4.5. Neuro-Activity-Based Path Planning
4.5.1. Forward Transmission
4.5.2. Backward Transmission with Synaptic Pruning
4.6. Integration of Neuro-Activity-Based Path Planning with Mobile Robot Control
4.7. The Analysis of the Time Complexity
- The size of the map;
- The ratio of free and occupied space on the map;
- The distance between the starting point and the destination;
- The strength of scope, ;
- The constant coefficient, C;
- The maximal potential value, ;
- The initial value of ;
- The friction force, ;
- , which influences the speed of the reduction in the potential energy.
5. Experimental Results
6. Conclusions
- Optimizing the time complexity of neuro-activity-based path-planning process;
- Adding more variables to the speed control, which can be extended to any number of variables. In this case, a rework of the optimization algorithm is needed;
- Optimizing the number of fuzzy rules using the bacterial evolutionary algorithm;
- Making path planning dynamic, so the robot can react to sudden obstacles;
- Enabling path planning on a topographic map, which requires a different mapping method because Turtlebot3 can only produce a two-dimensional map;
- Taking into account the movement of obstacles for the safety of the environment;
- Incorporating a reconnaissance function, i.e., planning a route through an unknown area;
- Designing an implementation for a robot that can transport objects; such a robot should strive for safety rather than speed if the object is heavy or fragile;
- Detecting obstacles with image processing. Security information should be based on the image. This would also avoid collisions with low obstacles;
- Upgrading optimization to a bacterial memetic algorithm;
- Integrating neutrosophic statistics into the control process. Neutrosophic statistics is an extension of classical statistics, and it is applied when the data is coming from an uncertain environment. This type of statistics uses sets instead of numbers to represent uncertain data. The sets contain numerical values that the data can be equal with. Neurosophic statistics was first proposed at the end of the 20th century, but it was only developed recently [45,46]. One of the potential applications is the generalization of fuzzy sets [47], which can also be applied in the current control process. Furthermore, it is worth mentioning that several parameters can have uncertain values. For example, the degree of safety can be uncertain because of measurement uncertainty, and there are different measurements that indicate the same level of safety. The other example is friction force in the neuro-activity-based path planning, which indicates how hard it is for the robot to move on the ground. Friction, in a physical sense, can have uncertain values, but this quantity in the neuro-activity-based path planning has a role that is similar to the cost values in case of cost function minimization-based algorithms, and these cost values can also be considered uncertain [48,49];
- Performing sensitivity analysis and investigating the stochastic nature of the applied evolutionary algorithm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mamdani, E.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- De Luca, F.; Calderaro, V.; Galdi, V. A Fuzzy Logic-Based Control Algorithm for the Recharge/V2G of a Nine-Phase Integrated On-Board Battery Charger. Electronics 2020, 9, 946. [Google Scholar] [CrossRef]
- Mosavi, A.; Qasem, S.N.; Shokri, M.; Band, S.S.; Mohammadzadeh, A. Fractional-Order Fuzzy Control Approach for Photovoltaic/Battery Systems under Unknown Dynamics, Variable Irradiation and Temperature. Electronics 2020, 9, 1455. [Google Scholar] [CrossRef]
- Anthony, M.; Prasad, V.; Kannadasan, R.; Mekhilef, S.; Alsharif, M.H.; Kim, M.K.; Jahid, A.; Aly, A.A. Autonomous Fuzzy Controller Design for the Utilization of Hybrid PV-Wind Energy Resources in Demand Side Management Environment. Electronics 2021, 10, 1618. [Google Scholar] [CrossRef]
- Memon, I.; Hasan, M.K.; Shaikh, R.A.; Nebhen, J.; Bakar, K.A.A.; Hossain, E.; Tunio, M.H. Energy-Efficient Fuzzy Management System for Internet of Things Connected Vehicular Ad Hoc Networks. Electronics 2021, 10, 1068. [Google Scholar] [CrossRef]
- Domingos, D.; Camargo, G.; Gomide, F. Autonomous Fuzzy Control and Navigation of Quadcopters. IFAC-PapersOnLine 2016, 49, 73–78. [Google Scholar] [CrossRef]
- Smith, S.; Rae, G.; Anderson, D.; Shein, A. Fuzzy logic control of an autonomous underwater vehicle. Control. Eng. Pract. 1994, 2, 321–331. [Google Scholar] [CrossRef]
- Cupertino, F.; Giordano, V.; Naso, D.; Delfine, L. Fuzzy control of a mobile robot. IEEE Robot. Autom. Mag. 2006, 13, 74–81. [Google Scholar] [CrossRef]
- Faisal, M.; Hedjar, R.; Sulaiman, M.A.; Al-Mutib, K. Fuzzy Logic Navigation and Obstacle Avoidance by a Mobile Robot in an Unknown Dynamic Environment. Int. J. Adv. Robot. Syst. 2013, 10, 37. [Google Scholar] [CrossRef]
- Singh, N.H.; Thongam, K. Mobile Robot Navigation Using Fuzzy Logic in Static Environments. Procedia Computer Science 2018, 125, 11–17. [Google Scholar] [CrossRef]
- Hartono, R.; Nizar, T. Speed Control of a Mobile Robot Using Fuzzy Logic Controller. IOP Conf. Ser. Mater. Sci. Eng. 2019, 662, 022063. [Google Scholar] [CrossRef]
- Mac, T.; Copot, C.; Keyser, R.; Tran, T.; Vu, T. MIMO Fuzzy Control for Autonomous Mobile Robot. J. Autom. Control. Eng. 2015, 3, 65–70. [Google Scholar] [CrossRef] [Green Version]
- Omrane, H.; Masmoudi, M.S.; Masmoudi, M. Fuzzy logic based control for autonomous mobile robot navigation. Comput. Intell. Neurosci. 2016, 2016, 9548482. [Google Scholar] [CrossRef] [Green Version]
- Kóczy, L.T.; Hirota, K. Rule interpolation by α -level sets in fuzzy approximate reasoning. BUSEFAL 1991, 46, 115–123. [Google Scholar]
- Kóczy, L.T.; Hirota, K. Rule interpolation in approximate reasoning based fuzzy control. In Proceedings of the 4th IFSA World Congress, Brussels, Belgium, 7–12 July 1991; pp. 89–92. [Google Scholar]
- Kóczy, L.T.; Hirota, K. Approximate reasoning by linear rule interpolation and general approximation. Int. J. Approx. Reason. 1993, 9, 197–225. [Google Scholar] [CrossRef] [Green Version]
- Kovács, S.; Kóczy, T.L. Application of an approximate fuzzy logic controller in an AGV steering system, path tracking and collision avoidance strategy. Fuzzy Set Theory Appl. 1999, 16, 456–467. [Google Scholar]
- Rubaai, A.; Young, P. Hardware/Software Implementation of Fuzzy-Neural-Network Self-Learning Control Methods for Brushless DC Motor Drives. IEEE Trans. Ind. Appl. 2016, 52, 414–424. [Google Scholar]
- Castillo, O.; Lizárraga, E.; Soria, J.; Melin, P.; Valdez, F. New approach using ant colony optimization with ant set partition for fuzzy control design applied to the ball and beam system. Inf. Sci. 2015, 294, 203–215. [Google Scholar]
- Nawa, N.; Furuhashi, T. Fuzzy system parameters discovery by bacterial evolutionary algorithm. IEEE Trans. Fuzzy Syst. 1999, 7, 608–616. [Google Scholar] [CrossRef]
- Shin, H.; Chae, J. A Performance Review of Collision-Free Path Planning Algorithms. Electronics 2020, 9, 316. [Google Scholar]
- Dijkstra, E. A Note on Two Problems in Connexion with Graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef] [Green Version]
- Likhachev, M.; Gordon, G.J.; Thrun, S. ARA*: Anytime A* with Provable Bounds on Sub-Optimality. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver and Whistler, BC, Canada, 8–13 December 2003; Thrun, S., Saul, L., Schölkopf, B., Eds.; pp. 767–774. [Google Scholar]
- Ferguson, D.; Stentz, A. Field D*: An Interpolation-Based Path Planner and Replanner. In Proceedings of the 12th International Symposium on Robotics Research, San Francisco, CA, USA, 12–15 October 2005; pp. 239–253. [Google Scholar]
- Quoy, M.; Moga, S.; Gaussier, P. Dynamical neural networks for planning and low-level robot control. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2003, 33, 523–532. [Google Scholar] [CrossRef]
- Yang, S.; Luo, C. A neural network approach to complete coverage path planning. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2004, 34, 718–724. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Shen, T.; Yang, S.; Liu, X.; Yang, R.; Cheng, L. A Path Planning Strategy with Ant Colony Algorithm for Series Connected Batteries. Electronics 2020, 9, 1816. [Google Scholar] [CrossRef]
- Botzheim, J.; Toda, Y.; Kubota, N. Bacterial memetic algorithm for offline path planning of mobile robots. Memetic Comput. 2012, 4, 73–86. [Google Scholar] [CrossRef]
- Botzheim, J.; Toda, Y.; Kubota, N. Path planning in probabilistic environment by bacterial memetic algorithm. In Intelligent Interactive Multimedia: Systems & Services; Watanabe, T., Watada, J., Takahashi, N., Howlett, R.J., Jain, L.C., Eds.; Smart Innovation, Systems and Technologies; Springer: Berlin/Heidelberg, Germany, 2012; Volume 14, pp. 439–448. [Google Scholar] [CrossRef]
- Botzheim, J.; Toda, Y.; Kubota, N. Bacterial memetic algorithm for simultaneous optimization of path planning and flow shop scheduling problems. Artif. Life Robot. 2012, 17, 107–112. [Google Scholar] [CrossRef]
- Lonklang, A.; Botzheim, J. Improved Rapidly Exploring Random Tree with Bacterial Mutation and Node Deletion for Offline Path Planning of Mobile Robot. Electronics 2022, 11, 1459. [Google Scholar] [CrossRef]
- Saputra, A.A.; Toda, Y.; Botzheim, J.; Kubota, N. Neuro-Activity-Based Dynamic Path Planner for 3-D Rough Terrain. IEEE Trans. Cogn. Dev. Syst. 2018, 10, 138–150. [Google Scholar] [CrossRef]
- Drobics, M.; Botzheim, J. Optimization of fuzzy rule sets using a bacterial evolutionary algorithm. Mathw. Soft Comput. 2008, 15, 21–40. [Google Scholar]
- Horvath, C.M.; Botzheim, J.; Thomessen, T.; Korondi, P. Bacterial memetic algorithm trained fuzzy system-based model of single weld bead geometry. IEEE Access 2020, 8, 164864–164881. [Google Scholar] [CrossRef]
- Kant, S.; Agarwal, D.; Shukla, P.K. A survey on fuzzy systems optimization using evolutionary algorithms and swarm intelligence. In Computer Vision and Robotics; Springer: Singapore, 2022; pp. 421–444. [Google Scholar]
- Shahidinejad, A.; Ghobaei-Arani, M.; Masdari, M. Resource provisioning using workload clustering in cloud computing environment: A hybrid approach. Clust. Comput. 2021, 24, 319–342. [Google Scholar] [CrossRef]
- Shakarami, A.; Shahidinejad, A.; Ghobaei-Arani, M. An autonomous computation offloading strategy in Mobile Edge Computing: A deep learning-based hybrid approach. J. Netw. Comput. Appl. 2021, 178, 102974. [Google Scholar] [CrossRef]
- Sánchez-Ibáñez, J.R.; Pérez-del Pulgar, C.J.; García-Cerezo, A. Path Planning for Autonomous Mobile Robots: A Review. Sensors 2021, 21, 7898. [Google Scholar] [CrossRef] [PubMed]
- Song, B.; Wang, Z.; Zou, L. An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve. Appl. Soft Comput. 2021, 100, 106960. [Google Scholar] [CrossRef]
- Zhang, Z.; He, R.; Yang, K. A bioinspired path planning approach for mobile robots based on improved sparrow search algorithm. Adv. Manuf. 2022, 10, 114–130. [Google Scholar] [CrossRef]
- Kovács, S.; Kóczy, T.L. The use of the concept of vague environment in approximate fuzzy reasoning. Fuzzy Set Theory Appl. 1997, 12, 169–181. [Google Scholar]
- Klawonn, F. Fuzzy Sets and Vague Environments. Fuzzy Sets Syst. 1994, 66, 207–221. [Google Scholar] [CrossRef]
- Huttenlocher, P.R. Synaptic density in human frontal cortex—Developmental changes and effects of aging. Brain Res. 1979, 163, 195–205. [Google Scholar]
- Chechik, G.; Meilijson, I.; Ruppin, E. Neuronal Regulation: A Mechanism for Synaptic Pruning During Brain Maturation. Neural Comput. 1999, 11, 2061–2080. [Google Scholar] [CrossRef]
- Smarandache, F. Introduction to Neutrosophic Statistics; Sitech & Education Publishing: Craiova, Romania, 2014. [Google Scholar] [CrossRef]
- Patro, S.; Smarandache, F. The Neutrosophic Statistical Distribution, More Problems, More Solutions. Neutrosophic Sets Syst. 2016, 12, 73–79. [Google Scholar]
- Smarandache, F. Neutrosophic set—A generalization of the intuitionistic fuzzy set. J. Def. Resour. Manag. 2010, 1, 107–116. [Google Scholar]
- Smarandache, F.; Vladareanu, L.; Broumi, S.; Bakali, A.; Akram, M. Applying Dijkstra Algorithm for Solving Neutrosophic Shortest Path Problem. In Proceedings of the 2016 International Conference on Advanced Mechatronic Systems, Melbourne, Australia, 30 November–3 December 2016; p. 1. [Google Scholar]
- Jan, N.; Aslam, M.; Ullah, K.; Mahmood, T.; Wang, J. An approach towards decision making and shortest path problems using the concepts of interval-valued Pythagorean fuzzy information. Int. J. Intell. Syst. 2019, 34, 2403–2428. [Google Scholar] [CrossRef]
- Szili, F.A. Intelligent Travel with Fuzzy Control for Mobile Robot. Available online: https://gitlab.com/Szilidam/intelligent-travel-with-fuzzy-control-for-mobile-robot (accessed on 10 April 2022).




















| Safe | Acceptable | Dangerous | |
|---|---|---|---|
| Slow | 2 | 2 | 1 |
| Medium | 2 | 2 | 0 |
| Fast | 0 | −1 | 0 |
| m | g | C | |||||
|---|---|---|---|---|---|---|---|
| 1.2 | 1 | 9.81 | 30 | 1.5 | 10 | 1 | 0 |
| R | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.05 | 0.2 | 10 | 0.8 | 0.3 | 0.7 | 10 | 0.5 | 0.8 | 1 |
| Mamdani Inference | Sugeno Inference | Interpolative Inference | |
|---|---|---|---|
| Time complexity of the inference (μs) | 68.964 | 19.996 | 597.452 |
| Duration of One Cost Function (s) | Number of Cost Function Calls during the Optimization Process (-) | Duration of the Optimization Process (min) | |
|---|---|---|---|
| Measurement result | 0.9173 | 18,400 | 281.3 |
| Mamdani Inference (Unit) | Sugeno Inference (Unit) | Interpolative Inference (Unit) | |
|---|---|---|---|
| 1. | 51.987 | 42.378 | 30.115 |
| 2. | 49.912 | 26.433 | 24.540 |
| 3. | 49.410 | 25.485 | 18.218 |
| 4. | 48.066 | 21.143 | 17.292 |
| 5. | 47.413 | 20.178 | 17.134 |
| 6. | 46.940 | 20.174 | 16.285 |
| 7. | 46.897 | 19.599 | 16.118 |
| 8. | 46.721 | 18.653 | 15.493 |
| 9. | 46.721 | 18.526 | 15.493 |
| 10. | 46.664 | 18.343 | 15.493 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szili, F.Á.; Botzheim, J.; Nagy, B. Bacterial Evolutionary Algorithm-Trained Interpolative Fuzzy System for Mobile Robot Navigation. Electronics 2022, 11, 1734. https://doi.org/10.3390/electronics11111734
Szili FÁ, Botzheim J, Nagy B. Bacterial Evolutionary Algorithm-Trained Interpolative Fuzzy System for Mobile Robot Navigation. Electronics. 2022; 11(11):1734. https://doi.org/10.3390/electronics11111734
Chicago/Turabian StyleSzili, Ferenc Ádám, János Botzheim, and Balázs Nagy. 2022. "Bacterial Evolutionary Algorithm-Trained Interpolative Fuzzy System for Mobile Robot Navigation" Electronics 11, no. 11: 1734. https://doi.org/10.3390/electronics11111734
APA StyleSzili, F. Á., Botzheim, J., & Nagy, B. (2022). Bacterial Evolutionary Algorithm-Trained Interpolative Fuzzy System for Mobile Robot Navigation. Electronics, 11(11), 1734. https://doi.org/10.3390/electronics11111734







