Effective Parametrization of Low Order Bézier Motion Primitives for Continuous-Curvature Path-Planning Applications
Abstract
:1. Introduction
Objectives Furthermore, Contributions
- Based on the findings of our literature review this is one of the few if not the first approach that apply third order Bézier curve motion primitives in path planning and takes into account the given requirements for initial and final position, orientation and curvature. The combined path using the proposed primitives has minimal required turns or oscillations between the initial and final configurations, since only a third order curve is used. Due to the small number of required parameters, the method is also suitable for use in path planning optimisers, since it reduces computational effort and improves convergence.
- We provide a new parametrization that allows an intuitive geometric interpretation of the curve and a simple algorithm to calculate its parameters. Parametrization is based on the initially available information, i.e., the position, orientation, and curvature requirements in the endpoints. The problem is solved by solving a system of two quadratic polynomial equations without the need for optimisation. It is therefore computationally very efficient.
- Practical directions for the construction of primitives and the related analysis of their performance are provided. The applicability of the proposed primitives is illustrated on typical path-planning scenarios.
2. Bézier Curves as Motion Primitives
2.1. Bézier Curves
2.2. The Curvature of Bézier Curves
2.3. Parametrization of Motion Primitives
- The position of both endpoints, i.e., and ;
- The orientation in both endpoints, i.e., angles and ; and
- The curvature in both endpoints, i.e., and .
2.4. Reconstruction of the Motion Primitive from the Boundary Conditions
- U-type and R-type functions are increasing while D-type and L-type are decreasing;
- Only U-type functions are convex while D-type, R-type, and L-type are concave.
- An increasing and a decreasing function can have at most one intersection;
- A decreasing convex function and a decreasing concave function can have at most two intersections (the same is true if both functions are increasing);
- Two decreasing concave functions (or any other of the three combinations decreasing-convex, increasing-concave, increasing-convex) can have more than two intersections.
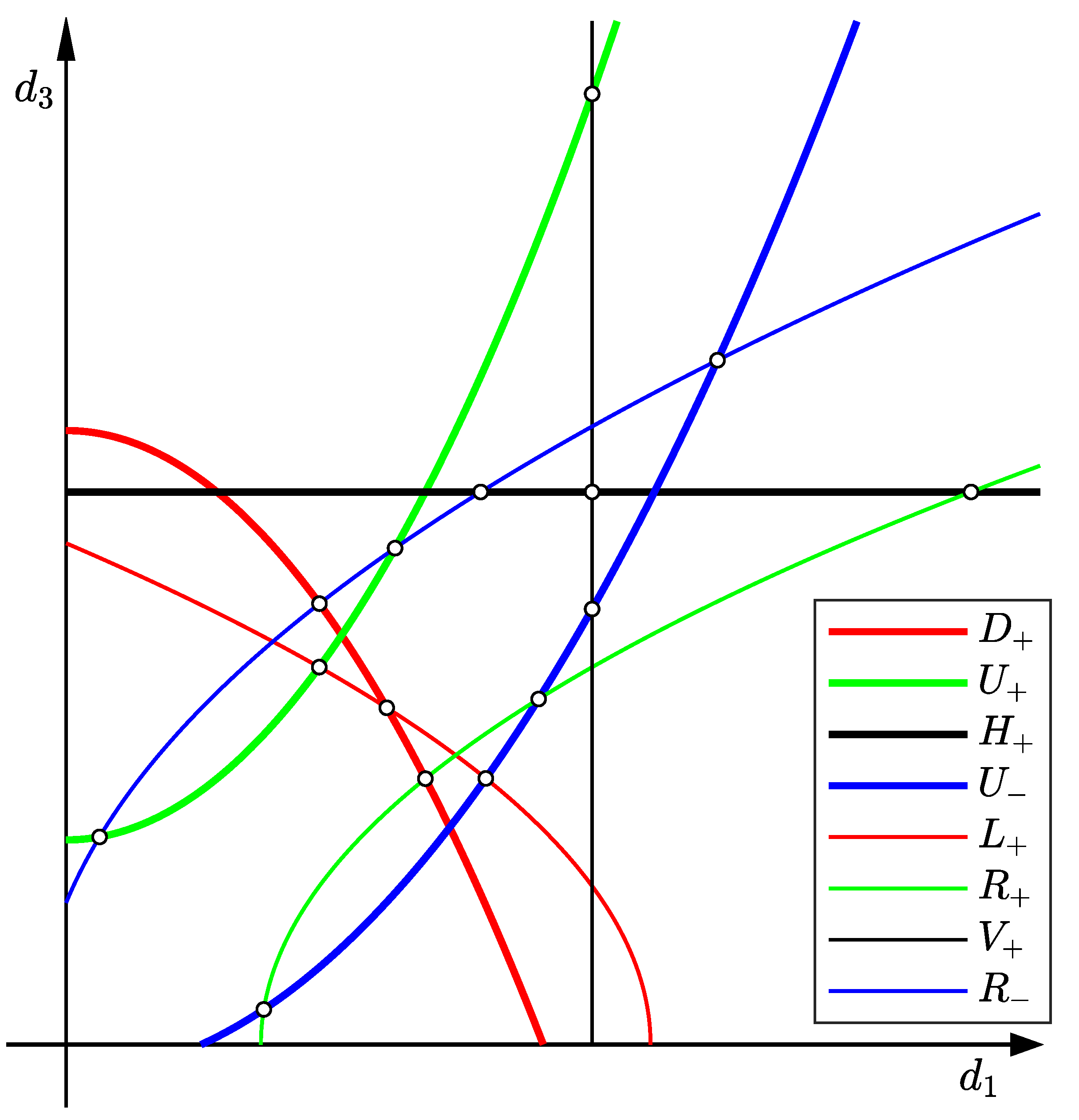
- One solution. This is the most frequent case that gives a unique Bézier curve.
- Two solutions. This happen rarely because the boundary conditions given above are quite restricting. An example is given in Figure 2 (the intersection of a green and a blue line).
- Three solutions. This can only happen if one function is and the other is and the parameters of both parabolas are extremely restricted. Two intersections lie very close to both axes. The solutions with very low values of and/or often result in a high-curvature path near the endpoints and should be avoided.
- No solutions. This happens when the parabolas do not have intersections in quadrant 1. Examples in Figure 2: two green lines, a black line, and a red line. We have to also mention here the cases where the parabolas do not even enter quadrant 1—the vertex is negative and the leading coefficient (or ) is negative.
2.5. Basic Motion Primitives
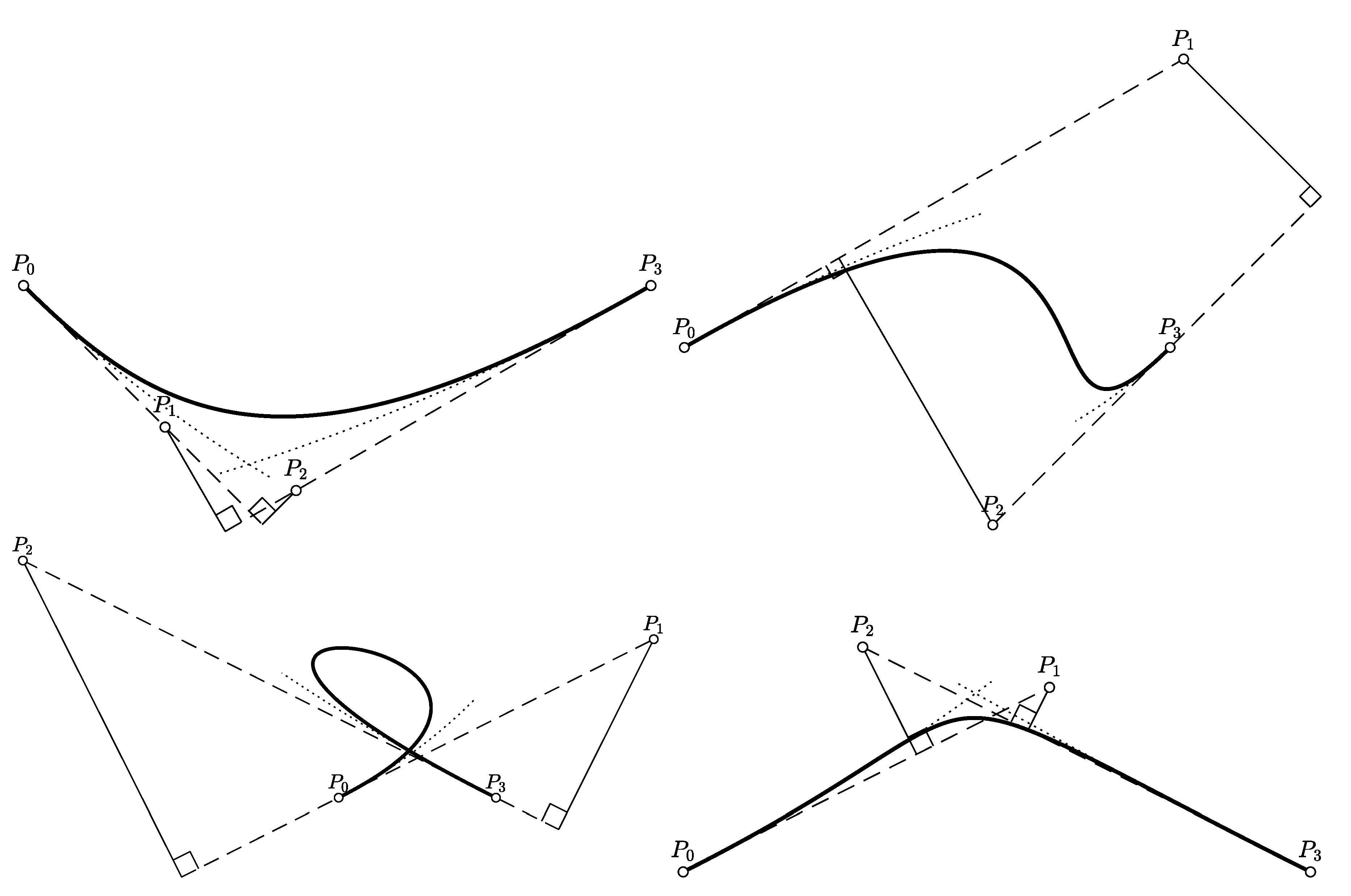
2.5.1. C-Shaped Primitive
2.5.2. S-Shaped Primitive
- parabola. The intersection exists if the point of entry of the parabola into the first quadrant lies below the vertex of the parabola. If this is not the case, the intersection appears by increasing the curvature of the parabola. An alternative solution is to change the sign of the parabola which turns the primitive to the loop-shaped or V-shaped curve (shown in the bottom part of Figure 3).
- parabola. The intersection exists if the vertex of the parabola is lower than the point where parabola crosses from quadrant 1 to quadrant 2. It there is no intersection, one can be obtained by changing the curvature of the parabola. This then changes the primitive into C-shaped one.
2.5.3. Loop-Shaped Primitive and V-Shaped Primitive
3. Construction of the Path from Motion Primitives
- Waypoints or intermediate points denoted by the sequence ( and are the initial and the final position, respectively);
- The orientation in the waypoints denoted by the sequence ( and are the initial and the final orientation, respectively);
- The curvature in the intermediate points denoted by the sequence .
| Algorithm 1: The algorithm for calculation of motion primitives from boundary conditions. |
In general, the solution of the system of equations in Equation (8)—or the intersection of parabolas in (9)—is obtained by following these steps:
|
3.1. The Algorithm for Proposing Suitable Orientations in Waypoints
3.2. The Algorithm for Proposing Suitable Curvatures in Waypoints
- follows directly from (12).
4. Examples and Comparisons
4.1. Example 1: A Path in a Given Corridor
4.2. Example 2: Environment with Random Obstacles—Comparison with an Existing Method
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Montemerlo, M.; Becker, J.; Bhat, S.; Dahlkamp, H.; Dolgov, D.; Ettinger, S.; Haehnel, D.; Hilden, T.; Hoffmann, G.; Huhnke, B.; et al. Junior: The Stanford entry in the Urban Challenge. J. Field Robot. 2008, 25, 569–597. [Google Scholar] [CrossRef] [Green Version]
- Likhachev, M.; Ferguson, D. Planning Long Dynamically-Feasible Maneuvers for Autonomous Vehicles. Int. J. Robot. Res. 2009, 28, 933–945. [Google Scholar] [CrossRef] [Green Version]
- Choset, H.; Lynch, K.; Hutchinson, S.; Kantor, G.; Burgard, W.; Kavraki, L.; Thrun, S. Principles of Robot Motion: Theory, Algorithms, and Implementations; MIT Press: Cambridge, MA, USA, 2005; p. 603. [Google Scholar]
- Webb, D.J.; van den Berg, J. Kinodynamic RRT*: Asymptotically optimal motion planning for robots with linear dynamics. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 5054–5061. [Google Scholar]
- Klančar, G.; Seder, M.; Blažič, S.; Škrjanc, I.; Petrović, I. Drivable Path Planning Using Hybrid Search Algorithm Based on E* and Bernstein–Bézier Motion Primitives. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 4868–4882. [Google Scholar] [CrossRef]
- Zhang, Q.; Song, Y.; Jiao, P.; Hu, Y. A Hybrid and Hierarchical Approach for Spatial Exploration in Dynamic Environments. Electronics 2022, 11, 574. [Google Scholar] [CrossRef]
- Pozna, C.; Precup, R.E.; Földesi, P. A novel pose estimation algorithm for robotic navigation. Robot. Auton. Syst. 2015, 63, 10–21. [Google Scholar] [CrossRef]
- Sánchez-Ibáñez, J.R.; Pérez-del Pulgar, C.J.; García-Cerezo, A. Path Planning for Autonomous Mobile Robots: A Review. Sensors 2021, 21, 7898. [Google Scholar] [CrossRef]
- Vaščák, J.; Hvizdoš, J. Vehicle navigation by fuzzy cognitive maps using sonar and RFID technologies. In Proceedings of the 14th IEEE International Symposium on Applied Machine Intelligence and Informatics, Herlany, Slovakia, 21–23 January 2016; pp. 75–80. [Google Scholar]
- Klančar, G.; Seder, M. Coordinated Multi-Robotic Vehicles Navigation and Control in Shop Floor Automation. Sensors 2022, 22, 1455. [Google Scholar] [CrossRef]
- Neto, A.A.; Macharet, D.G.; Campos, M.F.M. Feasible RRT-based path planning using seventh order Bézier curves. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 1445–1450. [Google Scholar] [CrossRef]
- Wang, H.; Li, G.; Hou, J.; Chen, L.; Hu, N. A Path Planning Method for Underground Intelligent Vehicles Based on an Improved RRT* Algorithm. Electronics 2022, 11, 294. [Google Scholar] [CrossRef]
- Zhang, T.; Mo, H. Reinforcement learning for robot research: A comprehensive review and open issues. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211007305. [Google Scholar] [CrossRef]
- Choi, J.W.; Curry, R.; Elkaim, G. Piecewise Bezier Curves Path Planning with Continuous Curvature Constraint for Autonomous Driving. In Machine Learning and Systems Engineering; Lecture Notes in Electrical Engineering 68; Springer Science + Business Media: Berlin/Heidelberg, Germany, 2010; pp. 31–45. [Google Scholar]
- Ghilardelli, F.; Gabriele, L.; Piazzi, A. Path Generation Using η4-Splines for a Truck and Trailer Vehicle. IEEE Trans. Autom. Sci. Eng. 2014, 11, 187–203. [Google Scholar] [CrossRef]
- Velenis, E.; Tsiotras, P. Minimum-Time Travel for a Vehicle with Acceleration Limits: Theoretical Analysis and Receding-Horizon Implementation. J. Optim. Theory Appl. 2008, 138, 275–296. [Google Scholar] [CrossRef]
- Chen, C.; He, Y.; Bu, C.; Han, J.; Zhang, X. Quartic Bezier Curve based Trajectory Generation for Autonomous Vehicles with Curvature and Velocity Constraints. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 6108–6113. [Google Scholar]
- Zdešar, A.; Škrjanc, I. Optimum Velocity Profile of Multiple Bernstein-BéZier Curves Subject to Constraints for Mobile Robots. ACM Trans. Intell. Syst. Technol. 2018, 9, 1–23. [Google Scholar] [CrossRef]
- Klančar, G.; Zdešar, A.; Blažič, S.; Škrjanc, I. Wheeled Mobile Robotics—From Fundamentals towards Autonomous Systems; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Loknar, M.B.; Blažič, S.; Klančar, G. Minimum-time velocity profile planning for planar motion considering velocity, acceleration and jerk constraints. Int. J. Control. 2021, 1–15. [Google Scholar] [CrossRef]
- Reeds, J.A.; Shepp, L.A. Optimal paths for a car that goes both forwards and backwards. Pac. J. Math. 1990, 145, 367–393. [Google Scholar] [CrossRef] [Green Version]
- Fraichard, T.; Scheuer, A. From Reeds and Shepp’s to continuous-curvature paths. IEEE Trans. Robot. 2004, 20, 1025–1035. [Google Scholar] [CrossRef] [Green Version]
- Brezak, M.; Petrović, I. Real-time Approximation of Clothoids With Bounded Error for Path Planning Applications. IEEE Trans. Robot. 2014, 30, 507–515. [Google Scholar] [CrossRef]
- Gim, S.; Adouane, L.; Lee, S.; Dérutin, J.P. Clothoids Composition Method for Smooth Path Generation of Car-Like Vehicle Navigation. J. Intell. Robot. Syst. Theory Appl. 2017, 88, 129–146. [Google Scholar] [CrossRef] [Green Version]
- Ibrahim, F.; Misro, M.Y.; Ramli, A.; Ali, J. Maximum safe speed estimation using planar quintic Bezier curve with C2 continuity. AIP Conf. Proc. 2017, 1870, 050006. [Google Scholar] [CrossRef]
- Misro, M.Y.; Ramli, A.; Ali, J. Construction of Quintic Trigonometric Bézier Spiral Curve. ASM Sci. J. 2019, 12, 208–215. [Google Scholar]
- Berglund, T.; Erikson, U.; Jonsson, H.; Mrozek, K.; Soderkvist, I. Automatic generation of smooth paths bounded by polygonal chains. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation (CIMCA), Las Vegas, NV, USA, 9–11 July 2001; pp. 528–535. [Google Scholar]
- Boryga, M.; Graboś, A. Planning of manipulator motion trajectory with higher-degree polynomials use. Mech. Mach. Theory 2009, 44, 1400–1419. [Google Scholar] [CrossRef]
- Piazzi, A.; Bianco, C.G.L.; Romano, M. η3-splines for the smooth path generation of wheeled mobile robots. IEEE Trans. Robot. 2007, 3, 1089–1095. [Google Scholar] [CrossRef]
- Fitter, H.N.; Pandey, A.B.; Patel, D.D.; Mistry, J.M. A Review on Approaches for Handling Bezier Curves in CAD for Manufacturing. Procedia Eng. 2014, 97, 1155–1166. [Google Scholar] [CrossRef] [Green Version]
- BiBi, S.; Abbas, M.; Misro, M.Y.; Hu, G. A Novel Approach of Hybrid Trigonometric Bézier Curve to the Modeling of Symmetric Revolutionary Curves and Symmetric Rotation Surfaces. IEEE Access 2019, 7, 165779–165792. [Google Scholar] [CrossRef]
- Meng, W.; Li, C.; Liu, Q. Geometric Modeling of C-Bézier Curve and Surface with Shape Parameters. Mathematics 2021, 9, 2651. [Google Scholar] [CrossRef]
- Maqsood, S.; Abbas, D.M.; Miura, K.; Majeed, A.; Iqbal, A. Geometric modeling and applications of generalized blended trigonometric Bézier curves with shape parameters. Adv. Differ. Equ. 2020, 2020, 550. [Google Scholar] [CrossRef]
- Zhang, B.; Zhu, D. A new method on motion planning for mobile robots using jump point search and Bezier curves. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211019220. [Google Scholar] [CrossRef]
- Manyam, S.G.; Casbeer, D.W.; Weintraub, I.E.; Taylor, C. Trajectory Optimization For Rendezvous Planning Using Quadratic Bézier Curves. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 1405–1412. [Google Scholar] [CrossRef]
- Han, L.; Yashiro, H.; Tehrani Nik Nejad, H.; Do, Q.H.; Mita, S. Bézier curve based path planning for autonomous vehicle in urban environment. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium, La Jolla, CA, USA, 21–24 June 2010; pp. 1036–1042. [Google Scholar] [CrossRef]
- Xu, L.; Cao, M.; Song, B. A new approach to smooth path planning of mobile robot based on quartic Bezier transition curve and improved PSO algorithm. Neurocomputing 2022, 473, 98–106. [Google Scholar] [CrossRef]
- Costanzi, R.; Fanelli, F.; Meli, E.; Ridolfi, A.; Allotta, B. Generic Path Planning Algorithm for Mobile Robots Based on Bézier Curves. IFAC-PapersOnLine 2016, 49, 145–150. [Google Scholar] [CrossRef]
- Simba, K.R.; Uchiyama, N.; Sano, S. Real-time smooth trajectory generation for nonholonomic mobile robots using Bézier curves. Robot. Comput.-Integr. Manuf. 2016, 41, 31–42. [Google Scholar] [CrossRef]
- Kallmann, M. Path Planning in Triangulations. In Proceedings of the Workshop on Reasoning, Representation, and Learning in Computer Games, International Joint Conference on Artificial Intelligence (IJCAI), Edinburgh, UK, 30 July–5 August 2005; pp. 49–54. [Google Scholar]
- Bonab, S.A.; Emadi, A. Optimization-based Path Planning for an Autonomous Vehicle in a Racing Track. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 3823–3828. [Google Scholar] [CrossRef]


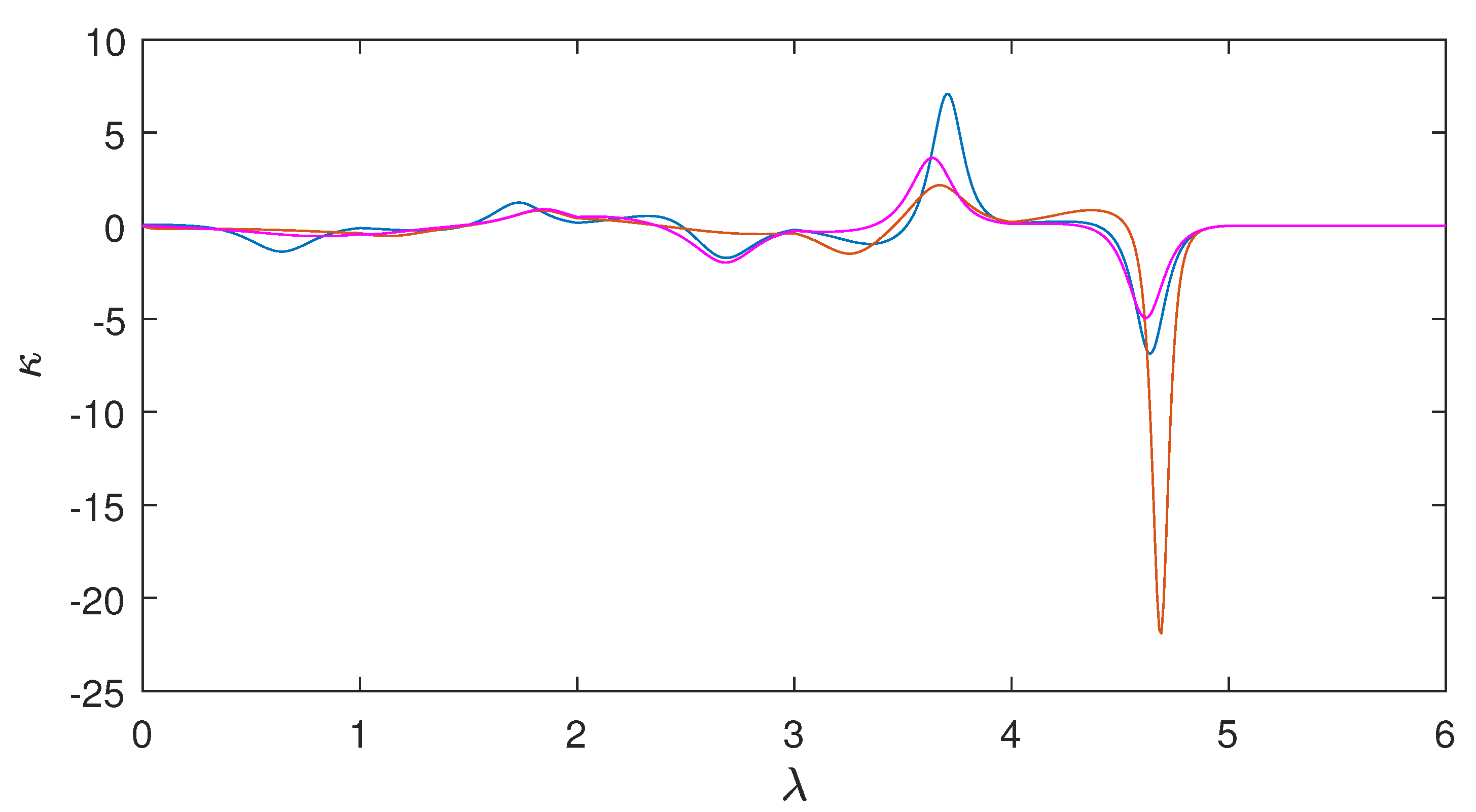
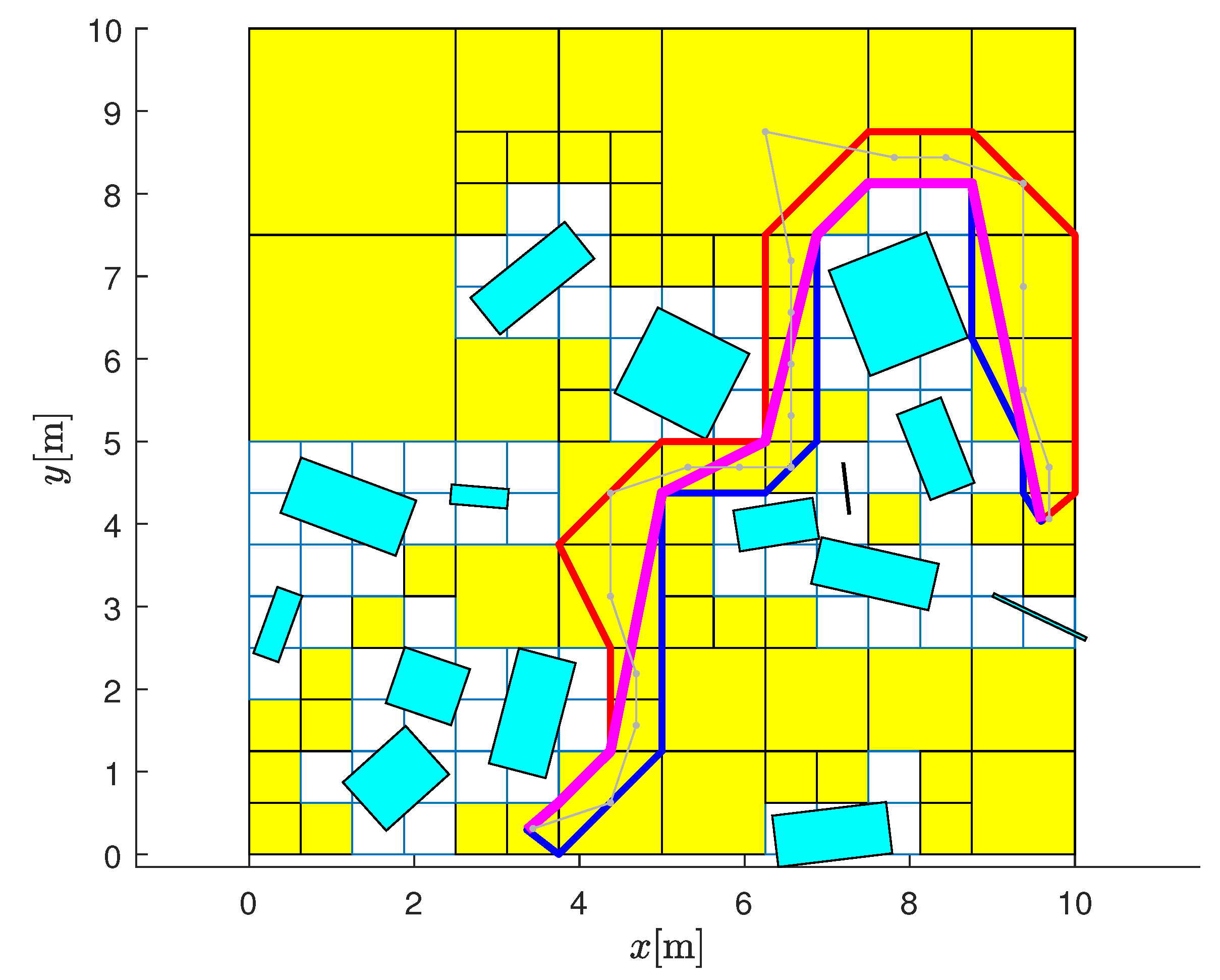
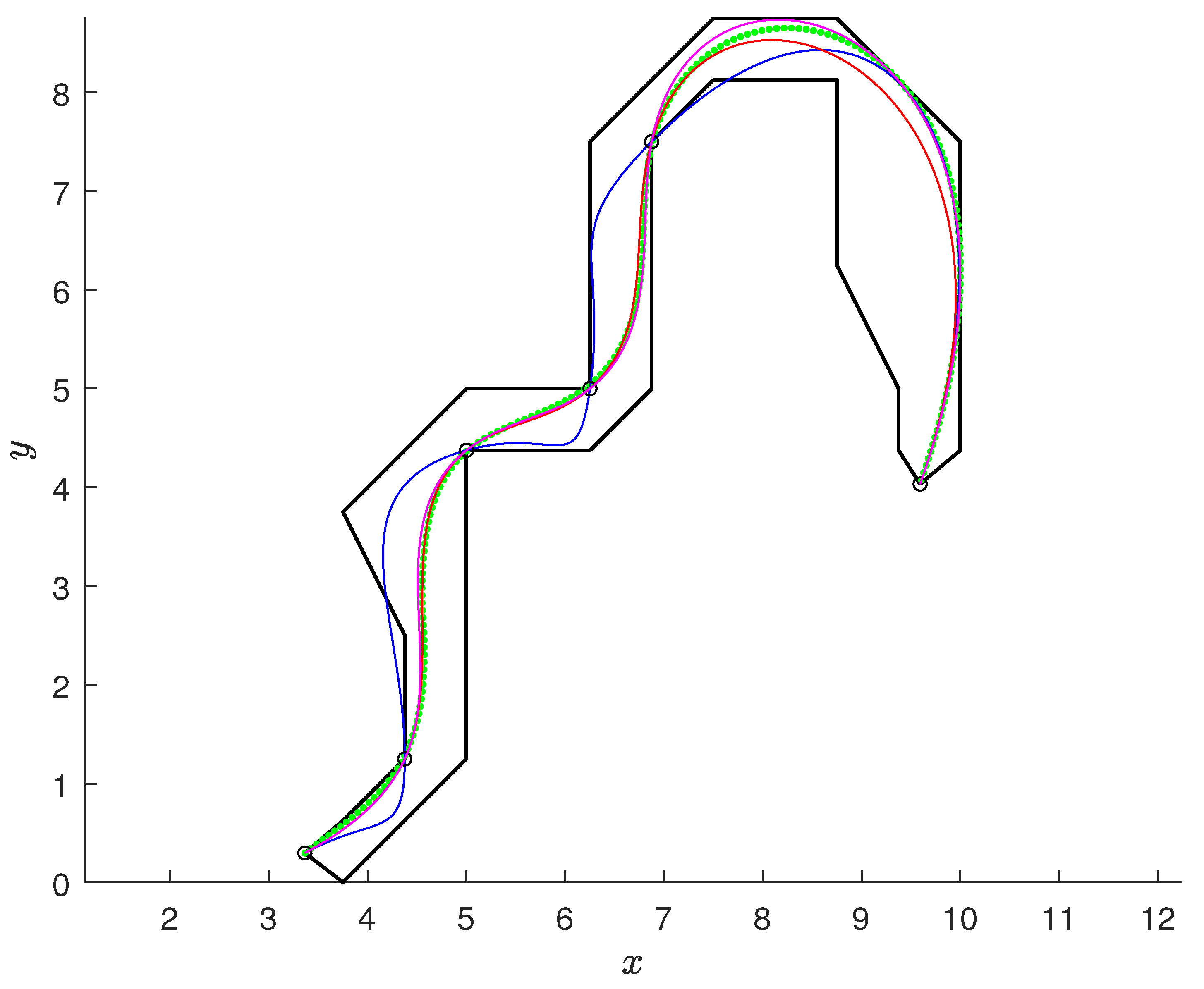
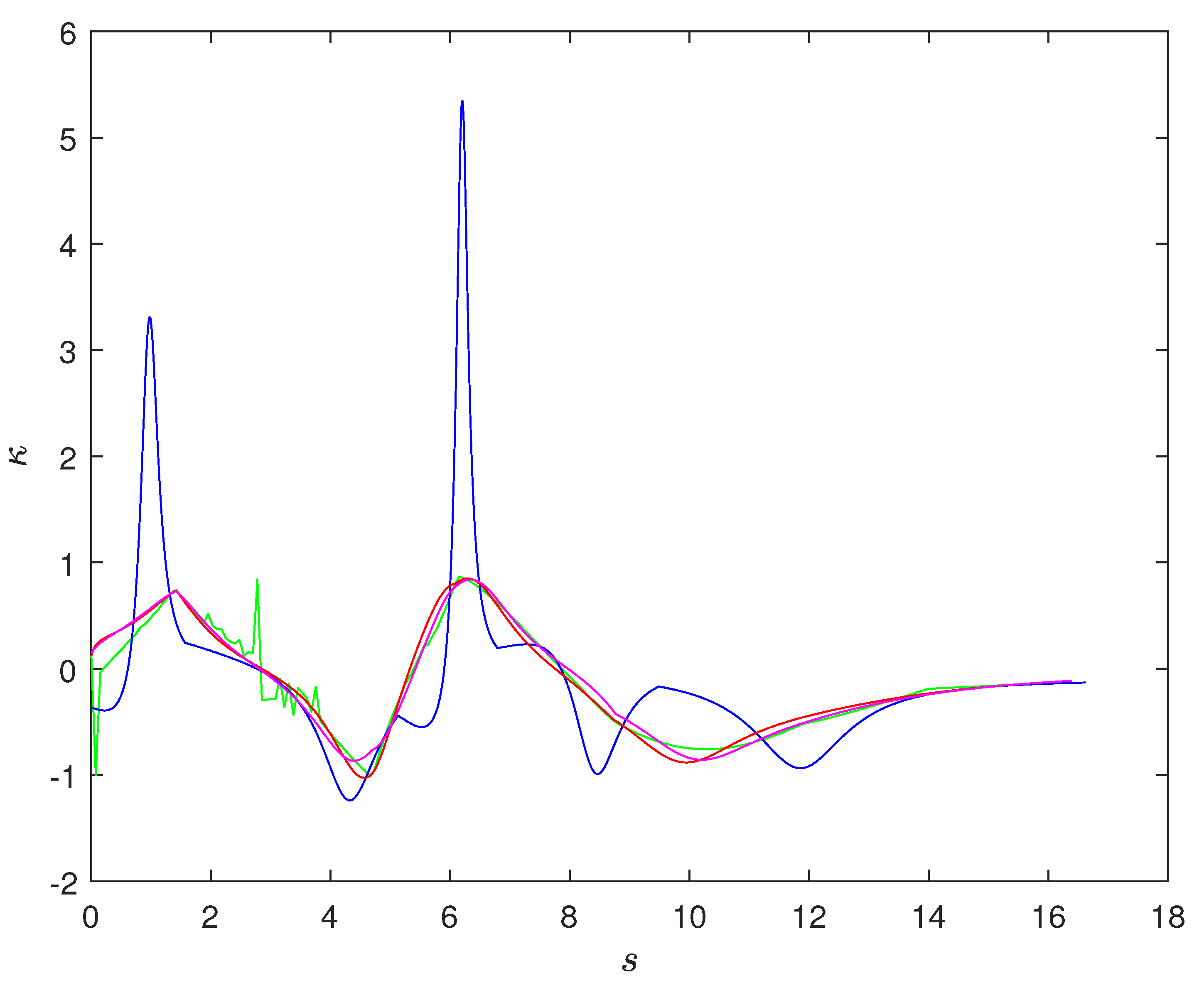
| Algorithm | Length | Average | Max | Min |
|---|---|---|---|---|
| funnel alg [40] | 16.1395 | 0.2415 | 0.8669 | |
| Section 3.1 and Section 3.2 | 16.6174 | 0.6825 | 5.3447 | |
| optimization | 16.3910 | 0.2451 | 0.8394 | |
| “filtering” of [40] | 15.9238 | 0.2576 | 0.8493 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blažič, S.; Klančar, G. Effective Parametrization of Low Order Bézier Motion Primitives for Continuous-Curvature Path-Planning Applications. Electronics 2022, 11, 1709. https://doi.org/10.3390/electronics11111709
Blažič S, Klančar G. Effective Parametrization of Low Order Bézier Motion Primitives for Continuous-Curvature Path-Planning Applications. Electronics. 2022; 11(11):1709. https://doi.org/10.3390/electronics11111709
Chicago/Turabian StyleBlažič, Sašo, and Gregor Klančar. 2022. "Effective Parametrization of Low Order Bézier Motion Primitives for Continuous-Curvature Path-Planning Applications" Electronics 11, no. 11: 1709. https://doi.org/10.3390/electronics11111709
APA StyleBlažič, S., & Klančar, G. (2022). Effective Parametrization of Low Order Bézier Motion Primitives for Continuous-Curvature Path-Planning Applications. Electronics, 11(11), 1709. https://doi.org/10.3390/electronics11111709







