FDTD-Based Electromagnetic Modeling of Dielectric Materials with Fractional Dispersive Response
Abstract
1. Introduction
2. Fractional Calculus in Electromagnetic Theory
2.1. Fractional Vector Calculus
2.2. Fractal Media
2.3. Dielectric Media
3. Fractional Dielectric Response Models
4. FDTD Modeling
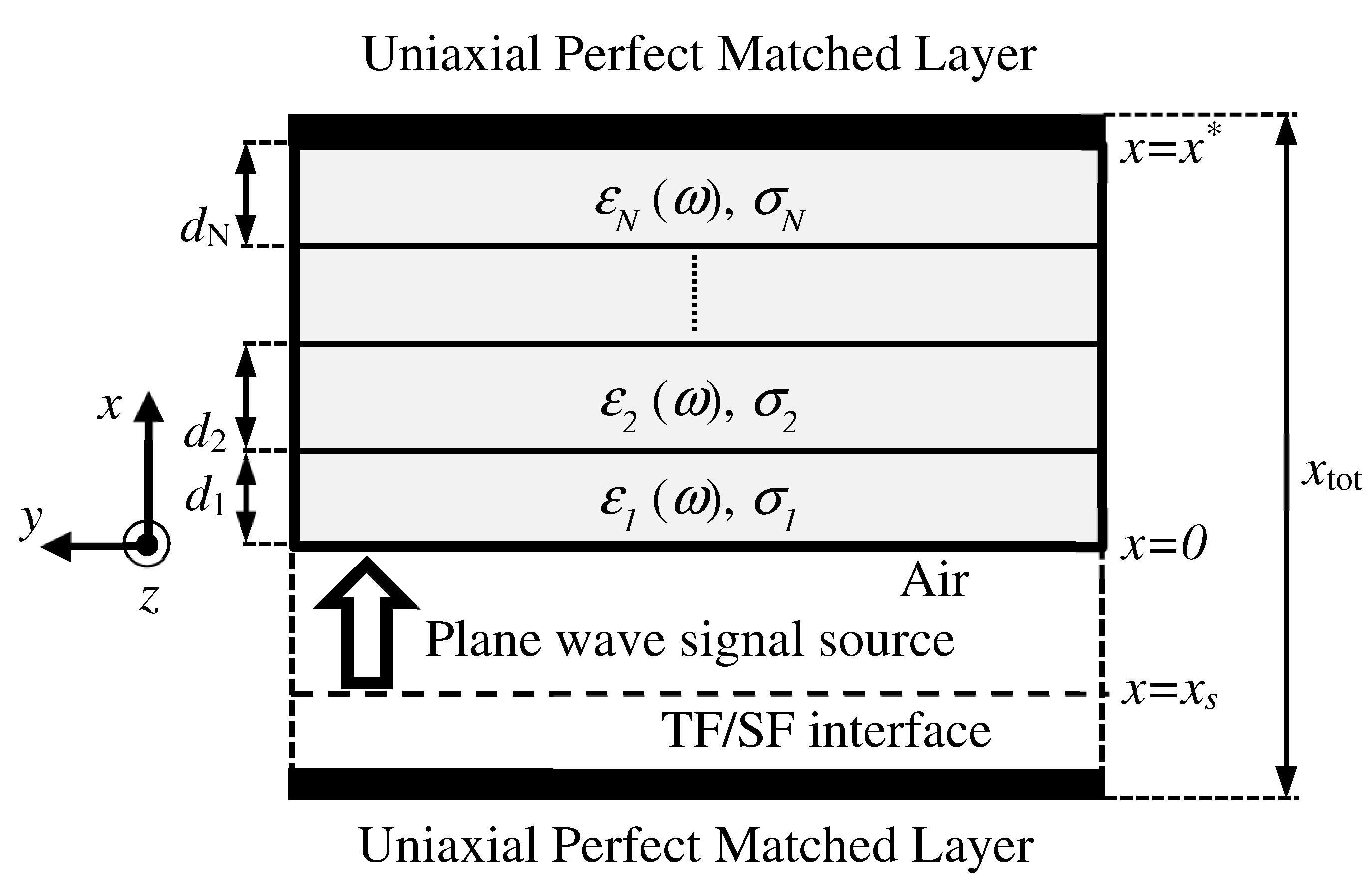
4.1. FDTD Scheme
4.2. Applications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| ADE | Auxiliary Differential Equation |
| CC | Cole–Cole |
| CD | Cole–Davidson |
| CFL | Courant–Friedrichs–Lewy |
| EM | Electromagnetic |
| EMM | Electromagnetic Metamaterial |
| EWQPSO | Enhanced Weighted Quantum Particle Swarm Optimization |
| FC | Fractional Calculus |
| FDTD | Finite Difference Time Domain |
| FO | Fractional Order |
| FILT | Fast Inverse Laplace Transform |
| FVC | Fractional Vector Calculus |
| GPR | Ground Penetrating Radar |
| HN | Havriliak–Negami |
| PDE | Partial Differential Equation |
| PSO | Particle Swarm Optimization |
| RC | Recursive Convolution |
| TF | Time Fractional |
| TFSF | Total-Field/Scattered-Field |
| TRD | Temporal Rrelaxation Distribution |
| UPML | Uniaxial Perfectly Matched Layer |
| ZT | Z-transform |
References
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simulat. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Bas, E.; Ozarslan, R. Real world applications of fractional models by Atangana–Baleanu fractional derivative. Chaos Solitons Fractals 2018, 116, 121–125. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier B.V.: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: New York, NY, USA, 2011. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Mescia, L.; Bia, P.; Caratelli, D. Fractional-Calculus-Based Electromagnetic Tool to Study Pulse Propagation in Arbitrary Dispersive Dielectrics. Phys. Status Solidi A 2019, 216, 1800557. [Google Scholar] [CrossRef]
- Garappa, R.; Mainardi, F.; Maione, G. Models of dielectric relaxation based on completely monotone functions. Fract. Calc. Appl. Anal. 2016, 19, 1105–1160. [Google Scholar] [CrossRef]
- Tarasov, V.E. On chain rule for fractional derivatives. Commun. Nonlinear Sci. Numer. Simulat. 2016, 30, 1–4. [Google Scholar] [CrossRef]
- Engheta, N. On Fractional Calculus and Fractional Multipoles in Electromagnetism. IEEE Trans. Antennas Propag. 1996, 44, 554–566. [Google Scholar] [CrossRef]
- Engheta, N. Use of fractional integration to propose some fractional solutions for the scalar Helmholtz equation. Prog. Electromagn. Res. 1996, 12, 107–132. [Google Scholar] [CrossRef]
- Engheta, N. Fractional curl operator in electromagnetics. Microw. Opt. Technol. Lett. 1998, 17, 86–91. [Google Scholar] [CrossRef]
- Veliev, E.I.; Ivakhnychenko, M.V.; Ahmedov, T.M. Fractional boundary conditions in plane waves diffraction on a strip. Prog. Electromagn. Res. 2008, 79, 443–462. [Google Scholar] [CrossRef][Green Version]
- Naqvi, Q.A.; Rizvi, A.A. Fractional dual solutions and corresponding sources. Prog. Electromagn. Res. 2000, 25, 223–238. [Google Scholar] [CrossRef]
- Naqvi, Q.A.; Murtaza, G.; Rizvi, A.A. Fractional dual solutions to Maxwell equations in homogeneous chiral media. Opt. Commun. 2000, 178, 27–30. [Google Scholar] [CrossRef]
- Hussain, A.; Naqvi, Q.A. Fractional curl operator in chiral medium and fractional non-symmetric transmission line. Prog. Electromagn. Res. 2006, 59, 199–213. [Google Scholar] [CrossRef]
- Naqvi, Q.A.; Abbas, M. Complex and higher order fractional curl operator in electromagnetics. Opt. Commun. 2004, 241, 349–355. [Google Scholar] [CrossRef]
- Ben Adda, F. Geometric interpretation of the differentiability and gradient of real order. Comptes Rendus L’Academie Des. Sci. Ser. Math. 1998, 8, 931–934. [Google Scholar]
- Meerschaert, M.M.; Mortensen, J.; Wheatcraft, S.W. Fractional vector calculus for fractional advection-dispersion. Phys. A Stat. Mech. Appl. 2006, 367, 181–190. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional vector calculus and fractional Maxwell’s equations. Ann. Phys. 2008, 323, 2756–2778. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Rivero, M.; Trujillo, J.J. From a generalised Helmholtz decomposition theorem to fractional Maxwell equations. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 1036–1049. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T.M. On fractional vectorial calculus. Bull. Pol. Acad. Sci. Tech. Sci. 2018, 66, 389–402. [Google Scholar]
- Cheng, J.; Dai, E. Higher-order fractional Green and Gauss formulas. J. Math. Anal. Appl. 2018, 462, 157–171. [Google Scholar] [CrossRef]
- Tarasov, V.E. General Fractional Vector Calculus. Mathematics 2021, 9, 2816. [Google Scholar] [CrossRef]
- Baleanu, B.; Golmankhaneh, A.K.; Baleanu, M.C. Fractional Electromagnetic Equations Using Fractional Forms. Int. J. Theor. Phys. 2009, 48, 2016. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Yépez-Martínez, H.; Escobar-Jiménez, R.F.; Astorga-Zaragoza, C.M.; Morales-Mendoza, L.J.; González-Lee, M. Universal character of the fractional space-time electromagnetic waves in dielectric media. J. Electromagn. Waves Appl. 2015, 29, 727–740. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Yépez-Martínez, H.; Calderón-Ramón, C.; Benavidez-Cruz, M.; Morales-Mendoza, L.J. Fractional electromagnetic waves in conducting media. J. Electromagn. Waves Appl. 2016, 30, 259–271. [Google Scholar] [CrossRef]
- Tararov, V.E.; Trujillo, J.J. Fractional power-law spatial dispersion in electrodynamics. Ann. Phys. 2013, 334, 1–23. [Google Scholar] [CrossRef]
- Stefanski, T.P.; Gulgowski, J. Formulation of Time-Fractional Electrodynamics Based on Riemann-Silberstein Vector. Entropy 2021, 23, 987. [Google Scholar] [CrossRef] [PubMed]
- Gulgowski, J.; Kwiatkowski, D.; Stefanski, T.P. Signal Propagation in Electromagnetic Media Modelled by the Two-Sided Fractional Derivative. Fractal Fract. 2021, 5, 10. [Google Scholar] [CrossRef]
- Zubair, M.; Mughal, M.J.; Naqvi, Q.A. An exact solution of the spherical wave equation in D-dimensional fractional space. J. Electromagn. Waves Appl. 2011, 25, 1481–1491. [Google Scholar] [CrossRef]
- Zubair, M.; Mughal, M.J.; Naqvi, Q.A. An exact solution of cylindrical wave equation for electromagnetic field in fractional dimensional space. Prog. Electromagn. Res. 2011, 114, 443–455. [Google Scholar] [CrossRef]
- Tarasov, V.E. Electromagnetic fields on fractals. Mod. Phys. Lett. A 2006, 21, 1587–1600. [Google Scholar] [CrossRef]
- Balankin, A.S.; Mena, B.; Patiño, J.; Morales, D. Electromagnetic fields in fractal continua. Phys. Lett. A 2013, 377, 783–788. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractal electrodynamics via non-integer dimensional space approach. Phys. Lett. A 2015, 379, 2055–2061. [Google Scholar] [CrossRef]
- Zubair, M.; Junaid Mughal, M.; Abbas Naqvi, Q. Electromagnetic Fields and Waves in Fractional Dimensional Space; Springer: Berlin, Germany, 2012. [Google Scholar]
- Zubair, M.; Mughal, M.J. Differential electromagnetic equations in fractional space. Prog. Electromagn. Res. 2011, 114, 255–269. [Google Scholar] [CrossRef]
- Zubair, M.; Mughal, M.J. On electromagnetic wave propagation in fractional space. Nonlinear Anal. Real World Appl. 2011, 12, 2844–2850. [Google Scholar] [CrossRef]
- Ostoja-Starzewski, M. Electromagnetism on anisotropic fractal media. Z. Angew. Math. Phys. 2013, 64, 381–390. [Google Scholar] [CrossRef]
- Asad, H.; Zubair, M.; Mughal, M.J. Reflection and transmission at dielectric-fractal interface. Prog. Electromagn. Res. 2012, 125, 543–558. [Google Scholar] [CrossRef][Green Version]
- Mescia, L.; Bia, P.; Caratelli, D. A novel ultrawideband FDTD numerical modeling of ground penetrating radar on arbitrary dispersive soils. In Proceedings of the IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; pp. 815–816. [Google Scholar]
- Di Matteo, A.; Pettinelli, E. Early-Time GPR Signal Attributes to Estimate Soil Dielectric Permittivity: A Theoretical Study. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1643–1654. [Google Scholar] [CrossRef]
- Mescia, L.; Bia, P.; Caratelli, D.; Gielis, J. Swarm intelligence for electromagnetic problem solving. In Handbook of Research on Soft Computing and Nature-Inspired Algorithms; Shandilya, S.K., Shandilya, K., Deep, A.K., Naga, K., Eds.; IGI Global: Hershey, PA, USA, 2017; pp. 69–100. [Google Scholar]
- Greiner, K.; Dubuc, D.; Chen, T.; Ertis, F.; Chretiennot, T.; Poupot, M.; Fournie, J.J. Recent advances in microwave-based dielectric spectroscopy at the cellular level for cancer investigations. IEEE Trans. Microw. Theory Tech. 2013, 61, 2023–2030. [Google Scholar] [CrossRef]
- Skierucha, W.; Wilczek, A.; Szyplowska, A. Dielectric spectroscopy in agrophysics. Int. Agrophys. 2012, 26, 187–197. [Google Scholar] [CrossRef]
- Asorey-Cacheda, R.; Canovas-Carrasco, S.; Garcia-Sanchez, A.J.; Garcia-Haro, J.A. An Analytical Approach to Flow-Guided Nanocommunication Networks. Sensors 2020, 20, 1332. [Google Scholar] [CrossRef]
- Akkaş, M.A. Nano-Sensor Modelling for Intra-Body Nano-Networks. Wirel. Pers. Commun. 2021, 118, 3129–3143. [Google Scholar] [CrossRef]
- Piccinni, G.; Avitabile, G.; Coviello, G.; Talarico, C. A novel optimization framework for the design of gilbert cell mixers. In Proceedings of the IEEE IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017. [Google Scholar]
- Piro, M.A.; Bia, P.; Boggia, G.; Caratelli, D.; Grieco, L.A.; Mescia, L. Terahertz electromagnetic field propagation in human tissues: A study on communication capabilities. Nano Commun. Netw. 2016, 10, 51–59. [Google Scholar] [CrossRef]
- Debye, P. Polar Molecules; Dover: New York, NY, USA, 1954. [Google Scholar]
- Hart, W.B. Multiterm Debye Dispersion Relations for Permittivity of Muscle. IEEE Trans. Biom. Eng. 1985, 32, 60–64. [Google Scholar] [CrossRef]
- Polk, C.; Postow, E. Biological Effects of Electromagnetic Fields; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Raju, G.G. Dielectrics in Electric Fields; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Kao, K.C. Dielectric Phenomena in Solids; Elsevier Academic Press: London, UK, 2004. [Google Scholar]
- Tuncer, E. Dielectric mixtures-importance and theoretical approaches. IEEE Electr. Insul. Mag. 2013, 29, 49–58. [Google Scholar] [CrossRef][Green Version]
- Singh, B.; Pratap, V.; Katiyar, M.; Abbas, S.M.; Sharma, Y.K.; Siddiqui, A.M.; Eswara Prasad, N. Engineering of dielectric composites on electromagnetic and microwave absorbing properties for operation in the X-band. J. Adv. Dielctr. 2021, 11, 2150001. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics, I. Alternating current characteristics. J. Chem. Phys. 1941, 9, 341–349. [Google Scholar] [CrossRef]
- Davidson, D.W.; Cole, R.H. Dielectric relaxation in glycerol, propylene glycol, and n-propanol. J. Chem. Phys. 1951, 19, 1484–1490. [Google Scholar] [CrossRef]
- Havriliak, S.; Negami, S. A Complex Plane Analysis of α-Dispersions in Some Polymer Systems. J. Polym. Sci. Part C 1966, 14, 99–117. [Google Scholar] [CrossRef]
- Havriliak, S., Jr.; Watts, D.G. Comparing graphical and statistical methods for analysing dielectric dispersions of polymers represented in the complex plane. Polymer 1986, 27, 1509–1512. [Google Scholar] [CrossRef]
- Williams, G.; Watts, D.C. Non-symmetrical dielectric relaxation behaviour arising from a simple empirical decay function. Trans. Faraday Soc. 1970, 66, 80–85. [Google Scholar] [CrossRef]
- Jonscher, A.K. Hopping losses in polarisable dielectric media. Nature 1974, 250, 191–193. [Google Scholar] [CrossRef]
- Raicu, V. Dielectric dispersion of biological matter: Model combining Debye-type and universal responses. Phys. Rev. E 1999, 60, 4677–4680. [Google Scholar] [CrossRef]
- Stanislavsky, A.; Weron, K.; Trzmiel, J. Subordination model of anomalous diffusion leading to the two-power-law relaxation responses. EPL 2010, 91, 40003. [Google Scholar] [CrossRef]
- Nigmatullin, N.N.; Ryabov, Y.E. Cole–Davidson dielectric relaxation as a self-similar relaxation process. Phys. Solid State 1997, 39, 87–90. [Google Scholar] [CrossRef]
- Novikov, V.V.; Privalko, V.P. Temporal fractal model for the anomalous dielectric relaxation of inhomogeneous media with chaotic structure. Phys. Rev. E 2001, 64, 031504. [Google Scholar] [CrossRef]
- Fu, J.Y. On the theory of the universal dielectric relaxation. Philos. Mag. 2014, 16, 1788–1815. [Google Scholar] [CrossRef]
- Wharmby, A.W.; Bagley, R.L. The application of the fractional calculus model for dispersion and absorption in dielectrics I. Terahertz waves. Int. J. Eng. Sci. 2015, 93, 1–12. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional integro-differential equations for electromagnetic waves in dielectric media. Theor. Math. Phys. 2009, 158, 355–359. [Google Scholar] [CrossRef]
- Nasrolahpour, H. Fractional electromagnetic metamaterials. Optik 2020, 203, 16396. [Google Scholar] [CrossRef]
- Stefanski, T.P. On possible applications of media described by fractional-order models in electromagnetic cloaking. Commun. Nonlinear Sci. Numer. Simulat. 2021, 99, 105827. [Google Scholar] [CrossRef]
- Stefanski, T.P.; Gulgowski, J. Signal propagation in electromagnetic media described by fractional-order models. Commun. Nonlinear Sci. Numer. Simulat. 2020, 82, 105029. [Google Scholar] [CrossRef]
- Mescia, L.; Bia, P.; Caratelli, D. Fractional derivative based FDTD modeling of transient wave propagation in Havriliak-Negami media. IEEE Trans. Microw. Theory Tech. 2014, 62, 1920–1929. [Google Scholar] [CrossRef]
- Caratelli, D.; Mescia, L.; Bia, P.; Stukach, O.V. Fractional-Calculus-Based FDTD Algorithm for Ultrawideband Electromagnetic Characterization of Arbitrary Dispersive Dielectric Materials. IEEE Trans. Antennas Propag. 2016, 64, 3533–3544. [Google Scholar] [CrossRef]
- Greenbaum, A.; Ishai, P.B.; Feldman, Y. Analysis of Experimental Data and Fitting Problems. In Dielectric Relaxation in Biological Systems: Physical Principles, Methods, and Applications; Raicu, V., Feldman, Y., Eds.; Oxford University Press: New York, NY, USA, 2015; pp. 170–185. [Google Scholar]
- Kalmykov, Y.P.; Coffey, W.T.; Crothers, D.S.F.; Titov, S.V. Microscopic models for dielectric relaxation in disordered systems. Phys. Rev. E 2004, 70, 041103. [Google Scholar] [CrossRef]
- Hilfer, R. Analytical representations for relaxation functions of glasses. J. Non-Crist. Solids 2002, 70, 122–126. [Google Scholar] [CrossRef]
- Zhao, D.; Sun, H. Anomalous relaxation model based on the fractional derivative with a Prabhakar-like kernel. Z. Angew. Math. Phys. 2019, 70, 42. [Google Scholar] [CrossRef]
- Sodhi, C.S.; Ozelim, L.C.S.M.; Rathie, P.N. Dielectric relaxation model of human blood as a superposition of Debye functions with relaxation times following a Modified-Weibull distribution. Heliyon 2021, 7, e06606. [Google Scholar] [CrossRef]
- Petreska, I.; Pejov, L.; Sandev, T.; Kocarev, L.; Metzler, R. Tuning of the Dielectric Relaxation and Complex Susceptibility in a System of Polar Molecules: A Generalised Model Based on Rotational Diffusion with Resetting. Fractal Fract. 2022, 6, 88. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media; Pergamon: New York, NY, USA, 1984; pp. 279–283. [Google Scholar]
- Ciancio, A.; Flora, B.F.F. Fractional Complex Permittivity Model of Media with Dielectric Relaxation. Fractal Fract. 2017, 1, 4. [Google Scholar] [CrossRef]
- Prokopidis, K.P.; Zografopoulos, D. A Unified FDTD/PML Scheme Based on Critical Points for Accurate Studies of Plasmonic Structures. J. Lightw. Technol. 2013, 21, 2467–2476. [Google Scholar] [CrossRef]
- Han, M.; Dutton, R.W.; Fan, S. Model Dispersive Media in Finite-Difference Time-Domain Method With Complex-Conjugate Pole-Residue Pairs. IEEE Microw. Wirel. Compon. Lett. 2006, 16, 119–121. [Google Scholar]
- Karpinski, K.; Zielinska-Raczynska, S.; Ziemkiewicz, D. Fractional Derivative Modification of Drude Model. Sensors 2021, 21, 4974. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.; Baek, J.W.; Jung, K.Y. Comprehensive Study on Numerical Aspects of Modified Lorentz Model-Based Dispersive FDTD Formulations. IEEE Trans. Antennas Propag. 2019, 67, 7643–7648. [Google Scholar] [CrossRef]
- Bia, P.; Mescia, L.; Caratelli, D. Fractional Calculus-Based Modeling of Electromagnetic Field Propagation in Arbitrary Biological Tissue. Math. Probl. Eng. 2016, 2016, 5676903. [Google Scholar] [CrossRef]
- Bia, P.; Caratelli, D.; Mescia, L.; Gielis, J. Analysis and synthesis of supershaped dielectric lens antennas. IET Microw. Antennas Propag. 2015, 9, 1497–1504. [Google Scholar] [CrossRef]
- Palma, G.; Bia, P.; Mescia, L.; Yano, T.; Nazabal, V.; Taguchi, J.; Moréac, A.; Prudenzano, F. Design of fiber coupled Er3+: Chalcogenide microsphere amplifier via particle swarm optimization algorithm. Opt. Eng. 2014, 53, 071805. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Kelley, D.F.; Luebbers, L.J. Piecewise linear recursive convolution for dispersive media using FDTD. IEEE Trans. Antennas Propag. 1996, 44, 792–797. [Google Scholar] [CrossRef]
- Giannakis, I.; Giannopoulos, A. A Novel Piecewise Linear Recursive Convolution Approach for Dispersive Media Using the Finite-Difference Time-Domain Method. IEEE Trans. Antennas Propag. 2014, 62, 2669–2678. [Google Scholar] [CrossRef]
- Chen, W.J.; Ma, P.; Tian, J. A Novel ADE-CN-FDTD with Improved Computational Efficiency for Dispersive Media. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 849–851. [Google Scholar] [CrossRef]
- Tian, H.; He, S.; Wang, M.; Li, G.; Yu, M.; Zhang, S.; Xu, J. Modified Lorentz Model-Based ADE-WLP-FDTD Method Simulation on THz Wave Propagation Properties of Tumor Tissue. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 2392–2396. [Google Scholar] [CrossRef]
- Sullivan, D.M. Z-transform theory and the FDTD method. IEEE Trans. Antennas Propag. 1996, 44, 28–34. [Google Scholar] [CrossRef]
- Nayyeri, V.; Soleimani, M.; Rashed-Mohassel, J.; Dehmollaian, M. FDTD Modeling of Dispersive Bianisotropic Media Using Z-Transform Method. IEEE Trans. Antennas Propag. 2011, 59, 2268–2279. [Google Scholar] [CrossRef]
- Kelley, D.F.; Destan, T.J.; Luebbers, R.J. Debye function expansions of complex permittivity using a hybrid particle swarm least squares optimization approach. IEEE Trans. Antennas Propag. 2007, 55, 1999–2005. [Google Scholar] [CrossRef]
- Wuren, T.; Takai, T.; Fujii, M.; Sakagami, I. Effective 2-Debye-Pole FDTD Model of Electromagnetic Interaction between Whole Human Body and UWB Radiation. IEEE Microw. Wirel. Comp. Lett. 2007, 17, 483–485. [Google Scholar] [CrossRef]
- Causley, M.F.; Petropoulos, P.G.; Jiang, S. Incorporating the Havriliak–Negami dielectric model in the FD-TD method. J. Comput. Phys. 2011, 230, 3884–3889. [Google Scholar] [CrossRef]
- Su, S.; Dai, W.; Haynie, D.T.; Simicevic, N. Use of the z-Transform to InvestigateNanopulse Penetration of Biological Matter. Bioelectromagnetics 2005, 28, 389–397. [Google Scholar] [CrossRef]
- Chakarothai, J. Novel FDTD Scheme for Analysis of Frequency-Dependent Medium Using Fast Inverse Laplace Transform and Prony’s Method. IEEE Trans. Antennas Propag. 2019, 67, 6076–6089. [Google Scholar] [CrossRef]
- Tofighi, M.R. FDTD Modeling of Biological Tissues Cole-Cole Dispersion for 0.5–30 GHz Using Relaxation Time Distribution Samples-Novel and Improved Implementations. IEEE Trans. Microw. Theory Tech. 2009, 57, 2588–2596. [Google Scholar] [CrossRef]
- Li, J.; Huang, Y.; Lin, Y. Developing finite element methods for Maxwell’s equations in a Cole–Cole dispersive medium. SIAM J. Sci. Comput. 2011, 33, 3153–3174. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, L.L.; Zeng, F. Analysis of a Backward Euler-type Scheme for Maxwell’s Equations in a Havriliak-Negami Dispersive Medium. Esaim Math. Model. Numer. Anal. 2021, 55, 479–506. [Google Scholar] [CrossRef]
- Bai, X.; Rui, H. A second-order space-time accurate scheme for Maxwell’s equations in a Cole–Cole dispersive medium. Eng. Comput. 2022. [Google Scholar] [CrossRef]
- Gedney, S.D. An anisotropic perfectly matched layer absorbingmedium for the truncation of FDTD lattices. IEEE Trans. Antennas Propagat. 1996, 44, 1630–1639. [Google Scholar] [CrossRef]
- Pereda, J.A.; Vielva, L.A.; Vegas, A.; Prieto, A. Analyzing the stability of the FDTD technique by combining the von Neumann method with the Routh–Hurwitz criterion. IEEE Trans. Microw. Theory Tech. 2001, 49, 371–377. [Google Scholar] [CrossRef]
- Yeh, P. Optical Waves in Layered Media; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Shivola, E. Electromagnetic Mixing Formulas and Applications; The Institution of Electrical Engineers: London, UK, 1999. [Google Scholar]
- Daniels, D.J. Ground Penetrating Radar, 2nd ed.; The Institution of Electrical Engineers: London, UK, 2004. [Google Scholar]
- Giannakis, I.; Giannopoulos, A.; Warren, C. A Realistic FDTD Numerical Modeling Framework of Ground Penetrating Radar for Landmine Detection. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 37–51. [Google Scholar] [CrossRef]
- Bobrov, P.P.; Repin, V.; Rodionova, O.V. Wideband Frequency Domain Method of Soil Dielectric Property Measurements. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2366–2372. [Google Scholar] [CrossRef]





| Layer | Thickness (mm) | Conductivity (S m−1) | Relaxation Time (ps) |
|---|---|---|---|
| 1 | 20 | 3.5 × 10−2 | 16 |
| 2 | 30 | 5 × 10−2 | 5.91 |
| 3 | 20 | 3 × 10−2 | 59.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mescia, L.; Bia, P.; Caratelli, D. FDTD-Based Electromagnetic Modeling of Dielectric Materials with Fractional Dispersive Response. Electronics 2022, 11, 1588. https://doi.org/10.3390/electronics11101588
Mescia L, Bia P, Caratelli D. FDTD-Based Electromagnetic Modeling of Dielectric Materials with Fractional Dispersive Response. Electronics. 2022; 11(10):1588. https://doi.org/10.3390/electronics11101588
Chicago/Turabian StyleMescia, Luciano, Pietro Bia, and Diego Caratelli. 2022. "FDTD-Based Electromagnetic Modeling of Dielectric Materials with Fractional Dispersive Response" Electronics 11, no. 10: 1588. https://doi.org/10.3390/electronics11101588
APA StyleMescia, L., Bia, P., & Caratelli, D. (2022). FDTD-Based Electromagnetic Modeling of Dielectric Materials with Fractional Dispersive Response. Electronics, 11(10), 1588. https://doi.org/10.3390/electronics11101588








