Detailed Placement and Global Routing Co-Optimization with Complex Constraints
Abstract
:1. Introduction
1.1. Previous Works
1.2. Our Works
- We propose an improved batch scheduling method which can increase the speed of scheduling the net into disjoint batches by 70× in this contest. Further, by combining FLUTE and maze routing, we propose a fast and effective preprocessing and refinement strategy;
- To find a proper destination for cell movement, a BFS-based approximate optimal addressing algorithm in 3D is designed. Further, we propose an optimal region selection algorithm based on the partial routing solution to jump out of the local optimal solution;
- According to the requirements of our work, four partial rip-up strategies for routing length optimization are presented to make a trade-off between quality and efficiency. Unlike previous works, we present a new routing cost function to consider this problem better. In addition, to improve the rerouting efficiency, we use the A* and the multi-source multi-sink maze routing algorithms to perform partial rerouting operations jointly;
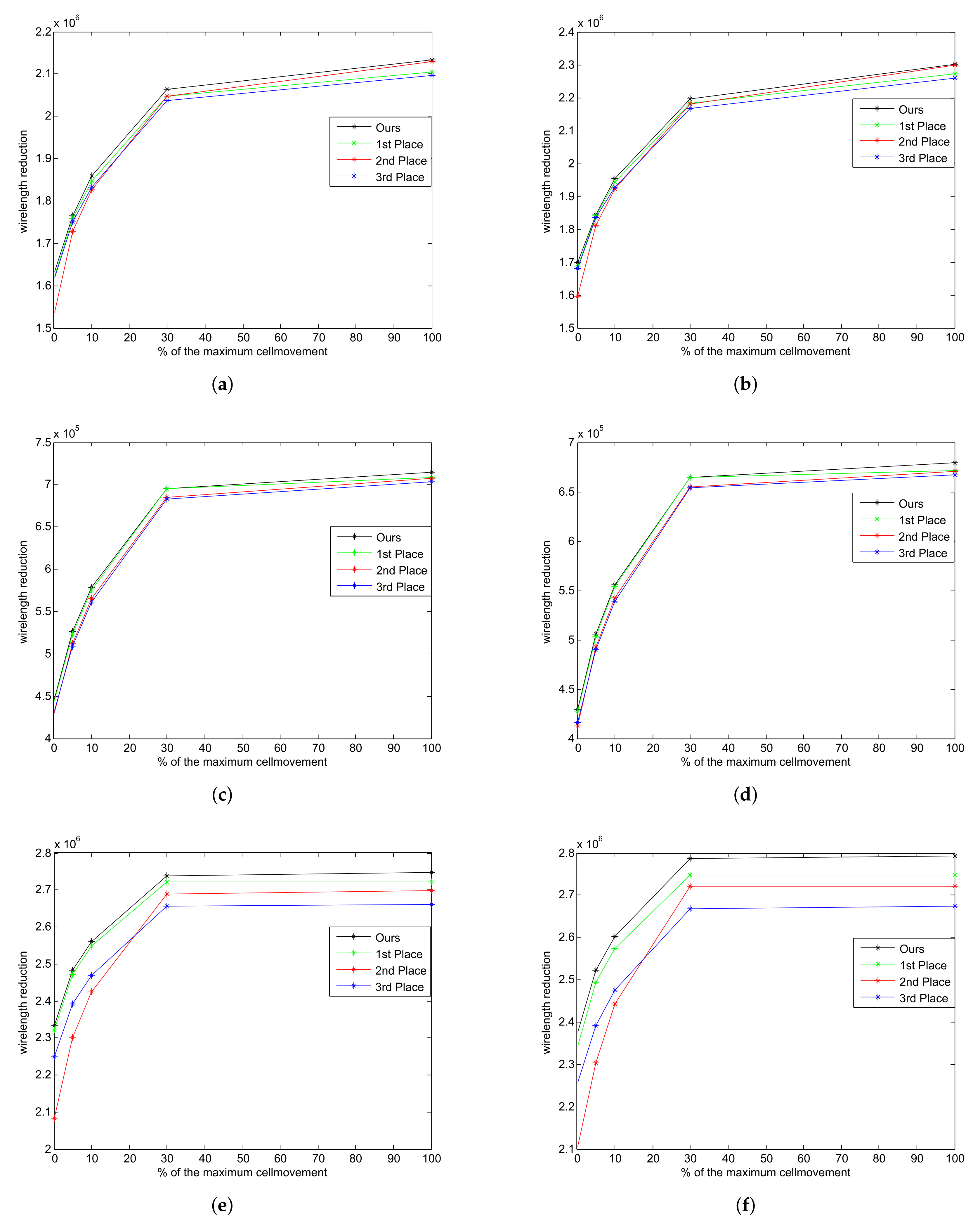
- Compared with the top 3 winners according to the 2020 ICCAD CAD contest benchmarks [21], experimental results show that our algorithm achieves the best routing length reduction for all cases with a shorter runtime. On average, our algorithm can improve 0.7%, 1.5%, and 1.7% for the first, second, and third place, respectively. In addition, we can still get the best results after relaxing the maximum cell movement constraint, which further illustrates the effectiveness of our algorithm.
2. Problem Description and Algorithm Flow
2.1. Problem Description
- No overflow gGrid constraint : Overflow is not allowed, which means the demand for a gGrid should not exceed its capacity;
- No open net constraint : The router should produce a routing solution with all pins of nets connected, i.e., having no open net;
- Maximum cell movement constraint : In order to maintain information of the given placement results and avoid generating completely altered placement results, the total number of moved cells during the cell movement should be constrained to 30% among all cells;
- Net-based minimum layer constraint : The net may have a minimum layer routing constraint . The pins whose z-coordinate are smaller than the minimum layer constraint need to be connected to the minimum layer through vias, and further, the -direction routing of this net will be only on or above the given minimum layer;
- Layer routing direction constraint : The routing direction is horizontal on the first layer , and it is different on any two adjacent layers. In other words, -direction routing must route on the odd/even layer, respectively.
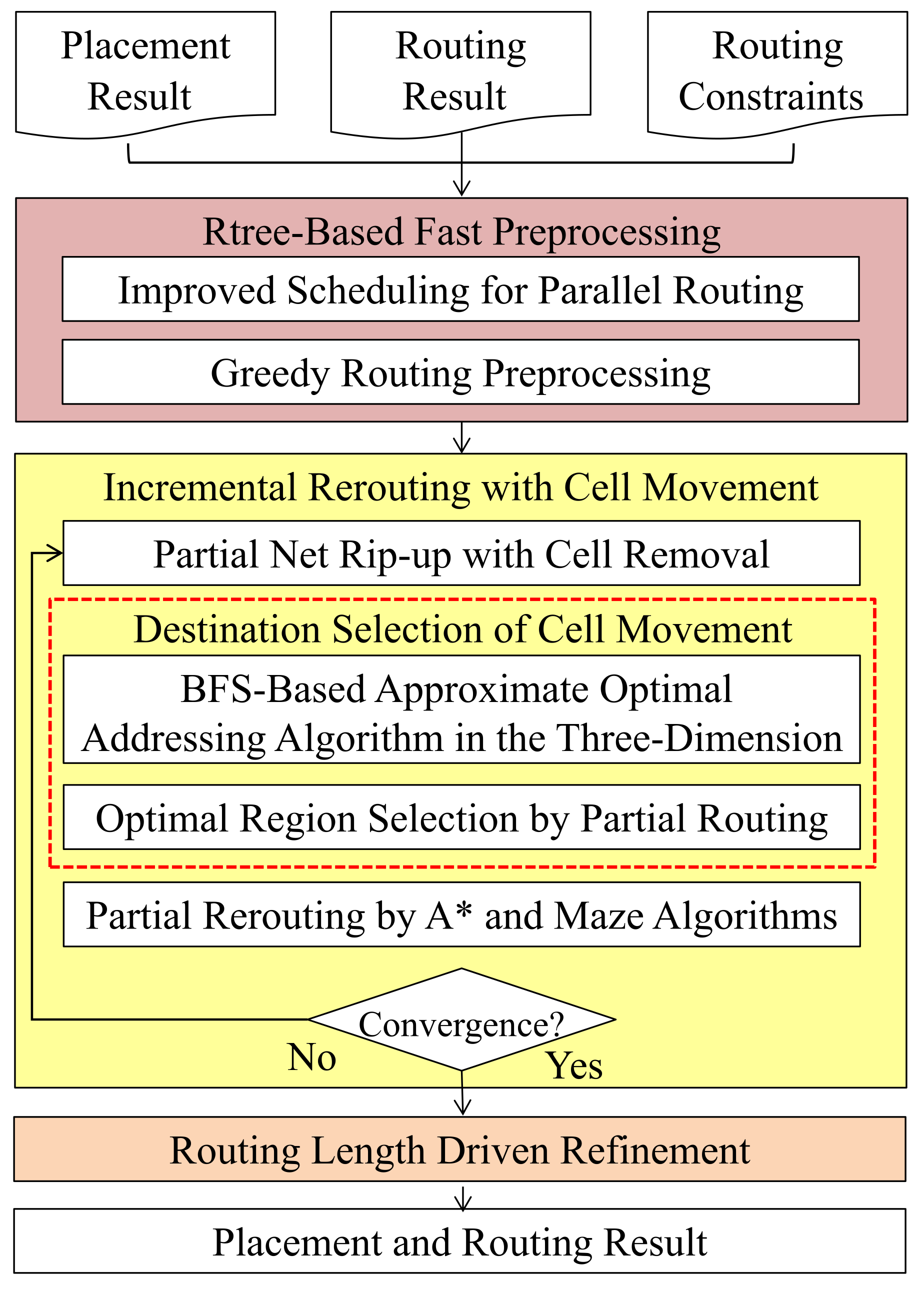
2.2. Our Algorithm Flow
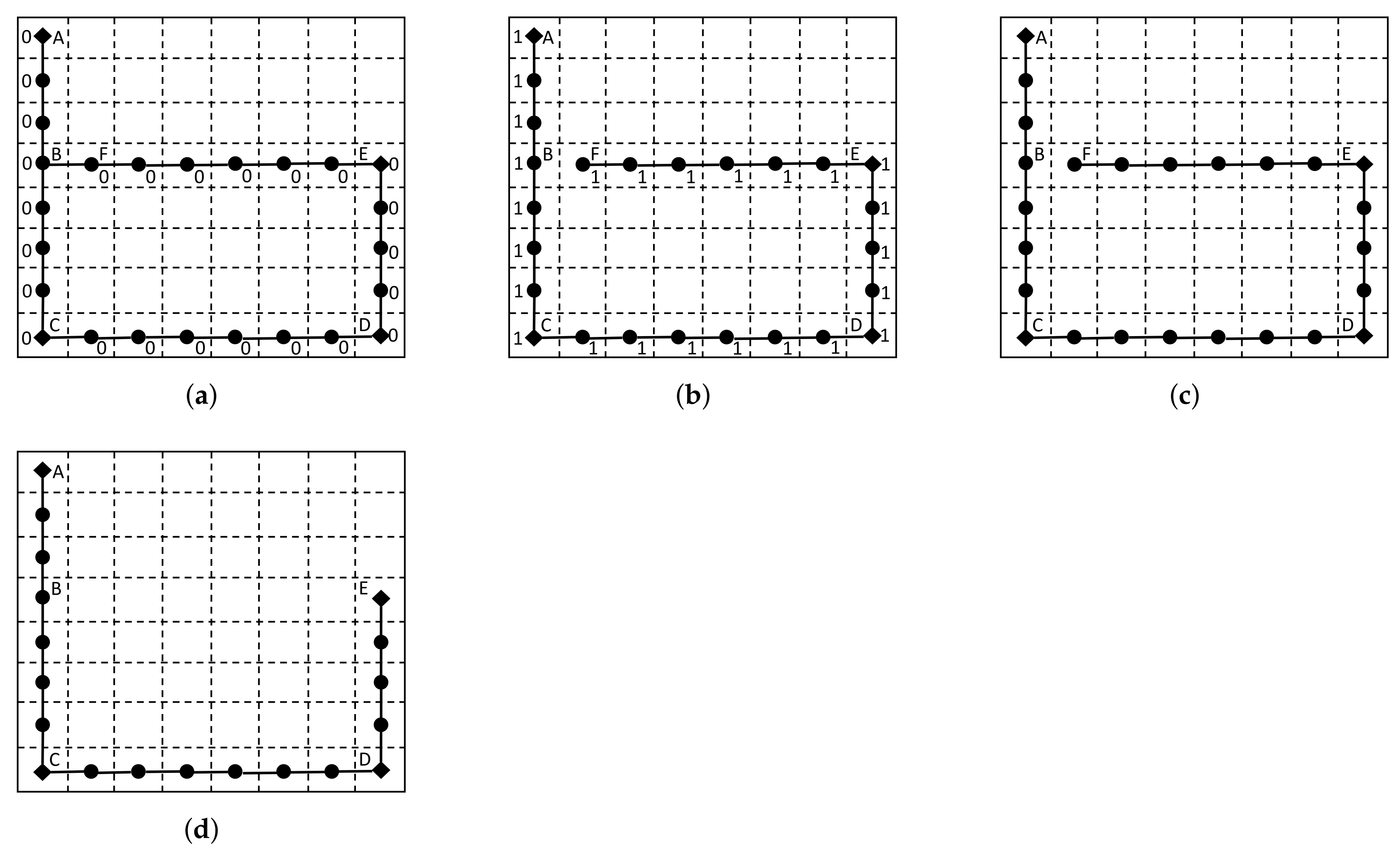
3. RTree-Based Fast Preprocessing
| Algorithm 1 Improved Scheduling for Parallel Routing. |
| Input: Nets; Output: BatchList;
|
| Algorithm 2 Greedy Routing Preprocessing. |
| Input: BatchList, Initial Global Routing; Output: Routing Result;
|
4. Incremental Rerouting with Cell Movement
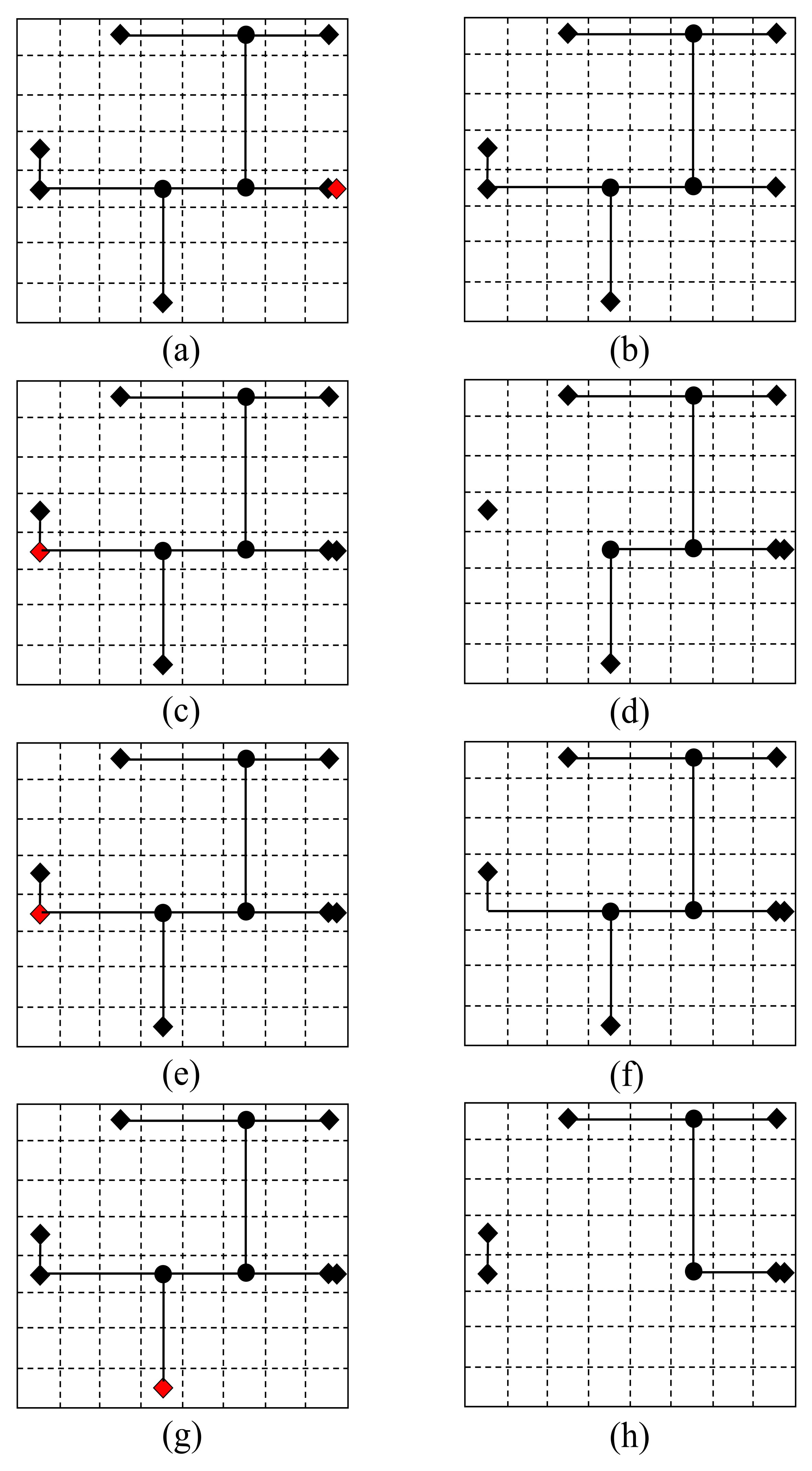
4.1. Partial Net Rip-Up with Cell Removal
4.2. Destination Selection of Cell Movement
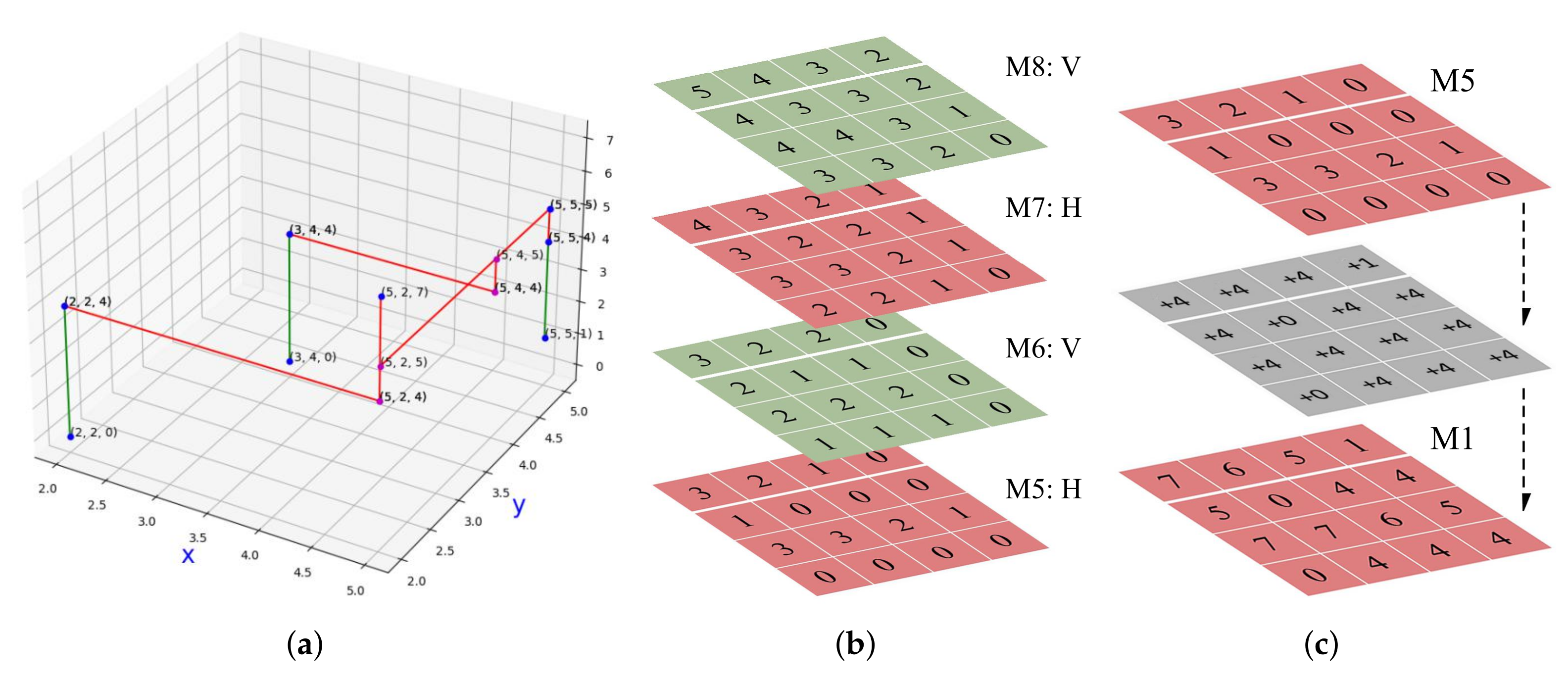
4.2.1. BFS-Based Approximate Optimal Addressing Algorithm in 3D
| Algorithm 3 The 3D BFS-based Approximate Optimal Addressing Algorithm. |
| Input: Removed cell i, the connected nets , rip-up routing length ; Output: Candidate destinations priority queue C;
|
4.2.2. Optimal Region Selection Using Partial Routing Solution
4.3. Partial Rerouting by A* and Maze Routing Algorithms
5. Routing Length Driven Refinement
| Algorithm 4 Routing Length Driven Refinement. |
| Input: BatchList, Global Routing Result; Output: Final Routing Result;
|
6. Experimental Results
6.1. Experimental Setup and Benchmarks
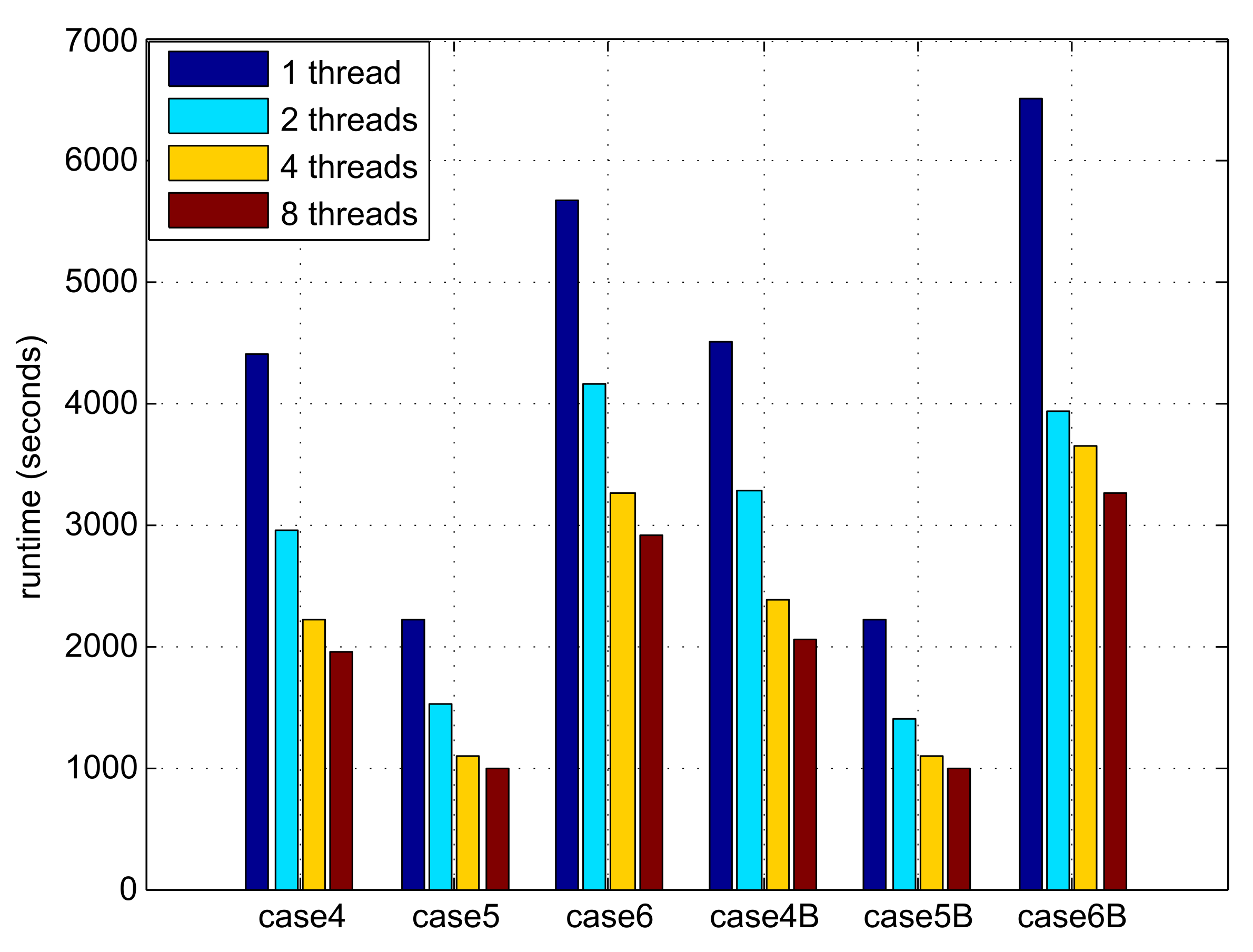
6.2. Parallel Technology
6.3. Comparison of Results with the Top Three Winners
6.4. Results with Relaxed Max Cell Movement Constraint
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alpert, C.J.; Mehta, D.P.; Sapatnekar, S.S. Handbook of Algorithm for Physical Design Automation; Auerbach Publications: New York, NY, USA, 2008. [Google Scholar]
- Kim, M.C.; Viswanathan, N.; Li, Z.; Alpert, C. ICCAD-2013 CAD contest in placement finishing and benchmark suite. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design, San Jose, CA, USA, 18–21 November 2013. [Google Scholar]
- Caldwell, A.E.; Kahng, A.B.; Markov, I.L. Optimal partitioners and end-case placers for standard-cell layout. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2000, 19, 1304–1313. [Google Scholar] [CrossRef]
- Chen, T.C.; Jiang, Z.W.; Hsu, T.C.; Chen, H.C.; Chang, Y.W. NTUplace3: An analytical placer for large-scale mixed-size designs with preplaced blocks and density constraints. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2008, 27, 1228–1240. [Google Scholar] [CrossRef] [Green Version]
- Pan, M.; Viswanathan, N.; Chu, C. An efficient and effective detailed placement algorithm. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design, San Jose, CA, USA, 6–10 November 2005; pp. 48–55. [Google Scholar]
- Chow, W.K.; Kuang, J.; He, X.; Cai, W.; Young, E.F. Cell Density-Driven Detailed Placement with Displacement Constraint. In Proceedings of the 2014 on International Symposium on Physical Design, Petaluma, CA, USA, 30 March–2 April 2014. [Google Scholar]
- Roy, J.A.; Markov, I.L. High-performance routing at the nanometer scale. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2008, 27, 1066–1077. [Google Scholar]
- Wu, T.H.; Davoodi, A.; Linderoth, J.T. Grip: Scalable 3d global routing using integer programming. In Proceedings of the 46th Annual Design Automation Conference, San Francisco, CA, USA, 26–31 July 2009. [Google Scholar]
- Liu, J.; Pui, C.W.; Wang, F.; Young, E.F.Y. Cugr: Detailed-routability-driven 3d global routing with probabilistic resource model. In Proceedings of the 2020 57th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 20–24 July 2020. [Google Scholar]
- Chu, C.; Wong, Y.C. Flute: Fast lookup table based rectilinear steiner minimal tree algorithm for vlsi design. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2007, 27, 70–83. [Google Scholar] [CrossRef]
- Liu, W.H.; Kao, W.C.; Li, Y.L.; Chao, K.Y. Nctu-gr 2.0: Multithreaded collision-aware global routing with bounded-length maze routing. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2013, 32, 709–722. [Google Scholar]
- Xu, Y.; Zhang, Y.; Chu, C. Fastroute 4.0: Global router with efficient via minimization. In Proceedings of the Asia and South Pacific Design Automation Conference (ASP-DAC), Yokohama, Japan, 19–22 January 2009. [Google Scholar]
- Chen, H.Y.; Hsu, C.H.; Chang, Y.W. High-performance global routing with fast overflow reduction. In Proceedings of the ACM/IEEE Design Automation Conference (DAC), Yokohama, Japan, 19–22 January 2009. [Google Scholar]
- Chang, Y.J.; Lee, Y.T.; Wang, T.C. Nthu-route 2.0: A fast and stable global router. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 10–13 November 2008. [Google Scholar]
- Pan, M.; Chu, C. IPR: An integrated placement and routing algorithm. In Proceedings of the ACM/IEEE Design Automation Conference (DAC), San Diego, CA, USA, 4–8 June 2007. [Google Scholar]
- Dai, K.R.; Lu, C.H.; Li, Y.L. GRPlacer: Improving routability and wire-length of global routing with circuit replacement. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 2–5 November 2009. [Google Scholar]
- Roy, J.A.; Viswanathan, N.; Nam, G.J.; Alpert, C.J.; Markov, I.L. CRISP: Congestion reduction by iterated spreading during placement. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 2–5 November 2009. [Google Scholar]
- Pan, M.; Chu, C. FastRoute: A Step to Integrate Global Routing into Placement. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 5–9 November 2006. [Google Scholar]
- He, X.; Chow, W.K.; Young, E.F. SRP: Simultaneous routing and placement for congestion refinement. In Proceedings of the ACM International Symposium on Physical design (ISPD), Stateline, NV, USA, 24–27 March 2013; pp. 108–113. [Google Scholar]
- Fontana, T.A.; Aghaeekiasaraee, E.; Netto, R.; Almeida, S.F.; Gandhi, U.; Tabrizi, A.F.; Westwick, D.; Behjat, L.; Güntzel, J.L. ILP-Based Global Routing Optimization with Cell Movements. In Proceedings of the IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Tampa, FL, USA, 7–9 July 2021. [Google Scholar]
- Hu, K.S.; Yang, M.J.; Yu, T.C.; Chen, G.C. ICCAD-2020 CAD contest in Routing with Cell Movement. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design, San Diego, CA, USA, 2–5 November 2020. [Google Scholar]
- Zou, P.; Lin, Z.; Ma, C.; Yu, J.; Chen, J. Late Breaking Results: Incremental 3D Global Routing Considering Cell Movement. In Proceedings of the 2021 58th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 5–9 December 2021; pp. 1366–1367. [Google Scholar]
- Guttman, A. R-trees: A dynamic index structure for spatial searching. In Proceedings of the 1984 ACM SIGMOD international Conference on Management of Data, Boston, MA, USA, 18–21 June 1984; pp. 47–57. [Google Scholar]
- Chen, G.; Pui, C.W.; Li, H.; Young, E.F.Y. CU: Detailed Routing by Sparse Grid Graph and Minimum-Area-Captured Path Search. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2020, 39, 1902–1915. [Google Scholar] [CrossRef]
- Pan, M.; Chu, C. FastRoute 2.0: A High-quality and Efficient Global Router. In Proceedings of the 2007 Asia and South Pacific Design Automation Conference, Yokohama, Japan, 23–26 January 2007. [Google Scholar]
- Lee, T.H.; Wang, T.C. Congestion-Constrained Layer Assignment for Via Minimization in Global Routing. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2008, 27, 1643–1656. [Google Scholar]
- Goto, S. An Efficient Algorithm for the Two-Dimensional Placement Problem in Electrical Circuit Layout. IEEE Trans. Circuits Syst. 1981, CAS-28, 12–18. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, SSC-4, 100–107. [Google Scholar] [CrossRef]
- Clow, G.W. A global routing algorithm for general cells. In Proceedings of the ACM/IEEE 21st Design Automation Conference, Albuquerque, NM, USA, 25–27 June 1984. [Google Scholar]
- 2020 CAD Contest at ICCAD on Routing with Cell Movement. Available online: http://iccad-contest.org/2020/problems.html (accessed on 1 November 2021).


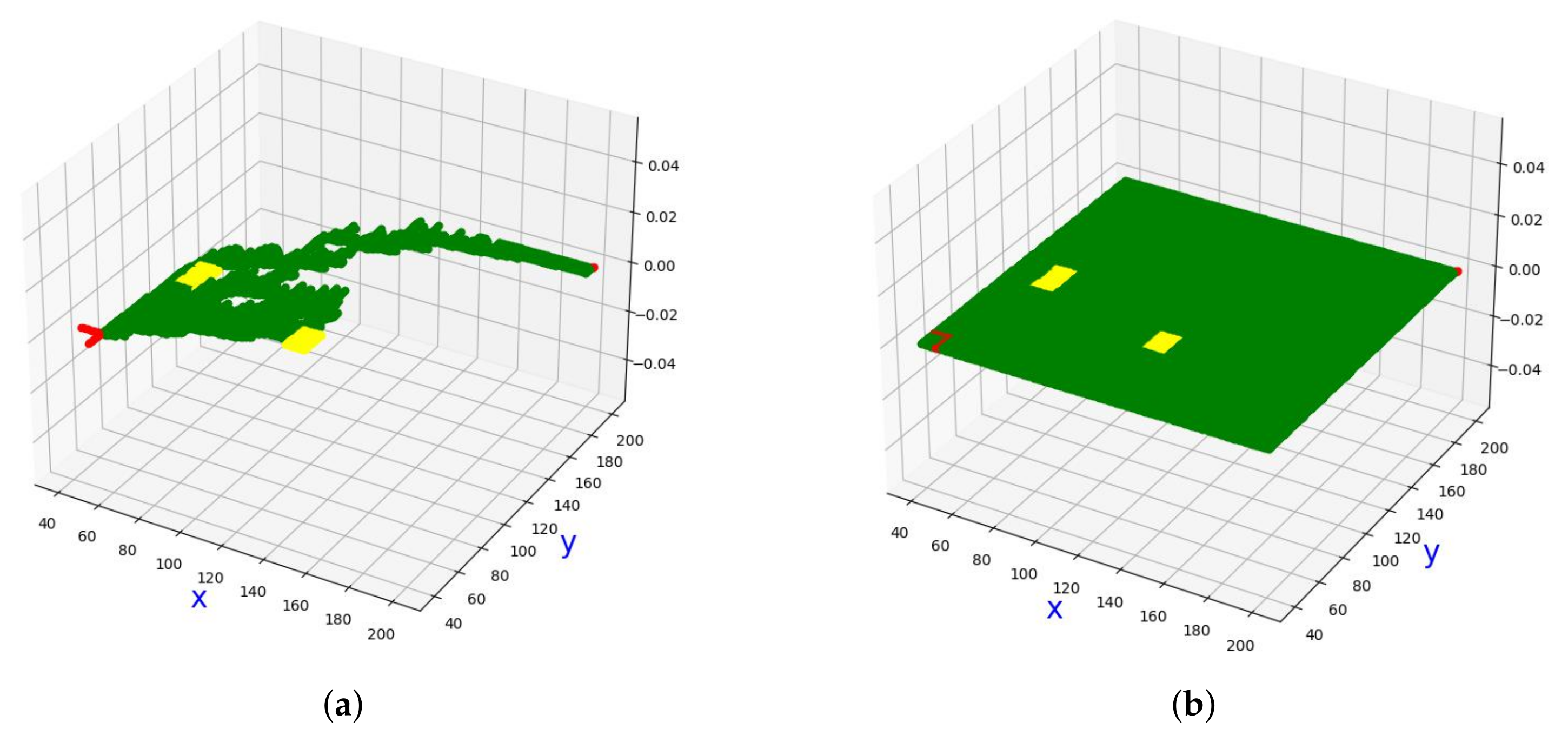

| Case | #gGrids | #Layers | #CellInsts | #Nets | Initial #Routes | Initial Length | Max Move |
|---|---|---|---|---|---|---|---|
| case1 | 5 × 5 | 3 | 8 | 6 | 42 | 64 | 2 |
| case2 | 4 × 4 | 3 | 6 | 6 | 20 | 30 | 3 |
| case3 | 27 × 33 | 7 | 2735 | 2644 | 26,046 | 32,600 | 820 |
| case4 | 277 × 277 | 12 | 204,206 | 179,996 | 3,530,382 | 4,680,681 | 61,261 |
| case5 | 104 × 103 | 16 | 96,682 | 92,546 | 1,404,555 | 1,763,627 | 29,004 |
| case6 | 237 × 236 | 16 | 352,269 | 332,080 | 4,575,644 | 7,188,481 | 105,680 |
| case3B | 29 × 29 | 7 | 2604 | 2563 | 24,829 | 29,748 | 781 |
| case4B | 277 × 277 | 12 | 207,347 | 183,137 | 3,661,438 | 4,886,698 | 62,204 |
| case5B | 104 × 103 | 16 | 96,689 | 92,559 | 1,368,552 | 1,721,530 | 29,006 |
| case6B | 237 × 236 | 16 | 352,234 | 332,045 | 4,685,372 | 7,340,802 | 105,670 |
| Case | No Parallel | Batch Scheduling [24] | Improved Batch Scheduling | |||||
|---|---|---|---|---|---|---|---|---|
| RL-Red. | R-Times | B-Times | RL-Red. | R-Times | B-Times | RL-Red. | R-Times | |
| case4 | 1,614,410 | 85 | 11.81 | 1,614,207 | 31 | 0.19 | 1,614,468 | 23 |
| case5 | 442,207 | 25 | 7.94 | 441,314 | 18 | 0.13 | 441,678 | 15 |
| case6 | 2,311,638 | 324 | 62.24 | 2,301,046 | 161 | 0.61 | 2,307,982 | 106 |
| case4B | 1,678,151 | 79 | 13.13 | 1,677,705 | 39 | 0.23 | 1,678,086 | 27 |
| case5B | 424,909 | 24 | 7.73 | 424,220 | 20 | 0.13 | 424,626 | 16 |
| case6B | 2,348,845 | 352 | 62.87 | 2,325,592 | 187 | 0.66 | 2,339,623 | 121 |
| Normalized | 1.001 | 2.629 | 73.044 | 0.998 | 1.391 | 1.000 | 1.000 | 1.000 |
| Case | First Place | Second Place | Third Place | Ours | ||||
|---|---|---|---|---|---|---|---|---|
| RL-Red. | Times | RL-Red. | Times | RL-Red. | Times | RL-Red. | Times | |
| case3 | 11,425 | 34 | 11,428 | 4 | 11,557 | 111 | 11,574 | 24 |
| case4 | 2,046,811 | 2221 | 2,048,105 | 804 | 2,037,598 | 3441 | 2,064,165 | 1952 |
| case5 | 695,219 | 903 | 685,173 | 183 | 682,963 | 1213 | 695,344 | 999 |
| case6 | 2,721,274 | 3171 | 2,687,926 | 2217 | 2,656,320 | 3511 | 2,737,732 | 2918 |
| case3B | 11,237 | 31 | 11,073 | 4 | 11,289 | 206 | 11,309 | 18 |
| case4B | 2,182,574 | 2299 | 2,180,172 | 786 | 2,167,411 | 3371 | 2,196,644 | 2050 |
| case5B | 664,347 | 886 | 654,797 | 237 | 654,183 | 1226 | 664,440 | 989 |
| case6B | 2,748,097 | 3406 | 2,722,222 | 2801 | 2,668,052 | 3514 | 2,787,052 | 3265 |
| Normalized | 0.993 | 1.160 | 0.985 | 0.402 | 0.983 | 2.986 | 1.000 | 1.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Huang, H.; Shi, R.; Li, X.; Zhang, X.; Chen, W.; Wang, J.; Zhu, Z. Detailed Placement and Global Routing Co-Optimization with Complex Constraints. Electronics 2022, 11, 51. https://doi.org/10.3390/electronics11010051
Huang Z, Huang H, Shi R, Li X, Zhang X, Chen W, Wang J, Zhu Z. Detailed Placement and Global Routing Co-Optimization with Complex Constraints. Electronics. 2022; 11(1):51. https://doi.org/10.3390/electronics11010051
Chicago/Turabian StyleHuang, Zhipeng, Haishan Huang, Runming Shi, Xu Li, Xuan Zhang, Weijie Chen, Jiaxiang Wang, and Ziran Zhu. 2022. "Detailed Placement and Global Routing Co-Optimization with Complex Constraints" Electronics 11, no. 1: 51. https://doi.org/10.3390/electronics11010051
APA StyleHuang, Z., Huang, H., Shi, R., Li, X., Zhang, X., Chen, W., Wang, J., & Zhu, Z. (2022). Detailed Placement and Global Routing Co-Optimization with Complex Constraints. Electronics, 11(1), 51. https://doi.org/10.3390/electronics11010051





