Optimization of Multi-Level Operation in RRAM Arrays for In-Memory Computing
Abstract
1. Introduction
2. Experimental Methodology
3. Modeling Methodology
4. Experimental and Modeling Results
5. VMM Architecture and Operational Results
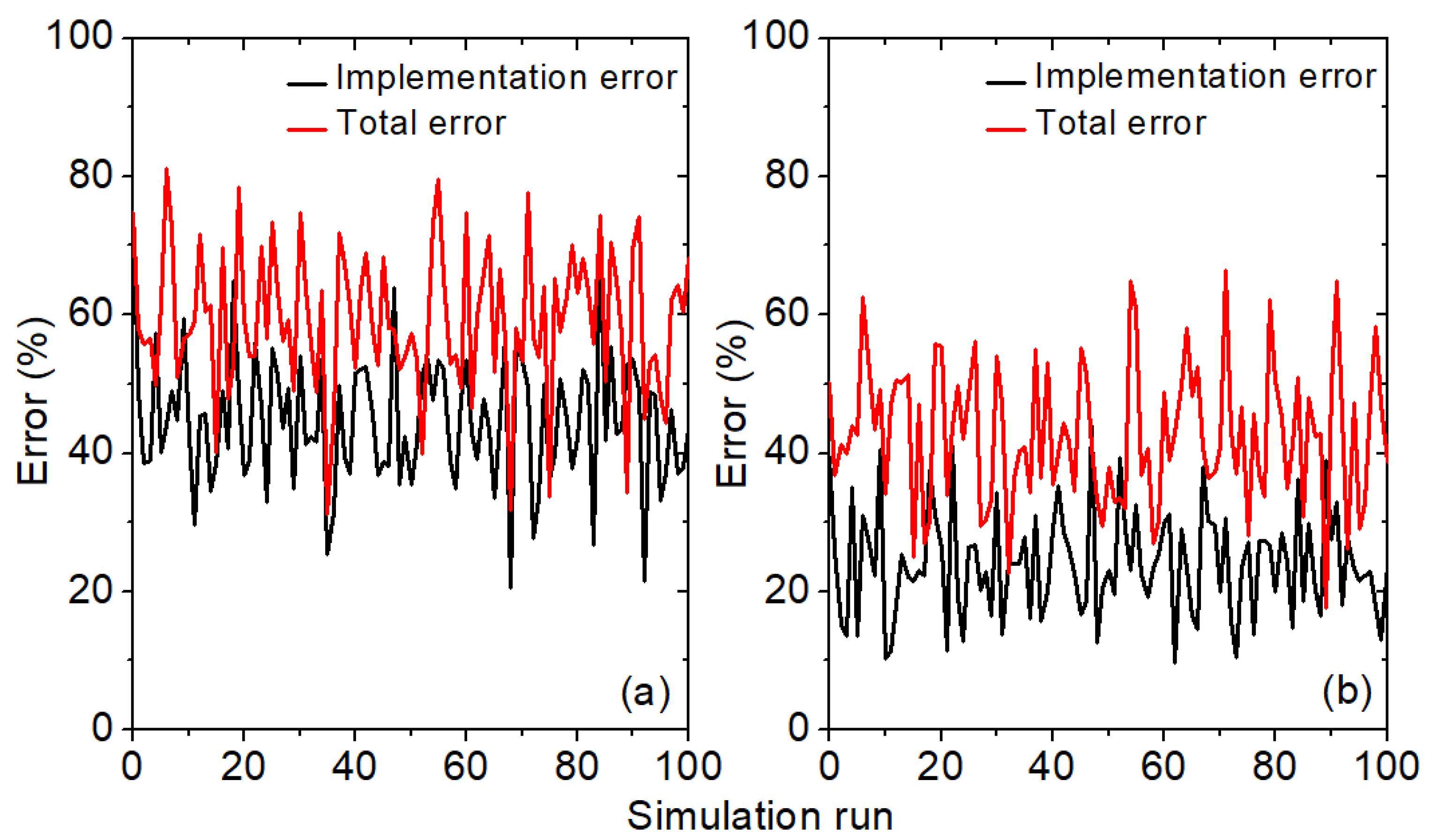
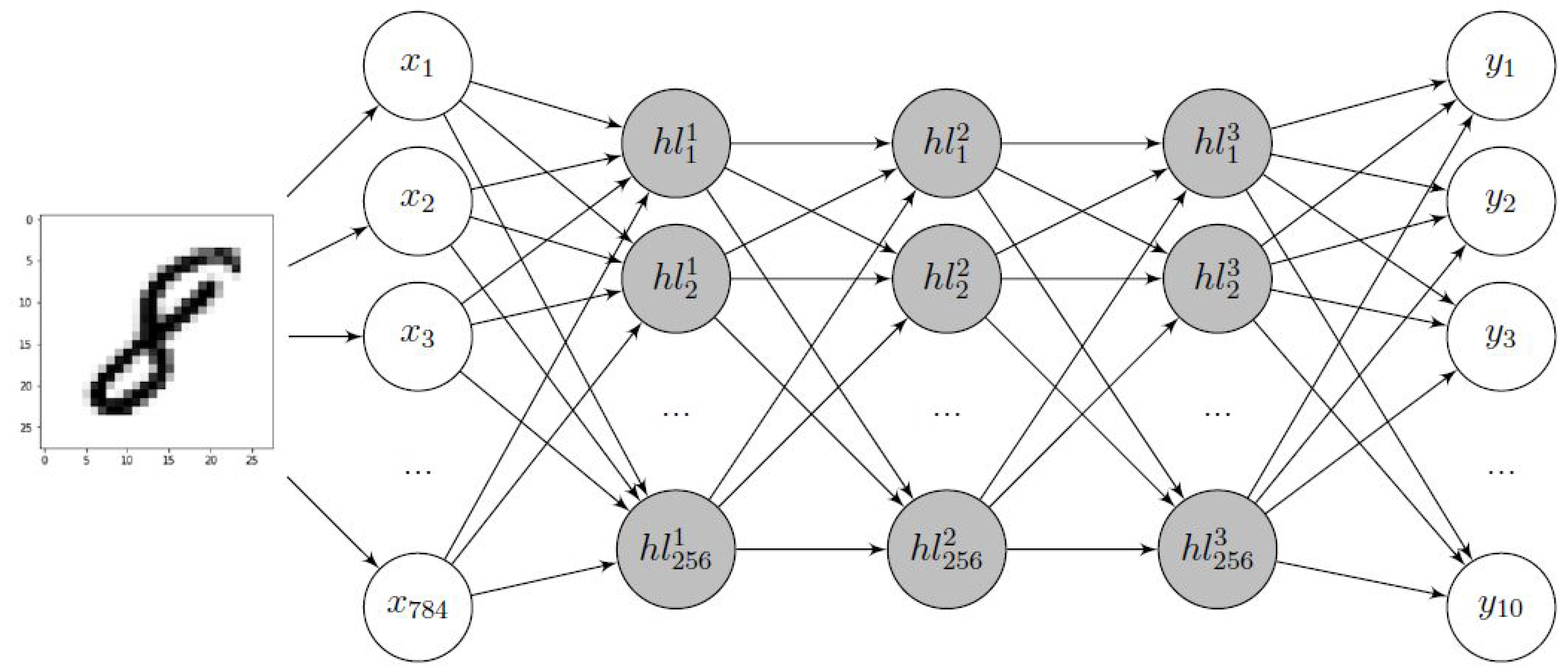
6. DNN Implementation
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| RRAM | Resistive Random Access Memory |
| M-ISPVA | Multi-Level Incremental Step Pulse with Verify Algorithm |
| VMM | Vector-Matrix-Multiplication |
| AI | Artificial Intelligence |
| IoT | Internet of Things |
| DNN | Deep Neural Network |
| SRAM | Static Random Access Memory |
| I | Target Read-out Current |
| V | Gate Voltage |
| DTD | Device-to-Device |
| CTC | Cycle-to-Cycle |
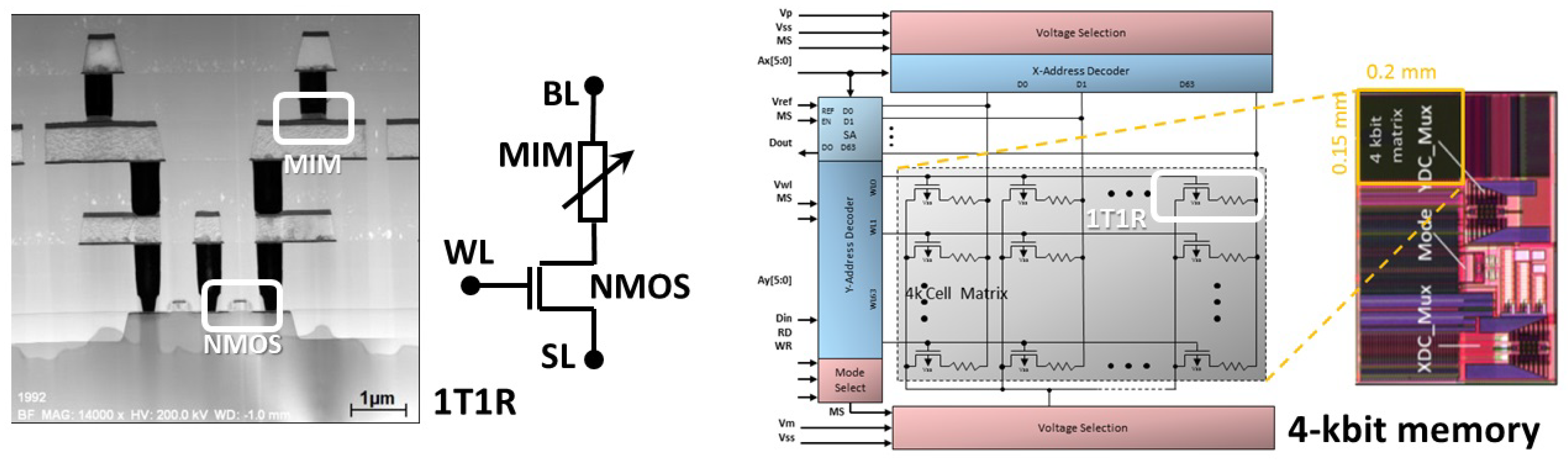
| 1T1R | 1-Transistor-1-Resistor |
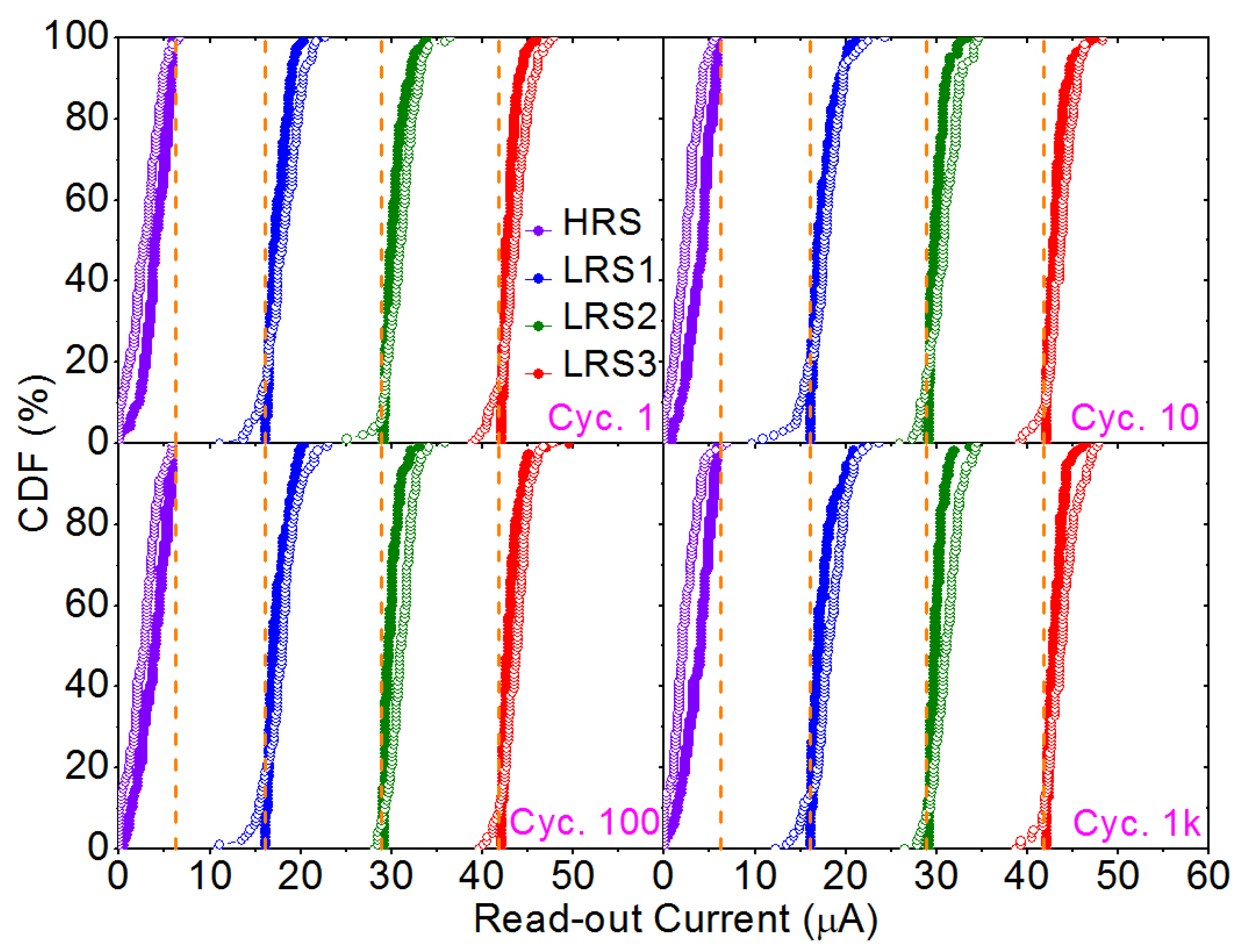
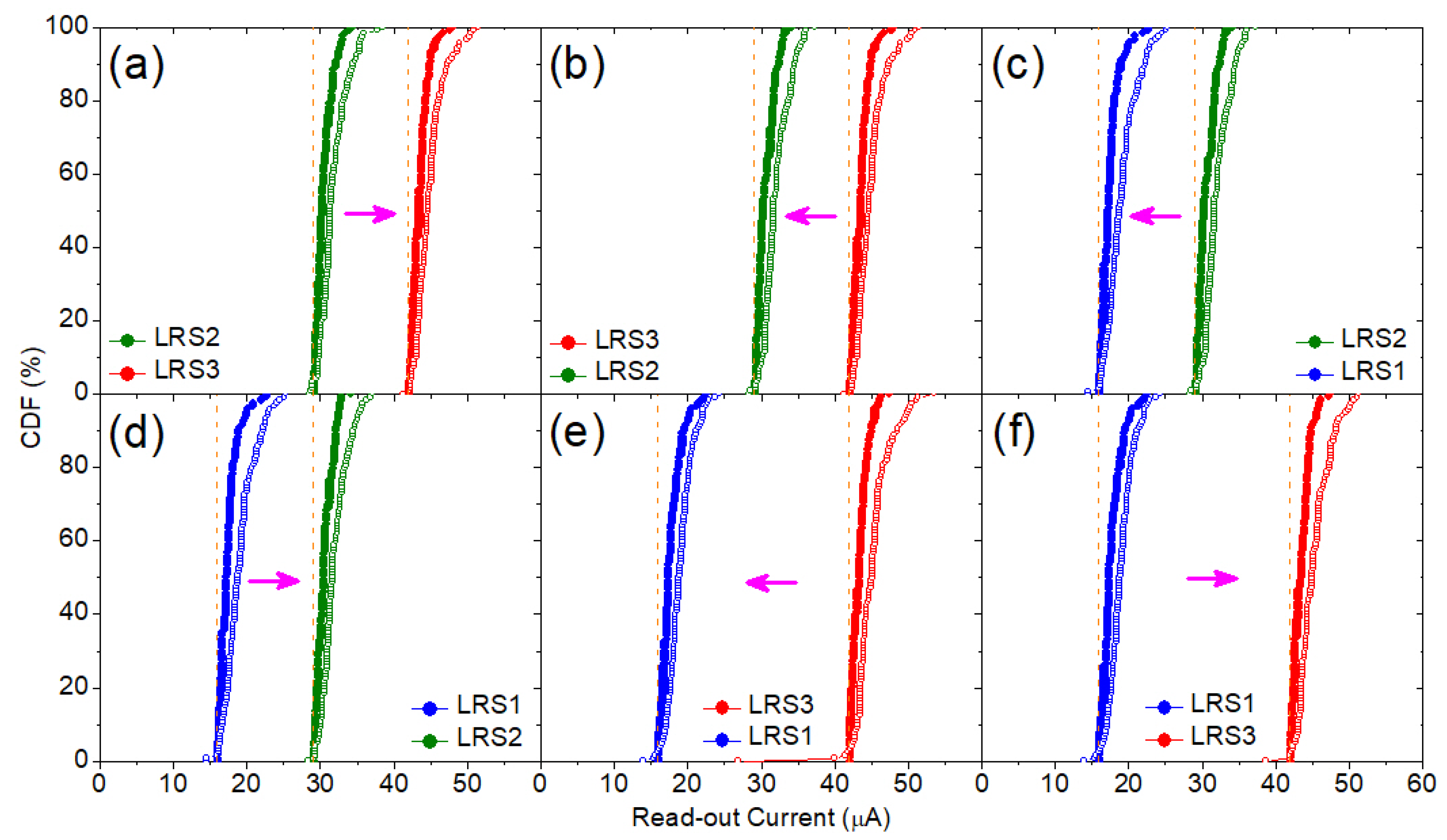
| LRS | Low Resistive State |
| WL | Word Line |
| MIM | Metal-Insulator-Metal |
| ALD | Atomic Layer Deposition |
| TEM | Transmission Electron Microscopy |
| BL | Bit Line |
| SL | Source Line |
| HRS | High Resistive State |
| CF | Conductive Filament |
| VAS | Voltage Amplitude Sweep |
| PW | Pulse Width |
| CDF | Cumulative Distribution Function |
| MLP | Multi-Layer Perceptron |
References
- Campbell, M.; Hoane, A.; Hsu, F.H. Deep Blue. Artif. Intell. 2002, 134, 57–83. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Wang, F.Y.; Zhang, J.J.; Zheng, X.; Wang, X.; Yuan, Y.; Dai, X.; Zhang, J.; Yang, L. Where does AlphaGo go: From church-turing thesis to AlphaGo thesis and beyond. IEEE/CAA J. Autom. Sin. 2016, 3, 113–120. [Google Scholar] [CrossRef]
- Burr, G.W.; Narayanan, P.; Shelby, R.M.; Sidler, S.; Boybat, I.; Di Nolfo, C.; Leblebici, Y. Large-scale neural networks implemented with non-volatile memory as the synaptic weight element: Comparative performance analysis (accuracy, speed, and power). In Proceedings of the 2015 IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 7–9 December 2015; pp. 4.4.1–4.4.4. [Google Scholar] [CrossRef]
- Mahapatra, N.R.; Venkatrao, B. The processor-memory bottleneck. XRDS: Crossroads ACM Mag. Stud. 1999, 5, 2. [Google Scholar] [CrossRef]
- Akopyan, F.; Sawada, J.; Cassidy, A.; Alvarez-Icaza, R.; Arthur, J.; Merolla, P.; Imam, N.; Nakamura, Y.; Datta, P.; Nam, G.J.; et al. TrueNorth: Design and Tool Flow of a 65 mW 1 Million Neuron Programmable Neurosynaptic Chip. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2015, 34, 1537–1557. [Google Scholar] [CrossRef]
- Davies, M.; Srinivasa, N.; Lin, T.H.; Chinya, G.; Cao, Y.; Choday, S.H.; Dimou, G.; Joshi, P.; Imam, N.; Jain, S.; et al. Loihi: A Neuromorphic Manycore Processor with On-Chip Learning. IEEE Micro 2018, 38, 82–99. [Google Scholar] [CrossRef]
- Di Ventra, M.; Pershin, Y.V. The parallel approach. Nat. Phys. 2013, 9, 200–202. [Google Scholar] [CrossRef]
- Ambrogio, S.; Narayanan, P.; Tsai, H.; Shelby, R.M.; Boybat, I.; Di Nolfo, C.; Sidler, S.; Giordano, M.; Bodini, M.; Farinha, N.C.P.; et al. Equivalent-accuracy accelerated neural-network training using analogue memory. Nature 2018, 558, 60–67. [Google Scholar] [CrossRef]
- Pei, J.; Deng, L.; Song, S.; Zhao, M.; Zhang, Y.; Wu, S.; Wang, G.; Zou, Z.; Wu, Z.; He, W.; et al. Towards artificial general intelligence with hybrid Tianjic chip architecture. Nature 2019, 572, 106–111. [Google Scholar] [CrossRef]
- Kim, K.H.; Gaba, S.; Wheeler, D.; Cruz-Albrecht, J.M.; Hussain, T.; Srinivasa, N.; Lu, W. A functional hybrid memristor crossbar-array/CMOS system for data storage and neuromorphic applications. Nano Lett. 2012, 12, 389–395. [Google Scholar] [CrossRef]
- Chu, M.; Kim, B.; Park, S.; Hwang, H.; Jeon, M.; Lee, B.H.; Lee, B.G. Neuromorphic Hardware System for Visual Pattern Recognition With Memristor Array and CMOS Neuron. IEEE Trans. Ind. Electron. 2015, 62, 2410–2419. [Google Scholar] [CrossRef]
- Zahari, F.; Hansen, M.; Mussenbrock, T.; Ziegler, M.; Kohlstedt, H. Pattern recognition with TiOx-based memristive devices. AIMS Mater. Sci. 2015, 2, 203–216. [Google Scholar] [CrossRef]
- Soudry, D.; Di Castro, D.; Gal, A.; Kolodny, A.; Kvatinsky, S. Memristor-based multilayer neural networks with online gradient descent training. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2408–2421. [Google Scholar] [CrossRef]
- Yao, P.; Wu, H.; Gao, B.; Tang, J.; Zhang, Q.; Zhang, W.; Yang, J.J.; Qian, H. Fully hardware-implemented memristor convolutional neural network. Nature 2020, 577, 641–646. [Google Scholar] [CrossRef]
- Ielmini, D.; Wong, H.S.P. In-memory computing with resistive switching devices. Nat. Electron. 2018, 1, 333–343. [Google Scholar] [CrossRef]
- Wong, H.S.P.; Lee, H.Y.; Yu, S.; Chen, Y.S.; Wu, Y.; Chen, P.S.; Lee, B.; Chen, F.T.; Tsai, M.J. Metal–Oxide RRAM. Proc. IEEE 2012, 100, 1951–1970. [Google Scholar] [CrossRef]
- Ielmini, D. Resistive switching memories based on metal oxides: Mechanisms, reliability and scaling. Semicond. Sci. Technol. 2016, 31, 063002. [Google Scholar] [CrossRef]
- Bai, Y.; Wu, H.; Wu, R.; Zhang, Y.; Deng, N.; Yu, Z.; Qian, H. Study of multi-level characteristics for 3D vertical resistive switching memory. Sci. Rep. 2014, 4, 5780. [Google Scholar] [CrossRef] [PubMed]
- Prakash, A.; Park, J.; Song, J.; Woo, J.; Cha, E.J.; Hwang, H. Demonstration of Low Power 3-bit Multilevel Cell Characteristics in a TaOx-Based RRAM by Stack Engineering. IEEE Electron Device Lett. 2015, 36, 32–34. [Google Scholar] [CrossRef]
- Stathopoulos, S.; Khiat, A.; Trapatseli, M.; Cortese, S.; Serb, A.; Valov, I.; Prodromakis, T. Multibit memory operation of metal-oxide bi-layer memristors. Sci. Rep. 2017, 7, 17532. [Google Scholar] [CrossRef]
- Liu, J.; Yang, H.; Ma, Z.; Chen, K.; Zhang, X.; Huang, X.; Oda, S. Characteristics of multilevel storage and switching dynamics in resistive switching cell of Al2O3/HfO2/Al2O3 sandwich structure. Semicond. Sci. Technol. 2018, 51, 025102. [Google Scholar] [CrossRef]
- Woo, J.; Moon, K.; Song, J.; Kwak, M.; Park, J.; Hwang, H. Optimized Programming Scheme Enabling Linear Potentiation in Filamentary HfO2 RRAM Synapse for Neuromorphic Systems. IEEE Trans. Electron Devices 2016, 63, 5064–5067. [Google Scholar] [CrossRef]
- Chen, J.; Wu, H.; Gao, B.; Tang, J.; Hu, X.S.; Qian, H. A Parallel Multibit Programing Scheme With High Precision for RRAM-Based Neuromorphic Systems. IEEE Trans. Electron Devices 2020, 67, 2213–2217. [Google Scholar] [CrossRef]
- Luo, Y.; Han, X.; Ye, Z.; Barnaby, H.; Seo, J.S.; Yu, S. Array-Level Programming of 3-Bit per Cell Resistive Memory and Its Application for Deep Neural Network Inference. IEEE Trans. Electron Devices 2020, 67, 4621–4625. [Google Scholar] [CrossRef]
- Perez, E.; Zambelli, C.; Mahadevaiah, M.K.; Olivo, P.; Wenger, C. Toward Reliable Multi-Level Operation in RRAM Arrays: Improving Post-Algorithm Stability and Assessing Endurance/Data Retention. IEEE J. Electron Devices Soc. 2019, 7, 740–747. [Google Scholar] [CrossRef]
- Milo, V.; Zambelli, C.; Olivo, P.; Perez, E.; Ossorio, O.G.; Wenger, C.; Ielmini, D. Low-energy inference machine with multilevel HfO2 RRAM arrays. In Proceedings of the ESSDERC 2019—49th European Solid-State Device Research Conference (ESSDERC), Cracow, Poland, 23–26 September 2019; pp. 174–177. [Google Scholar] [CrossRef]
- Milo, V.; Zambelli, C.; Olivo, P.; Pérez, E.; Mahadevaiah, K.M.; Ossorio, G.O.; Wenger, C.; Ielmini, D. Multilevel HfO2-based RRAM devices for low-power neuromorphic networks. APL Mater. 2019, 7, 081120. [Google Scholar] [CrossRef]
- Jiang, H.; Han, L.; Lin, P.; Wang, Z.; Jang, M.H.; Wu, Q.; Barnell, M.; Yang, J.J.; Xin, H.L.; Xia, Q. Sub-10 nm Ta Channel Responsible for Superior Performance of a HfO2 Memristor. Sci. Rep. 2016, 6, 28525. [Google Scholar] [CrossRef]
- Zhao, M.; Wu, H.; Gao, B.; Zhang, Q.; Wu, W.; Wang, S.; Xi, Y.; Wu, D.; Deng, N.; Yu, S.; et al. Investigation of Statistical Retention of Filamentary Analog RRAM for Neuromorphic Computing. In Proceedings of the IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 2–6 December 2017; pp. 39.4.1–39.4.4. [Google Scholar] [CrossRef]
- Shim, W.; Luo, Y.; Seo, J.S.; Yu, S. Impact of Read Disturb on Multilevel RRAM based Inference Engine: Experiments and Model Prediction. In Proceedings of the 2020 IEEE International Reliability Physics Symposium (IRPS), Dallas, TX, USA, 28 April–30 May 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Grossi, A.; Zambelli, C.; Olivo, P.; Miranda, E.; Stikanov, V.; Walczyk, C.; Wenger, C. Electrical characterization and modeling of pulse-based forming techniques in RRAM arrays. Solid-State Electron. 2016, 115, 17–25. [Google Scholar] [CrossRef]
- Pérez, E.; Mahadevaiah, M.K.; Zambelli, C.; Olivo, P.; Wenger, C. Characterization of the interface-driven 1st Reset operation in HfO2-based 1T1R RRAM devices. Solid-State Electron. 2019, 159, 51–56. [Google Scholar] [CrossRef]
- Perez-Avila, A.J.; Gonzalez-Cordero, G.; Perez, E.; Quesada, E.P.B.; Kalishettyhalli Mahadevaiah, M.; Wenger, C.; Roldan, J.B.; Jimenez-Molinos, F. Behavioral modeling of multilevel HfO2-based memristors for neuromorphic circuit simulation. In Proceedings of the 2020 XXXV Conference on Design of Circuits and Integrated Systems (DCIS), Segovia, Spain, 18–20 November 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Miranda, E.A.; Walczyk, C.; Wenger, C.; Schroeder, T. Model for the Resistive Switching Effect in HfO2 MIM Structures Based on the Transmission Properties of Narrow Constrictions. IEEE Electron Device Lett. 2010, 31, 609–611. [Google Scholar] [CrossRef]
- Nayak, P.; Zhang, D.; Chai, S. Bit Efficient Quantization for Deep Neural Networks. arXiv 2019, arXiv:1910.04877. [Google Scholar]
- Fantini, A.; Goux, L.; Degraeve, R.; Wouters, D.J.; Raghavan, N.; Kar, G.; Belmonte, A.; Chen, Y.Y.; Govoreanu, B.; Jurczak, M. Intrinsic switching variability in HfO2 RRAM. In Proceedings of the 2013 5th IEEE International Memory Workshop, Monterey, CA, USA, 26–29 May 2013; pp. 30–33. [Google Scholar] [CrossRef]
- Grossi, A.; Nowak, E.; Zambelli, C.; Pellissier, C.; Bernasconi, S.; Cibrario, G.; El Hajjam, K.; Crochemore, R.; Nodin, J.F.; Olivo, P.; et al. Fundamental variability limits of filament-based RRAM. In Proceedings of the 2016 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2016; pp. 4.7.1–4.7.4. [Google Scholar] [CrossRef]
- LeCun, Y.; Cortes, C.; Burges, C.J. The MNIST Database of Handwritten Digits. 1999. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 5 April 2021).
- Popescu, M.C.; Balas, V.E.; Perescu-Popescu, L.; Mastorakis, N. Multilayer perceptron and neural networks. WSEAS Trans. Circuits Syst. 2009, 8, 579–588. [Google Scholar]
- Brodersen, K.H.; Ong, C.S.; Stephan, K.E.; Buhmann, J.M. The Balanced Accuracy and Its Posterior Distribution. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 3121–3124. [Google Scholar] [CrossRef]
- Covi, E.; Brivio, S.; Serb, A.; Prodromakis, T.; Fanciulli, M.; Spiga, S. Analog Memristive Synapse in Spiking Networks Implementing Unsupervised Learning. Front. Neurosci. 2016, 10, 482. [Google Scholar] [CrossRef] [PubMed]



| Non-Optimized | Optimized | |||||||
|---|---|---|---|---|---|---|---|---|
| Operation | (μA) | (V) | VAS (V) | PW (μs) | (μA) | (V) | VAS (V) | PW (μs) |
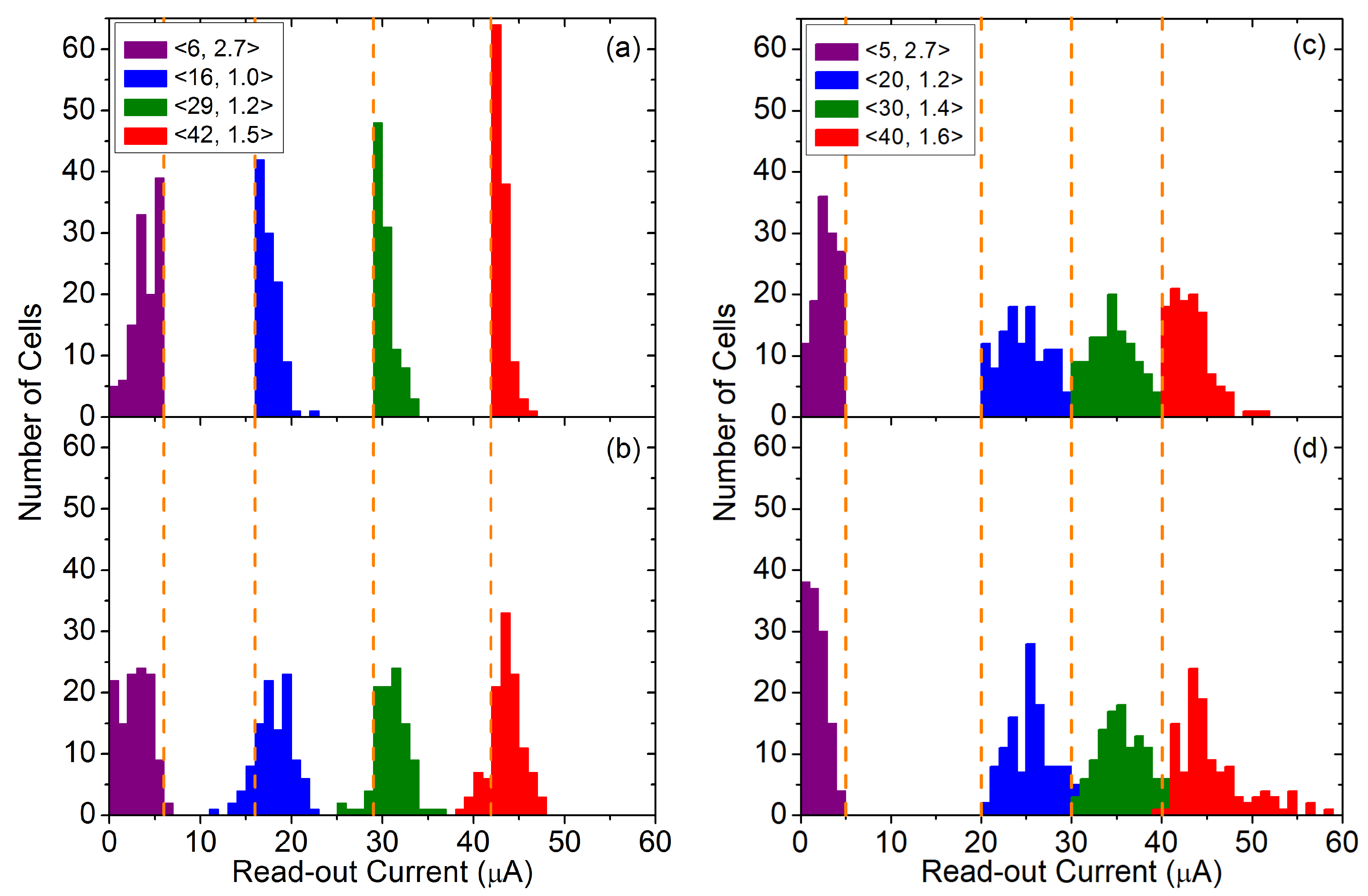
| Forming | 42 | 1.5 | 2.5–5.0 (0.01) | 10 | 42 | 1.5 | 2.5–5.0 (0.01) | 10 |
| Reset | 6 | 2.7 | 0.5–2.5 (0.1) | 1 | 6 | 2.7 | 0.5–2.5 (0.1) | 1 |
| Set | 20, 30, 40 | 1.2, 1.4, 1.6 | 0.5–2.5 (0.1) | 1 | 16, 29, 42 | 1.0, 1.2, 1.5 | 0.5–2.5 (0.1) | 1 |
| Read-out | - | 1.7 | 0.2 | 1 | - | 1.7 | 0.2 | 1 |
| HRS | LRS1 | LRS2 | LRS3 | ||
|---|---|---|---|---|---|
| Non-optimized | 1.70 | 25.66 | 35.81 | 44.78 | |
| 1.52 | 2.73 | 3.03 | 2.87 | ||
| Optimized | 2.85 | 18.08 | 31.01 | 43.59 | |
| 1.85 | 1.96 | 1.60 | 1.55 | ||
| Non-Optimized | Optimized | |||
|---|---|---|---|---|
| Training | 63.3 | 8.5 | 69.3 | 4.8 |
| Test | 63.8 | 8.5 | 69.9 | 4.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez, E.; Pérez-Ávila, A.J.; Romero-Zaliz, R.; Mahadevaiah, M.K.; Pérez-Bosch Quesada, E.; Roldán, J.B.; Jiménez-Molinos, F.; Wenger, C. Optimization of Multi-Level Operation in RRAM Arrays for In-Memory Computing. Electronics 2021, 10, 1084. https://doi.org/10.3390/electronics10091084
Pérez E, Pérez-Ávila AJ, Romero-Zaliz R, Mahadevaiah MK, Pérez-Bosch Quesada E, Roldán JB, Jiménez-Molinos F, Wenger C. Optimization of Multi-Level Operation in RRAM Arrays for In-Memory Computing. Electronics. 2021; 10(9):1084. https://doi.org/10.3390/electronics10091084
Chicago/Turabian StylePérez, Eduardo, Antonio Javier Pérez-Ávila, Rocío Romero-Zaliz, Mamathamba Kalishettyhalli Mahadevaiah, Emilio Pérez-Bosch Quesada, Juan Bautista Roldán, Francisco Jiménez-Molinos, and Christian Wenger. 2021. "Optimization of Multi-Level Operation in RRAM Arrays for In-Memory Computing" Electronics 10, no. 9: 1084. https://doi.org/10.3390/electronics10091084
APA StylePérez, E., Pérez-Ávila, A. J., Romero-Zaliz, R., Mahadevaiah, M. K., Pérez-Bosch Quesada, E., Roldán, J. B., Jiménez-Molinos, F., & Wenger, C. (2021). Optimization of Multi-Level Operation in RRAM Arrays for In-Memory Computing. Electronics, 10(9), 1084. https://doi.org/10.3390/electronics10091084








