Abstract
Item Response Theory (IRT) evaluates, on the same scale, examinees who take different tests. It requires the linkage of examinees’ ability scores as estimated from different tests. However, the IRT linkage techniques assume independently random sampling of examinees’ abilities from a standard normal distribution. Because of this assumption, the linkage not only requires much labor to design, but it also has no guarantee of optimality. To resolve that shortcoming, this study proposes a novel IRT based on deep learning, Deep-IRT, which requires no assumption of randomly sampled examinees’ abilities from a distribution. Experiment results demonstrate that Deep-IRT estimates examinees’ abilities more accurately than the traditional IRT does. Moreover, Deep-IRT can express actual examinees’ ability distributions flexibly, not merely following the standard normal distribution assumed for traditional IRT. Furthermore, the results show that Deep-IRT more accurately predicts examinee responses to unknown items from the examinee’s own past response histories than IRT does.
1. Introduction
As a rapidly growing area of e-assessment, E-testing involves the delivery of examinations and assessments on screen, using either local systems or web-based systems. In general, e-testing provides automatic assemblies of uniform test forms, for which each form comprises a different set of items but which still has equivalent measurement accuracy [1,2,3,4,5,6,7,8,9,10]. Uniform test forms are assembled for which all forms have equivalent qualities for equal evaluation of examinees who have taken different test forms. Examinees’ test scores should be guaranteed to become equivalent, even if different examinees with the same ability take different tests. However because it is difficult to develop perfectly uniform test forms, the calibration process is fundamentally important when multiple test forms are used. To resolve this difficulty, IRT has been used as a calibration method. Reports of the literature describe that Item Response Theory (IRT) offers the following benefits [11,12]:
- One can estimate examinees’ abilities while minimizing the effects of heterogeneous or aberrant items that have low estimation accuracy.
- IRT produces examinee ability estimates on a single scale, even for results obtained from different tests.
- IRT predicts an individual examinee’s correct response probability to an item from the examinee’s past response histories.
Evaluating abilities of numerous examinees on a single scale requires linkage of examinees’ abilities estimated from different tests [12,13,14,15]. However, linkage techniques of IRT assume random sampling of examinees’ abilities from a standard normal distribution. Because of this assumption, the IRT linkage theoretically has no guarantee for its optimality. Nevertheless, it requires much labor to design [16,17,18,19]. In addition, examinees’ abilities have no guarantee of being sampled randomly from a standard normal distribution.
To resolve difficulties of linkage, this study proposes a novel Item Response Theory based on deep learning, Deep-IRT, without assuming random sampling of examinees’ abilities from a statistical distribution. The proposed method represents a probability for an examinee to answer an item correctly based on the examinee’s ability parameter and the item’s difficulty parameter. The main contributions of this study are presented below:
- Based on deep learning technology, a novel IRT is proposed. It requires no linkage procedures because it does not assume random sampling of examinees.
- Deep-IRT estimated examinees’ abilities with high accuracy when the examinees are not sampled randomly from a single distribution or when there are no common items among the different tests.
- Deep-IRT can express actual examinees’ abilities distributions flexibly. It does not follow a standard normal distribution.
- The proposed method provides more reliable and robust ability estimation for actual data than IRT does.
In the study of artificial intelligence, researchers have recently developed deep learning methods that incorporate IRT for knowledge tracing [20,21,22,23]. Nevertheless, these methods have not achieved interpretable parameters for examinee ability and item difficulty because each examinee parameter depends on each item. Estimating interpretable parameters is the most important task in the field of test theory. To increase the interpretability of the parameters, the proposed method estimates parameters using two independent networks: an examinee network and an item network. However, generally speaking, independent networks are known to have less prediction accuracy than dependent networks have. Recent studies of deep learning have demonstrated that redundancy of parameters (deep layers of hidden variables) reduces generalization error, contrary to Occam’s razor [24,25,26,27]. Based on reports of state-of-the-art studies, the proposed method constructs two independent redundant deep networks: an examinee network and an item network. The present study uses the term “deep learning” in the sense of learning neural networks with a deep layer of hidden variables. Therefore, the proposed method is expected to have highly interpretable parameters without impairment of the estimation accuracy.
Simulation experiments demonstrate that the proposed Deep-IRT estimates examinees’ abilities more accurately than IRT does when examinees’ abilities are not sampled randomly from a single distribution or when no common items exist among the different tests. Experiments conducted with actual data demonstrated that the proposed method provides more reliable and robust ability estimation than IRT does. Furthermore, Deep-IRT more accurately predicted examinee responses to unknown items from the examinee’s past response histories than IRT does.
2. Related Works
For knowledge tracing [28,29,30,31,32,33,34], the task of tracking the knowledge states of different learners over time, several deep IRT methods that have been developed in the domain of artificial intelligence combine IRT with a deep learning method [20,21,22,23,27]. Cheng and Liu [21] proposed deep IRT based Long-short term memory (LSTM) [35] to estimate item discrimination and difficulty parameters by extracting item text information. Yeung [20] and Gan et al. [23] used the dynamic key-value memory network (DKVMN) [21] based on a Memory-Augmented Neural Network and attention mechanisms that trace a learner’s knowledge state. Ghosh et al. [22] used attention mechanisms that incorporates a forgetting function of the past learner’s response data. Ghosh et al. used a Rasch model [13,36] incorporating the learner’s ability parameters and the item’s difficulty parameter.
These deep knowledge tracing methods have not achieved interpretable parameters for learner ability and item difficulty, which are extremely important in the field of test theory. In addition, these earlier deep knowledge tracing methods estimate time-series changes of an examinee’s abilities to capture the examinee’s growth for knowledge tracing. However, the examinees’ ability change is not considered in the field of test theory because the purpose of testing is estimating an examinee’s current ability.
Consequently, earlier deep knowledge tracing methods [20,21,22,23,27] emphasized not a test theory but a knowledge tracing task. By contrast, this study proposes an IRT model based on deep learning as a novel test theory. Herein, we designate the proposed IRT as “Deep-IRT”: a novel test theory.
3. Item Response Theory
This section briefly introduces IRT and a two-parameter logistic model (2PLM), which is an extremely popular IRT model as a test theory. For the two-parameter logistic model, denotes the response of examinee i to item j (1, …, n) as
In the two parameter logistic model, the probability of a correct answer given to item j by examinee i with ability parameter is assumed as
where is the j-th item’s discrimination parameter expressing the discriminatory power for examinee’s abilities, and where is the j-th item’s difficulty parameter expressing the degree of difficulty. From Bayes’ theorem, the posterior distribution of an ability parameter is given as
where is a marginal distribution:
The parameters are estimated using the expected a priori (EAP) method, which is known to maximize the prediction accuracy theoretically as
Because calculating the parameters analytically is difficult, numerical calculation methods such as Markov Chain Monte Carlo methods (MCMC) are generally used.
Here, prior distribution indicates the examinees’ ability distribution. The examinees’ abilities are assumed to be sampled randomly from . Therefore, comparing the examinees’ abilities as estimated from different tests requires a linkage that scales those abilities on the same scale using common examinees or items among the tests.
Evaluating examinees’ abilities on the same scale requires linkage of examinees’ abilities as estimated from different tests [12,13,14,15]. Many researchers have developed IRT linkage and calibration methods. Linkage and calibration methods for IRT are divisible into separate calibrations, calibrations with fixed common item parameters, and concurrent calibrations as follows [37,38,39,40]:
- Common-item non-equivalent group linkage: transforming scales of parameters into common scales using common items such as substituting the means and deviations of the item parameter estimates of common items [41,42,43,44,45,46,47,48,49].
- Concurrent calibration: Item parameters for different tests are estimated together using common items [37,50].
- Fixed common item parameters: fixing the common item parameters and calibrating only the pretest items so that the item parameter estimates of the pretest are of the same scale as the common item parameters [51,52].
Even though linkage requires much labor to design, no linkage method can fully represent the joint probability distribution. Particularly when examinees are not sampled randomly from a certain statistical distribution, the linkage accuracy is greatly decreased [16,17,18,19]. In addition, examinees’ abilities might not be sampled randomly from the standard normal distribution.
4. Deep-IRT
To resolve the difficulties described above, this study proposes a novel Item Response Theory based on Deep Learning: Deep-IRT. To increase the interpretability of the parameters, Deep-IRT estimates parameters using two independent networks: an examinee network and an item network. However, in general, independent networks are known to have less prediction accuracy than dependent networks have. Recent studies of deep learning have demonstrated that redundancy of parameters (deep layers of hidden variables) reduces generalization error, contrary to Occam’s razor [24,25,26,27]. Based on state-of-the-art reports, Deep-IRT constructs two independent redundant deep networks: an examinee network and an item network. Deep-IRT is expected to have highly interpretable parameters without impairment of the estimation accuracy.
4.1. Method
This subsection presents an explanation of the Deep-IRT method. This method uses two independent neural networks: Examinee Layer and Item Layer. Using outputs of both networks, a probability for an examinee to answer an item correctly is calculated. Figure 1 presents a brief illustration.
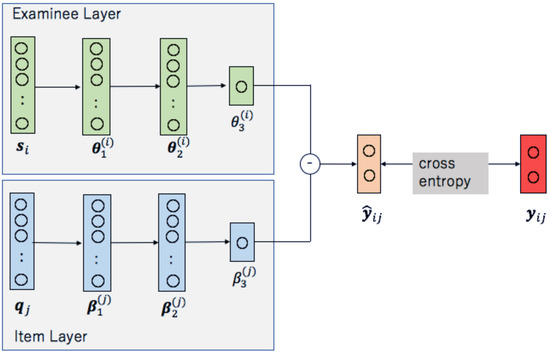
Figure 1.
Outline of Deep-IRT.
To express the i-th examinee, the encode of Examinee Layer is a one-hot vector , where I represents the number of examinees. The i-th element is 1; the other elements are 0s. The Examinee Layer comprises three layers as described below:
Here, we use the hyperbolic tangent as an activation function:
In addition, and are the weight matrices given as
Therein, is the weight vector given as
In addition, and are the bias parameters vectors; is the bias parameter. In this study, we consider the last layer as the ith examinee’s ability parameter. An overview of the calculation in terms of the Examinee Layer is presented in Figure 2. Weight matrix W represents an estimate of the relation between an examinee’s ability and all other examinees’ abilities. Therefore, Deep-IRT does not require assumption of random sampling examinees’ abilities from a statistical distribution because it estimates an examinees’ ability by adjusting the other examinees’ ability estimates.
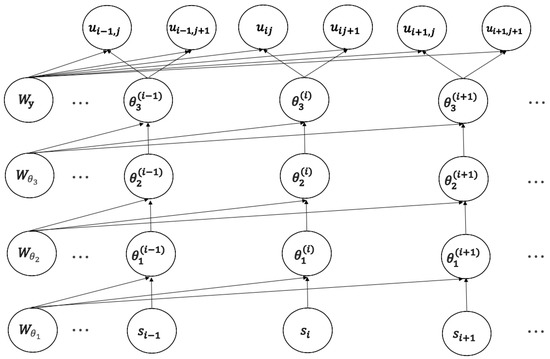
Figure 2.
Examinee layer structure.
Similarly, to express the j-th item, the encoding of the Item Layer is a one-hot vector , where J stands for the number of items. The j-th element is 1; the other elements are 0s. The Item Layer consists of three layers as follows:
In addition, and are the weight matrices given as presented below:
Here, is the weight vector given as shown below:
Additionally, and are the bias parameters’ vectors. is the bias parameter. For this study, we consider the last layer as the j th item’s difficulty parameter. Similarly to the sampling of examinees, this method does not assume random sampling of item difficulty parameters from a statistical distribution.
Then, Deep-IRT represents an examinee’s correct response probability to an item using the difference between the examinee’s ability parameter and the item difficulty parameter. Specifically, examinee i’s correct response probability to j’s item is described using a hidden layer as
Here, and are the weight vector and bias’ parameters vector.
Deep-IRT does not assume random sampling of examinees’ abilities and item difficulties from any statistical distribution. Instead, it uses a deep learning method to estimate the relation between an examinees’ ability and all other examinees’ abilities by maximizing the prediction accuracy of examinees’ responses. The unique feature of this method is to estimate an examinee’s ability by adjusting the other examinees’ ability estimates. Because of this property, this method requires no linkage procedure.
4.2. Learning Parameters
In general, deep learning methods learn their parameters using the back-propagation algorithm by minimizing a loss function. The loss function of the proposed Deep-IRT employs cross-entropy, which reflects classification errors. It is calculated from the predicted responses and the true responses as
Like other machine learning techniques, deep learning methods are biased to data they have encountered before. Therefore, the generalization capacity of the methods depends on the training data, which leads to sub-optimal performance. Consequently, Deep-IRT cannot predict responses of examinees or items accurately with an extremely small number of (in)correct answers. To overcome this shortcoming, cost-sensitive learning, which weights minority data over majority, has been used widely [53]. Therefore, we add the loss function based on a cost-sensitive approach as
where stands for a group of examinees whose correct answer rates are less than , denotes a group of examinees whose correct answer rates are more than , signifies a group of items of which correct answer rates are less than , and represents a group of items with correct answer rates that are more than . Here, and are tuning parameters.
All of the parameters are learned simultaneously using a popular optimization algorithm: adaptive moment estimation [54].
5. Simulation Experiments
This section presents evaluation of the performances of Deep-IRT using simulation data according to earlier IRT studies of the linkage or the multi-population [55,56].
5.1. Experiment Settings
We implemented Deep-IRT using Chainer (https://chainer.org/ (accessed on 23 April 2021)), a popular framework for neural networks. The values of tuning parameters are presented in Table 1.

Table 1.
Values of tuning parameters.
For implementation of IRT, we employ 2PLM and estimate the parameters using EAP estimation with the MCMC algorithm. The prior distributions are
Estimation Accuracy
For this experiment, we evaluate root mean square error (RMSE), Pearson’s correlation coefficient, and the Kendall rank correlation coefficient between the estimated abilities and the true values. For calculation of RMSE, the estimated abilities of Deep-IRT are standardized.
5.2. Estimation Accuracy for Randomly Sampled Examinee Data
To underscore the effectiveness of Deep-IRT for data of examinees’ abilities that are not randomly sampled, this subsection presents evaluation of the estimation accuracy with changing examinee assignments for different tests. The procedures of this experiment are explained hereinafter.
This experiment generates 10 test data that have no common examinees. In addition, the k-th test () has common items only among the -th test and the -th test.
The true parameters were generated randomly:
Here, the simulation data were generated based on 2PLM in the following two ways. The first way is that examinees are assigned randomly to each test from Equation (17). The other way is that examinees are assigned systematically to each test as described below.
- Examinees are sampled randomly from Equation (17).
- The examinees are sorted in order of their ascending ability. Furthermore, the examinees are divided equally into groups of 10 examinees in order of their respective abilities.
- The k th examinee group is assigned to the k-th test.
Table 2 demonstrates the average of estimation accuracies for each condition. Results of the random assignment condition show that IRT outperforms Deep-IRT. The reason is that the condition is an ideal situation for IRT because the data are generated randomly from the IRT model. However, for a small number of examinees or items, the differences between IRT and Deep-IRT become smaller.

Table 2.
Parameter estimation accuracies.
In contrast, the results obtained for the systematically assignment condition show Deep-IRT without assuming randomly sampling examinees outperforms IRT with that assumption. Furthermore, Deep-IRT suppresses the decline of accuracy in cases without common items among different tests. These results are expected to be beneficial for applying Deep-IRT with actual data.
5.3. Estimation Accuracy for Multi-Population Data
As described earlier, IRT assumes that examinees’ abilities follow a standard normal distribution. Furthermore, it is known that no optimal linkage occurs under the assumption [17]. Additionally, no guarantee exists that examinees’ abilities follow a standard normal distribution. When the assumption is violated, ability estimation accuracy of IRT becomes extremely worse, even without the linkage problem. However, because Deep-IRT does not assume random sampling from a statistical distribution, robust ability estimation is expected to be provided even when the IRT presumption is violated. To demonstrate the benefits of the proposed method, this subsection evaluates estimation accuracies of IRT and Deep-IRT when examinees’ abilities follow multiple populations.
For this experiment, the abilities of examinees taking different tests are assumed to be sampled from different populations. For this study, we assume two tests including 50 items. The abilities of the tests are sampled randomly from and .
Table 3 shows the average of estimation accuracies with different ability distributions and the number of common items. The standard deviation of each distribution was ascertained so that the total abilities’ standard deviation is close to 1.0. Here, Wilcoxon’s signed rank test is applied to infer whether the accuracies of IRT and Deep-IRT are significantly different. The results showed that when the difference between and becomes small, IRT provides significantly high accuracy because the distribution approaches a single normal distribution. By contrast, as the difference between and becomes large, Deep-IRT estimates examinees’ abilities accurately. Therefore, Deep-IRT is robust for estimation of examinees’ abilities when they follow different distributions. The results also show that, when there is no common item, Deep-IRT estimates the examinees’ abilities more accurately than IRT does. Consequently, Deep-IRT can estimate examinees’ abilities accurately without common items.

Table 3.
Estimation accuracies for multi-population data.
Next, we demonstrate that Deep-IRT can accommodate abilities with multiple populations. Specifically, we generate abilities according to multiple populations for data and in Table 3. Figure 3 shows histograms of the true abilities, the estimated abilities using IRT, and the estimated abilities using Deep-IRT. Figure 3 shows that Deep-IRT clearly estimates a bimodal distribution as the ability distribution similar to the true distribution. The result demonstrates that Deep-IRT flexibly expresses actual examinees’ abilities distributions that do not follow a standard normal distribution.
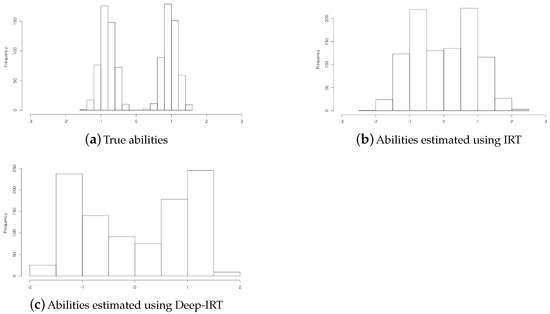
Figure 3.
Histograms of estimated abilities for multi-population data.
Next, we evaluate the estimated ability distributions of IRT and Deep-IRT using a fitting score to the true distribution as
where represents the number of examinees who took the k-th test. In addition, is the estimated ability of i-th examinee for the k-th test. In addition, is the likelihood of estimated abilities given the true ability distribution as
If the method fits the true distribution, then the estimated distribution approaches the true distribution. The fitting score of IRT is −1633.4. That of Deep-IRT is −1437.1. The latter is higher than the former. Therefore, Deep-IRT expresses the examinees’ ability distributions more accurately than IRT does.
6. Actual Data Experiments
The simulation experiments suggested that Deep-IRT might estimate examinees’ abilities with high accuracy for actual data. This section evaluates the effectiveness of Deep-IRT using actual datasets.
6.1. Actual Datasets
For this experiment, we use the following actual datasets. Here, we present “Rate.Sparse” which is the average rate of items that an examinee did not address in the learning process.
- Information datasets consist of two test data (Information 1, 2) related to information technology. Information 1 has 169 examinees over 50 items. Information 2 has 266 examinees over 50 items. The tests were conducted of the learning management system, “Samurai” developed by [57,58,59]. Rate.Sparse is 0%.
- The critical thinking dataset has 1221 undergraduate examinees over 179 items about critical thinking. Rate.Sparse is 87.8%.
- Program datasets consist of two test data (Program 1, 2) about programming. Program 1 has 93 examinees over 13 items. Rate.Sparse is 0%. Program 2 has 74 examinees over 19 items with 6.8% Rate.Sparse.
- Practice Exam dataset consists of two test data for high school students. Each test relates to mathematics and physics. Mathematics data have 12,348 examinees over 48 items. Physics data have 9172 examinees over 24 items. The respective values of Rate.Sparse are 16.4% and 12.0%.
- Assistments dataset is the 2009–2010 dataset of Assistments (https://sites.google.com/site/assistmentsdata/\home/assistment-2009-2010-data (accessed on 23 April 2021).), which is a large dataset that is used widely for knowledge tracing. Here, we removed examinees answering only one item and items answered by fewer than 30 examinees. For that reason, our dataset has 3941 examinees over 2921 items with 84.4% Rate.Sparse.
- CDM datasets, which are widely used open datasets, are included in the R package CDM [60]. We used two datasets: ECPE and TIMSS. ECPE data include those for 2922 examinees over 28 language-related items. TIMSS data include those for 757 examinees over 23 math items. Rate.Sparse is 0%.
- Statistics dataset includes those of 26 undergraduate examinees over 25 items about statistics. Rate.Sparse is 33.8%.
- Information Ethics dataset has 31 undergraduate examinees over 90 items related to information ethics. Rate.Sparse is 46.3%.
- Engineer Ethics dataset has 85 undergraduate examinees over 69 items related to engineer ethics. Rate.Sparse is 26.4%.
- Classi datasets consist of three test data for high school examinees: tests relate to physics, chemistry, and biology. The tests were conducted on the web-based system, “Classi (https://classi.jp (accessed on 23 April 2021).)” using a tablet. Datasets have 239, 1139, and 192 examinees, respectively, and 119, 364, and 114 items. The respective values of Rate.Sparse are 92.4%, 96.4%, and 93.5%.
6.2. Reliability of Ability Estimation
This subsection presents evaluation of the reliability of abilities estimation of Deep-IRT. Because the true values of parameters are unknown, we evaluate the reliabilities as follows: (1) Each dataset is divided equally into two sets of data. (2) Parameters of each method are estimated for the divided data from each dataset. (3) The RMSE and correlation between the two sets of the estimated parameters from the two divided datasets are calculated. (4) These procedures are repeated 10 times. The average of the RMSEs and correlations is calculated. Table 4 presents the results. Here, a Wilcoxon signed rank test is applied to infer whether the reliabilities of IRT and Deep-IRT are significantly different.

Table 4.
Reliability of ability parameter estimation.
Table 4 shows that Deep-IRT provides more reliable ability estimates than IRT does. In particular, regarding the average of Kendall rank correlation coefficient, which is known to provide a robust estimate for aberrant values, Deep-IRT outperforms IRT significantly. Results indicate that Deep-IRT can estimate parameters more reliably than IRT does for actual test data. It is surprising that Deep-IRT outperforms IRT for small datasets such as Program 1, Program 2, Statistics, Information Ethics, and Engineer Ethics. This result indicates Deep-IRT as effective even for small datasets. For Practice_Math, Practice_Physics, and ASSISTMENTS, IRT has a higher Kendall rank correlation coefficient than Deep-IRT does because the ability estimation of IRT tends to become stable when the dataset becomes large. IRT has that stability because it is guaranteed to converge asymptotically to the true joint probability distribution.
6.3. Prediction of Responses to Unknown Items
In the field of artificial intelligence in education, the prediction of examinee’s responses to unknown items from the examinee’s past response history becomes important for adaptive learning systems [20,30,32,61,62]. Reportedly, the prediction accuracy of IRT is the highest for the problem [63]. This subsection presents comparison of the prediction accuracy of Deep-IRT with that of IRT. Specifically, using ten-fold cross validation, the parameters are learned from training data and are used to predict responses in the remaining data. Then, we calculate the accuracy rates for the cross validation experiments. Here, a Wilcoxon signed rank test is applied to infer whether the respective accuracies of IRT and Deep-IRT are significantly different.
Table 5 shows the results: the average of F1 value of Deep-IRT is significantly higher than that of IRT. Deep-IRT can predict examinees’ responses to unknown items more accurately than IRT can. It is noteworthy that Deep-IRT does not always outperform for large data. For ASSISTMENTS and Critical Thinking, IRT provides better performance than Deep-IRT does because ASSISTMENTS and Critical Thinking have high values of Rate.Sparse. Deep-IRT might be weak in dealing with sparse datasets. In contrast, for datasets with low values of Rate.Sparse, Deep-IRT outperforms IRT even for small datasets. Generally speaking, the IRT prediction accuracy increases along with the number of examinees. Therefore, IRT has high prediction accuracies for Practice_Math and Practice_Physics.

Table 5.
Prediction accuracies of responses to unknown items.
Furthermore, Figure 4 depicts histograms of abilities estimated from Practice_Math, where the prediction accuracy of IRT is higher than that of Deep-IRT. Figure 5 depicts histograms of abilities estimated from Classi_Biology data, where the prediction accuracy of Deep-IRT is higher than that of IRT. Figure 4 shows estimates conducted using both methods for the ability distribution similar to the standard normal distribution. In contrast, Figure 5 shows that Deep-IRT expresses a multi modal distribution, although IRT estimates a unimodal distribution. Deep-IRT can predict responses to unknown items because it can flexibly express distributions of various abilities.
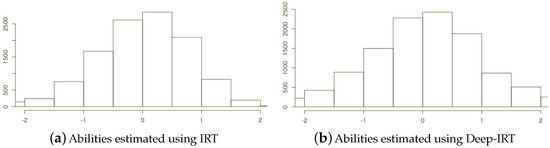
Figure 4.
Histograms of abilities estimated using IRT and Deep-IRT for Practice_Math data.
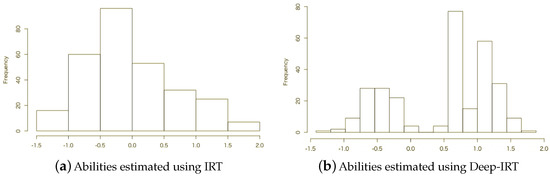
Figure 5.
Histograms of abilities estimated using IRT and Deep-IRT for Classi_Biology data.
7. Conclusions
This study examines a novel test theory based on deep learning: Deep-IRT. To increase the interpretability of the parameters, Deep-IRT estimates parameters using two independent networks: an examinee network and an item network. However, generally speaking, independent networks are known to have less prediction accuracy than dependent networks have. Recent studies of deep learning have indicated that redundancy of parameters reduces generalization error, contrary to Occam’s razor [24,25,26,27]. Based on reports of state-of-the-art research, Deep-IRT was constructed to have two independent redundant deep networks. Therefore, Deep-IRT has high interpretable parameters without impairment of the estimation accuracy. The main contributions of Deep-IRT are presented below:
- (1)
- Deep-IRT does not assume random sampling of examinees’ abilities from a statistical distribution because the weight matrix of the ability parameters estimates the relation between an examinee’s ability and all other examinees’ abilities.
- (2)
- Deep-IRT estimates examinees’ abilities with high accuracy when the examinees are not sampled randomly from a single distribution or when no common items exist among the different tests.
- (3)
- Deep-IRT flexibly expresses actual examinees’ ability distributions that do not follow a standard normal distribution.
Experiments conducted using actual data demonstrated that Deep-IRT provided more reliable and robust ability estimation than IRT did. Furthermore, Deep-IRT more accurately predicted examinee responses to unknown items from the examinee’s past response histories than IRT did. Results showed that Deep-IRT is effective even for small datasets. However, the results also suggest that Deep-IRT might be weak in dealing with sparse data. To estimate an examinee’s ability for sparse data robustly, one must improve the estimation methods. One potential means of doing so is optimizing the number of hidden layers of each neural network.
Furthermore, as another subject of future work, we expect to incorporate Deep-IRT with (CAT) [64,65] to improve the examinee’s ability estimation accuracy in an actual environment.
Author Contributions
Conceptualization, methodology, E.T., R.K., and M.U.; validation, R.K.; writing—original draft preparation, E.T. and R.K.; writing—review and editing, M.U.; funding acquisition, M.U. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by JSPS KAKENHI Grant Numbers JP19H05663 and JP19K21751.
Conflicts of Interest
The authors declare that they have no conflict of interest. The funders had no role in the design of the study, in the collection, analyses, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
References
- Songmuang, P.; Ueno, M. Bees Algorithm for Construction of Multiple Test Forms in E-Testing. IEEE Trans. Learn. Technol. 2011, 4, 209–221. [Google Scholar] [CrossRef]
- Ishii, T.; Songmuang, P.; Ueno, M. Maximum Clique Algorithm for Uniform Test Forms Assembly. In Proceedings of the 16th International Conference on Artificial Intelligence in Education, Memphis, TN, USA, 9–13 July 2013; Volume 7926, pp. 451–462. [Google Scholar] [CrossRef]
- Ishii, T.; Songmuang, P.; Ueno, M. Maximum Clique Algorithm and Its Approximation for Uniform Test Form Assembly. IEEE Trans. Learn. Technol. 2014, 7, 83–95. [Google Scholar] [CrossRef]
- Ishii, T.; Ueno, M. Clique Algorithm to Minimize Item Exposure for Uniform Test Forms Assembly. In Proceedings of the International Conference on Artificial Intelligence in Education, Madrid, Spain, 22–26 June 2015; pp. 638–641. [Google Scholar] [CrossRef]
- Ishii, T.; Ueno, M. Algorithm for Uniform Test Assembly Using a Maximum Clique Problem and Integer Programming. In Proceedings of the Artificial Intelligence in Education, Wuhan, China, 28 June–1 July 2017; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 102–112. [Google Scholar] [CrossRef]
- Lin, Y.; Jiang, Y.S.; Gong, Y.J.; Zhan, Z.H.; Zhang, J. A Discrete Multiobjective Particle Swarm Optimizer for Automated Assembly of Parallel Cognitive Diagnosis Tests. IEEE Trans. Cybern. 2018, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Vie, J.J.; Popineau, F.; Bruillard, E.; Bourda, Y. Automated Test Assembly for Handling Learner Cold-Start in Large-Scale Assessments. Int. J. Artif. Intell. Educ. 2018, 28. [Google Scholar] [CrossRef]
- Rodríguez-Cuadrado, J.; Delgado-Gómez, D.; Laria, J.; Rodriguez-Cuadrado, S. Merged Tree-CAT: A fast method for building precise Computerized Adaptive Tests based on Decision Trees. Expert Syst. Appl. 2019, 143, 113066. [Google Scholar] [CrossRef]
- Linden, W.; Jiang, B. A Shadow-Test Approach to Adaptive Item Calibration. Psychometrika 2020, 85. [Google Scholar] [CrossRef]
- Ren, H.; Choi, S.; Linden, W. Bayesian adaptive testing with polytomous items. Behaviormetrika 2020, 47. [Google Scholar] [CrossRef]
- Lord, F.; Novick, M. Statistical Theories of Mental Test Scores; Addison-Wesley: Boston, MA, USA, 1968; p. xiii. 274p. [Google Scholar]
- Van der Linden, W.J. Handbook of Item Response Theory, Volume Three: Applications; Chapman and Hall/CRC Statistics in the Social and Behavioral Sciences; Chapman and Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]
- Lord, F. Applications of Item Response Theory to Practical Testing Problems; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1980. [Google Scholar]
- Van der Linden, W.J. Handbook of Item Response Theory, Volume Two: Statistical Tools; Chapman and Hall/CRC Statistics in the Social and Behavioral Sciences; Chapman and Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]
- Joo, S.H.; Lee, P.; Stark, S. Evaluating Anchor-Item Designs for Concurrent Calibration With the GGUM. Appl. Psychol. Meas. 2017, 41, 83–96. [Google Scholar] [CrossRef]
- Ogasawara, H. Standard Errors of Item Response Theory Equating/Linking by Response Function Methods. Appl. Psychol. Meas. 2001, 25, 53–67. [Google Scholar] [CrossRef]
- van der Linden, W.; Barrett, M.D. Linking Item Response Model Parameters. Psychometrika 2016, 81, 650–673. [Google Scholar] [CrossRef]
- Andersson, B. Asymptotic Variance of Linking Coefficient Estimators for Polytomous IRT Models. Appl. Psychol. Meas. 2018, 42, 192–205. [Google Scholar] [CrossRef]
- Barrett, M.D.; van der Linden, W.J. Estimating Linking Functions for Response Model Parameters. J. Educ. Behav. Stat. 2019, 44, 180–209. [Google Scholar] [CrossRef]
- Yeung, C. Deep-IRT: Make Deep Learning Based Knowledge Tracing Explainable Using Item Response Theory. In Proceedings of the 12th International Conference on Educational Data Mining, EDM, Montreal, QC, Canada, 2–5 July 2019. [Google Scholar]
- Cheng, S.; Liu, Q. Enhancing Item Response Theory for Cognitive Diagnosis. CoRR 2019, abs/1905.10957. Available online: http://xxx.lanl.gov/abs/1905.10957 (accessed on 23 April 2021).
- Ghosh, A.; Heffernan, N.; Lan, A.S. Context-Aware Attentive Knowledge Tracing. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, CA, USA, 23–27 August 2020. [Google Scholar]
- Gan, W.; Sun, Y.; Sun, Y. Knowledge Interaction Enhanced Knowledge Tracing for Learner Performance Prediction. In Proceedings of the 2020 Seventh International Conference on Behavioural and Social Computing (BESC), Bournemouth, UK, 5–7 November 2020; pp. 1–6. [Google Scholar] [CrossRef]
- He, H.; Huang, G.; Yuan, Y. Asymmetric Valleys: Beyond Sharp and Flat Local Minima. In Advances in Neural Information Processing Systems 32; Curran Associates, Inc.: New York City, NY, USA, 2019; pp. 2553–2564. [Google Scholar]
- Morcos, A.; Yu, H.; Paganini, M.; Tian, Y. One ticket to win them all: Generalizing lottery ticket initializations across datasets and optimizers. In Advances in Neural Information Processing Systems 32; Curran Associates, Inc.: New York City, NY, USA, 2019; pp. 4932–4942. [Google Scholar]
- Nagarajan, V.; Kolter, J.Z. Uniform convergence may be unable to explain generalization in deep learning. In Advances in Neural Information Processing Systems 32; Curran Associates, Inc.: New York City, NY, USA, 2019; pp. 11615–11626. [Google Scholar]
- Tsutsumi, E.; Kinoshita, R.; Ueno, M. Deep-IRT with independent student and item networks. In Proceedings of the 14th International Conference on Educational Data Mining, EDM, Paris, France, 29 June–2 July 2021. [Google Scholar]
- Corbett, A.T.; Anderson, J.R. Knowledge tracing: Modeling the acquisition of procedural knowledge. User Model. User-Adapt. Interact. 1994, 4, 253–278. [Google Scholar] [CrossRef]
- González-Brenes, J.; Huang, Y.; Brusilovsky, P. Fast: Feature-aware student knowledge tracing. In Proceedings of the NIPS 2013 Workshop on Data Driven Education, Lake Taho, NV, USA, 9–10 December 2013. [Google Scholar]
- Piech, C.; Bassen, J.; Huang, J.; Ganguli, S.; Sahami, M.; Guibas, L.J.; Sohl-Dickstein, J. Deep Knowledge Tracing. In Advances in Neural Information Processing Systems 28; Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; Curran Associates, Inc.: New York City, NY, USA, 2015; pp. 505–513. [Google Scholar]
- Khajah, M.; Lindsey, R.V.; Mozer, M.C. How Deep is Knowledge Tracing? arXiv 2016, arXiv:1604.02416. [Google Scholar]
- Zhang, J.; Shi, X.; King, I.; Yeung, D.Y. Dynamic Key-Value Memory Network for Knowledge Tracing. In Proceedings of the 26th International Conference on World Wide Web, WWW ’17, Perth, Australia, 3–7 May 2017; International World Wide Web Conferences Steering Committee: Geneva, Switzerland, 2017; pp. 765–774. [Google Scholar]
- Vie, J.; Kashima, H. Knowledge Tracing Machines: Factorization Machines for Knowledge Tracing. arXiv 2018, arXiv:1811.03388. [Google Scholar] [CrossRef]
- Pandey, S.; Karypis, G. A Self-Attentive model for Knowledge Tracing. In Proceedings of the International Conference on Education Data Mining, Montreal, QC, Canada, 2–5 July 2019. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Rasch, G. Probabilistic Models for Some Intelligence and Attainment Tests; MESA Press: San Diego, CA, USA, 1993. [Google Scholar]
- Hanson, B.A.; Béguin, A.A. Obtaining a Common Scale for Item Response Theory Item Parameters Using Separate Versus Concurrent Estimation in the Common-Item Equating Design. Appl. Psychol. Meas. 2002, 26, 3–24. [Google Scholar] [CrossRef]
- Hu, H.; Rogers, W.T.; Vukmirovic, Z. Investigation of IRT-Based Equating Methods in the Presence of Outlier Common Items. Appl. Psychol. Meas. 2008, 32, 311–333. [Google Scholar] [CrossRef]
- Kolen, M.J.; Brennan, R.L. Test Equating, Scaling, and Linking: Methods and Practices, 2nd ed.; Springer: New York City, NY, USA, 2004. [Google Scholar]
- Gonzãlez, J.; Wiberg, M. Applying Test Equating Methods: Using R; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Marco, G.L. Item Characteristic Curve Solutions to Three Intractable Testing Problems. J. Educ. Meas. 1977, 14, 139–160. [Google Scholar] [CrossRef]
- Loyd, B.H.; Hoover, H.D. Vertical Equating Using the Rasch Model. J. Educ. Meas. 1980, 17, 179–193. [Google Scholar] [CrossRef]
- Haebara, T. Equating Logistic Ability Scales by a Weighted Least Squares Method. Jpn. Psychol. Res. 1980, 22, 144–149. [Google Scholar] [CrossRef]
- Stocking, M.L.; Lord, F.M. Developing a Common Metric in Item Response Theory. Appl. Psychol. Meas. 1983, 7, 201–210. [Google Scholar] [CrossRef]
- Arai, S.; Mayekawa, S. A Comparison of Equating Methods and Linking Designs for Developing an Item Pool Under Item Response Theory. Behaviormetrika 2011, 38, 1–16. [Google Scholar] [CrossRef]
- Sansivieri, V.; Wiberg, M.; Matteucci, M. A Review of Test Equating Methods with a Special Focus on IRT-Based Approaches. Statistica 2018, 77, 329–352. [Google Scholar] [CrossRef]
- He, Y.; Cui, Z. Evaluating Robust Scale Transformation Methods With Multiple Outlying Common Items Under IRT True Score Equating. Appl. Psychol. Meas. 2020, 44, 296–310. [Google Scholar] [CrossRef]
- Robitzsch, A. Robust Haebara Linking for Many Groups: Performance in the Case of Uniform DIF. Psych 2020, 2, 155–173. [Google Scholar] [CrossRef]
- Robitzsch, A.; Lüdtke, O. Supplemental Material: A Review of Different Scaling Approaches under Full Invariance. Psych. Test Assess. Model 2020, 62, 233–279. [Google Scholar] [CrossRef]
- Bock, R.D.; Zimowski, M.F. Multiple Group IRT. In Handbook of Modern Item Response Theory; Springer: Berlin/Heidelberg, Germany, 1997; pp. 433–448. [Google Scholar]
- Jodoin, M.; Keller, L.; Swaminathan, H. A Comparison of Linear, Fixed Common Item, and Concurrent Parameter Estimation Equating Procedures in Capturing Academic Growth. J. Exp. Educ. 2003, 71, 229–250. [Google Scholar] [CrossRef]
- Li, Y.; Tam, H.; Tompkins, L.J. A Comparison of Using the Fixed Common-Precalibrated Parameter Method and the Matched Characteristic Curve Method for Linking Multiple-Test Items. Int. J. Test. 2004, 4, 267–293. [Google Scholar] [CrossRef]
- Shen, W.; Wang, X.; Bai, X.; Zhang, Z. DeepContour: A deep convolutional feature learned by positive-sharing loss for contour detection. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3982–3991. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Kilmen, S.; Demirtasli, N. Comparison of Test Equating Methods Based on Item Response Theory According to the Sample Size and Ability Distribution. Procedia Soc. Behav. Sci. 2012, 46, 130–134. [Google Scholar] [CrossRef]
- Uysal, I.; Kilmen, S. Comparison of Item Response Theory Test Equating Methods for Mixed Format Tests. Int. Online J. Educ. Sci. 2016, 8, 1–11. [Google Scholar] [CrossRef]
- Ueno, M. Animated agent to maintain learner’s attention in e-learning. In Proceedings of the E-Learn: World Conference on E-Learning in Corporate, Government, Healthcare, and Higher Education 2004; Nall, J., Robson, R., Eds.; Association for the Advancement of Computing in Education (AACE): Washington, DC, USA, 2004; pp. 194–201. [Google Scholar]
- Ueno, M. Data Mining and Text Mining Technologies for Collaborative Learning in an ILMS “Samurai”. In Proceedings of the ICALT ’04 Proceedings of the IEEE International Conference on Advanced Learning Technologies, Joensuu, Finland, 30 August–1 September 2004; pp. 1052–1053. [Google Scholar] [CrossRef]
- Ueno, M. Intelligent LMS with an agent that learns from log data. In Proceedings of E-Learn: World Conference on E-Learning in Corporate, Government, Healthcare, and Higher Education 2005; Richards, G., Ed.; Association for the Advancement of Computing in Education (AACE): Vancouver, BC, Canada, 2005; pp. 3169–3176. [Google Scholar]
- George, A.C.; Robitzsch, A.; Kiefer, T.; Groß, J.; Ünlü, A. The R Package CDM for Cognitive Diagnosis Models. J. Stat. Softw. Artic. 2016, 74, 1–24. [Google Scholar] [CrossRef]
- Ueno, M.; Miyazawa, Y. Probability Based Scaffolding System with Fading. In Proceedings of the Artificial Intelligence in Education—17th International Conference, AIED, Madrid, Spain, 21–25 June 2015; pp. 237–246. [Google Scholar] [CrossRef]
- Ueno, M.; Miyazawa, Y. IRT-Based Adaptive Hints to Scaffold Learning in Programming. IEEE Trans. Learn. Technol. 2018, 11, 415–428. [Google Scholar] [CrossRef]
- Wilson, K.H.; Karklin, Y.; Han, B.; Ekanadham, C. Back to the basics: Bayesian extensions of IRT outperform neural networks for proficiency estimation. In Proceedings of the 9th International Conference on Educational Data Mining, Raleigh, NC, USA, 29 June– 2 July 2016; Volume 1, pp. 539–544. [Google Scholar]
- Ueno, M.; Pokpong, S. Computerized Adaptive Testing Based on Decision Tree. In Proceedings of the Advanced Learning Technologies (ICALT), 2010 IEEE Tenth International Conference, Sousse, Tunisia, 5–7 July 2010; pp. 191–193. [Google Scholar]
- Ueno, M. Adaptive testing based on Bayesian decision theory. In Proceedings of the International Conference on Artificial Intelligence in Education, Memphis, TN, USA, 9–13 July 2013; pp. 712–716. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).