Next Article in Journal
HEVC Fast Intra-Mode Selection Using World War II Technique
Next Article in Special Issue
Coreset Clustering on Small Quantum Computers
Previous Article in Journal
An Integrated Framework for Traceability and Impact Analysis in Requirements Verification of Cyber–Physical Systems
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Electronics
Volume 10
Issue 8
10.3390/electronics10080984
electronics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Automated Quantum Hardware Selection for Quantum Workflows

by
Benjamin Weder
*,
Johanna Barzen
,
Frank Leymann
and
Marie Salm
University of Stuttgart, Institute of Architecture of Application Systems, Universitätsstraße 38, 70569 Stuttgart, Germany
*
Author to whom correspondence should be addressed.
Electronics 2021, 10(8), 984; https://doi.org/10.3390/electronics10080984
Submission received: 25 March 2021 / Revised: 15 April 2021 / Accepted: 17 April 2021 / Published: 20 April 2021
(This article belongs to the Special Issue Quantum Computing System Design and Architecture)
Browse Figures
Review Reports Versions Notes

Abstract

:
The execution of a quantum algorithm typically requires various classical pre- and post-processing tasks. Hence, workflows are a promising means to orchestrate these tasks, benefiting from their reliability, robustness, and features, such as transactional processing. However, the implementations of the tasks may be very heterogeneous and they depend on the quantum hardware used to execute the quantum circuits of the algorithm. Additionally, today’s quantum computers are still restricted, which limits the size of the quantum circuits that can be executed. As the circuit size often depends on the input data of the algorithm, the selection of quantum hardware to execute a quantum circuit must be done at workflow runtime. However, modeling all possible alternative tasks would clutter the workflow model and require its adaptation whenever a new quantum computer or software tool is released. To overcome this problem, we introduce an approach to automatically select suitable quantum hardware for the execution of quantum circuits in workflows. Furthermore, it enables the dynamic adaptation of the workflows, depending on the selection at runtime based on reusable workflow fragments. We validate our approach with a prototypical implementation and a case study demonstrating the hardware selection for Simon’s algorithm.

1. Introduction

In recent years, various advances have been made in the development of quantum computers, quantum algorithms, and corresponding software tools [1,2,3]. Additionally, quantum advantage has already been shown for some problems [4,5]. Thus, quantum computing is expected to enable breakthroughs in different application areas, such as machine learning, chemistry, or scientific simulations [6,7]. However, today’s quantum computers only provide a limited number of qubits and short decoherence times [8,9]. This limits the maximum width, i.e., the number of required qubits, and depth, i.e., the number of sequentially executable gates of quantum circuits [10,11]. However, the width and depth of a quantum circuit depend on the input data for the implemented quantum algorithm, e.g., the number to factorize for Shor’s algorithm [10,12]. Furthermore, different quantum computers provide diverse characteristics, and periodic re-calibrations change them over time, e.g., their decoherence times or readout-errors [13]. Additionally, a set of quantum hardware simulators is available, e.g., included in Software Development Kits (SDKs), such as Qiskit [14]. Therefore, the selection of suitable quantum hardware, i.e., a quantum computer or a corresponding simulator, to execute a certain quantum circuit is a complex task and it has to be done based on the input data, the resulting quantum circuit properties, and the current characteristics of the available quantum hardware [8,10].
In addition to the execution of quantum circuits, quantum algorithms often require algorithm-specific pre- or post-processing tasks, e.g., Shor’s [12] or Simon’s algorithm [15]. Furthermore, there may be algorithm-independent tasks, such as mitigating readout-errors after the execution of a quantum circuit [8,16,17]. Thus, workflows can be used to orchestrate these tasks to benefit from their advantages, such as scalability, reliability, robustness, and comprehensive error handling mechanisms [18,19,20]. To ease the modeling of such quantum workflows and increase the reuse of implementations for the various tasks, we introduced the Quantum Modeling Extension (QuantME) [21] for imperative workflow languages, such as BPMN [22] or BPEL [23]. Thereby, QuantME provides modeling constructs for the different frequently occurring tasks abstracting from the underlying technical details. However, the various pre-processing, quantum circuit execution, and post-processing tasks are implemented differently, depending on the quantum hardware to use [14,17]. For example, because an SDK enabling the execution on this quantum hardware must be utilized [10]. This means, to support the selection of suitable quantum hardware based on the input data at runtime, all possible alternative implementations for the tasks would have to be modeled in the workflow [21]. However, because of the large and steadily growing software landscape in the quantum computing area, this would clutter the workflow model and require updating the workflow every time, e.g., a new software tool, quantum computer, or simulator is released [2,14,24].
In this paper, we introduce an approach to automatically select suitable quantum hardware for the execution of quantum circuits in workflows and to dynamically adapt the workflows, depending on the selection at runtime. Therefore, we (i) present a new QuantME modeling construct to model subprocesses in a workflow, for which the required quantum hardware should be selected automatically based on the quantum circuit to be executed. Additionally, we (ii) propose an approach to dynamically replace the tasks in the subprocesses by reusable workflow fragments implementing the required functionality for the selected quantum hardware. Thereby, the workflow fragments may be heterogeneous and use, e.g., different SDKs, compilers, optimizers, or APIs of the various quantum hardware providers. Furthermore, (iii) the services that are needed by the workflow fragments are automatically deployed on-demand to avoid a complex manual deployment and additional costs for the used hardware. Finally, (iv) a prototypical implementation of our concept and a case study validating its practical feasibility is presented.
The remainder of the paper is structured, as follows: Section 2 presents the fundamentals and the problem statement of our work. Afterward, Section 3 discusses related work regarding the dynamic adaptation of workflows, the on-demand provisioning of services, and the selection of suitable quantum hardware. In Section 4, an overview of our quantum hardware selection approach for workflows is given. Subsequently, Section 5 introduces the system architecture, our prototypical implementation, and validates our approach with a case study. Finally, Section 6 provides a conclusion and outlook.

2. Fundamentals & Problem Statement

In this section, we introduce the fundamentals about quantum computing, the limitations of today‘s quantum computers, and the problem of selecting suitable quantum hardware for a certain quantum computation. Afterward, we show how workflow technologies can be used to orchestrate the different tasks that are required to execute a quantum algorithm and present the problem statement that underlies our work.

2.1. NISQ Era & Quantum Hardware Selection

When considering the gate-based quantum computing model, quantum algorithms are implemented by so-called quantum circuits [2,25]. A universal quantum circuit consists of a set of gates and measurements operating on different qubits [3]. However, computations on today’s quantum computers are affected by various kinds of noise, such as gate-errors, qubit decoherence, or readout-errors [8,17]. This noise leads to errors in computations and restricts the maximum circuit depth of the executable quantum circuits [11]. Furthermore, the available quantum computers only provide a small number of qubits. Therefore, they are referred to as Noisy Intermediate Scale Quantum (NISQ) computers [9].
However, the various quantum computers differ significantly concerning characteristics, such as the number of provided qubits, their connectivities, or the fidelities of the implemented gates [8,10]. Additionally, some of their characteristics change between different re-calibrations, e.g., the decoherence times of the qubits [13]. Moreover, a quantum compiler has to map the quantum circuit to the qubits and gates provided by the quantum computer before executing it [26,27]. The resulting depth and width of the compiled quantum circuit may differ because of diverse connectivities or physically implemented gate sets of the quantum computers [28]. Therefore, the selection of suitable quantum hardware to execute a certain quantum circuit is a complex task [10,11]. In order to overcome this problem, different benchmarks [4,29,30] and metrics, such as the total quantum factor (TQF) [31], quantum volume [32], or the epsilon metric [8,11], were developed to assess and compare the capabilities of quantum computers or to directly estimate whether a quantum circuit can be executed on a given quantum computer.
In previous work, we introduced the NISQ Analyzer [10], which automatically selects suitable quantum hardware for the execution of a quantum algorithm based on given input data. For this purpose, the corresponding quantum circuit is compiled for the different available quantum computers and simulators to retrieve its hardware-dependent depth and width. Subsequently, the NISQ Analyzer determines whether the width of the compiled quantum circuit is smaller or equal to the number of provided qubits [10]. In addition, the depth of the compiled quantum circuit is compared to the estimated maximum executable depth of the quantum computers. This maximum executable depth is estimated by dividing the average decoherence time of the qubits by the maximum gate time [31]. For the decoherence times of the qubits and the maximum gate time, the NISQ Analyzer uses up-to-date provenance data [33] about the available quantum hardware. These data are, e.g., retrieved from the API of the corresponding quantum hardware provider if available or otherwise determined by executing respective calibration circuits [8,16]. Finally, the NISQ Analyzer returns the set of quantum computers and simulators, providing enough qubits and a sufficient maximum executable depth to successfully execute the circuit [10].

2.2. Quantum Workflows & QuantME

The execution of quantum algorithms typically includes classical pre- and post-processing tasks before and after executing the corresponding quantum circuits [8,17]. For example, the generation of an initialization circuit to prepare the initial state in the register of the quantum hardware depending on the input data [34]. Furthermore, the impact of readout-errors can be reduced using classical post-processing [16]. Additionally, some algorithms also require algorithm-specific tasks, e.g., Shor’s [12] or Simon’s algorithm [15]. Moreover, variational algorithms, such as VQE [35] or QAOA [36], perform multiple iterations of quantum and classical processing until the result converges [8,37].
Therefore, workflow technology can be utilized to orchestrate all of the required pre-processing, quantum circuit execution, and post-processing tasks of quantum algorithms [21]. For this, the tasks are specified in so-called workflow models and connected through control and data flow edges to define their execution order and the data that have to be exchanged between them [19,38]. Subsequently, the workflow model can be executed automatically using a workflow engine. Thereby, workflows provide different benefits, such as robustness, reliability, scalability, and transactional processing [18,39]. Furthermore, they enable the specification of alternative control flows in the presence of failures, e.g., if a quantum computer is down for maintenance or if the user passes an invalid access token [40,41]. However, existing workflow languages do not provide explicit modeling constructs that are required for quantum computing related tasks [21].
To overcome these issues and ease the modeling and execution of quantum workflows, we introduced the Quantum Modeling Extension (QuantME) [21]. QuantME provides modeling constructs for different frequently occurring tasks, as well as specific configuration attributes to customize them. It can be applied to various imperative workflow languages, such as BPMN [22] or BPEL [23]. In this work, we use the BPMN concepts and their graphical notation to describe our approach. Figure 1 provides an overview of the QuantME modeling constructs. For example, there exists the Data Preparation Task, which generates an initialization circuit depending on the input data and the encoding specified in the configuration attributes and adds it to the beginning of the quantum circuit to execute [21]. This means that it generates an executable quantum circuit that is based on the input data and the base circuit for the quantum algorithm. Furthermore, the Quantum Circuit Execution Task executes the resulting initialized quantum circuit on the quantum hardware defined in the configuration attributes of the task. In addition to the new modeling constructs for the different tasks, QuantME also introduces two new data objects to transfer quantum circuits or probability distributions that result from a circuit execution between the tasks. A detailed discussion of all QuantME modeling constructs and their configuration attributes can be found in [21]. In order to avoid the need to extend the target workflow engine to understand the new modeling constructs and retain the portability of the workflows, the QuantME modeling constructs are replaced by reusable workflow fragments [42] implementing their functionality before deploying the workflow. Thereby, the selection of a suitable workflow fragment for the replacement depends on the configuration attributes of the modeling construct, such as the quantum hardware to use. These workflow fragments can be heterogeneous and use various SDKs, compilers, optimizers, or APIs of different quantum hardware providers.

2.3. Problem Statement

Various tasks in a quantum workflow have to be implemented differently, depending on the quantum hardware that should be used for the execution of a certain quantum algorithm or the corresponding quantum circuit, as outlined in the previous section [21]. However, the depth and width of the quantum circuit depend on the input data, which is usually not known when modeling the workflow [10]. Thus, the selection of suitable quantum hardware to execute a quantum circuit can only be done at the workflow runtime. However, the modeling of all possible alternative tasks clutters the workflow model. Furthermore, the resulting workflow model would then have to be adapted whenever a new alternative task is available, e.g., because a new quantum computer is released or a new readout-error mitigation technique is proposed. Thus, an approach to abstractly model the different tasks in the workflow and dynamically replace them with suitable workflow fragments based on the selected quantum hardware at runtime is needed. Hence, our first research question is as follows: “How can tasks in a quantum workflow be modeled independent of the quantum hardware to use and be dynamically replaced by workflow fragments providing the required functionality for the automatically selected quantum hardware?”
However, the workflow fragments may require services that are not always-on and must be deployed before executing the workflow fragments [40]. The manual deployment of these services is complex, time-consuming, and error-prone [43]. Additionally, the deployment of the services for all available workflow fragments would incur additional monetary costs for the used hardware, even if the services are not needed when another workflow fragment is selected. Hence, the required services for the selected workflow fragment should be automatically deployed on-demand. Therefore, the second research question for this work is as follows: “How can the workflow fragment implementing a certain task, as well as the corresponding services, be deployed on-demand during workflow runtime?”

3. Related Work

In this section, we discuss related work concerning the dynamic adaptation of workflows during runtime, the on-demand provisioning of services, and the selection of suitable quantum hardware to execute a given quantum circuit.
Several works cover the dynamic adaptation of workflows during runtime based on the current context or situation. Mundbrod et al. [44] present the concept of Context-aware Process Injection to dynamically adapt business workflows. Thereby, it enables the automated injection of workflow fragments at design and runtime based on the current context, e.g., the available resources or the customer request. Bucchiarone et al. [45] propose an extension for existing workflow languages, called Adaptable Pervasive Flows. In addition to the existing modeling constructs, they enable annotating goals, preconditions, and effects to tasks. Based on these annotations, the abstract tasks that are modeled in a workflow are dynamically replaced by fine-grained workflow fragments at runtime. Képes et al. [46] introduce an approach to adapt workflows based on the current situation. Therefore, they use a repository with workflow fragments defining the action that they implement and the situation when they can be used. Based on this repository, workflow fragments in traditional workflows are detected and replaced by abstract tasks. Subsequently, a service bus is called by the abstract tasks during runtime, which discovers and invokes a suitable workflow fragment. However, the presented works are not tailored to the peculiarities and requirements in the quantum computing domain. Therefore, the specification of the selection rules or situations to choose a workflow fragment based on the quantum hardware selection is a complex and error-prone task, which required mathematical knowledge regarding quantum computing, as well as technical knowledge about workflow technologies. Furthermore, an additional task performing the hardware selection has to be added to the workflows or an external service must be integrated into the approaches to adapt the current context or situation based on the quantum circuit to execute. In contrast, our approach abstracts from these details and provides a new modeling construct explicitly defining the relevant configuration attributes for the hardware selection, guiding quantum experts in the modeling of hardware-independent quantum workflows. Additionally, we provide a graphical notation and a corresponding modeling tool, which facilitates the modeling and understanding of quantum workflows.
AgentWork [47] is a workflow engine supporting the runtime adaptation of workflows by adding or removing tasks based on rules. Thereby, it is intended for use cases, where the modeling of alternative control flow is not sufficient or it would result in a very complex workflow model. For example, if an adaptation is required when a value exceeds a certain threshold which must be continuously monitored. Therefore, the workflow engine performs the adaptation if necessary. Rinderle et al. [48,49] introduced an adaptive workflow engine, called AristaFlow. It enables ad-hoc adaptations of running workflow instances, as well as their automated migration, if a new version of the corresponding workflow model is available. However, the AgentWork and AristaFlow workflow engines must be extended to support the quantum hardware selection at workflow runtime. This would lead to a technology lock-in and reduce the portability of the workflow models. Furthermore, their corresponding workflow languages do not provide explicit modeling constructs for quantum computing related tasks. Instead, our modeling extension eases the modeling of such tasks, is applicable to various imperative workflow languages, such as BPEL or BPMN (see Section 2.2), and it can be mapped to native modeling constructs of the extended workflow language. Therefore, the portability between different workflow engines supporting the same workflow language is retained.
Dynamic binding or late binding are concepts used in Service-oriented Computing (SoC) to describe the required functionality for a service in an abstract manner and to discover a suitable service using a service registry at runtime, which is then invoked by a service bus [38,50,51]. However, the functionality required to implement a QuantME modeling construct typically comprises several complex tasks, and wrapping them into one large service would reduce the reusability. Further, the required functionality is very heterogeneous, and the required services are currently not hosted by a provider and registered in a service registry. Finally, the usage of workflow fragments eases the later analysis of the results, as all of the steps are modeled explicitly instead of hiding them in a service.
Different research works investigate the automated deployment of the required services for a workflow execution. Qasha et al. [52] provide a framework for enabling the specification of workflows together with the execution environment of the necessary services based on TOSCA. Hence, the services can be automatically deployed using a TOSCA-compliant deployment system. To automatically deploy and scale the services that are needed to execute a BPEL workflow, Dörnemann et al. [53] introduce a concept based on an extended load balancer. Thus, it has the capabilities to deploy and decommission the services, depending on the current workload. However, both of the approaches do not support providing the services on-demand. Hence, the services for all available workflow fragments would have to be deployed before the workflow execution, incurring additional monetary costs. Vukojevic-Haupt et al. [54] present an approach for the on-demand deployment of infrastructure, middleware, and services that are required for the execution of scientific workflows. This means that, if a workflow should be executed, they first deploy the workflow engine and upload the workflow. During workflow runtime, the service invocations are sent to a service bus, which determines whether the required service is already running and forwards the request to it. Otherwise, the service is deployed on-demand using so-called service packages, containing all required information for the service deployment. Although the approach enables the on-demand deployment of services, it does currently not support the dynamic adaptation of workflows during runtime.
Some works provide concepts to determine the capabilities of quantum computers or the resource requirements of quantum circuits, not already discussed in Section 2.1. For example, Suchara et al. [55] present the Resource Estimator Toolbox, which estimates the number of qubits and gates required to execute a quantum algorithm based on the algorithm description. However, they do not compare the results to available quantum computers to determine the suitable quantum hardware for the execution. JavadiAbhari et al. [56] propose ScaffCC, a compilation framework for quantum circuits. During the compilation, they track the properties of the quantum circuits, such as their width or depth. However, the compilation is hardware-independent, and therefore, a mapping to the qubits and gate sets provided by the different quantum computers has to be done before using these properties for the selection of suitable quantum hardware. The t|ket〉 [28] compiler validates whether a quantum circuit is executable on a quantum computer, e.g., by comparing the width of the circuit to the number of provided qubits, but does not take into account the depth. Finally, different benchmarks are used to assess the capabilities of quantum computers, e.g., based on error-correction codes [30], the sampling of pseudo-random quantum circuits [4], or the Bars and Stripes machine learning data set [29]. Nevertheless, the benchmarks only provide a means to compare different quantum computers and they do not enable determining whether a quantum computer can execute a given quantum circuit.

4. Automated Quantum Hardware Selection Approach

In this section, we introduce our automated quantum hardware selection approach for quantum workflows. First, we present a new QuantME modeling construct to enable the definition of subprocesses, for which the required quantum hardware should be dynamically selected during workflow runtime based on the quantum circuit to execute. Subsequently, we show how these subprocesses are replaced by reusable workflow fragments, depending on the selected quantum hardware.

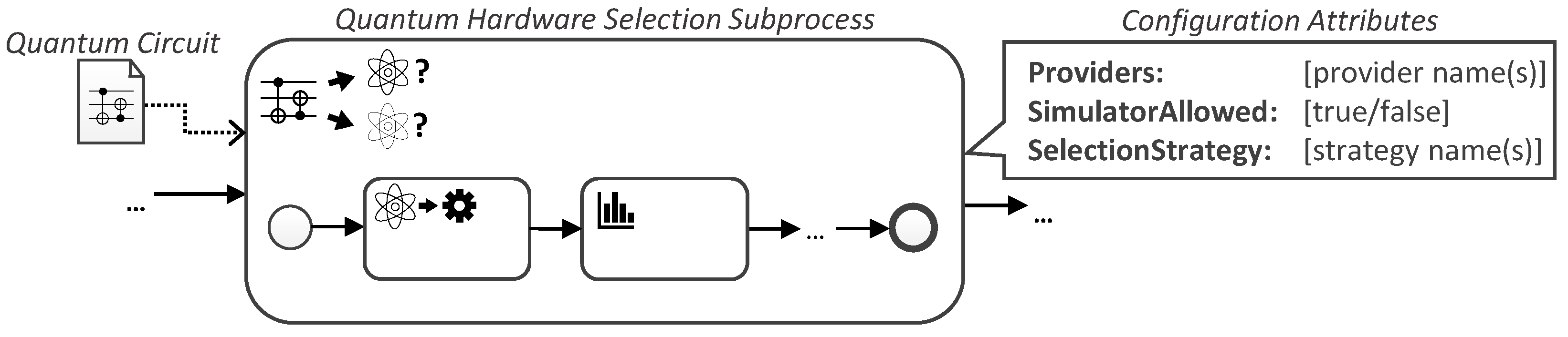
4.1. Quantum Hardware Selection Subprocess

In order to abstractly model tasks in a quantum workflow, for which the quantum hardware should be selected automatically during runtime, we introduce a new subprocess, called Quantum Hardware Selection Subprocess. Figure 2 shows the visual representation of the new subprocess. It has the semantics to perform the selection of suitable quantum hardware for a given quantum circuit and to execute all contained tasks, depending on this selection. Therefore, the Quantum Hardware Selection Subprocess always requires an ingoing Quantum Circuit Object (see Section 2.2) with the quantum circuit to conduct the selection for. The subprocess may comprise tasks to execute the quantum circuit and to mitigate the readout-errors, as depicted in Figure 2. However, it can also contain additional pre- and post-processing tasks if they depend on the quantum hardware.
The Quantum Hardware Selection Subprocess has three configuration attributes: (i) an optional Providers defining a list of quantum hardware providers to use for the hardware selection, (ii) SimulatorAllowed specifying whether simulators should also be included in the hardware selection, and (iii) an optional SelectionStrategy to select one concrete quantum computer or simulator for the execution if multiple can successfully execute the given quantum circuit. Thereby, the specification of a provider list enables the user to restrict the selection to a certain set of providers, e.g., based on the available credentials or trust in the providers. Furthermore, the analysis of the quantum hardware and quantum circuit may result in multiple quantum computers or simulators that can execute the circuit [10]. Therefore, for the selection of the concrete quantum hardware to use, different selection strategies can be defined, e.g., minimizing the monetary costs, using the quantum hardware with the shortest queue size, or preferring quantum computers to simulators. Finally, multiple strategies can be combined, e.g., first minimizing the costs and then selecting from the remaining quantum hardware while using the shortest queue size.

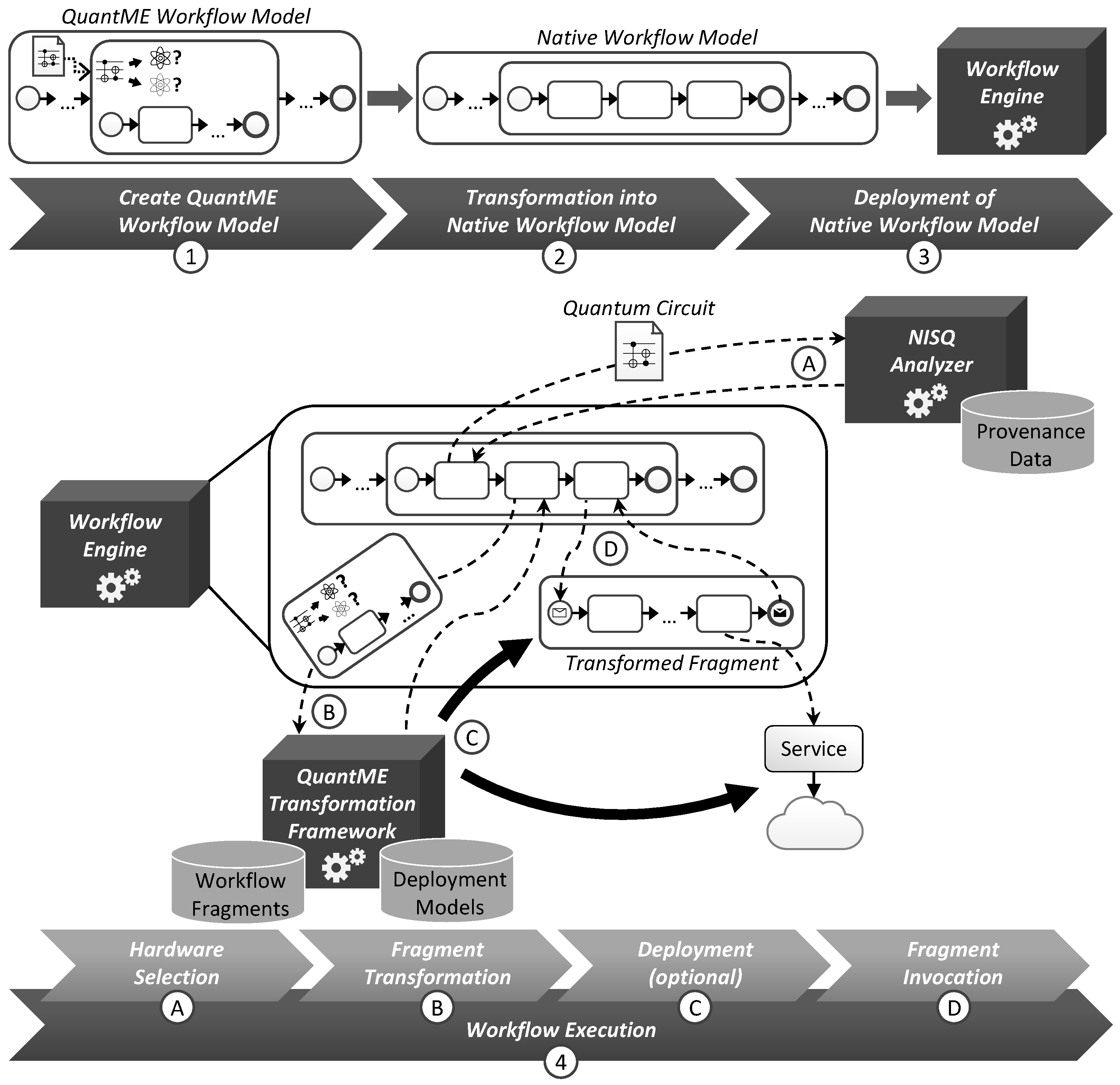
4.2. Automated Hardware Selection and Dynamic Workflow Adaptation

In the following, we introduce our approach for the hardware-independent modeling of quantum workflows and their dynamic adaptation during runtime based on the automatically selected quantum hardware. Figure 3 provides an overview of the approach, which consists of four steps that are presented in this section.
First, a QuantME workflow model implementing the quantum workflow is created. Thereby, it may orchestrate the different pre-processing, quantum circuit execution, and post-processing tasks of one or multiple quantum algorithms. The QuantME workflow model can contain the QuantME modeling constructs discussed in Section 2.2, as well as the newly introduced Quantum Hardware Selection Subprocess. Furthermore, it may comprise native modeling constructs of the used workflow language, e.g., to enable human tasks, service invocations, or the execution of scripts [21].
However, existing workflow engines cannot process the QuantME modeling constructs without extending them to understand their semantics [21]. Additionally, the extension of a workflow engine would reduce the portability of the workflows between other workflow engines that support the same workflow language, which is one of the benefits of using a standardized workflow language, such as BPMN or BPEL. Therefore, the QuantME workflow model is transformed into a native workflow model in the second step of our approach. The native workflow model only contains native modeling constructs of the used workflow language and, hence, the portability of the workflow model is retained. For this transformation, reusable workflow fragments are utilized to iteratively replace the QuantME modeling constructs [21,42]. However, the Quantum Hardware Selection Subprocess has to be handled differently, as the contained QuantME modeling constructs can only be transformed after the hardware selection during workflow runtime. Thus, it is replaced by a traditional subprocess performing the hardware selection, the transformation of the QuantME modeling constructs, and the invocation of the resulting workflow fragment. Section 4.3 discusses the replacement of Quantum Hardware Selection Subprocesses in detail. After the transformation, the native workflow model is deployed to a workflow engine in the third step and it can be instantiated by passing the required input data.
The workflow is executed in the fourth step of our approach. If the original QuantME workflow model does not contain a Quantum Hardware Selection Subprocess, it can be executed without the need for a hardware selection at runtime. Otherwise, the hardware selection and the dynamic workflow adaptation are done in four steps when a traditional subprocess replacing a Quantum Hardware Selection Subprocess is reached during workflow execution (see steps A–D in Figure 3).
First, the quantum circuit to select suitable quantum hardware for is sent to the NISQ Analyzer (step A). The NISQ Analyzer compiles the quantum circuit for the different available quantum computers or simulators. Thereby, the list of quantum computers and simulators to consider may be restricted to certain quantum hardware providers, depending on the configuration attributes of the Quantum Hardware Selection Subprocess. In the same way, simulators are only included if this is defined in the corresponding configuration attribute. Subsequently, the NISQ Analyzer uses up-to-date provenance data about the quantum hardware, such as the number of qubits or their decoherence times, to determine which quantum hardware can successfully execute the given quantum circuit [10,33]. Finally, it returns the list of suitable quantum hardware to the workflow. An error is thrown if none of the quantum computers and simulators is suitable to execute the quantum circuit. Such errors can be handled by attaching an error boundary event to the Quantum Hardware Selection Subprocess and defining an alternative control flow. In the case of multiple suitable quantum computers or simulators, the concrete quantum hardware to use is selected in the workflow based on the specified selection strategy, which is implemented by another workflow fragment (see Section 4.3).
After selecting the quantum hardware, the workflow fragment that is defined within the Quantum Hardware Selection Subprocess must be transformed to enable its execution by the workflow engine (step B). For this, the workflow fragment, as well as the selected quantum hardware, are forwarded to the QuantME Transformation Framework, which was also used for the transformation in step two of the approach. The QuantME Transformation Framework accesses a workflow fragment repository [57] and retrieves the transformed fragment, comprising only native modeling constructs. Thereby, it is configured to use the selected quantum hardware. If the transformed fragment was already deployed as a workflow model to the workflow engine, the corresponding endpoint is returned [40].
Otherwise, the transformed fragment must first be uploaded to the workflow engine (step C). Furthermore, it may require services for its execution that are not always-on and cannot be reused from a previous workflow execution [40]. Hence, these services have to be deployed on-demand before executing the transformed fragment [54]. For this, the QuantME Transformation Framework uses a repository with deployment models for the services. Such a deployment model contains all of the required information to deploy a service or application [43]. Thus, a deployment system, such as Kubernetes, Terraform, or the OpenTOSCA Container, can be used for the automatic deployment of the services [40,58]. If there are multiple deployment models for a service available, the selected quantum hardware can also be taken into account when choosing one of them for the deployment. For example, the deployment of a service performing the optimization in a variational algorithm might be more efficient using the IBM cloud if a quantum computer from IBM is selected and in Rigetti’s quantum-classical cloud platform if a quantum computer from Rigetti should be utilized [3,59]. Finally, the QuantME Transformation Framework performs the binding between the transformed fragment and the deployed services to enable their invocation [18,38].
In the last step of the workflow execution, the transformed and deployed fragment is invoked by the workflow (step D). Therefore, all of the required data are passed from the workflow to the transformed fragment, e.g., the quantum circuit to execute or the access token to use. Finally, the transformed fragment is executed, accesses the deployed services, and returns the results to the workflow.

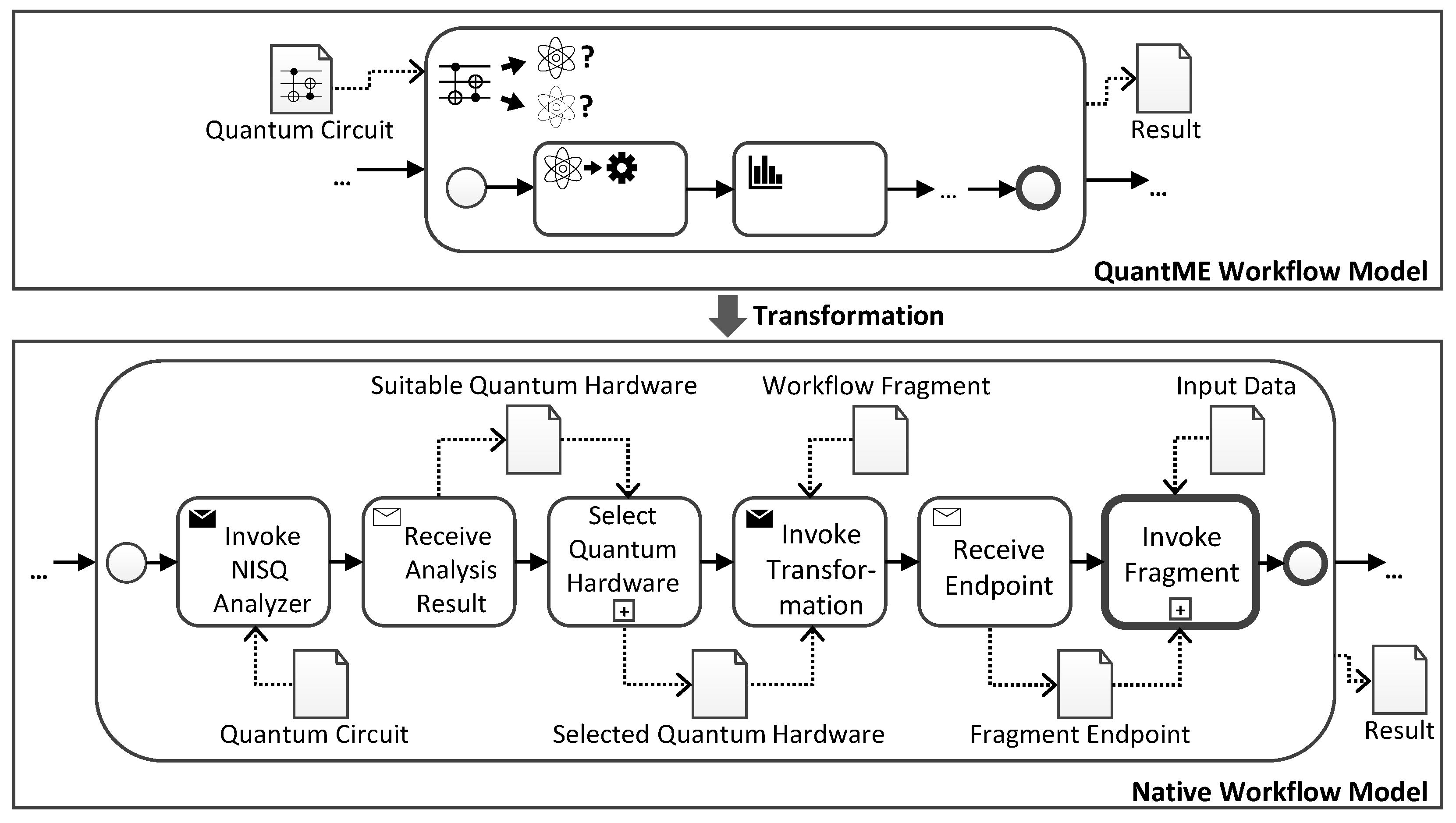
4.3. Transformation into Native Workflow Models

QuantME workflow models are transformed into native workflow models before deploying and executing them, as outlined in the previous section. Thereby, the QuantME modeling constructs that are summarized in Section 2.2 are replaced by reusable workflow fragments depending on their configuration attributes, as discussed in [21]. However, in the following, we present the transformation rule for the new Quantum Hardware Selection Subprocesses, as depicted in Figure 4.
Quantum Hardware Selection Subprocesseses are transformed into traditional subprocesses comprising six activities, independent of the contained workflow fragment. These activities are intended to orchestrate the hardware selection, transformation, and fragment invocation steps performed during workflow execution in our approach. Therefore, the resulting subprocesses only differ in the used data while orchestrating these steps. In the following, the six different activities are described:
  • First, the NISQ Analyzer is invoked with the ingoing quantum circuit from the Quantum Hardware Selection Subprocess, which is stored in a traditional data object after the transformation.
  • Afterward, the result from the NISQ Analyzer is received, and the list of suitable quantum hardware is added to a new data object.
  • Next, one of the suitable quantum computers or simulators has to be chosen depending on the selection strategy defined in the configuration attributes of the subprocess. Thereby, the implementation of this activity can, e.g., be done using a script task if the quantum hardware with the shortest queue size should be used. Another selection strategy could include a manual selection and, thus, would be implemented by a human task. Hence, new selection strategies can be added as plugins with the corresponding implementation of the selection task. For this, the implementation of the selection activity is defined as a workflow fragment. These workflow fragments are then automatically injected during transformation based on the configured selection strategy.
  • Subsequently, the transformation of the workflow fragment specified within the Quantum Hardware Selection Subprocess has to be performed. For this, the selected quantum hardware, as well as the workflow fragment to transform, are sent to the QuantME Transformation Framework. Thereby, the workflow fragment is serialized and stored in a separate data object, which can, e.g., be done using the XML syntax for BPMN [22]. The result of the transformation is a workflow model, which is assembled from multiple workflow fragments, depending on the QuantME tasks within the subprocess [21].
  • The transformed workflow model is deployed after the successful transformation, and the corresponding endpoint is received by the workflow.
  • In the last step, the deployed workflow model is invoked with the input data. Thereby, the input data comprises any ingoing data object to the replaced Quantum Hardware Selection Subprocess including the quantum circuit to execute. Finally, the result of the invocation is stored in the data object outside the subprocess, which can be accessed by subsequent tasks in the workflow. The invocation of the transformed workflow fragment is done using a call activity in BPMN. However, if such an activity is not supported by the used workflow language, then it can be split into a send and receive task, as shown for the invocation of the NISQ Analyzer.

5. System Architecture & Prototypical Validation

In this section, we prove the practical feasibility of our automated quantum hardware selection approach by presenting a system architecture in which it can be realized. Further, our prototypical implementation of this architecture and a case study is described.

5.1. System Architecture

The overall system architecture to support our approach is shown in Figure 5. It consists of extensions of the QuantME Transformation Framework [21,60] depicted on the left and the NISQ Analyzer [10,61] represented on the right. Thereby, newly added components are dark, extended components are grey, and existing unchanged components are light. The QuantME Transformation Framework provides a Graphical Workflow Modeler to enable the modeling of BPMN workflows supporting the QuantME modeling constructs. Thus, it is extended with the new Quantum Hardware Selection Subprocess. Furthermore, an HTTP REST API can be used to trigger the transformation of QuantME workflow models and the deployment of the required services for workflows. The transformation of QuantME workflow models to native workflow models is performed by the QuantME Transformer, which is extended with the transformation rule presented in Section 4.3. Thereby, it provides a plug-in system for the different selection strategies that can be defined for a Quantum Hardware Selection Subprocess. The newly added Deployment Orchestrator is in charge of deploying workflow models, as well as their required services. Hence, it enables uploading BPMN workflow models to the Camunda Engine [62], a state-of-the-art BPMN workflow engine. Additionally, the Deployment Orchestrator uses the OpenTOSCA Container [58,63], a TOSCA-compliant deployment system, to automatically deploy the services required by a workflow [40,64]. However, it is plugin-based and can be extended to support other workflow engines or deployment systems. Another component is the QuantME Validator, which is used by the Graphical Workflow Modeler to determine if the configuration attributes of the QuantME modeling constructs are valid and to mark errors during modeling. Finally, the QuantME Repository manages all of the data within the framework. This includes a repository with Workflow Fragments for the transformation, as well as Deployment Models for the service deployment. Thereby, the Deployment Models repository contains a set of TOSCA Service Templates for the required services [64]. These Service Templates comprise all needed information to deploy an instance of the corresponding service and can be consumed by a TOSCA-compliant deployment system, such as the OpenTOSCA Container [40,58]. However, also other kinds of deployment models, e.g., supported by Kubernetes or Terraform, can be stored and used for the service deployment after extending the Deployment Orchestrator accordingly.
The workflows executed by the Camunda Engine send a request to the NISQ Analyzer when hardware selection is required (see step 4A in Figure 3). Thus, they use the HTTP REST API of the NISQ Analyzer. The Selector component performs the selection of suitable quantum hardware based on defined Selection Rules, as described in Section 2.1. It uses the Connector to retrieve current characteristics of the available quantum computers and simulators from QProv [65], e.g., the decoherence times of the various qubits. QProv is a provenance system for quantum computing periodically analyzing and collecting the characteristics of quantum hardware from various vendors. The Selector also uses the Connector to interact with the Compilation Services compiling the quantum circuits and determining the hardware-dependent depth and width for the different quantum computers and simulators. In addition to the provenance data that are required by the NISQ Analyzer, further data, such as the current queue size, are retrieved and returned to the workflow together with the suitable quantum hardware. Therefore, it can be used for the selection strategy of the Quantum Hardware Selection Subprocess (see Section 4.1).

5.2. Prototypical Implementation

In order to realize the QuantME Transformation Framework, we extended the Camunda Modeler [66], which is an open-source BPMN workflow modeler. It is implemented as a desktop application using the Electron framework, comprising a graphical user interface and a Node.js backend. Thus, we extended the graphical user interface to support the QuantME modeling constructs, as well as buttons to trigger the transformation and deployment functionalities. Furthermore, an HTTP REST API was implemented using the Express framework to enable the invocation of the QuantME Transformation Framework by workflows. In order to implement the transformation and deployment functionalities, corresponding plugins were added to the Camunda Modeler. The reusable workflow fragments necessary for the transformation are stored in a Github repository using the BPMN XML syntax [22]. For the deployment of the services, the required deployment models are managed by a Winery [67] instance. Winery is a graphical modeling tool for TOSCA-based deployment models. Therefore, the deployment models are exported and uploaded to the OpenTOSCA Container to create service instances.
An in-depth description of the existing implementations of the NISQ Analyzer, the defined selection rules, and the Compilation Services can be found in [10]. We extended the Selector of the NISQ Analyzer to support the selection of suitable quantum computers based on a certain quantum circuit besides the selection that is based on a higher-level quantum algorithm and its input data. Furthermore, the Connector is extended to call QProv for retrieving the most recent characteristics of the available quantum computers as basis for the selection.

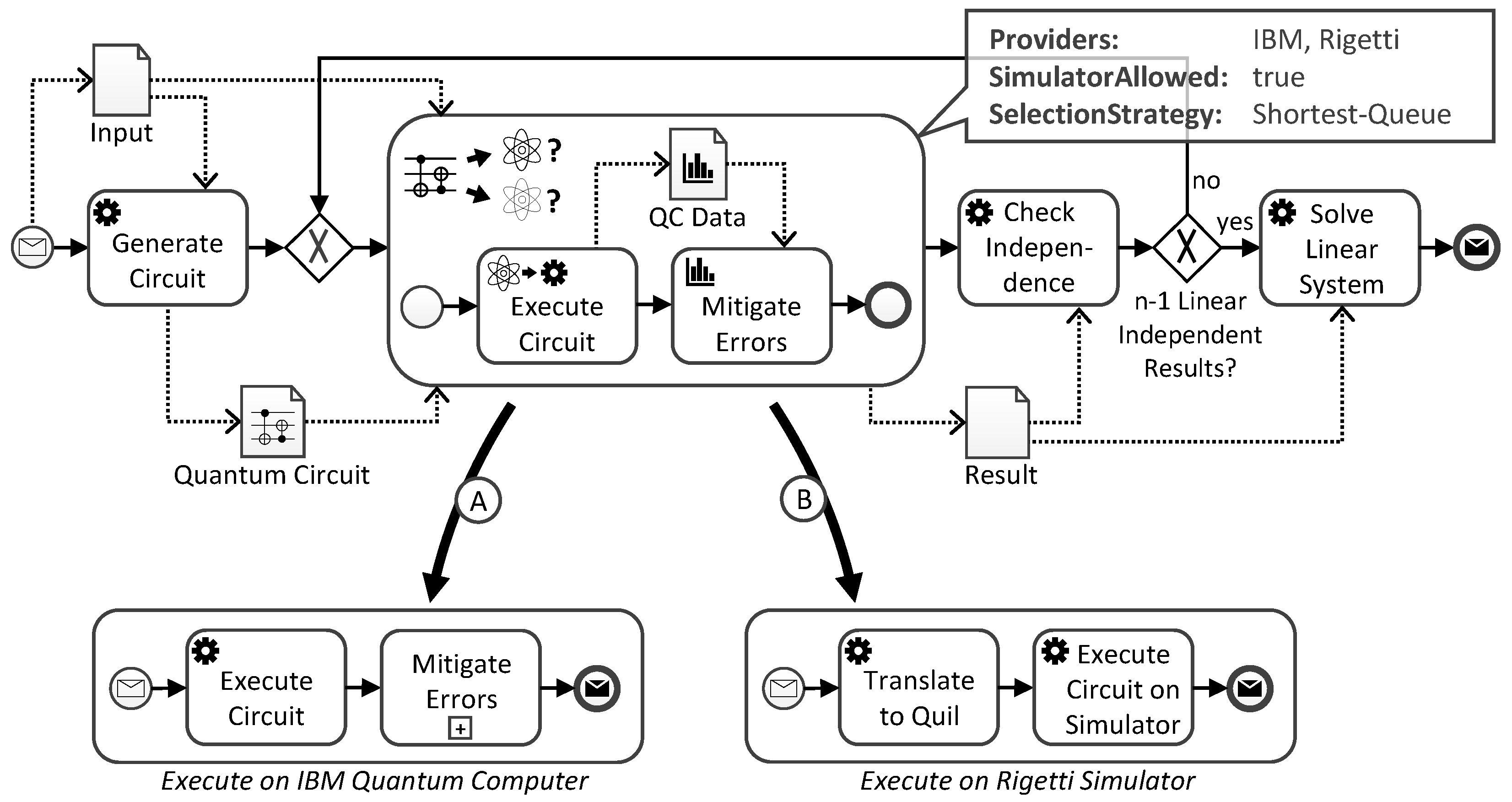
5.3. Case Study

We demonstrate the usage of the new Quantum Hardware Selection Subprocess to model a workflow implementing Simon’s algorithm [15] in a hardware-independent manner to validate our approach. Thus, the quantum hardware is selected at runtime based on the given input data, and the workflow is dynamically adapted. Figure 6 gives an overview of the corresponding workflow model, as well as the workflow fragments that can be used to replace the Quantum Hardware Selection Subprocess, depending on the hardware selection. The presented workflow model, the transformed native workflow model, and detailed instructions on how to set up the required environment and execute the workflow using the Camunda Engine are available on Github (see [68]).
The purpose of Simon’s algorithm is to determine whether a given function f ( x ) : { 0 , 1 } n → { 0 , 1 } n is bijective or not. If it is bijective, then there exists a secret bit string s which applied to an arbitrary element using xor leads to the second element that is mapped to the same target element. Thus, this secret bit string has to be found with a minimum number of function calls by a quantum computer. Thereby, the input of the quantum workflow is the oracle implementing the function f, as well as the access keys for the different quantum hardware providers that should be included in the hardware selection. Then, the required quantum circuit for Simon’s algorithm is generated based on the given oracle. For this, the functionality provided by Qiskit [69] is used. Therefore, the resulting quantum circuit is defined in the assembly language OpenQASM [70] and passed to the Quantum Hardware Selection Subprocess. The configuration attributes of the subprocess specify, that quantum computers and simulators from IBM and Rigetti should be utilized for the hardware selection. Furthermore, Shortest-Queue is used as the selection strategy, which means from the quantum computers and simulators capable of executing the quantum circuit the one with the shortest queue is chosen.
Within the Quantum Hardware Selection Subprocess, the quantum circuit is first executed on the automatically selected quantum hardware. Afterward, the readout-errors are mitigated based on classical post-processing [16]. Thereby, the QuantME tasks in the subprocess are implemented by two different workflow fragments, depending on the hardware selection, as depicted at the bottom of Figure 6.
If a quantum computer from IBM is selected, the transformation of the Quantum Hardware Selection Subprocess results in the workflow fragment on the left (see A). First, the quantum circuit is executed while using Qiskit and, then, the readout-errors are mitigated utilizing current provenance data about the used quantum computer. Thereby, the mitigation requires performing multiple tasks [8,16]. Due to space reasons, it is represented as a collapsed subprocess and the expanded subprocess is depicted in Figure 7. In the following, the different tasks of the subprocess are described:
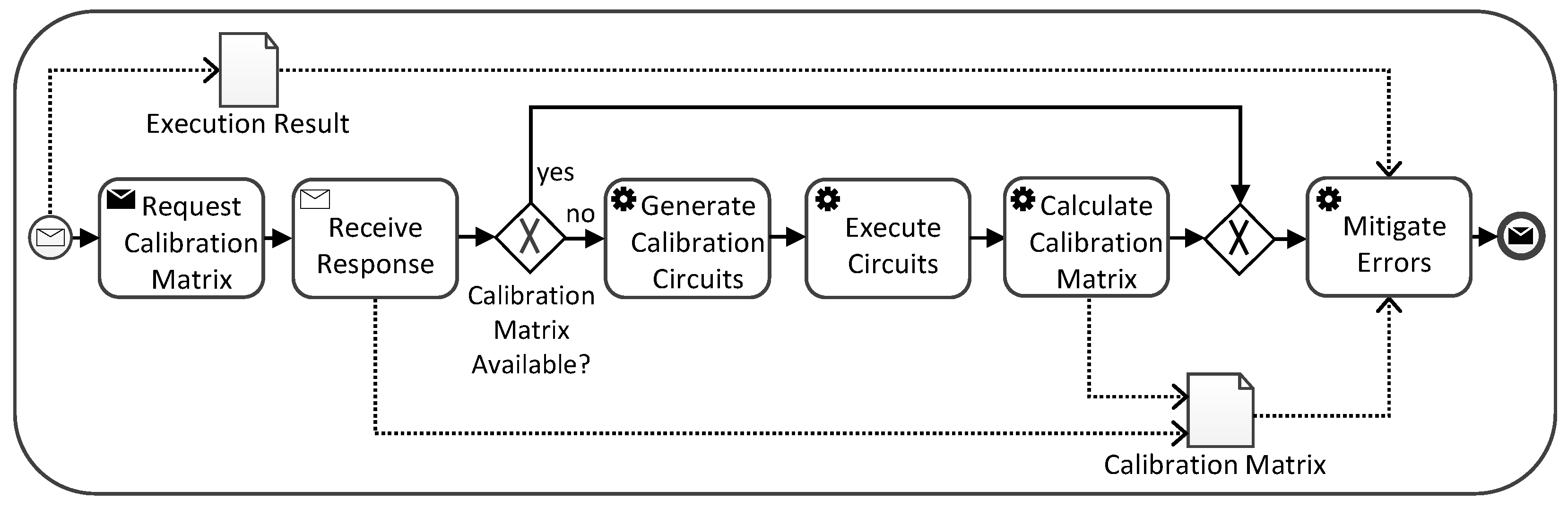
  • First, the calibration matrix for the mitigation is requested from a provenance system, such as QProv (see Section 5.1). Thereby, the calibration matrix differs for various quantum computers and, thus, it depends on the hardware selection [16].
  • Afterward, the response from the provenance system is received, containing the calibration matrix for the quantum computer if available. Hence, it does not have to be separately determined for the current workflow execution, reducing the number of quantum circuits to execute and increasing the efficiency [8].
  • However, if no up-to-date calibration matrix is available for the selected quantum computer, it can also be directly calculated in the workflow. For this, the corresponding calibration circuits are generated in the next task.
  • Subsequently, the calibration circuits are executed on the quantum computer.
  • Based on the results from the calibration circuit executions, the calibration matrix can be determined and is stored in a designated data object.
  • Finally, the received or calculated calibration matrix is used to mitigate the readout-errors in the execution results that are passed to the subprocess as input. Thereby, different readout-error mitigation or unfolding techniques are available [71,72], and in our example, the so-called matrix inversion technique is used. Hence, the calibration matrix is inverted and multiplied with the execution results to retrieve mitigated results.
In contrast, if the simulator from Rigetti is selected, the quantum circuit must be translated from OpenQASM to Quil first (see B in Figure 6). After this, the circuit can be executed using the Forest SDK [73] and the workflow fragment terminates without applying readout-error mitigation to the results. The reason for this is that we use a simulator without noise model and, hence, no mitigation is needed.
The outcome of the two alternative workflow fragments is stored in the result data object. In the next step, it is verified how many of the already received results are linearly independent. Thereby, Simon’s algorithm requires n − 1 linearly independent results. Thus, an exclusive gateway is used to execute the quantum circuit again until n − 1 results are received. The quantum circuit to execute does not differ between the iterations, and the characteristics of the quantum computers do not change significantly in this time interval [13]. Therefore, the hardware selection does not need to be repeated. Instead, the endpoint of the workflow fragment to execute is stored in the first iteration and, then, it can be directly invoked in all further iterations. When n − 1 linearly independent results are received, the linear system of equations is solved using a service task. This leads to the searched bit string s, which is returned to the user.

6. Conclusions and Future Work

In this paper, we introduced an approach for the automated quantum hardware selection for quantum workflows. For this, (i) QuantME was extended with a new modeling construct in order to enable the specification of subprocesses, containing tasks for which the required quantum hardware should be selected automatically during workflow runtime based on the quantum circuit to execute. Therefore, it enables the modeling of quantum workflows independent of a certain quantum computer or simulator to use. Furthermore, (ii) we presented an approach to dynamically replace the abstract tasks in the subprocesses by reusable workflow fragments, depending on the selected quantum hardware. Moreover, (iii) the required services of the workflow fragments are automatically deployed on-demand if they are not already running to avoid a complex and time-consuming manual deployment or the need to deploy all possible services before the workflow execution. We validated the technical feasibility of our approach by a prototypical implementation.
In future work, we will investigate new metrics for improving the estimates if a certain quantum circuit is executable on a quantum computer. For this, we plan to use machine learning techniques and analyze how such metrics can be derived from collected provenance data. Furthermore, our approach is based on the availability of suitable workflow fragments, e.g., for the execution on different quantum computers or the implementation of a certain unfolding technique. Therefore, we will develop additional workflow fragments and provide them in our repository. Additionally, quantum algorithms are currently often developed using python scripts or Jupyter notebooks. Thus, we will evaluate how quantum workflows can be generated out of such scripts to enable benefiting from their advantages, such as reliability, robustness, or scalability.

Author Contributions

Conceptualization, B.W., J.B., F.L., and M.S.; methodology, B.W.; software, B.W.; validation, B.W.; investigation, B.W., J.B., F.L., and M.S.; resources, B.W.; writing—original draft preparation, B.W.; writing—review and editing, J.B., F.L., and M.S.; visualization, B.W.; supervision, F.L.; project administration, J.B. and F.L.; funding acquisition, F.L. All authors have read and agreed to the published version of the manuscript.

Funding

The authors would like to thank the German Research Foundation (DFG) for financial support of the project within the Cluster of Excellence in Simulation Technology (EXC 2075–390740016) at the University of Stuttgart. This work was partially funded by the BMWi project PlanQK (01MK20005N).

Acknowledgments

We are grateful to IBM for providing open access to its quantum computers.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Acín, A.; Bloch, I.; Buhrman, H.; Calarco, T.; Eichler, C.; Eisert, J.; Esteve, D.; Gisin, N.; Glaser, S.J.; Jelezko, F.; et al. The quantum technologies roadmap: A European community view. New J. Phys. 2018, 20, 080201. [Google Scholar] [CrossRef]
  2. LaRose, R. Overview and Comparison of Gate Level Quantum Software Platforms. Quantum 2019, 3, 130. [Google Scholar] [CrossRef] [Green Version]
  3. Leymann, F.; Barzen, J.; Falkenthal, M.; Vietz, D.; Weder, B.; Wild, K. Quantum in the Cloud: Application Potentials and Research Opportunities. In Proceedings of the 10th International Conference on Cloud Computing and Services Science (CLOSER). SciTePress, Prague, Czech Republic, 7–9 May 2020; pp. 9–24. [Google Scholar] [CrossRef]
  4. Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; Martinis, J.M.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  5. Zhong, H.S.; Wang, H.; Deng, Y.H.; Chen, M.C.; Peng, L.C.; Luo, Y.H.; Qin, J.; Wu, D.; Ding, X.; Hu, Y.; et al. Quantum computational advantage using photons. Science 2020, 370, 1460–1463. [Google Scholar] [CrossRef]
  6. Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef]
  7. National Academies of Sciences, Engineering, and Medicine. Quantum Computing: Progress and Prospects; National Academies Press: Washington, DC, USA, 2019. [Google Scholar]
  8. Leymann, F.; Barzen, J. The bitter truth about gate-based quantum algorithms in the NISQ era. Quantum Sci. Technol. 2020, 5, 044007. [Google Scholar] [CrossRef]
  9. Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
  10. Salm, M.; Barzen, J.; Breitenbücher, U.; Leymann, F.; Weder, B.; Wild, K. The NISQ Analyzer: Automating the Selection of Quantum Computers for Quantum Algorithms. In Proceedings of the 14th Symposium and Summer School on Service-Oriented Computing (SummerSOC), Crete, Greece, 13–19 September 2020; Springer: Berlin, Germany, 2020; pp. 66–85. [Google Scholar] [CrossRef]
  11. Salm, M.; Barzen, J.; Leymann, F.; Weder, B. About a Criterion of Successfully Executing a Circuit in the NISQ Era: What wd≪1/ϵeff Really Means. In Proceedings of the 1st ACM SIGSOFT International Workshop on Architectures and Paradigms for Engineering Quantum Software (APEQS), ACM, Virtual, New York, NY, USA, 9 November 2020; pp. 10–13. [Google Scholar] [CrossRef]
  12. Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef] [Green Version]
  13. Tannu, S.S.; Qureshi, M.K. Not All Qubits Are Created Equal: A Case for Variability-Aware Policies for NISQ-Era Quantum Computers. In Proceedings of the 24th International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS), ACM, Providence, RI, USA, 13–17 April 2019; pp. 987–999. [Google Scholar] [CrossRef]
  14. Vietz, D.; Barzen, J.; Leymann, F.; Wild, K. On Decision Support for Quantum Application Developers: Categorization, Comparison, and Analysis of Existing Technologies. In Proceedings of the 21st International Conference on Computational Science (ICCS), Krakow, Poland, 16–18 June 2021; Springer: Berlin, Germany, 2021. [Google Scholar]
  15. Simon, D.R. On the Power of Quantum Computation. SIAM J. Comput. 1997, 26, 1474–1483. [Google Scholar] [CrossRef]
  16. Maciejewski, F.B.; Zimborás, Z.; Oszmaniec, M. Mitigation of readout noise in near-term quantum devices by classical post-processing based on detector tomography. Quantum 2020, 4, 257. [Google Scholar] [CrossRef]
  17. Weder, B.; Barzen, J.; Leymann, F.; Salm, M.; Vietz, D. The Quantum Software Lifecycle. In Proceedings of the 1st ACM SIGSOFT International Workshop on Architectures and Paradigms for Engineering Quantum Software (APEQS), ACM, Virtual, New York, NY, USA, 9 November 2020; pp. 2–9. [Google Scholar] [CrossRef]
  18. Leymann, F.; Roller, D. Production Workflow: Concepts and Techniques; Prentice Hall PTR: Hoboken, NJ, USA, 2000. [Google Scholar]
  19. Ellis, C.A. Workflow Technology. Comput. Support. Coop. Work Trends Softw. Ser. 1999, 7, 29–54. [Google Scholar]
  20. Leymann, F.; Karastoyanova, D.; Papazoglou, M.P. Business Process Management Standards. In Handbook on Business Process Management 1; Springer: Berlin, Germany, 2010; pp. 513–542. [Google Scholar] [CrossRef]
  21. Weder, B.; Breitenbücher, U.; Leymann, F.; Wild, K. Integrating Quantum Computing into Workflow Modeling and Execution. In Proceedings of the 13th IEEE/ACM International Conference on Utility and Cloud Computing (UCC), Leicester, UK, 7–10 December 2020; pp. 279–291. [Google Scholar] [CrossRef]
  22. OMG. Business Process Model and Notation (BPMN) Version 2.0; Object Management Group: Needham, MA, USA, 2011. [Google Scholar]
  23. OASIS. Web Services Business Process Execution Language (WS-BPEL) Version 2.0; Organization for the Advancement of Structured Information Standards: Burlington, MA, USA, 2007. [Google Scholar]
  24. Zhao, J. Quantum Software Engineering: Landscapes and Horizons. arXiv 2020, arXiv:2007.07047. [Google Scholar]
  25. Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
  26. Heyfron, L.E.; Campbell, E.T. An efficient quantum compiler that reduces T count. Quantum Sci. Technol. 2018, 4, 015004. [Google Scholar] [CrossRef] [Green Version]
  27. Khatri, S.; LaRose, R.; Poremba, A.; Cincio, L.; Sornborger, A.T.; Coles, P.J. Quantum-assisted quantum compiling. Quantum 2019, 3, 140. [Google Scholar] [CrossRef]
  28. Sivarajah, S.; Dilkes, S.; Cowtan, A.; Simmons, W.; Edgington, A.; Duncan, R. t|ket〉: A Retargetable Compiler for NISQ Devices. Quantum Sci. Technol. 2020. [Google Scholar] [CrossRef]
  29. Benedetti, M.; Garcia-Pintos, D.; Perdomo, O.; Leyton-Ortega, V.; Nam, Y.; Perdomo-Ortiz, A. A generative modeling approach for benchmarking and training shallow quantum circuits. NPJ Quantum Inf. 2019, 5, 1–9. [Google Scholar] [CrossRef]
  30. Knill, E.; Laflamme, R.; Martinez, R.; Negrevergne, C. Benchmarking Quantum Computers: The Five-Qubit Error Correcting Code. Phys. Rev. Lett. 2001, 86, 5811–5814. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  31. Sete, E.A.; Zeng, W.J.; Rigetti, C.T. A Functional Architecture for Scalable Quantum Computing. In Proceedings of the IEEE International Conference on Rebooting Computing, San Diego, CA, USA, 17–19 October 2016; pp. 1–6. [Google Scholar] [CrossRef]
  32. Bishop, L.; Bravyi, S.; Cross, A.; Gambetta, J.; Smolin, J. Quantum Volume Technical Report. 2017. Available online: http://book.itep.ru/depository/quant_comp/quant_volume.pdf (accessed on 19 April 2021).
  33. Herschel, M.; Diestelkämper, R.; Ben Lahmar, H. A Survey on Provenance: What for? What Form? What from? VLDB J. 2017, 26, 881–906. [Google Scholar] [CrossRef]
  34. Cortese, J.A.; Braje, T.M. Loading Classical Data into a Quantum Computer. arXiv 2018, arXiv:1807.02500. [Google Scholar]
  35. Kandala, A.; Mezzacapo, A.; Temme, K.; Takita, M.; Brink, M.; Chow, J.M.; Gambetta, J.M. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 2017, 549, 242–246. [Google Scholar] [CrossRef]
  36. Farhi, E.; Goldstone, J.; Gutmann, S. A Quantum Approximate Optimization Algorithm. arXiv 2014, arXiv:1411.4028. [Google Scholar]
  37. McClean, J.R.; Romero, J.; Babbush, R.; Aspuru-Guzik, A. The theory of variational hybrid quantum-classical algorithms. New J. Phys. 2016, 18, 023023. [Google Scholar] [CrossRef]
  38. Leymann, F.; Roller, D.; Schmidt, M. Web services and business process management. IBM Syst. J. 2002, 41, 198–211. [Google Scholar] [CrossRef]
  39. Greenfield, P.; Fekete, A.; Jang, J.; Kuo, D. Compensation is Not Enough. In Proceedings of the 7th IEEE International Enterprise Distributed Object Computing Conference (EDOC), Brisbane, QLD, Australia, 19 September 2003; pp. 232–239. [Google Scholar] [CrossRef]
  40. Weder, B.; Breitenbücher, U.; Képes, K.; Leymann, F.; Zimmermann, M. Deployable Self-contained Workflow Models. In Proceedings of the 8th European Conference on Service-Oriented and Cloud Computing (ESOCC), Crete, Greece, 28–30 September 2020; Springer: Berlin, Germany, 2020; pp. 85–96. [Google Scholar] [CrossRef]
  41. Eder, J.; Liebhart, W. Workflow Recovery. In Proceedings of the First International Conference on Cooperative Information Systems (IFCIS), Brussels, Belgium, 19–21 June 1996; pp. 124–134. [Google Scholar] [CrossRef]
  42. Eberle, H.; Unger, T.; Leymann, F. Process Fragments. In On the Move to Meaningful Internet Systems (OTM); Springer: Berlin, Germany, 2009; pp. 398–405. [Google Scholar] [CrossRef]
  43. Breitenbücher, U.; Binz, T.; Képes, K.; Kopp, O.; Leymann, F.; Wettinger, J. Combining Declarative and Imperative Cloud Application Provisioning based on TOSCA. In Proceedings of the International Conference on Cloud Engineering (IC2E), Boston, MA, USA, 11–14 March 2014; pp. 87–96. [Google Scholar] [CrossRef]
  44. Mundbrod, N.; Grambow, G.; Kolb, J.; Reichert, M. Context-Aware Process Injection: Enhancing Process Flexibility by Late Extension of Process Instances. In On the Move to Meaningful Internet Systems (OTM); Springer: Berlin, Germany, 2015; pp. 127–145. [Google Scholar] [CrossRef]
  45. Bucchiarone, A.; Marconi, A.; Pistore, M.; Raik, H. Dynamic Adaptation of Fragment-based and Context-aware Business Processes. In Proceedings of the 19th International Conference on Web Services (ICWS), Honolulu, HI, USA, 24–29 June 2012; pp. 33–41. [Google Scholar] [CrossRef]
  46. Képes, K.; Breitenbücher, U.; Sáez, S.G.; Guth, J.; Leymann, F.; Wieland, M. Situation-Aware Execution and Dynamic Adaptation of Traditional Workflow Models. In Proceedings of the 5th European Conference on Service-Oriented and Cloud Computing (ESOCC), Vienna, Austria, 5–7 September 2016; Springer: Berlin, Germany, 2016; pp. 69–83. [Google Scholar] [CrossRef] [Green Version]
  47. Müller, R.; Greiner, U.; Rahm, E. AgentWork: A workflow system supporting rule-based workflow adaptation. Data Knowl. Eng. 2004, 51, 223–256. [Google Scholar] [CrossRef]
  48. Rinderle-Ma, S.; Reichert, M. Advanced Migration Strategies for Adaptive Process Management Systems. In Proceedings of the 12th IEEE Conference on Commerce and Enterprise Computing, Shanghai, China, 10–12 November 2010; pp. 56–63. [Google Scholar] [CrossRef] [Green Version]
  49. Dadam, P.; Reichert, M. The ADEPT project: A decade of research and development for robust and flexible process support. Comput. Sci. Res. Dev. 2009, 23, 81–97. [Google Scholar] [CrossRef] [Green Version]
  50. Garofalakis, J.; Panagis, Y.; Sakkopoulos, E.; Tsakalidis, A. Contemporary Web Service Discovery Mechanisms. J. Web Eng. 2006, 5, 265–290. [Google Scholar]
  51. Schonenberg, H.; Mans, R.; Russell, N.; Mulyar, N.; van der Aalst, W. Process Flexibility: A Survey of Contemporary Approaches. In Advances in Enterprise Engineering I; Springer: Berlin, Germany, 2008; pp. 16–30. [Google Scholar] [CrossRef]
  52. Qasha, R.; Cala, J.; Watson, P. Towards Automated Workflow Deployment in the Cloud using TOSCA. In Proceedings of the 8th International Conference on Cloud Computing (CLOUD), New York, NY, USA, 27 June–2 July 2015; pp. 1037–1040. [Google Scholar] [CrossRef]
  53. Dörnemann, T.; Juhnke, E.; Freisleben, B. On-Demand Resource Provisioning for BPEL Workflows Using Amazon’s Elastic Compute Cloud. In Proceedings of the 9th IEEE/ACM International Symposium on Cluster Computing and the Grid, Shanghai, China, 18–21 May 2009; pp. 140–147. [Google Scholar] [CrossRef]
  54. Vukojevic-Haupt, K.; Karastoyanova, D.; Leymann, F. On-demand Provisioning of Infrastructure, Middleware and Services for Simulation Workflows. In Proceedings of the 6th International Conference on Service Oriented Computing and Applications (ICSOC), Koloa, HI, USA, 16–18 December 2013; pp. 91–98. [Google Scholar] [CrossRef]
  55. Suchara, M.; Kubiatowicz, J.; Faruque, A.; Chong, F.T.; Lai, C.Y.; Paz, G. QuRE: The Quantum Resource Estimator Toolbox. In Proceedings of the 31st International Conference on Computer Design (ICCD), Asheville, NC, USA, 6–9 October 2013; pp. 419–426. [Google Scholar] [CrossRef] [Green Version]
  56. JavadiAbhari, A.; Patil, S.; Kudrow, D.; Heckey, J.; Lvov, A.; Chong, F.T.; Martonosi, M. ScaffCC: A Framework for Compilation and Analysis of Quantum Computing Programs. In Proceedings of the 11th ACM Conference on Computing Frontiers, ACM, Cagliari, Italy, 20–22 May 2014. [Google Scholar] [CrossRef]
  57. Schumm, D.; Karastoyanova, D.; Leymann, F.; Strauch, S. Fragmento: Advanced Process Fragment Library. In Proceedings of the 19th International Conference on Information Systems Development, Prague, Czech Republic, 25–27 August 2010; Springer: Berlin, Germany, 2010; pp. 659–670. [Google Scholar] [CrossRef]
  58. Binz, T.; Breitenbücher, U.; Haupt, F.; Kopp, O.; Leymann, F.; Nowak, A.; Wagner, S. OpenTOSCA - A Runtime for TOSCA-based Cloud Applications. In Proceedings of the 11th International Conference on Service-Oriented Computing (ICSOC), Berlin, Germany, 2–5 December 2013; Springer: Berlin, Germany, 2013; pp. 692–695. [Google Scholar] [CrossRef] [Green Version]
  59. Karalekas, P.J.; Tezak, N.A.; Peterson, E.C.; Ryan, C.A.; da Silva, M.P.; Smith, R.S. A quantum-classical cloud platform optimized for variational hybrid algorithms. Quantum Sci. Technol. 2020, 5, 024003. [Google Scholar] [CrossRef] [Green Version]
  60. University of Stuttgart. QuantME Transformation Framework—Source Code. 2021. Available online: https://github.com/UST-QuAntiL/QuantME-TransformationFramework (accessed on 19 April 2021).
  61. University of Stuttgart. NISQ Analyzer—Source Code. 2021. Available online: https://github.com/UST-QuAntiL/nisq-analyzer (accessed on 19 April 2021).
  62. Camunda. Camunda BPMN Workflow Engine. 2021. Available online: https://camunda.com/products/camunda-bpm/bpmn-engine (accessed on 19 April 2021).
  63. University of Stuttgart. OpenTOSCA Container - Source Code. 2021. Available online: https://github.com/OpenTOSCA/container (accessed on 19 April 2021).
  64. OASIS. Topology and Orchestration Specification for Cloud Applications (TOSCA) Version 1.0; Organization for the Advancement of Structured Information Standards: Burlington, MA, USA, 2013. [Google Scholar]
  65. University of Stuttgart. QProv—Source Code. 2021. Available online: https://github.com/UST-QuAntiL/qprov (accessed on 19 April 2021).
  66. Camunda. Camunda BPMN Modeler. 2021. Available online: https://camunda.com/products/camunda-bpm/modeler (accessed on 19 April 2021).
  67. University of Stuttgart. Winery—Source Code. 2021. Available online: https://github.com/OpenTOSCA/winery (accessed on 19 April 2021).
  68. University of Stuttgart. QuantME Use Case Repository—Source Code. 2021. Available online: https://github.com/UST-QuAntiL/QuantME-UseCases (accessed on 19 April 2021).
  69. IBM. Qiskit. 2021. Available online: https://qiskit.org (accessed on 19 April 2021).
  70. Cross, A.W.; Bishop, L.S.; Smolin, J.A.; Gambetta, J.M. Open Quantum Assembly Language. arXiv 2017, arXiv:1707.03429. [Google Scholar]
  71. Brenner, L.; Balasubramanian, R.; Burgard, C.; Verkerke, W.; Cowan, G.; Verschuuren, P.; Croft, V. Comparison of unfolding methods using RooFitUnfold. Int. J. Mod. Phys. A 2020, 35, 2050145. [Google Scholar] [CrossRef]
  72. Nachman, B.; Urbanek, M.; de Jong, W.A.; Bauer, C.W. Unfolding Quantum Computer Readout Noise. NPJ Quantum Inf. 2020, 6, 1–7. [Google Scholar] [CrossRef]
  73. Rigetti. Docs for the Forest SDK. 2021. Available online: http://docs.rigetti.com (accessed on 19 April 2021).
Electronics 10 00984 g001 550
Figure 1. Overview of the QuantME modeling constructs (based on [21]).
Figure 1. Overview of the QuantME modeling constructs (based on [21]).
Electronics 10 00984 g001
Electronics 10 00984 g002 550
Figure 2. Graphical notation of the Quantum Hardware Selection Subprocess.
Figure 2. Graphical notation of the Quantum Hardware Selection Subprocess.
Electronics 10 00984 g002
Electronics 10 00984 g003 550
Figure 3. Automated selection of quantum hardware for quantum workflows.
Figure 3. Automated selection of quantum hardware for quantum workflows.
Electronics 10 00984 g003
Electronics 10 00984 g004 550
Figure 4. The transformation rule of the Quantum Hardware Selection Subprocess.
Figure 4. The transformation rule of the Quantum Hardware Selection Subprocess.
Electronics 10 00984 g004
Electronics 10 00984 g005 550
Figure 5. System architecture for the automated quantum hardware selection.
Figure 5. System architecture for the automated quantum hardware selection.
Electronics 10 00984 g005
Electronics 10 00984 g006 550
Figure 6. Executing Simon‘s algorithm using dynamically selected quantum hardware.
Figure 6. Executing Simon‘s algorithm using dynamically selected quantum hardware.
Electronics 10 00984 g006
Electronics 10 00984 g007 550
Figure 7. Subprocess to mitigate readout-errors in the results of a quantum circuit execution.
Figure 7. Subprocess to mitigate readout-errors in the results of a quantum circuit execution.
Electronics 10 00984 g007
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Weder, B.; Barzen, J.; Leymann, F.; Salm, M. Automated Quantum Hardware Selection for Quantum Workflows. Electronics 2021, 10, 984. https://doi.org/10.3390/electronics10080984

AMA Style

Weder B, Barzen J, Leymann F, Salm M. Automated Quantum Hardware Selection for Quantum Workflows. Electronics. 2021; 10(8):984. https://doi.org/10.3390/electronics10080984

Chicago/Turabian Style

Weder, Benjamin, Johanna Barzen, Frank Leymann, and Marie Salm. 2021. "Automated Quantum Hardware Selection for Quantum Workflows" Electronics 10, no. 8: 984. https://doi.org/10.3390/electronics10080984

APA Style

Weder, B., Barzen, J., Leymann, F., & Salm, M. (2021). Automated Quantum Hardware Selection for Quantum Workflows. Electronics, 10(8), 984. https://doi.org/10.3390/electronics10080984

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop