Hierarchic Clustering-Based Face Enhancement for Images Captured in Dark Fields
Abstract
1. Introduction
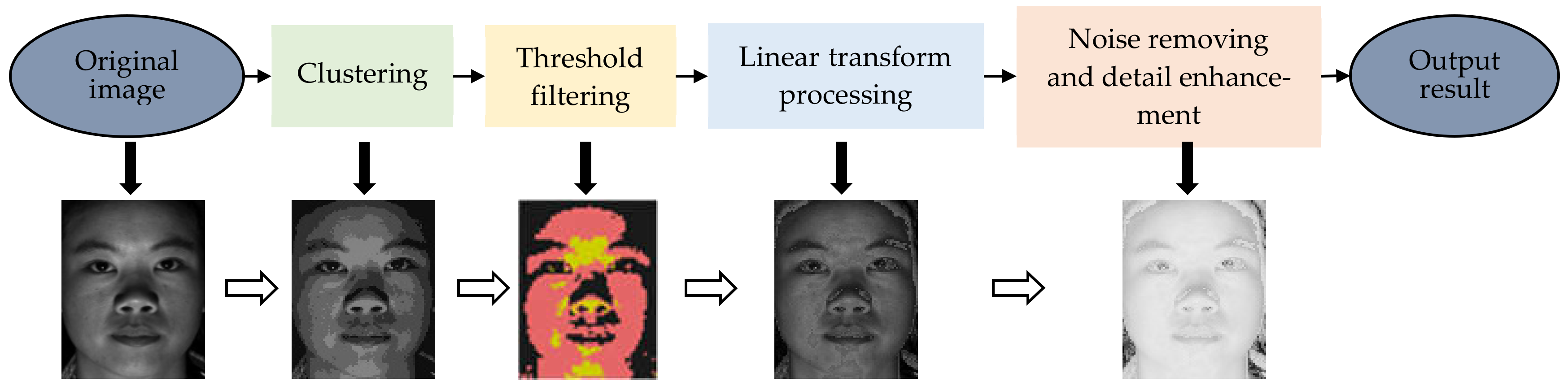
2. Proposed Algorithm
2.1. Initial Clustering of Face Image
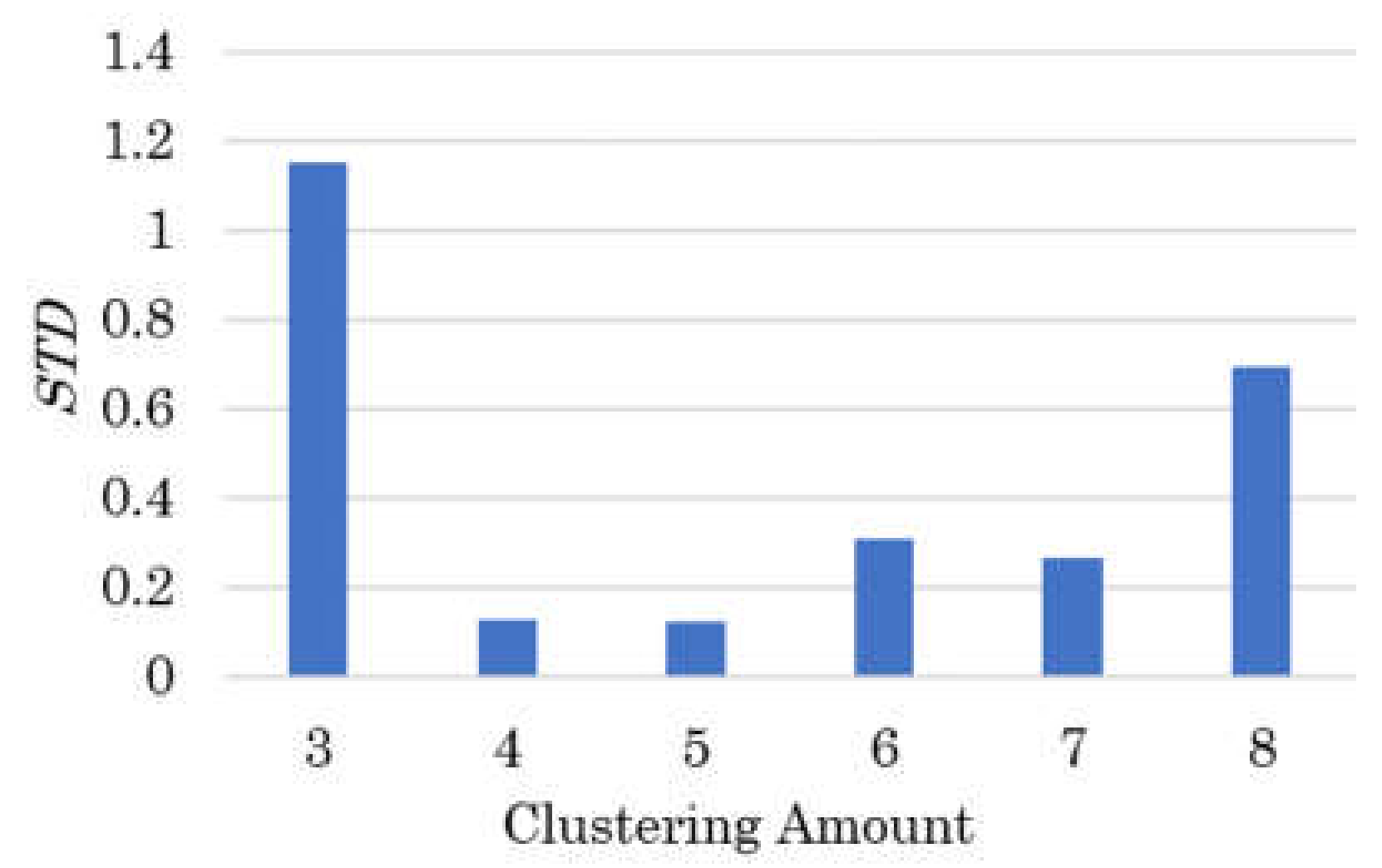
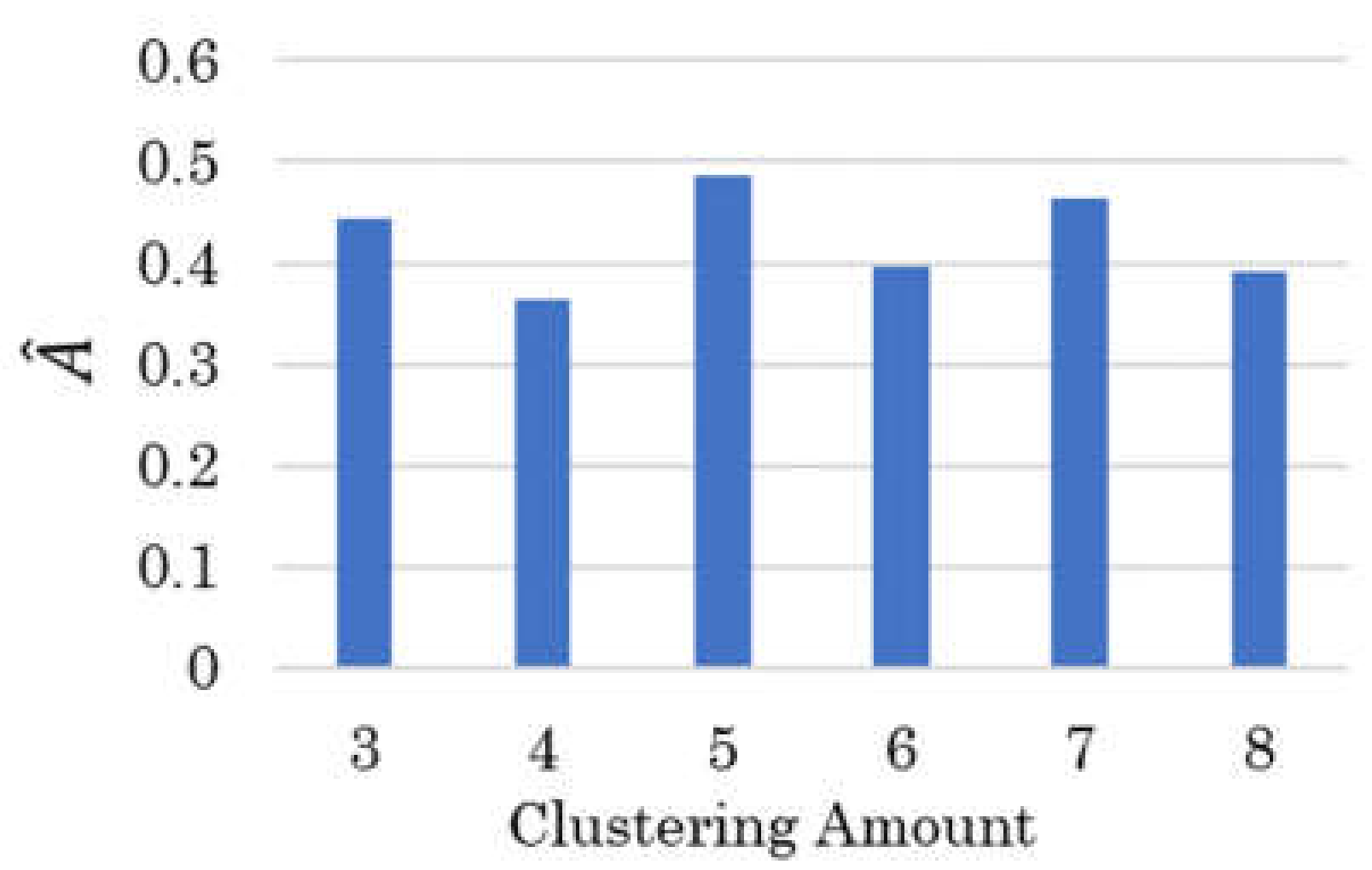
2.2. Dimension Reduction of Face Clustering
2.3. Intensity Mapping of over Dark or over Bright Region
2.4. Contrast Enhancement and Noise Removement
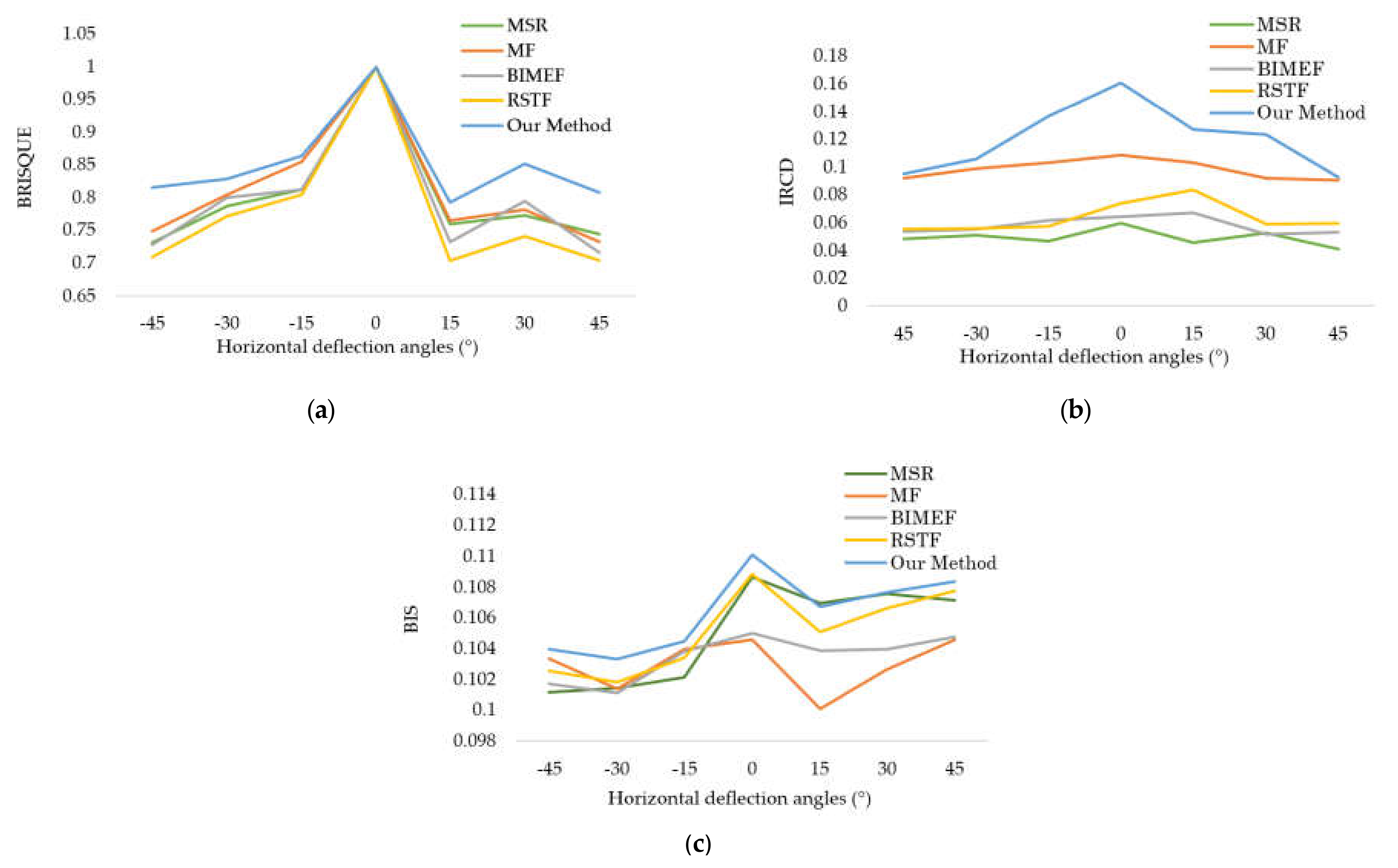
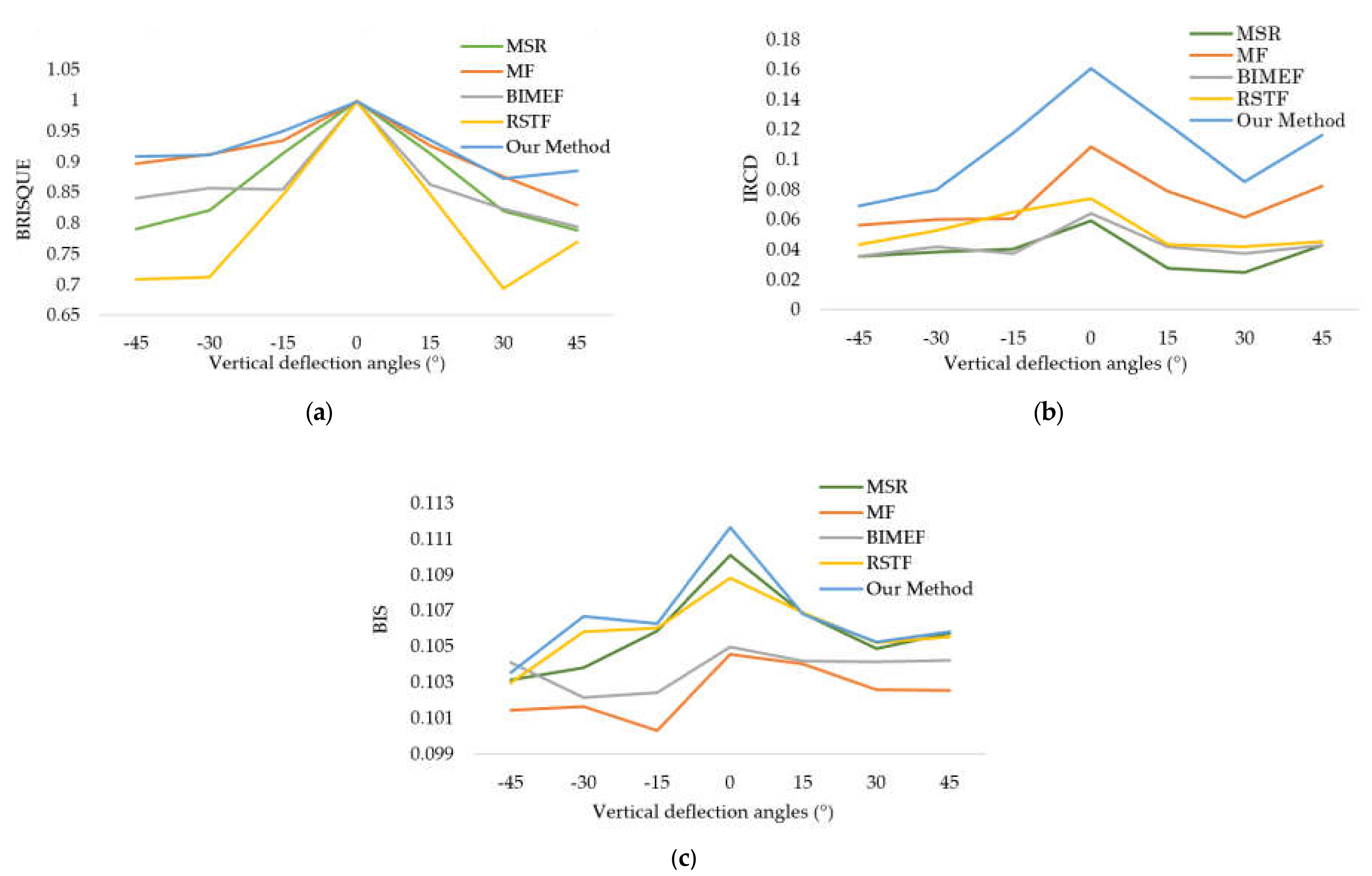
3. Experiments
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, W.; Chellappa, R.; Phillips, P.J.; Rosenfeld, A. Face recognition: A literature survey. ACM Comput. Surv. 2003, 35, 399–458. [Google Scholar] [CrossRef]
- Wang, W.; Wu, X.; Yuan, X.; Gao, Z. An experiment-based review of low-light image enhancement methods. IEEE Access 2020, 8, 87884–87917. [Google Scholar] [CrossRef]
- Wang, M.; Chen, C.; Pan, J.; Zhu, Y.; Chang, X. A relative radiometric calibration method based on the histogram of side-slither data for high-resolution optical satellite imagery. Remote Sens. 2018, 10, 381. [Google Scholar] [CrossRef]
- Das, S.; Gulati, T.; Mittal, V. Histogram equalization techniques for contrast enhancement: A review. Int. J. Comput. Appl. 2015, 114, 32–36. [Google Scholar] [CrossRef]
- Mathias, A.; Tsamene, D. Enhancing gray scale images for face detection under unstable lighting condition. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 12–20. [Google Scholar]
- Liu, B.; Wang, X.; Jin, W.; Chen, Y.; Liu, C.; Liu, X. Infrared image detail enhancement based on local adaptive gamma correction. Chin. Opt. Lett. 2012, 10, 25–29. [Google Scholar]
- Fan, C.; Zhang, F. Homomorphic filtering based illumination normalization method for face recognition. Pattern Recogn. Lett. 2011, 32, 1468–1479. [Google Scholar] [CrossRef]
- Shim, H.; Luo, J.; Chen, T. A subspace model-based approach to face relighting under unknown lighting and poses. IEEE Trans. Image Process. 2008, 17, 1331–1341. [Google Scholar] [CrossRef]
- Lagorce, X.; Orchard, G.; Galluppi, F.; Shi, B.E.; Benosman, R.B. HOTS: A hierarchy of event-based time-surfaces for pattern recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1346–1359. [Google Scholar] [CrossRef]
- Karczmarek, P.; Pedrycz, W.; Kiersztyn, A.; Rutka, P. A study in facial features saliency in face recognition: An analytic hierarchy process approach. Soft Comput. 2017, 21, 7503–7517. [Google Scholar] [CrossRef]
- Fnaiech, A.; Sahli, H.; Sayadi, M.; Gorce, P. Fear facial emotion recognition based on angular deviation. Electronics 2021, 10, 358. [Google Scholar] [CrossRef]
- Lecca, M. STAR: A segmentation-based approximation of point-based sampling milano Retinex for color image enhancement. IEEE Trans. Image Process. 2018, 27, 5802–5812. [Google Scholar] [CrossRef]
- Ren, X.; Yang, W.; Cheng, W.; Liu, J. LR3M: Robust low-light enhancement via low-rank regularized Retinex model. IEEE Trans. Image Process. 2020, 29, 5862–5876. [Google Scholar] [CrossRef]
- Park, S.; Yu, S.; Kim, M.; Park, K.; Paik, J. Dual autoencoder network for Retinex-based low-light image enhancement. IEEE Access 2018, 6, 22084–22093. [Google Scholar] [CrossRef]
- Devi, G.S.; Rabbani, M.M.A. Image contrast enhancement using histogram equalization with fuzzy approach on the neighbourhood metrics (FANMHE). In Proceedings of the International Conference on Wireless Communications, Signal Processing and Networking, Chennai, India, 23–25 March 2016. [Google Scholar]
- Lin, P.T.; Lin, B.R. Fuzzy automatic contrast enhancement based on fuzzy C-means clustering in CIELAB color space. In Proceedings of the IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications, Auckland, New Zealand, 29–31 August 2016. [Google Scholar]
- Zhong, X.; Wen, X.; Zhu, D. Lookup-table-based inverse model for human skin reflectance spectroscopy: Two-layered Monte Carlo simulations and experiments. Opt. Express 2014, 22, 1852–1864. [Google Scholar] [CrossRef]
- Sánchez-Reyes, L.-M.; Rodríguez-Reséndiz, J.; Salazar-Colores, S.; Avecilla-Ramírez, G.N.; Pérez-Soto, G.I. A High-accuracy mathematical morphology and multilayer perceptron-based approach for melanoma detection. Appl. Sci. 2020, 10, 1098. [Google Scholar] [CrossRef]
- Bijl, A.F. A Comparison of Clustering Algorithms for Face Clustering. Ph.D. Thesis, University of Groningen, Groningen, The Netherlands, 2018. [Google Scholar]
- Challa, A.; Danda, S.; Sagar, B.S.D.; Najman, L. Power spectral clustering. J. Math. Imaging Vis. 2020, 62, 1195–1213. [Google Scholar] [CrossRef]
- Saxena, A.; Prasad, M.; Gupta, A.; Bharill, N.; Patel, O.P.; Tiwari, A.; Er, M.J.; Ding, W.; Lin, C. A review of clustering techniques and developments. Neurocomputing 2017, 267, 664–681. [Google Scholar] [CrossRef]
- Ahmad, A.U.; Starkey, A. Application of feature selection methods for automated clustering analysis: A review on synthetic datasets. Neural Comput. Appl. 2018, 29, 317–328. [Google Scholar] [CrossRef]
- Giampietro, C.; Roberto, G. Towards a generalized beer-lambert law. Fractal Fract. 2018, 2, 8. [Google Scholar]
- Masuda, Y.; Yamashita, T.; Hirao, T.; Takahashi, M. An innovative method to measure skin pigmentation. Skin Res. Tech. 2009, 15, 224–229. [Google Scholar] [CrossRef]
- Tsumura, N.; Ojima, N.; Sato, K.; Shiraishi, M.; Shimizu, H.; Nabeshima, H.; Akazaki, S.; Hori, K.; Miyake, Y. Image-based skin color and texture analysis/synthesis by extracting hemoglobin and melanin information in the skin. ACM Trans. Graph. 2003, 22, 770–779. [Google Scholar] [CrossRef]
- Blondel, W.; Delconte, A.; Khairallah, G.; Marchal, F.; Gavoille, A.; Amouroux, M. Spatially-resolved multiply-excited autofluorescence and diffuse reflectance spectroscopy: SpectroLive medical device for skin in vivo optical biopsy. Electronics 2021, 10, 243. [Google Scholar] [CrossRef]
- Li, P.; Wang, H.; Li, Y.; Liu, M. Analysis of face detection based on skin color characteristic and AdaBoost algorithm. J. Phys. Conf. Ser. 2020, 1601, 052019. [Google Scholar] [CrossRef]
- Georghiades, A.S.; Belhumeur, P.N.; Kriegman, D.J. From Few to Many: Illumination cone models for face recognition under variable lighting and pose. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 643–660. [Google Scholar] [CrossRef]
- Fu, X.; Zeng, D.; Huang, Y.; Liao, Y.; Ding, X.; Paisley, J. A fusion-based enhancing method for weakly illuminated images. IEEE Trans. Signal Process. 2016, 129, 82–96. [Google Scholar] [CrossRef]
- Wang, W.; Wei, C.; Yang, W.; Liu, J. GLADNet: Low-light enhancement network with global awareness. In Proceedings of the IEEE International Conference on Automatic Face and Gesture Recognition, Xi’an, China, 15–19 May 2018. [Google Scholar]
- Seyedali, M. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef]
- Chandra, R.; An-Nissa, S.; Zamzami, E.M. Comparative analysis of eigenface and learning vector quantization (lvq) to face recognition. J. Phys. Conf. Ser. 2020, 1566, 012012. [Google Scholar] [CrossRef]
- Mittal, A.; Moorthy, A.K.; Bovik, A.C. No-reference image quality assessment in the spatial domain. IEEE Trans Image Process. 2012, 21, 4695–4708. [Google Scholar] [CrossRef]
- Liu, H.; Lu, H.; Zhang, Y. Image enhancement for outdoor long-range surveillance using IQ-learning multiscale Retinex. IET Image Process. 2017, 11, 786–795. [Google Scholar] [CrossRef]
- De, K.; Masilamani, V. No-reference image sharpness measure using discrete cosine transform statistics and multivariate adaptive regression splines for robotic applications. Procedia Comput. Sci. 2018, 133, 268–275. [Google Scholar] [CrossRef]
- Liang, J.; Wang, J.; Quan, Y.; Chen, T.; Liu, J.; Ling, H.; Xu, Y. Recurrent exposure generation for low-light face detection. arXiv 2020, arXiv:2007.10963. [Google Scholar]
- Guo, Y.; Ke, X.; Ma, J.; Zhang, J. A pipeline neural network for low-light image enhancement. IEEE Access 2019, 7, 13737–13744. [Google Scholar] [CrossRef]


| Clustering Algorithms | ||||
|---|---|---|---|---|
| K-Means | BIRCH | Agglomerative Clustering | DBSCAN | |
| Times (s) | 0.8112 | 2.2448 | 490.0283 | 266.2787 |
| Image ID | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Image 1 | Image 2 | Image 3 | Image 4 | Image 5 | Image 6 | Image 7 | Image 8 | ||
| Gray value of clustering center | 1 | 0.0592 | 0.0472 | 0.0423 | 0.0369 | 0.0356 | 0.0329 | 0.0680 | 0.0771 |
| 0.1922 | 0.1959 | 0.1772 | 0.1427 | 0.1796 | 0.2000 | 0.3087 | 0.2335 | ||
| 0.3039 | 0.3648 | 0.3071 | 0.2470 | 0.3412 | 0.4005 | 0.5340 | 0.3812 | ||
| 0.4033 | 0.5343 | 0.4986 | 0.3864 | 0.4753 | 0.6122 | 0.7449 | 0.5282 | ||
| 0.5234 | 0.7554 | 0.8097 | 0.5176 | 0.6506 | 0.8244 | 0.9427 | 0.7397 | ||
| Threshold | 0.2117 | 0.0666 | 0.1098 | 0.1176 | 0.0784 | 0.0352 | 0.0941 | 0.1882 | |
| 0.5019 | 0.6588 | 0.5647 | 0.5215 | 0.6627 | 0.7451 | 0.9921 | 0.7176 | ||
| Intensity region | Low | ||||||||
| Middle | |||||||||
| High | - | - | - | ||||||
| Evaluation Algorithms | ||||||||
|---|---|---|---|---|---|---|---|---|
| Original Image | MSR | MF | BIMEF | RSTF | Mini-Type Version of Our Method | Our Method | ||
| FRR | Sparse Representation-based method | 83.3333 | 86.6667 | 94.8148 | 84.8148 | 81.4815 | 93.9541 | 96.2963 |
| PCA-based method | 60.0000 | 77.0370 | 80.7407 | 68.8889 | 67.4074 | 89.4318 | 93.3333 | |
| IQAM | BRISQUE | 0.9179 | 0.8173 | 0.8923 | 0.8788 | 0.8554 | 0.9127 | 0.9509 |
| IRCD | 0.1047 | 0.1087 | 0.1046 | 0.1050 | 0.1088 | 0.1093 | 0.1101 | |
| BIS | 0.0558 | 0.0457 | 0.1032 | 0.0668 | 0.0832 | 0.1115 | 0.1271 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, N.; Liu, H.; Zhang, Z. Hierarchic Clustering-Based Face Enhancement for Images Captured in Dark Fields. Electronics 2021, 10, 936. https://doi.org/10.3390/electronics10080936
Zheng N, Liu H, Zhang Z. Hierarchic Clustering-Based Face Enhancement for Images Captured in Dark Fields. Electronics. 2021; 10(8):936. https://doi.org/10.3390/electronics10080936
Chicago/Turabian StyleZheng, Na, Haoting Liu, and Zhiqiang Zhang. 2021. "Hierarchic Clustering-Based Face Enhancement for Images Captured in Dark Fields" Electronics 10, no. 8: 936. https://doi.org/10.3390/electronics10080936
APA StyleZheng, N., Liu, H., & Zhang, Z. (2021). Hierarchic Clustering-Based Face Enhancement for Images Captured in Dark Fields. Electronics, 10(8), 936. https://doi.org/10.3390/electronics10080936






