Arbitrary Configurable 20-Channel Coincidence Counting Unit for Multi-Qubit Quantum Experiment
Abstract
1. Introduction
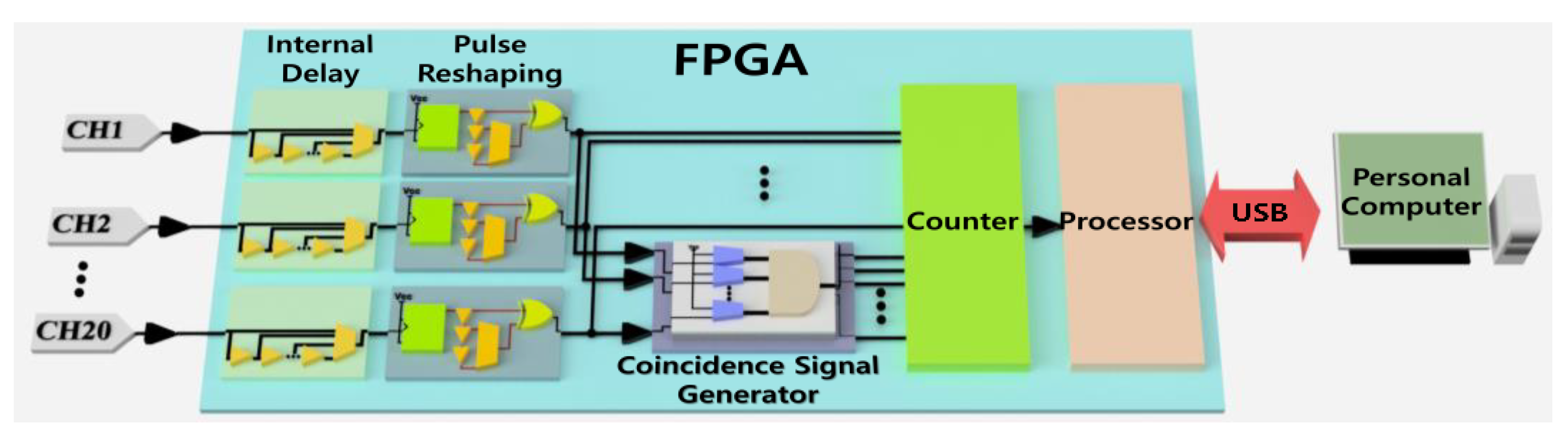
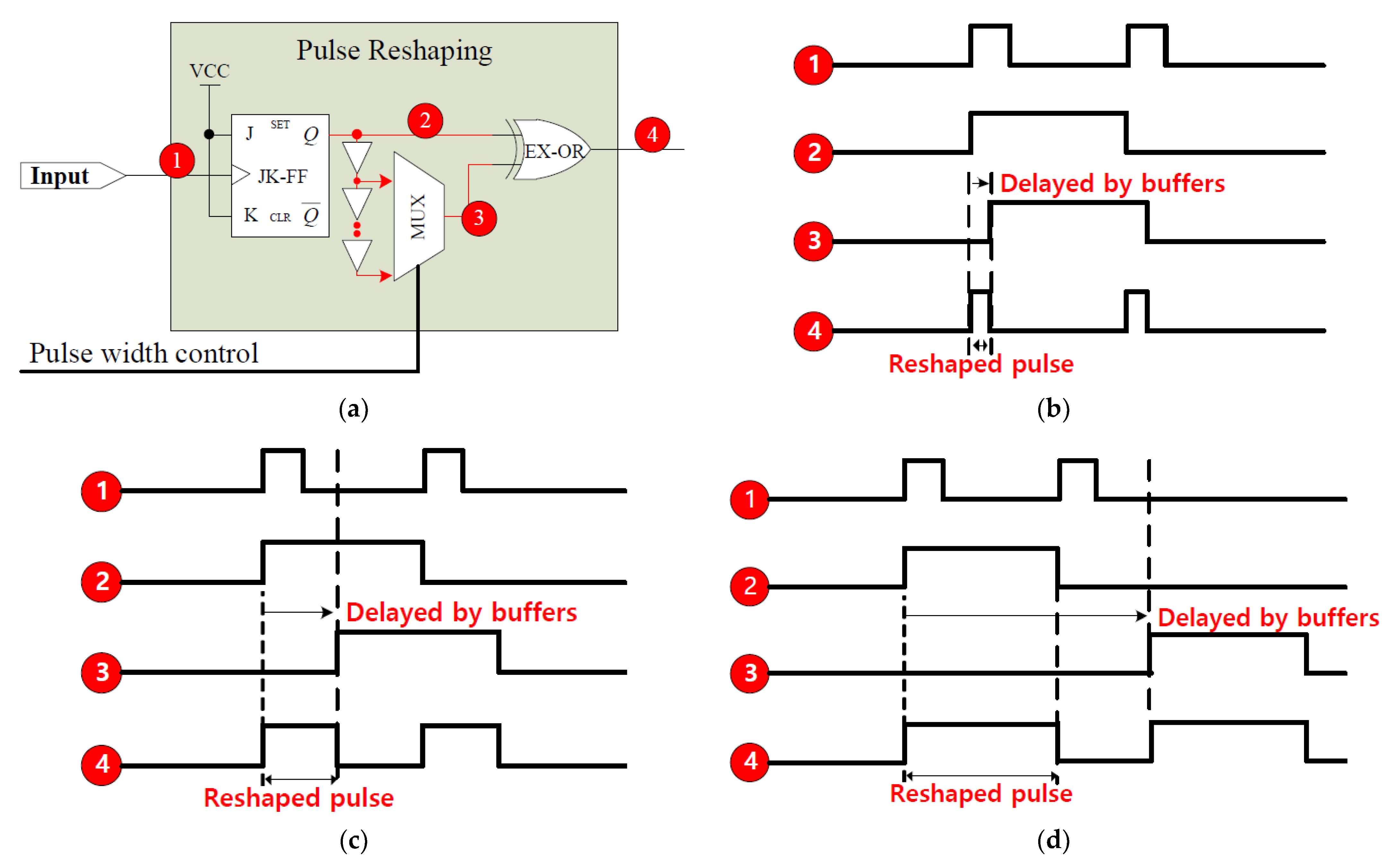
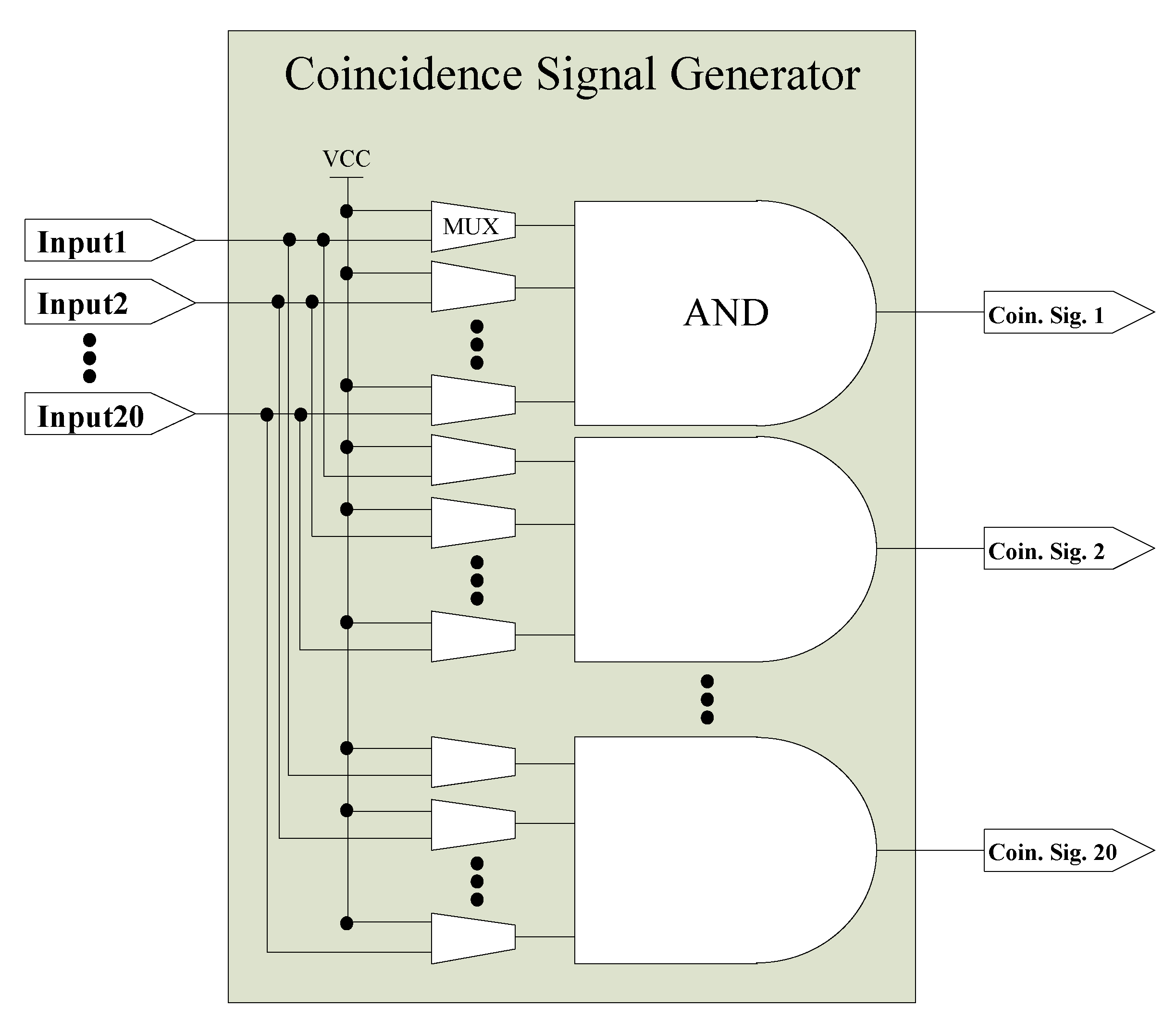
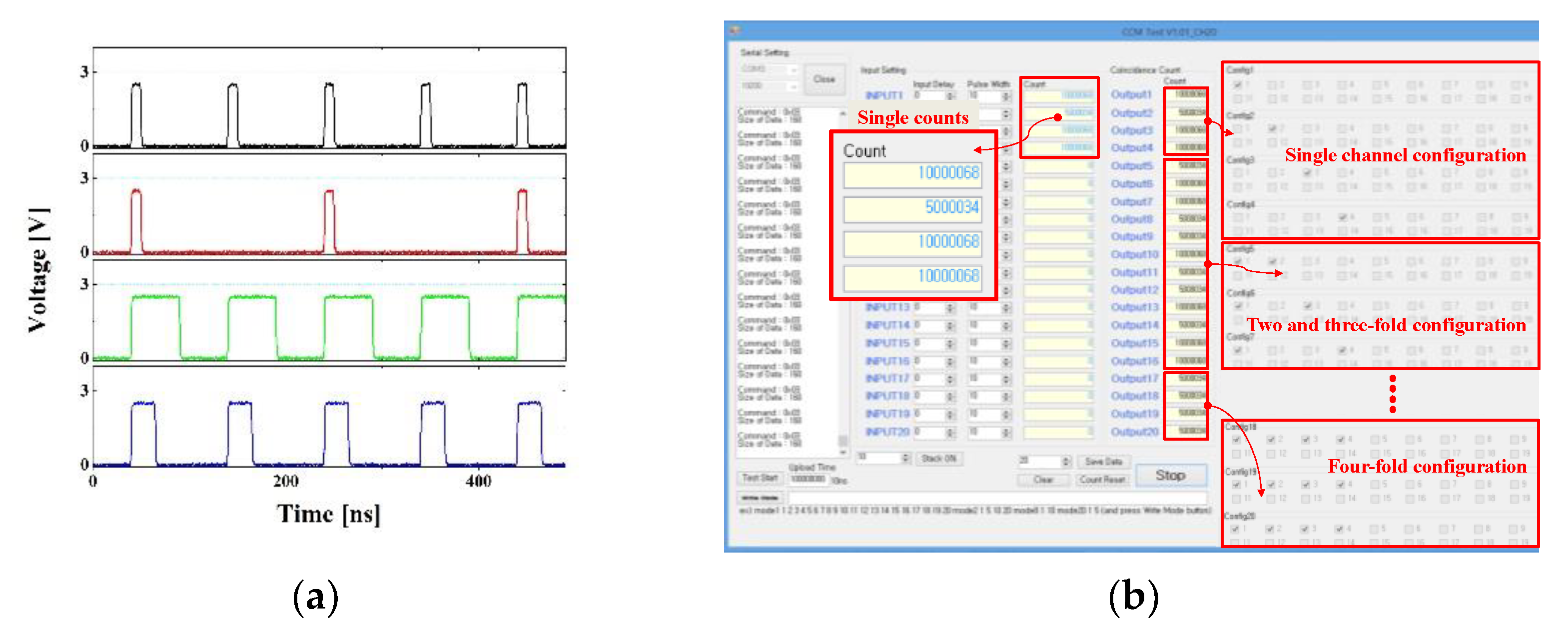
2. Materials and Methods
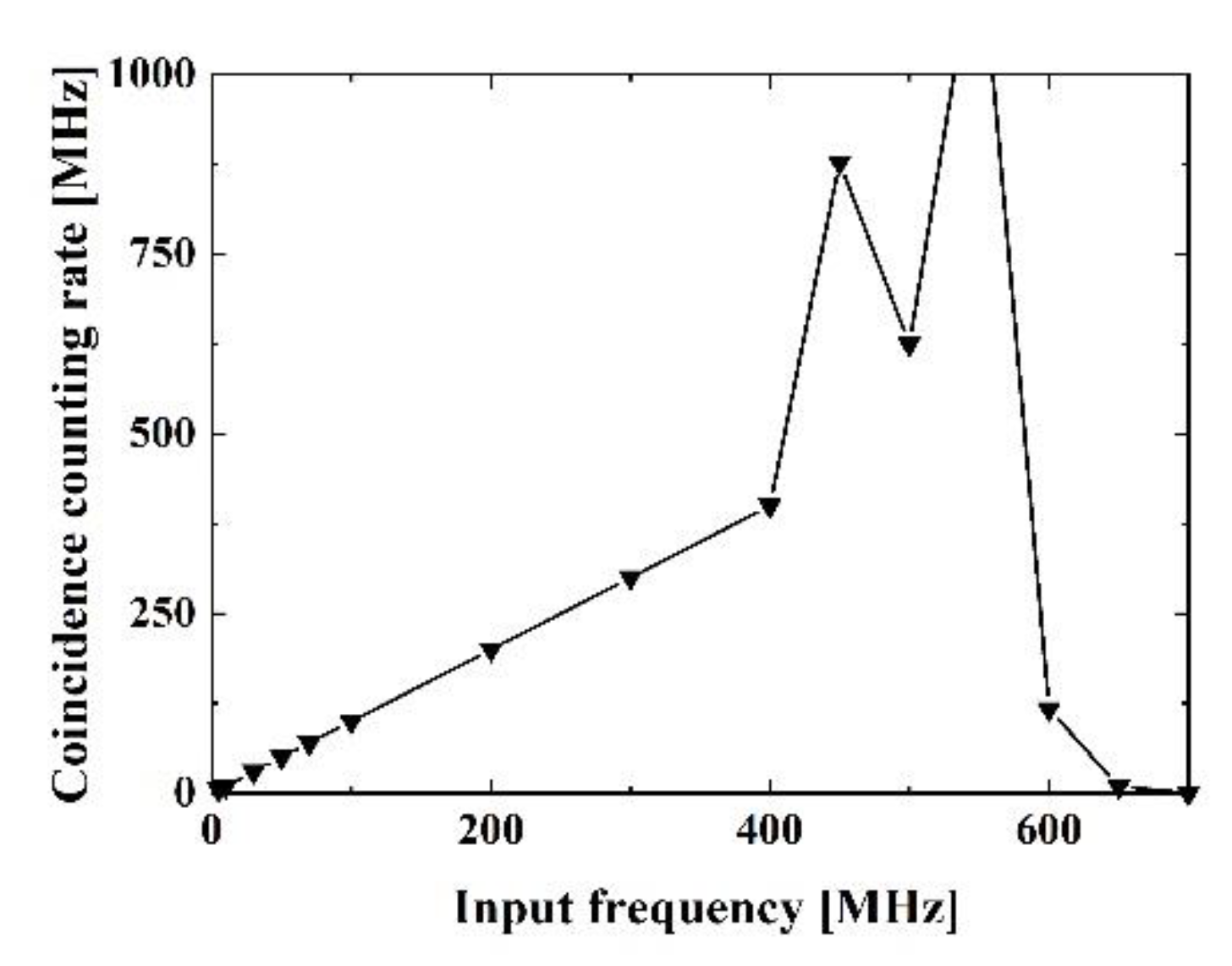
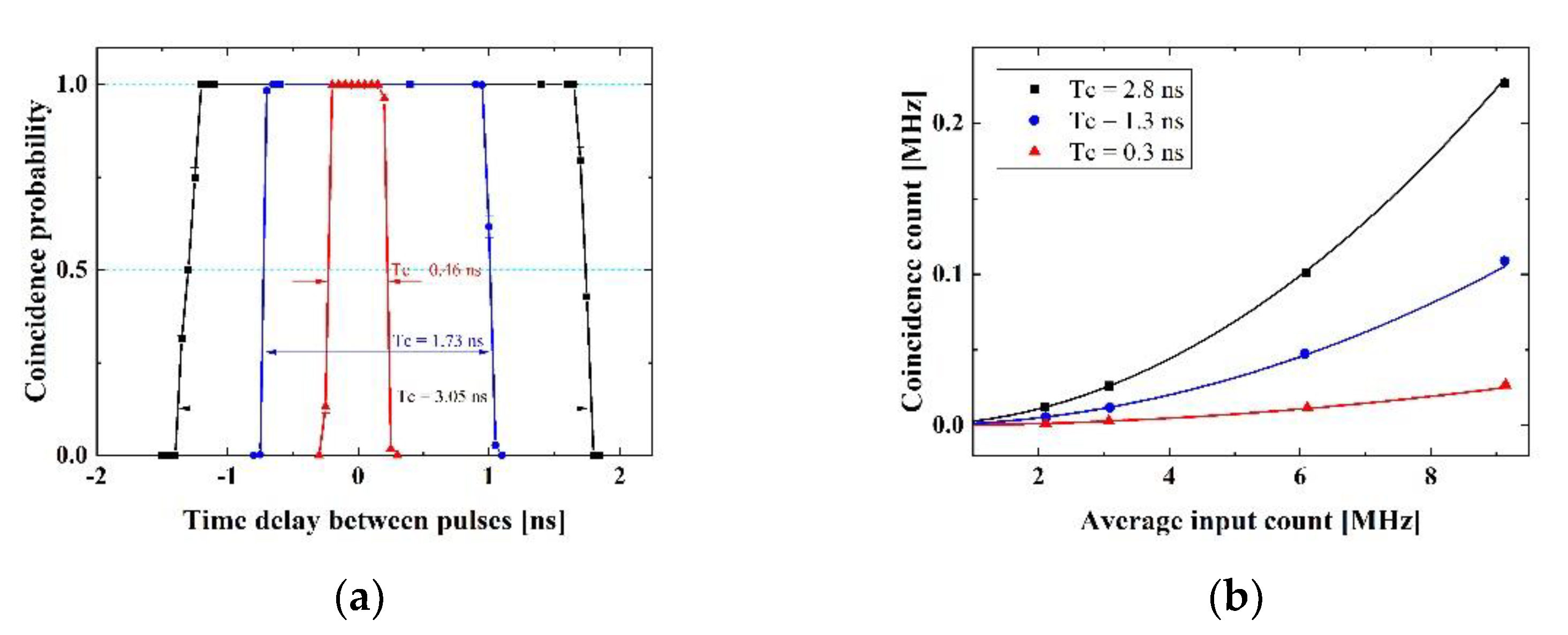
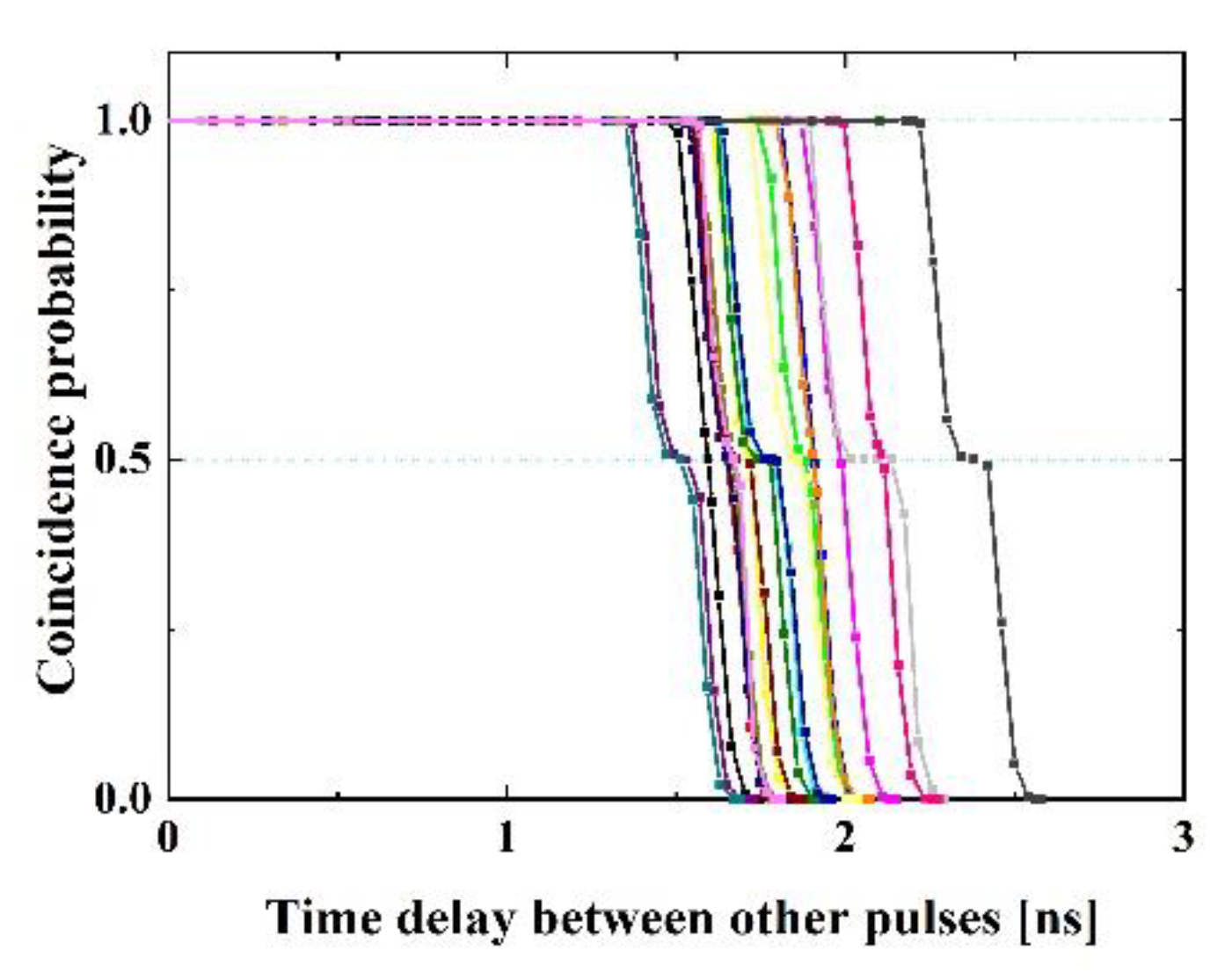
3. Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kwon, O.; Cho, Y.-W.; Kim, Y.-H. Single-mode coupling efficiencies of type-II spontaneous parametric down-conversion: Collinear, noncollinear, and beamlike phase matching. Phys. Rev. A 2008, 78, 053825. [Google Scholar] [CrossRef]
- Kwon, O.; Ra, Y.-S.; Kim, Y.-H. Observing photonic de Broglie waves without the maximally-path-entangled| N, 0〉+| 0, N〉 state. Phys. Rev. A 2010, 81, 063801. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Kwon, O.; Lee, S.M.; Lee, J.-C.; Kim, H.; Choi, S.-K.; Park, H.S.; Kim, Y.-H. Observation of Young’s double-slit interference with the three-photon N00N state. Opt. Express 2011, 19, 24957–24966. [Google Scholar] [CrossRef]
- Pan, J.-W.; Chen, Z.-B.; Lu, C.-Y.; Weinfurter, H.; Zeilinger, A.; Żukowski, M. Multiphoton entanglement and interferometry. Rev. Mod. Phys. 2012, 84, 777–838. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Slattery, O.; Kuo, P.S.; Tang, X. Conditions for two-photon interference with coherent pulses. Phys. Rev. A 2013, 87, 063843. [Google Scholar] [CrossRef]
- Ra, Y.-S.; Tichy, M.C.; Lim, H.-T.; Kwon, O.; Mintert, F.; Buchleitner, A.; Kim, Y.-H. Observation of detection-dependent multi-photon coherence times. Nat. Commun. 2013, 4, 2451. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Kim, Y.-S.; Lee, S.-Y.; Han, S.-W.; Moon, S.; Kim, Y.-H.; Cho, Y.-W. Direct quantum process tomography via measuring sequential weak values of incompatible observables. Nat. Commun. 2018, 9, 192. [Google Scholar] [CrossRef]
- Pramanik, T.; Cho, Y.-W.; Han, S.-W.; Lee, S.-Y.; Kim, Y.-S.; Moon, S. Revealing hidden quantum steerability using local filtering operations. Phys. Rev. A 2019, 99, 030101. [Google Scholar] [CrossRef]
- Cho, Y.-W.; Kim, Y.; Choi, Y.-H.; Kim, Y.-S.; Han, S.-W.; Lee, S.-Y.; Moon, S.; Kim, Y.-H. Emergence of the geometric phase from quantum measurement back-action. Nat. Phys. 2019, 15, 665–670. [Google Scholar] [CrossRef]
- Pramanik, T.; Cho, Y.-W.; Han, S.-W.; Lee, S.-Y.; Moon, S.; Kim, Y.-S. Nonlocal quantum correlations under amplitude damping decoherence. Phys. Rev. A 2019, 100, 042311. [Google Scholar] [CrossRef]
- Lo, H.-K.; Curty, M.; Qi, B. Measurement-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Chen, T.-Y.; Wang, L.-J.; Liang, H.; Shentu, G.-L.; Wang, J.; Cui, K.; Yin, H.-L.; Liu, N.-L.; Li, L.; et al. Experimental Measurement-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2013, 111, 130502. [Google Scholar] [CrossRef]
- Tang, Z.; Liao, Z.; Xu, F.; Qi, B.; Qian, L.; Lo, H.-K. Experimental Demonstration of Polarization Encoding Measurement-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2014, 112, 190503. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Kwon, O.; Woo, M.; Oh, K.; Han, S.-W.; Kim, Y.-S.; Moon, S. Plug-and-play measurement-device-independent quantum key distribution. Phys. Rev. A 2016, 93, 032319. [Google Scholar] [CrossRef]
- Park, C.H.; Woo, M.K.; Park, B.K.; Lee, M.S.; Kim, Y.-S.; Cho, Y.-W.; Kim, S.; Han, S.-W.; Moon, S. Practical Plug-and-Play Measurement-Device-Independent Quantum Key Distribution with Polarization Division Multiplexing. IEEE Access 2018, 6, 58587–58593. [Google Scholar] [CrossRef]
- Acremann, Y.; Chembrolu, V.; Strachan, J.P.; Tyliszczak, T.; Stöhr, J. Software defined photon counting system for time resolved x-ray experiments. Rev. Sci. Instruments 2007, 78, 14702. [Google Scholar] [CrossRef] [PubMed]
- Zhong, H.-S.; Li, Y.; Li, W.; Peng, L.-C.; Su, Z.-E.; Hu, Y.; He, Y.-M.; Ding, X.; Zhang, W.; Li, H.; et al. 12-Photon Entanglement and Scalable Scattershot Boson Sampling with Optimal Entangled-Photon Pairs from Parametric Down-Conversion. Phys. Rev. Lett. 2018, 121, 250505. [Google Scholar] [CrossRef] [PubMed]
- Zhong, H.-S.; Wang, H.; Deng, Y.-H.; Chen, M.-C.; Peng, L.-C.; Luo, Y.-H.; Qin, J.; Wu, D.; Ding, X.; Hu, Y.; et al. Quantum computational advantage using photons. Science 2020, 370, 1460. [Google Scholar]
- Crotti, M.; Rech, I.; Ghioni, M. Four Channel, 40 ps Resolution, Fully Integrated Time-to-Amplitude Converter for Time-Resolved Photon Counting. IEEE J. Solid-State Circuits 2011, 47, 699–708. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, W.; Yu, X.; Jiang, Q.; Zheng, L.; Sun, W. A hybrid time-to-digital converter based on residual time extraction and amplification. Microelectron. J. 2017, 63, 148–154. [Google Scholar] [CrossRef]
- Arabul, E.; Rarity, J.; Dahnoun, N. FPGA based fast integrated real-time multi coincidence counter using a time-to-digital converter. In Proceedings of the IEEE 2018 7th Mediterranean Conference on Embedded Computing (MECO), Budva, Montenegro, 10–14 June 2018; pp. 1–4. [Google Scholar]
- Li, W.; Hu, Y.; Zhong, H.-S.; Wang, Y.-F.; Wang, X.-L.; Peng, C.-Z.; Jiang, X. Time-tagged coincidence counting unit for large-scale photonic quantum computing. Rev. Sci. Instruments 2018, 89, 103113. [Google Scholar] [CrossRef]
- Machado, R.; Cabral, J.; Alves, F.S. All-Digital Time-to-Digital Converter Design Methodology Based on Structured Data Paths. IEEE Access 2019, 7, 108447–108457. [Google Scholar] [CrossRef]
- Chen, P.; Lan, J.-T.; Wang, R.-T.; Qui, N.M.; Marquez, J.C.J.S.; Kajihara, S.; Miyake, Y. High-Precision PLL Delay Matrix With Overclocking and Double Data Rate for Accurate FPGA Time-to-Digital Converters. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2020, 28, 904–913. [Google Scholar] [CrossRef]
- Gaertner, S.; Weinfurter, H.; Kurtsiefer, C. Fast and Compact Multichannel Photon Coincidence Unit for Quantum Information Processing. Rev. Sci. Instruments 2005, 76, 123108. [Google Scholar] [CrossRef]
- Branning, D.; Bhandari, S.; Beck, M. Low-cost Coincidence-Counting Electronics for Undergraduate Quantum Optics. Am. J. Phys. 2009, 77, 667–670. [Google Scholar] [CrossRef]
- Branning, D.; Khanal, S.; Shin, Y.H.; Clary, B.; Beck, M. Note: Scalable Multiphoton Coincidence-Counting Electronics. Rev. Sci. Instruments 2011, 82, 016102. [Google Scholar] [CrossRef]
- Ko, G.B.; Yoon, H.S.; Kwon, S.I.; Hong, S.J.; Lee, N.S.; Lee, J.S. Development of FPGA-based Coincidence Units with Veto Function. Biomed. Eng. Lett. 2011, 1, 27–31. [Google Scholar] [CrossRef]
- Zhu, F.-M.; Hsieh, S.; Yen, W.; Chou, H. A digital coincidence measurement system using FPGA techniques. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2011, 652, 454–457. [Google Scholar] [CrossRef]
- DE2-115 CCU. Available online: http://people.whitman.edu/~beckmk/QM/circuit/circuit.html (accessed on 19 January 2021).
- Park, B.K.; Kim, Y.-S.; Kwon, O.; Han, S.-W.; Moon, S. High-performance reconfigurable coincidence counting unit based on a field programmable gate array. Appl. Opt. 2015, 54, 4727–4731. [Google Scholar] [CrossRef]
- Zhang, C.; Li, W.; Hu, Y.; Yang, T.; Jin, G.; Jiang, X. 48-channel coincidence counting system for multiphoton experiment. Rev. Sci. Instruments 2016, 87, 113107. [Google Scholar] [CrossRef]
- Gupta, A.K.; Prasad, R.S.; Srivani, L.; Murthy, D.T.; Panigrahi, B.K.; Raghavan, G. Design and Development of Flexible and Low-Cost Coincidence Counting Unit. In Proceedings of the 2018 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 16–17 March 2018; pp. 1–4. [Google Scholar]
- Arabul, E.; Paesani, S.; Tancock, S.; Rarity, J.G.; Dahnoun, N. A Precise High Count-Rate FPGA Based Multi-Channel Coincidence Counting System for Quantum Photonics Applications. IEEE Photon- J. 2020, 12, 1–14. [Google Scholar] [CrossRef]
- Eckart, C.; Shonka, F.R. Accidental Coincidences in Counter Circuits. Phys. Rev. 1938, 53, 752–756. [Google Scholar] [CrossRef]


| Resource | Utilization/Available |
|---|---|
| Total logic elements | 17,476/22,320 (78%) |
| Registers | 4101/22,320 (18%) |
| Pins | 27/154 (18%) |
| Memory | 279,552/608,256 (46%) |
| PLL | 1/4 (25%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, B.K.; Kim, Y.-S.; Cho, Y.-W.; Moon, S.; Han, S.-W. Arbitrary Configurable 20-Channel Coincidence Counting Unit for Multi-Qubit Quantum Experiment. Electronics 2021, 10, 569. https://doi.org/10.3390/electronics10050569
Park BK, Kim Y-S, Cho Y-W, Moon S, Han S-W. Arbitrary Configurable 20-Channel Coincidence Counting Unit for Multi-Qubit Quantum Experiment. Electronics. 2021; 10(5):569. https://doi.org/10.3390/electronics10050569
Chicago/Turabian StylePark, Byung Kwon, Yong-Su Kim, Young-Wook Cho, Sung Moon, and Sang-Wook Han. 2021. "Arbitrary Configurable 20-Channel Coincidence Counting Unit for Multi-Qubit Quantum Experiment" Electronics 10, no. 5: 569. https://doi.org/10.3390/electronics10050569
APA StylePark, B. K., Kim, Y.-S., Cho, Y.-W., Moon, S., & Han, S.-W. (2021). Arbitrary Configurable 20-Channel Coincidence Counting Unit for Multi-Qubit Quantum Experiment. Electronics, 10(5), 569. https://doi.org/10.3390/electronics10050569






