Abstract
The use of non-local self-similarity prior between image blocks can improve image reconstruction performance significantly. We propose a compressive sensing image reconstruction algorithm that combines bilateral total variation and nonlocal low-rank regularization to overcome over-smoothing and degradation of edge information which result from the prior reconstructed image. The proposed algorithm makes use of the preservation of image edge information by bilateral total variation operator to enhance the edge details of the reconstructed image. In addition, we use weighted nuclear norm regularization as a low-rank constraint for similar blocks of the image. To solve this convex optimization problem, the Alternating Direction Method of Multipliers (ADMM) is employed to optimize and iterate the algorithm model effectively. Experimental results show that the proposed algorithm can obtain better image reconstruction quality than conventional algorithms with using total variation regularization or considering the nonlocal structure of the image only. At 10% sampling rate, the peak signal-to-noise ratio gain is up to 2.39 dB in noiseless measurements compared with Nonlocal Low-rank Regularization (NLR-CS). Reconstructed image comparison shows that the proposed algorithm retains more high frequency components. In noisy measurements, the proposed algorithm is robust to noise and the reconstructed image retains more detail information.
1. Introduction
Compressive sensing (CS) [1,2,3] is a burgeoning signal acquisition and reconstruction method that breaks through the frequency limit of the Nyquist–Shannon sampling theorem. CS theory points out that the perfect reconstruction of an original signal can be realized by using a small number of random measurements if the signal is sparse or can be sparsely expressed in a certain transform domain, such as Discrete Cosine Transform (DCT) and Discrete Wavelet Transform (DWT). The measurements are generated by a random Gaussian matrix or partial Fourier matrix in the way of sampling and data compressing at the same time. CS has the advantages of low sampling rate and high acquisition efficiency, which has been widely used in various fields including 3 D imaging [4], video acquisition [5], image encryption transmission [6], optical microscopy [7], target tracking [8], digital holography [9] and multimode fiber [10,11]. The accurate and high-quality reconstruction of signal is the core of the research of CS. In the process of image reconstruction, the prior information of image plays an important role. How to fully explore the prior information of image as much as possible and construct effective constraint becomes the key of image reconstruction. The most commonly used image prior is sparse prior, that is, building a sparse model based on sparse representation in a transform domain to obtain the optimal solution. The classical reconstruction algorithms mainly include greedy algorithms and convex optimization algorithms. The greedy algorithms based on the l0 norm minimization model include Orthogonal Match Pursuit (OMP) [12], Subspace Pursuit (SP) [13], Compressed Sampling Match Pursuit (CoSaMP) [14], etc; The convex optimization algorithms based on the l1 norm minimization model include Basis Pursuit (BP) [15], Iterative Shrinkage Threshold (IST) [16], Gradient Projection (GP) [17], Total Variation (TV) [18], etc.
Among them, the total variation algorithm uses the sparse gradient prior as a constraint to reconstruct the image, which can remove the noise and retain the detail information of the image better. However, some problems such as staircase effect still exist in the total variation algorithm. Many variants are proposed and applied to CS reconstruction gradually, such as fractional-order total variation [19], reweighted total variation [20] and bilateral total variation [21], etc. These reconstruction algorithms using the image sparse prior have achieved good image reconstruction performance. Recently, image restoration models based on nonlocal self-similarity prior have received extensive attention. With the application of nonlocal self-similarity prior [22,23,24] in image denoising, many researchers applied it to CS to realize image reconstruction. Zhang et al. [25] introduced nonlocal mean filter as a regularization term into the total variation model and used the correlation of noise between image blocks to set weights for filtering, which achieves excellent constraint and reconstruction results. Egiazarian et al. [26] presented an algorithm for joint filtering in block matching and sparse three-dimensional transformation domain, which is based on the nonlocal self-similarity among image blocks. Through the collaborative Wiener filtering of similar blocks in the wavelet transform domain, excellent denoising effect and reconstruction performance are achieved. Dong et al. [27] further explored the relationship between structured sparsity and nonlocal self-similarity of images; They presented a nonlocal low-rank regularized image reconstruction algorithm, which takes full advantage of the low-rank features of similar image blocks, removes redundant information and artifacts effectively in images and achieves excellent image restoration results by combining sparse encoding of images.
At present, reconstruction algorithms utilize the non-local self-similarity of image by adopting a block matching strategy to get similar image blocks. Since there are some duplicate structures in the image and the disturb of noise, the optimization model based on low-rank instead of sparsity constraint will inevitably remove these duplicate structures, and result in the problems of over-smoothing and edge information degradation of the reconstructed image [19]. In this paper, we add the bilateral total variation constraint as a global information prior to the reconstruction model based on nonlocal low-rank to propose an optimized scheme. The bilateral total variation operator is used to enhance the texture details of the reconstructed image. The low-rank minimization problem of the original image is usually non-convex and difficult to solve. The Weighted Nuclear Norm (WNN) [28] is employed to approximate the image low-rank in our model. In the stage of solving the optimization problem, the Alternating Direction Method of Multipliers (ADMM) [29] is used to iterate the model effectively.
The remainder of this paper is organized as follows: In Section 2, we introduce our reconstruction model combining bilateral total variation and weighted nuclear norm low-rank regularization. In Section 3, the process of using ADMM to recover compressed images is described. In Section 4, we evaluate the performance of the proposed algorithm and other mainstream CS algorithms. In Section 5, we give a conclusion.
2. Reconstruction Algorithm Combining Bilateral Total Variation and Nonlocal Low-Rank Regularization
According to CS theory, given a one-dimensional discrete vector signal with length N, the measured value can be obtained by M random projection:
where is the sampling matrix. Since , Equation (1) is an underdetermined equation and has no unique solution, it is impossible to reconstruct the original signal x directly with the measured value y. However, when the measurement matrix satisfies the restricted isometry property (RIP) [1,2], which means the length of measured value y collected by the measurement matrix must be longer than the sparsity of the signal x, CS theory can guarantee the accurate reconstruction of sparse (or compressible) signal x.
According to the sparse prior of signal x, the traditional optimization algorithm can be written in the following unconstrained form:
where is the fidelity term of reconstruction, is the sparse regularization term of signal, and is the properly selected regularization parameter.
2.1. The Bilateral Total Variation Model
For an image x, its total variation model is defined as:
where , and represent the gradient difference operators in the horizontal and vertical directions respectively, , , corresponds to the pixel position in the image x. The gradient of the image can be used as the reconstruction constraint to retain the detail information of the image. However, restoring the image with only the traditional total variation constraint has staircase effect in the smooth region. The local details of image are easy to be lost since the penalty of gradient is uniform. Therefore, the reweighted total variation method [20] is proposed, which applies a certain weight to the gradient to avoid local over-smoothing and staircase effect. The reweighted total variation model is defined as:
where , is a small positive constant, weight is iteratively updated by image x.
The bilateral filtering [30] is a non-linear filtering method, which combines the spatial proximity and pixel value similarity of the image. Considering both spatial information and gray level similarity, it can achieve edge preserving and noise reduction. We introduce bilateral filtering into the total variation model. The bilateral total variation model is defined as:
where represents that the image is shifted l pixel horizontally, represents that the image is shifted t pixels vertically, represents the difference of image x at each pixel scale. Weight is used to control the spatial attenuation of the regularization term, and is the window size of the filter kernel.
The bilateral total variation model is essentially an extension of the traditional total variation model. When the weight , set or , define , is the unit matrix, then the bilateral total variation model is transformed into:
it can be seen that the above expression is consistent with Equation (3) of the total variation model.
For the reweighted bilateral total variation model, it can be expressed in the following form:
here we set the weight .
2.2. The Weighted Nuclear Norm Low-Rank Model
The image restoration model based on image nonlocal self-similarity prior consists of two parts: one is the block matching strategy used to characterize the image self-similarity, the other is the low-rank approximation used to characterize the sparsity constraint. The block matching strategy refers to block grouping of similar blocks for an image x. For a n × n block at position i in the image, m similar image blocks are searched based on Euclidean distance in the search window (e.g., 20 × 20), i.e., , , where T is a predefined threshold, and denotes the collection of positions corresponding to those similar blocks. After block grouping, we obtain a data matrix , where each column of denotes a block similar to (including itself).
Due to the similar structure of these image blocks, the matrix composed by them has the property of low-rank. There is also noise pollution in the actual image x, so the similar block matrix can be modeled as: , where and represent low-rank matrix and Gaussian noise matrix respectively. Then, the low-rank matrix can be recovered by solving the following optimization problems:
where is a similar block matrix composed of each image block after block matching, i.e., . The solution of Equation (8) is a rank minimization problem, which is non-convex and difficult to solve. In this paper, the Weighted Nuclear Norm (WNN) [28] is used to replace the rank of matrix. For a matrix X, its weighted nuclear norm is defined as:
where corresponds to the j-th singular value in X, is the weight assigned to the corresponding . As we all know, the larger singular value in X, the more important characteristic component in matrix. So the larger singular value should give a smaller shrinkage in weight distribution. Here, we set the weight , and is a small positive constant.
In this way, the optimization problem of replacing the rank of matrix with weighted nuclear norm is transformed into:
2.3. The Joint Model
We add the proposed bilateral total variation constraint as a global information prior to the reconstruction based on the weighted nuclear norm low-rank model, and get the following joint model:
The joint reconstruction model seems to be relatively complicated. In order to facilitate the calculation, we simplify the bilateral total variation term, replace by , and define , Equation (11) can be abbreviated as:
3. Compressed Image Reconstruction Process
The ADMM [29] can be used to solve the optimization problem of Equation (12) to recover image x. First, auxiliary variables are introduced for replacement:
using the augmented Lagrangian function, Equation (13) is transformed into an unconstrained form:
where and are penalty parameters, and and are Lagrange multipliers. Then the multiplier iteration is adopted as follows:
where k is the number of iterations. According to the ADMM, the original problem can be divided into the following four sub-problems to solve.
3.1. Solving the Sub-Problem of
Having fixed , the optimization problem of is as follows:
this optimization problem of the weighted nuclear norm is generally solved by singular value threshold (SVT) [31] operation:
where is the singular value decomposition of , and is the threshold operator to perform threshold operation on each element in the diagonal matrix :
here , and is the weight, as described in Section 2.2, we set , and the singular value of is sorted in descending order, so the weight is increasing. In order to reduce the amount of computation, we relocate similar blocks every T iterations rather than searching similar blocks in every iteration.
3.2. Solving the Sub-Problem of
Having fixed , the optimization problem of is as follows:
Equation (19) has a closed-form solution:
where is the diagonal matrix, each term in it corresponds to the image pixel position, and its value is the number of overlapping image blocks covering the pixel position. is the average value result of blocks, that is, average the similar blocks collected by each image block.
3.3. Solving the Sub-Problem of
Having fixed , the optimization problem of is as follows:
Equation (21) can be solved according to soft threshold shrinkage [32]:
The soft threshold shrinkage operator . The gradient weight is updated according to the following form:
where is a small positive constant, and the weight is updated according to the gradient at the pixel point in the k-th iteration of image.
3.4. Solving the Sub-Problem of
Having fixed , the optimization problem of is as follows:
Equation (24) has a closed-form solution:
Since the inverse of matrix in Equation (25) is large, it is not easy to solve directly. Here, we use the conjugate gradient algorithm [33] to deal with this problem.
After solving each sub-problem, the multipliers are updated according to Equation (15). The whole process of image reconstruction is summarized in Algorithm 1. A description of the relevant symbols is given in Appendix A.
| Algorithm 1: The proposed CS reconstruction algorithm |
| Input: The measurements and sampling matrix Initialization: The traditional CS algorithm (DCT, DWT, etc.) is used to estimate the initial image ; Set parameters ; Set the nuclear norm weight ; Set the gradient weight ; Outer loop: for do Using the similar block matching strategy to search and group the similar blocks in the image to get the similar block matrix ; Set ; Inner loop: for each block in do Update weight: ; Calculate according to Equation (17); End for Calculate according to Equation (20); Calculate according to Equation (22), update the gradient weight according to Equation (23); Calculate according to Equation (25); Update Lagrange multipliers according to Equation (15); if , relocate the similar blocks position and update similar blocks grouping; End for Output: The final reconstructed image . |
4. Experiments
We compare the proposed algorithm with several mainstream CS algorithms, including TVAL3 [32], TVNLR [25], BM3D-CS [26] and NLR-CS [27]. The comparison algorithms are all based on the total variation constraint ([25,32]) or non-local redundant structure of the image ([26,27]). These algorithms are obtained through the website of the relevant authors. All experimental results are obtained by running Matlab R2016b on a personal computer equipped with an Intel®Core™i5 processor and 8 GB memory running the Windows 10 operating system. We choose eight standard images and two resolution charts from the USC-SIPI image database to test the performance of our algorithm. All the test images are 256 × 256 gray-scale images, as shown in Figure 1. In order to evaluate the reconstruction performance objectively, we choose peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) as evaluation indexes. PSNR and SSIM are calculated as follows:

Figure 1.
Standard test images used in experiments. From left to right, first row: Barbara, Boats, Cameraman, Foreman, House; second row: Peppers, Monarch, Parrots, Testpat1, Testpat2.
In the above formulas, MSE is the mean square error, x is the reference image, y is the reconstructed image, and their size is M × N. The larger the PSNR value, the closer y and x are, which means the better the evaluation result of image quality is. , are the mean value of x and y, , are the standard deviation of x and y, respectively, and is the covariance between two images. and are small positive constants. The value of SSIM is between 0 and 1, and the larger the value, the better the image quality.
In order to make full use of the nonlocal self-similarity features in images as much as possible, it is necessary to select an appropriate block matching strategy. First of all, we give the PSNR results and the reconstruction time of the Monarch image reconstructed by the proposed algorithm. In Figure 2a, we set different image block sizes () and search window sizes (). It can be seen that with the increase of image block size, the reconstruction time of the proposed algorithm is significantly shortened. With the increase of the search window size, the reconstruction time of the image will increase linearly. In general, the PSNR of the image does not change significantly. In Figure 2b, we set different number of similar blocks (). It can also be seen that when the number of similar blocks is similar, the improvement of PSNR of image reconstructed by the proposed algorithm is relatively consistent with the increase of reconstruction time. However, when the number of selected similar blocks increases to a certain amount (), the changes of the two are completely opposite. Moreover, when too many similar blocks are selected (), the reconstruction time of the image will increase dramatically.
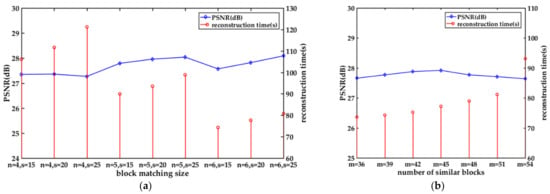
Figure 2.
The PSNR (dB) and reconstruction time(s) of the Monarch image with different (a) block sizes () and search window size (), (b) number of similar blocks () reconstructed by the proposed algorithm.
4.1. Parameters Selection
Since our proposed algorithm combines bilateral total variation, it is necessary to select appropriate spatial attenuation term and filter window size . Figure 3 shows the PSNR results and reconstruction time of the Monarch image reconstructed by the proposed algorithm with corresponding bilateral parameters. With the increase of spatial attenuation term , the PSNR of the image gradually increases, reaching the peak at , and then decreases slightly, but decreases sharply when . When the filter window size and , the reconstruction results of the algorithm is approximately the same, but the final decline of the latter is faster. When , the overall PSNR results are worse than the former two. In addition, we compared the corresponding reconstruction time. It can be found that the main factor affecting the reconstruction time of the algorithm is the filter window size . The change of spatial attenuation term makes the reconstruction time fluctuate slightly, but the change is not significant. When and , their reconstruction times are close to each other, and the latter is slightly longer. When , the reconstruction time seems to be much longer. A larger filter window size obviously increases the reconstruction time of the algorithm.
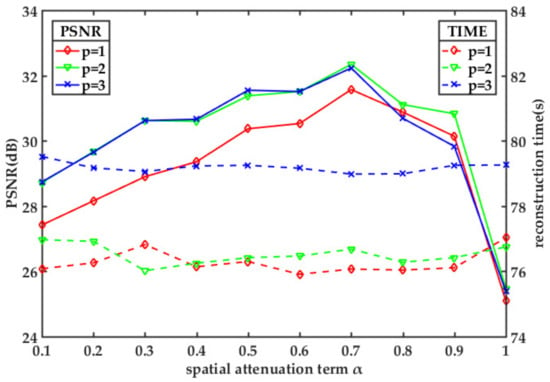
Figure 3.
The PSNR (dB) and reconstruction time(s) of the Monarch image with different spatial attenuation term and filter window size reconstructed by the proposed algorithm.
In the experiment, the sampling matrix is a partial Fourier matrix. In the block matching strategy, based on the previous discussion, we select an image block with the size of and the number of similar blocks is for trade-off between PSNR and reconstruction time. In order to reduce the computational complexity, we extract an image block every 5 pixels along the horizontal and vertical directions, and the search window size of block matching is . Lagrange multipliers and are initially set to null matrix, K = 100, T = 4, i.e., the total number of iterations is 100, and the similar block positions are relocated every 4 iterations. The initial image is estimated by the same standard DCT algorithm as NLR-CS. The regularization parameters are set separately according to different sampling rates. According to the analysis results of Figure 3, we choose to set the spatial attenuation weight of bilateral total variation term to 0.7, and the filter window size . The penalty parameter used in ADMM iteration . We first present the experimental results for noiseless CS measurements and then report the results using noisy CS measurements.
4.2. Noiseless CS Measurements
Table 1 shows the PSNR and SSIM of the proposed algorithm and comparison algorithms at different sampling rates (5%, 10%, 15%, 20%, 25%) respectively. It can be seen from Table 1 that at a lower sampling rate, the total variation model based on the sparse gradient prior, including TVAL3 and TVNLR, is worse than other algorithms. In contrast, BM3D-CS and NLR-CS can extract the nonlocal self-similarity prior information of the image, so even if the sampling rate is very low, the PSNR reconstructed by these algorithms are also great. The proposed algorithm, owing to the joint total variation and nonlocal rank minimization, achieves better reconstruction performance than NLR-CS. For example, at 10% sampling rate, different test images in Table 1 can have different PSNR gain of 1.86 dB, 1.38 dB, 1.44 dB, 2.08 dB, 2.06 dB, 1.96 dB, 1.48 dB, 1.22 dB, 2.17 dB and 2.39 dB respectively. For a more intuitive comparison, we selected the Cameraman and Peppers images to draw the corresponding PSNR curves. The results are shown in Figure 4. It can be seen that our proposed algorithm achieves better PSNR at each sampling rate. When reconstructing Testpat1 image, we find that the PSNR result of BM3D-CS is better than that of NLR-CS and the proposed algorithm. We speculate that the initial image estimated by the standard DCT algorithm affects the performance of the proposed algorithm. It also can be seen that at a lower sampling rate, the SSIM of TVAL3 and TVNLR are relatively lower, while those of nonlocal self-similarity algorithms are relatively higher. Among them, the SSIM of the proposed algorithm is closer to 1, which indicates that the reconstructed image quality is better.

Table 1.
The PSNR (dB, left) and SSIM (right) of test images at different sampling rates reconstructed by the proposed algorithm and comparison algorithms. The best performance algorithm is shown in bold.
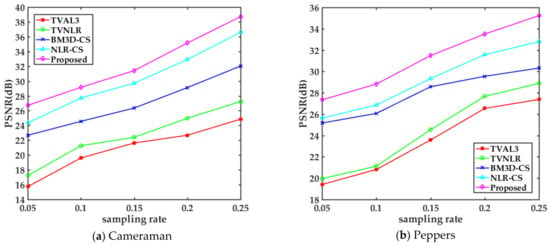
Figure 4.
The PSNR (dB) curves of the (a) Cameraman and (b) Peppers images reconstructed at different sampling rates reconstructed by different algorithms.
In order to compare the reconstructed image quality subjectively, Figure 5 shows the results of reconstruction of five test images (Boats, Cameraman, House, Peppers, Testpat2) by the proposed algorithm and comparison algorithms at 10% sampling rate. There are a lot of nonlocal similar redundant structures in these images, so we choose them for comparison. The above comparison results show that at a lower sampling rate, the details of TVAL3 and TVNLR are seriously lost. For the House image, the texture of the house becomes very blurred, and the bricks and tiles on the eaves of the house cannot be distinguished. The image reconstructed by BM3D-CS with nonlocal similar structure is better, but there are still some artifacts, and the details are also blurred. NLR-CS and the proposed algorithm look clearer visually. Because the proposed algorithm adds bilateral total variation as a constraint to the nonlocal low-rank sparse model, compared with NLR-CS, it plays an important role in maintaining edge texture. Compared with the bricks and tiles details in the middle area on the right side of the image, we can see that the texture of the proposed algorithm is richer, while the NLR-CS is too smooth. Similarly, for the Boats image, we can see from the local detail image that the result of NLR-CS reconstruction is too smooth resulting in a serious loss of rope details, while the details of the proposed algorithm look better.

Figure 5.
Comparison of reconstruction results of five test images with (a) TVAL3, (b) TVNLR, (c) BM3D-CS, (d) NLR-CS, (e) Proposed algorithm at 10% sampling rate. The lower right or left corner of the image is the selected local detail image.
In order to compare the texture details of the reconstructed image more intuitively, we use DCT to separate the high and low frequency components of the test images. Figure 6 shows the comparison of high frequency details of the reconstructed Cameraman and Peppers images. It can be seen from Figure 6 that there are many artifacts in the image restored by BM3D-CS, resulting in a large number of artifacts interfering with high frequency components and serious loss of details. The high frequency details of TVAL3 and TVNLR are obviously less. Compared with NLR-CS, the proposed algorithm can reconstruct the high frequency profile more clearly and more details of the texture can be found. Figure 7 shows the relative errors and SSIM results of high frequency components of the Cameraman image restored by different algorithms at different sampling rates (5%, 10%, 15%, 20%, 25%). In Figure 7a, the relative errors of TVAL3, TVNLR and BM3D-CS are relatively large at a low sampling rate, but with the increase of sampling rates, the relative errors will decrease greatly. The relative errors of NLR-CS are very low at the beginning. With the increase of sampling rates, the amplitude of NLR-CS decreases slightly, but it is always in the leading position. The downward trend of our proposed algorithm is similar to that of NLR-CS, and its relative errors are lower. The SSIM curve in Figure 7b seems to be consistent, but the result of the proposed algorithm is always optimal. It is worth noting that both in Figure 7a,b it can be seen that the recovery results of BM3D-CS are relatively poor. Obviously, as shown in Figure 6, the high frequency details of the algorithm are seriously damaged due to the interference of artifacts. The comparison of the above results shows that the proposed algorithm can retain more details of high frequency components of the restored image.
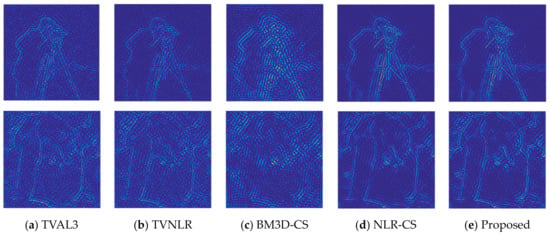
Figure 6.
Comparison of high frequency details of the Cameraman(top) and Peppers(bottom) images with (a) TVAL3, (b) TVNLR, (c) BM3D-CS, (d) NLR-CS, (e) Proposed algorithm at 10% sampling rate.
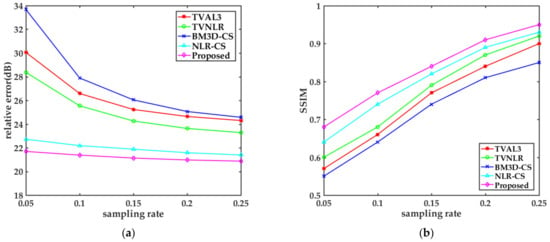
Figure 7.
The (a) relative error(dB) and (b) SSIM of high frequency components of the Cameraman image at different sampling rates reconstructed by different algorithms.
4.3. Noisy CS Measurements
We also test the robustness of the proposed algorithm to noisy measurements, by adding Gaussian noise to CS measurements, and the variation of standard deviation of noise will produce a signal-to-noise ratio (SNR) between 10 dB and 30 dB. In order to compare the results reasonably, we choose a 20% sampling rate to evaluate algorithms. Table 2 shows the PSNR results of test images reconstructed by different comparison algorithms under different SNR conditions. As can be seen from Table 2, it is different from noiseless CS measurements. In noisy CS measurements, the anti-noise performance of the algorithm based on total variation model is obviously inferior to that based on nonlocal self-similarity prior. For a more intuitive comparison, we selected the Boats and Parrots images to draw the corresponding PSNR curves. The results are shown in Figure 8. It can be seen that the reconstruction performance of each comparison algorithm is relatively poor at low SNR, but the reconstruction algorithms based on nonlocal self-similarity prior are much better than those based on sparse gradient prior. At the beginning, the proposed algorithm has no difference with BM3D-CS and NLR-CS. With the improvement of SNR, the PSNR of TVAL3 and TVNLR increased significantly, at higher SNR, the PSNR improvement of them became gentle. In contrast, the reconstruction performance of the proposed algorithm and NLR-CS are improved steadily, and there is a certain disparity between the proposed algorithm and BM3D-CS at higher SNR. Compared with NLR-CS, the proposed algorithm achieves better reconstruction results under all SNR, although the gain amplitude of PSNR is not large. Figure 9 shows the subjective visual comparison results of the reconstruction of the Boats and Parrots images by each algorithm from noisy measurements. Here noise environment with SNR of 25 dB is selected. It can be seen from Figure 9 that even if the sampling rate is increased, the quality of image restoration is much worse than that of noiseless measurements. From the perspective of local detail images, the reconstruction algorithm based on nonlocal self-similarity prior is better. There are still some artifacts in BM3D-CS. Compared with NLR-CS, the texture details of the proposed algorithm are richer, such as the details of parrot head feathers. The comparison between PSNR and subjective quality results shows that the proposed algorithm is robust to noisy measurements.

Table 2.
The PSNR (dB) of test images reconstructed at 20% sampling rate from noisy measurements (SNR = 10, 15, 20, 25, 30 dB). The best performance algorithm is shown in bold.
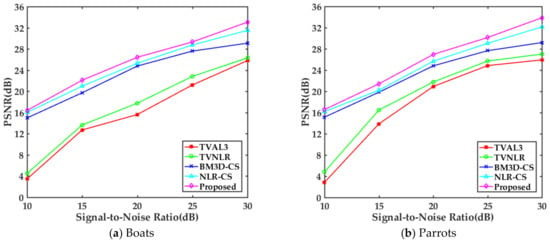
Figure 8.
The PSNR (dB) curves of the (a) Boats and (b) Parrots images reconstructed at 20% sampling rate from noisy measurements.

Figure 9.
Comparison of reconstruction results of the Boats and Parrots images with (a) TVAL3, (b) TVNLR, (c) BM3D-CS, (d) NLR-CS, (e) Proposed algorithm at 20% sampling rate from noisy measurements (SNR = 25 dB). The lower right corner of the image is the selected local detail image.
4.4. Reconstruction Time
Figure 10 shows the average reconstruction time required by several comparison algorithms to restore ten test images at different sampling rates (5%, 10%, 15%, 20%, 25%). All the results were compared in the same iterative environment. From Figure 10, the reconstruction time of TVAL3 which based on total variation model is quite short, because of utilizing the steepest descent method, the advantage of this algorithm is fast reconstruction. The reconstruction time of BM3D-CS is relatively short, because the processing of its similar blocks is carried out in the wavelet transform domain.
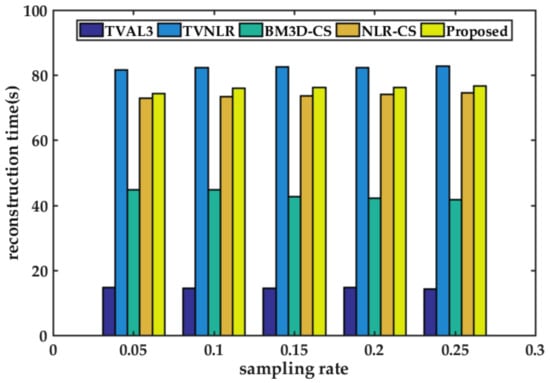
Figure 10.
The average reconstruction time(s) of ten test images reconstructed by different algorithms at different sampling rates. The results are obtained by running Matlab R2016 b on a personal computer with Win10 operating system, Intel®Core™i5 processor and 8 GB memory.
As the nonlocal filtering operation takes a lot of time in iteration, the reconstruction time of TVNLR is the longest. Compared with TVAL3, the computational complexity of the model increases due to the consideration of nonlocal structure information, similar block searching and matching. The reconstruction time of NLR-CS and the proposed algorithm is relatively longer, because the low-rank approximation of similar blocks requires singular value decomposition of the matrix, and the computational complexity will be further increased. Although the reconstruction time of the proposed algorithm will be a little longer, the reconstruction quality is improved significantly by adding bilateral total variation constraints for a joint solution. Compared with NLR-CS, the average time increase is about only 3 seconds, the performance gain is acceptable.
5. Discussion and Conclusions
In this paper, we proposed a CS image reconstruction algorithm, which combines bilateral total variation and weighted nuclear norm low-rank regularization. In this algorithm, the bilateral total variation constraint is added to the reconstruction model based on nonlocal low-rank as a global information prior, and the texture details of the reconstructed image are enhanced by using the bilateral total variation operator to maintain the edge of the image. Experimental results on standard test images demonstrate that the proposed algorithm works well. Compared with traditional algorithms which using total variation constraint or considering image nonlocal structure only, although the reconstruction time of the algorithm increases a little, the proposed algorithm obtains better reconstruction results both subjectively and objectively, and retains more detail information of the image, which shows the effectiveness of the proposed algorithm.
Author Contributions
Concept and structure of this paper, K.Z.; resources, Y.Q. and H.Z.; writing—original draft preparation, K.Z.; writing—review and editing, Y.Q., H.R. and Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (NSFC) (61675184 and 61405178).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Description of relevant symbols in Algorithm 1.
Table A1.
Description of relevant symbols in Algorithm 1.
| Symbol | Description | Symbol | Description |
|---|---|---|---|
| CS | compressive sensing | sampling matrix | |
| DCT | discrete cosine transform | ADMM iterations | |
| DWT | discrete wavelet transform | relocate similar blocks threshold | |
| measured value | nuclear norm weight | ||
| reconstructed image | gradient weight | ||
| regularization parameter | similar block matrix | ||
| regularization parameter | low-rank matrix | ||
| spatial attenuation weight | auxiliary variable | ||
| filter window size | auxiliary variable | ||
| penalty parameter | Lagrange multiplier | ||
| penalty parameter | Lagrange multiplier |
References
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J.; Tao, T. Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information. IEEE Trans. Inf. Theory 2006. [Google Scholar] [CrossRef]
- Candès, E.J.; Wakin, M.B. An Introduction to Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Sun, M.J.; Edgar, M.P.; Gibson, G.M.; Sun, B.; Radwell, N.; Lamb, R.; Padgett, M.J. Single-pixel three-dimensional imaging with time-based depth resolution. Nat. Comm. 2016, 7, 12010. [Google Scholar] [CrossRef]
- Zhang, Y.; Edgar, M.P.; Sun, B.; Radwell, N.; Gibson, G.M.; Padgett, M.J. 3D single-pixel video. J. Opt. 2016, 18, 035203. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, B.; Zhou, N. A novel image compression–encryption hybrid algorithm based on the analysis sparse representation. Opt. Comm. 2017, 392, 223–233. [Google Scholar] [CrossRef]
- Rodriguez, A.D.; Clemente, P.; Tajahuerce, E.; Lancis, J. Dual-mode optical microscope based on single-pixel imaging. Optics Lasers Eng. 2016, 82, 87–94. [Google Scholar] [CrossRef]
- Shi, D.; Yin, K.; Huang, J.; Yuan, K.; Zhu, W.; Xie, C.; Liu, D.; Wang, Y. Fast tracking of moving objects using single-pixel imaging. Opt. Comm. 2019, 440, 155–162. [Google Scholar] [CrossRef]
- Martínez-León, L.; Clemente, P.; Mori, Y.; Climent, V.; Tajahuerce, E. Single-pixel digital holography with phase-encoded illumination. Opt. Express 2017, 25, 4975–4984. [Google Scholar] [CrossRef]
- Amitonova, L.V.; Boer, J.F.D. Compressive imaging through a multimode fiber. Opt. Lett. 2018, 43, 5427. [Google Scholar] [CrossRef] [PubMed]
- Lan, M.; Guan, D.; Gao, L.; Li, J.; Yu, S.; Wu, G. Robust compressive multimode fiber imaging against bending with enhanced depth of field. Opt. Express 2019, 27, 12957–12962. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.; Dahmen, W.; Devore, R. Orthogonal Matching Pursuit under the Restricted Isometry Property. Constr. Approx. 2017, 45, 113–127. [Google Scholar] [CrossRef]
- Han, X.; Zhao, G.; Li, X.; Shu, T.; Yu, W. Sparse signal reconstruction via expanded subspace pursuit. J. Appl. Remote Sens. 2019, 13, 1. [Google Scholar] [CrossRef]
- Tirer, T.; Giryes, R. Generalizing CoSaMP to Signals from a Union of Low Dimensional Linear Subspaces. Appl. Comput. Harmonic Anal. 2017. [Google Scholar] [CrossRef]
- Zeng, K.; Erus, G.; Sotiras, A.; Shinohara, R.T.; Davatzikos, C. Abnormality Detection via Iterative Deformable Registration and Basis-Pursuit Decomposition. IEEE Trans. Med. Imaging 2016, 35, 1937–1951. [Google Scholar] [CrossRef] [PubMed]
- Bayram, I. On the convergence of the iterative shrinkage/thresholding algorithm with a weakly convex penalty. IEEE Trans. Signal Process. 2016, 64, 1597–1608. [Google Scholar] [CrossRef]
- Gong, B.; Liu, W.; Tang, T.; Zhao, W.; Zhou, T. An Efficient Gradient Projection Method for Stochastic Optimal Control Problems. SIAM J. Num. Anal. 2017, 55, 2982–3005. [Google Scholar] [CrossRef]
- Vishnevskiy, V.; Gass, T.; Szekely, G.; Tanner, C.; Goksel, O. Isotropic Total Variation Regularization of Displacements in Parametric Image Registration. IEEE Trans. Med. Imaging 2017, 36, 385–395. [Google Scholar] [CrossRef]
- Chen, H.; Qin, Y.; Ren, H.; Chang, L.; Zheng, H. Adaptive weighted high frequency iterative algorithm for fractional-order total variation with nonlocal regularization for image reconstruction. Electronics 2020, 9, 1103. [Google Scholar] [CrossRef]
- Candès, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing Sparsity by Reweighted l1 Minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Farsiu, S.; Robinson, M.D.; Elad, M.; Milanfar, P. Fast and robust multiframe super resolution. IEEE Trans. Image Process. 2004, 13, 1327–1344. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 60–65. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K.O. Image restoration by sparse 3D transform-domain collaborative filtering. In Proceedings of the Image Processing: Algorithms and Systems VI, San Jose, CA, USA, 28 January 2008. [Google Scholar]
- Dong, W.; Zhang, L.; Shi, G. Nonlocally Centralized Sparse Representation for Image Restoration. IEEE Trans. Image Process. 2012, 22. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, S.; Zhao, D.; Xiong, R.; Ma, S. Improved total variation based image compressive sensing recovery by nonlocal regularization. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS), Beijing, China, 19–23 May 2013; pp. 2836–2839. [Google Scholar]
- Egiazarian, K.; Foi, A.; Katkovnik, V. Compressed Sensing Image Reconstruction via Recursive Spatially Adaptive Filtering. In Proceedings of the IEEE Conference on Image Processing, San Antonio, TX, USA, 17–19 September 2007. [Google Scholar]
- Dong, W.; Shi, G.; Li, X.; Ma, Y.; Huang, F. Compressive Sensing via Nonlocal Low-Rank Regularization. IEEE Trans. Image Process. 2014, 23, 3618–3632. [Google Scholar] [CrossRef] [PubMed]
- Gu, S.; Zhang, L.; Zuo, W.; Feng, X. Weighted Nuclear Norm Minimization with Application to Image Denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. In Proceedings of the IEEE Conference on Computer Vision, Bombay, India, 7 January 1998. [Google Scholar]
- Cai, J.F.; Candès, E.J.; Shen, Z. A Singular Value Thresholding Algorithm for Matrix Completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Li, C.; Yin, W.; Jiang, H.; Zhang, Y. An efficient augmented Lagrangian method with applications to total variation minimization. Computat. Optim. Appl. 2013, 56, 507–530. [Google Scholar] [CrossRef]
- Nazareth, J.L. Conjugate gradient method. WIREs Computat. Stat. 2009, 1, 348–353. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).