Statistical Beamforming Techniques for Power Domain NOMA System
Abstract
:1. Introduction
Paper Contributions
- (a)
- Unlike the existing works which employ approximate characterization to derive outage probabilities, such as Gaussian or Chi-square distribution assumption, this work derives closed form expression for the outage probabilities for both near and far users in the multi-user NOMA system without imposing such assumptions. To elaborate further, we use the exact characterization of the ratio of IQF of the form (the notation represents the weighted norm defined as ) where is a scalar quantity, is a complex circular Gaussian vector, and and are certain weighting matrices.
- (b)
- This work proposes two techniques to obtain an optimal solution for beam vectors which rely on the derived outage probabilities. More precisely, these techniques are as follows:
- (i)
- To obtain the optimal beam vectors by minimizing the total beam power while constraining the outage probabilities to the QoS threshold.
- (ii)
- To obtain the optimal beam vectors by minimizing the outage probabilities while constraining the total beam power.
- (c)
- It is important to highlight that the proposed methods require only statistical CSI in contrast to the existing works in [5,18], which employ the knowledge of instantaneous CSI. Thus, the proposed methods do not require pilot transmission for channel estimation and hence, can provide better spectral efficiency in contrast to the existing methods, which need pilot transmission.
2. Materials and Methods
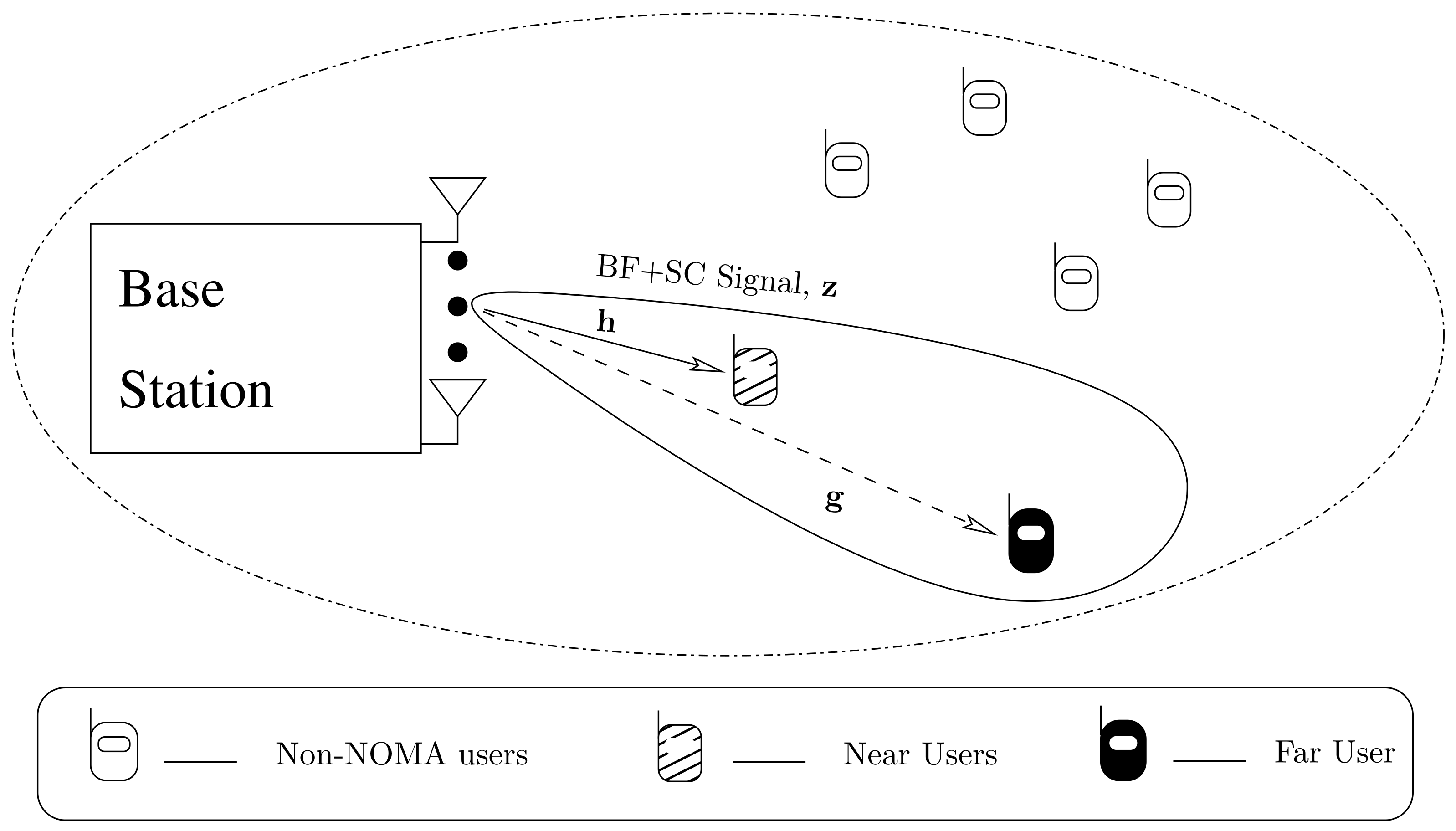
2.1. System Model
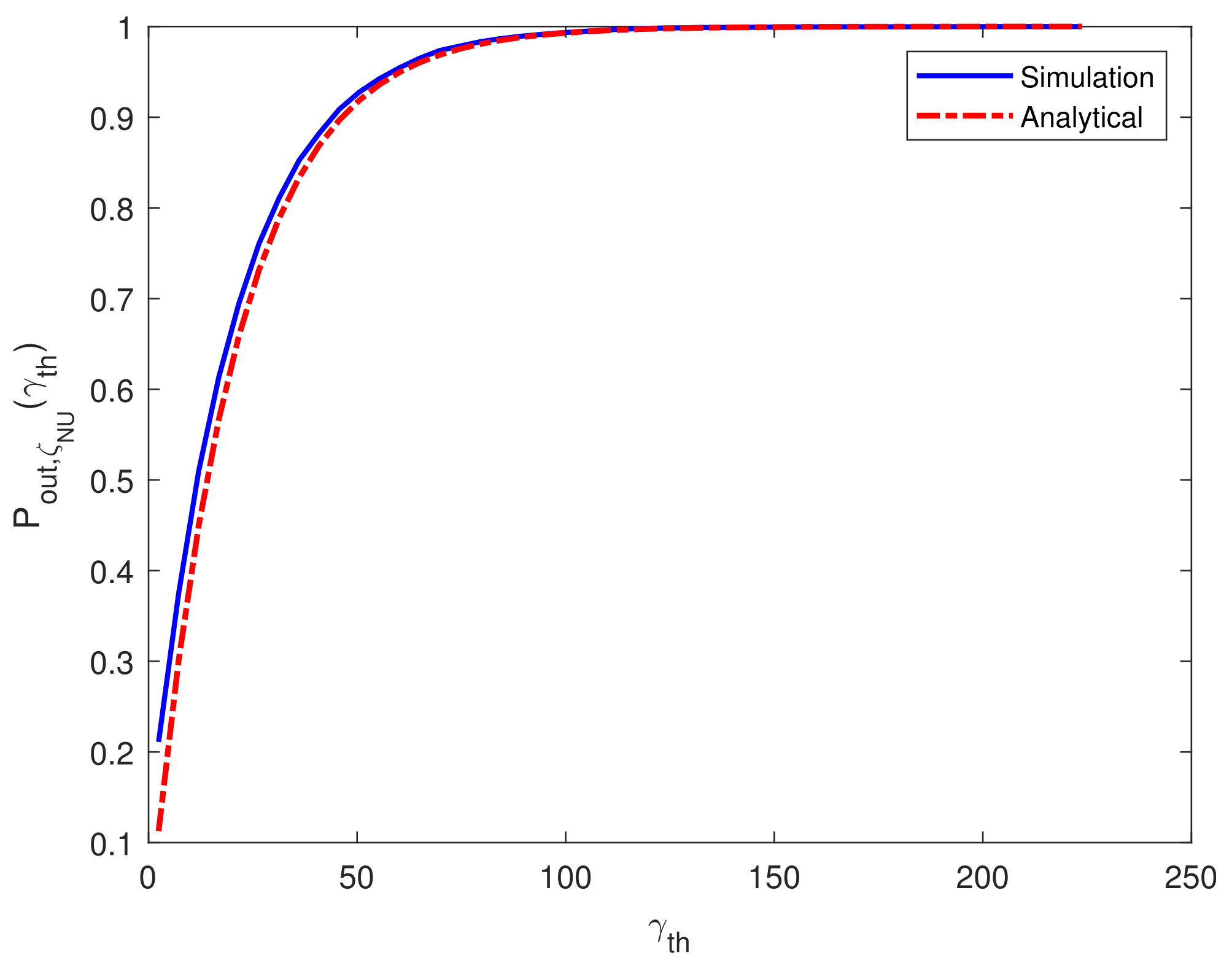
2.2. Derivation of Outage Probabilities
2.3. Design of Optimized Beamvectors for the NOMA System
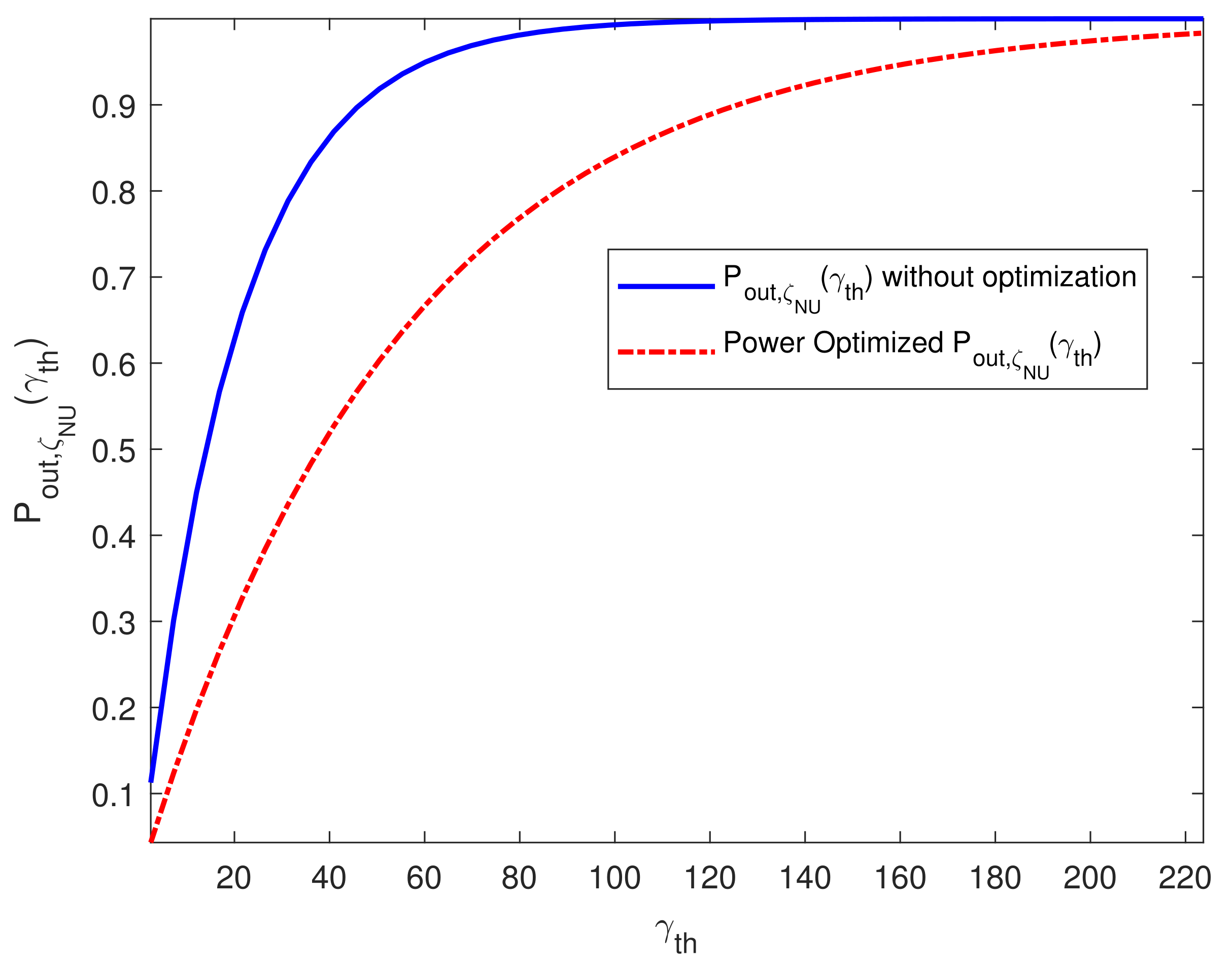
2.3.1. Task 1: Beam Power Minimization While Constraining the Outage Probabilities
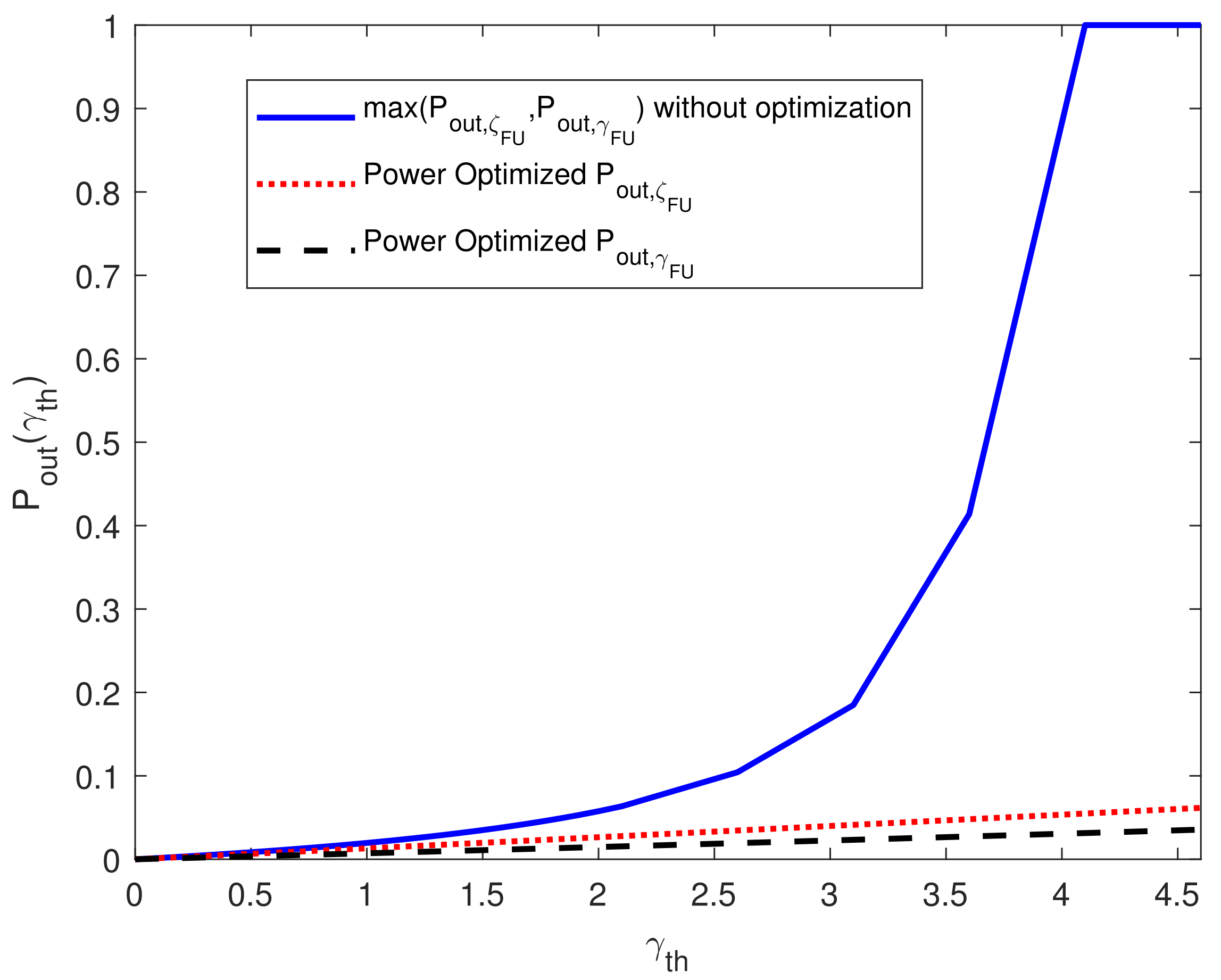
2.3.2. Task 2: Outage Probabilities Minimization While Constraining the Transmit Beam Powers
| Algorithm 1 NOMA-BeamformingOptimization Algorithm. |
|
3. Results and Discussion
3.1. Results for Task 1
3.2. Results for Task 2
4. Conclusions
- By minimizing the total beam powers while constraining the outage probabilities for near and far users;
- By minimizing the total outage probabilities in the system while constraining the beam powers.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Overview of Sequential Quadratic Programming
Appendix B. Evaluation of required Gradient Vectors for the Proposed Method
References
- Mohamed, E.M. Joint users selection and beamforming in downlink millimetre-wave NOMA based on users positioning. IET Commun. 2020, 14, 74–81. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Yuan, Y.; Han, S.; Chih-Lin, I.; Wang, Z. Non-orthogonal multiple access for 5G: Solutions, challenges, opportunities, and future research trends. Commun. Mag. 2015, 53, 74–81. [Google Scholar] [CrossRef]
- Agiwal, M.; Roy, A.; Saxena, N. Next generation 5G wireless networks: A comprehensive survey. Commun. Surv. Tutor. 2016, 18, 1617–1655. [Google Scholar] [CrossRef]
- Ding, J.; Cai, J.; Yi, C. An Improved Coalition Game Approach for MIMO-NOMA Clustering Integrating Beamforming and Power Allocation. Trans. Veh. Technol. 2019, 68, 1672–1687. [Google Scholar] [CrossRef]
- Choi, J. On generalized downlink beamforming with NOMA. J. Commun. Netw. 2019, 68, 1672–1687. [Google Scholar] [CrossRef]
- Aldebes, R.; Dimyati, K.; Hanafi, E. Game-theoretic power allocation algorithm for downlink NOMA cellular system. Electron. Lett. 2019, 55, 1361–1364. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, J.; Xiao, Z.; Cao, X.; Wu, D.O.; Xia, X. Joint Power Control and Beamforming for Uplink Non-Orthogonal Multiple Access in 5G Millimeter-Wave Communications. Trans. Wireless Commun. 2018, 17, 6177–6189. [Google Scholar] [CrossRef] [Green Version]
- Choi, J. Repetition-Based NOMA Transmission and Its Outage Probability Analysis. IEEE Trans. Veh. Technol. 2020, 69, 5913–5922. [Google Scholar] [CrossRef] [Green Version]
- Garcia, C.E.; Camana, M.R.; Koo, I. Joint Beamforming and Artificial Noise Optimization for Secure Transmissions in MISO-NOMA Cognitive Radio System with SWIPT. Electronics 2020, 9, 1948. [Google Scholar] [CrossRef]
- Ribeiro, F.; Guerreiro, J.; Dinis, R.; Cercas, F.; Jayakody, D. Multi-user detection for the downlink of NOMA systems with multi-antenna schemes and power-efficient amplifiers. Phys. Commun. 2019, 33, 199–205. [Google Scholar] [CrossRef]
- Kassir, A.; Dziyauddin, R.A.; Kaidi, H.M.; Izhar, M.A.M. Power Domain Non Orthogonal Multiple Access: A Review. In Proceedings of the 2018 2nd International Conference on Telematics and Future Generation Networks (TAFGEN), Kuching, Malaysia, 24–26 July 2018. [Google Scholar]
- Guerreiro, J.; Dinis, R.; Carvalho, P.; Silva, M. Nonlinear Effects in NOMA Signals: Performance Evaluation and Receiver Design. In Proceedings of the 2019 IEEE 90th Vehicular Technology Conference (VTC2019-Fall), Waikoloa, HI, USA, 22–25 September 2019. [Google Scholar]
- Clerckx, B.; Mao, Y.; Schober, R.; Jorswieck, E.; Love, D.J.; Yuan, J.; Hanzo, L.; Li, G.Y.; Larsson, E.G.; Caire, G. Is NOMA efficient in multi-antenna networks? A critical look at next generation multiple access techniques. IEEE Open J. Commun. Soc. 2021, 2, 1310–1343. [Google Scholar]
- Al-Naffouri, T.Y.; Moinuddin, M.; Ajeeb, N.; Hassibi, B.; Moustakas, A.L. On the distribution of indefinite quadratic forms in Gaussian random variables. Trans. Commun. 2016, 64, 153–165. [Google Scholar] [CrossRef]
- Panier, E.R. An active set method for solving linearly constrained nonsmooth optimization problems. Math. Program. 1987, 37, 269–292. [Google Scholar]
- Lucidi, S. Recursive quadratic programming algorithm that uses an exact augmented lagrangian function. J. Optim. Theory Appl. 1990, 67, 227–245. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, Springer Series in Operations Research and Financial Engineering, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Choi, J. Minimum Power Multicast Beamforming With Superposition Coding for Multiresolution Broadcast and Application to NOMA Systems. Trans. Commun. 2015, 63, 791–800. [Google Scholar] [CrossRef]
- Hassan, A.K.; Moinuddin, M.; Al-Saggaf, U.M.; Al-Naffouri, T.Y. Performance Analysis of Beamforming in MU-MIMO Systems for Rayleigh Fading Channels. Access 2017, 5, 3709–3720. [Google Scholar] [CrossRef] [Green Version]
- Broyden, C.G. The convergence of a class of double-rank minimization algorithms. II. The new algorithm. J. Inst. Math. Appl. 1970, 6, 222–231. [Google Scholar] [CrossRef] [Green Version]
- Fletcher, R. A new approach to variable metric algorithms. Comput. J. 1970, 6, 317–322. [Google Scholar] [CrossRef] [Green Version]
- Goldfarb, D. A family of variable-metric methods derived by variational means. Math. Comput. 1970, 24, 23–26. [Google Scholar] [CrossRef]
- Shanno, D.F. Conditioning of quasi-Newton methods for function minimization. Math. Comput. 1970, 24, 647–656. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Wright, M.H. Numerical Linear Algebra and Optimization; Addison Wesley: Boston, MA, USA, 1991. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aljohani, A.J.; Moinuddin, M. Statistical Beamforming Techniques for Power Domain NOMA System. Electronics 2021, 10, 3064. https://doi.org/10.3390/electronics10243064
Aljohani AJ, Moinuddin M. Statistical Beamforming Techniques for Power Domain NOMA System. Electronics. 2021; 10(24):3064. https://doi.org/10.3390/electronics10243064
Chicago/Turabian StyleAljohani, Abdulah Jeza, and Muhammad Moinuddin. 2021. "Statistical Beamforming Techniques for Power Domain NOMA System" Electronics 10, no. 24: 3064. https://doi.org/10.3390/electronics10243064
APA StyleAljohani, A. J., & Moinuddin, M. (2021). Statistical Beamforming Techniques for Power Domain NOMA System. Electronics, 10(24), 3064. https://doi.org/10.3390/electronics10243064





