A New Approach to the Development of Additive Fibonacci Generators Based on Prime Numbers
Abstract
1. Introduction
2. Related Works
3. Case Study
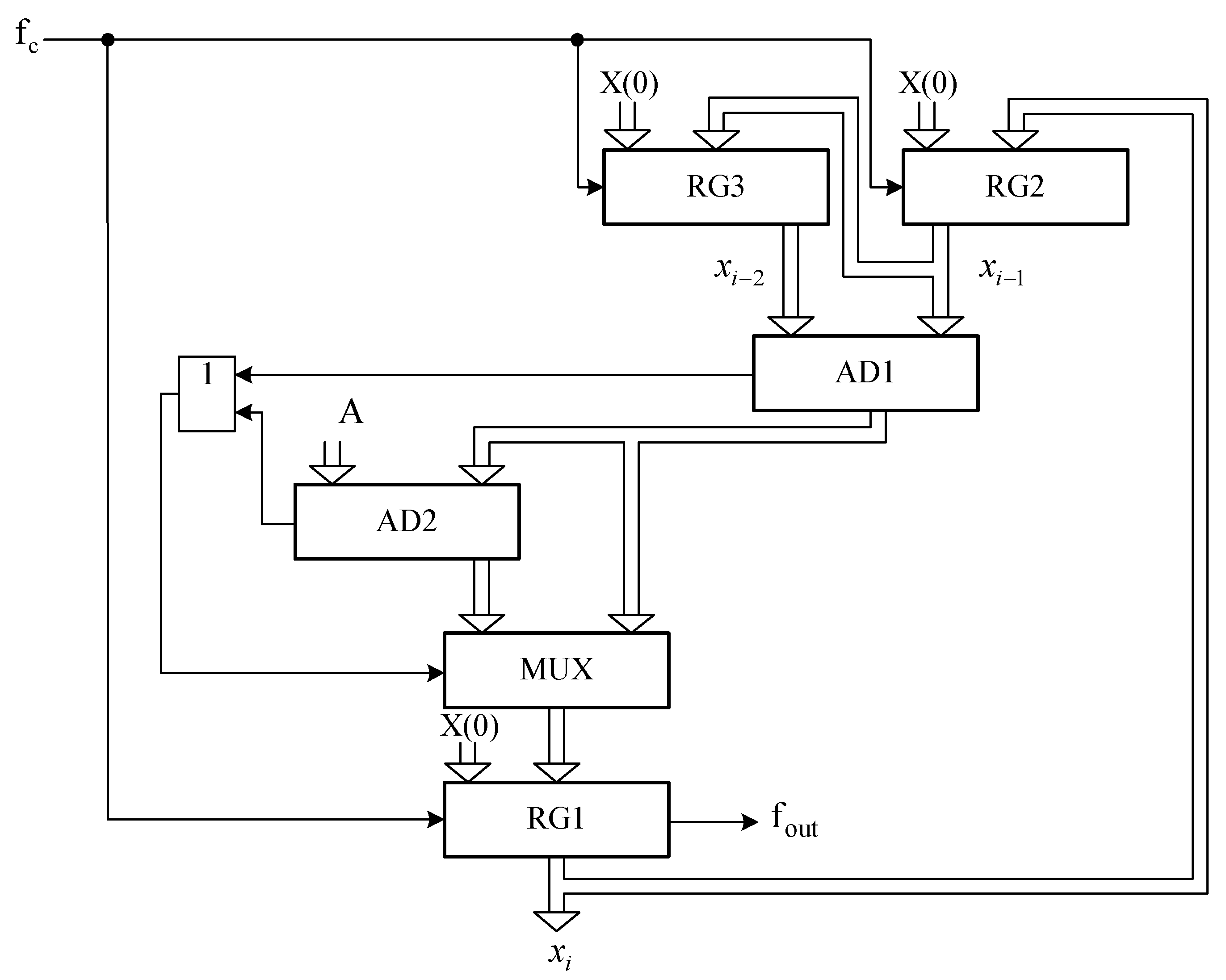
3.1. The Structure Schema and the Work Principle of the New AFG
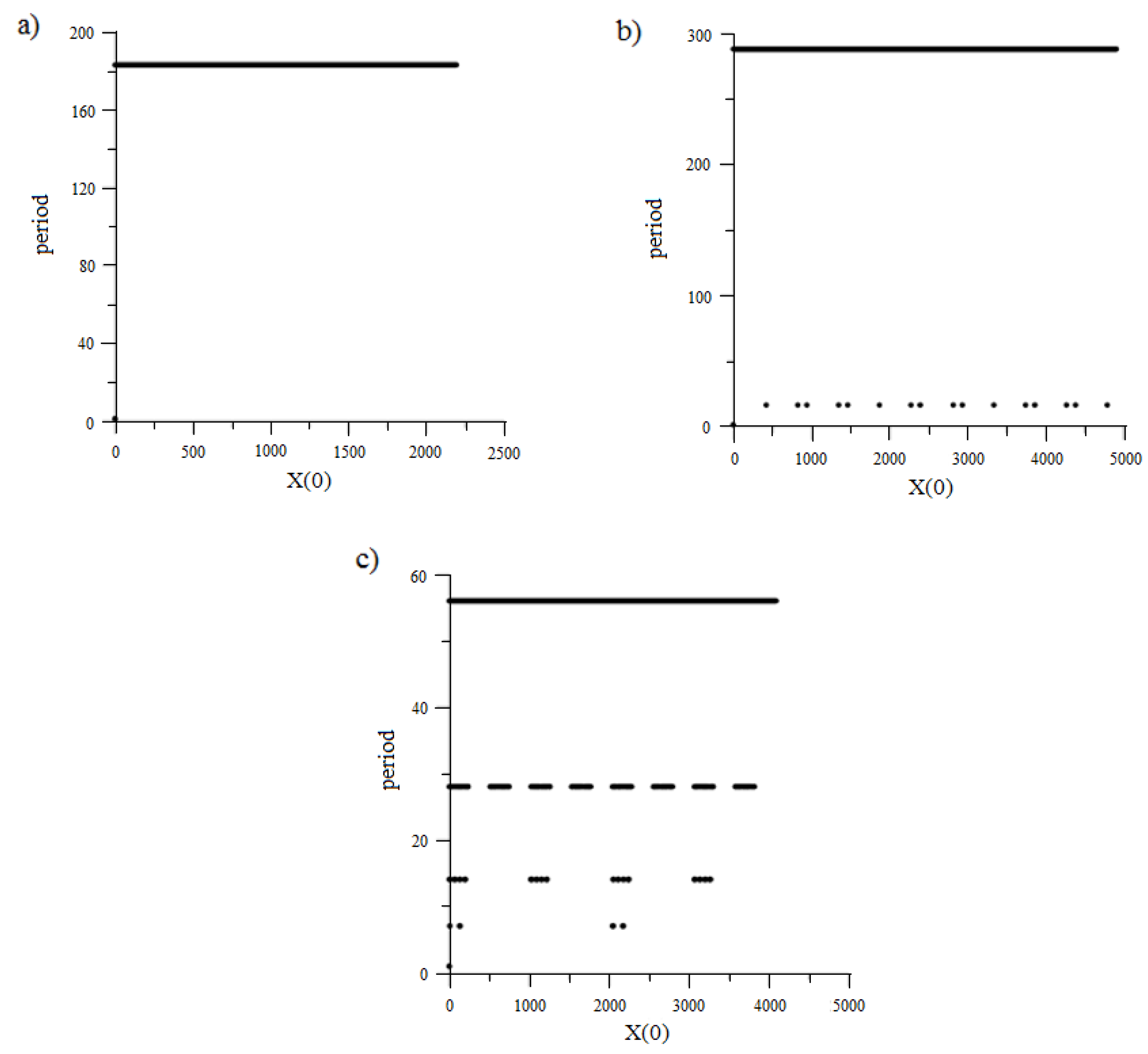
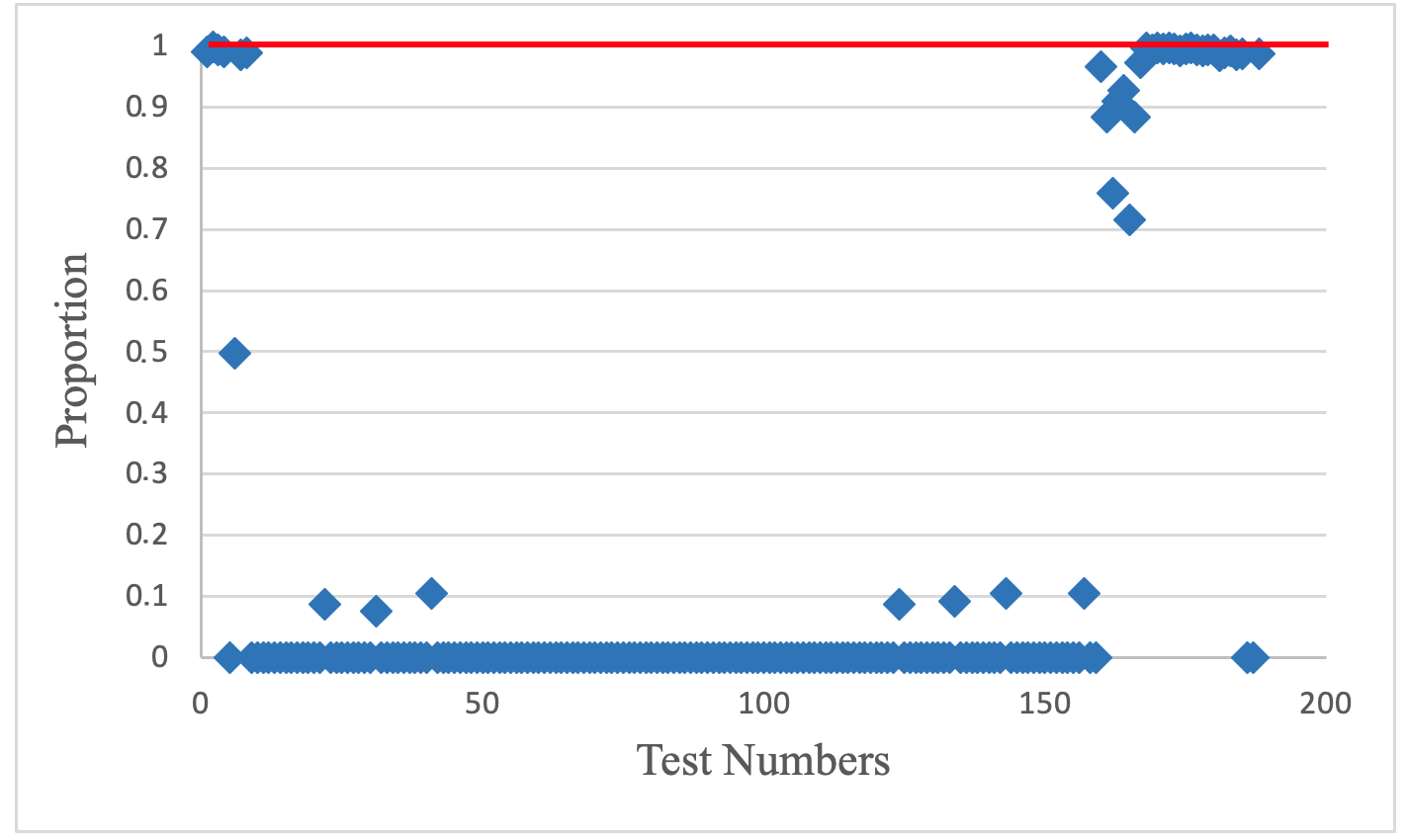
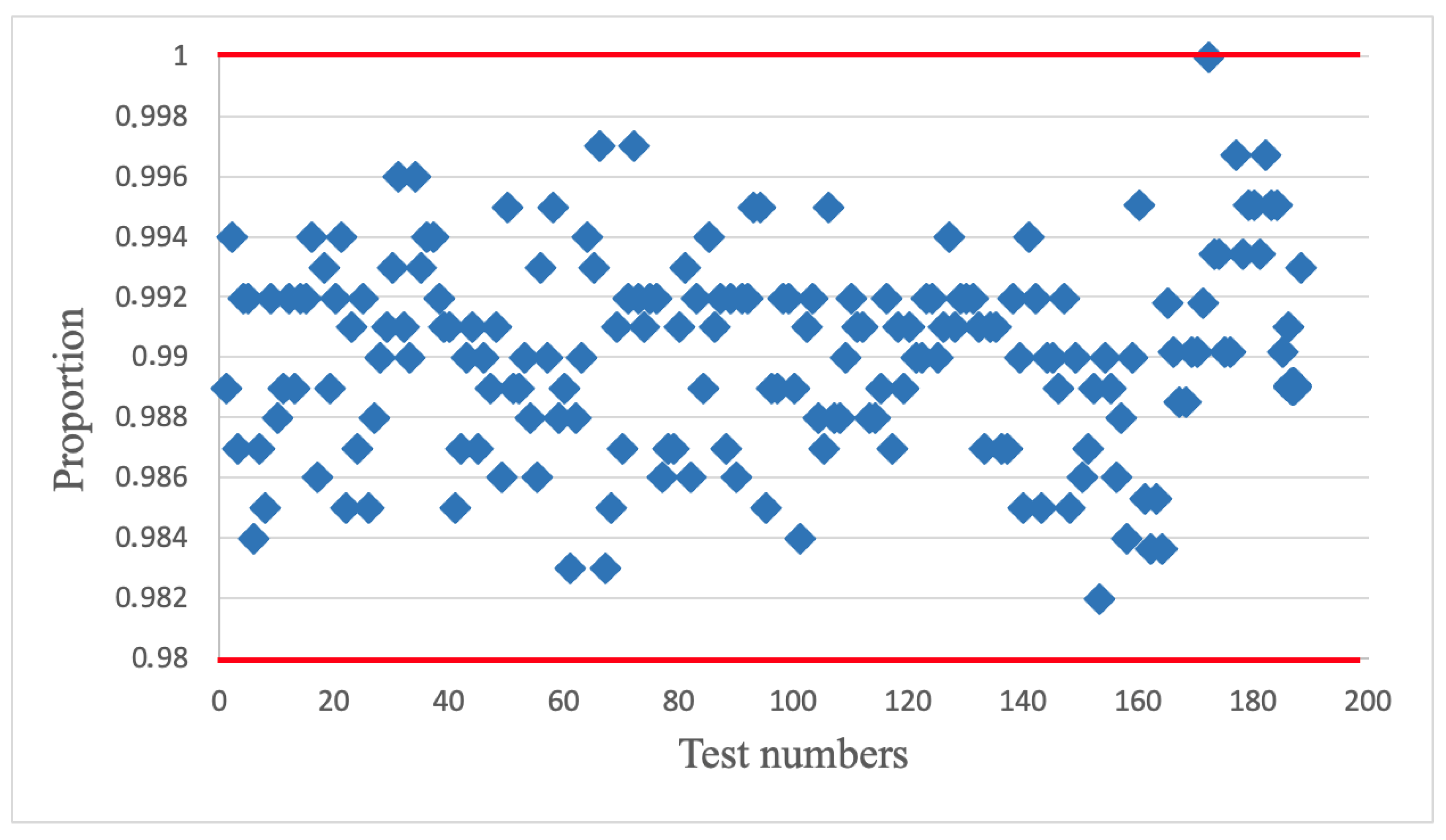
3.2. Research of the New AFG Characteristics
- A new type of AFG, in which the modulus of recurrent equations is a prime number (Figure 1), differs favourably from classical AFG, in which the modulus of recurrent equations is a power of 2, in the absence or relatively small number of “weak keys” (in which the repetition period of the pseudo-random sequence is small);
- In AFG of a new type (Figure 1), there are values of the module for which there are no “weak keys”.
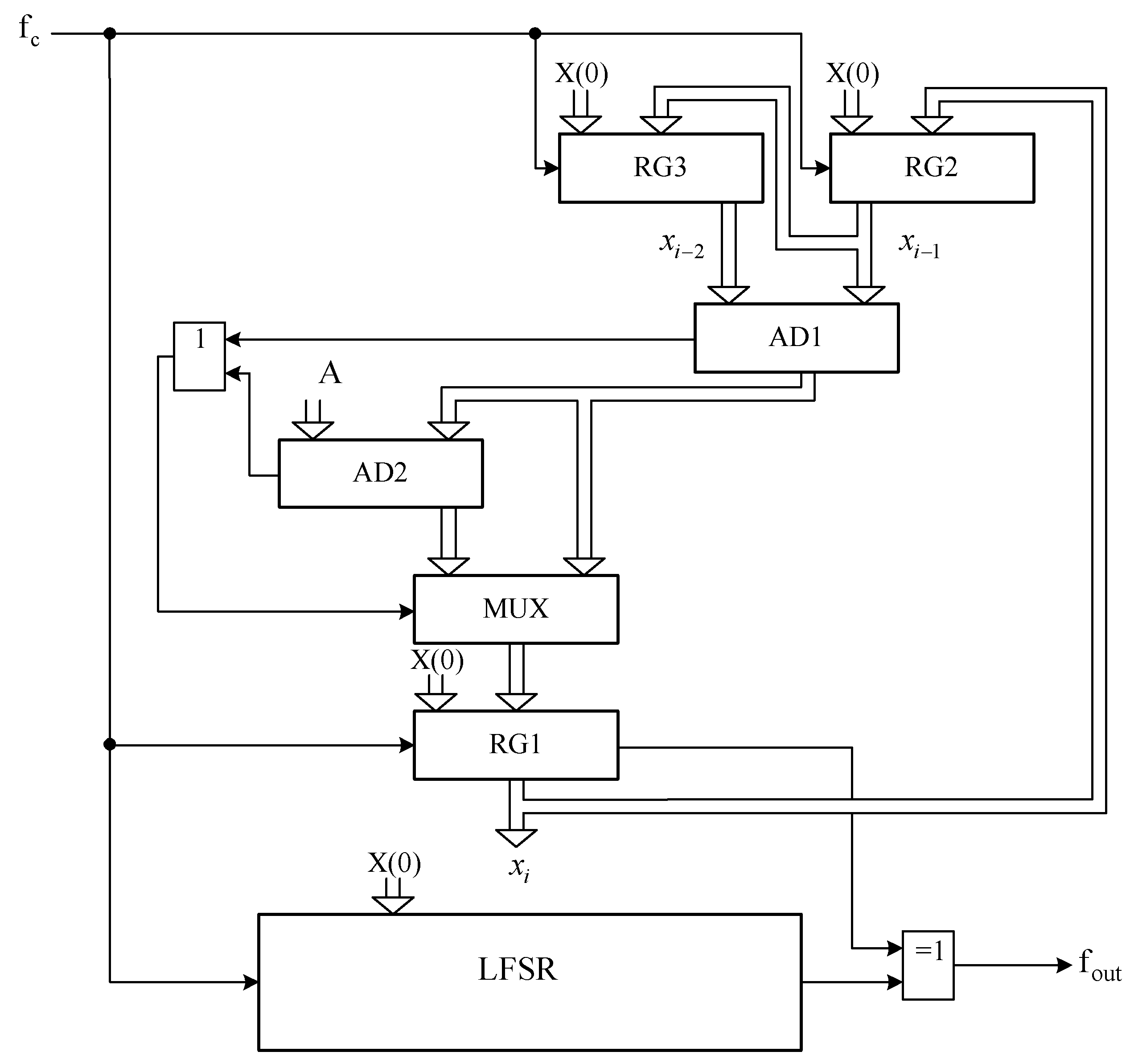
3.3. Structure Scheme and Operation Principle of the Combined PRBSG
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Cardell, S.D.; Requena, V.; Fuster-Sabater, A.; Orue, A.B. Randomness Analysis for the Generalized Self-Shrinking Sequences. Symmetry 2019, 11, 1460. [Google Scholar] [CrossRef]
- Blanco, A.; Orúe, A.B.; López, A.; Martín, A. On-the-Fly Testing an Implementation of Arrow Lightweight PRNG Using a LabVIEW Framework. In Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2019; pp. 175–184. [Google Scholar]
- Orúe, A.B.; Encinas, L.H.; Fernández, V.; Montoya, F. A Review of Cryptographically Secure PRNGs in Constrained Devices for the IoT. In Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2017; pp. 672–682. [Google Scholar]
- Murillo-Escobar, M.A.; Cruz-Hernández, C.; Cardoza-Avendaño, L.; Méndez-Ramírez, R. A novel pseudorandom number generator based on pseudorandomly enhanced logistic map. Nonlinear Dyn. 2017, 87, 407–425. [Google Scholar] [CrossRef]
- Meranza-Castillón, M.O.; Murillo-Escobar, M.A.; López-Gutiérrez, R.M.; Cruz-Hernández, C. Pseudorandom number generator based on enhanced Hénon map and its implementation. J. AEU-Int. J. Electron. Commun. 2019, 107, 239–251. [Google Scholar] [CrossRef]
- Hamza, R. A novel pseudo random sequence generator for image-cryptographic applications. J. Info. Secur. Appl. 2017, 35, 119–127. [Google Scholar] [CrossRef]
- Ivanov, M.A.; Chugunkov, I.V. Theory, Application and Evaluation of the Quality of Pseudorandom Consequences Generators; KUDITS-OBRAZ: Moskow, Russia, 2003; p. 240. [Google Scholar]
- Schneier, B. Applied Cryptography: Protocols, Algorithms, and Source Code in C; John Wiley & Sons: Hoboken, NJ, USA, 2007; p. 675. [Google Scholar]
- Orue, A.B.; Montoya, F.; Encinas, L.H. Trifork, a New Pseudorandom Number Generator Based on Lagged Fibonacci Maps. J. Comput. Sci. Eng. 2010, 2, 46–51. [Google Scholar]
- Maksymovych, V.; Harasymchuk, O.; Mandrona, M. Additive Fibonacci Generators Using Prime Numbers. In Proceedings of the VIIth International Scientific and Technical Conference “Information protection and Information Systems Security”, Lviv, Ukraine, 30–31 May 2019; pp. 66–68. [Google Scholar]
- Mandrona, M.; Maksymovych, V.; Harasymchuk, O.; Kostiv, Y. Generator of pseudorandom bit sequence with increased cryptographic immunity. Metall. Min. Ind. 2014, 6, 24–28. [Google Scholar]
- Aluru, S. Lagged Fibonacci Random Number Generators for Distributed Memory Parallel Computers. J. Parallel Distrib. Computing 1997, 45, 1–12. [Google Scholar] [CrossRef][Green Version]
- Mandrona, M.; Maksymovych, V. Investigation of the statistical characteristics of the modified Fibonacci generators. J. Autom. Inf. Sci. 2014, 46, 48–53. [Google Scholar] [CrossRef]
- Baldoni, S.; Battisti, F.; Carli, M.; Pascucci, F. On the Use of Fibonacci Sequences for Detecting Injection Attacks in Cyber Physical Systems. IEEE Access 2021, 9, 41787–41798. [Google Scholar] [CrossRef]
- Agarwal, A.; Agarwal, S.; Singh, B.K. Algorithm for data encryption & decryption using Fibonacci primes. J. Math. Control. Sci. Appl. 2020, 6, 63–71. [Google Scholar]
- Yacoab, M.; Sha, M.; Mustaq Ahmed, M. Secured Data Aggregation Using Fibonacci Numbers and Unicode Symbols for Wsn. Int. J. Comput. Eng. Technol. 2019, 10, 218–225. [Google Scholar] [CrossRef]
- Wang, J.; Przystupa, K.; Maksymovych, V.; Stakhiv, R.; Kochan, O. Computer Modelling of Two-level Digital Frequency Synthesizer with Poisson Probability Distribution of Output Pulses. Meas. Sci. Rev. 2020, 20, 65–72. [Google Scholar] [CrossRef]
- Maksymovych, V.; Mandrona, M.; Garasimchuk, O.; Kostiv, Y. A study of the characteristics of the Fibonacci modified additive generator with a delay. J. Autom. Inf. Sci. 2016, 48, 76–82. [Google Scholar] [CrossRef]
- Maksymovych, V.; Mandrona, M.; Harasymchuk, O. Dosimetric Detector Hardware Simulation Model Based on Modified Additive Fibonacci Generator. Adv. Intell. Syst. Comput. 2020, 938, 162–171. [Google Scholar]
- NIST SP 800-22 version 1a. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; NIST: Gaithersburg, MD, USA, 2010; p. 131.

| Prime Numbers, Max and Min Repetition Period Values | ||||||||
|---|---|---|---|---|---|---|---|---|
| m | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 |
| period | 7 | 13 | 24 4 | 48 6 | 120 10 | 183 | 288 16 | 180 9 |
| m | 23 | 29 | 31 | 37 | 41 | 43 | 47 | 53 |
| period | 506 22 | 871 | 993 | 1368 36 | 1723 | 231 21 | 2257 | 1404 |
| m | 59 | 61 | 67 | 71 | 73 | 79 | 83 | 89 |
| period | 58 | 930 | 4488 66 | 5113 | 5403 | 3120 | 2296 82 | 3960 44 |
| m | 97 | 101 | 103 | 107 | 109 | 113 | 127 | 131 |
| period | 3116 | 100 50 | 3536 | 2862 | 1485 | 4256 | 16,257 | |
| Prime Numbers, Repetition Period Values | ||||
|---|---|---|---|---|
| m | 8191 | 9973 | 65,537 (Fermat number) | 2,147,483,647 (Marsenn number) |
| period | 22,366,291 | 99,46,728 | 1,431,699,455 | >1010 |
| m Values, Max and Min Repetition Period Values | ||||||||
|---|---|---|---|---|---|---|---|---|
| m | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
| period | 7 | 14 7 | 28 7 | 56 7 | 112 7 | 224 7 | 448 7 | 896 7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maksymovych, V.; Harasymchuk, O.; Karpinski, M.; Shabatura, M.; Jancarczyk, D.; Kajstura, K. A New Approach to the Development of Additive Fibonacci Generators Based on Prime Numbers. Electronics 2021, 10, 2912. https://doi.org/10.3390/electronics10232912
Maksymovych V, Harasymchuk O, Karpinski M, Shabatura M, Jancarczyk D, Kajstura K. A New Approach to the Development of Additive Fibonacci Generators Based on Prime Numbers. Electronics. 2021; 10(23):2912. https://doi.org/10.3390/electronics10232912
Chicago/Turabian StyleMaksymovych, Volodymyr, Oleh Harasymchuk, Mikolaj Karpinski, Mariia Shabatura, Daniel Jancarczyk, and Krzysztof Kajstura. 2021. "A New Approach to the Development of Additive Fibonacci Generators Based on Prime Numbers" Electronics 10, no. 23: 2912. https://doi.org/10.3390/electronics10232912
APA StyleMaksymovych, V., Harasymchuk, O., Karpinski, M., Shabatura, M., Jancarczyk, D., & Kajstura, K. (2021). A New Approach to the Development of Additive Fibonacci Generators Based on Prime Numbers. Electronics, 10(23), 2912. https://doi.org/10.3390/electronics10232912











