1. Introduction
The recent decade has witnessed a tremendous growth of Internet traffic, which is expected to continue climbing for the foreseeable future. Recently, Spectrum-sliced Elastic Optical Path (SLICE) networks [
1,
2,
3] have come to light as a promising solution to resolve this traffic explosion. In traditional Wavelength Division Multiplexing (WDM) networks, spectrum resources are coarsely managed at the level of wavelengths (that are separated from each other with fixed guard-bands). In SLICE networks, a traffic demand is accommodated with a group of consecutive sub-carriers, and neighboring sub-carriers can overlap partially in the spectrum domain [
1,
2,
3]. As a single sub-carrier has a finer granular than a wavelength and consecutive sub-carriers can overlap without the fixed guard-bands, SLICE networks can better deliver both sub-wavelength and super-wavelength traffic accommodation [
2]. In addition, SLICE networks have other inherent advantages such as enhanced signal quality and extended reachability [
2].
It remains a challenging but fundamental problem to efficiently allocate lightpaths in SLICE networks to accommodate traffic demands, which is known as the Routing and Spectrum Allocation (RSA) problem [
4]. The challenges originate from three major constraints. First, one has to allocate continuously free sub-carriers along a path to fulfill the demand. Second, the chosen free sub-carriers should as well be consecutive ones in the spectrum domain (i.e., the
sub-carrier consecutiveness constraint). Third, the guard-bands between lightpaths are not predetermined and have to be decided at run time. The RSA problem is shown to be NP-Hard [
4], and the solutions to the RSA problem can be classified into two categories. First, optimal solutions provided by link-based, path-based, and channel-based Integer Linear Programming (ILP) models. We note that channel-based models inherently capture the second and third constraints above explicitly, thus leading to a compact formulation. Second, sub-optimal heuristic algorithms and meta-heuristic algorithms. Overall, ILP-based approaches demand prohibitive computational time, which limits their applicability in reality; and methods that are heuristic in nature lack guaranteed closeness to the optimal solution.
We seek to avoid the above limitations of existing approaches, and propose a novel primal-dual solution framework to the RSA problem in this paper. Inspired by a compact channel-based ILP solution, we explore the relaxation and decomposition of the model based on the dual variables or Lagrange multipliers of complex coupling constraints, which leads to an upper bound (UB) of the problem. The dual multipliers obtained from above are then fed into a Primal algorithm for obtaining a lower bound (LB) of the problem. Our framework employs these two processes to update the UB and LB iteratively, resulting in a near-optimal solution with a per-instance guarantee on its closeness to the optimal solution.
The rest of the paper is organized as follows. In
Section 2, we present the network model, the definition, and a compact ILP model of the studied problem. In
Section 3, we explore relaxation and decomposition of the ILP model, and propose an exact solution to the resulting problem. In
Section 4, we present the primal-dual framework. In
Section 5, we evaluate the proposed framework. In
Section 6, we review related literature, and we conclude this work in
Section 7.
2. Network Model, Problem Definition, and a Channel-Based ILP Model
In this section, we present the network model, problem definition and complexity, and a channel-based ILP model of the studied problem.
2.1. Network Model
A SLICE network is modeled as a graph
:
V consists of nodes of the network;
E contains the set of directional fibers connecting nodes in
V; and
S is the group of sub-carriers on each fiber. The set of traffic demands is denoted as
D = {
} (
), and
denotes the required number of sub-carriers for demand
.
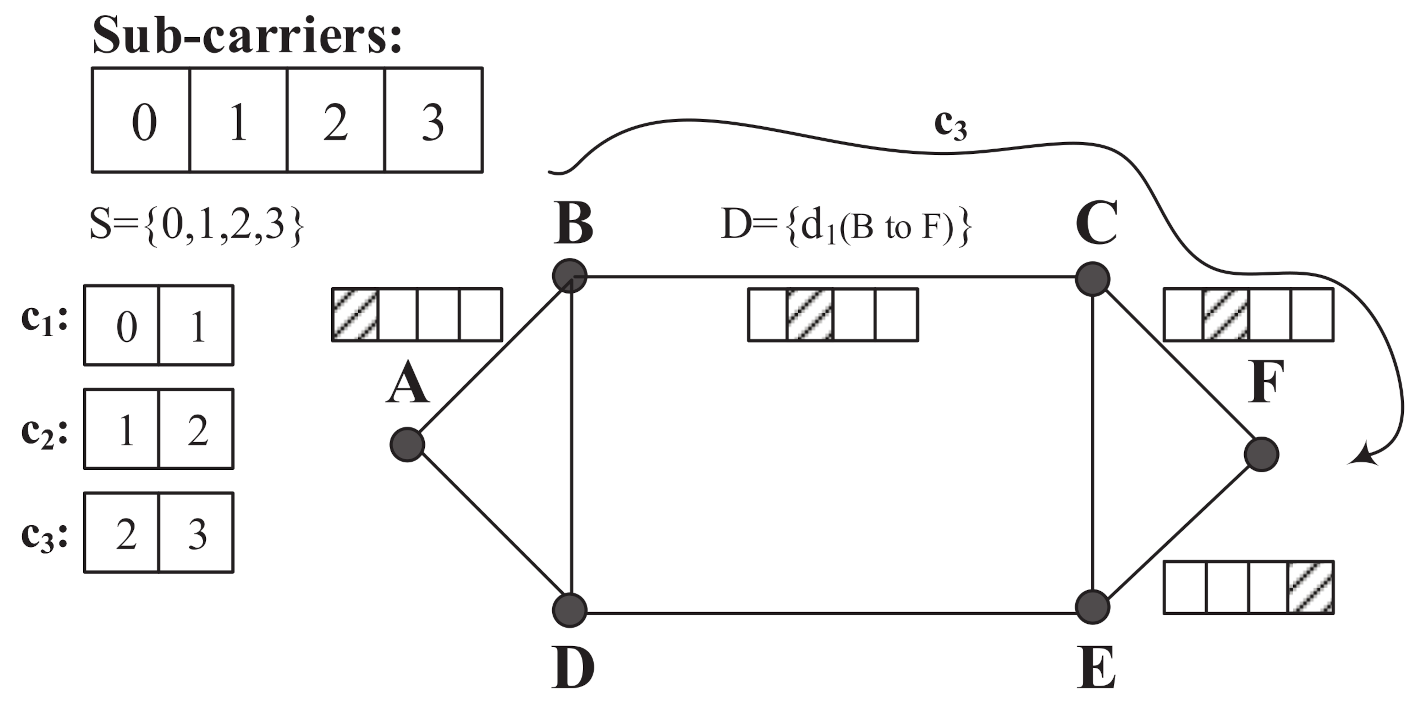
Figure 1 shows an example of the SLICE network with six nodes and
(i.e.,
) for each fiber. In
Figure 1, the sub-carrier usage of fiber links are only shown for those with partial sub-carriers occupied (i.e., in shadow). In addition, for this example, there is only one demand
(from node
B to node
F) in the set
D.
The sub-carrier consecutiveness constraint requires the allocation of a block of
consecutive sub-carriers for a demand
d. This requirement can be explicitly captured with the concept of channel [
5,
6]. Note that we exclude the consideration of guard-bands in this paper since which can as well be treated as part of the channel [
4,
5]. In
Figure 1, for example, assuming that the demand size of
is 2, one can have three channels of
,
, and
, with two sub-carriers each. Some of the channels, however, cannot be used to accommodate demands when sub-carriers within are occupied. For instance, in
Figure 1, for the request
of size 2 between
B and
F along the path
B-
C-
F, only channel
can be allocated.
Definition 1. Channel—Achannelis a block of consecutive sub-carriers of size for a request d.
2.2. Problem Definition
The formal definition of the studied problem is stated below.
Definition 2. Routing and Spectrum Allocation with Optimal Revenue (ROR)—given the demand set D, and a SLICE network , the ROR problem aims to achieve the maximum revenue by satisfying requests from D with available channels along the routes of requests.
Note that our general definition leaves the freedom for exact ways of defining the revenue. Some typical definitions of revenue, however, are addressed in the subsection below. We further note that the ROR problem is NP-Hard, as shown in Theorem 1.
Theorem 1. The ROR problem is NP-Hard.
Proof of Theorem 1. One can simply reduce a regular RSA problem [
4] to the ROR problem by setting the revenue of each request to be the same. Thus the ROR problem is NP-Hard. □
2.3. A Channel-Based Model for the ROR Problem
Next we adapt the channel-based ILP model from [
5] and present it below, which adopts the following variables/notations.
| : | 0 if demand d is not accommodated, 1 otherwise; |
| : | 1 for the chosen channel c along the chosen path p, 0 otherwise; |
| : | the path set for demand d; |
| : | the channel set for demand d; |
| : | the revenue factor for accepting demand d; |
| : | 1 if path p includes e (∈ E) as an edge, 0 otherwise; |
| : | 1 if channel c contains sub-carrier s, 0 otherwise. |
Each demand is associated with a revenue factor
, which may reflect the incentive of accepting demand
d. The resulting objective of maximizing the total revenue is expressed as in Equation (
1). We discuss two typical ways of defining
. One can set
for
, then revenue is reflected as the total number of accepted requests in Equation (
2). Likewise, one can set
, then revenue is reflected as the total volume of accommodated requests as in Equation (
3).
There are only two groups of constraints in this compact model (and the sub-carrier consecutiveness constraint is already taken into account implicitly). The constraints of Equation (
4) ensure that demand
d is accepted when one and only one channel along its route is chosen (i.e.,
). In addition, Equation (
5) is employed to avoid a sub-carrier clash, which happens only when two conditions are both satisfied: first, a given sub-carrier appears in overlapping channels of multiple requests; the given sub-carrier is over a common fiber link that resides in paths of those requests.
One well-known issue with a model that is path-based in nature is the potential exponential number of path-related variables (i.e., ). Interestingly, with our proposed framework, we can obtain solutions based on the above model without this issue.
3. Resolve the Channel-Based Model: Relaxation, Decomposition and Channel-Graph-Based Algorithm
In this section, we apply relaxation, and decomposition in sequence to the channel-based model, resulting in a simplified model that can be exactly resolved by a Channel-Graph-based algorithm.
3.1. Relaxation of the Channel-Based Model
Note that the most complex constraints of the channel-based ROR model lie in Equation (
5). We take the dual variables of Equation (
5) (i.e.,
(≥0)), and apply Lagrange relaxation to the constraints of Equation (
5) (with the aim of simplifying the channel-based model). The revised objective is shown in Equation (
6). The resulting Relaxed model consists of Equation (
6) and Equation (
7), and is referred to as the R model hereafter.
It remains to address two issues to resolve the original ROR problem. First, one needs to find the optimal for the R model, which essentially solves the dual problem of the R model and can be addressed with a Sub-gradient algorithm. Second, one needs to resolve the R model at any given dual variables , namely the R() model, which is further elaborated below.
3.2. Decomposition of the R() Model
It can be observed that, in the R(
) model, for a given demand
d, constraints of Equation (
7) are not coupled with that of any other demands. This observation inspires us to further decompose the R(
) model on a per-demand basis. The resulting model consists of Equation (
8), and Equation (
9) as the objective and constraints, respectively. Note that the term
in the objective of Equation (
6) is a constant at any fixed dual variables, thus it is excluded in Equation (
8).
We refer to above Decomposed Relaxed model as the DR model. Note that after the DR model for each demand is resolved, one can combine the solutions to resolve the R() model.
3.3. Channel-Graph-Based Algorithm for the DR Model
Now we design a polynomial time algorithm to resolve the DR model based on the concept of Channel-Graph. A Channel-Graph is a snapshot of the network at a particular channel, thus there are at most
Channel-Graphs for a demand
d. An example of the Channel-Graph (CG) construction for the six-node network in
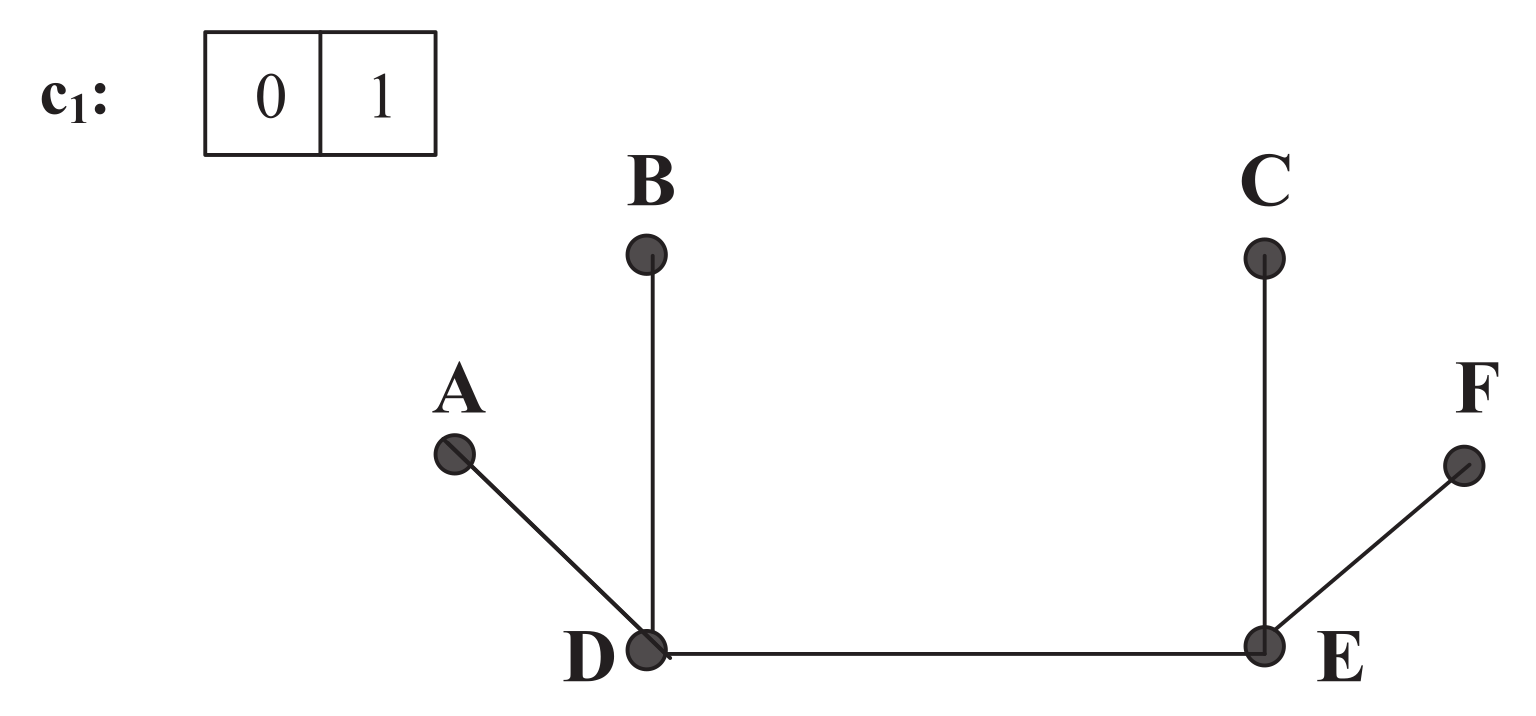
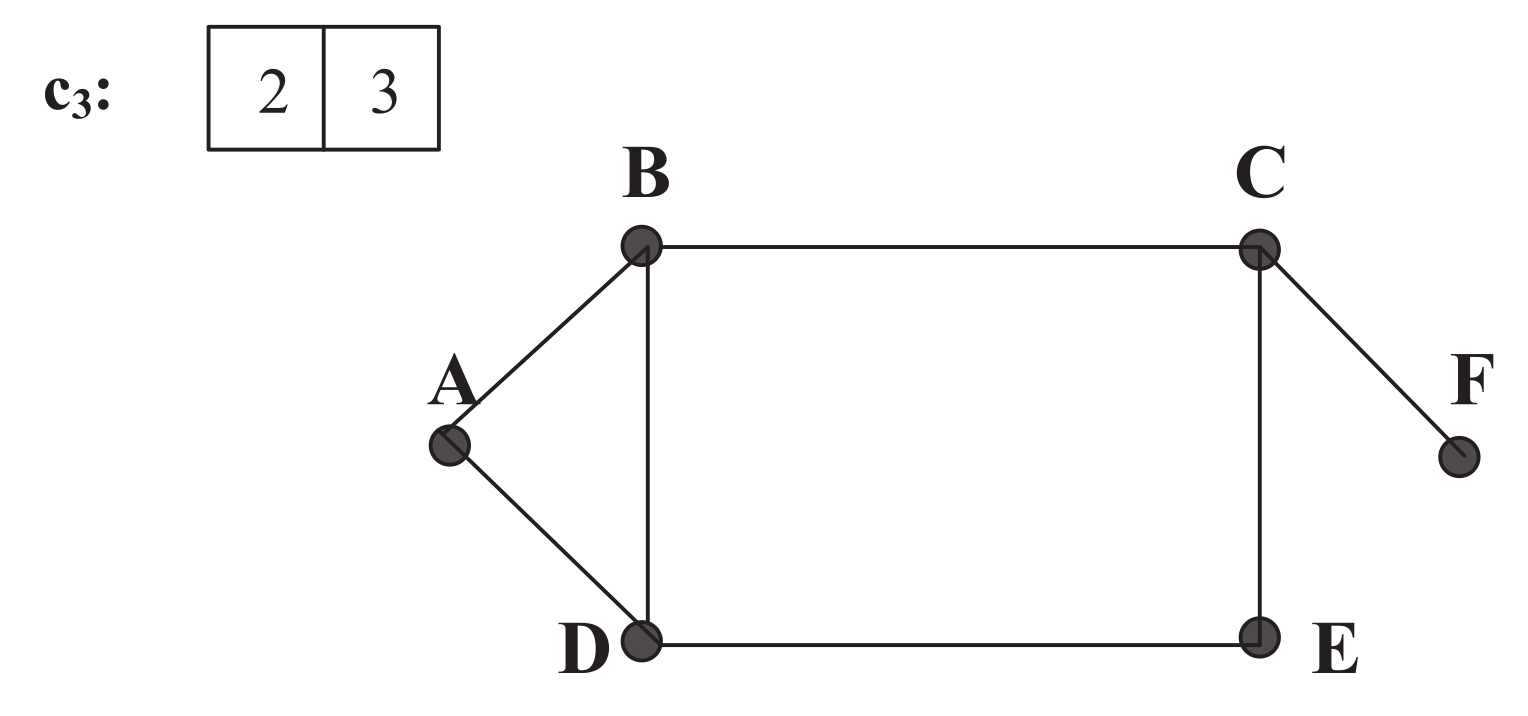
Figure 1 is shown in
Figure 2,
Figure 3 and
Figure 4. We assume that the demand
has a size of 2, which leads to three possible channels:
,
, and
in
Figure 1, with respective Channel-Graphs shown in
Figure 2,
Figure 3 and
Figure 4. As an example, in
Figure 2 of channel
, link
A-
B, link
B-
C, and link
C-
F are removed from the original network due to the occupancy of sub-carriers of
(i.e., Sub-carrier 0 or 1) on those three links.
Based on the channel-graphs, Algorithm 1 provides an exact solution for the DR model of each demand. Variable i in Line 1 is the index of all possible channels for demand d (i.e., ). Lines 4 to 7 construct the channel-graph for each channel (say c), and assign the weight of an edge e as . The rational of this weight assignment is further elaborated below in the proof of Theorem 2. Lines 8 to 12 employ the Dijkstra’s algorithm for the shortest path over all channel-graphs to decide the best channel (i.e., ) and path (i.e., ). represents the weight of the found shortest path. As shown in Lines 14 to 17, a demand is accepted (i.e., , and ) if (i.e., non-negative revenue). As shown in Theorem 2, we claim that Algorithm 1 exactly resolves the DR model.
Theorem 2. Algorithm 1 resolves DR model of a demand d optimally.
Proof of Theorem 2. For a given demand
d, note that the corresponding DR model only has a single constraint in Equation (
9). Equation (
9) essentially corresponds to a path and channel selection for demand
d (i.e.,
). With the constructed channel-graphs, we can separately examine the objective of the model per channel if the weight of the edges in each channel-graph is properly assigned. For a demand
d, the maximization of the objective is equivalent to the minimization of the term
. We reformulate this term as
. This inspires us to assign weight as
for link
e on the channel
c, thus the minimum weight path over all channel-graphs of demand
d leads to the minimization of the term
, and further the optimization of the DR model. □
| Algorithm 1 Channel-Graph-Based Algorithm for DR Model of Demand d. |
- 1:
- 2:
- 3:
for do - 4:
Make a copy of the original network, namely - 5:
for all Link do - 6:
Remove e from if Channel i is not available on e, otherwise: - 7:
- 8:
end for - 9:
Obtain the minimum weight path on using Dijkstra’s algorithm (assume that the found path p has weight W) - 10:
if then - 11:
- 12:
- 13:
- 14:
end if - 15:
- 16:
end for - 17:
- 18:
if then - 19:
- 20:
- 21:
end if
|
With the exact solution of DR model, we can resolve the R() by combining the results from each demand . It now remains to find the optimal dual variables to resolve the original problem, which is elaborated in the next section.
4. The Primal-Dual Framework for the ROR Problem
We present the solution framework in this section, focusing on two major components of this framework: the Primal algorithm, and a Sub-gradient algorithm. Note that the Primal algorithm addresses the ROR problem directly (i.e., the primal problem), while the Sub-gradient algorithm finds the optimal (which essentially resolves the dual problem of ROR). We hence refer to the framework as the primal-dual framework.
4.1. The Primal Algorithm
Note that the solution obtained by Algorithm 1 may not be feasible for the ROR problem as Equation (
5) is relaxed. We need an algorithm that directly solves the ROR problem for a definite feasible solution, which is presented in Algorithm 2, namely the Primal algorithm. As the solution found by Algorithm 2 is feasible, the associated revenue is adopted as a
lower bound (LB) for that of the ROR problem.
| Algorithm 2 The Primal Algorithm for the ROR Problem. |
- 1:
for all do - 2:
for all do - 3:
- 4:
end for - 5:
end for - 6:
Arrange demands in D in descending order based on the value of - 7:
for all do - 8:
W ← ∞ - 9:
for all Channel do - 10:
Obtain the minimum-weight path on the current channel-graph of d using Dijkstra’s algorithm (assume that the found path p has weight ) - 11:
if ≤ W then - 12:
W ← - 13:
* ← p - 14:
* ← - 15:
end if - 16:
end for - 17:
for all Channel-Graph do - 18:
for all * do - 19:
Remove e from - 20:
end for - 21:
end for - 22:
end for
|
Following the descending order of (i.e., the revenue found by Algorithm 1), Algorithm 2 sequentially accepts demands in D. In Lines 5–7, we assign the weight () of edge e on as . Note that this weight reflects the extent that the corresponding constraints are violated after the relaxation. The minimum-weight path found (i.e., path * along channel *) in Lines 7 to 12 attempts to achieve the least violation of the original constraints. As Channel * is planned to be reserved along path *, we remove corresponding edges from other channel-graphs to prevent the related sub-carriers from being used again in Lines 13 to 15.
4.2. The Sub-Gradient Algorithm for the R Model
The Sub-gradient Algorithm is an iterative process that is guaranteed to converge to the best dual variable or Lagrange multiplier (i.e.,
) [
7]. The objective of the found solution with a Sub-gradient Algorithm is an
upper bound (UB) of that of the original problem [
7]. The Sub-gradient Algorithm is reflected in Algorithm 3 (excluding Line 11). In Algorithm 3,
i is the iteration number. The dual variable in Iteration
i is denoted as
, and hence the
R model of the current iteration is denoted as
. In Lines 8 to 10, Algorithm 1 resolves the decomposed
model (i.e., the DR model), and updates UB and/or LB (if better UB and/or LB are found). The dual variables are updated in each iteration by taking the violations of the relaxed constraints of the original model into account in Lines 12 to 13, where
is a standard scalar [
7].
4.3. Summary of the Overall Framework
The Primal-Dual framework presented in Algorithm 3 iteratively maintains an upper bound and lower bound for the original ROR problem from the Sub-gradient algorithm and the Primal algorithm, respectively. Line 11 applies the Primal algorithm to obtain a feasible solution to the ROR problem in each iteration. There are two possible stopping criteria (i.e., Line 16): the maximum iteration number (i.e., ) and the value of = . The second criteria is reached when the upper bound and lower bound are close enough (e.g., , and is a small number that can be customized as an input).
It is worth noting that the proposed framework bears a few important merits. First, our framework stays away from directly solving any time-prohibitive ILP models (even though it is derived from a channel-based model). Second, our framework avoids exploring the exponential number of potential paths. DR model is exactly solved with the simple Dijkstra’s algorithm following a proper link weight assignment (Line 8 of Algorithm 1). Likewise, in the Sub-gradient algorithm, only selected paths in the current iteration (i.e., for which = 1) contribute to the updating of the dual variables in Line 13 of Algorithm 3. Third, with either stopping criteria in Line 16 of Algorithm 3, the obtained solution has a guaranteed closeness to the optimal solution as shown in Theorem 3 below, where is the revenue from the optimal solution.
Theorem 3. The framework can obtain a feasible solution with a revenue no less than *.
Proof of Theorem 3. First note that the solution found by the Primal algorithm or the one with LB updated in Line 10 of Algorithm 3 is always feasible. We have , where denotes the obtained revenue from the framework. As , we have . □
| Algorithm 3 The Primal-Dual Framework for the ROR Problem. |
- 1:
for all , do - 2:
- 3:
end for - 4:
Revenue of accommodating all demands - 5:
- 6:
- 7:
- 8:
repeat - 9:
Apply Algorithm 1 to resolve the decomposed model, and update the UB if needed - 10:
if The solution in the above step is feasible then - 11:
Update the LB if needed - 12:
end if - 13:
Apply the Primal algorithm, and update the LB if needed - 14:
for all , do - 15:
- 16:
end for - 17:
- 18:
- 19:
until is small enough
|
5. Performance Evaluation
In this section, the proposed framework is evaluated and analyzed. The NSFNET network is used as the network topology with
= 40. The demand set
D consists of a demand from each node-pair, with
as an integer number uniformly distributed within
(
x is an integer number) for each demand
d. For each experiment, average performance based on hundreds of instances (at the same setting) are collected and reported below. Furthermore, the proposed framework does not require an ILP solver such as ILOG CPLEX [
8] as a polynomial-time algorithm (i.e., Algorithm 1) is proposed to address the DR model.
5.1. The Impact of the Stopping Criteria
As we discuss above, we have two stopping criteria: the maximum iteration number, and the closeness of the current solution (i.e., ). We investigate the impact of these two criteria to uncover some insights on the choice of these two parameters.
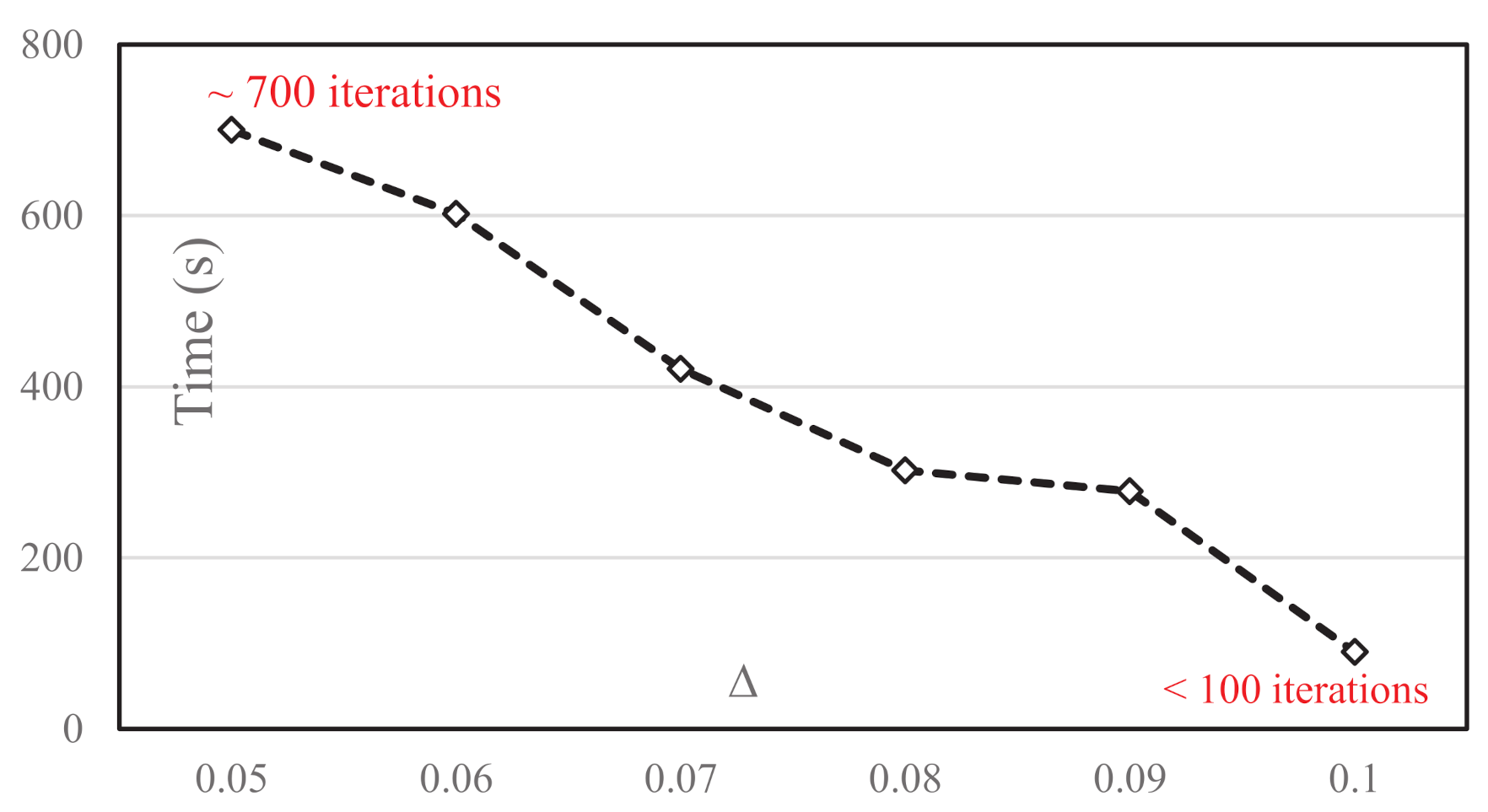
We first investigate the impact of parameter of
on computational time in
Figure 5 where the X-axis is the
value and the Y-axis is the computational time needed to achieve the respective
. Clearly, with the increase of
, the required computational time decreases as the larger
s correspond to lower revenues. Approximately, to achieve
, 700 iterations are consumed while less than 100 iterations are needed to achieve
. The best
achieved in
Figure 5 is
. One question arises is:
Do more iterations lead to a further decrease in Δ?. We investigate this problem below.
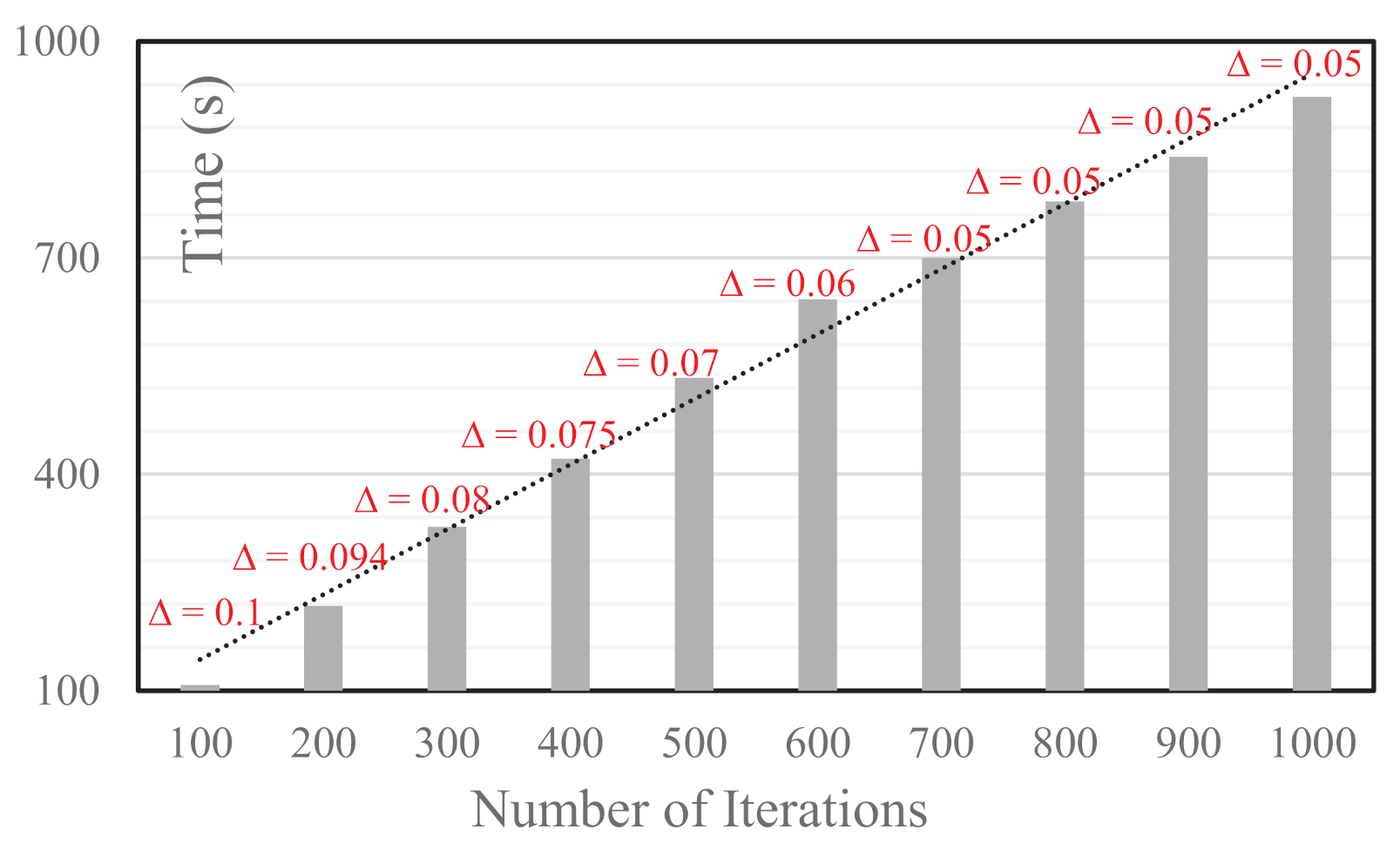
Figure 6 plots the trend of computational time (i.e., the Y-axis) as the number of iterations (i.e., the X-axis) grows. Evidently, it reveals an almost linear increase of time with the growth of the number of iterations. This observation is to be expected. Note that, however, an increasing number of iterations
does not lead to definite performance improvement based on the labeled
value in
Figure 6. When the number of iterations is at the lower end, its increase leads to an evident increase in performance (i.e., the decrease in
). When the number of iterations reaches a larger value (e.g., 700 in
Figure 5), a further increase does not lead to revenue increase as
already converges to the optimal value. Based on the above discussion, in reality, depending on time-sensitivity and the solution quality requirement, one can trade-off along these two dimensions.
5.2. Performance in Revenue
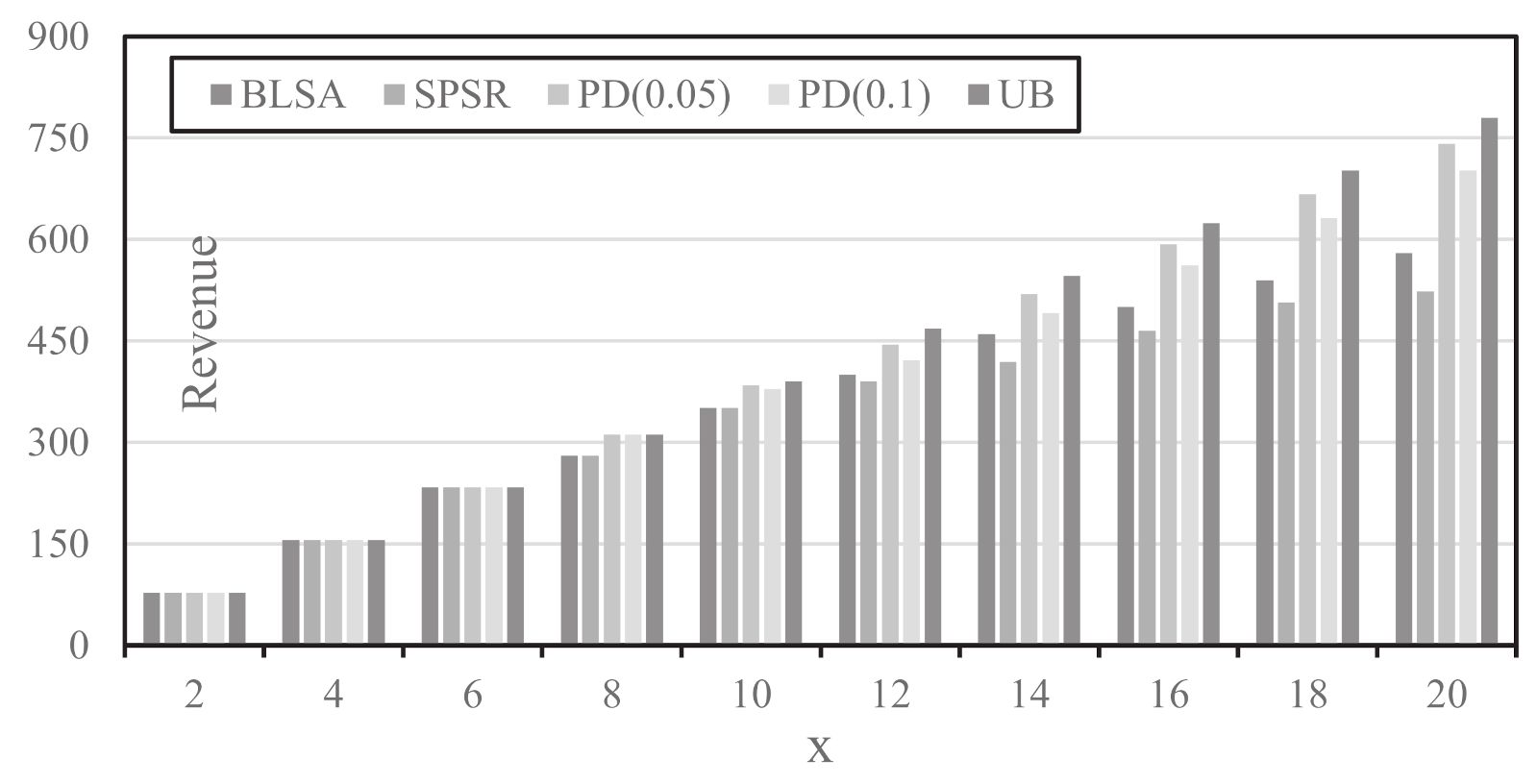
We further study the performance of the proposed framework by examining the achieved revenue, and the SPSR (Shortest Path with Maximum Spectrum Reuse) and BLSA (Balanced Load Spectrum Assignment) algorithms (which are commonly adopted as benchmark algorithms in the literature) from [
4] are used for comparison. The major difference between SPSR and BLSA lies in the routing: the shortest-path routing is used in the former; and load-balanced routing is used in the latter. The maximum iteration number (i.e.,
) is set to be 700. The performance comparison is shown in
Figure 7 where the X-axis of
Figure 7 corresponds to
x or the maximum value for demands between node-pairs and the Y-axis shows the revenue by setting
for each demand
d. In
Figure 7, PD(n) represents the proposed Primal-Dual framework when setting
. UB refers to the upper bound that is obtained by the Sub-gradient algorithm (while LB matches the respective revenue from PD(n) solution). From
Figure 7, with a light traffic load (e.g.,
), all schemes demonstrate a similar performance as all requests are accommodated with all schemes. With the increase of the load, the proposed schemes achieve higher revenue than that of BLSA and SPSR. The performance difference even enlarges with the further increase of traffic load. The PD(
) scheme apparently outperforms the PD(
) scheme in most cases at the expense of a possible longer computational time.
6. Related Work
The Routing and Spectrum Allocation (RSA) problem shares similarity with the Routing and Wavelength Assignment (RWA) problem in WDM networks. The latter has been extensively studied in the literature (see, e.g., [
9,
10,
11,
12,
13,
14]), however, the solutions to RWA problem cannot be applied to RSA due to two major reasons. First, in RWA, a traffic demand is typically accommodated as a lightpath at the granular of individual wavelength. In SLICE networks, however, one may have to allocate a group of
consecutive sub-carriers [
2]. Second, RWA problem is guard-band-oblivious since guard-bands are predetermined and fixed in WDM networks. In the RSA problem, however, guard-bands between lightpaths have to be determined at run time [
4].
After being introduced by a group of pioneering work [
2,
4,
15,
16], there have been extensive studies on the RSA problem [
17]. We classify those solutions based on two different criteria. According to the nature of the adopted methodologies, those solutions can be broadly classified into two categories. First, optimal ILP-based approaches that provide exact solutions to the RSA problem, which can be further divided into three types: link-based models [
4], path-based models [
15], and channel-based models [
5]. ILP models typically are limited to small size RSA problem instances due to the prohibitive computational time. Second, non-optimal solutions to the RSA problem, which include heuristic algorithm and meta-heuristic algorithms. Non-optimal solutions typically divide the routing and spectrum allocation process into two sub-problems (i.e., routing sub-problem, and spectrum allocation sub-problem) and solves the two problems in sequence [
4,
18]. Meta-heuristic approaches employ varieties of methodologies including tabu-search [
19], differential evolution [
20,
21], ant colony optimization [
21], bee colony optimization [
22], Genetic algorithm [
18], as well as AI/ML (Artificial Intelligence/Machine Learning) techniques (e.g., [
23,
24], and see [
25] for a comprehensive discussion). The main drawback of heuristic/meta-heuristic algorithms is the lack of a guaranteed closeness to the optimal solution. These limitations of existing approaches partially motivated this work.
Alternatively, we can classify the RSA problem based on the employed physical constraints, resulting in many variations of the RSA problem. When the modulation level of the signal is introduced to RSA, the resulting problem is referred to as the RMLSA (Routing, Modulation Level, and Spectrum Allocation) problem [
26,
27,
28]. The study in [
29] in fact further incorporated the consideration of signal regeneration in RMLSA (as well as survivability). When physical layer security (e.g., eavesdropping) is taken into account, the resulting RSA problem adds in security-awareness [
30]. The RSA problem can also consider the physical layer power spectral density [
31]. With the emerging of Space Division Multiplexing (SDM) technologies, the RSA variant further addresses the assignment of fiber cores, which is referred to as the Routing, Modulation, Spectrum, and Core Allocation (RMSCA) problem in this context [
32,
33,
34]. RSA can also be studied under other assumptions including: RSA for multi-cast traffic [
35], RSA allowing delayed decision [
36], and RSA with the presence of multiple fibers [
37], to name a few. It is worth mentioning that the RSA problem overlaps with the Optical Virtual Network Embedding (OVNE) problem in SLICE networks [
6,
38,
39,
40]. The OVNE problem contains an instance of the RSA problem in the link mapping process where bandwidth requests between virtual nodes are instantiated as lightpaths of SLICE networks. The framework presented in this work mainly addresses the baseline RSA problem, and extensions to the above variations of the RSA problem will be explored in the future.