Rapid Detection of Small Faults and Oscillations in Synchronous Generator Systems Using GMDH Neural Networks and High-Gain Observers
Abstract
:1. Introduction
- -
- A systematic FDI procedure with the capacity of rapid detection of small faults and oscillations in the SG system is presented.
- -
- A differential flatness approach is employed to model the SG system in a Brunovsky form utilizable for the FDI procedure.
- -
- A bank of a practically implementable high-gain observer is developed for state estimation of the SG system in both healthy and faulty mode.
- -
- A computationally efficient and real-time implementable GMDHNN is developed to approximate unknown dynamics and fault functions in the SG system.
- -
- A decision-making mechanism for the detection of small oscillation and fault occurrence based on an average L1-norm criterion is proposed.
2. Technical Preliminaries and Problem Description
2.1. Technical Preliminaries
2.2. Problem Description
- (1)
- The dynamic model of SG should be in a Brunovsky form, as described in system (1).
- (2)
- The SG states in the nominal form should be estimated robustly.
- (3)
- The unknown dynamics in (2) and (3) should be approximated accurately.
- (4)
- A bank of dynamical estimators should be developed to produce fault residual and consequently detect the real-time fault occurrence at .
3. The SG Model
3.1. Third Order SG Model
3.2. Flatness-Based SG Model
4. FDI Design Process
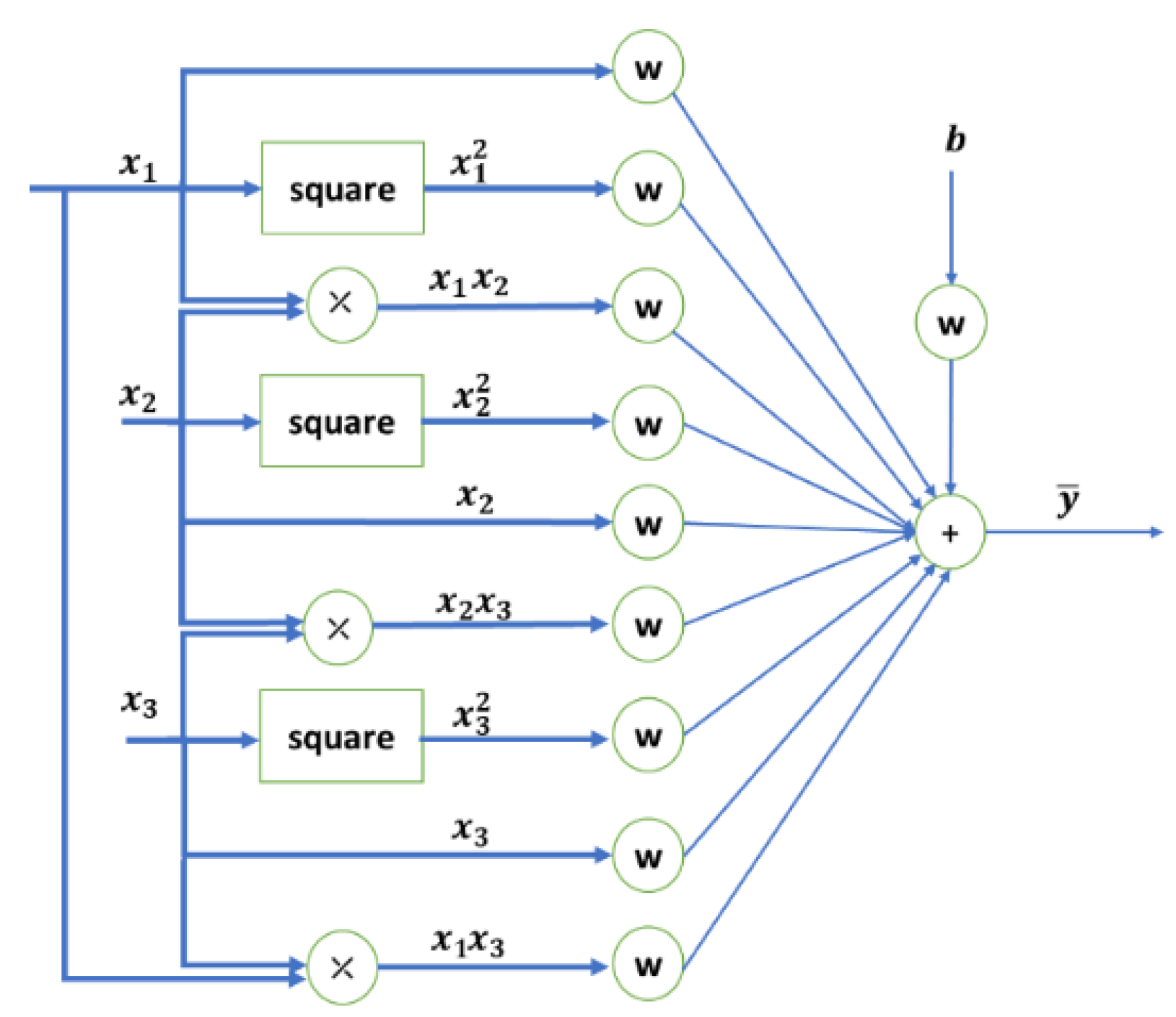
4.1. The Essence of GMDH Neural Network
- -
- Step 1: Neurons with inputs consist of all possible couple of input variables that are are developed.
- -
- Step 2: The neurons with higher error rates are ignored and other neurons are utilized to construct the next layer. In this regard, each neuron is used to calculate the quadratic polynomial.
- -
- Step 3: The second layer is constructed via the output of the first layer and hence, a higher-order polynomial is developed. Then, Step 2 is repeated to determine the optimal output utilized for the next layer input. This process is continued until the termination condition is fulfilled, i.e., the function approximation is achieved with the desired accuracy.
4.2. High-Gain Observer Design
4.3. FDI Mechanism
| Algorithm 1 FDI Mechanism |
High-gain Observer
|
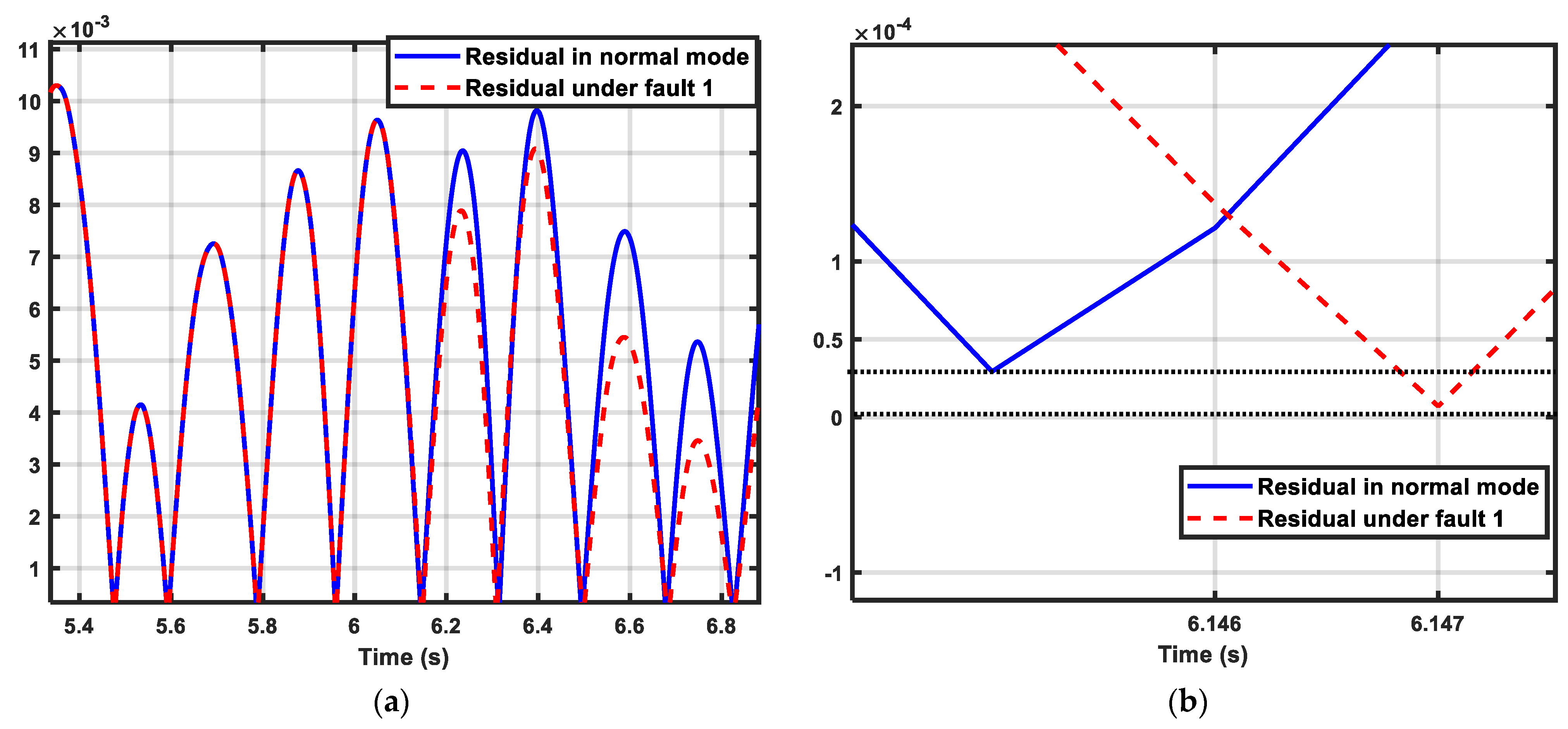
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Habibi, H.; Howard, I.; Simani, S. Reliability improvement of wind turbine power generation using model-based fault detection and fault tolerant control: A review. Renew. Energy 2019, 135, 877–896. [Google Scholar] [CrossRef]
- Habibi, H.; Howard, I.; Simani, S.; Fekih, A. Decoupling Adaptive Sliding Mode Observer Design for Wind Turbines Subject to Simultaneous Faults in Sensors and Actuators. IEEE/CAA J. Autom. Sin. 2021, 8, 837–847. [Google Scholar] [CrossRef]
- Isermann, R. Process fault detection based on modeling and estimation methods—A survey. Automatica 1984, 20, 387–404. [Google Scholar] [CrossRef]
- Wu, Y.; Zhao, D.; Liu, S.; Li, Y. Fault detection for linear discrete time-varying systems with multiplicative noise based on parity space method. ISA Trans. 2021. [Google Scholar] [CrossRef] [PubMed]
- de Morais, A.P.; Bretas, A.S.; Brahma, S.; Cardoso, G. High-sensitivity stator fault protection for synchronous generators: A time-domain approach based on mathematical morphology. Int. J. Electr. Power Energy Syst. 2018, 99, 419–425. [Google Scholar] [CrossRef]
- Doorwar, A.; Bhalja, B.; Malik, O.P. A new internal fault detection and classification technique for synchronous generator. IEEE Trans. Power Deliv. 2018, 34, 739–749. [Google Scholar] [CrossRef]
- Oliveira, M.O.; Bretas, A.; Ferreira, G.D. Adaptive differential protection of three-phase power transformers based on transient signal analysis. Int. J. Electr. Power Energy Syst. 2014, 57, 366–374. [Google Scholar] [CrossRef]
- Chen, T.; Hill, D.J.; Wang, C. Distributed Fast Fault Diagnosis for Multimachine Power Systems via Deterministic Learning. IEEE Trans. Ind. Electron. 2019, 67, 4152–4162. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S.K.; Patton, R.J. Sliding mode observers for fault detection and isolation. Automatica 2000, 36, 541–553. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis With Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques Part II: Fault Diagnosis with Knowledge-Based and Hybrid/Active Approaches. IEEE Trans. Ind. Electron. 2015, 62, 1. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.; Kambli, R.; Wagh, S.; Kazi, F. Support-Vector-Machine-Based Proactive Cascade Prediction in Smart Grid Using Probabilistic Framework. IEEE Trans. Ind. Electron. 2015, 62, 2478–2486. [Google Scholar] [CrossRef]
- Huang, Y.-C. Fault section estimation in power systems using a novel decision support system. IEEE Trans. Power Syst. 2002, 17, 439–444. [Google Scholar] [CrossRef]
- Kezunovic, M. Smart Fault Location for Smart Grids. IEEE Trans. Smart Grid 2011, 2, 11–22. [Google Scholar] [CrossRef]
- Lee, H.-J.; Ahn, B.-S.; Park, Y.-M. A fault diagnosis expert system for distribution substations. IEEE Trans. Power Deliv. 2000, 15, 92–97. [Google Scholar]
- Lin, X.; Ke, S.; Li, Z.; Weng, H.; Han, X. A Fault Diagnosis Method of Power Systems Based on Improved Objective Function and Genetic Algorithm-Tabu Search. IEEE Trans. Power Deliv. 2010, 25, 1268–1274. [Google Scholar] [CrossRef]
- Xu, L.; Chow, M.-Y. A Classification Approach for Power Distribution Systems Fault Cause Identification. IEEE Trans. Power Syst. 2006, 21, 53–60. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Xu, Y.; Luo, F.; Dong, Z.Y.; Peng, Y. Power system fault diagnosis based on history driven differential evolution and stochastic time domain simulation. Inf. Sci. 2014, 275, 13–29. [Google Scholar] [CrossRef]
- Chen, M.; Shi, P.; Lim, C.-C. Adaptive Neural Fault-Tolerant Control of a 3-DOF Model Helicopter System. IEEE Trans. Syst. Man Cybern. Syst. 2015, 46, 260–270. [Google Scholar] [CrossRef] [Green Version]
- Taimoor, M.; Aijun, L.; Samiuddin, M. Sliding mode learning algorithm based adaptive neural observer strategy for fault estimation, detection and neural controller of an aircraft. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 2547–2571. [Google Scholar] [CrossRef]
- Yin, S.; Xiao, B.; Ding, S.X.; Zhou, D. A Review on Recent Development of Spacecraft Attitude Fault Tolerant Control System. IEEE Trans. Ind. Electron. 2016, 63, 3311–3320. [Google Scholar] [CrossRef]
- Li, H.; Shi, P.; Yao, D.; Wu, L. Observer-based adaptive sliding mode control for nonlinear Markovian jump systems. Automatica 2016, 64, 133–142. [Google Scholar] [CrossRef]
- Shoaib, M.A.; Khan, A.Q.; Mustafa, G.; Gul, S.T.; Khan, O.; Khan, A.S. A framework for observer-based robust fault detection in nonlinear systems with application to synchronous generators in power systems. IEEE Trans. Power Syst. 2021, 1. [Google Scholar] [CrossRef]
- Silvio, S.; Fantuzzi, C.; Jon Patton, R. Model-based fault diagnosis techniques. In The Model-Based Fault Diagnosis in Dynamic Systems Using Identification Techniques; Springer: London, UK, 2003; pp. 19–60. [Google Scholar]
- Spurgeon, S.K. Sliding mode observers: A survey. Int. J. Syst. Sci. 2008, 39, 751–764. [Google Scholar] [CrossRef]
- Tan, C.P.; Edwards, C. Sliding mode observers for detection and reconstruction of sensor faults. Automatica 2002, 38, 1815–1821. [Google Scholar] [CrossRef]
- Yan, X.-G.; Edwards, C. Nonlinear robust fault reconstruction and estimation using a sliding mode observer. Automatica 2007, 43, 1605–1614. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, L.; Shi, P.; Zhao, Y. Fault Estimation Sliding-Mode Observer with Digital Communication Constraints. IEEE Trans. Autom. Control. 2018, 63, 3434–3441. [Google Scholar] [CrossRef]
- Chen, W.; Chowdhury, F.N. A synthesized design of sliding-mode and Luenberger observers for early detection of incipient faults. Int. J. Adapt. Control. Signal Process. 2010, 24, 1021–1035. [Google Scholar] [CrossRef]
- Veluvolu, K.; Defoort, M.; Soh, Y. High-gain observer with sliding mode for nonlinear state estimation and fault reconstruction. J. Frankl. Inst. 2014, 351, 1995–2014. [Google Scholar] [CrossRef]
- Veluvolu, K.C.; Kim, M.; Lee, D. Nonlinear sliding mode high-gain observers for fault estimation. Int. J. Syst. Sci. 2011, 42, 1065–1074. [Google Scholar] [CrossRef]
- Liu, J.; Luo, W.; Yang, X.; Wu, L. Robust Model-Based Fault Diagnosis for PEM Fuel Cell Air-Feed System. IEEE Trans. Ind. Electron. 2016, 63, 3261–3270. [Google Scholar] [CrossRef] [Green Version]
- Fridman, L.; Shtessel, Y.; Edwards, C.; Yan, X.-G. Higher-order sliding-mode observer for state estimation and input reconstruction in nonlinear systems. Int. J. Robust Nonlinear Control. 2008, 18, 399–412. [Google Scholar] [CrossRef]
- Rios, H.; Punta, E.; Fridman, L. Fault Detection and Isolation for Nonlinear Non-Affine Uncertain Systems via Sliding-Mode Techniques. Int. J. Control. 2016, 90, 1–22. [Google Scholar] [CrossRef]
- Fridman, L.; Levant, A.; Davila, J. High-Order Sliding-Mode Observer for Linear Systems with Unknown Inputs. In International Workshop on Variable Structure Systems, 2006. VSS’06; IEEE: Piscataway, NJ, USA, 2006; Volume 5. [Google Scholar] [CrossRef]
- Defoort, M.; Veluvolu, K.C.; Rath, J.J.; Djemai, M. Adaptive sensor and actuator fault estimation for a class of uncertain Lipschitz nonlinear systems. Int. J. Adapt. Control Signal Proc. 2016, 30, 271–283. [Google Scholar] [CrossRef]
- Gou, B.; Xu, Y.; Xia, Y.; Wilson, G.; Liu, S. An Intelligent Time-Adaptive Data-Driven Method for Sensor Fault Diagnosis in Induction Motor Drive System. IEEE Trans. Ind. Electron. 2019, 66, 9817–9827. [Google Scholar] [CrossRef]
- Freire, N.M.; Estima, J.O.; Cardoso, A.J.M. A new approach for current sensor fault diagnosis in PMSG drives for wind energy conversion systems. IEEE Trans. Ind. Appl. 2013, 50, 1206–1214. [Google Scholar] [CrossRef]
- Ferrari, R.M.; Parisini, T.; Polycarpou, M.M. A robust fault detection and isolation scheme for a class of uncertain input-output discrete-time nonlinear systems. In Proceedings of the 2008 American Control Conference, Seattle, WD, USA, 11–13 June 2008; pp. 2804–2809. [Google Scholar]
- Wang, C.; Chen, T. Rapid Detection of Small Oscillation Faults via Deterministic Learning. IEEE Trans. Neural Netw. 2011, 22, 1284–1296. [Google Scholar] [CrossRef]
- Zhang, X.; Polycarpou, M.; Parisini, T. A robust detection and isolation scheme for abrupt and incipient faults in nonlinear systems. IEEE Trans. Autom. Control. 2002, 47, 576–593. [Google Scholar] [CrossRef]
- De Leon-Morales, J.; Busawon, K.; Acha-Daza, S. A robust observer-based controller for synchronous generators. Int. J. Electr. Power Energy Syst. 2001, 23, 195–211. [Google Scholar] [CrossRef]
- Mahmud, M.; Pota, H.; Hossain, M. Full-order nonlinear observer-based excitation controller design for interconnected power systems via exact linearization approach. Int. J. Electr. Power Energy Syst. 2012, 41, 54–62. [Google Scholar] [CrossRef] [Green Version]
- Fliess, M.; Lévine, J.; Martin, P.; Rouchon, P. Flatness and defect of non-linear systems: Introductory theory and examples. Int. J. Control. 1995, 61, 1327–1361. [Google Scholar] [CrossRef] [Green Version]
- Anastasakis, L.; Mort, N. The Development of Self-Organization Techniques in Modelling: A Review of the Group Method of Data Handling (GMDH); Research Report; Department of Automatic Control and Systems Engineering, University of Sheffield: Sheffield, UK, 2001. [Google Scholar]
- Kondo, T. GMDH neural network algorithm using the heuristic self-organization method and its application to the pattern identification problem. In Proceedings of the 37th SICE Annual Conference, Chiba, Japan, 29–31 July 1998; International Session Papers. pp. 1143–1148. [Google Scholar]
- Elbaz, K.; Shen, S.-L.; Zhou, A.; Yin, Z.-Y.; Lyu, H.-M. Prediction of Disc Cutter Life During Shield Tunneling with AI via the Incorporation of a Genetic Algorithm into a GMDH-Type Neural Network. Engineering 2021, 7, 238–251. [Google Scholar] [CrossRef]
- Roshani, M.; Sattari, M.A.; Ali, P.J.M.; Roshani, G.H.; Nazemi, B.; Corniani, E.; Nazemi, E. Application of GMDH neural network technique to improve measuring precision of a simplified photon attenuation based two-phase flowmeter. Flow Meas. Instrum. 2020, 75, 101804. [Google Scholar] [CrossRef]
- Witczak, M.; Korbicz, J.; Mrugalski, M.; Patton, R.J. A GMDH neural network-based approach to robust fault diagnosis: Application to the DAMADICS benchmark problem. Control. Eng. Pract. 2006, 14, 671–683. [Google Scholar] [CrossRef]
- Patan, K.; Witczak, M.; Korbicz, J. Towards Robustness in Neural Network Based Fault Diagnosis. Int. J. Appl. Math. Comput. Sci. 2008, 18, 443–454. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Hill, D.J. Deterministic learning and nonlinear observer design. Asian J. Control. 2010, 12, 714–724. [Google Scholar] [CrossRef]
- Khalil, H.K.; Praly, L. High-gain observers in nonlinear feedback control. Int. J. Robust Nonlinear Control. 2014, 24, 993–1015. [Google Scholar] [CrossRef]
- Hassan, K. High-Gain Observers in Nonlinear Feedback Control; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2017. [Google Scholar]
- Chen, T.; Wang, C.; Hill, D.J. Small oscillation fault detection for a class of nonlinear systems with output measurements using deterministic learning. Syst. Control Lett. 2015, 79, 39–46. [Google Scholar] [CrossRef]
- Aghababa, M.P.; Marinescu, B.; Xavier, F. Observer-based tracking control for single machine infinite bus system via flatness theory. Int. J. Electr. Comput. Eng. 2021, 11, 1186–1199. [Google Scholar] [CrossRef]
- Anene, E.; Aliyu, U.; Levine, J.; Venayagamoorthy, G.K. Flatness-Based Feedback Linearization of a Synchronous Machine Model with Static Excitation and Fast Turbine Valving. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–6. [Google Scholar]
- Hu, Y.; Wang, H.; Yazdani, A.; Man, Z. Adaptive full order sliding mode control for electronic throttle valve system with fixed time convergence using extreme learning machine. Neural Comput. Appl. 2021, 1–13. [Google Scholar] [CrossRef]
- Ye, M.; Wang, H.; Yazdani, A.; He, S.; Ping, Z.; Xu, W. Discrete-time integral terminal sliding mode-based speed tracking control for a robotic fish. Nonlinear Dyn. 2021, 1–12. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Cao, Z.; Zheng, J.; Yu, M.; Yazdani, A.; Shahnia, F. Fast nonsingular terminal sliding mode control for permanent-magnet linear motor via ELM. Neural Comput. Appl. 2020, 32, 14447–14457. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Ma, M.; Yu, M.; Yazdani, A.; Chen, L. Active Front Steering-Based Electronic Stability Control for Steer-by-Wire Vehicles via Terminal Sliding Mode and Extreme Learning Machine. IEEE Trans. Veh. Technol. 2020, 69, 14713–14726. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghanooni, P.; Habibi, H.; Yazdani, A.; Wang, H.; MahmoudZadeh, S.; Mahmoudi, A. Rapid Detection of Small Faults and Oscillations in Synchronous Generator Systems Using GMDH Neural Networks and High-Gain Observers. Electronics 2021, 10, 2637. https://doi.org/10.3390/electronics10212637
Ghanooni P, Habibi H, Yazdani A, Wang H, MahmoudZadeh S, Mahmoudi A. Rapid Detection of Small Faults and Oscillations in Synchronous Generator Systems Using GMDH Neural Networks and High-Gain Observers. Electronics. 2021; 10(21):2637. https://doi.org/10.3390/electronics10212637
Chicago/Turabian StyleGhanooni, Pooria, Hamed Habibi, Amirmehdi Yazdani, Hai Wang, Somaiyeh MahmoudZadeh, and Amin Mahmoudi. 2021. "Rapid Detection of Small Faults and Oscillations in Synchronous Generator Systems Using GMDH Neural Networks and High-Gain Observers" Electronics 10, no. 21: 2637. https://doi.org/10.3390/electronics10212637
APA StyleGhanooni, P., Habibi, H., Yazdani, A., Wang, H., MahmoudZadeh, S., & Mahmoudi, A. (2021). Rapid Detection of Small Faults and Oscillations in Synchronous Generator Systems Using GMDH Neural Networks and High-Gain Observers. Electronics, 10(21), 2637. https://doi.org/10.3390/electronics10212637











