Abstract
The field of autonomous driving vehicles is growing and expanding rapidly. However, the control systems for autonomous driving vehicles still pose challenges, since vehicle speed and steering angle are always subject to strict constraints in vehicle dynamics. The optimal control action for vehicle speed and steering angular velocity can be obtained from the online objective function, subject to the dynamic constraints of the vehicle’s physical limitations, the environmental conditions, and the surrounding obstacles. This paper presents the design of a nonlinear model predictive controller subject to hard and softened constraints. Nonlinear model predictive control subject to softened constraints provides a higher probability of the controller finding the optimal control actions and maintaining system stability. Different parameters of the nonlinear model predictive controller are simulated and analyzed. Results show that nonlinear model predictive control with softened constraints can considerably improve the ability of autonomous driving vehicles to track exactly on different trajectories.
1. Introduction
The rapid and widespread development of advanced technologies in robotics, automation, IT, and high-speed communication networks has caused the application of autonomous driving vehicles to grow constantly and change society. Controllers for autonomous driving vehicles and driver-assistance systems can be based on model-free or model-based algorithms. For model-free controllers, the feedback error and the control action are mostly created from fuzzy logic, neural networks, AI, and haptic-based virtual and augmented reality. Recent research on haptic motion tracking for virtual and augmented reality can be found in [1]. However, due to the length limit of this paper, we mainly focus on the latest research on model-based controllers using objective functions subject to dynamic constraints.
Controllers designed for autonomous driving systems can be implemented with conventional PID, H2, and H∞ feedback controllers. An adaptive PID controller with the integration of multi-sensor navigation and trajectory tracking is presented in [2]; this controller can maintain system stability and handle the instantaneous trajectory error. A new conventional controller based on sliding mode and fuzzy logic is introduced in [3]; the authors presented a new robust adaptive controller for trajectory-tracking and lane-keeping in autonomous driving vehicles dealing with unstructured uncertainties and disturbances. Path-tracking issues in controlling autonomous driving vehicles with integral sliding mode are also presented in [4]; the authors designed the radial basis function neural network, nonlinear feedback-based integral sliding mode controller, and extended Kalman filter to ensure system stability and minimize tracking error.
A new conventional method of active disturbance rejection control based on PID, nonlinear feedback, and robust control based on the extension of the vehicle model is referred to in [5]; this method deals with varying velocity and uncertain lateral disturbances, feedforward, and feedback to control the lateral and longitudinal motion. A brief comparison among trajectory tracking controllers for autonomous driving vehicles is presented in [6]; this paper summarizes conventional control methods of H2, H∞, PID, sliding mode, and linear quadratic regulators (LQR). Authors in [7] showed that LQR strategies are more suitable for and robust against system uncertainties and measurement noises. Model Predictive Control (MPC) is developed from LQG algorithms. LQG refers to infinite horizon optimization, and the algorithms are much simpler and deal with disturbance rejection better, while MPC refers to finite-horizon optimization and the algorithms are more complex and necessary to perform more complicated calculations online. However, MPC shows better trajectory tracking and considerably smoother control action changes [8].
LQR and linear matrix inequalities (LMI) are widely applied to online control optimizers subject to dynamic constraints, for which conventional controllers cannot be used. A new method for the autonomous driving vehicle using a Lyapunov function based on LQR–LMI algorithms is proposed in [9]. In this model-based controller’s LQR and MPC, the system is considered fully modeled, and all states are considered fully observed. The mismatch between the model and the real vehicle, as well as noises and uncertainties from the system, are not considered. Therefore, several linear quadratic Gaussian (LQG) methods are studied and applied with Gaussian noises, as well as uncertain measured outputs, where the full system states may not need to be observed. The design of LQG with an adaptive Q-matrix improves the vehicle’s tracking performance in [10]; this method can better handle the model–plant mismatch and noises.
Recent research on model-based MPC methods for controlling autonomous vehicles is enormous. Research highlighting recent MPC references is found in [11,12,13,14,15,16,17,18,19,20,21]. A new presentation of robust MPC (RMPC) subject to the uncertain system using LMIs subject to input- and output-saturated constraints is presented in [11]; this paper describes a new RMPC method with polytopic uncertainties and constraints for linear time-varying (LTV). This RMPC can maintain system stability amid the presence of system uncertainties. Reference [12] presents the generation of feasible paths for autonomous mobile robots and nonlinear model predictive control (NMPC); several NMPC methods are developed and compared to show the ability of NMPC to maintain system stability and trajectory tracking ability.
Reference [13] presents a controller for an autonomous vehicle steering system in a MIMO system; a new adaptive MPC (AMPC) is implemented. This AMPC provides better trajectory tracking performance for dynamic changing systems. Reference [14] develops a new fault-tolerant AMPC algorithm for robust trajectory tracking control in autonomous vehicles. This method includes AMPC and a novel Kalman filter; the proposed method can detect and isolate faults and maintain system stability. Reference [15] presents the implementation of MPC-based trajectory tracking with hard constraints on outputs and inputs; in this method, the nonlinear model is linearized and discretized. A review of shared control for automated vehicles for advanced driver-assistance systems (ADAS) is presented in [16]. Most of the controllers recently used in autonomous systems are LQ, H2, H∞, LMI–H∞, LMI–LQ, and MPC; however, there has still been no attempt to develop MPC with softened constraints. Reference [17] introduces a novel method of MPC with PID for control of autonomous vehicles’ tracking trajectories; the PID provides feedback from the MPC optimizer. Simulations show good performance of trajectory tracking and speed tracking. Reference [19] and partly [18] present a new MPC proposal for autonomous driving vehicles; the MPC optimizer calculates the optimal inputs of the steering wheel and vehicle speed, subject to the vehicle’s physical constraints. Finally, [20] and [21] present novel control algorithms based on fuzzy control for intelligent vehicle lane change and tracking setpoints for RMPC.
In recent reference reviews, there is still a lack of MPC applications with softened constraints. The idea of this paper comes from the fact that MPC is a finite horizon optimizer subject to dynamic constraints. If we include all constraints in the optimizer, the MPC will have many constraints on states, inputs, and outputs, and, therefore, the optimizer may not find a solution. Since the MPC is designed for an online calculation, any infeasible solution is not tolerated. Thus, it would be better if some constraints were converted from the vehicle dynamics into softened constraints, which will widen the ability of the MPC optimizer to find a solution and will considerably improve the stability and robustness of the MPC controller.
The structure of this paper is as follows: Section 2 introduces the vehicle modeling and constraints; Section 3 presents the NMPC with hard constraints; Section 4 presents the new NMPC with softened constraints; Section 5 illustrates the two schemes’ performance; finally, Section 6 is our conclusion and recommendation.
2. Vehicle Modeling and Constraints
This paper mainly uses vehicle dynamics modeling and constraints from the reference book [22], where the vehicle is a four-wheel model. This vehicle is assumed to be totally identified on x and y coordinates at the center of the rear wheels by the Global Positioning System (GPS). The vehicle body angle, θ, and the steering angle, ϕ, are also always identified by the 3D sensor system embedded into the vehicle. The distance between the center of the front wheels and the rear wheels is called the vehicle wheelbase, l, and the rolling radius of the vehicle wheel is r, as shown in Figure 1.
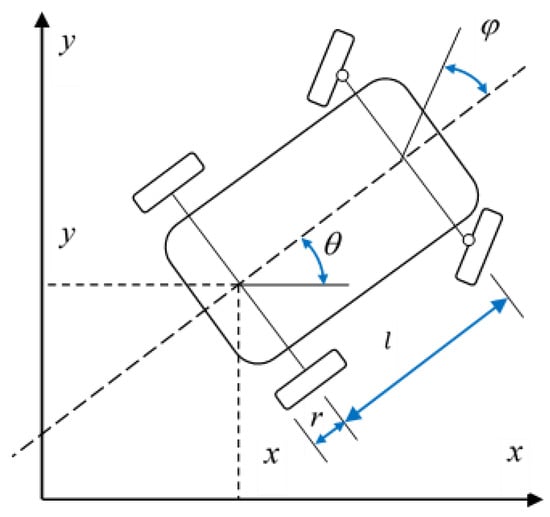
Figure 1.
Vehicle modeling.
The vehicle steering wheel can rotate at a hard limit angle of ±675 degrees and make the front wheels turn at hard angle ranges of ±45 degrees. From now on, for simplicity purposes, we will call the vehicle steering wheel angle the vehicle front wheels angle because this angle is used to calculate the vehicle movement direction. In all calculations and simulations from now on, we use the vehicle wheelbase l = 2 m and the wheel rolling radius r = 0.25 m. It is assumed that all of the vehicle parameters are totally identified and always measured by x, y, θ, and ϕ. Therefore, the vehicle can be totally controlled by the two inputs, , and (the angular velocity of the vehicle driven rolling wheels and the steering wheel).
The vehicle dynamics in [22] show that the vehicle can move forward and in reverse, as well as be driven by the front wheels or by the rear wheels. Equation (1) shows the vehicle moving forward and driven by the rear wheels.
Equation (2) shows the vehicle driven by the rear wheels but moving in reverse speed. In the calculations and simulations, we assign the reverse speed with a negative sign.
Finally, Equation (3) shows the vehicle driven by front wheels and moving forwards, where we control the vehicle speed from the front rolling wheels.
In the above equations, [x, y, θ, ϕ]′ are the vehicle states and outputs. The two control inputs are the vehicle rolling wheel angular velocity, v_1, and the steering wheel angular velocity, v_2. Therefore, rv_1 is the vehicle speed in kilometers per hour (km/h), and v_2 is the vehicle steering angular velocity in revolutions per minute (rpm).
A real vehicle always has a strict steering angle limit at:
The vehicle represented in Equations (1) and (2), or (3) can be controlled by tracking a given trajectory from a given starting position to a given destination position. It is assumed that the vehicle must start from an initial position [x0, y0, θ0, ϕ0 ] at the time t = 0, and move to the destination at the end of a trajectory [xT, yT, θT, ϕT] at the time t = T.
In vehicle dynamics, vehicle tire slip will take place when the vehicle speed is greater than 12 km/h. Then, vehicle sideslip will increase exponentially when the vehicle speed exceeds 67 km/h. Therefore, the vehicle steering angle must always be strictly constrained by the vehicle speed, as shown in Figure 2.
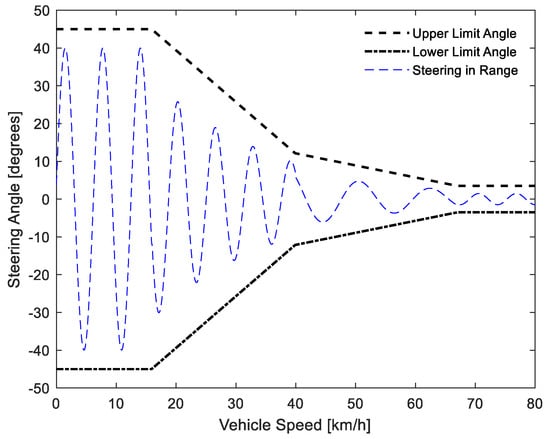
Figure 2.
Vehicle steering angle vs. vehicle speed.
Figure 2 shows that, at low speeds of less than 16 km/h, the steering angle can move almost freely within its limit of ±45 degrees. The steering angle will be reduced to less than ±12 degrees when the vehicle speed increases from 16 km/h to 40 km/h. Then, the limit of the steering angle will rapidly reduce to less than ±4 degrees as the vehicle speed exceeds 67 km/h. These dynamic constraints can be changed into softened constraints in order to widen the ability of the MPC controller to find a solution. The basic MPC algorithms will be presented in the next part.
3. NMPC with Hard Constraints
Vehicle models in (1)–(3) are all nonlinear forms and can be linearized and transformed into discretized time models. Equations (1)–(3) can be considered as the first-order continuous derivative equation as:
where x is the state variables, , and u are the inputs, . The first order nonlinear in (5) can be approximated in a Taylor series at any referenced position of for , that:
in which and are the Jacobean function of and , moving around the referenced positions .
Substituting (6) for , we can obtain an approximation linear form for the continuous time :
in which the approximation of , and ,
The continuous approximation form of in Equation (7) can be transferred into the discrete-time form in and , with being the length of the sampling interval or the computer scanning speed. The discrete inputs will be kept at constant values from the time interval k to . The discrete form for an NMPC optimizer can now be written as:
in which
and
In those approximation-discretized vehicle dynamics, there are two control inputs of vehicle speed, , and the steering angular velocity, . There are four measured outputs, . These outputs will be updated at each time interval. The discretized vehicle dynamics in (8) is the time-variant model, since this system is dependent on the updating time interval or computer scanning speed, .
The MPC algorithms for these vehicle dynamics can be expressed in finite-horizon prediction outputs and inputs. For simplicity, from now on, we assign the horizon output as equal to the horizon input, or . The MPC objective function for the vehicle tracking trajectory subject to hard constraints will be:
subject to:
, and , , for ,
, and , for ,
, and , for ,
, , , ,
where are the state variables at the present discrete time (k) and is the solution of the predictive input horizon from k to Nu. Additionally, Ny is the predictive output horizon; are the outputs at the present discrete time (k), are the tracking trajectory setpoints; are the input predictive increments, and ; , are the weighting matrices for outputs and inputs, respectively.
By substituting , Equation (9) can be rewritten as
subject to the linear matrices inequality (LMI), , where the column vector is the optimization vector, , and H, F, Y, G, W, E are obtained from Q and R and in (9), as only the optimizer vector U is needed, the term involving Y is usually removed from (10). The optimization problem (10) is a quadratic program (QP). The MPC optimizer will calculate the optimal input vector subject to the hard constraints of the inputs, , and ; of the outputs , and ; and of the input increments . However, only the first input increment, , is taken into the implementation. Then, the optimizer will update the outputs and states variables with the new update input and repeat the calculation for the next time interval. Therefore, the MPC is also called the receding time horizon control. A diagram control system for this NMPC is shown in Figure 3.
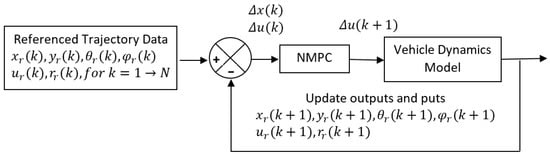
Figure 3.
NMPC diagram system.
The NMPC optimizer in Figure 3 receives the online optimal control action, , feeds into the vehicle dynamics model, and updates the current update states, inputs, and outputs. The update states, inputs, and outputs will be feedback and compared to the reference trajectory data. The new differences of states, inputs, and outputs then feed into the NMPC optimizer for the next online optimal input calculation.
In the next part, we present the development of NMPC with softened constraints.
4. NMPC with Softened Constraints
When all constraints are set as hard constraints, difficulties will arise since the controller may not find a solution satisfying all constraints and the controller may become infeasible.
In reality, some physical constraints can be violated a little during the evolution of the system, since some initial conditions may lead to some violations in constraints. Therefore, we can consider and assign some constraints as softened constraints in order to increase the probability of the MPC finding an optimal solution. The softened constraints can be formulated into the following form:
where is assigned as big values as a weighting factor (), and are the constraints’ penalty terms () added into the MPC objective function. and are the corresponding matrix of the hard constraints. Some hard constraints can be converted to the softened form. The new MPC algorithm subject to softened constraints can be written as:
subject to (11) and:
, and , , for ,
, and , for ,
, and , for ,
, , ,,
where , , and ; is the additional penalty matrix (generally and assigned to small values). In this new NMPC, the penalty term of softened state constraints is added into the objective function with positive definite and symmetric matrix ; this term penalizes violations of softened constraints, and, when possible, the free constrained solution will be returned.
Now, this NMPC calculates the new optimization vector , and the new NMPC computational algorithms will be:
subject to ,
where is the optimization vector, and , and matrices for inequality constraints H, F, G, W, and E are obtained from Equation (10).
To illustrate the ability of the new controller, we tested the two NMPC schemes in (9) and in (12) with the following simple example, considering the below nonlinear system:
It is assumed that this system in (14) is subjected to the hard state and input constraints and . The linearized approximation of this system from (7) is: , in which and . The weighting matrices are chosen as . The weighting matrices for softened constraints are chosen as . It is assumed that the system is starting from an initial state position, . Figure 4 shows the performance of two NMPC schemes; this initial state position x0 does not lead to any violation of states and input ( and ). In this , the solutions of the two control schemes are always available. We can see that the NMPC with a softened state approaches the asymptotic point faster than with the hard constraints. This means that if we loosen some constraints, the optimizer can generate easier optimal inputs, and the system will be more stable.
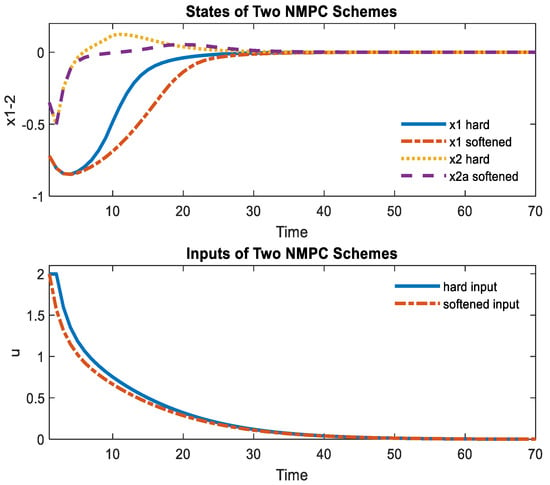
Figure 4.
Comparison of two RMPC schemes.
Now, it is interesting to see in Figure 4 that both schemes have and , almost reaching the hard constraint of . These states still have not violated the state constraints, but if we select some other initial positions , it may lead to some state and input violations.
Now, if we select , this initial condition will lead to violations of the state and the input constraints as and . These violations make the RMPC with hard constraints infeasible. Meanwhile, the RMPC scheme with softened constraints will still work well and easily find optimal input solutions, as shown in Figure 5. After a short transitional period, the fully constrained solution is returned, or there is no more constraint violation.
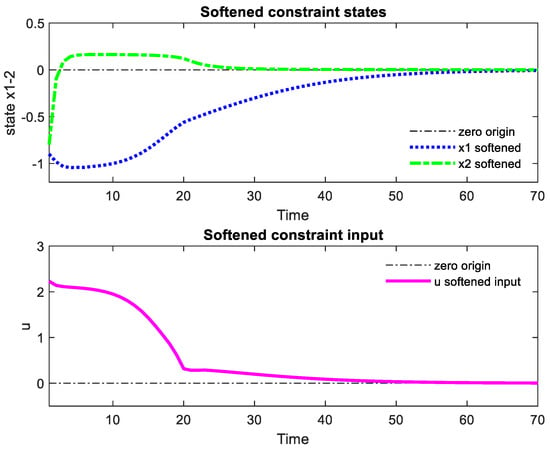
Figure 5.
Softened constraint RMPC.
The two NMPC schemes will be further analyzed and simulated in the next part with different trajectories and control parameters.
5. NMPC Tracking Trajectory Performance
First, we tested the two NMPC schemes tracking on a full circle from an initial position outside. In this example, we select an initial position of . The constraints are imposed on this vehicle as: the input limits, , ; the increase of input limits, , ; and the coordinate limits, , and ; in our NMPC algorithms, the predictive horizons are set with . The state and the input penalty matrices are set with and . The performance of the two MPC schemes is shown in Figure 6.
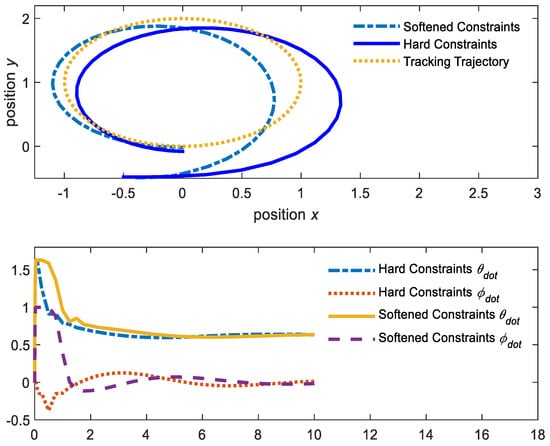
Figure 6.
NMPC schemes tracking a circle.
Figure 6 shows that the softened constraints scheme reaches setpoints faster than the hard constraints scheme. The control input actions of the softened constraints scheme are also likely smoother than the hard constraints scheme. However, the softened constraints scheme is more complex and leads to a longer elapsed CPU time (0.89 s) vs. the hard constraints scheme (0.74 s).
Next, we tested these two schemes tracking on real polynomial trajectories with different MPC control parameters to have a closer look at the ability of each scheme. Now, we assumed a feasible polynomial trajectory from x0, y0 of [0, 0] to xT, yT of [10, 10]. The vehicle is starting from an initial condition at , and arriving at the destination condition at The prediction horizon is set with ; the penalty matrices for states and inputs are set with and . The vehicle speed vs. the steering angular velocity is fully controlled. The performance of the two schemes is shown in Figure 7.
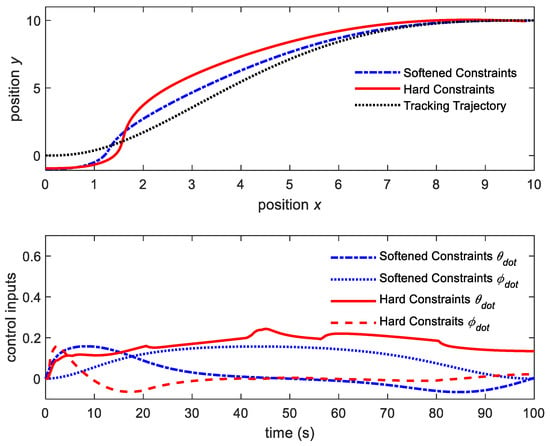
Figure 7.
NMPC schemes’ tracking trajectory.
Figure 7 shows that the softened constraints scheme is faster to track on the trajectory and always maintains smaller tracking errors than the hard constraints scheme. The control inputs of the softened scheme are also smoother. The hard constraints scheme has more difficulty driving the vehicle tracking to the trajectory. However, the elapsed CPU time of the softened scheme becomes a great challenge for the computer system. The elapsed CPU time for the softened constraints scheme is 4.27 s, while the time for the hard constraints scheme is only 2.45 s for the whole trajectory control.
In order to shorten the CPU elapsed time, we tried to reduce the MPC prediction horizon. However, a too-short prediction horizon will lead to harder control actions and the system becoming infeasible and unstable. Figure 8 shows the performance of the two schemes with a shorter state and input prediction horizon of .
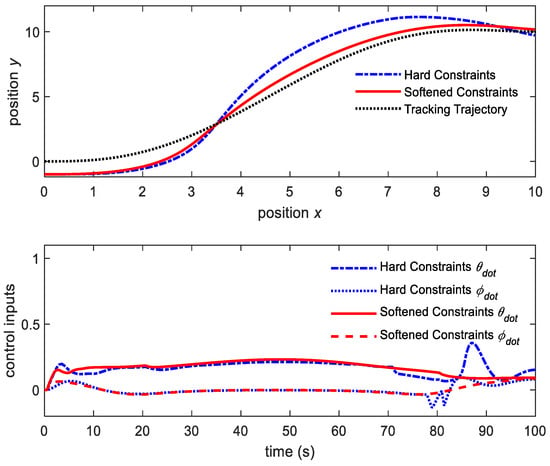
Figure 8.
NMPC schemes with shortened prediction horizon of N = 5.
When we shorten the state and control prediction horizon to Ny = Nu = 5, both schemes are still stable and work well. However, the hard constraints scheme is likely to generate harder control actions and has more difficulty approaching the trajectory. However, the hard constraints scheme needs only 1.84 s of elapsed CPU time, while the softened scheme consumes 3.23 s of elapsed CPU time for the whole drive.
If we lengthen the prediction horizon, the system will become looser and more flexible, but it will considerably lengthen the CPU time and cause larger tracking errors. Figure 9 shows the performance of the softened constraints scheme with the control horizon of Ny = Nu = 10 vs. Ny = Nu = 30.
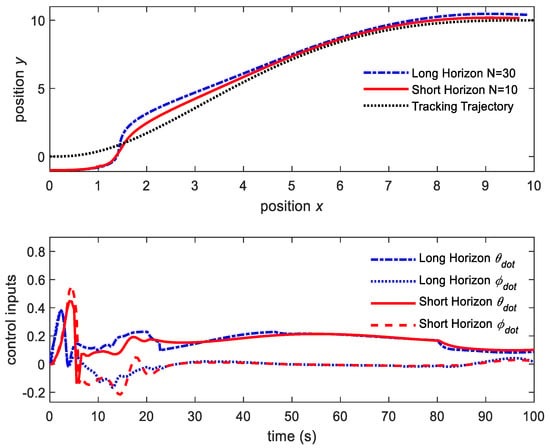
Figure 9.
NMPC schemes with N = 10 vs. N = 30.
The short control prediction horizon leads to harder control actions, and the system approaches the setpoint faster. However, the longer horizon leads to smoother control actions, and the system becomes looser and more stable. The elapsed CPU time for the long prediction horizon N = 30 is 7.65 s, considerably greater than the elapsed CPU time for the short prediction horizon N = 10, which is 4.47 s.
In MPC algorithms, the CPU discrete time interval or computer scanning speed is also an important factor affecting their performance. The MPC discretized system is a time-variant model and depends on the length of the time intervals or the computer scanning speed. Figure 10 shows the performance of the two schemes with a scanning time interval of 0.1 s vs. 0.5 s.
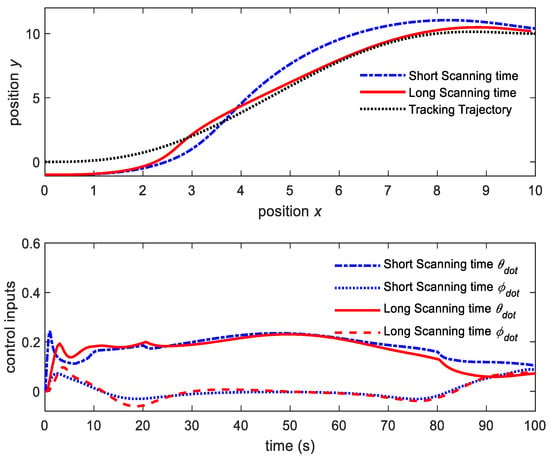
Figure 10.
NMPC schemes with short vs. long time intervals.
A scanning speed that is too fast will lead to instability. The control system will become more sensitive and more difficult to control. When the scanning time interval is set at 0.1 s, the elapsed CPU time will be 21.74 s. While the scanning time interval is set at a slower speed of 0.5 s, the elapsed CPU time reduces to only 4.15 s.
Finally, we illustrate the run of different state and input penalty matrices, Q and R. If we set R to a larger value than Q, it means that a small change of input will lead to a large value at the objective function. The control system becomes less sensitive and more stable. However, it becomes more difficult to track the setpoints. On the other hand, if we set R to a much smaller value than Q, the control actions will become harder, and the system will approach the setpoints faster. However, the system will become less stable. Figure 11 shows the performance of the softened constraints scheme with R = 60 and R = 1.
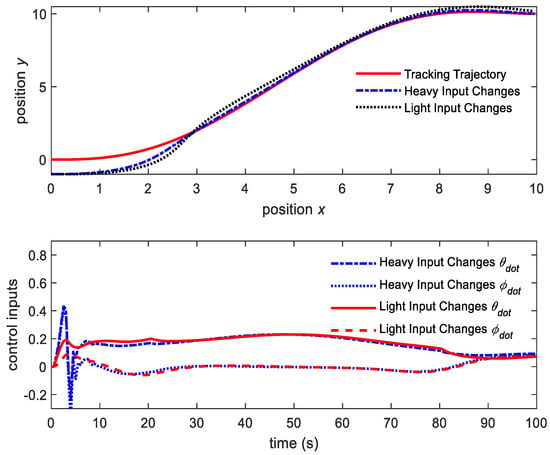
Figure 11.
NMPC with light vs. heavy input matrices R = 60 vs. R = 1.
If we set the input penalty matrix to R = 60, the control system becomes less sensitive to any change of the inputs, since the inputs can be changed only in small increments (Light Input Changes). The system is smoother and more stable. However, the tracking errors become larger. If we set the input penalty matrix to R = 1, the inputs can change in larger increments (Heavy Input Changes), and the tracking errors are smaller. However, the control system will become less stable.
The above simulations of both NMPC schemes for tracking different trajectories with different control parameters show that the NMPC scheme with softened constraints is more stable but requires more elapsed CPU time and is more complicated in terms of programming.
6. Conclusions
Due to the recent advances in computer calculation capability, the complexity in programming and the CPU elapsed time are almost no longer limitations of the NMPC scheme with softened constraints. Controllers for autonomous driving vehicles need a combination of advanced techniques, including neural networks, AI, GPS, LIDAR, high-speed internet, and online video and image processing. This proposed NMPC scheme with softened constraints can be applied to autonomous driving vehicles and further intelligent control techniques. Several physical constraints can be converted into softened constraints. This loosens up the capabilities of NMPC, and the systems become more stable. The constrained violations usually take place in short transitional periods until the optimizer finds the optimal control actions that fully satisfy all constraints. In our next research, we will investigate and apply this scheme to real vehicle systems.
Author Contributions
Conceptualization, T.M.V.; methodology, T.M.V.; formal analysis, T.M.V.; writing—original draft preparation, T.M.V. and R.M.; writing—review and editing, R.M. and J.C.; supervision, J.H. All authors have read and agreed to the published version of the manuscript.
Funding
The result was obtained through financial support from the Ministry of Education, Youth and Sports in Czechia and the European Union in the framework of the project “Modular platform for autonomous chassis of specialized electric vehicles for freight and equipment transportation”, Reg. No. CZ.02.1.01/0.0/0.0/16_025/0007293. This work also was partly supported by the Student Grant Scheme at the Technical University of Liberec through project nr. SGS-2021-3059.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study. Participants were informed that their responses to the questionnaire would be treated entirely anonymously and confidentially.
Data Availability Statement
The data are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Minh, V.T.; Katushin, N.; Pumwa, J. Motion tracking glove for augmented reality and virtual reality. Paladyn J. Behav. Robot. 2019, 10, 160–166. [Google Scholar] [CrossRef]
- Zhao, P.; Chen, J.; Song, Y.; Tao, X.; Xu, T.; Mei, T. Design of a Control System for an Autonomous Vehicle Based on Adaptive-PID. Int. J. Adv. Robot. Syst. 2012, 9, 11. [Google Scholar] [CrossRef]
- Taghavifar, H.; Rakheja, S. Path-tracking of autonomous vehicles using a novel adaptive robust exponential-like-sliding-mode fuzzy type-2 neural network controller. Mech. Syst. Signal Process. 2019, 130, 41–55. [Google Scholar] [CrossRef]
- Hu, C.; Wang, Z.; Taghavifar, H.; Na, J.; Qin, Y.; Guo, J.; Wei, C. MME-EKF-Based Path-Tracking Control of Autonomous Vehicles Considering Input Saturation. IEEE Trans. Veh. Technol. 2019, 68, 5246–5259. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Gao, S.; Wang, Y.; Wang, P.; Zhou, Y.; Xu, Y. Robust trajectory tracking control for autonomous vehicle subject to velocity-varying and uncertain lateral disturbance. Arch. Transp. 2021, 57, 7–23. [Google Scholar] [CrossRef]
- Calzolari, D.; Schurmann, B.; Althoff, M. Comparison of trajectory tracking controllers for autonomous vehicles. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 1–8. [Google Scholar]
- Varma, B.; Swamy, N.; Mukherjee, S. Trajectory Tracking of Autonomous Vehicles Using Different Control Techniques (PID vs. LQR vs. MPC). In Proceedings of the 2020 International Conference on Smart Technologies in Computing, Electrical and Electronics (ICSTCEE), Bengaluru, India, 9–10 October 2020; pp. 84–89. [Google Scholar]
- Jezierski, A.; Mozaryn, J.; Suski, D. A Comparison of LQR and MPC Control Algorithms of an Inverted Pendulum. In 2017 Trends in Advanced Intelligent Control, Optimization and Automation; Springer: Kraków, Poland, 2017; pp. 65–76. [Google Scholar]
- Alcala, E.; Puig, V.; Quevedo, J.; Escobet, T.; Comasolivas, R. Autonomous vehicle control using a kinematic Lyapunov-based technique with LQR-LMI tuning. Control. Eng. Pract. 2018, 73, 1–12. [Google Scholar] [CrossRef]
- Lee, K.; Jeon, S.; Kim, H.; Kum, D. Optimal Path Tracking Control of Autonomous Vehicle: Adaptive Full-State Linear Quadratic Gaussian (LQG) Control. IEEE Access 2019, 7, 109120–109133. [Google Scholar] [CrossRef]
- Vu, T.M.; Nitin, A. Robust Model Predictive Control for Input Saturated and Softened State Constraints. Asian J. Control. 2005, 7, 319–325. [Google Scholar]
- Minh, V.T. Nonlinear Model Predictive Controller and Feasible Path Planning for Autonomous Robots. Open Comput. Sci. 2016, 6, 178–186. [Google Scholar] [CrossRef]
- Reda, A.; Bouzid, A.; Vásárhelyi, J. Model Predictive Control for Automated Vehicle Steering. Acta Polytech. Hung. 2020, 17, 163–182. [Google Scholar] [CrossRef]
- Geng, K.; Liu, S. Robust Path Tracking Control for Autonomous Vehicle Based on a Novel Fault Tolerant Adaptive Model Predictive Control Algorithm. Appl. Sci. 2020, 10, 6249. [Google Scholar] [CrossRef]
- Chen, S.; Chen, H.; Negrut, D. Implementation of MPC-Based Trajectory Tracking Considering Different Fidelity Vehicle Models. J. Beijing Inst. Technol. 2020, 29, 303–316. [Google Scholar]
- Marcano, M.; Díaz, S.; Pérez, J.; Irigoyen, E. A Review of Shared Control for Automated Vehicles: Theory and Applications. IEEE Trans. Hum.-Mach. Syst. 2020, 50, 475–491. [Google Scholar] [CrossRef]
- Chen, S.; Chen, H. MPC-based path tracking with PID speed control for autonomous vehicles. IOP Conf. Ser. Mater. Sci. Eng. 2020, 892, 3702–3720. [Google Scholar] [CrossRef]
- Minh, V.T.; Moezzi, R.; Dhoska, K.; Pumwa, J. Model Predictive Control for Autonomous Vehicle Tracking. Int. J. Innov. Technol. Interdiscip. Sci. 2021, 4, 560–603. [Google Scholar]
- Wang, J.; Teng, F.; Li, J.; Zang, L.; Fan, T.; Zhang, J.; Wang, X. Intelligent vehicle lane change trajectory control algorithm based on weight coefficient adaptive adjustment. Adv. Mech. Eng. 2021, 13, 1–16. [Google Scholar] [CrossRef]
- Cao, H.; Zoldy, M. MPC Tracking Controller Parameters Impacts in Roundabouts. Mathematics 2021, 9, 1394. [Google Scholar] [CrossRef]
- Vu, T.M.; Hashim, F. Tracking setpoint robust model predictive control for input saturated and softened state constraints. Int. J. Control. Autom. Syst. 2011, 9, 958–965. [Google Scholar]
- Minh, V.T. Advanced Vehicle Dynamics; Universiti of Malaya Press: Kuala Lumpur, Malaysia, 2012; p. 265, ISBN: 9789831005446 9831005449. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).