Joint Diagnosis of RIS and BS for RIS-Aided Millimeter-Wave System

Abstract

Recently, the reconfigurable intelligent surface (RIS)-aided communication system has emerged as a promising candidate for future millimeter-wave wireless communications. Due to the short wavelength of millimeter wave, the antennas on the base station (BS) and the elements on the RIS can be densely packed. It usually causes the BS and RIS to be blocked by rain, snow, or dust, which will change the channel’s characteristics and decrease the performance of communication system. In order to solve this problem, we propose an iterative compressed sense based algorithm for joint estimating the blockage coefficients of RIS and BS. Then, for the complete blockage scenario, we propose a low complexity algorithm for estimating the blockage coefficients. Our simulation results demonstrate the superior performance of the proposed algorithm to existing ones.

1. Introduction

As a new technology for next generation wireless networks, RIS integrates a large number of passive reflection units with low hardware cost and energy consumption for intelligent transmission, which can improve the spectrum efficiency and the coverage capability of the communication system [1]. There are numerous literatures on the beamforming design of the BS and RIS to maximize the system capacity, which needs to know the channel state information perfectly [2]. However, since the passive RIS elements cannot perform signal processing, channel estimation for RIS-aided systems is challenging.

The channel estimation of RIS-aided systems has been studied by some literatures, recently [3,4,5,6,7]. Specifically, a novel message-passing based algorithm has been proposed in [3] to factorize the cascaded channel by utilizing the slow-varying characteristics of channel and the sparsity of the hidden channel. C. Hu et al. have proposed a two-timescale channel estimation framework to achieve accurate channel estimation with low pilot overhead [4]. A non-iterative two-stage RIS-aided channel estimation algorithm has been introduced in [5] which has low computational complexity. An aggregated channel estimation approach has been proposed in [6,7] to reduce the required overhead of channel estimation with sufficient information for data processing. Above all, channel estimation methods assume an ideal scenario of non-blockage on the BS and RIS. However, there is always a possibility of failure of one or more elements in the large array, which will affect the quality of service of communication systems significantly [8,9]. Additionally, the BS and RIS are easily blocked by rain, water, and snow. References [9,10] pointed out that the blocked probability of RIS and BS is 0.4 and 0.1, where the blockage of RIS and BS affects the quality of service of communication systems significantly. Thus, the array under test (AUT) technique is proposed [9,11]. This technique compares the received signal affected by faulty antennas with the signal generated by the ideal channel with free-antennas. Specifically, E. Eltayeb et al. have proposed a compressed sensing based method to diagnose the faulty antennas at BS [9]. R. Sun et al. have proposed an atomic norm based algorithm for detecting the faulty elements on the RIS [11]. Nevertheless, the diagnosis algorithm proposed in [9] is suitable for the scenario where the BS is blocked but the RIS is free. Furthermore, the diagnosis algorithm proposed in [11] is suitable for the scenario where the RIS is blocked but the BS is free. However, when the blockage occurs on the BS and RIS at the same time, the above algorithms are not valid. Because the blockage of RIS and BS are affecting the received signal together, it is hard to separate and estimate them.

To the best of our knowledge, this is the first contribution proposing diagnosis method for an RIS-aided system considering the scenario where blockages occur both at the BS and RIS. The diagnostic techniques are used to locate faulty reflecting elements and retrieve failure parameters for RIS systems. Specifically, we formulate the diagnosis model for RIS and BS. Then, we propose an iterative algorithm, named Algorithm 1, for joint estimation of the RIS blockage and BS blockage. Next, for the complete blockage scenario, we propose a low complexity algorithm compared to Algorithm 1. Our simulation results demonstrate the superior performance of the proposed algorithms compared to existing ones.

Notation: We use the following notations throughout the paper. We let a, $\mathbf{a}$, $\mathbf{A}$ represent the scalar, vector, and matrix respectively; ${(·)}^{\mathrm{T}}$, ${(·)}^{\mathrm{H}}$, and ${(·)}^{-1}$ denote the transpose, conjugate transpose, and inverse of a matrix, respectively;

Algorithm 1 Proposed algorithm.

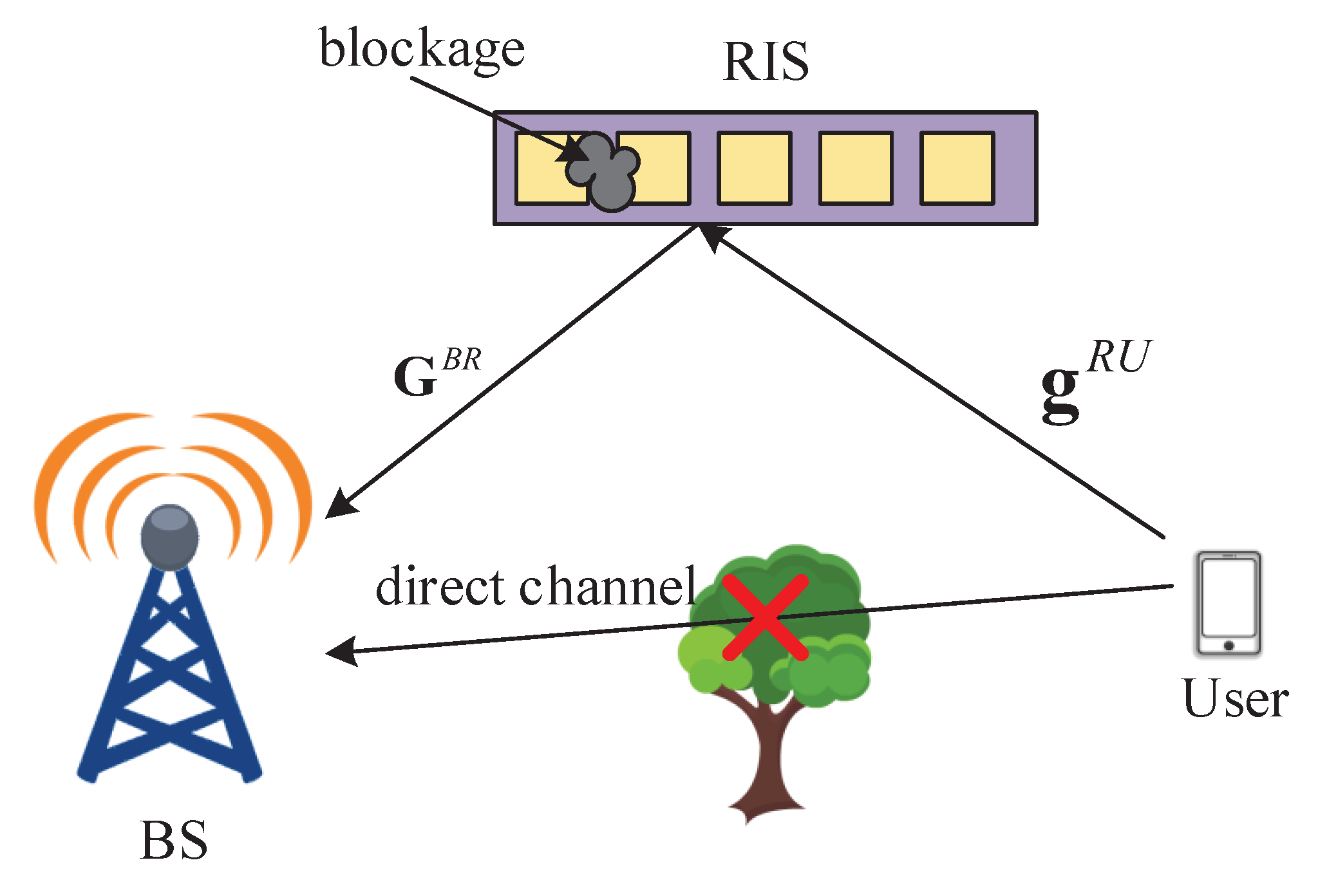
2. System Model

As shown in Figure 1, we consider the RIS-aided communication system in the uplink, where the base station (BS) is equipped with $(N\times 1)$-uniform linear array (ULA) and the RIS is equipped with $(M\times 1)$- ULA (this algorithm can be also readily extended to uniform planar array (UPA) at BS or RIS.) [12]. We neglect the channel between the BS and user [13]. We consider that there is only one line-of-sight (LoS) path between the BS and RIS (Due to the high path loss of the millimeter wave band, the first scattering path is 13 dB lower than the main path in the LOS channel model [14]. Thus, the LOS channel model is widely used in the RIS-aided mmwave MIMO system [10]. Furthermore, from Equation (7) we find that the proposed algorithm in this paper is not sensitive to the multipath channels). Thus, the BS-RIS channel ${\mathbf{G}}^{\mathrm{BR}}$ can be expressed as

$$\begin{array}{c}\hfill {\mathbf{G}}^{\mathrm{BR}}=c^{\mathrm{BR}}{\mathbf{a}}_N\left({\vartheta }^{BR}\right){\mathbf{a}}_M^{\mathrm{H}}\left({\overline{\vartheta }}^{BR}\right),\end{array}$$

(1)

where $c^{\mathrm{BR}}$ denotes the complex channel gains. Furthermore, we define the equivalent angle of aperture (AoA) and angle of departure (AoD) from RIS to BS as ${\vartheta }^{BR}=dsin\left({\varphi }^{\mathrm{BR}}\right)/\lambda$ and ${\overline{\vartheta }}^{BR}=dsin\left({\overline{\varphi }}^{\mathrm{BR}}\right)/\lambda$, where ${\varphi }^{\mathrm{BR}}$ and ${\overline{\varphi }}^{\mathrm{BR}}$ denotes the AoA/AoD from RIS to BS. The scaler d and $\lambda$ denote the antenna spacing and the signal wavelength, and typically we have $d/\lambda =1/2$. The steering vector is defined as

$$\begin{array}{cc}\hfill {\mathbf{a}}_M\left(\vartheta \right)& ={[1,e^{j2\pi \vartheta },\cdots ,e^{j2\pi (M-1)\vartheta }]}^{\mathrm{T}}\in {\mathbb{C}}^{M\times 1}\hfill \\ \hfill {\mathbf{a}}_N\left(\vartheta \right)& ={[1,e^{j2\pi \vartheta },\cdots ,e^{j2\pi (N-1)\vartheta }]}^{\mathrm{T}}\in {\mathbb{C}}^{N\times 1}.\hfill \end{array}$$

(2)

Similarly, the RIS-user channel ${\mathbf{g}}^{\mathrm{RU}}$ can be expressed as

$$\begin{array}{c}\hfill {\mathbf{g}}^{\mathrm{RU}}=c^{\mathrm{RU}}\mathbf{a}\left({\upsilon }^{\mathrm{RU}}\right),\end{array}$$

(3)

where $c^{\mathrm{BR}}$ denotes the complex channel gains. We have ${\vartheta }^{RU}=dsin\left({\varphi }^{\mathrm{RU}}\right)/\lambda$, where ${\varphi }^{\mathrm{RU}}$ denotes the AoD from the user to BS. Thus, without RIS blockage and BS blockage, the uplink signal received by the BS can be expressed as

$$\begin{array}{c}\hfill \mathbf{y}\left(t\right)={\mathbf{G}}^{\mathrm{BR}}\mathrm{diag}\left(\mathit{\theta }\left(t\right)\right){\mathbf{g}}^{\mathrm{RU}}x\left(t\right)+\mathbf{n}\left(t\right),\end{array}$$

(4)

where $\mathbf{y}\left(t\right)\in {\mathbb{C}}^{N\times 1}$ and $\mathbf{n}\left(t\right)\in {\mathbb{C}}^{N\times 1}$ denote the received signal and the Gaussian noise vector at the t-th time slot. We consider the transmit symbol $x\left(t\right)$ as 1 for simply. The vector $\mathit{\theta }\left(t\right)={[e^{j{\mathit{\theta }}_1},\cdots ,e^{j{\mathit{\theta }}_N}]}^{\mathrm{T}}$ with ${\mathit{\theta }}_n\in [0,2\pi )$ denotes the phase coefficients of RIS. We consider that the phase coefficients of RIS are generated randomly, which is adopted in reference [13], investigating the channel estimation for a RIS-aided communication system. However, in practice, the RS/RIS may be blocked by the rain, snow, or dust, which will change the channel characteristics and decrease the performance of systems such as sum-rate. In addition, we usually choose cheap antennas and cheap elements on the BS and RIS for reducing the cost, which also causes the blockage to occur. We defined that $\mathbf{b}\in {\mathbb{C}}^{\mathbf{N}\times \mathbf{1}}$ denotes the blockage coefficient vector of BS, whose n-th element $b_n$ is the random complex random variable with a modulus less than 1. Particularly, if the n-th antenna on BS is completely blocked, we have $b_n=0$. If the n-th antenna on BS is free, we have $b_n=1$. We define the blockage coefficient vector of RIS as $\overline{\mathbf{b}}\in {\mathbb{C}}^{M\times 1}$, which has the similar definition to the definition of $\mathbf{b}$ [10,11]. Thus, with the blockage, the received signal on the BS can be expressed as

$$\begin{array}{c}\hfill \mathbf{y}\left(t\right)=\mathrm{diag}\left(\mathbf{b}\right){\mathbf{G}}^{BR}\mathrm{diag}(\overline{\mathbf{b}}\circ \mathit{\theta }\left(t\right)){\mathbf{g}}^{RU}x\left(t\right)+\mathbf{n}\left(t\right).\end{array}$$

(5)

We define that $\mathbf{b}={\mathbf{1}}_N+\mathbf{s}$ and $\overline{\mathbf{b}}={\mathbf{1}}_M+\overline{\mathbf{s}}$, where $\mathbf{s}$ and $\overline{\mathbf{s}}$ denote the offset coefficients of BS and RIS, respectively. Usually, the RIS or BS is partially blocked. Thus, the offset coefficients $\mathbf{s}$ and $\overline{\mathbf{s}}$ are usually sparse, that is, there are a small number of non-zero elements in vector $\mathbf{s}$ and $\overline{\mathbf{s}}$. If we can estimate the offset coefficients, the blockage coefficients can be obtained. Then, (5) can be rewritten as

$$\begin{array}{c}\hfill \mathbf{y}\left(t\right)=\mathrm{diag}({\mathbf{1}}_N+\mathbf{s}){\mathbf{G}}^{\mathrm{BR}}\mathrm{diag}({\mathbf{g}}^{\mathrm{RU}}\circ \mathit{\theta }\left(t\right))({\mathbf{1}}_M+\overline{\mathbf{s}})+\mathbf{n}\left(t\right).\end{array}$$

(6)

Then, combining T time slots, we have

$$\begin{array}{c}\hfill \mathbf{y}=\left[\begin{array}{c}\mathrm{diag}({\mathbf{1}}_N+\mathbf{s})\mathbf{H}\left(1\right)({\mathbf{1}}_M+\overline{\mathbf{s}})\\ ⋮\\ \mathrm{diag}({\mathbf{1}}_N+\mathbf{s})\mathbf{H}\left(T\right)({\mathbf{1}}_M+\overline{\mathbf{s}})\end{array}\right]+\mathbf{n},\end{array}$$

(7)

where $\mathbf{y}={[{\mathbf{y}}^{\mathrm{T}}\left(1\right),\cdots ,{\mathbf{y}}^{\mathrm{T}}\left(T\right)]}^{\mathrm{T}}\in {\mathbb{C}}^{TN\times 1}$ and $\mathbf{n}={[{\mathbf{n}}^{\mathrm{T}}\left(1\right),\cdots ,{\mathbf{n}}^{\mathrm{T}}\left(T\right)]}^{\mathrm{T}}\in {\mathbb{C}}^{TN\times 1}$. The equivalent cascaded channel $\mathbf{H}\left(t\right)$ can be expressed as $\mathbf{H}\left(t\right)={\mathbf{G}}^{\mathrm{BR}}\mathrm{diag}({\mathbf{g}}^{\mathrm{RU}}\circ \mathit{\theta }\left(t\right))$. In the next section, we propose a compressed-based algorithm for joint estimation of the RIS blockage coefficients and the BS blockage coefficients according to the received signal $\mathbf{y}$ shown in (7).

Figure 1. RIS-aided communication system with RIS blockage and BS blockage.

3. Proposed Algorithm

From Equation (6), we find that the received signal $\mathbf{y}\left(t\right)$ is affected by the RIS blockage and the BS blockage simultaneously. We call this effect the blockage coupling. Due to the effect of blockage coupling, the blockage estimation method proposed in [10,11] for the scenario where the RIS is blocked and the BS is free cannot be applied for the scenario considered in this paper. In this paper, we assume that the cascaded channel information ${\mathbf{G}}^{\mathrm{BR}}\mathrm{diag}\left({\mathbf{g}}^{RU}\right)$ is known.

3.1. Algorithm 1 for the Partial Blockage Scenario

In this subsection, we will propose an iterative compressed-based algorithm for the joint estimation of the RIS blockage and BS blockage. We define ${\mathbf{s}}^i$ and ${\overline{\mathbf{s}}}^i$ as the estimation of RIS/BS blockage in the i-th iteration.

In the first stage, we estimate the blockage coefficient vector of RIS. We split the Equation (7) and have

$$\begin{array}{c}\hfill \overline{\mathbf{y}}=\mathbf{A}{\overline{\mathbf{s}}}^{i+1}+\mathbf{n},\end{array}$$

(8)

where $\overline{\mathbf{y}}\in {\mathbb{C}}^{NT\times 1}$ and $\mathbf{A}\in {\mathbb{C}}^{NT\times M}$ can be defined as

$$\begin{array}{c}\hfill \overline{\mathbf{y}}=\mathbf{y}-\left[\begin{array}{c}\mathbf{H}\left(1\right){\mathbf{1}}_M\\ ⋮\\ \mathbf{H}\left(T\right){\mathbf{1}}_M\end{array}\right]-\left[\begin{array}{c}\mathrm{diag}\left({\mathbf{s}}^i\right)\mathbf{H}\left(1\right){\mathbf{1}}_M\\ ⋮\\ \mathrm{diag}\left({\mathbf{s}}^i\right)\mathbf{H}\left(T\right){\mathbf{1}}_M\end{array}\right],\end{array}$$

(9)

and

$$\begin{array}{c}\hfill \mathbf{A}=\left[\begin{array}{c}\mathrm{diag}({\mathbf{1}}_N+{\mathbf{s}}^i)\mathbf{H}\left(1\right)\\ ⋮\\ \mathrm{diag}({\mathbf{1}}_N+{\mathbf{s}}^i)\mathbf{H}\left(T\right)\end{array}\right].\end{array}$$

(10)

From (9) and (10), we observe that the vector $\overline{\mathbf{y}}$ and matrix $\mathbf{A}$ are the function of ${\mathbf{s}}^i$ and $\mathbf{H}\left(t\right)$. Thus, the problem of estimating the spare vector ${\overline{\mathbf{s}}}^{i+1}$ becomes the sparse recovery problem. In this way, we utilize the OMP algorithm for estimating ${\overline{\mathbf{s}}}^{i+1}$. The details are shown in Steps 4–8 of Algorithm 1. Furthermore, we do not know the number of the RIS blockage in advance, thus, we need to design an appropriate stop condition to terminate the algorithm. The stop condition can be expressed as $\frac{\left|\right|{\mathbf{r}}^j{\left|\right|}_2^2}{{\left|\right|\mathbf{y}\left|\right|}_2^2}\ge \xi$, which is shown in Step 3. Actually, due to the impact of the inaccurate BS blockage ${\mathbf{s}}^i$ estimation in the initial iterative process, the error $\frac{\left|\right|{\mathbf{r}}^j{\left|\right|}_2^2}{{\left|\right|\mathbf{y}\left|\right|}_2^2}$ is usually large. After multiple iterations, we can have the accurate estimation of BS blockage, thus, the error $\frac{\left|\right|{\mathbf{r}}^j{\left|\right|}_2^2}{{\left|\right|\mathbf{y}\left|\right|}_2^2}$ is small. Thus, the stop condition can be designed dynamically, that is, we set the value of $\xi$ large in the initial process and decrease the value of $\xi$ appropriately after multiple iterations.

In the second stage, we estimate the blockage vector of BS. We reshape the Equation (7) and have

$$\begin{array}{c}\hfill \tilde{\mathbf{Y}}=\mathrm{diag}\left({\mathbf{s}}^{i+1}\right)\mathbf{B}+\mathbf{N},\end{array}$$

(11)

where $\tilde{\mathbf{Y}}=[\tilde{\mathbf{y}}\left(1\right),\tilde{\mathbf{y}}\left(2\right),\cdots ,\tilde{\mathbf{y}}\left(T\right)]\in {\mathbb{C}}^{N\times T}$, $\mathbf{N}=[\mathbf{n}\left(1\right),\mathbf{n}\left(2\right),\cdots ,\mathbf{n}\left(T\right)]\in {\mathbb{C}}^{N\times T}$, and $\tilde{\mathbf{y}}\left(t\right)$ can be expressed as

$$\begin{array}{c}\hfill \tilde{\mathbf{y}}\left(t\right)=\mathbf{y}\left(t\right)-\mathbf{H}\left(t\right){\mathbf{1}}_M-\mathbf{H}\left(t\right){\overline{\mathbf{s}}}^{i+1}.\end{array}$$

(12)

Additionally, the matrix $\mathbf{B}$ can be expressed as

$$\begin{array}{c}\hfill \mathbf{B}=[\mathbf{H}\left(1\right)({\mathbf{1}}_M+{\overline{\mathbf{s}}}^{i+1}),\mathbf{H}\left(2\right)({\mathbf{1}}_M+{\overline{\mathbf{s}}}^{i+1}),\cdots ,\mathbf{H}\left(T\right)({\mathbf{1}}_M+{\overline{\mathbf{s}}}^{i+1})]\in {\mathbb{C}}^{N\times T}.\end{array}$$

From (12) and (13), we find that matrix $\tilde{\mathbf{Y}}$ and $\mathbf{B}$ are functions of the RIS blockage ${\overline{\mathbf{s}}}^{i+1}$ and $\mathbf{H}\left(t\right)$. In addition, we observe that the k-th row of matrix $\tilde{\mathbf{Y}}$ is affected by the k-th element of ${\mathbf{s}}^{i+1}$ and that the other elements of the vector ${\mathbf{s}}^{i+1}$ have no effect on the k-th row of matrix $\tilde{\mathbf{Y}}$. Thus, the k-th element of ${\mathbf{s}}^{i+1}$ can be obtained by the following equation, which is shown as

$$\begin{array}{c}\hfill {\tilde{\mathbf{Y}}}_{k,:}={\mathbf{B}}_{k,:}{s}_k+{\mathbf{N}}_{k,:},\end{array}$$

(13)

where ${\tilde{\mathbf{Y}}}_{k,:}$, ${\mathbf{B}}_{k,:}$ and ${\mathbf{N}}_{k,:}$ denote the k-th row of matrix $\tilde{\mathbf{Y}}$, $\mathbf{B}$ and $\mathbf{N}$, respectively. Similarly, $s_k$ denotes the k-th elements of ${\mathbf{s}}^{i+1}$. Thus, we can utilize the least squares (LS) estimator to estimate $s_k$, which can be expressed as

$$\begin{array}{c}\hfill LS:s_k={\left({\mathbf{B}}_{k,:}{\left({\mathbf{B}}_{k,:}\right)}^{\mathrm{H}}\right)}^{-1}{\tilde{\mathbf{Y}}}_{k,:}{\left({\mathbf{B}}_{k,:}\right)}^{\mathrm{H}}.\end{array}$$

(14)

Repeat the above process until the number of iterations reaches $N_{iter}$. We can then obtain the accurate estimation of $\mathbf{s}$ and $\overline{\mathbf{s}}$.

Next, we analyze the complexity of Algorithm 1. The complexity mainly comes from Steps 4, 6, and 10. In Step 4, the complexity can be expressed as $\mathcal{O}\left(MNT\right)$. In Steps 6 and 10, the complexity can be expressed as $\mathcal{O}(NT{\left(N_R\right)}^2+{N_R}^3)$ and $\mathcal{O}\left(TN\right)$, where $N_R$ denotes the number of the non-zero element in $\overline{\mathbf{s}}$. After $N_{iter}$ iterations, the total complexity can be expressed as $\mathcal{O}\left(N_{iter}(N_R(MNT+NT{\left(N_R\right)}^2+{N_R}^3)+N^{2}T)\right)$.

3.2. Fast Algorithm for the Completely Blockage Scenario

In this subsection, we consider the scenario where RIS and BS are completely blocked [15]. We find that the Algorithm 1 needs multiple iterations to obtain the BS and RIS blockage coefficients, which leads the complexity of Algorithm 1 to be large. Motivated by this, we propose fast Algorithm for estimating the BS and RIS blockage coefficients without iteration.

In the first stage, we estimate the BS blockage coefficient vector. Due to the fact that we consider the scenario of complete blockage, that is, if the n-th antenna on the BS is blocked, we have $1+s_n=0$, and we can obtain the estimation of $s_n$ by judging whether $y_n\left(t\right)$ is equal to 0 according to (5), where $y_n\left(t\right)$ denotes the n-th element of $\mathbf{y}\left(t\right)$. However, due to the effect of the noise, the value of the received signal $y_n\left(t\right)$ may be large even if $1+s_n=0$, which leads us to judge an blocked antenna as free. In order to decrease the effect of noise, we appropriately design the phase coefficients of RIS $\mathit{\theta }\left(t\right)$. Specifically, according to (5), in the n-th time slot, we have

$$\begin{array}{c}\hfill y_n\left(n\right)=(1+s_n){\left[{\mathbf{G}}^{BR}\mathrm{diag}(\overline{\mathbf{b}}\circ {\mathbf{g}}^{RU})\right]}_{n,:}\mathit{\theta }\left(n\right)+n_n\left(n\right).\end{array}$$

(15)

We can increase the amplitude of ${\left[{\mathbf{G}}^{BR}\mathrm{diag}(\overline{\mathbf{b}}\circ {\mathbf{g}}^{RU})\right]}_{n,:}\mathit{\theta }\left(n\right)$ to decrease the effect of noise $n_n\left(n\right)$. Due the fact that the element of $\overline{\mathbf{b}}$ is either 1 or 0, and we know the cascaded channel ${\mathbf{G}}^{BR}\mathrm{diag}(\overline{\mathbf{b}}\circ {\mathbf{g}}^{RU})$, the optimal solution of $\mathit{\theta }\left(n\right)$ for maximizing the function $|{\left[{\mathbf{G}}^{BR}\mathrm{diag}(\overline{\mathbf{b}}\circ {\mathbf{g}}^{RU})\right]}_{n,:}\mathit{\theta }\left(n\right)|$ can be expressed as ${\mathit{\theta }}_m\left(t\right)=e^{-2j\pi \angle {\left[{\mathbf{G}}^{BR}\mathrm{diag}(\overline{\mathbf{b}}\circ {\mathbf{g}}^{RU})\right]}_{n,m}}$, where $\angle \left(x\right)$ denotes the angle of complex x. After N time slots, we can get the estimation of BS blockage coefficients $\mathbf{b}$.

In the second stage, we estimate the RIS blockage coefficient vector $\overline{\mathbf{s}}$. In this stage, we combine T time slots and the phase coefficients of RIS are generated randomly. According to (6), by combining the T time slots, we have

$$\begin{array}{c}\hfill \overline{\overline{\mathbf{y}}}=\overline{\overline{\mathbf{H}}}\overline{\mathbf{s}}+\overline{\overline{\mathbf{n}}},\end{array}$$

(16)

where $\overline{\overline{\mathbf{y}}}={[{\overline{\overline{\mathbf{y}}}}^{\mathrm{T}}\left(1\right),\cdots ,{\overline{\overline{\mathbf{y}}}}^{\mathrm{T}}\left(T\right)]}^{\mathrm{T}}$, and where $\overline{\overline{\mathbf{y}}}\left(n\right)$ can be expressed as $\overline{\overline{\mathbf{y}}}\left(n\right)={\mathbf{y}}_{{\mathcal{I}}^{BS},:}\left(n\right)-{\mathbf{H}}_{{\mathcal{I}}^{BS},:}\left(n\right){\mathbf{1}}_{M\times 1}$. In addition, $\overline{\overline{\mathbf{H}}}$ can be expressed as $\overline{\overline{\mathbf{H}}}=[{\mathbf{H}}_{{\mathcal{I}}^{BS},:}\left(1\right);\cdots ;{\mathbf{H}}_{{\mathcal{I}}^{BS},:}\left(T\right)]$. The vector ${\mathcal{I}}^{BS}$ denotes the index of non-zero element of $\mathbf{s}$, which is obtained in the first stage. We observe that the Equation (16) is similar to (8). Thus, we can utilize the OMP algorithm on (16) to estimate the RIS blockage coefficients $\overline{\mathbf{s}}$.

Next, we analyze the complexity of fast Algorithm. The total complexity of fast Algorithm is $\mathcal{O}(MNT+NT{\left(N_R\right)}^2+{\left(N_R\right)}^3+NT)$. Compared to the complexity of Algorithm 1, the complexity of fast Algorithm is lower than that of Algorithm 1. Furthermore, the number of pilot symbols used in the proposed algorithm in this paper is similar to the algorithm of [9,11]. Our algorithms can be extended to multi-user scenarios. When we adopt the orthogonal code, the code words used by each user are orthogonal, and the algorithms can be used separately without affecting each other, which can realize the multi-user diagnosis.

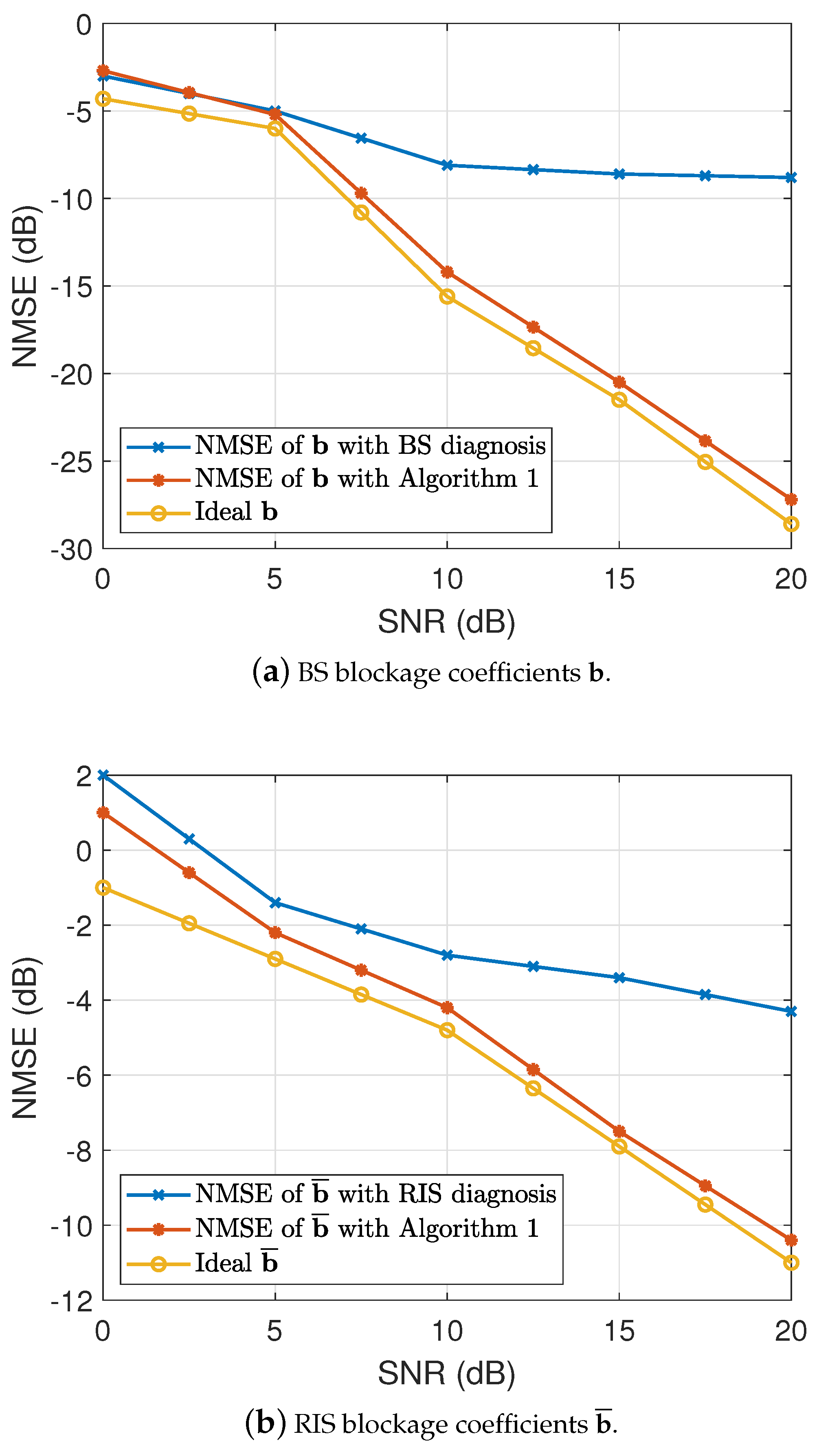
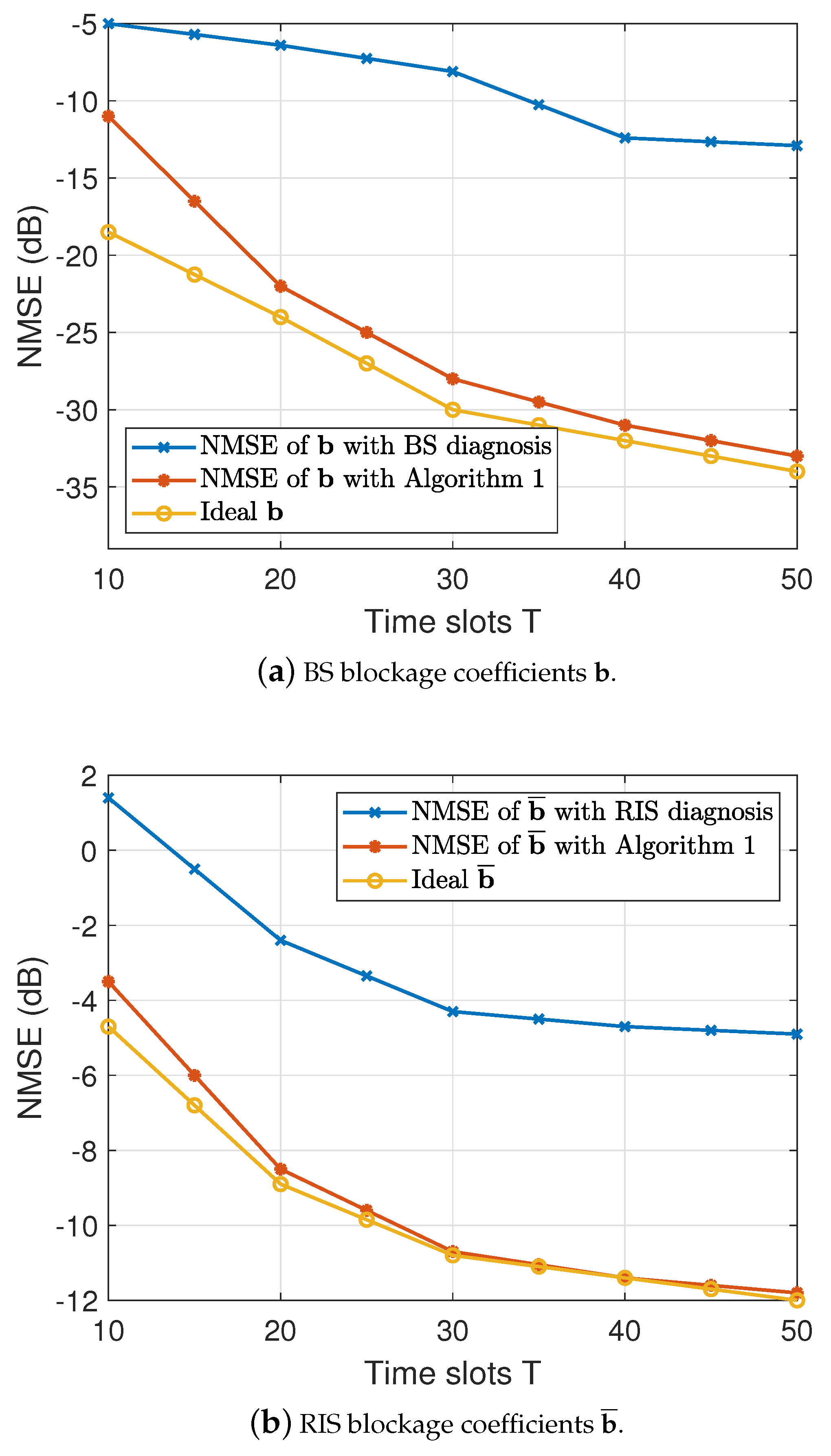
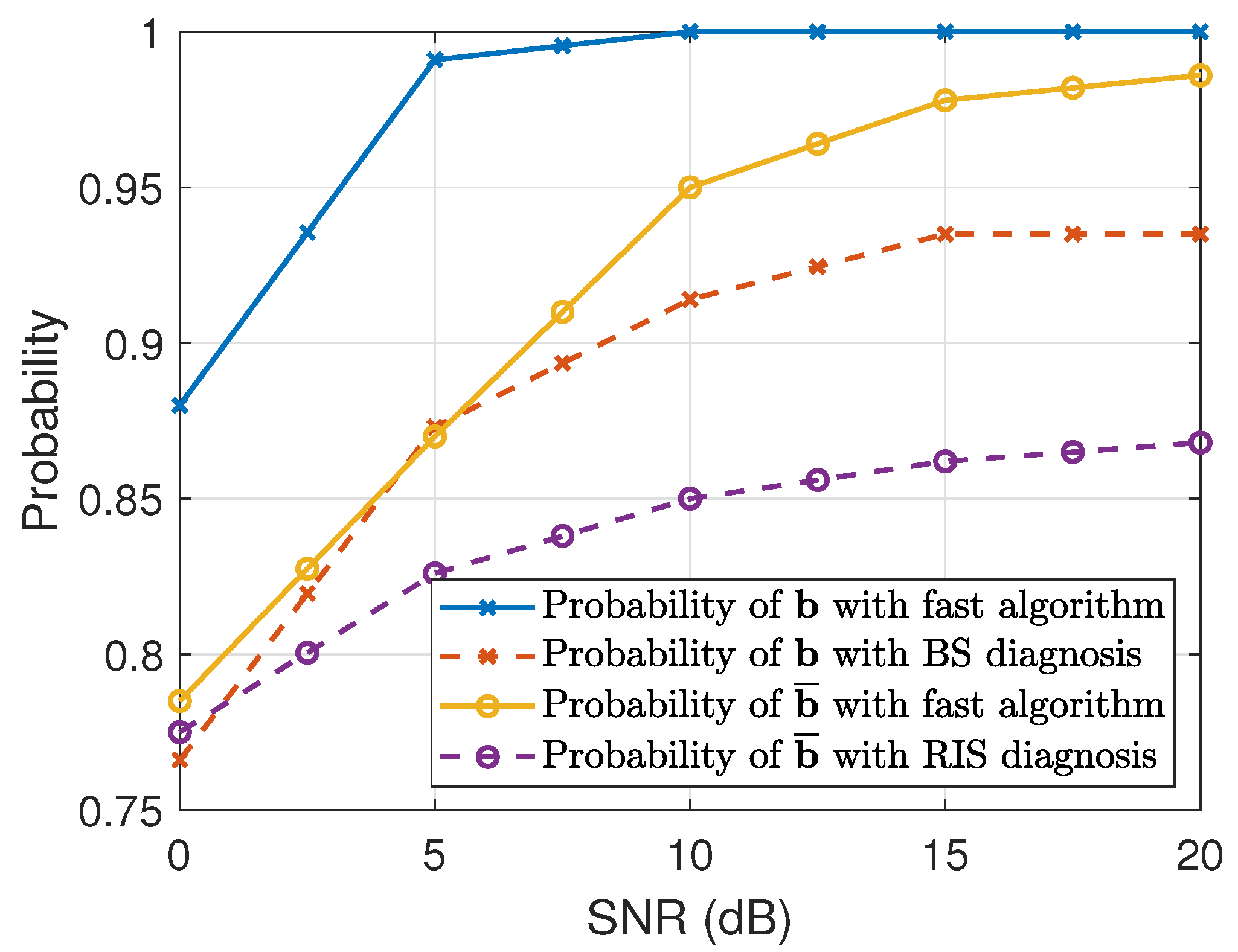
4. Simulation Results

In this section, we show the performance of the proposed Algorithm 1 and fast Algorithm using simulations. The system parameters are set as follows: We consider that the RIS is equipped with 100 elements and the BS is equipped with 10 antennas; The number of the BS-RIS channel path is 1, and the number of the RIS-user channel path is 1; The AoA from RIS to BS ${\varphi }_{l_1}^{\mathrm{BR}}$, AoD from RIS to BS ${\overline{\varphi }}_{l_1}^{\mathrm{BR}}$ and AoD from the user to BS ${\varphi }_{l_2}^{\mathrm{RU}}$ are randomly chosen from $[-\pi /2,\pi /2]$; We set the probability of blocked RIS and blocked BS as $0.2$. We define the normalized mean-squared error (NMSE) of vector $\mathbf{x}$ as ${\mathrm{NMSE}}_{\mathbf{x}}=\frac{E\left(\right||\widehat{\mathbf{x}}-\mathbf{x}|{|}_2^2)}{E\left(\right|\left|\mathbf{x}\right|{|}_2^2)}$, where $\widehat{\mathbf{x}}$ denotes the estimation of $\mathbf{x}$.

Figure 2 shows the NMSE performance of the RIS blockage coefficient and BS blockage coefficient against SNR. We set the time slots T as 30. The curve NMSE of $\mathbf{b}$ with [9] denotes the NMSE of BS blockage coefficient $\mathbf{b}$ estimated by the traditional diagnosis method for BS proposed in [9], which ignores the effect of RIS blockage. The curve Ideal $\mathbf{b}$ denotes the NMSE of BS blockage coefficient $\mathbf{b}$ estimated by the method proposed in [9], where the RIS blockage is known in advance. The curve NMSE of $\overline{\mathbf{b}}$ with [11] denotes the NMSE of RIS blockage coefficient $\overline{\mathbf{b}}$ estimated by the traditional diagnosis method for RIS proposed in [11], which ignores the effect of BS blockage. The curve Ideal $\overline{\mathbf{b}}$ denotes the NMSE of RIS blockage coefficient $\overline{\mathbf{b}}$ estimated by the method proposed in [11], where the BS blockage is known in advance. From Figure 2, we observe that the proposed Algorithm 1 can jointly estimate the RIS blockage and BS blockage, accurately. The NMSE performance of method [9,11] is poor, due to the effect of RIS blockage and BS blockage, respectively.

Figure 2. NMSE performance against SNR.

Figure 3 shows the NMSE of RIS blockage coefficient and BS blockage coefficient against time slots T. The SNR is set as 20 dB. We observe that the estimated performance increases as the time slots T increase.

Figure 3. NMSE performance against time slots T.

Figure 4 shows the probability of successful diagnosis against the SNR, where we only consider the completely blockage scenario. We observe that the proposed fast Algorithm can detect the location of completely blockage, accurately.

Figure 4. The probability of successful diagnosis.

5. Conclusions

In the paper, we have studied the joint blockage coefficients estimation problem for RIS-aided millimeter-wave systems. By exploiting the sparsity of the RIS blockage coefficient and BS blockage coefficient, we have proposed an iterative algorithm, which can simultaneously estimate the BS and RIS blockage coefficients. Then, for the complete blockage scenario, we propose a low complexity algorithm. Simulation results have verified that the proposed algorithm is superior to existing ones.