Abstract
In recent years, systems that monitor and control home environments, based on non-vocal and non-manual interfaces, have been introduced to improve the quality of life of people with mobility difficulties. In this work, we present the reconfigurable implementation and optimization of such a novel system that utilizes a recurrent neural network (RNN). As demonstrated in the real-world results, FPGAs have proved to be very efficient when implementing RNNs. In particular, our reconfigurable implementation is more than 150× faster than a high-end Intel Xeon CPU executing the reference inference tasks. Moreover, the proposed system achieves more than 300× the improvements, in terms of energy efficiency, when compared with the server CPU, while, in terms of the reported achieved GFLOPS/W, it outperforms even a server-tailored GPU. An additional important contribution of the work discussed in this study is that the implementation and optimization process demonstrated can also act as a reference to anyone implementing the inference tasks of RNNs in reconfigurable hardware; this is further facilitated by the fact that our C++ code, which is tailored for a high-level-synthesis (HLS) tool, is distributed in open-source, and can easily be incorporated to existing HLS libraries.
1. Introduction
Several applications that monitor and control home living environments have recently been introduced. These applications usually utilize complex deep neural networks and can improve the quality of life for people with disabilities. Even though those applications may not seem to be ’processing demanding’, the fact that, in certain cases, they simultaneously classify the inputs from several humans (e.g., in a rehabilitation center or a nursery home [1]), significantly increases the processing demands.
Nowadays, recurrent neural network (RNN)-based approaches are commonly used to monitor and control home application domains, in order to model high level representations and capture complex relationships, which are often hidden in raw data, especially during the training. RNNs have the capability of propagating information from previous time-steps to the current process while LSTM networks are special architectures of RNNs, which proved to be highly accurate. Although, RNNs that are composed of LSTM modules are commonly used for pattern recognition in several application areas, such as speech and handwriting recognition [2,3,4,5], a number of works use RNNs in non-vocal applications, using electroencephalogram (EEG) [6,7,8,9,10].
In [6], the authors present a design of RNNs for detecting sleep stages from single channel EEG signals recorded at home by non-expert users, reporting the effect of data set size, architecture choices, regularization, and personalization on the classification performance. The authors in [7] propose and validate a deep learning model to decode gait phases from electroencephalography (EEG) using LSTM recurrent neural network. In [8], various models consisting of LSTM networks are proposed for classifying emotions through processed EEG recordings and then compared based on their accuracy. In [9], the authors design a CRNN model, which is a combination of CNN and RNN/LSTM networks, for Parkinson’s disease classification using EEG signals. The authors in [10] present a software application that assists people with mobility difficulties, such as elderly or people with motor neuron diseases. This system utilizes a recurrent neural network (RNN) and electroencephalography (EEG) signals to recognize and classify the intent of the user and control the moves of a robot as well as the operation of household appliances. In this paper, the model proposed in [10] is exploited because it displays a noticeably high accuracy, utilizes raw EEG data, contrasting most mentioned designs that need preprocessing, and classifies the signals to five different classes, dissimilar with most that trigger binary values, resulting in a more functional and intriguing application.
In this work, (i) an RNN consisting of two long short-term memory (LSTM) modules was developed using Python and TensorFlow [11] based on [10], and (ii) it was optimized for high-end Xilinx Alveo U200 Field-programmable gate array (FPGA) in order to increase the throughput and decrease the power consumption. Even though there exist several automated tools/flows for implementing NNs described in TensorFlow in reconfigurable hardware, such as hls4ml [12], Xilinx ML-Suite [13], and Vitis AI [14], none of them fully support the implementation of LSTMs in high-end FPGAs. It should be noted that a preliminary beta-version of LSTM was added to Vitis AI; however, this version only supports Alveo U25 and Alveo U50 cards, and its code is not officially listed in the Vitis AI repository and/or support document.
The overall contributions of this paper can be summarized in the following points:
- A novel FPGA-based intent recognition system to process EEG signals was developed and optimized for Xilinx Alveo U200 high-end FPGA.
- A C++-based RNN intent recognition model was developed eliminating one layer from the original implementation [10].
- The complete design flow with optimizations are analytically presented, while basic modules are distributed as open-source [15]; thus, the proposed design approach can act as a valuable reference for anyone implementing complex RNNs/LSTMs in high-end FPGA devices for mobility difficulty applications; this is very important, since currently there are no FPGA-tailored LSTM implementations freely available.
- A thorough evaluation of the proposed implementation is presented in terms of performance and power efficiency, and the real-world experiments demonstrate that the proposed implementation is an order of magnitude faster (and more energy efficient) than a state-of-the-art Intel CPU, while it is very likely that also outperforms several GPUs.
2. Literature Review
As demonstrated in several recent papers, FPGAs show great potential when executing RNNs and LSTMs, in terms of both performance and energy consumption. In [16], an FPGA-based accelerator for an LSTM model, utilized in speech recognition, achieves a speedup of 20.18× over a single-threaded software implementation while it is 5.41 times faster than a 16-thread implementation. Furthermore, the FPGA implementation outperforms the Intel Xeon E5-2430 CPU, when executing single-threaded software, by approximately two orders of magnitude, in terms of energy efficiency. In [17], an LSTM implementation on an FPGA is 21× faster than on an ARM Cortex-A9 CPU. In [18], the authors propose GRNN, a GPU-based RNN-LSTM inference library, which outperforms, by up to 17.5× in terms of latency reduction, the most efficient, optimized for multi-core server CPUs, inference library. The authors of [19] propose a multi-FPGA platform for the optimization of deep RNNs and LSTM/LSTMP cells. The implementation of a single-layer LSTM-RNN on the Flow-in-Cloud (FiC) system achieves a speedup of 31× over an Intel CPU and 2× over a GPU. Moreover, a four-layer LSTM-RNN in the same system is 61× and 5× faster than a CPU and GPU, respectively, while it provides a power efficiency up to 12 GOPS/W when handling 8-bit numbers. The authors in [20] present an LSTM-based architecture that can facilitate brain–computer interfaces with detecting common EEG artifacts from multiple channels. The FPGA-based model displays lower power consumption than ARM CPU implementation deeming it suitable for low power and wearable applications. In [21], the authors propose a compact LSTM inference kernel (CLINK) that can be employed to neurofeedback devices for efficiently processing EEG signals. The FPGA implementation is designed for low power consumption considering the real-time requirements of these applications. Reference [22] demonstrates a hybrid model of CNN and LSTM architectures that collects EEG signals and controls a hexapod robot. The classification model achieves accuracy of 84.69% and is implemented effectively in FPGA. Lastly, reference [23] presents an FPGA-based implementation of the BiLSTM neural network by investigating the effects of quantization and utilizing a parameterizable architecture for parallelization of the hardware. The results of [23] indicate a higher throughput compared to other FPGA-based implementations of RNNs when utilizing 1- to 8-bit precision on a Zynq UltraScale+. The main differences between all those implementations and the FPGA-based system, which is presented in this paper, are that: (a) the listed systems/approaches utilize very different LSTMs to the one implemented in this work, and (b) most of the presented systems support up to 8-bit numbers; such numbers significantly decrease the accuracy of the proposed model as demonstrated in Section 4.2.1.
Moreover, several researchers have proposed pruning algorithms for higher acceleration of RNNs when executed in FPGAs. The authors in [24] propose a reconfigurable system that is 43× faster and 40× more energy efficient than an Intel Core i7 5930k CPU. In [25], several FPGA-tailored pruning methods are demonstrated, achieving considerably high throughput and energy efficiency. These methods are orthogonal to the presented implementation approach and, thus, they can additionally be applied to further increase the performance and the energy efficiency of the targeted system.
3. Background
The reference model [10] is a seven-layer RNN consisting of one input layer, five hidden layers, two of which are LSTMs, and one output layer. The first, second, third, and seventh layers of the model implement the following function, which represents the connection between two sequential layers:
where i denotes the i-th layer.
The weights between layer i and layer i + 1 are denoted as and the biases of the i-th layer are denoted as . The sizes of , and are correspondingly [, 1, ], [, ] and [, 1], where represents the number of input signals that will be classified and denotes the dimension of the layer. Conclusively, consists of different EEG signals, each of which has values, and can be alternative denoted as where j represents the j-th EEG sample. In this model, is equal to 7000, are equal to 64 and finally equals 6.
The fifth and sixth layers are LSTM layers, each one consisting of timesteps, and they are connected by the following functions:
where , , and represent the input gate, forget gate, output gate, and input modulation gate, respectively, ⊙ denotes the element-wise multiplication, represents the state (memory) of the j-th time-step in the i-th layer and W, and b represent the appropriate weights and biases. The size of the four gates as well as at each timestep is [1, ], where equals 64.
The fourth layer of the model reconstructs the resulting table of the previous layer, namely . The table is converted into an appropriate variable (tensor) which is used as the input to TensorFlow’s LSTM module in the fifth layer. The final predicted results are obtained in the seventh layer; the position of the maximum number in each row indicates in which class each signal is classified.
4. Materials and Methods
4.1. Design Flow and High-Level Optimizations
Usually NN-based applications are implemented in Python, utilizing the basic modules provided by certain AI libraries (i.e., mostly TensorFlow or Keras). Normally, the underlying library modules can also be used for the development of a corresponding C++ model because TensorFlow supports a C++ application programming interface (API) and Keras has some external open-source tools that can perform this conversion. However, neither the TensorFlow C++ API nor the Keras-tailored external applications currently fully support the implementation of RNN and LSTM models in C++. Hence, there are currently no automated design flows that can take as input a description of an RNN and/or LSTM in TensorFlow or Keras and transform it to C/C++ functions that can be handled by an FPGA-tailored HLS tool.
As a result, in order to implement the proposed reconfigurable system, each TensorFlow module is replaced by hand-made C++ functions, implementing the same functionality. Thus, all the equations listed in Section 3 are implemented by C++ operations and loops while all the variables are mapped to tables of the same size. Additionally, the fourth layer is unnecessary in the developed C++ code because all the data are saved in simple tables, and not in TensorFlow-friendly structures, which would need reconstruction. Thus, the developed C++ model has one layer less than the original one. After the initial development, the functionality of the code is verified by applying the same inputs to the C++ code and to the original Python/TensorFlow models and to examine the output.
In order to further optimize the proposed system, the two LSTM layers are combined to be executed in a fully pipelined manner, without the use of any HLS hardware directives/pragmas. Specifically, the computation of the first row of table begins just after the calculation of the first row of table , and this continues until table is fully populated. This optimization significantly decreases the overall latency and increases the throughput, while preserving the recurrent connection between the two LSTM layers.
Figure 1 demonstrates the original computation flow (left) and the proposed one (right); n denotes the number of inputs used for inference.
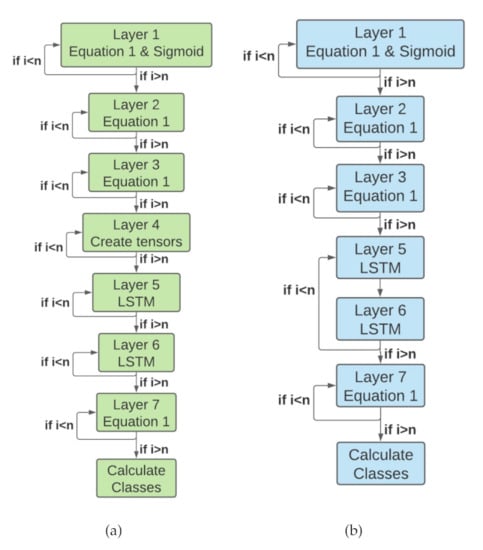
Figure 1.
(a) original and (b) optimized computation flow.
4.2. Optimizations for Reconfigurable Implementation
4.2.1. Quantization
In order to create an optimal reconfigurable module, the ability of FPGAs to efficiently handle numbers of arbitrary bit-lengths is exploited; thus, both the integers and the floating-point numbers that are involved are quantized. In order to end up with the best quantized numbers, a space exploration of the different configurations is performed with the aim to achieve high classification accuracy at high throughput.
In order to identify the optimal quantization point, three categories for the numbers utilized in the models are created, namely one for the integers and two for the different decimals (i.e., weights and intermediate data). In the following tables, the quantized size of the integers is represented with <k> (which is the corresponding bit length), while for the decimals, a fixed-point representation and the <a,b> notation is utilized; a is the total number of bits and b denotes the bits corresponding to the integer part.
The first combinations tested are presented in Table 1 and the results triggered in Table 2. As clearly demonstrated, and expected, as the bit-widths increase, the accuracy and the latency increase as well. In between the third and sixth cases, latency is relatively stable, but accuracy decreases significantly. Therefore, the optimal point is somewhere in between those cases. Exploiting further the combinations in this range, the ones presented in Table 3 are explored and the results triggered are displayed in Table 4. As clearly demonstrated, the optimal combination is the seventh one in Table 3, and this is what was adopted for the implementation of the created module.

Table 1.
First set of quantized numbers.

Table 2.
Accuracy and latency of the first set of quantized numbers.

Table 3.
Final sets of quantized numbers.

Table 4.
Accuracy and latency of the final sets of quantized numbers.
4.2.2. Hardware-Oriented Optimizations
In order to accelerate the execution of the operations involved in Equations (1) and (), the corresponding data, namely , and , were placed into registers (instead of the on-chip BRAM) to allow for the fully pipelined processing of the matrices elements. Moreover, four identical circuits for the multiplications and the additions involved are included, to be able to perform four operations in parallel. As demonstrated in the experimental results, more parallel units cannot be employed due to the lack of available DSPs in the targeted FPGA.
Furthermore, Equations (2)–(5) are independent of one another; thus, there are four parallel units calculating them, while for Equations (6) and (7), since one-dimensional tables are utilized, they are again placed into registers, to allow for the fully pipelined processing of the vector elements (i.e., the calculation of one vector element is initiated on each clock cycle).
Figure 2 depicts the architecture of the modules implementing the operations Equations (1) and (8), respectively. Furthermore, in Figure 3, a simplified architecture of the block implementing the basic LSTM operations (2)–(7) is presented.
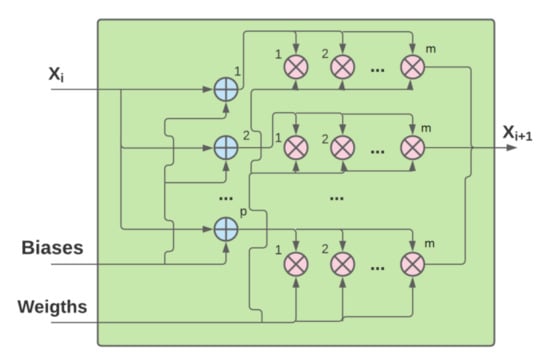
Figure 2.
Architecture of modules implementing formulas (1) and (8).
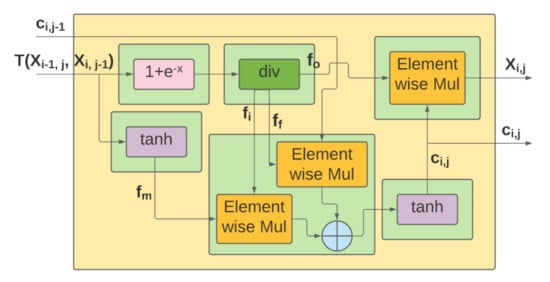
Figure 3.
Architecture of modules implementing the basic LSTM operations.
In order to further demonstrate the created design, mainly, the optimization flow, and facilitate anyone designing such modules using HLS FPGA-tailored tools, some pieces of the developed code, including the utilized HLS pragmas, are listed below.
In this example module, the temporary gates array is utilized for storing all the values of the four LSTM cell’s gates (forget, input, output, and input modulation gate) and the temporary registers (gates_tmp, gates_tmp2, gates_tmp3, and gates_tmp4) are created for efficiently calculating gates array. Moreover, the inputs array has the results of the previous timestep and the tables w_all and b_all have the values of the LSTM cell weights and biases, respectively.
| //gates array for storing all values of LSTM cell’s gates |
| #pragma HLS array_partition variable=gates complete dim=1 |
| #pragma HLS array_partition variable= ff cyclic factor=m dim=1 //forget gate |
| #pragma HLS array_partition variable= fi cyclic factor=m dim=1 //input gate |
| #pragma HLS array_partition variable= fo cyclic factor=m dim=1 //output gate |
| #pragma HLS array_partition variable= fm cyclic factor=m dim=1 //input modulation gate |
| loop1:for(int j=0;j<4*m;j=j+1){ |
| #pragma HLS unroll factor=m/4 |
| //gates array is calculated through the four |
| //registers gates_tmp, gates_tmp2, gates_tmp3 and gates_tmp4 |
| dtype gates_tmp = b_all[j]; //first register is initialized with LSTM cell’s biases |
| dtype gates_tmp2 = 0; //the rest are initialized with zero |
| dtype gates_tmp3 = 0; |
| dtype gates_tmp4 = 0; |
| #pragma HLS pipeline II=1 |
| //the values of the previous timestep (inputs) are multiplied with the LSTM |
| //cell’s weights (w_all) and then the biases (b_all) are added through gates_tmp |
| loop2:for(int k=0;k<m/2;k=k+1){ |
| gates_tmp=gates_tmp+inputs[k]*w_all[k][j]; |
| } |
| loop3:for(int k=m/2;k<m;k=k+1){ |
| gates_tmp2=gates_tmp2+inputs[k]*w_all[k][j]; |
| } |
| loop4:for(int k=m;k<3*m/2;k=k+1){ |
| gates_tmp3=gates_tmp3+inputs[k]*w_all[k][j]; |
| } |
| loop5:for(int k=3*m/2;k<2*m;k=k+1){ |
| gates_tmp4=gates_tmp4+inputs[k]*w_all[k][j]; |
| } |
| gates[j] = gates_tmp + gates_tmp2 + gates_tmp3 + gates_tmp4; |
| } |
| //calculate each LSTM cell’s gate utilizing gates array |
| loop6:for(intj=0;j<m;j=j+1){ |
| #pragma HLS unroll factor=m/2 |
| #pragma HLS pipeline II=1 |
| ff[j]= (1+hls::exp((dtype)-(gates[j+2*m]+1))); |
| fi[j]= (1+hls::exp((dtype)-(gates[j]))); |
| fo[j]= (1+hls::exp((dtype)-(gates[j+3*m]))); |
| fm[j]= tanhf((dtype)gates[j+m]); |
| } |
In order to map the , , , arraysm as well as the gates array to individual registers, for the reasons described in the previous paragraph, the array_partition pragma is applied into their single dimension. Then, in order to initiate one calculation in each clock cycle, as also described above, the pipeline pragma with the initiation interval (II) equal to 1 is utilized. Hence, loop2, loop3, loop4, and loop5 are completely unrolled in their k-th dimension, creating (m is equal to the dimension of layer ) identical modules, implementing the calculations listed in each loop’s body, which all operate in parallel. It should be noticed that four identical loops (instead of one) are used to calculate the total result of gates in order to minimize the pipeline depth. Finally, the pragma unroll is used in loop1, to create identical copies of the optimized nested loop modules.
The rest of the loops of the LSTM layer are accelerated in a similar way to that demonstrated in loop6. First, the processing is pipelined and one operation starts in every clock cycle (through the pipeline pragma with initiation interval (II) equal to 1). Then, two modules that are placed in parallel in each pipeline stage are created (through the pragma unroll factor equal to ). This approach of having two parallel modules per pipeline stage is proven to be more efficient (i.e., higher performance to resources ratio) than when the operations of the loop are fully parallelized.
5. Results and Discussion
5.1. Reference Execution Time
In order to evaluate the efficiency of the designed system, it is compared with the reference software executed on a high-end server CPU. In particular, the original Python model, as well as the hand-developed C++ model, with all the high-level optimizations, are executed in an Intel® Xeon® CPU E5-2620 v4 in a single thread. The C++ code is compiled with the g++ compiler with optimization level. The execution times are presented in Table 5.

Table 5.
Performance & Power Efficiency Analysis on Intel® Xeon® CPU E5-2620 v4.
5.2. Hardware Execution Time
In order to analyze the efficiency of the presented approach and highlight the different design aspects that increase the performance and/or decrease the power consumption, both the non-optimized initial C++ model and the fully optimized one are implemented on Xilinx Alveo U200 FPGA. Moreover, the performance (and later the power consumption) of the system is measured when it is clocked at 100, 200, and 300 MHz, as presented in Table 6. Those results clearly demonstrate that the proposed system is 68 times faster when clocked at 100 MHz and more than 152 times faster when clocked at 300 MHz, when compared to the reference Python/TensorFlow model. Furthermore, this created reconfigurable system is 17.4× faster at 100 MHz, 28× faster at 200 MHz, and 39× faster at 300 MHz than the hand-made C++ model executed on the Intel Xeon E5-2620 v4 CPU.

Table 6.
Performance and power efficiency analysis on Alveo U200.
Regarding the comparison with a multi-threaded CPU code and a GPU, several researchers have reported that the maximum speedup they have achieved, for different real-world LSTM networks, when compared with the single threaded TensorFlow-based CPU implementations, is from 10× to 61× [18,19,26]. This is well below what was measured in this implementation; therefore, it is firmly concluded that the proposed system clearly outperforms any GPU and/or multi-threaded CPU software implementations.
Looking at the comparison between the initial implementation in the FPGA (i.e., without any hardware-oriented optimizations) and the final optimized one, the presented optimizations have triggered a more than 500× speedup. This is a clear indication that, in order to get the best out of the FPGA resources, it is not suggested to just synthesize existing C++ code developed for software execution; instead the designer should apply several manual hardware-tailored optimizations, such as the ones presented in the last section, to implement an efficient FPGA-based system.
5.3. Performance over Power Efficiency
In order to compare the overall efficiency of the presented system with that triggered by the reference software approach, the GFLOPS/Watt for each implementation is measured.
The power consumption of the original Python/TensorFlow application, as well as the manually-made C++ one, when executed on the server CPU, is reported by the Intel pcm-power utility[27]. Based on those measurements, the Python/TensorFlow software and the C++ one achieve 0.017 and 0.068 GFLOPS/W, respectively (Table 5). For the proposed hardware implementation, the total on-chip power is reported by the Xilinx Power Estimator (XPE) tool to be 8.1 watts at 100 MHz, 14.5 watts at 200 MHz, and 20.9 watts at 300 MHz; based on those numbers, the achieved GFLOPS/Watt for the FPGA system are listed in Table 6. This table clearly demonstrates that this novel system achieves up to 303× and 77× higher energy efficiency than the Python/TensorFlow and C++ software implementations respectively. As a comparison, in [28], the FPGAs were reported to provide up to 28.7 higher performance per watt than the corresponding GPU implementations for several LSTM models. Moreover, as stated in [29], the actual achieved performance in a GPU, for LSTM networks, ranges from 17.85% to 25% of the peak reported performance of the GPU; thus, for an NVIDIA Tesla K80 GPU, this translates from 3.33 to 4.66 GFLOPS/W of achieved performance. As a result, the created system, which triggers 5.29 GFLOPS/W, can outperform such a GPU. Looking at the price comparison, although the Intel Xeon CPU E5-2620 v4 costs an order of magnitude less than Xilinx Alveo U200 FPGA, the presented results demonstrate that the FPGA achieves at least two orders of magnitude higher energy efficiency.
Finally, Table 7 presents the hardware cost for the optimized reconfigurable implementation. Due to the high levels of parallelism imposed by the optimizations, the critical factor is the number of DSPs, since more than 80% of them are utilized.

Table 7.
Hardware cost on the Alveo U200 device.
6. Conclusions
In this paper, the implementation of an RNN-based system for intent recognition in a high-end Xilinx Alveo FPGA is presented. The design flow and optimizations, as well as the performance and energy consumption of the final prototype are displayed. The proposed implementation outperforms the original software, which utilizes an optimized AI library and is executed on a high-end Intel® Xeon® CPU, by a factor of over 152× in terms of latency, and over 300× in terms of energy efficiency, while it outperforms, in terms of reported achieved GFLOPS/W, and a server-tailored GPU.
The presented detailed design and optimization flow, as well as the fact that the code is distributed in open-source, is expected to facilitate anyone implementing LSTM modules in reconfigurable systems; this is even more important, since currently there is no automated tool/library handling such neural networks, and the implemented modules can easily be incorporated into existing libraries and tools.
7. Future Work
The interconnection of the demonstrated reconfigurable system with several wireless EEG capturing modules is considered a future extension of this study. In that respect, there will be a complete system that can be utilized in a nursery home and/or a rehabilitation center, and efficiently identify several human intentions, causing a significant improvement in the quality of life of people with mobile difficulties. It should be noted that, by collecting the data from numerous users in a single point, the accuracy of the overall system is higher than in the case where there are smaller distributed systems, each working with a single human.
Author Contributions
Conceptualization and methodology, K.T. and I.P.; methodology, K.T., I.P., and N.T.; software, validation, investigation K.T., N.T.; data curation, K.T. and I.P.; writing—original draft preparation, K.T; writing—review and editing, N.T., K.T., I.P.; supervision and project administration, I.P. All authors have read and agreed to the published version of the manuscript.
Funding
Hellenic Foundation for Research and Innovation (H.F.R.I.) under the “First Call for H.F.R.I. Research Projects to support faculty members and researchers and the procurement of high-cost research equipment grant”, project id: 2198.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The proposed methodology in this study, including the source code, is distributed as open-source (i.e., the optimized FPGA-based LSTM and the rest of the layers for intent recognition as illustrated in Figure 1b). In addition, the same repository contains the appropriate dataset for the FPGA acceleration of the RNN-LSTM model.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, S.K.; Ahn, J.; Shin, J.; Lee, J. Application of Machine Learning Methods in Nursing Home Research. Int. J. Environ. Res. Public Health 2020, 17, 6234. [Google Scholar] [CrossRef] [PubMed]
- Sak, H.; Senior, A.; Beaufays, F. Long short-term memory recurrent neural network architectures for large scale acoustic modeling. In Proceedings of the 15th Annual Conference of the International Speech Communication Association, INTERSPEECH, Singapore, 14–18 September 2014; pp. 338–342. [Google Scholar]
- Fernández, S.; Graves, A.; Schmidhuber, J. An Application of Recurrent Neural Networks to Discriminative Keyword Spotting. In Artificial Neural Networks—ICANN 2007; de Sá, J.M., Alexandre, L.A., Duch, W., Mandic, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 220–229. [Google Scholar]
- Graves, A.; Liwicki, M.; Fernández, S.; Bertolami, R.; Bunke, H.; Schmidhuber, J. A Novel Connectionist System for Unconstrained Handwriting Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 855–868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bresch, E.; Großekathöfer, U.; Garcia-Molina, G. Recurrent Deep Neural Networks for Real-Time Sleep Stage Classification From Single Channel EEG. Front. Comput. Neurosci. 2018, 12, 85. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tortora, S.; Ghidoni, S.; Chisari, C.; Micera, S.; Artoni, F. Deep learning-based BCI for gait decoding from EEG with LSTM recurrent neural network. J. Neural Eng. 2020, 17, 046011. [Google Scholar] [CrossRef] [PubMed]
- Jeevan, R.K.; S.P., V.M.R.; Shiva Kumar, P.; Srivikas, M. EEG-based emotion recognition using LSTM-RNN machine learning algorithm. In Proceedings of the 1st International Conference on Innovations in Information and Communication Technology (ICIICT), Chennai, India, 25–26 April 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Lee, S.; Hussein, R.; McKeown, M.J. A Deep Convolutional-Recurrent Neural Network Architecture for Parkinson’s Disease EEG Classification. In Proceedings of the 2019 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Ottawa, ON, Canada, 11–14 November 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Zhang, X.; Yao, L.; Huang, C.; Sheng, Q.; Wang, X. Intent recognition in smart living through deep recurrent neural networks. In Lecture Notes in Computer Science, Proceedings of the 24th International Conference on Neural Information Processing (ICONIP 2017); Liu, D., Zhao, D., Xie, S., El-Alfy, E., Li, Y., Eds.; Springer Nature: New York, NY, USA, 2017; Volume 10635, pp. 748–758. [Google Scholar] [CrossRef] [Green Version]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Duarte, J.; Han, S.; Harris, P.; Jindariani, S.; Kreinar, E.; Kreis, B.; Ngadiuba, J.; Pierini, M.; Rivera, R.; Tran, N.; et al. Fast inference of deep neural networks in FPGAs for particle physics. J. Instrum. 2018, 13, P07027. [Google Scholar] [CrossRef]
- Xilinx ML Suite: A Development Stack for ML Inference on Xilinx Hardware Platforms, GitHub Repository. 2019. Available online: https://github.com/Xilinx/ml-suite (accessed on 13 October 2021).
- Kathail, V. Xilinx Vitis Unified Software Platform. In FPGA ’20: Proceedings of the 2020 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays; Association for Computing Machinery: New York, NY, USA, 2020; pp. 173–174. [Google Scholar] [CrossRef] [Green Version]
- Tsantikidou, K. A Novel FPGA-Based Intent Recognition System Utilizing Deep Recurrent Neural Networks, GitHub Repository. 2021. Available online: https://github.com/ntampouratzis/FPGA-based-LSTM (accessed on 13 October 2021).
- Guan, Y.; Yuan, Z.; Sun, G.; Cong, J. FPGA-based accelerator for long short-term memory recurrent neural networks. In Proceedings of the 22nd Asia and South Pacific Design Automation Conference (ASP-DAC), Jeju Island, Korea, 22–25 January 2018; pp. 629–634. [Google Scholar] [CrossRef]
- Chang, A.X.M.; Martini, B.; Culurciello, E. Recurrent Neural Networks Hardware Implementation on FPGA. arXiv 2015, arXiv:1511.05552. [Google Scholar]
- Holmes, C.; Mawhirter, D.; He, Y.; Yan, F.; Wu, B. GRNN: Low-Latency and Scalable RNN Inference on GPUs. In EuroSys ’19: Proceedings of the Fourteenth EuroSys Conference 2019; Association for Computing Machinery: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Yuxi, S.; Hideharu, A. FiC-RNN: A multi-FPGA acceleration framework for deep recurrent neural networks. IEICE Trans. Inf. Syst. 2020, E103D, 2457–2462. [Google Scholar] [CrossRef]
- Hasib-Al-Rashid; Manjunath, N.K.; Paneliya, H.; Hosseini, M.; Hairston, W.D.; Mohsenin, T. A Low-Power LSTM Processor for Multi-Channel Brain EEG Artifact Detection. In Proceedings of the 21st International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 25–26 March 2020; pp. 105–110. [Google Scholar] [CrossRef]
- Chen, Z.; Howe, A.; Blair, H.T.; Cong, J. CLINK: Compact LSTM Inference Kernel for Energy Efficient Neurofeedback Devices. In ISLPED ’18: Proceedings of the International Symposium on Low Power Electronics and Design; Association for Computing Machinery: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Mwata-Velu, T.; Ruiz-Pinales, J.; Rostro-Gonzalez, H.; Ibarra-Manzano, M.A.; Cruz-Duarte, J.M.; Avina-Cervantes, J.G. Motor Imagery Classification Based on a Recurrent-Convolutional Architecture to Control a Hexapod Robot. Mathematics 2021, 9, 606. [Google Scholar] [CrossRef]
- Rybalkin, V.; Pappalardo, A.; Ghaffar, M.M.; Gambardella, G.; Wehn, N.; Blott, M. FINN-L: Library Extensions and Design Trade-off Analysis for Variable Precision LSTM Networks on FPGAs. arXiv 2018, arXiv:1807.04093. [Google Scholar]
- Han, S.; Kang, J.; Mao, H.; Hu, Y.; Li, X.; Li, Y.; Xie, D.; Luo, H.; Yao, S.; Wang, Y.; et al. ESE: Efficient Speech Recognition Engine with Compressed LSTM on FPGA. arXiv 2016, arXiv:1612.00694. [Google Scholar]
- Wang, S.; Lin, P.; Hu, R.; Wang, H.; He, J.; Huang, Q.; Chang, S. Acceleration of LSTM With Structured Pruning Method on FPGA. IEEE Access 2019, 7, 62930–62937. [Google Scholar] [CrossRef]
- Mahjoub, A.B.; Atri, M. Implementation of convolutional-LSTM network based on CPU, GPU and pynq-zl board. In Proceedings of the 2019 IEEE International Conference on Design Test of Integrated Micro Nano-Systems (DTS), Gammarth, Tunisia, 28 April–1 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Intel Processor Counter Monitor (PCM), GitHub Repository. 2021. Available online: https://github.com/opcm/pcm (accessed on 13 October 2021).
- Yazdani, R.; Ruwase, O.; Zhang, M.; He, Y.; Arnau, J.; González, A. LSTM-Sharp: An Adaptable, Energy-Efficient Hardware Accelerator for Long Short-Term Memory. arXiv 2019, arXiv:1911.01258. [Google Scholar]
- MaliŢa, M.; Popescu, G.V.; Ştefan, G.M. Heterogeneous Computing System for Deep Learning. In Deep Learning: Concepts and Architectures; Pedrycz, W., Chen, S.M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 287–319. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).