Abstract
Convolutional Neural Network (CNNs) models’ size reduction has recently gained interest due to several advantages: energy cost reduction, embedded devices, and multi-core interfaces. One possible way to achieve model reduction is the usage of Rotation-invariant Convolutional Neural Networks because of the possibility of avoiding data augmentation techniques. In this work, we present the next step to obtain a general solution to endowing CNN architectures with the capability of classifying rotated objects and predicting the rotation angle without data-augmentation techniques. The principle consists of the concatenation of a representation mapping transforming rotation to translation and a shared weights predictor. This solution has the advantage of admitting different combinations of various basic, existing blocks. We present results obtained using a Gabor-filter bank and a ResNet feature backbone compared to previous other solutions. We also present the possibility to select between parallelizing the network in several threads for energy-aware High Performance Computing (HPC) applications or reducing the memory footprint for embedded systems. We obtain a competitive error rate on classifying rotated MNIST and outperform existing state-of-the-art results on CIFAR-10 when trained on up-right examples and validated on random orientations.
1. Introduction
In recent years, Convolutional Neural Networks (CNNs) have the highest accuracy rate on state-of-the-art image classification tasks [1,2,3]. Usually, to obtain these results, the networks are trained for a couple of days or weeks. This training time comes from feeding the network with different image transformations to increase the generalization potential (data-augmentation technique).
As the number of transformations increases, the training time increases consequently. It has been tested and demonstrated that a data augmented model has up to 600% training part than the non-augmented model [4]. Hence, the usage of data augmentation techniques results in increased energy consumption
Recently, the increased training time of models in terms of millions of parameters has become a concern. While these models’ accuracy is off-charts compared to traditional approaches, better usage of the network’s internal resources would result in more energy-efficient algorithms. The best scenario would be to achieve the same accuracy level while minimizing parameters, reducing training time and energy costs. This scenario would lead to faster inference times and reduced environmental costs associated with the network’s training time.
One possible approach to reduce the number of parameters needed is to endow the network with properties that it usually obtains via data augmentation. It is common knowledge that CNNs are translation invariant up to some extent. This property states that the network can find the features for image classification (i.e., a cat or dog’s ear) despite the feature’s position on the image. Unfortunately, this invariance property is not present for rotated versions of the features. The rotation-invariance property is the network’s capability to predict the class regardless of the object’s orientation.
It is desirable for deep learning applications (i.e., face recognition apps on cellphone, drone aerial imagery for embedded devices) to obtain rotation-invariance properties. As more applications appear oriented towards cellphones and embedded devices, the energy constraints become a challenge. Most of these applications find a trade-off between the inference times, memory access, or cloud solutions to run in battery enabled devices [5]. The recent trends also converge toward High-Performance Computing (HPC) data-centers to run the training or serve several inference instances of these networks. In the last years, reducing power and energy consumption has become one of the most critical factors of large-scale HPC systems [6,7,8] and studied on partially functional complex networks with energy restrictions [9]. There exist several possible solutions, like hardware infrastructure change to micro-architectural solutions. The usual solutions seem to converge towards the parallelism associated with CNNs and running the code efficiently instead of focusing purely on high-accuracy performance [6].
The reduction of the CNN models is a possible axis that could be beneficial to HPC. This reduction can come from obtaining networks with fewer trainable parameters or a highly parallelizable neural network architecture [10]. Reduced and efficient models have also contributed to the state-of-the-art moving quickly to field-programmable gate array (FPGA) hardware accelerators targeting both HPC and embedded applications [11,12,13].
A closer inspection of state-of-the-art networks shows that the first layer filters are usually low complexity filters (i.e., edge detectors) in several orientations. Furthermore, these filters are not bound by any relation nor respect any prior ordering on them. These filters usually contain several rotated copies of almost the same filter. This phenomenon happens even though the network trains each filter independently from each other. For example, the network independently creates several, almost identical, rotated copies of an edge detector. Several state-of-the-art approaches have studied this phenomenon and proposed to rotate the inner filters of the CNNs to obtain rotation-invariance. While most of these solutions find a trade-off between complexity and model size, most of them are one-shot solutions suited to a unique architecture.
In this work, we propose to use this filter knowledge to generate a trainable ensemble of filters from a mother filter. This oriented decomposition results in a roto-translational feature space that allows the rotation invariant prediction of the class and angle prediction using the filters’ position. Training a few mother filters and then rotating and ordering them in an ordered set can provide the network with angular information, optimizing the subsequent class-predicting model’s size. The presented model also includes the possibility to select between parallelism or memory footprint reduction (for HPC or embedded solutions) due to the multi-threaded nature possibility of our proposal.
In Section 2, we present a short state-of-the-art survey of the methods that tackle the rotation invariance problem. Section 3 presents the network’s theoretical foundation and explains the network’s two main stages that allow the possibility of rotation-invariant properties. Finally, in Section 4, we show the results with different oriented features and backbones and compare them with current state-of-the-art approaches. In Section 5, we conclude and describe future works.
2. Related Works
As mentioned previously, a low-footprint network allows reducing the energy spent on training and inference. Thus, the main challenge is to design a network invariant to the image transformations allowing to preserve the accuracy of state-of-the-art networks while keeping the number of trainable parameters low. In this sense, here, we present a state-of-the-art survey of works involved in rotation-invariant networks.
In the literature, two main strategies exist to endow a network with rotation invariance: (i) modify the input image by several images (data-augmentation) (ii) modification of the inner filters of the network. The second one has recently gained attention with different approaches: continuous rotation approaches and discrete angular sampling of the filters. As the main scope of this work is on reducing neural networks, we will present results in the (ii) group, as data-augmentation has demonstrated to increase training time and network size.
Recent works in state-of-the-art converge in providing rotation invariance properties by encoding it in the neural networks’ internal filters. Typically, some of these approaches try to find a trade-off between the number of features needed to get a good prediction accuracy and network size.
These approaches modify the network’s inner filters in some way (i.e., rotation) to decompose the input image into several orientations. The act of sampling the input allows some of these approaches to obtain rotation-invariant features; hence, the network acquires rotation invariant properties. The main challenge of these works is to find a trade-off between the angular sampling (fine-grained sampling needs more memory and network size) to obtain good accuracy and a reasonable network size.
2.1. Continuous Filter Sampling
In the continuous sampling, we can find Worral et al.’s work that achieves a good trade-off between angular sampling and size in their Harmonic Networks [14] work. The authors use circular harmonics, returning a maximum response, and they achieve continuous angular sampling by constructing any angular filter using the linear combination of a set of base filters.
Other approaches use a similar Harmonic approach to obtain continuous sampling; Cohen et al. [15] use a spherical cross-correlation in their Spherical CNN work. They introduce a set of building blocks to obtain a rotation-equivariant cross-correlation in spherical images. Furthermore, they present results on up-right training and rotated samples validation; however, the computational cost of the spherical space remains very high. Cohen et al. address the reduction of the computational cost in their Icosahedral CNN [16] by sub-sampling the spherical space; the results achieve better computational cost than the previous approach, but the rotation-equivariance is affected.
Continuous sampling approaches reach competitive accuracy and rotation invariant properties. The main drawback of these approaches is the computation involved to obtain continuous sampling. For example, Worral et al. need to add a process to maintain the rotation order’s disentanglement that is a product of the combination of complex features [14]. This process leads to increased network size, training time, and network complexity.
2.2. Discrete Angular Sampling
The counterpart of the continuous approach is to use a finite number of angular samples. Works in this group sample the input by several angles that become a hyper-parameter of the network. Most of these approaches use a fixed angular sampling adequate to the application and the dataset. For example, Cohen et al. [17] find a trade-off between angular sampling and network size. They use a symmetry group composed of 90-degree rotations and pool over the group. Pooling in the first layers discards important angular information, as explained in their paper. Usually, using multiples of 90-degree orientation steps avoid interpolation problems. The main problem is that using only 90 degrees multiples, the network cannot generalize the data orientation and predict smaller angles.
Several previous works use the oriented filter decomposition with group convolution-based predictors. To mention some, Sifre and Mallat introduced the Scattering transform-based networks in [18]. They use Scattering transforms to generate rotation-equivariant feature extractors. Marcos at al. [19] introduce a CNN architecture encoding rotation equivariance, called Rotation Equivariant Vector Field Networks (RotEqNet). The network applies one filter at different orientations and extracts a vector field feature map, encoding the maximum activation in terms of magnitude and angle. Zhou et al. [20] propose the Oriented Response Networks (ORN) to have Active Rotating Filters. These filters rotate during convolution and produce maps with location and orientation explicitly encoded. An extension to ORN is the Rotation Invariant Local Binary Networks [21]. The authors replace the first convolutional layer for steerable modules that can be inserted into traditional CNNs. In RotDCF [22], the authors demonstrate the benefits of decomposing the convolution filters leading to implicit regularization and robust representations; they present results on rotated samples validation up to 60°. The main limitation of these approaches is the high number of parameters to learn, the computational complexity, and the fixed number of angular sampling they present.
Follman et al. [23] achieve rotational invariance by rotating the filters and then back-rotating the generated feature map by the negative angle of the filter. Weiler et al. [24] introduces the rotation-equivariant CNN with learnable steerable filters. Their SF-CNN allows choosing an arbitrary angular sampling. The idea of learning steerable filters inspired layers based on the Gabor filter bank [25]. Whereas the obtained accuracy is very competitive, the authors present results only for four different orientations, and the number of parameters increases to almost 2 million parameters on the MNIST dataset. While these approaches introduce a lower sampling complexity, they do not provide the roto-translational space to achieve equivariance or angular prediction.
Oyallon and Mallat [26] first present the roto-translational feature space; in their work, they use a non-trainable Scattering transform oriented feature space. Nevertheless, they do not use these oriented feature space properties to obtain an angular prediction. To the best of our knowledge, the first work that uses a translating predictor over an oriented feature space is from Rodriguez et al. [27]. In their work, they use the Scattering transform for the orientation filter decomposition. They apply a predictor to the roto-translational feature space to make the input’s angular prediction. The accuracy of both of these works is deeply affected by the non-trainability of the Scattering filters involved in the oriented filter decomposition stage.
Our prediction model uses a set of features generated by one mother filter. These features, oriented and ordered, form a representation space where translation covaries with the input rotation. A subsequent predictor scans over this representation space and predicts the class and angle of the input. As the rotation invariance is the product of the feature space’s roto-translational properties and not of the translating predictor, the shared weight predictor keeps a small footprint in the network. Using this approach, the user can select the angular sampling as a network hyper-parameter to adapt the angular resolution to the user’s needs.
Furthermore, in the literature we can find references that study the vulnerability of networks based on sampling techniques [28]. In the case of angular sampling techniques, this would mean losing orientation information caused by the attack. The worst case would result in the network’s accuracy reduction or the loss of rotation invariance properties. The oriented sampling and shared weight predictor presented in this work make a possible solution against these attacks as the predictor learns from each translation and becomes rotation sensitive. If an oriented wavelet is missing, the predictor has enough information from the complete filter ensemble and the other translations to complete the inference.
In the following section, we present the methodology in which we base our rotation invariant network. We detail how we obtain a roto-translational feature space and how the shared weight predictor is applied to the feature space to obtain the class and angle prediction.
3. Methodology
In this work, we propose a convolutional network architecture (Figure 1) with rotation-invariant properties and prediction of the angle without angle labels. With rotation-invariant properties, we refer to the network’s capability to correctly predict the class despite the orientation of the object in the input. Furthermore, it can predict the angle by fostering the angle information from the relative position of the network’s inner filters.
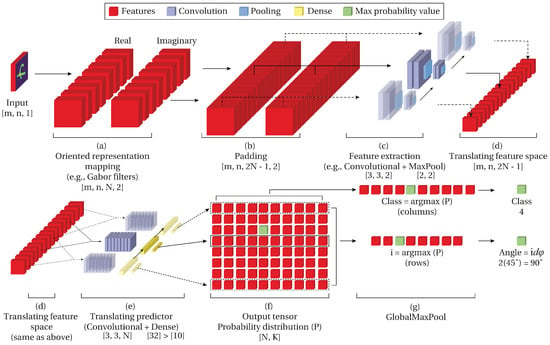
Figure 1.
Rotational Invariant CNN architecture. Input is class number 4 rotated 90° clockwise. (, convolutions in (c,e) scan each place with shared weights).
For easier understanding, we divide the intuition behind the network into two parts. First, the generation of a feature space that translates with respect to the rotation of the input image (roto-translational feature space) (Figure 1 upper row). Second, a predictor that scans the generated roto-translational feature space and outputs a prediction for each of the translations (Figure 1 lower row). The result of these two processes is a probability distribution that contains a prediction for each translation. Then, the class is obtained from the prediction, and the angle from the relative position of the maximum predicted class.
3.1. Oriented Representation Mapping
Oriented representation mapping is the result of two operations: oriented components, based on wavelet theory [29], and re-orientation of such components. First, we start by obtaining a set of oriented components from the input image x (Figure 2a). An oriented component is obtained by the product where is the orientation of an oriented edge detector g. Furthermore, we have a set of orientations such as , with where N is the number of orientations in which we want to decompose the input image. This means that the set contains N oriented components (features) of the input image . Furthermore, we can define as the angular sampling magnitude in degrees for a filter with periodicity . Then the orientation of the filter in the position i position is .
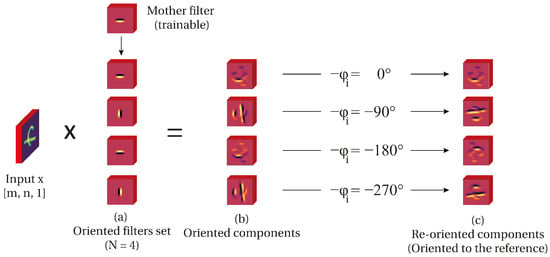
Figure 2.
Oriented mapping. First, the image is decomposed by a set of N oriented components. Second, the result is re-oriented to the reference. This becomes a roto-translational feature stage.
Is straightforward to see that the input image of size [m, n] is decomposed in N oriented components of the same size generating a feature space with size [m, n, N] (Figure 2b). This can be observed in Figure 2b where each feature is an oriented component in the angle .
Second, let be a transformation rotating the support by the angle . Then we compensate the rotation by rotating the support degrees. This re-orientation results in all the feature components to be aligned to the referential orientation (Figure 2c).
Then we can define as an oriented feature representation of :
Definition 1
(oriented feature representation).Let Φ be a mapping , and a feature representation of
containing oriented components of , and re-oriented to align with the referential orientation .
A cyclic permutation of the elements in the axis N of the oriented features is then observed. This permutation is cyclic with period equal to N and the last element replaces the first one. We refer to this permutation as translation, and denotes a translation over the filters in the N axis of i times. The same oriented features in Figure 3c are located at when the input rotates (Figure 3f).
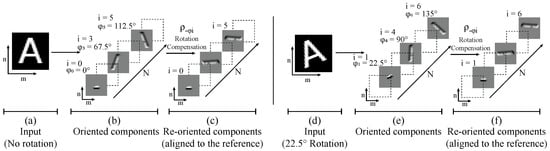
Figure 3.
Oriented representation mapping to obtain roto-translational feature space. Left side: Up-right oriented input (a), and the oriented components (b) generate a translating output product of the rotation compensation (c). Right side: Rotated input (d) and the oriented components (e) with output translated by one space over axis N (f).
As a consequence of the oriented decomposition of the input () and the re-orientation () the oriented features in translate i times following magnitude (Figure 3). Experimental results demonstrate that the transformation is necessary to obtain a roto-translational feature space. Without this transformation the oriented feature space does not translate and the prediction accuracy is heavily affected.
The oriented components of the input can be obtained with several approaches. Previous works [27,30] used the Scattering transform and Steerable filters. We propose the usage of trainable Gabor filters that can offer a higher degree of freedom to fit the data. The implementation aspects of trainable Gabor filters are explained in the next section. Furthermore, in the result section we compare the Steerable filters approach with the Gabor filters generation of the oriented features.
Gabor Filters
Gabor filters offer a higher degree of flexibility than previous works approaches [27,30], especially in the sense that the angular and frequency selectivity can be learned independently; they can generate an oriented feature space and trained to fit the training data. A 2D Gabor filter can be defined as an oriented sine (imaginary part of the filter) or cosine (real part) modulated by a 2D Gaussian function [31]. The shape of the Gabor function is defined by the frequency, the orientation of the sinusoid, and the scale of the Gaussian function [32].
Consider the rotation matrix in 2D space:
Let and divide the rotation matrix by their magnitude:
We obtain the respective real and imaginary components of the Gabor function in which corresponds to the filter’s angular selectivity and to the frequency selectivity of the filter.
The parameters become trainable parameters of the network and are updated by the back-propagation algorithm (Figure 4). Recalling as a list of N orientations, Gabor filters can generate an oriented filter g separated in real and imaginary components.

The presented Gabor methodology then generates an oriented filter bank with a set of orientations that allows the extraction of the oriented components of the input by the convolution operation (Equation (1)). We implement this operation as a 2D Convolution with as many Gabor filters as orientations N. Each one of these filters is oriented as and the shape is determined by the Equation (4) (for the real part filter bank) and Equation (5) (for the imaginary part).
The wavelet re-orientation stage () is then applied to these oriented components to obtain the oriented components re-oriented to the referential orientation . This means that each filter of the bank is rotated by a fixed angle calculated by its position i on the bank using bilinear interpolation. As consequence of this Gabor methodology we obtain a roto-translational feature space (Figure 3). The number of oriented components is then defined as a network hyper-parameter, hence the user selects the number of oriented components N that conform the oriented feature space. In this work, we present different N values and results with .
3.2. Feature Extraction
The most typical feature extraction stage in the literature is stacked convolutions with increasing filters over the depth. Usually, these convolutions are followed up by a batch normalization operation and activation. The feature extraction stage has recently moved to architectures that contain connection skipping and the depth of hundreds of layers. Following the state-of-the-art implementations, we connect the feature extraction stage to the representation mapping’s oriented feature representation.
This feature extraction stage’s main challenge is to preserve the roto-translational feature properties of the oriented feature space. As the translation occurs in the extra dimension of size N, we apply the feature extraction to the feature space dimensions that do not have translation [m, n]. This means that input gets decomposed in oriented components by a set of oriented filters (previous subsection) and generates a roto-translational feature space with m, n, N, channels) where refers to the dimensions of the space. To preserve the translation axis, then the feature extraction is applied to the m, n, and channels axis (Figure 1c). A straightforward way to obtain this is with a 3D Convolution with a window size of one in the translation axis, for example, with for a square kernel support of size 3. This implementation way allows the convolutional backbone to extract and refine the feature space’s useful features in the same way as the feature extraction stages from the state-of-the-art architectures.
Gabor filters output two channels, the product of the real filter response and the imaginary filters response. Furthermore, it can be possible for the Gabor filters approach to use more than one mother filter and generate as many pairs of real and imaginary filters as necessary. Nevertheless, in this work, we have used a single mother filter in all the experiments.
If observed, this feature extraction convolutional backbone is applied to a 3-axis tensor height, weight, channels). The current state-of-the-art networks use a similar shape as the network’s input. This opens the possibility of changing the convolutional backbone to a known state-of-the-art architecture such as ResNet. While the convolutional backbone reaches state-of-the-art results on the MNIST dataset, a more robust backbone is needed for more challenging datasets such as CIFAR-10. To prove this, we propose applying a ResNet backbone to the oriented feature space to extract and refine the features. The translation is then preserved on the additional axis as the backbones’ convolution window does not affect this dimension.
State-of-the-Art Architectures as Backbone (ResNet)
The output shape of the Gabor filter approach opened a new possibility to explore: exploring the usage of state-of-the-art backbones (i.e., ResNet). If the connections are managed correctly, it opens the possibility to use a known network as a plug and play backbone of the rotation invariant network. In other words, it is possible to use these networks potential to refine the features (Figure 5).
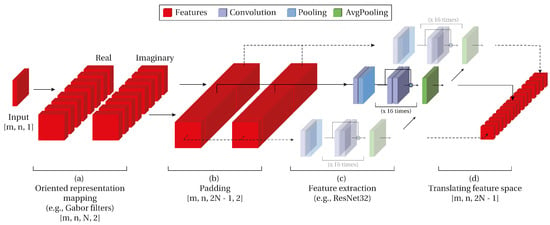
Figure 5.
The backbone feature extraction is applied to each filter of the oriented feature space. ResNet used as backbone example. Output is a translating feature space. (Image blocks with ).
The first challenge is to adapt the shapes and connections between the custom Gabor layer and the possible backbones. Usually, networks have an input with width, height, channels). This means that the expected input of these networks are not prepared for the dimension N containing the orientations product of the Gabor layer. One way to achieve this shape adaptation is to use the backbone predictor on each one of the filters (apply it on one orientation instead of the complete translation of size N) (Figure 5c). Then, concatenate the outputs and apply a translating convolution hence obtaining the same behavior of having a prediction for each position on the roto-translation feature space.
Several questions could arise when following this methodology. First, the roto-translational properties of the feature space are preserved on the architecture. This is possible because the backbone network is applied to each filter individually and the position of the filter is preserved in the output of this layer.
Another concern comes in the form of the size of the network. As we use a backbone network, the number of trainable parameters increases quickly. For example, using a ResNet20 with 438 k parameters multiplicated by 16 orientations would mean about 7 M trainable parameters. Sharing weights allows the backbone to learn from the different orientations and be implemented once in memory hence keeping the network size constant for any number of orientations N.
This means that the network could be benefited from the usage of any state-of-the-art backbone network instead of the convolutional backbone presented previously. With this the network is able to predict class and the angle without any angular labeling on the training stage. As the network with this backbone is complex enough, we opted for testing ResNet backbones on the CIFAR-10 dataset.
3.3. Translating Predictor
As a result of the input decomposition presented in the last section, we obtain an oriented feature representation space. This oriented feature space contains features ordered in increasing magnitude. As a consequence of this transformation, the feature space translates over this depth axis of size in a cyclic form.
When we rotate the input the oriented feature is translated i spaces over the N axis. The translation of the filters is proportional to the magnitude of the input’s angle and covariates following . This means that for any input rotation a translation i exists in the oriented feature space up to . Then is possible to find a translation for an almost unrotated version of the input.
It is possible to find the position i corresponding to the almost unrotated version of the input using a cyclic convolutional predictor over the feature space. This predictor with an attention window of size N reads each translation and obtains a prediction for each position i. Hence, the predictor will output a higher probability on the translation i that corresponds to the unrotated input (the same orientation of the training samples). Consequently, the linear distance of the position i where the maximum probability is obtained to the reference orientation becomes the input angle .
A straightforward way to implement this cyclic convolutional predictor is to pad the feature space by itself and then applying this convolution over the translation N axis. This is implemented as a 3D Convolution with a kernel size of (3, 3, N) that scans each one of the translations . Then a fully-connected layer with size K (number of classes) generates a class prediction for each one of the translations (Figure 1e). The number of classes K is determined by the problem and dataset used in training (i.e., MNIST contains ten classes one for each digit in the dataset).
The output contains N predictions in the form of a probabilistic distribution with a higher value on the translation corresponding to almost the same orientation of the input with slightly lower values at the neighbor positions of the maximum value. A max-pooling operation over the N axis and the K axis outputs the angular and class prediction, respectively (Figure 1f). This max-pooling operation over the output reinforces the convolutional shared predictor on the correct orientation while not updating it at the other orientations. This implementation model allows the proposed prediction model to have rotation-invariant properties angular prediction.
In conclusion, following this method, we obtain a convolutional neural network with rotation invariant properties. This network can predict the input class and angle. The angle is predicted using the relative position i, where the highest prediction is present. As this position is proportional to the rotation of the input (roto-translational feature space), then the angle can be fostered from the translation information ().
This work presents results with two alternatives for the oriented feature space and results with two different backbones: convolutional and different sizes of ResNet. In the following section, we describe the results obtained on the MNIST dataset and CIFAR-10 dataset and compare them with the state-of-the-art approaches.
3.4. Memory-Footprint vs. Data Parallelism
One of the main advantages of this approach is the capability of selecting between memory-footprint and data parallelism. Our network uses a set of shared weights convolutions for the feature extraction and for the translating predictor explained previously. This means that the number of parameters is kept low while keeping high accuracy. A closer look at the data dependency between the layers demonstrates that each filter can be processed independently, speeding up the inference process.
For the inference step, instead of a shared weight convolution scanning each filter position, we can implement N instances of the feature extraction and translating predictor and process each position i in parallel. This would mean an increase in the memory size of N times the operation size but speed the inference time N times. An HPC center with several cores could run each orientation in a core as the memory is usually not a limitation in these devices.
On the other hand, the user could select to implement the feature extraction and translating predictor as a single instance scanning each orientation i. This would mean a low-footprint network (10 k learnable parameters) at the expense of augmenting the inference time N times.
The network flexibility between memory footprint and parallelism would allow benefits on several applications. Usually, neural networks require large amounts of on-chip memories that occupy significant chip area, making impractical their realization on small footprint devices [33]. Shared weights and the presented methodology allows the implementation of the network in these limited memory embedded devices. For the parallelism, there exist some efforts on deeply pipelined multi-FPGA implementations [11] which could benefit both from the low-footprint size and to run in parallel pipelines.
4. Results
We evaluate different options for the proposed stages of the architecture. For the oriented feature generators we test Steerable and Gabor filters on the MNIST dataset, and for the feature extractors we test convolutional and ResNet on CIFAR-10 dataset. To test rotational-invariance we train the network with up-right samples (all the samples in the same orientation) and validate with randomly rotated samples. We train the network for 200 epochs using the Adam loss function on a Titan Xp GPU with 16 GB VRAM; unless noted the angular sampling is . This N value allows a direct comparison between our approach and state-of-the-art approaches but can be changed by the user as a network hyper-parameter.
4.1. MNIST
For the MNIST dataset we have trained the network using up-right samples and validated it on randomly rotated samples. This type of validation ensures that the rotation invariance property is adquired by the network. We present results using two different oriented feature filters using Steerable filters and Gabor filters approaches.
We present the rotation-invariant approaches in Table 1. The presented results include the cases when the network is trained on up-right samples and validated on random orientations. Some of the presented approaches obtain the rotation invariant property by increasing the number of parameters over 100 k. Usually, they are group-convolution-based approaches that lose the orientation of the input to ensure the invariance. Instead, we preserve the orientation as a different axis of the network and use it to predict the angle.

Table 1.
Obtained error rate MNIST dataset (training: up-right/validation: rotated).
The nearest approach in parameter terms is Covariant CNN [27] with lower accuracy; this is mostly due to the static nature of their scattering filters approach instead of trainable ones like the presented on this work.
As observed in Table 1 the Gabor filters approach has a lower number of parameters while achieving higher accuracy (best values are depicted in bold); this is mostly caused by the degrees of freedom of this approach. The Steerable filters need to be circular to keep their steerability properties while the Gabor ones have better angular and frequency selectivity. Our results demonstrate the capability of the added functions to endow with rotation invariance and angular prediction properties to neural networks. Furthermore, the number of parameters has been kept lower than 10 k.
4.2. CIFAR-10
We tested the capability of our approach on the CIFAR-10 dataset. We opted for Gabor Filters as oriented filters decomposition function because it showed better adaptive capabilities and have higher degree of freedom. We tested two different feature extractors: convolutional and ResNet.
For the first one, the convolutional feature extractor, we have three 2D Convolution stages with filters number increasing with the depth. Each one of the convolutional stages is followed up by a BatchNormalization layer following the state-of-the-art implementations. The convolutional feature extractor shows error rate up to 28% with 238 k learned parameters. Increasing the number of filters, hence the number of trainable parameters, shows no improvement over this point. In conclusion, higher number of filters in the convolutional feature extraction approach tend to overfit the dataset quickly.
For the ResNet feature extractor, we test different depths of the network; with ResNet20 we obtain 21% error rate and preserve the rotation invariance properties. Having more layers on this type of feature extractor did not improve the error rate further than 21%; this means that the network tend to overfit quickly with deeper feature extractors.
Table 2 condenses the results with Gabor oriented filters and these two different feature extractors (best values are depicted in bold). We compare these results with previous state-of-the-art implementations on CIFAR-10 dataset when trained on up-right and validated on randomly oriented samples. In general, we observe an accuracy increase over previous methods (Figure 6a) with both approaches. For both feature extractors (Convolutional, Gabor) we find the same error rate with approximately 240 k parameters; more filters in the convolutional feature extractor did not improve the error rate. Nevertheless, ResNet improves the error rate by 6% until 21% error rate is reached. When comparing the ResNet feature extractor with the original ResNet (Figure 6b) we observe that our proposal achieves rotation-invariance having around 80% accuracy; the original ResNet20 accuracy drops when tested with non-upright samples. Increasing the number of orientations did not result in an increase on accuracy.

Table 2.
Obtained error rate CIFAR-10 dataset (training: up-right/validation: rotated).
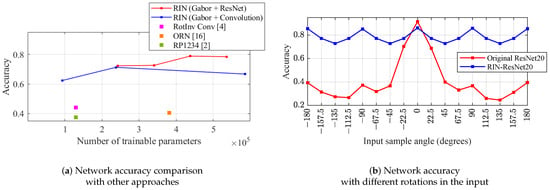
Figure 6.
Accuracy values forthe proposed architecture on CIFAR-10 (training: up-right/validation: rotated).
5. Conclusions
In this paper, we propose a prediction model based on an oriented feature representation mapping and a translating predictor. The concatenation of these two allows the usual convolutional networks to obtain rotational invariance properties. The oriented features have roto-translational properties between the input and an additional axis proportional to the angular sampling of the input. The translational predictor uses the translating feature space to obtain a set of probabilities for each possible discrete orientations of the input. The maximum value of this set contains the prediction for the class and orientation.
We present results obtained with different oriented features mapping as Steerable and Gabor filters for the MNIST dataset. The mapping generated by Steerable filters demonstrates to increase the accuracy results compared to previous state-of-the-art implementations on the MNIST dataset; their main drawback is the circular shape that limits the filter flexibility to adapt to the data. Gabor filters present higher flexibility than Steerable ones; with Gabor filters, one can either prefer a better angular or frequency selectivity. Results on the MNIST dataset show a slight reduction of the error rate (Steerable: 2.05%, Gabor: 1.71%), with the Gabor implementation being almost five times smaller than the first one. These results demonstrate the limited capabilities of the Steerable filters to fit the data. Both of these approaches outperform the previous Scattering approach error rate of 17.21%.
This reduction in the model’s size opens the possibility to use these networks in low-memory devices like embedded devices or smartphones. For example, aerial/satellite imagery applications on UAV could be benefited from low-footprint rotation-invariant networks opening the possibility of inference on-site. Furthermore, the reduced model represents an enhancement in energy reduction for reduced training time and less memory access on the inference. The obtention of these results without data augmentation also opens the possibility to focus on developing efficient networks and using the inner filter resources adequately. One example of this is the usage of the relative position of the filters to obtain rotation invariance properties and angular prediction without angle labels.
Furthermore, we tested the proposed prediction model with different feature extractors: convolutional and ResNet. In both cases, we use the headless architecture (feature extraction stage). To validate these feature extractors, we trained them on the CIFAR-10 dataset. Both implementations outperformed (Convolutional: 19.98%, ResNet: 11.95%) previous state-of-the-art error rates when trained and validated on up-right samples. Furthermore, these implementations demonstrated to acquire the rotation-invariant properties and angular prediction capabilities described in the paper.
The low footprint of the presented work opens the possibility for implementation in embedded, mobile, and other resource-limited devices. As this model offers the flexibility between memory footprint or multi-thread parallelism, it allows to target the hardware efficiently when more cores are available (e.g., HPC centers) or memory-constrained hardware (e.g., FPGA, single-board computers). In the end, this means better resource usage and energy consumption reduction for inference. In future works, we expect to test the model with other state-of-the-art feature extraction stages and validate the rotation-invariant properties in harder datasets as faces or food. Furthermore, a deeper analysis of the multi-threading advantages and memory constraints are expected in the near future.
Author Contributions
R.R.S.: manuscript writing and editing, E.D.: final version editing and checking, P.D.: final version editing and checking. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gu, Y.; Wang, Y.; Li, Y. A survey on deep learning-driven remote sensing image scene understanding: Scene classification, scene retrieval and scene-guided object detection. Appl. Sci. 2019, 9, 2110. [Google Scholar] [CrossRef]
- Alom, M.Z.; Taha, T.M.; Yakopcic, C.; Westberg, S.; Sidike, P.; Nasrin, M.S.; Hasan, M.; Van Essen, B.C.; Awwal, A.A.; Asari, V.K. A state-of-the-art survey on deep learning theory and architectures. Electronics 2019, 8, 292. [Google Scholar] [CrossRef]
- Véstias, M.P. A survey of convolutional neural networks on edge with reconfigurable computing. Algorithms 2019, 12, 154. [Google Scholar] [CrossRef]
- O’Gara, S.; McGuinness, K. Comparing Data Augmentation Strategies for Deep Image Classification; IMVIP; Technological University Dublin: Dublin, Ireland, 2019. [Google Scholar]
- Zhang, C.; Patras, P.; Haddadi, H. Deep learning in mobile and wireless networking: A survey. IEEE Commun. Surv. Tutor. 2019, 21, 2224–2287. [Google Scholar] [CrossRef]
- Maiterth, M.; Wilde, T.; Lowenthal, D.; Rountree, B.; Schulz, M.; Eastep, J.; Kranzlmüller, D. Power aware high performance computing: Challenges and opportunities for application and system developers—Survey & tutorial. In Proceedings of the International Conference on High Performance Computing & Simulation (HPCS), Genoa, Italy, 17–21 July 2017; pp. 3–10. [Google Scholar]
- Rofouei, M.; Stathopoulos, T.; Ryffel, S.; Kaiser, W.; Sarrafzadeh, M. Energy-aware high performance computing with graphic processing units. In Proceedings of the Workshop on Power Aware Computing and System, San Diego, CA, USA, 7 December 2008. [Google Scholar]
- Zong, Z.; Ge, R.; Gu, Q. Marcher: A heterogeneous system supporting energy-aware high performance computing and big data analytics. Big Data Res. 2017, 8, 27–38. [Google Scholar] [CrossRef]
- Shang, Y. Vulnerability of networks: Fractional percolation on random graphs. Phys. Rev. E 2014, 89, 012813. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Khan, S.U.; Chen, D.; KołOdziej, J.; Ranjan, R.; Xu, C.Z.; Zomaya, A. Energy-aware parallel task scheduling in a cluster. Future Gener. Comput. Syst. 2013, 29, 1661–1670. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, D.; Sun, J.; Sun, G.; Luo, G.; Cong, J. Energy-efficient CNN implementation on a deeply pipelined FPGA cluster. In Proceedings of the 2016 International Symposium on Low Power Electronics and Design, San Francisco, CA, USA, 19–21 August 2016; pp. 326–331. [Google Scholar]
- Gai, K.; Qin, X.; Zhu, L. An energy-aware high performance task allocation strategy in heterogeneous fog computing environments. IEEE Trans. Comput. 2020. [Google Scholar] [CrossRef]
- Abdelouahab, K.; Pelcat, M.; Serot, J.; Berry, F. Accelerating CNN inference on FPGAs: A survey. arXiv 2018, arXiv:1806.01683. [Google Scholar]
- Worrall, D.E.; Garbin, S.J.; Turmukhambetov, D.; Brostow, G.J. Harmonic deep: Networks translation and rotation equivariance. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar] [CrossRef]
- Cohen, T.S.; Geiger, M.; Koehler, J.; Welling, M. Spherical CNNs. ICLR. 2018. Available online: http://xxx.lanl.gov/abs/1801.10130 (accessed on 21 December 2020).
- Cohen, T.; Weiler, M.; Kicanaoglu, B.; Welling, M. Gauge equivariant convolutional networks and the icosahedral CNN. In Proceedings of the 36th International Conference on Machine Learning, (ICML 2019), Long Beach, CA, USA, 18–23 January 2019; pp. 1321–1330. [Google Scholar]
- Cohen, T.; Welling, M. Group equivariant convolutional networks. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 2990–2999. [Google Scholar]
- Sifre, L.; Mallat, S. Rotation, scaling and deformation invariant scattering for texture discrimination. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Portland, Oregon, 23–28 June 2013; pp. 1233–1240. [Google Scholar] [CrossRef]
- Marcos, D.; Volpi, M.; Komodakis, N.; Tuia, D. Rotation equivariant vector field networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; Volume 2017, pp. 5058–5067. [Google Scholar] [CrossRef]
- Zhou, Y.; Ye, Q.; Qiu, Q.; Jiao, J. Oriented response networks. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; Volume 2017, pp. 4961–4970. [Google Scholar] [CrossRef]
- Shin, C.; Yun, J. Deep rotating kernel convolution neural network. In Proceedings of the 2019 Third IEEE International Conference on Robotic Computing (IRC), Naples, Italy, 25–27 February 2019; pp. 441–442. [Google Scholar]
- Gao, L.; Li, H.; Lu, Z.; Lin, G. Rotation-equivariant convolutional neural network ensembles in image processing. In Adjunct Proceedings of the 2019 ACM International Joint Conference on Pervasive and Ubiquitous Computing and Proceedings of the 2019 ACM International Symposium on Wearable Computers, London, UK, 9–10 September 2019; Association for Computing Machinery: New York, NY, USA, 2019. [Google Scholar]
- Follmann, P.; Bottger, T. A rotationally-invariant convolution module by feature map back-rotation. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision, WACV 2018, Lake Tahoe, NV, USA, 12–15 March 2018; Volume 2018, pp. 784–792. [Google Scholar] [CrossRef]
- Weiler, M.; Hamprecht, F.A.; Storath, M. Learning steerable filters for rotation equivariant CNNs. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 849–858. [Google Scholar] [CrossRef]
- Luan, S.; Chen, C.; Zhang, B.; Han, J.; Liu, J. Gabor convolutional networks. IEEE Trans. Image Process. 2018, 27, 4357–4366. [Google Scholar] [CrossRef] [PubMed]
- Oyallon, E.; Mallat, S. Deep roto-translation scattering for object classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 2865–2873. [Google Scholar]
- Rodriguez Salas, R.; Dokladalova, E.; Dokladal, P. Rotation invariant CNN using scattering transform for image classification. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 654–658. [Google Scholar] [CrossRef]
- Shang, Y. Subgraph robustness of complex networks under attacks. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 821–832. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing, Third Edition: The Sparse Way, 3rd ed.; Academic Press, Inc.: Cambridge, MA, USA, 2008. [Google Scholar]
- Rodriguez Salas, R.; Dokládal, P.; Dokladalova, E. RED-NN: Rotation-Equivariant Deep Neural Network for Classification and Prediction of Rotation. 2019. Available online: https://hal.archives-ouvertes.fr/hal-02170933 (accessed on 1 January 2021).
- Szeliski, R. Computer Vision: Algorithms and Applications; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Petkov, N. Biologically motivated computationally intensive approaches to image pattern recognition. Future Gener. Comput. Syst. 1995, 11, 451–465. [Google Scholar] [CrossRef]
- Seto, K.; Nejatollahi, H.; An, J.; Kang, S.; Dutt, N. Small memory footprint neural network accelerators. In Proceedings of the 20th International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 6–7 March 2019; pp. 253–258. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).