1. Introduction
In the last two decades, automation and control have become a topic of interest for researchers from different areas. Mainly in industrial robotics [
1,
2] and in the medical area’s robotic systems. There is a wide variety of automation and control; however, the medical area has been greatly benefited; below, some works related to this area are mentioned, such as tele-operated surgery [
3], surgical pattern cutting [
4]. According to Shademan et al., an industrial robot’s precision offers excellent advantages in this area [
5]. The trajectory of a robotic arm has been a subject widely studied by different researchers using different techniques. These techniques help us to understand and make different tasks; for example, in the industries, a robot arm makes repeated work where it is making a trajectory. This topic has been improved throughout time, and nowadays, some related works with robotic assistance arms have been developed [
6,
7,
8] to help people with physical disabilities to become more independent in daily life. According to the works in [
9,
10], the most commonly used methods to calculate trajectories in robotic arms are cubic polynomials [
11], trapezoidal trajectory [
12], and the Euler angles [
10]. With these methods, it is possible to obtain smooth motions in the joint space, and these movements are predictable in the task space.
However, these methods present specific problems when calculating the trajectory. According to the work of Sidobre and Desormeaux [
11], with cubic polynomials, it is difficult to calculate the trajectory in an optimal time; that is, there is no freedom to take a trajectory with a time of 1 s or another to ensure accurate results in the trajectory. Hence, to obtain an accurate trajectory, it is necessary to estimate the optimal time, and therefore, more calculations are required. According to [
13], the (N-1)-order polynomials present other disadvantages when generating the trajectories. First, it is only possible to generate velocity and acceleration for a determinate position, and it is not possible to change those positions. Second, when the polynomial order increases, the robotic arm acquires an oscillatory behavior, which causes an unnatural response, and therefore, the precision of the trajectory decreases. Third, the constraint equations system is difficult to solve, and compile-time is increased as a result. Finally, the polynomial coefficients have to be recomputed every time that a new endpoint is assigned.
In relation to the trapezoidal trajectory, there are some disadvantages. According to [
12], although it does not require many computations, this trapezoidal profile requires additional response-time and has a constant acceleration, velocity, and deceleration regions, which means, large jerk causes vibrations which restrict position accuracy. Finally, another method that is very popular to calculate the trajectory of a robotic arm is Euler angles. According to [
10] which can cause malfunction of robots with systematic errors and lead to undesirable results because of the nonlinearity of the three Euler angles.
In addition to the disadvantages presented in each of the methods, it is essential to mention that when estimating the velocity and the acceleration in a real application, these calculations can be affected by noise during the process. As an alternative to this problem, some authors [
14,
15,
16] have proposed different approaches to reducing possible measurement errors and noise. In the work of Mercorelli [
14] a velocity estimator based on current measurements is proposed. In another work [
15] a derived approximation structure is proposed to estimate velocity by measuring position. In [
16] the authors have proposed an adaptive algorithm to calculate a signal’s derivative with convergence in infinite time.
Some work has proposed to use a touch screen for robotic control as an alternative solution to help people with physical disabilities, providing an intuitive interface. Makwana and Tandon [
17] have proposed controlling a robotic wheelchair using a touch screen to improve a person’s movements with physical disabilities. Similarly, Bularka et al. [
18] present an alternative to control a robotic arm using the accelerometer of a watch and a smartphone; control is carried out using finger gestures on the touch screen or moving the phone in the air. The authors in [
19] present solutions for robotic control using the potential advantages of smartphones so that people with a physical disability can interact with the environment in a friendly way.
Another problem related to robotic arms control is when a joystick or another kind of sensor is used. According to [
20], some inconveniences can be presented, for example, it has been proved that controlling a robotic arm by voice commands lack high reliability, or when using keyboards, joystick or model controls to generate a robotic arm trajectory. However, these techniques are unsatisfactory because disabled persons cannot provide inputs to keyboard and joysticks for a sustained period.
To solve all problems mentioned regarding arm control and the calculation of their trajectory, first of all, it has been considered an LCD touch screen to generate the end-point motion of the robot because the control is intuitive, the people are more familiarized using an LCD touch screen due to they use smartphones, laptops, etc.; which count with an LCD touch screen to work. Also, the idea to use an LCD touch screen to control an anthropomorphic robotic arm with just one finger and using the distribution function proposed, it is a great option to help physically disabled people in their quotidian lives with an exact, fast and comfortable option to control the robotic arm. Concerning the problems mentioned above when calculating a robotic arm’s trajectory, it is proposed to use a distribution function, named distribution function-(), that allows the calculation of an exact trajectory and for any parameter. For example, the velocity and acceleration can be chosen without affecting the desired position and the initial position by changing one parameter and making one calculation to generate the trajectory planning.
The remainder of this paper is organized as follows:
Section 2 introduces an overview of previous related works on the application of different techniques to generate the trajectory of a robotic arm.
Section 3 describes how the LCD touch screen works in order to understand the algorithm operation.
Section 4 presents the proposed algorithm to generate a safe and fast trajectory; it includes the conditions, the linear transformation as baseline to calculate the inverse-kinematic with the distribution function and its properties to generate de trajectory and finally how is calculated the velocity and acceleration.
Section 5, simulation and results, and designs land on the code using the Arduino Mega microcontroller to obtain the end-point of the robotic arm and MATLAB to generate the trajectory.
Section 6 mentions a critical discussion of the results obtained with the proposed algorithm compared to the algorithm of cubic polynomials. Finally,
Section 7 summarizes the conclusions of the paper and indicates further work.
2. Related Works
Most robotic applications are currently related to industrial robot arms; therefore, it is essential to know the main concepts in robotics, such as kinematics, dynamics, movement planning, computer vision, and control. In this sense, robotic control is considered the core part when planning trajectories and the most used technique to achieve a specific position is inverse-kinematics.
Liu et al. [
21] analyzed the Denavit-Hartenberg (DH) method for planning trajectories with multiple manipulators; besides, the authors solved the inverse kinematics equation employing the matrix operation algebraic method. In another work [
22], the authors proposed the exponential product method based on screw theory to avoid the singularity problem. They used different analytical, geometric, and algebraic methods combined with the Paden-Kahan subproblem and the matrix theory. Other works [
23,
24,
25,
26,
27] proposed conventional tools to discover the robot manipulator’s kinematic solutions.
Other methods have been used to control a robotic arm; for example, the authors [
28] designed and programmed an interface with open control algorithms to generate and control three types of movements: joint interpolation, linear interpolation, and circular arcs. The results have been tested on the CompactRIO industrial controller. According to the results obtained, some position errors were found in the end effector, and the process shows oscillations on the desired coordinates. In the work of Barghi-Jond et al. [
29] proposed the use of 3rd, 4th and 5th-degree polynomial trajectory to present three problems of optimization of trajectories, and it has been mentioned that the slowest trajectory occurs when there is a high-degree polynomial. The coefficients of the polynomial cannot get frequently.
In other work [
30], the authors have used artificial intelligence to optimize trajectory planning; mainly, this work is focused on an improved genetic algorithm. The authors mention that the polynomial interpolation method is an excellent option to study robot obstacle avoidance due to the complexity of this method. Then, the trajectory of the robot’s joints is planned by the quantic polynomial; however, the optimal time of this method is 13.729 s because a smooth motion is presented at this time, and the trajectory planning presents oscillations. Other authors [
31] used trapezoidal motion to generate trajectories; nevertheless, it is necessary to reduce the residual vibration in acceleration and deceleration. According to [
12], the trapezoidal trajectory has a constant velocity and acceleration, and a large jerk causes vibration, the accuracy of the results decreases and requires an additional response time.
In another research work [
32], the authors have proposed optimizing the trajectory planning using the Gaussian distribution.
The research of robotics applied in the area of assistance and rehabilitation has in-creased considerably, kinds of research works have focused on motion planning using manipulators with different degrees of freedom to allow the independence of patients who require rehabilitation or assistance in daily life activities [
33,
34]. Most of the research related to the trajectory generation for assistance or rehabilitation manipulators are based on the use of different techniques such as: forward and inverse-kinematic analysis [
35,
36], DH method [
37], the Jacobian Equation [
38], the geodetic curves [
39], and the minimum jerk algorithm [
40], among others. All methods are used in order to improve the safety and the experience of patients who need to perform human-robot interaction to recover the functional impairment or to help the functional rehabilitation of people with loss of autonomy [
41,
42,
43].
As a result of the analysis of the related works, it can be highlighted there are several research works that present solutions both Robotic controls, as well as robotics, applied in the area of assistance and rehabilitation. However, several disadvantages in these algorithms are presented, the trajectory can oscillate between feasible and infeasible during optimization, and it needs an optimization process which implies more calculations to generate an optimized trajectory. Moreover, the solutions presented by the authors were applied with joystick MATLAB, Lab-VIEW, industrial controller CompactRIO and camera. This implies that people are dependent or require help from other people to control these devices. In addition, the trajectory captured in these devices is slower and more complex to generate the trajectory of a robotic arm, and the short trajectories cannot be calculated.
3. LCD Touch Screen Operation
Nowadays, using joystick is widespread and other types of electronics devices to control a robotic arm, whatever is the kind of robotic arm; cartesian, SCARA, cylindrical, delta, spherical, and anthropomorphic. Nevertheless, these sensors that are used as control tools could have problems when it is implemented within particular characteristics, and it cannot meet the necessities or expectations to get the maximum utilization. These problems are due to constant effort requirement and waiting time while a force is being applied until the robotic arm gets the desired position, without mentioning that it is needed to coordinate. Supposing that the patient is sick of diabetics (in the case of hypoglycemia), lupus, or another disease that impedes good coordination, so in this case, joystick could be a difficult tool used by patients who present these cases. Therefore, it has been thought in those cases and has been implemented the LCD touch screen rather than joystick or another device. Before to start explaining about the algorithm to obtain the trajectory of the anthropomorphic robotic arm using the LCD touch screen as a control.
First, how the LCD touch screen works, it has to be explained. Arduino Mega was utilized to program the interface and get the data to obtain the end-position of the robotic arm; it was used the libraries Adafruit_TFTLCD.h, Adafruit_GFX.h and TouchScreen.h. Then, the interface was programmed to reference the task space such as it can be observed in
Figure 1a, so, four right triangles with equal areas, each time that the LCD touch was touched, it gives us a coordinate between 123 and 932 in the axis
X and, 897 and 128 in the axis
Y. This coordinate is processed using MATLAB to obtain a coordinate
where
and
. So, every coordinate which is less than 527.5 and greater or equal to 123, that means
and, if a coordinate greater than 527.5 is given and less or equal to 932, then
. this is the same for
; if a coordinate between 128 and 512.5 is given, then
, and if a coordinate between 512.5 and 897 is given, then
. Note that 527.5 is the middle point in the axis
X of the LCD touch screen and 512.5 is the middle point of the axis
Y of the LCD touch screen. Taking the coordinates
, it can be started to work with the algorithm presented in the next section.
4. Algorithm Description
The proposed algorithm has been thought for the anthropomorphic robotic arm, which has three rotation joints, and it has been inspired in third-order polynomial time scaling to propose the distribution function, which is discussed through this paper. In the next section, it is going to talk more about this distribution function. First, it is necessary to speak of the first conditions, second establish the linear transformation as baseline to calculate the inverse-kinematic with the distribution function and its properties to generate de trajectory and finally calculating the velocity and acceleration.
4.1. Nomenclature
: coordinate in the axis X obtained from the LCD Touch screen.
coordinate in the axis Y obtained from the LCD Touch screen.
angle to obtain the direction of the coordinate obtained from the LCD Touch screen.
total angle rotation of the first joint of the robotic arm.
final position.
initial position.
final time of the trajectory.
: parameter to change the shape of the trajectory, velocity, acceleration, and Jerk.
constant greater to 1.
: parameter used to generate the trajectory through the time.
4.2. Description of Conditions
The joint which is more nearly to the base of the robotic arm has to rotate greater or equal to 0 degrees and equal or less to 180 degrees, and that would be represented
, where
represents the first-joint degrees with a clockwise or counterclockwise rotation, depending on the point that has been touched on the LCD touch screen. Then, it can be obtained the coordinate
which gives another datum to obtain
that represent the degrees of the condition that
is positioned which is going to be calculated as follow:
where
must be strictly differently than zero in the first part of (1) and for when
then
.
are represented like intervals,
is contained in (
),
is contained in
((
) degrees) and
is contained in
and for when
happens, the gripper is located from the negative
coordinate because the direction of α provokes a direction with a negative x value. this means, for example, that
is the lowest position in the axis
that the gripper can get and
is the highest position that the gripper can reach in the axis
. These boundaries are given by the robotic arm dimensions, for example, suppose that each link measure 1 unit and we have three links, then the maximum height that is possible to make is 3 units seen from the base of the robotic arm to the gripper and height that is possible to make is 0 units seen from the base.
Therefore, to represent a coordinate which was touched on the LCD touch screen, four conditions are presented which the values of
and
are greater or equal than to each other, it means, two cases where
or
occur. The four conditions are represented in four right triangles which represent the workspace of the LCD touch screen. The conditions and its equations are described in [
44]. These conditions are the baseline to calculate the inverse-kinematics.
4.3. Linear Transformation
Three different values have been defined, which are obtained from the LCD touch screen; then the robotic arm needs to get the point in the space that was touched in the LCD touch screen, so a linear transformation is required to know where the gripper is. It can be constructed a vector
which the linear transformation work with it, also
is defined such as depth-location of the gripper point,
is the height location of the gripper point and
is the direction where
and
are located such as it was defined in
Figure 1a. In summary, when a point in the LCD touch screen is touched, this point is seen from the top view and then, the linear transformation is used to see the same point but with side view. So, the linear transformation is defined first:
and
whatever real number to avoid collision between links for when
rotates counterclockwise such as is presented in
Figure 1a and
is defined in [
44]:
If
has to rotate clockwise, so the second linear transformation is used.
That means α needs to rotate inversely; therefore, the conditions are switched of its place, the first condition to the fourth condition and the second condition to the third condition, such as it is shown in
Figure 1b and
is the direction of
where the coordinate is located in the condition to arrive.
For example, an initial coordinate
is given which is located in the fourth condition from
Figure 1a and
then
and
is selected, then
which is obtained that
that means
and the third condition is the final position that is wanted to get to, then observing it in the second condition from
Figure 1b, then
and
, note that
and
, then, applying (3).
Therefore
where
and
was got, then
that is
with
and since
and
that means
seen from
Figure 1b, multiplying by
then
and adding
it is had
, that means
. Therefore effectively
is located in the third condition from
Figure 1a or in the second condition from
Figure 1b and
rotates
clockwise to get to third condition from
Figure 1a.
Another example, an initial coordinate
is given which is in the third condition seen from
Figure 1a and the second condition is the final position that is wanted to get to, then it is had
and
then
where
is obtained and
. Calculating the new point
which is in the second condition from
Figure 1a and calculating with the linear transformation (3) it is had a
and
is needed due to
and
are located in the third condition seen from
Figure 1b.
Then:
where
is obtained and
is defined with
, that means
, then
multiplying by -1 and adding 180, it is got
, then
with
, therefore
is located in the third condition seen from
Figure 1b or
second condition that is seen from
Figure 1a, then,
(first-joint degree) has to rotate
clockwise starting to
and getting
which is in the second condition from
Figure 1a. In a similar way, the other remaining cases can be proven and for when the first joint rotates counterclockwise, the (2) linear transformation is used and
in the first condition,
in the second condition,
in the third condition, and
in the fourth condition and
is defined in [
44] for each condition.
In this way, the degree’s condition can be found with the second linear transformation, and it can find the degrees that the first-joint has been moved with the coordinate that has been touched. Having said that, it is used the geometry method from [
45] to calculate the inverse-kinematics. The equations were represented in the most convenient way to obtain results. Then, the equations are presented below:
And:
where
and
are the final position of the second-joint and third-joint and
and
are the length of the second link and third link. This inverse kinematic is for a 2 DOF robotic arm, we can use these formulas to get the position (
) with a direction of
which represents the degrees that the first-joint has to rotate. This algorithm can be implemented to a robotic arm with more degrees of freedom as long as exist a geometric method to calculate the degree of the second-joint to the n-joint. For example, supposing that a 6DOF manipulator is used, the formulas could be used to calculate the inverse kinematic of 5DOF manipulator presented in [
46].
4.4. Distribution and Trajectory Function
The next distribution function has been proposed because is too easy to calculate the trajectory for whatever point; moreover, it is exact, due to the degree or radians are ordained in the whole interval
which is the number
the final position, so, if the final position is 180 degree, that means
, or if the final position is
that means
. In this way, the radians or degrees between 0 and
radians (180 degrees) are represented in the interval
with the number
with whatever time of interest (
). The distribution function with parameters
and
is represented below.
where
is a natural number greater than 1,
, it can help to reduce the value of the parameter
, and different velocities, accelerations, and different shapes of the trajectory can be obtained.
Moreover, the function
is a distribution function because it fulfils the characteristics of a distribution function that has been proved in [
47]. Once the distribution function-(
) has been presented, it is proposed how the trajectory function-(
) using the Equation (8) must work in order to compute a safe and fast point-to-point trajectory.
The distribution function has to get to the final position
in the start position which is
where it belongs to
. As it was mentioned before, reducing the compile time is wanted; the computation of the function is necessary to reduce. Also, it is wanted to have an exact trajectory, which means, with high accuracy in the results. Thereby, one parameter is assigned to each join space trajectory; for these reasons, the next characteristic is introduced. Exist a number
for whatever
and
such that
and
, and for when
gets to
, then the equalization is fulfilled:
then:
Then
, and for when
is approaching to
(
), occurs:
For when
, then:
In this way, the trajectory is made from an initial position greater than the final position, which means .
Using the Equation (8) and adding
, the trajectory function-(
) is defined and used for calculating the linear and curved motion trajectory in order to obtain the final position from the LCD touch screen. The trajectory function-(
) is presented below:
where
is a real number such that
. When
is so close to 1, large values of
are presented and that could provoke great magnitudes of velocity, acceleration and Jerk. Then,
is used to take advantages of non-large values of
and allows us to show other advantages for when
. Then
is used to get the results using the algorithm proposed and show some examples to obtain different shape of trajectories, implementing the function (13) and calculating the parameter
with (11) and (12).
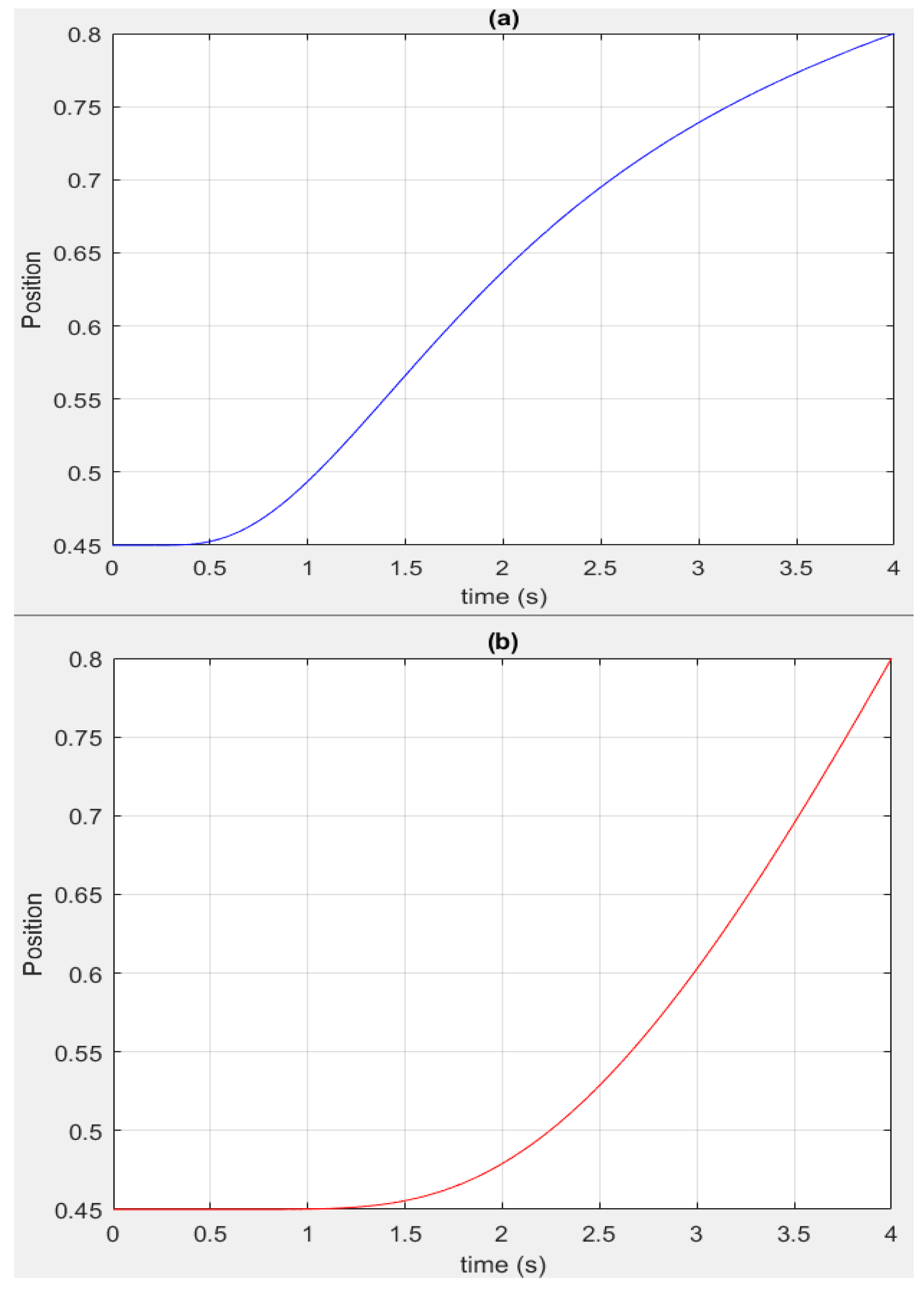
Example 1: It is used Equation (11) to compute
using
and
with
and
, two different trajectories are generated with the same end-point
calculated by (13:
) such as it is shown in
Figure 2.
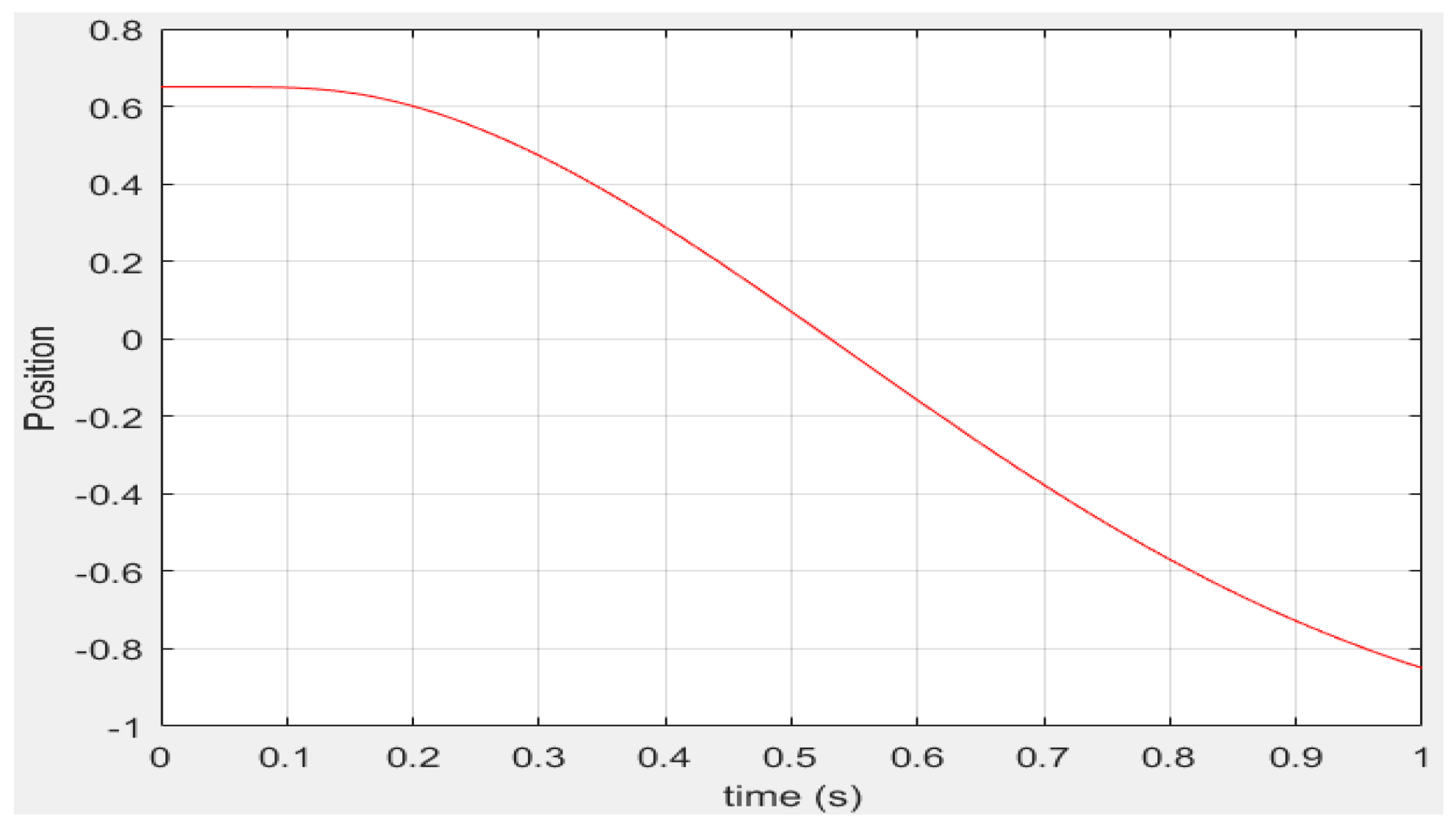
Example 2: When the 2nd condition is used, then, ζ is calculated by using the Equation (12). Then, a decreasing trajectory is presented. In this example the final position is
and the trajectory starts in 0.65, this means
.
Figure 3 represents the trajectory with a total time equal to 1 and using a parameter
and ζ = 0.53915881.
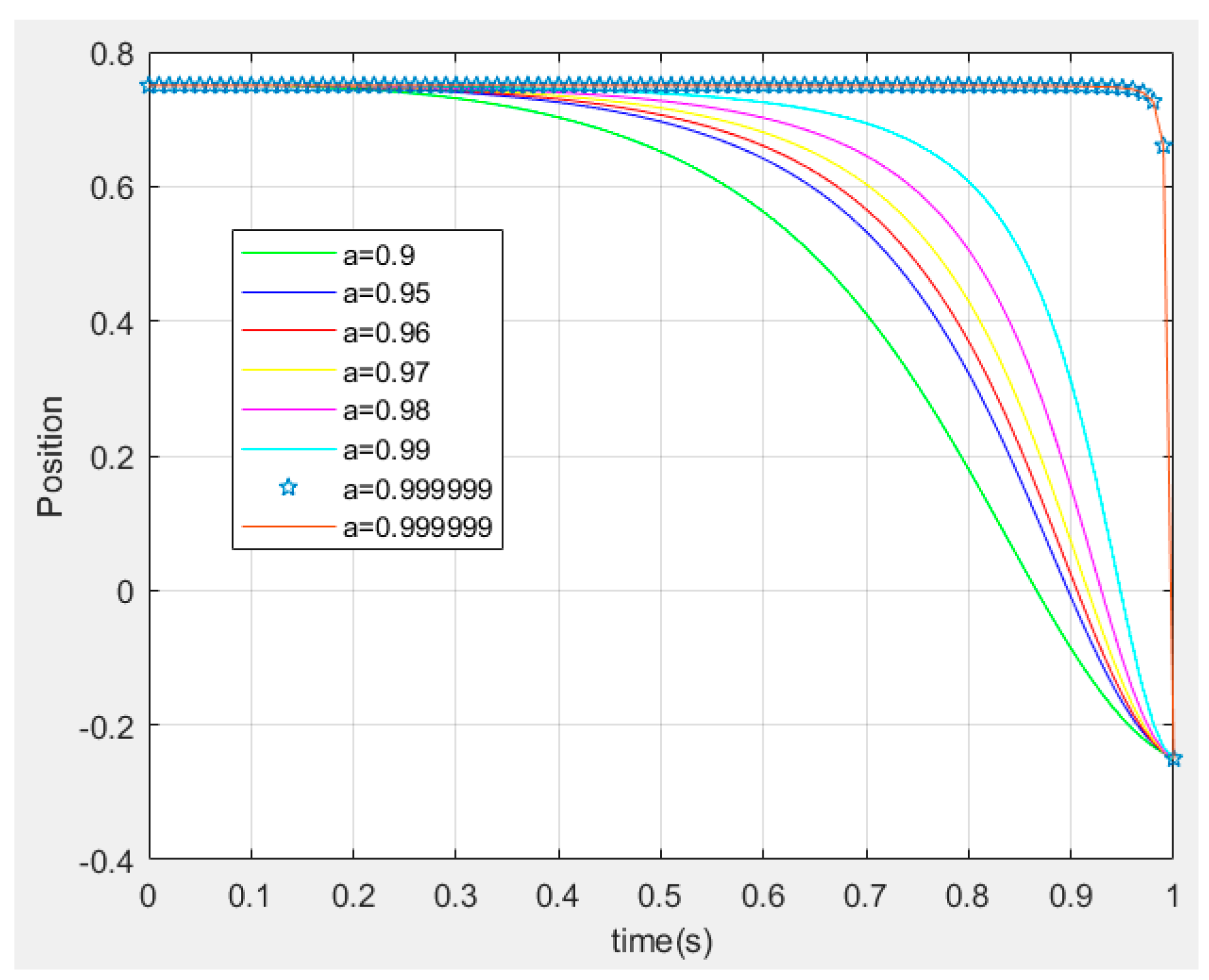
Example 3: Different shapes of trajectory have been presented at this moment, but this characteristic can increase if the parameter
is changed (see
Figure 4). Moreover, the velocity, acceleration, and Jerk can increase and decrease in order to obtain linear or curved trajectories as well as diversity to generate trajectories.
This property is only presented when the total time of the trajectory is equal to 1 because
is not enough small for when
is
(the reader can draw the function
and
to get a better idea). However, a curved motion can be obtained even when the total time is greater than 1, for example in
Figure 5, different curved motions are shown.
4.5. Calculation of Velocity and Acceleration
Finally, in order to generate a safe and fast trajectory, the velocity and acceleration calculation must be obtained. Getting the position from it can be obtained and to obtain the velocity and acceleration respectively.
The velocity is represented below:
Note that
is effectively a density function, according to [
40]; therefore,
is always positive
, only in cases that the distribution function is used as a trajectory function and
takes negative values (for example
or
), the density function that is to say the velocity function can be positive and pass to a negative values.
Then, according to [
48], the acceleration is represented below:
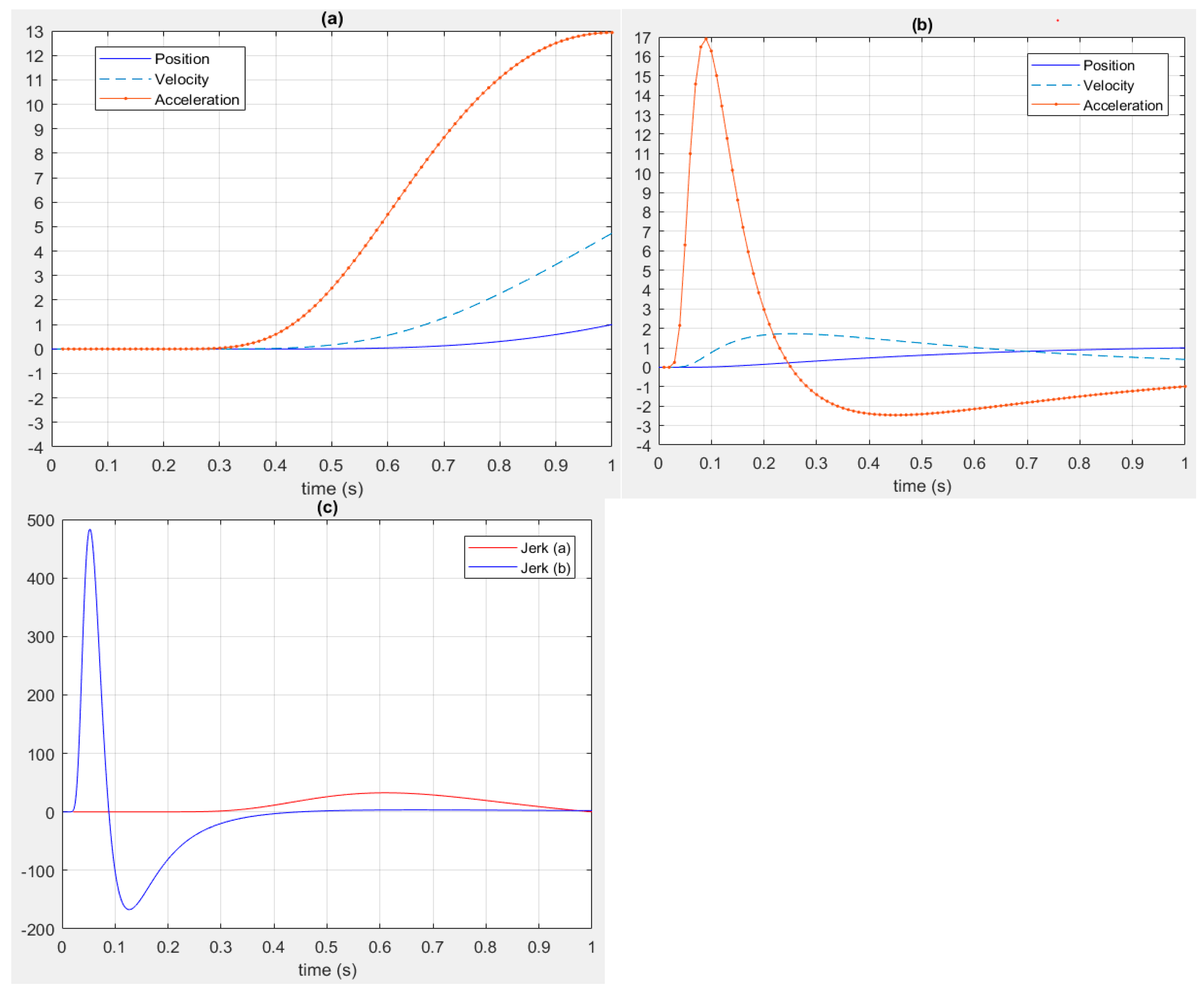
Then, the position, velocity, acceleration and Jerk (the derivative of the acceleration) is obtained and shown in
Figure 6 for when
with different value of
.
Changing the value of , a smooth trajectory can be obtained. Note that the velocity, acceleration and Jerk start at 0 and also these functions are finites, moreover, the Jerk is continuous and can approximate to 0 for using different values of . This is an advantage characteristic when the function is used because it generates smooth trajectories, and we can take care of the robotic arm quality.
To obtain the trajectories in Matlab, the function (13) is multiplied by , therefore the units are and for the velocity and acceleration respectively. The position is obtained in radians using the Equations (6) and (7) to obtain the inverse kinematic and the gripper position.
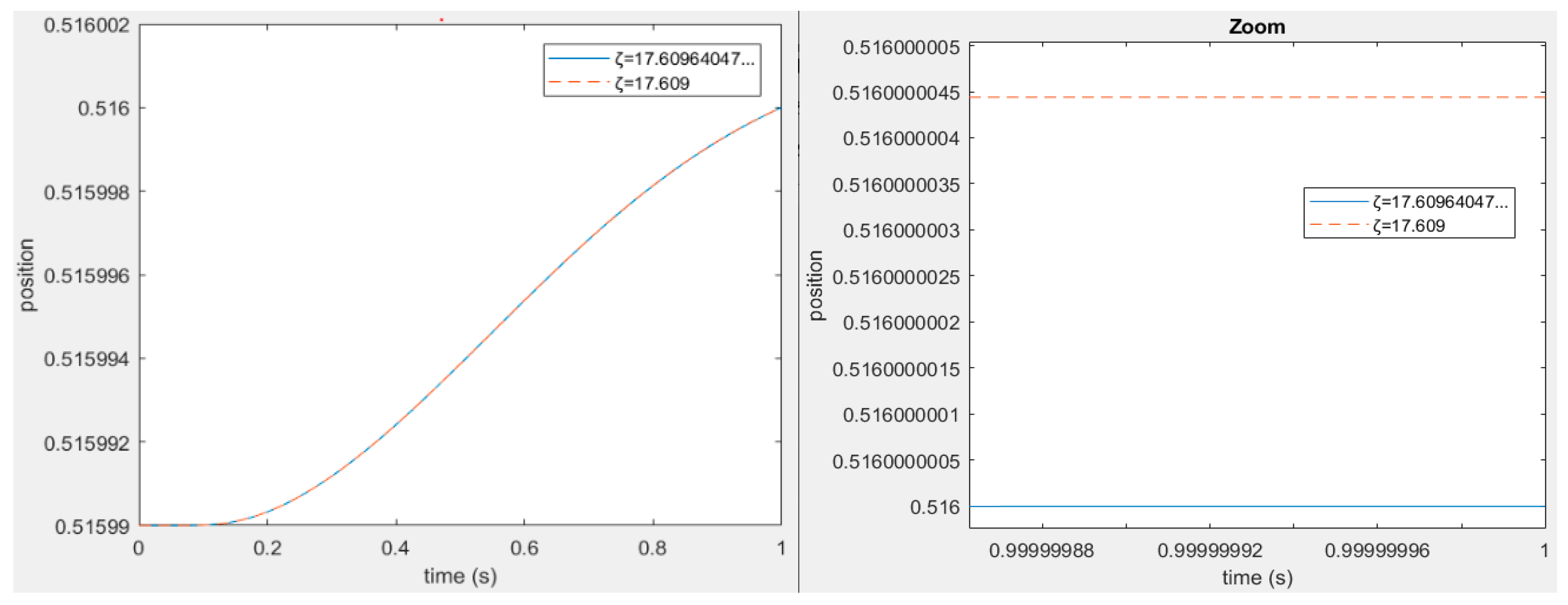
It is necessary to emphasize that the final result using the function (13) and a parameter ζ with three decimals are not affected in precision (see
Figure 7). Also, to generate the desired point-to-point trajectory just require one computation with high exactitude. To show this, a short trajectory is generated using ζ = 17.609 and the resulting trajectory is compared with the resulting trajectory with ζ calculated by using the function (13), which value is 17.6096404.
5. Simulation and Results
First, the LCD touch screen is used in Arduino Mega and it is connected to MATLAB, where the data is read, then, the simulation and the results obtained are found in the guide of MATLAB. The guide shows the results of position, velocity, and acceleration which are in the next tables, with velocity and acceleration graphs. With the coordinates
, the degrees of the second and third articulation are calculated with the function (9) and (10), and the degrees of the first articulation is calculated depending on the four conditions where the coordinate
are located. Secondly, the degrees are switched (
) in the closed interval
or
, and finally, the trajectory is calculated, with the current position encrypted and calculating the parameter
. In
Figure 8, the whole process and position-zero are represented.
This process is repeated the times as much as the trajectory is calculated with the LCD touch screen and the initial position is
in each joint (that means
and
are equal to zero, which are presented in
Figure 8). In
Table 1,
is between
degrees and
, with the different coordinates
represented as a division of
over
, and the value of each
, velocity and acceleration of the joint-2, joint-3 and joint-
(or joint-1). In
Figure 9 the position, velocity, and acceleration vectors are shown for the first condition, the trajectory animation is shown using the example of the last result from the
Table 1 with
and
and the gripper is in the end-point (1,1,45) according to the linear transformation in the Equation (2).
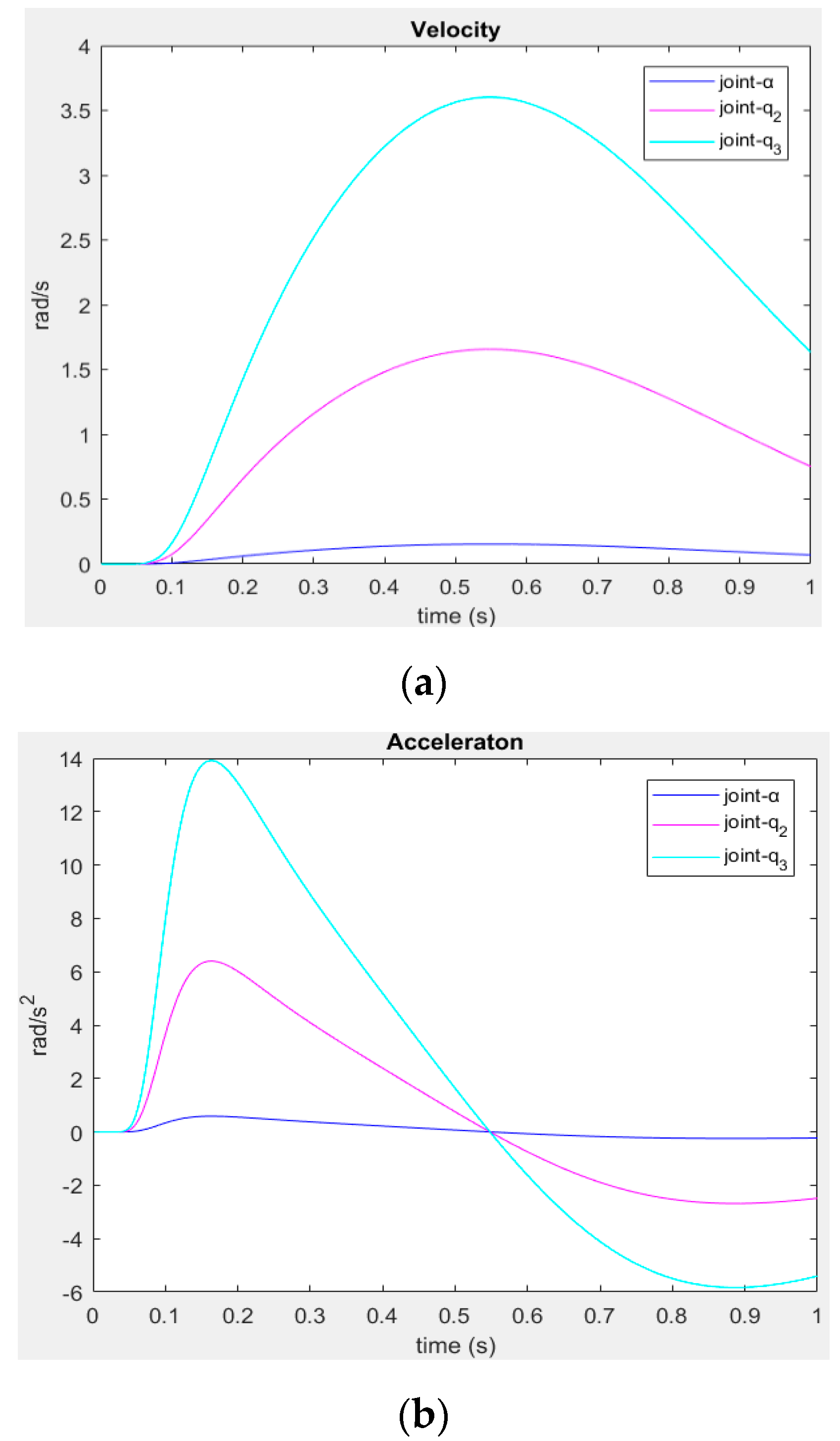
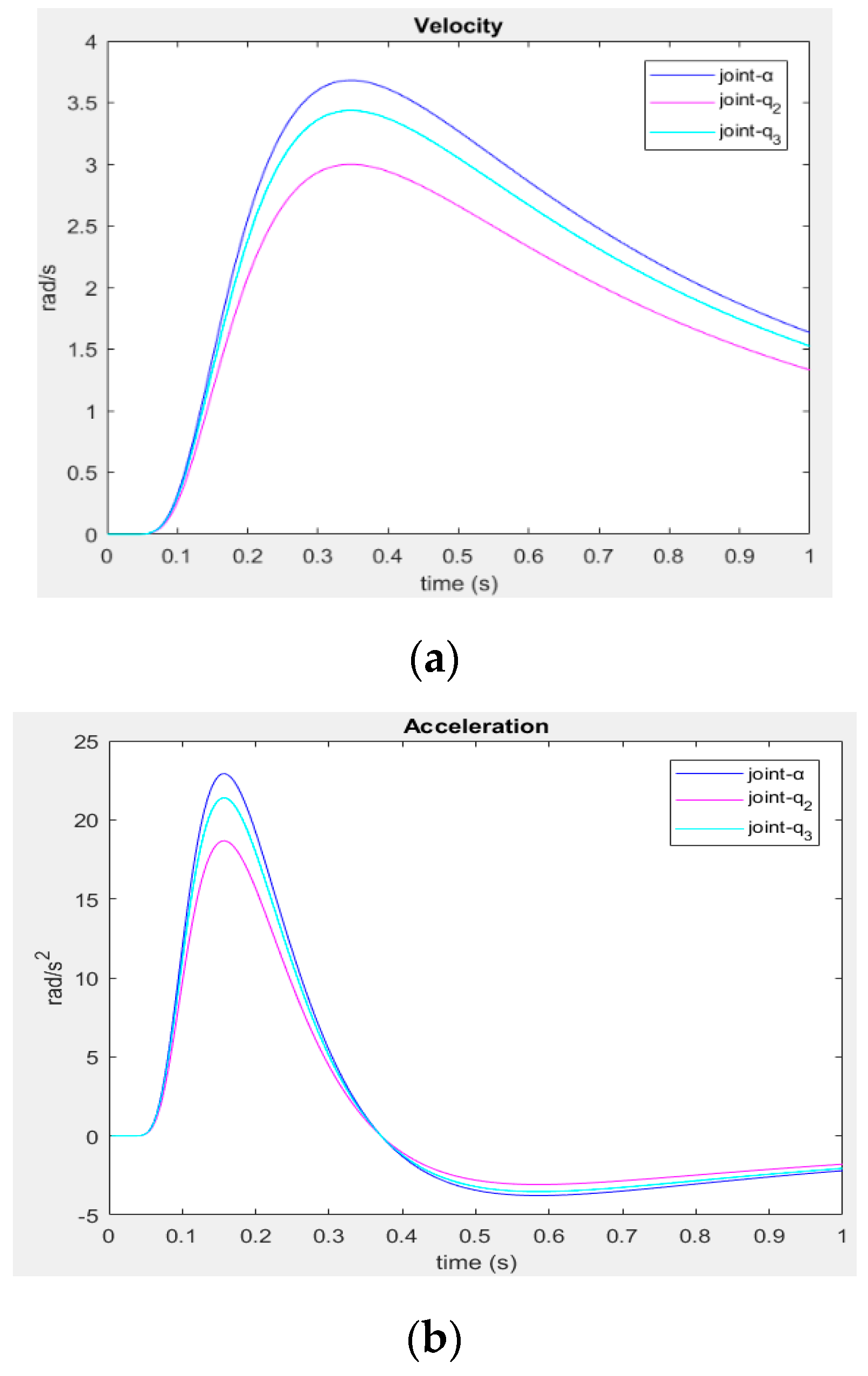
In
Figure 10 the velocity functions have the maximum value in the same point of the domain of
, which means, a linear-motion is obtained. In
Table 2 the results of the second condition are shown, taking deferent values greater than zero of
and
to generate a curved-motion and starting in
for when
.
The maximums of each acceleration are located almost in the same location at the domain of
, then, and a curve-motion is presented due to the maximum values of the acceleration are not close and the acceleration functions are different distributed through the time (see
Figure 11).
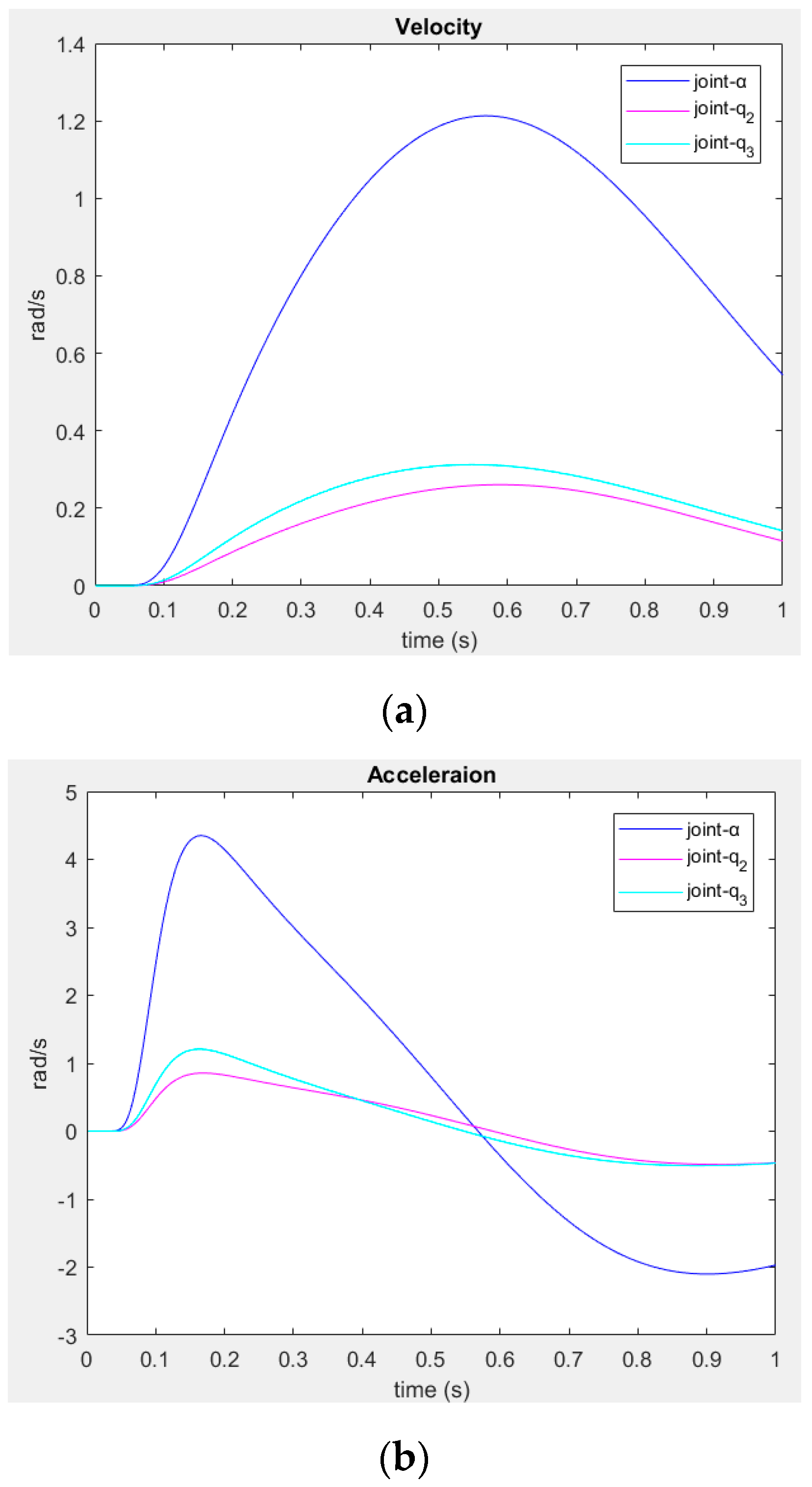
Table 3 shows the results of the trajectory in the third condition, using
.
According to
Table 3, most of the time, a linear motion is presented, and also, the trajectory is smooth and equilibrated (see
Figure 12).
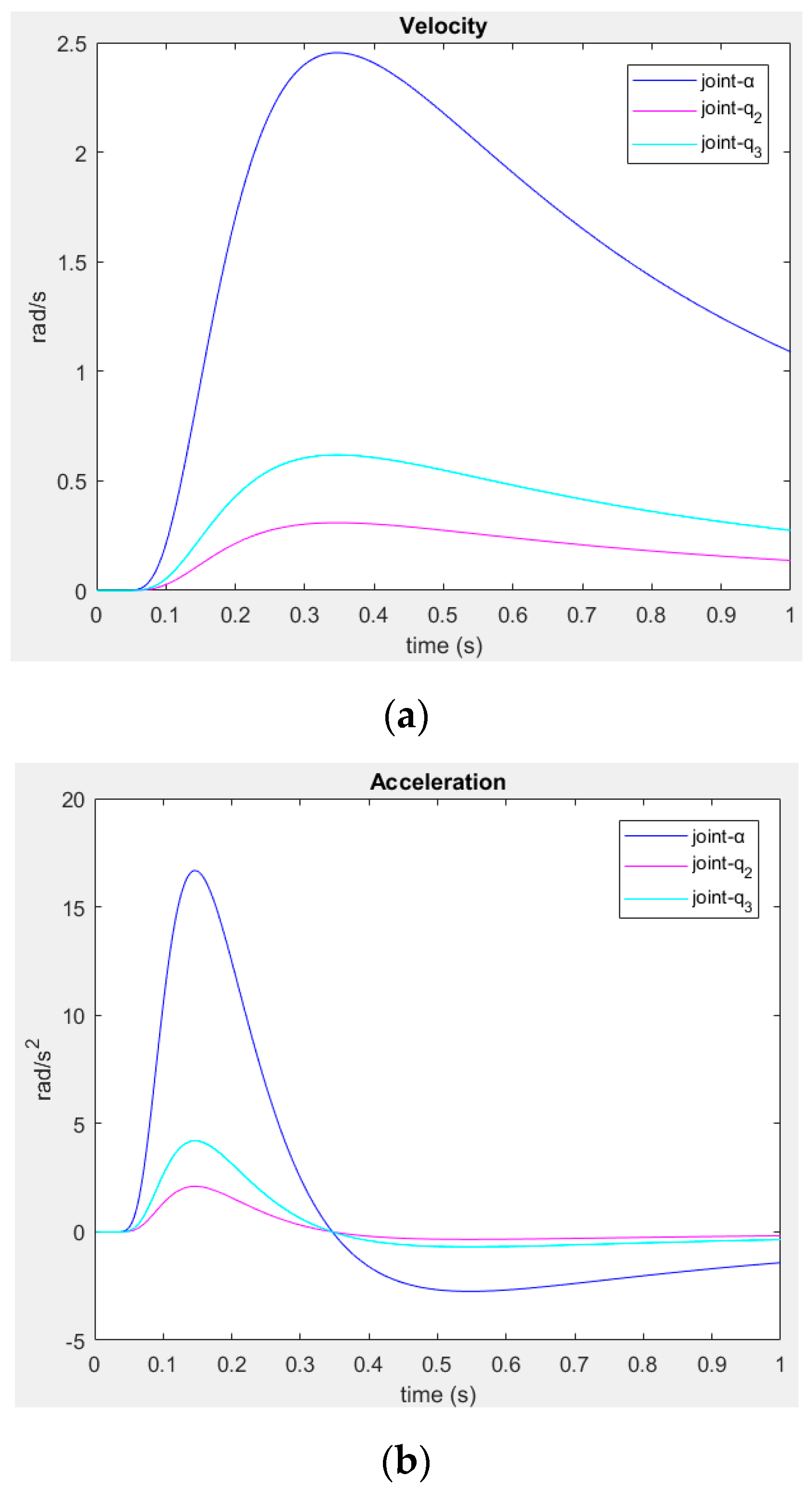
In
Table 4, the fourth condition is showed; it is had a
to observe the velocity and acceleration behavior, the numbers
and
have been changed through the fourth condition.
As can be noted in
Figure 10,
Figure 11,
Figure 12 and
Figure 13, different motions are presented because the parameter
has been changed through the four conditions. The maximums of the acceleration function are almost located closet of each other in the domain of
such as it was presented in
Table 4. Most of the time, a smooth trajectory is obtained (this depends on the values
and
chosen) because the velocity is suitably distributed through the time and, therefore, the acceleration too (see
Figure 13). Therefore, the velocity has to be conveniently distributed through the time to have a smoother trajectory using the parameter
and
.
6. Discussion
The trajectory obtained in the four conditions is exact and comfortable to obtain a safe and fast trajectory. It is not necessary to calculate and make restrictions such as polynomials trajectory, and it is not presented oscillations and inexactitudes in the end-point. Moreover, the general problem of all methods to calculate the trajectory is the presentation of oscillations and using the distribution function presented; the oscillation is eliminated in any case. Also, with this algorithm, it has been decreased the process of calculation and hence the compile time reduced.
The velocity and acceleration calculated using this distribution function can be modified according to the desired kind of movement, so, it can be had many options according to obtain the best safe and fast trajectory, unlike other methods. That is, the trajectory has only one option to generate the velocity and acceleration for a specific start-point and end-point, and most of the time, oscillations occur in large jerks, and the accuracy of the results decreases in smaller trajectories.
It is important to highlight that the algorithms mentioned in the related works, in addition to using the algorithm to calculate the trajectory, usually use other techniques such as an additional feedback control algorithm or employ a time-based profile generator to calculates key times, and in this way, to obtain the optimal time calculations and reduce unnatural behavior, with this proposed algorithm no further calculations are necessary, this distribution function only performs a calculation and as a result a faster and safer process is obtained to calculate the trajectory as well as showed in the results, the trajectory is always accurate with a determinate shape of the trajectory according to the parameter (a).
In
Table 5, it is presented different end-position of each condition and it has been compared the values of the end-position using the distribution function proposed and cubic polynomial with a trajectory of 1 s. It can be observed that the results of the cubic polynomials are inaccurate while the distribution function is accurate.
Figure 14 shows these simulated results in MATLAB with an anthropomorphic robotic arm. It can be clearly seen that the trajectory of the joint -α rotates starting in position zero
and gets to the end-position equal to 1, that means, 180 degrees or
radians. It is used the distribution function presented with a total time of 1 s, as it can be noted, the result of the end-position is 3.14159...radians, that means 180 degrees, unlike cubic polynomial, the result of the end-position is 3.0533 radians which is 174.941204 degrees. Therefore, the distribution function proposed is more accurate than cubic polynomials and present a smooth trajectory, according to the velocities and acceleration obtained.
Note that the gripper is situated in the coordinate
and the input coordinate is
and y = 1, that means
(obtained from the LCD Touch screen) with α=180 then
seen from condition 4
Figure 1a or
(input) seen from condition
Figure 1b. Then, α determinates the sense of
touched in the LCD Touch screen, no matter which is the sense of the input value of X.
7. Conclusions
A novel algorithm for the trajectory calculation of a robotic arm using an LCD touch screen with the distribution function has been proposed. This proposal is easy to carry out to get a safe and fast trajectory results. Moreover, the distribution function is exact when the calculation of
is correct, and just one computation has to be it to obtain the trajectory (see
Table 5). The way to calculate
has a simple formula to get the trajectory in an easy way to interpret. The function starts in
and gets to
when the time is complete
, similar to the n-order polynomial, but, in a different way to the trajectory method mentioned and whatever another technique. The distribution function calculates the trajectory with one computation which implies a faster process to calculate the trajectory in whatever time of interest. Also, the velocity and the acceleration functions do not implement always the same values, because these can be modified to obtain a smoother trajectory just changing the parameter
or
and it can be obtained a curved or linear motion. The polynomial trajectory increments its coefficients to obtain a smoother trajectory, and the function proposed has the advantage to get the flattest trajectory changing the parameter
and different motions such as linear or curve motion.
In future works, the value of
can be optimized because it can help to make different economics controls and electronics designs such as the control touch presented in this paper, but now, in a more direct way such as the PID controller. Another future work can be developed for adding more joints to the robotic arm using this method and getting an inverse-kinematics in function to the axis X and Y. Also, another interesting future work is using the method proposed in the work of Mercorelli [
14] to estimate the velocity and acceleration in the presence of noise and combine the properties and advantages of using the trajectory function-(
) presented in this work. Finally, the parameter
could be defined as a variable to obtain many via points with great accuracy and convenient velocity/acceleration functions, but this is another proposed for future work.