Abstract
The development of convolutional neural networks for deep learning has significantly contributed to image classification and segmentation areas. For high performance in supervised image segmentation, we need many ground-truth data. However, high costs are required to make these data, so unsupervised manners are actively being studied. The Mumford–Shah and Chan–Vese models are well-known unsupervised image segmentation models. However, the Mumford–Shah model and the Chan–Vese model cannot separate the foreground and background of the image because they are based on pixel intensities. In this paper, we propose a weakly supervised model for image segmentation based on the segmentation models (Mumford–Shah model and Chan–Vese model) and classification. The segmentation model (i.e., Mumford–Shah model or Chan–Vese model) is to find a base image mask for classification, and the classification network uses the mask from the segmentation models. With the classifcation network, the output mask of the segmentation model changes in the direction of increasing the performance of the classification network. In addition, the mask can distinguish the foreground and background of images naturally. Our experiment shows that our segmentation model, integrated with a classifier, can segment the input image to the foreground and the background only with the image’s class label, which is the image-level label.
1. Introduction
Presently, automatic image segmentation tasks are required to obtain accurate information about each region of an image because the number of images continues to surge. With the development of convolutional neural network (CNN) [1] in deep learning, there are many works for image segmentation. However, to achieve high performance of segmentation result in an supervised manner [2], the convolutional neural network (CNN) requires many ground truth data that show the area of the objects at the pixel level. Creating each of these data is cumbersome and requires much time and other resources. Some works solve image segmentation problems in unsupervised manners [3]. Mumford–Shah functional [4] and Chan–Vese algorithm [5,6,7] are well-known models for classical unsupervised image segmentation problems.
However, since the Mumford–Shah functional and Chan–Vese algorithm rely on pixel intensities and the objective functions are non-convex, these models cannot distinguish between the foreground and background of images, and the foreground and background results are changed depending on the initialized value of the networks’ weights. To solve this problem, we propose a segmentation model that is integrated with a classifier for image segmentation. In our work, the segmentation model, which solves the Chan–Vese algorithm or Mumford–Shah functional, is used for the region proposals. Since these two algorithms minimize their objective functions with a curve in a level-set method [8], which evolves the initial surface defined as a function by minimizing the energy function, these algorithms can detect the edges of the images. With this segmentation model, we can get more precise boundaries. However, as we mentioned above, the results of the Chan–Vese algorithm and Mumford–Shah functional cannot distinguish the foreground and the background of the image alone. Therefore, the regions divided by these segmentation model alone have no meaning. To solve this problem, we integrate the segmentation model with the classifier. With the classifier, the detected meaningless regions by the output mask of the segmentation model become foreground regions. Furthermore, we propose a simple loss that can distinguish the background more precisely. With this simple loss, we can obtain more meaningful foreground regions. One thing to note is that with our classification loss, the classifier can extract the foreground regions alone. However, the regions’ boundaries are not precise. Therefore, the segmentation model and the classifier work to complement each other.
For our experiment, we used the dog-and-cat dataset from kaggle [9] and PASCAL VOC 2012 [10] as a dataset. To this end, the contributions of this work are as follows:
- We integrate the segmentation model with a classifier to solve the image segmentation problem.
- We use the Mumford–Shah functional and the Chan–Vese algorithm for the segmentation model. Furthermore, with the segmentation model, we can achieve more accurate boundaries.
- For the classifier, we propose a loss function that can meaningfully distinguish between the background and the foreground.
2. Related Works
2.1. Image Segmentation
Image segmentation refers to labeling each pixel of an image to a particular class, and it aims to separate a given image into several meaningful regions for more manageable analyses. It has been approached in classical manners such as those of Osher et al. [8] and Lloyd et al. [11]. However, with the development of convolutional neural networks (CNNs) [1] in deep learning, many studies solve the image segmentation problem through CNN. In this paper, we detect the foreground and the background of the input images by generating the binarized segmentation masks.
2.1.1. Classical Image Segmentation
The classical image segmentation methods are mostly based on mathematical or statistical methods. Tobias et al. [12] and Arifin et al. [13] use the characteristic histogram, Ma et al. [14] approach the segmentation problem with edge and boundary detection. Furthermore, classical variational methods solve the problem with clustering. These classical variational methods minimize their objective functions such the as Mumford–Shah functional [4].
2.1.2. Supervised Image Segmentation
To achieve high image segmentation performance in a supervised manner [2] with CNN-based models, UNet [15] uses skip connections between contracting and expansive parts. Furthermore, FCN [16] changes the fully connected layer to fully convoluntional network to preserve the location information. However, even though these methods have led to high performance, supervised learning has a considerable limitation: it must have ground truth for all training data.
2.1.3. Unsupervised Image Segmentation
To overcome the limitations of the supervised methods, some works solve the image segmentation problem with unsupervised methods [3] with CNN. These unsupervised learning methods segment images without any ground truth data. Usually, these unsupervised manners use the objective functions of the classical variational approach [4,5,6,7]. Similar to our work, Kim et al. [17] also minimizes the pixel-wise constant Mumford–Shah functional. However, the main difference is [17] uses pixel-level labels, but we use image-level labels for image segmentation for a weakly supervised method.
2.1.4. Weakly Supervised Image Segmentation
Although deep learning methods based on CNN can optimize the objective functions of the classical variational method, the results are not accurate because most of the objective functions are non-convex functions. Thus, many weakly supervised methods solve the image segmentation problem with much more simple objective functions and use given ground-truth class labels for segmentation. Zhou et al. [18] use global average pooling layers instead of fully connected layers with a classifier to visualize the most prominent part of the input image. Selvaraju et al. [19] uses the gradient to overcome the limitation of [18], such that [18] cannot be applied to the models without global average pooling layers. Lee et al. [20] extract the class activation map from a randomly selected feature map of classifier for their seed loss and combine it with the boundary loss, which consists of a conditional random field. More simply, Huang et al. [21] use only one class activation map for their seed loss. Wang et al. [22] construct a pixel correlation module to solve the problem that the class activation map is not consistent when the input resolutions change. References [20,21,22] use the class activation map of [18] for segmentation, but our work does not use class activation map. Instead, we directly extract the foreground regions by generating a binary mask from the input image, not from the feature maps of the classifier, which can enhance the classification confidence of the classifier. Similarly, Zolna et al. [23] generates a binary mask for input image, using classifiers to find all parts of the image that any classifier could use. Furthermore, Araslanov et al. [24] uses the classification loss to generate a mask and uses a local mask refinement module called PAMR to refine the mask. Unlike the method of elaborating the boundaries of segmentation areas detected by these works, we used the Chan–Vese model or the Mumford–Shah model.
2.2. Mumford–Shah Functional and Chan–Vese Algorithm
The Mumford–Shah functional [4] and Chan–Vese algorithm [5,6,7] are well-known approaches that solve the image segmentation problem in the classical method. These methods find optimal segmentation results, which minimize specific energy functions.
2.2.1. Chan–Vese Algorithm
The edge gradient-based energy function that [25,26,27] proposed cannot segment the images well when the edges are too smooth or the noises are too big. The Chan–Vese model [5] defines a region-based energy function based on Mumford–Shah functional [4]. The original Mumford–Shah functional is (1).
The energy function that Chan–Vese model [5] proposes is (2)
where C is the curve at the Level-Set Method [8], and are fixed parameters. is the length of the curve C. is the area of the region inside C that is added to the original Mumford–Shah [4]. The equation of the original Mumford–Shah functional for segmentation is (1). and are constants depending on C, since is the average value inside C and is the average value outside C. Furthermore, is a given input image. In this energy function, the first term controls the length of C. The second term controls the area of C to control its size. The third and fourth terms are used to control the difference between the piece-wise constant model’s result and the input image . To solve (2) with level-set method [8], Reference [5] uses Heavyside function H, and the one-dimensional Dirac measure . These are defined in (3).
With this H and , the energy function (2) can be re-formulated to (4).
where is a bounded open subset of and is a zero level set of a Lipschitz function that represent the curve C. Furthermore, and are calculated with (5).
2.2.2. Mumford–Shah Functional
2.3. Region of Interest Detection
Detecting the regions of the input image that stimulate the deep learning network is called Region of Interest detection. Li et al. [28] makes the soft masks for input images with classification loss. Fong et al. [29] makes spatial perturbation masks that maximally affect a model’s output. More simply, Singh et al. [30] use randomly generated hidden image patches for each image at every iteration. Fong et al. [31] optimize the objective function with binarized masks that resize the area of input images. Furthermore, Jaderberg et al. [32] transform the input image with affine transformation matrix via classification loss.
3. Method
In this section, we describe two network structures and two corresponding loss functions for each network that segments the input image to the foreground and the background. Each network consists of a segmentation stage and a classification stage that classifies the segmentation results of the segmentation stage. As we mentioned, segmented results by the Mumford–Shah model and Chan–Vese model can detect the edges of the objects very precisely, but the results do not mean the foreground and the background. Since these two models segment the input images with pixel-intensity, the segmented regions consist of pixels with similar intensity. In our work, we use a classifier like [33,34,35,36], to make each segmented region, which is the result of the segmentation stage, meaning the foreground or the background. As shown in [18,19], some areas of the image, not the entire area, have a significant impact on the classifier. Therefore, when we train the classifier with multiplication of the outputs of the segmentation stage and the input image, the meaningless regions become the foreground and the background. Notice that the outputs of the segmentation stage are binarized with 0 and 1 to detect the foreground area of the input image. When we set the mask as and the input image as I, means the foreground and .⊙ means the element-wise multiplication. However, we use as the foreground regions and as the background regions, because it shows better results experimentally. In our experiment, the classifier is trained to classify the as the foreground (i.e., image-level label) and as the background. For the foreground, we use the cross-entropy loss between the ground-truth image class label and the output of the classifier. Furthermore, for the background, we construct a loss. We explain this background loss in (13).
3.1. Network Structure
For our experiment, we exploit the network structure of [23]. We do not need to make additional encoders with this structure because all the decoders directly use classifiers’ feature maps. Furthermore, for the classifier, we use ResNet-18 [37] structure. We experiment with two network structures. The first network, Figure 1, is composed of the Chan–Vese energy function, and the second network, shown in Figure 2, is composed of piecewise-smooth Mumford–Shah energy function. In Figure 1 and Figure 2, , , and are the classification score of the original input image, foreground image, and background image, respectively. Notice that because we use a same classifier for the original image, foreground image, and background image like Siamese networks [38], which share the weights, the classifier’s weights are updated by the , , and . We indicate the classifier as in each of Figure 1 and Figure 2. is the generated binary mask and is the reversed generated mask. Furthermore, in Figure 2, F is the foreground matrix and B is the background matrix for the calculation of the piecewise smooth Mumford–Shah functional loss (10).
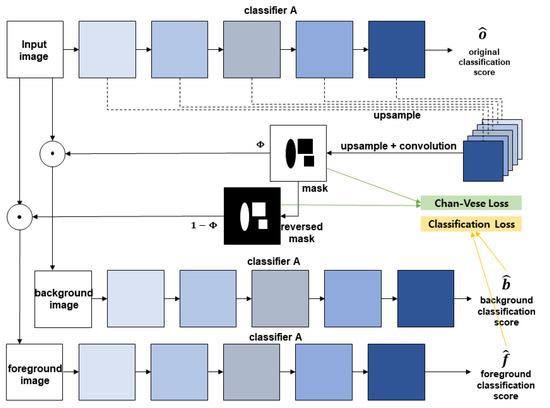
Figure 1.
Illustration of the first network when the loss is composed of Chan–Vese energy function.
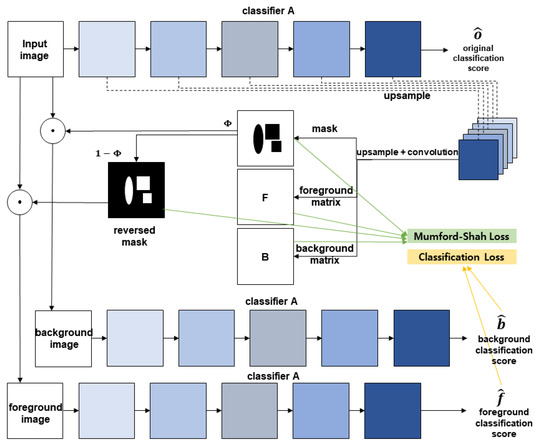
Figure 2.
Illustration of the second network when the loss is composed of piecewise-smooth Mumford–Shah energy function.
3.1.1. Network with Chan–Vese Energy Function
The mask is a one-channel image and has the same height and width as the input image. Furthermore, since we use the sigmoid function instead of the HeavySide function (3), the mask has only 0.1 values when the regularization term is used together. The upsampled feature maps from the used for the original input image are concatenated and pass convolutional layers. The output of the last convolutioinal layers is a mask that shows the background of the image. To get the foreground of the image, we reverse the mask by subtracting the mask from 1. The foreground image and background image pass the classifier, which we use for the original image. The classifies the original images, the foreground, and the background of the input image. and are used for Chan–Vese loss (7) and (8). and are used for classification loss (14).
3.1.2. Network with Piecewise-Smooth Mumford–Shah Energy Function
As in Figure 1, we use ResNet-18 for the , and the mask is a one-channel image and has same the height and length as the input image. The only difference is that there are three decoders. The first one is for a mask , the second one is for a foreground matrix F, and the last one is for a background matrix B. The foreground matrix F and the background matrix B are three-channel images and have the same height and length as the input image. , , F, and B are used for Mumford–Shah loss (10). and are used for classification loss (14).
3.2. Loss Function
Our total loss (6) can be divided into two parts. The first part is a segmentation loss for the segmentation stage, and the second part is a classification loss for the classification stage.
uses either the energy function of the Chan–Vese algorithm (4) or the energy function of the Mumford–Shah, neither of which calculates the mean values of the each region, for our deep learning network, reflecting some modification. is composed of classification loss about the foreground region and the background region.
3.2.1.
- Chan–Vese Energy Function for Segmentation: To apply the Chan–Vese algorithm to our network, we modify (4) to (7). Where I is the input image, is the mask, and is the derivative of the mask with forward difference.Furthermore, and the are calculated with (8). The is the mean value of the first region, and the is the mean value of the second region.In (7), the first term and the second term divide the input image into two regions with similar pixel intensity. With the , which only has values 0 and 1, and the constant mean value , the first term only considers the first regions regardless of the second regions, and the first regions are grouped into the pixels of similar value. Similarly, with the and the constant mean value , the second term only considers the second regions regardless of the other regions and the pixel values in the second regions have similar values. The third term controls the regions’ size of the mask, and the fourth term controls the noise of the mask. We call each loss term foreground fidelity, background fidelity, mask region regularization, and mask smooth regularization. For a given mini-batch of training set {(, )(, )} when the is the ground-truth image level labels (i.e., images class labels) of mini-batch of input images , we set (7) as (9). is the sum of the foreground fidelity term and the background fidelity term. is the regularization of , and M is the size of mini-batch.
- Piecewise-smooth Mumford–Shah Energy Function for Segmentation: As with the relationship between (4) and traditional piecewise-smooth Mumford–Shah Energy Function, the differences between each loss function of our two networks are that constant values and of (7) are changed to (i.e., foreground matrix) and (i.e., background matrix). The loss function is (10).The terms in are foreground fidelity, background fidelity, mask region regularization, mask smooth regularization, foreground smooth regularization, and background smooth regularization in order. With the and the foreground matrix , the first term only considers the remained regions by the regardless of the other regions, and the remained regions resemble the same regions of the input image. Same as the first term, the remaining regions of the input image by the second term depend on the . The foreground smooth regularization and the background smooth regularization work with the foreground fidelity and the background fidelity, respectively, to control the smooth of the foreground matrix and the background matrix. These terms work closely with mask smooth regularization and adjust the smooth of the mask. The effect of the mask region regularization and the mask smooth regularization are the same as (7). Furthermore, we set (10) as (11), where is the sum of the foreground fidelity term and the background fidelity term. Furthermore, is the summation of the regularizations of , F, and B.
Notice that the divided regions of these two models’ outputs are not the foreground and the background of the input images. The Chan–Vese algorithm and the Mumford–Shah functional cannot distinguish the foreground and the background, because these energy functions are based on pixel intensities, like K-means clustering [11]. Because these two models divide the images into two regions regardless of the meaning of each region, we use a classifier to make each region be the foreground and the background of the input images. We use this as a regional proposal to the next stage (i.e., classifier).
3.2.2.
Our classification loss (12) consists of the foreground classification loss and the background classification loss.
The is a classification loss for the foreground image (i.e., ), and the is a classification loss for the background image (i.e., ). Operator ⊙ means element-wise multiplication. , , and are the vectors and the size is . The values of the vectors are the probabilities corresponding to each class. For the foregrounds, we use cross-entropy loss. However, it is impossible to find common features of the backgrounds with a classifier because the components of the backgrounds are too diverse to assign them to the same label. Therefore, we formulate a loss (13) that can distinguish the background from the foreground.
To minimize this (13), all the values of , meaning probability values belonging to each class, must be 0.5. This means that the backgrounds do not belong to any given class. In (13), the constant inside the log is set to 4 to make the minimum zero. With the foreground loss and our background loss, we set (12) as (14).
With this (12), the proposed regions from gradually change into the regions that have the meaning of foreground.
3.3. Algorithm
We solve the two-stage segmentation problem with the Stochastic Gradient Descent (SGD) [39] method. For convenience, we rearrange the terms as follows; the classifier C, the decoder D, the mask , the foreground matrix F, and the background matrix B. The only difference between using (7) and using (10) for segmentation is the number of D.
3.3.1. Chan–Vese Algorithm
First, to extract the feature maps l, which are the input of the decoder D, we use the original input Image I. Using the original image for the classifier is more helpful for to detect the whole part of the foreground of I.
With the feature maps l from the classifier C and the original image I, the D generates the .
With the , we compute the and with (8) and get the probability of foreground and background . The probability refers to the degree to which foreground and background belong to a particular class.
The loss function for the Chan–Vese algorithm for the mini-batch i at step t is
The parameters of each network’s component are updated by gradient descent algorithm. Where is the parameters of the networks, is the learning rate at step t, and is the cross entropy loss, .
We show this process with Algorithm 1.
| Algorithm 1 Chan–Vese Segmentation Algorithm. |
|
3.3.2. Piecewise-Smooth Mumford–Shah Algorithm
The differences with the Chan–Vese algorithm are shown in (21).
Therefore, the loss function for the Mumford–Shah Algorithm about the mini-batch i at step t is
Furthermore, the parameters of the networks are updated:
This process is shown in Algorithm 2.
| Algorithm 2 Mumford–Shah Segmentation Algorithm. |
|
4. Experimental Results
4.1. Training and Testing Details
For training, we use ResNet-18 [37] as a classifier. Since we use the classifier’s feature maps for the decoder’s input, we do not construct a encoder. This is more efficient because we do not need additional parameters [23]. Furthermore, for the decoder that generates the masks, we upsample the each feature map of the classifier to and apply a convolution layer with the ReLU activation function to make each input’s channel be 64 since the last feature map of the classifier has 64 channels and the first feature map’s size is . Furthermore, after concatenating the all upsampled feature maps, we apply a convolution layer (kernel with a size of 3, stride 1, and padding 1), upsample to , and apply the sigmoid function to make the mask within 0 and 1. For the pre-processing, we resize the input images to the and normalize the input images value from 0 to 1 by , when I is the input image and is the value of pixel. Furthermore, for each dataset [9,10], we train and evaluate the network separately.
Furthermore, for the test to generate the masks, we use the same pre-processing for the input images. The network for the test is shown in Figure 3. The is our segmentation result for an input image, which segments the input image to the foreground and the background.
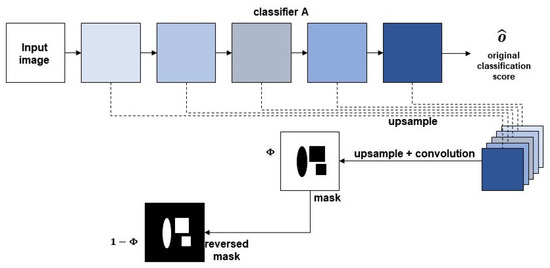
Figure 3.
Illustration of the network for the testing.
4.2. Qualitative Comparisons
With the [9] dataset, we conducted three additional experiments to show the effectiveness of each loss term (classification loss (12) and segmentation loss (7),(10)): Generate mask only with classification loss, Chan–Vese network without any classification loss, and Mumford_Shah network without any classification loss. The experiment “Generate mask only with classification loss” is conducted through the structure of Figure 1, except for the Chan–Vese loss. In this experiment, the entire loss consists only of classification loss (12), and the generated masks are learned only by classification loss, similarly to [23]. For the two experiments “Chan–Vese network without any classification loss” and “Mumford_Shah network without any classification loss”, we make an auto-encoder network. For the encoder, we use the Vgg-16 [40], and the decoder is constructed symmetrically with the encoder using the transposed convolution. There are no skip connections between the encoder and the decoder. In these two experiments, only the segmentation loss (Chan–Vese loss (7) and Mumford–Shah loss (10)) affects the masks.
Figure 4 shows the results of these three experiments and our main two experiments’ (Figure 1 and Figure 2) results. For the baseline, we use the results of CASM [23] that segments the image to the foreground and the background, because we use the same network structure as CASM. For each set of result images, the first row is the input image, the second row is the generated mask, the third row is the foreground image (i.e., ), and the last row is the background image (i.e., ). When we observe Figure 4b, it is remarkable that when we use our classification loss (12) and a regularization term for segmentation (i.e., using Figure 1 except the Chan–Vese loss to classify the as the foreground and classify the as the background), we can get the area of the foreground. However, we cannot detect the whole area of the object. With Figure 4c,d, applying the Chan–Vese loss (7) and the Mumford–Shah loss (10) without classification loss (12) to the our simple auto-encoder can achieve a precise boundary of the object. However, the inside of the mask is not homogeneous. This is because (7) and (10) are minimized when pixels of similar intensity of the image are grouped together. Furthermore, the mask cannot detect the object as the foreground, since (7) and (10) are the functions of the intensity of the pixels. To make each region detected by the mask have the meaning of the foreground or the background, we concatenate the Chan–Vese loss (7) and the Mumford–Shah loss (10) with the classification loss (12) to make our total loss (6). The results of our total loss are in Figure 4e,f. The result of total loss combining Chan–Vese loss and classification loss is Figure 4e, and the result of total loss combining Mumford-Shan loss and classification loss is Figure 4e. Comparing the results of Figure 4c,d with those of Figure 4e,f shows that the area that was detected as black by the mask changed to the white area. This means that the mask finally detects the object as the foreground. Furthermore, when we compare with the baseline Figure 4a, we can get a more precise boundary since the Chan–Vese loss or the Mumford–Shah loss is used in addition to the classification loss as the segmentation loss. Figure 5 and Figure 6 show more segmentation results when using our total loss (6). Figure 5 is the result with the [9] dataset and uses our total loss (6), where the is composed of the Mumford–Shah functional. In Figure 5, the first column is the input images, the second column is the generated masks (i.e., ) by our total loss (6), the third column is the foreground images (i.e., ), and the last column is the background images (i.e., ). We can see that the masks detect the dogs and cats very accurately, and the boundaries resemble the shape of the dogs and cats. Furthermore, there are no parts of the dogs and cats in the background images. In Figure 6, we additionally add the ground-truth masks in the second column. When we compare the ground-truth mask (second column) and the generated mask by our total loss (6), we could get masks of very similar shape to the ground-truth masks even if the objects classified as foreground are small. However, when we use the PASCAL VOC dataset, we assume that the one image has only one image-level label, although there are multiple objects since our mask segments the image as the foreground and the background.

Figure 4.
The original input images (i.e., I) are in the first row. The second row shows the masks (i.e., . The foreground (i.e., ) images are in the third row, and the background (i.e., ) images are in the last row. The result images are randomly selected form the validation set.

Figure 5.
The result of the Mumford–Shah network with ResNet-18 as a classifier.

Figure 6.
The segmentation results with PascalVOC dataset. In each group, the first column is the input image, the second column is the ground truth binary mask, the third column is the generated binary mask by our Mumford–Shah network, the fourth column is the foreground region, and the fifth column is the background region calculated by the generated binary mask.
4.3. Quantitative Comparison
Since we assume that the one image has only one image-level class label, we calculate the mean IoU (intersection of union) for each image-level class label, not for the entire dataset. Table 1 shows the mean IoU calculated only for images belonging to each class. We show the results for four classes (dog, cat, horse, and cow) with a high IoU and for two classes (car, person) with a low IoU. When we compare the results of Baseline and our results (fourth row and fifth row of Table 1), our total loss (6) gets a higher mean IoU.

Table 1.
Mean Intersection of Union of each class label.
5. Discussions and Conclusions
Unlike other weakly supervised image segmentation, we assume that the one image only has one image-level label. Therefore, with our network and loss, we only can get the foreground and the background of the image. However, the segmentation energy functions of the Chan–Vese model or the Mumford–Shah model, which are revised to be applied in the deep learning framework, are efficient to get the precise boundaries of the objects. Furthermore, we do not optimize these energy functions with conventional level-set method. Instead, we optimize them with the stochastic gradient descent method, since these energy functions’ elements are the output of the deep learning network. Because we use deep learning, the initial curve of the level-set method is not important, and the number of regions is fixed as two (the foreground and the background). Furthermore, with the classifier, the meaningless regions are changed to the foreground and the background, since the classifier needs the foreground regions to classify the image. Moreover, through our background loss, which acts similarly to assigning a background image to a new class label, the classification loss (12) with two regularizers (15) can also get the mask. Therefore, with our work, we can get the foreground and the background, although the image only has an image level class label and not other information. However, our networks have one significant limitation. Since we use the classifier’s feature maps as the input of the decoder, the results change significantly with the classifier’s performance. Therefore, we construct a new network that does not depend on the classifier for the following study.
Author Contributions
Conceptualization, H.-T.C. and B.-W.H.; methodology, H.-T.C. and B.-W.H.; software, H.-T.C.; validation, H.-T.C. and B.-W.H.; formal analysis, H.-T.C.; investigation, H.-T.C.; resources, B.-W.H.; data curation, H.-T.C.; writing—original draft preparation, H.-T.C.; writing—review and editing, H.-T.C.; visualization, H.-T.C.; supervision, B.-W.H.; project administration, B.-W.H.; funding acquisition, B.-W.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Chung-Ang University Research Scholarship Grants in 2019 and the Korea government (MSIT): IITP-2021-0-01574, High-Potential Individuals Global Training Program.
Data Availability Statement
The datasets presented in this study are openely available in http://host.robots.ox.ac.uk/pascal/VOC/voc2012/ (accessed on 15 September 2021) and https://www.kaggle.com/c/dogs-vs-cats-redux-kernels-edition/data (accessed on 15 September 2021).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- O’Shea, K.; Nash, R. An introduction to convolutional neural networks. arXiv 2015, arXiv:1511.08458. [Google Scholar]
- Cunningham, P.; Cord, M.; Delany, S.J. Supervised Learning. In Machine Learning Techniques for Multimedia: Case Studies on Organization and Retrieval; Cord, M., Cunningham, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 21–49. [Google Scholar] [CrossRef]
- Ghahramani, Z. Unsupervised Learning. In Advanced Lectures on Machine Learning: ML Summer Schools 2003, Canberra, Australia, February 2–14, 2003, Tübingen, Germany, August 4–16, 2003, Revised Lectures; Bousquet, O., von Luxburg, U., Rätsch, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 72–112. [Google Scholar] [CrossRef]
- Mumford, D.B.; Shah, J. Optimal approximations by piecewise smooth functions and associated variational problems. Commun. Pure Appl. Math. 1989, 42, 577–685. [Google Scholar] [CrossRef] [Green Version]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Getreuer, P. Chan-vese segmentation. Image Process. Line 2012, 2, 214–224. [Google Scholar] [CrossRef]
- Cohen, R. The chan-vese algorithm. arXiv 2011, arXiv:1107.2782. [Google Scholar]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton–Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef] [Green Version]
- Dogs, vs. Cats Redux: Kernels Edition. Available online: https://www.kaggle.com/c/dogs-vs-cats-redux-kernels-edition/overview (accessed on 15 September 2016).
- Everingham, M.; Van Gool, L.; Williams, C.K.; Winn, J.; Zisserman, A. The pascal visual object classes (voc) challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef] [Green Version]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Tobias, O.J.; Seara, R. Image segmentation by histogram thresholding using fuzzy sets. IEEE Trans. Image Process. 2002, 11, 1457–1465. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arifin, A.Z.; Asano, A. Image segmentation by histogram thresholding using hierarchical cluster analysis. Pattern Recognit. Lett. 2006, 27, 1515–1521. [Google Scholar] [CrossRef]
- Ma, W.Y.; Manjunath, B.S. EdgeFlow: A technique for boundary detection and image segmentation. IEEE Trans. Image Process. 2000, 9, 1375–1388. [Google Scholar] [PubMed] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Kim, B.; Ye, J.C. Mumford–Shah loss functional for image segmentation with deep learning. IEEE Trans. Image Process. 2019, 29, 1856–1866. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26–30 June 2016; pp. 2921–2929. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Lee, J.; Kim, E.; Lee, S.; Lee, J.; Yoon, S. Ficklenet: Weakly and semi-supervised semantic image segmentation using stochastic inference. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5267–5276. [Google Scholar]
- Huang, Z.; Wang, X.; Wang, J.; Liu, W.; Wang, J. Weakly-supervised semantic segmentation network with deep seeded region growing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7014–7023. [Google Scholar]
- Wang, Y.; Zhang, J.; Kan, M.; Shan, S.; Chen, X. Self-supervised equivariant attention mechanism for weakly supervised semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–18 June 2020; pp. 12275–12284. [Google Scholar]
- Zolna, K.; Geras, K.J.; Cho, K. Classifier-agnostic saliency map extraction. Comput. Vis. Image Underst. 2020, 196, 102969. [Google Scholar] [CrossRef] [Green Version]
- Araslanov, N.; Roth, S. Single-stage semantic segmentation from image labels. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–18 June 2020; pp. 4253–4262. [Google Scholar]
- Caselles, V.; Kimmel, R.; Sapiro, G. Geodesic active contours. Int. J. Comput. Vis. 1997, 22, 61–79. [Google Scholar] [CrossRef]
- Malladi, R.; Sethian, J.A.; Vemuri, B.C. Topology-independent shape modeling scheme. In Geometric Methods in Computer Vision II; International Society for Optics and Photonics: Washington, DC, USA, 1993; Volume 2031, pp. 246–258. [Google Scholar]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active contour models. Int. J. Comput. Vis. 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Li, K.; Wu, Z.; Peng, K.C.; Ernst, J.; Fu, Y. Tell me where to look: Guided attention inference network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9215–9223. [Google Scholar]
- Fong, R.C.; Vedaldi, A. Interpretable explanations of black boxes by meaningful perturbation. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3429–3437. [Google Scholar]
- Singh, K.K.; Lee, Y.J. Hide-and-seek: Forcing a network to be meticulous for weakly-supervised object and action localization. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 3544–3553. [Google Scholar]
- Fong, R.; Patrick, M.; Vedaldi, A. Understanding deep networks via extremal perturbations and smooth masks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 2950–2958. [Google Scholar]
- Jaderberg, M.; Simonyan, K.; Zisserman, A. Spatial transformer networks. Adv. Neural Inf. Process. Syst. 2015, 28, 2017–2025. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Boston, MA, USA, 7–12 June 2015; pp. 1440–1448. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 28, 91–99. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Koch, G.; Zemel, R.; Salakhutdinov, R. Siamese neural networks for one-shot image recognition. In Proceedings of the 2015 ICML Deep Learning Workshop, Lille, France, 10–11 June 2015; Volume 2. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).