1. Introduction
Amongst the test equipment needed to install and maintain state-of-the-art fiber optic communication systems, the optical time-domain reflectometer (OTDR) remains the troubleshooting and fault locating tool of choice for fiber characterization in terms of identification and localization of various refractive and reflexive events, e.g., breaks, as well as for measuring attenuation, splice and connector insertion/return losses [
1,
2,
3].
Moreover, in contrast to legacy OTDRs designed to out-of-service test inactive (“dark”) fibers only, the new OTDR generation is equipped with filtered ports, enabling in-service measurements on active fibers carrying live traffic, by generating pulses at 1625 nm or 1650 nm wavelength, which do not belong to the windows used for optical transmission of user traffic [
1].
Specifically, concerning the long-distance measurements, especially the far-end events visibility and measurement accuracy, the crucial OTDR attribute is dynamic range, which is the difference between the backscatter level at the front end and the noise floor at the far end of the fiber. Consequently, the dynamic range determines how far downstream the fiber can the strongest (i.e., of longest duration) transmitted optical pulse reach, also taking into account OTDR span reduction introduced by connectors, splices, and splitters. Consequently, the dynamic range should be about 5 to 8 dB larger than the maximal loss that the OTDR can measure [
1,
4,
5,
6,
7,
8].
On the other hand, looking from the bottom up, the lower boundary determining the OTDR dynamic range is the noise floor value, which is (mostly) where the signal-to-noise ratio (SNR) equals unity, and is observed against the longest pulse width, after the three-minute averaging time [
9].
With this regard, still many older-generation OTDR units have insufficient dynamic range to test the far end of long fibers. For example, out of a typical dynamic range of, say, 35 dB, by subtracting attenuations of splices, just about 30 dB remains usable. This implies a considerable reduction of distance span which can be reliably tested with such OTDR units, which reduces their application range and therefore makes them left unused in test tools inventories of network operators [
1].
However, in this paper, we introduce a simple and cost-effective solution to reactivate such OTDRs and make them capable of reaching significantly farther along the fiber, by extending their dynamic range. With this regard, for constant laser saturation power level determined by the chosen pulse width, lowering the OTDR noise floor is the only option for widening the dynamic range, and thus extending the distance range. This makes sense, as the OTDR receiver noise figure is anything but small, since it is mostly determined by the large noise figure of the passive optical directional coupler (ODC) [
3] the very first block which the returning backscatter passes through before entering the detector.
We inserted a low-noise high-gain optical preamplifier in front of the OTDR, thus making the noise figure of the cascade dominantly determined by the (lower) noise figure of the optical preamplifier, which, according to our preliminary tests in this research-motivating framework of a network operator environment, enabled the OTDR to reach considerably farther along the same fiber under test.
As to our best knowledge, no similar investigation has been reported in public literature, the problem identification could not be reviewed in the standard way by citing detailed achievements and drawbacks of formerly published related solutions, to serve as our motivation for proposing a better approach.
Instead, we consider the other investigations involving dynamic range enhancements (e.g., optimizing its balance with dead zones) complementary rather than mutually exclusive with the proposed model, and therefore, we placed the comments on the related references in a separate
Section 4.3. about potential model enhancements “on top of” distance span extension that we proposed in this work.
Accordingly, in
Section 2, we present the analysis of all relevant aspects of OTDR measurements, with an accent on dynamic range, noise floor reduction, and distance range extension, whereas in
Section 3, we express the preliminary test results, which are discussed in
Section 4. Conclusions are summarized in
Section 5.
2. Analysis
Essentially, an OTDR inserts a pulsed signal into the fiber, from which a small portion that is commonly referred to as Rayleigh backscatter, is continuously reflected back by irregularities in the optical fiber structure, with the appropriate delays of the reflections expressed as the power loss versus distance, by appropriately scaling the time axis in relation to the speed of light in the fiber determining its refraction index.
Accordingly, an OTDR comprises a microprocessor, a pulse trigger and generator, a laser diode, an optical coupler, a detector, an analog-to-digital converter, and a display,
Figure 1.
When the test is started, the microprocessor sends a set of instructions to the trigger and generator that tells the laser to send a pulse. The pulses then pass through the directional optical coupler to the OTDR port and into the fiber being tested. In the reverse direction, the ODC channels the reflected signal away from the originating laser and into the detector mostly the avalanche photodiode (APD). Then the signal passes through the analog-to-digital converter to the microprocessor for analysis and display. The processor then averages the data to improve the SNR and displays the points that make up the fiber trace or waveform.
The trace is a collection of tens of thousands of sampling points. Because of the OTDR’s limited display resolution, not all of these data points can be displayed, so each point on the screen represents an average of a dozen sampling points.
2.1. Basic OTDR Model
More precisely, when the OTDR transmits the light pulse of power
P0 into the fiber, then the power
PT(
z) of the pulse propagating downstream the fiber, is the exponential function of distance
z of the observation point from the fiber near-end (OTDR):
where
α = αs + αa is the sum of the scattering and absorption losses expressed in dB/km.
The total scattered power at distance
z is:
where
α′
s = 0.23
·αs and Δ
z denote the fiber loss and the light pulse length, respectively.
The latter can be expressed as:
where
w,
vgr,
ngr, and
c denote the pulse duration, the group velocity in the fiber, the group refractive index (justifiably approximated by the ordinary index
n), and the speed of light in vacuum, respectively.
Determined by the fiber numerical aperture, i.e., by limited efficiency of an optical fiber to confine the incident light, only a certain part
S < 1 of the scattered light travels back to the OTDR (and is being subjected to equal loss, as during forward propagation), and reaches the observation point (that is
z apart from the OTDR) with the total backscattered power:
where
Ts is the transmission coefficient of the OTDR directional coupler.
So, the maximal backscattered power at the input of the fiber, i.e., at
z = 0, is:
Analogously, the backscattering power reflected from the end of the fiber (
z =
L) is:
The signal returning to the OTDR consists of both Rayleigh scattering and Fresnel reflections, where the latter is much stronger than the former. Rayleigh backscattering comes from the natural reflection and absorption of impurities inside the optical fiber. It enables calculating the level of fiber attenuation as a function of distance, which is represented by the constantly falling apart of an OTDR trace. However, Fresnel reflection occurs when the light pulse light hits an abrupt change in refraction index, which causes a strong reflection back, and therefore enables detection of physical events along with the fiber link identifiable by spikes in OTDR trace due to connectors, mechanical splices, bulkheads, fiber breaks or opened connectors (the higher the spike with respect to the backscatter levels, the greater the reflectance). Non-reflective events are caused by fusion splices or bending, and are visible as discrete drops in backscatter level,
Figure 2.
In order to apply Equation (5) to estimate the maximal backscattered power at 1550 nm and 1300 nm, we need to adopt some typical parameters’ values, such as the ones in
Table 1.
For example, quite a low backscatter power level
PBS(0) being about 50 dB below the incidence power level
P0, is close to the noise floor of the receiver, and is therefore commonly referred to as Noise Equivalent Power (NEP) [
10], so that the SNR must be increased by averaging, which effectively reduces NEP to:
where
n is the count of averaged samples.
As the OTDR sends light pulses repetitively into the fiber, the responses are computationally averaged, which reduces the receiver noise floor
NEPeff,
Figure 3.
2.2. OTDR Performance Parameters–Dynamic Range and Distance Span
An OTDR’s performance can be accurately evaluated by briefly examining the following key specifications: dynamic range and dead zone caused by the high-return-power Fresnel reflection (mostly from the fiber near-end first connector) that saturates the OTDR detector, disabling detection of events or measuring within that zone of the OTDR trace.
As it was pointed out above, dynamic range is defined as the difference (in dBs) between the maximal backscattered power Equation (5) at the input of the fiber, and the effective noise equivalent power Equation (7):
where the latter is sometimes related to the peak noise floor, implying a 2.2 dB smaller dynamic range than it is with SNR = 1.
Dynamic range depends on the setup parameters’ values. The main influences are pulse width, optimization mode, and wavelength.
From a top-down point of view, longer pulses provide larger dynamic range and, consequently, fiber end visibility but also worse event resolution and longer attenuation dead zone,
Figure 4.
On the other hand, from the bottom-up perspective, with already chosen pulse width, dynamic range can be increased by lowering
NEPeff. A way to do it is averaging, as it is already elaborated above and illustrated in
Figure 3, where significant improvements are achieved within the first three minutes of averaging, implying no need for a longer average time.
As it was pointed out above, dynamic range determines the maximal length of fiber that the longest pulse can reach; the larger the dynamic range, the longer the distance. So, if either the loss of a fiber under test is too high, or the dynamic range is insufficient, the far end of the fiber disappears in the noise, whereas in the opposite case, it is visible above the noise floor, and it is possible to detect the break. As connectors, splices, and splitters reduce the maximal fiber length that an OTDR can span, averaging for a longer period and using the proper distance range setup, is the key to increase the maximal measurable distance.
A good rule of thumb is to choose an OTDR with a dynamic range that enables the trace to remain at least 6 dB and 3 dB above the noise, in order to allow measuring of a 0.1 dB splice and detect a break, respectively. This requires the dynamic range to be at least 5 to 8 dB larger than the total optical transmission system loss [
4] to be encountered.
Consequently, a single-mode OTDR with a 35 dB dynamic range has a usable dynamic range of approximately 30 dB. Assuming typical single-mode fiber attenuation of 0.20 dB/km at 1550 nm, and splices every 2 km (loss of 0.1 dB per splice), such OTDR will be able to accurately certify distances of up to 120 km.
Accordingly, subtracting attenuations of all discrete loss events, the maximal distance could be approximately calculated by dividing the rest of the dynamic range of the OTDR by the attenuation (per distance unit) of the fiber [
4].
The end of the fiber can be seen as a reflective or non-reflective event, which condition is characterized by the noise after the event indicating the actual fiber end or brake, which may not necessarily be reflective.
2.3. OTDR Receiver Noise Floor Model
As we are interested here in lowering the OTDR noise floor (NEP) to widen the dynamic range, and thus extend the distance span, let us relate NEP to the commonly used receiver inherent noise descriptor—the noise figure, which is generally accepted as a measure of the excess noise that a device itself adds to the incoming noise.
Moreover, as we are to enhance the OTDR receiver by inserting a new front-end block, let us recall that the noise characteristics of a receiver cascade of blocks are commonly modeled by the noise figure.
2.3.1. Noise Floor vs. Noise Figure
Concretely, the noise figure expresses how much larger is the noise power spectral density
Pno at the receiver output than the input noise power spectral density
Pni multiplied by the transmission gain
G of the device, assuming shot noise at the input [
11]:
From Equation (9), it follows that the noise floor
NEPeff is linear with the noise figure
F:
However, the noise figure is rarely given in OTDR technical specifications; rather it is the noise floor that can be found or easily calculated from common OTDR parameters such as its output optical power level and dynamic range.
Nevertheless, due to linear relationship Equation (10), our considerations of reducing the OTDR receiver noise figure are directly applicable to the targeted reduction of its noise floor
NEPeff and consequent extension of its dynamic range and, finally, distance span [
1].
Furthermore, as can be seen in
Figure 1, the OTDR backscatter receiver path includes the ODC and the APD detector. Let us consider the noise contribution (in terms of noise figure) of each of these, and then of the whole cascade.
2.3.2. APD Noise Figure
APD is widely used in test instrumentation, offering NEP lesser than 10
−15 W/Hz
½ [
12,
13] determined mostly by shot noise due to stochastic behavior of photons and signal multiplication therefore the name: Poisson noise, which is sometimes also referred to as “gain noise” [
11], and described by the excess noise factor ENF [
12]. Moreover, a number of other affecters determine the APD noise floor, among them the reverse bias voltage and load. As related to the latter, Johnson noise is caused by the thermal motion of charged particles in a resistive element, and is typically much stronger than the intrinsic shot noise for low bandwidth applications, when the effective noise floor is therefore to the large extent determined by the load resistance.
2.3.3. ODC Noise Figure
On its way to APD, the backscattered signal firstly transverses the ODC, which not only introduces its intrinsic insertion loss between the input and the designated output, but also absorption and backscattering caused by imperfections in the fused region, always creating an excess loss that is a source of excess noise.
Moreover, the noise figure of a passive device is simply equal to its attenuation, implying that the SNR at the ODC output is that much lower than at the input, i.e., that the ODC insertion loss effectively makes it a noise generator whose power is linear with the attenuation [
3].
Therefore, insertion loss of an ODC is the important OTDR system design parameter. For a high-quality ODC, both the directionality and the reflection should be typically lower than −55 dB (with optical terminators at unused connector ports) [
3].
2.3.4. Noise Figure of Cascaded ODC and APD
Finally, as the OTDR backscatter signal receiver is, in fact, an APD, preceded by the ODC, we recall that, generally, the noise figure
F1,2 of the cascaded two blocks is to the large extent determined by the noise figure
F1 of the first block (with large gain
G1 >> 1) in the series:
The above classic relation describes that the second stage is fed with noise well above the shot noise limit (assuming that the first stage has significant gain). Therefore, the excess noise of the second stage is not very relevant (unless it is very strong), and it does not contribute significantly to the noise figure of the cascade.
However, in the case of the OTDR receiver, not only is the older-generation APD quite noise-rich [
1], but the passive front-end ODC with insertion loss
ADC (equal to its NF), deteriorates the noise figure of the cascade Equation (11) even further to:
From Equation (12), it implies that, for the class of older-generation OTDRs represented by the one under test here, we can justifiably consider the OTDR receiver noise figure, and thereby the OTDR noise floor, relatively high.
This motivates the investigation of reducing the OTDR noise floor by inserting a low-noise-figure high-gain optical preamplifier in front of the OTDR through the enhanced branching provided by means of a low-insertion-loss optical circulator (rather than ODC).
This would make the noise figure of the cascade dominantly determined by the (lower) noise figure of the front-end optical amplifier (OA).
2.3.5. Noise Figure of OA with Small-Loss Coupling
While the noise figure of electronic amplifiers is defined around the thermal noise, it is the shot noise that matters here, as the photon energy is far below the thermal one [
14,
15,
16].
Wide wavelength band, flat gain over a large dynamic gain range, high saturated output power, and low noise are the main features that state-of-the-art erbium-doped fiber amplifiers (EDFA) provide [
14,
15,
16].
Since the doped fiber of the fiber amplifier and the fiber of the transmission line are generally compatible, high coupling efficiency is feasible. This leads to a low noise figure in the range of 4–6 dB for fiber pre-amplifier(s) used at the far end of a link [
17,
18,
19], which should provide high gain, often in the range of 30 dB, in order to enable error-free information transport.
On the other hand, optical circulator (OC) is a passive optical component widely used in lightwave communications to separate optical signals traveling in opposite directions over optical fiber, and so, for example, enable bi-directional transmission over a single fiber [
3].
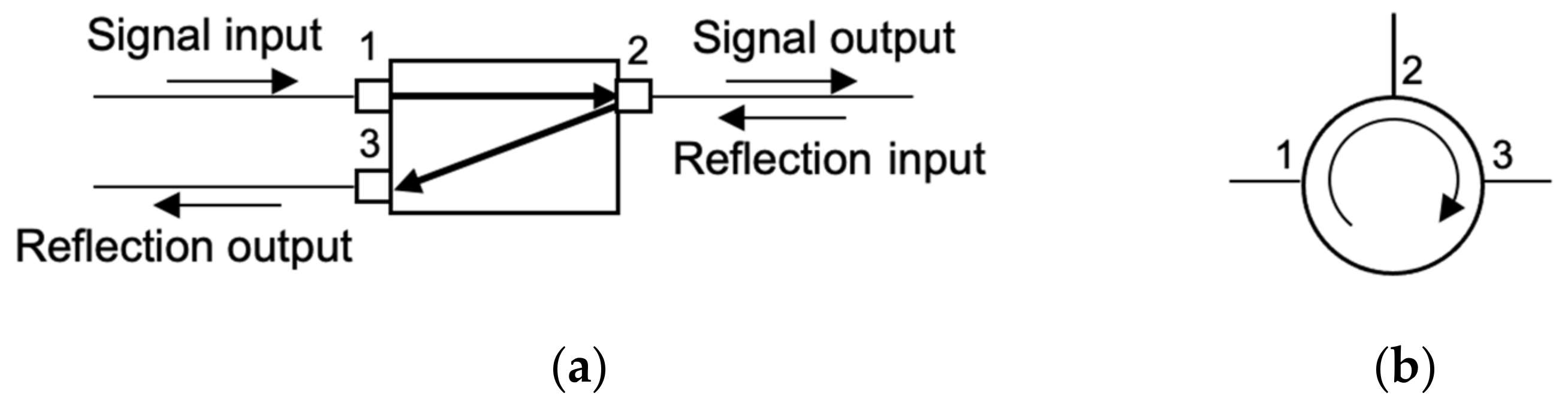
OC is based on the nonreciprocal polarization of the optical signal by the Faraday effect. It is a 3-port or a 4-port device as illustrated for the former one in
Figure 5a, where “1” denotes the input port, and “2” is the output port. The signal reflected back into port 2 will be redirected (with minimal loss) to port 3, and not to port 1,
Figure 5a.
In OC, light entering any port exits from the next one pointed to by the arrow in the symbolic OC presentation in
Figure 5b.
Because of its high isolation of direct from reflected light, and its low insertion loss (of a fraction of dB), OC is used in various optical devices and fiber optic sensors.
Accordingly, as ODC used within the OTDR under test to separate the optical signals of opposite directions, provides a considerable intrinsic insertion loss, in our OTDR preamplifier solution, we used OC as the signal separation front-end, rather than ODC [
3,
4].
3. OTDR Dynamic Range and Distance Span Extension by Inserting Front-End OA
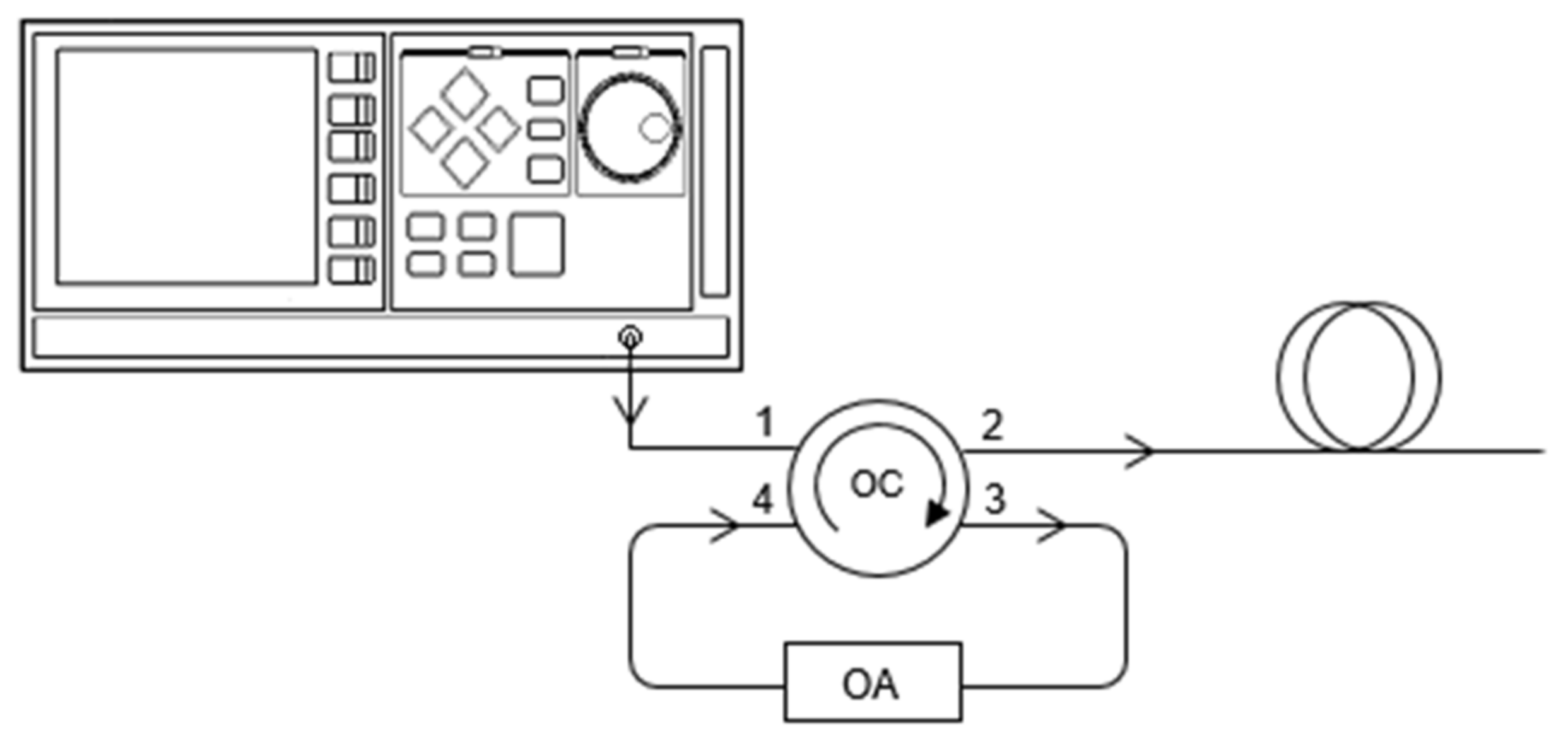
Let us consider now the noise figure of the cascaded 4-port OC, OA, and OTDR, constituting the test configuration presented in
Figure 6.
The OC port 2 is isolated from the adjacent OC port 3, as these are externally interconnected by the OA.
We will first model the dynamic range (and consequent distance span) extension, and then verify the estimated values by the measured ones [
20,
21].
3.1. Dynamic Range and Distance Span Extension Prediction Model
From Equation (11), analogously to Equation (12), the noise figure of the cascaded OC and OA is:
Furthermore, as 0 <
AOC <<
ADC, and 1 <
FOA <<
FAPD, from Equation (12) and Equation (13), it implies that:
Consequently, taking into account Equation (11), the noise figure of the whole cascade consisting of the 4-port OC, OA, and OTDR, presented in
Figure 6, is:
where we considered
GOC+OA ≈
GOA >>
AOC (quite justifiably as
GOA is of the order of 10
3 and thereby much larger than the OC insertion loss
AOC).
Thereby, recalling Equation (12), from Equation (15) it is obvious that:
i.e., that introducing the OTDR front-end optical pre-amplifier significantly reduces the noise figure, and thereby widens the dynamic range.
Coming out of Equation (10), reducing the noise figure, i.e., the SNR degradation by the OTDR receiver chain adding its own inherent noise, would reduce the OTDR noise floor – the lower bound of the OTDR dynamic range (where SNR=1), and thus widen the dynamic range for Δ
DR as it implies from Equation (8):
From Equation (10), it is obvious that, for certain input noise power
Pni, the noise floor
NEPOTDR for the OTDR alone is:
whereas for the cascaded OC, OA, and OTDR, it is:
So, the noise floor reduction (and consequent dynamic range extension) as a benefit of inserting the preamplifier, can be obtained if we divide Equation (18) by Equation (19), or perform the subtraction in dB units.
However, the OTDR noise figure FOTDR (specifically its constituents ADC and FAPD) and gain GOTDR are rarely given in technical specifications, whereas its noise floor NEPOTDR (in dB units) can be easily estimated by subtracting the specified dynamic range from the maximal output optical power level.
On the contrary, the OA noise figure FOA and gain GOA is always specified, whereas it is not the case with the OA noise floor NEPOA.
Considering the OTDR alone, the SNR at its receiver output is:
where
Sinp is the input signal power, and introducing the optical pre-amplifier implies the following SNR at the OTDR receiver output:
Furthermore, considering Equations (20) and (21) simplifies to:
The noise floor reduction (and consequent dynamic range extension Δ
DR) as a result of inserting a preamplifier is obtained dividing Equation (22) by Equation (20) as it follows:
In dB units, Equation (23) can be expressed as:
The dynamic range extension Equation (24) implies the following distance range extension:
3.2. Dynamic Range and Distance Span Extension Prediction Values
Let us make an exemplar prediction of dynamic range extension and distance span extension by means of Equations (23) and (24), as well as Equation (25), respectively, adopting common values for the relevant parameters of interest:
By conducting measurement, we found the OTDR noise floor NEPOTDR value to be close to −50 dBm, which corresponds to NEPOTDR = 10 nW on the linear scale.
Furthermore, let us suppose the EDFA preamplifier gain
GOA of 30 dB and the noise figure
FOA of 6 dB [
22]. The latter implies the OA noise floor spectral density value of 10
−5 nW/Hz
1/2 [
11], so that the noise bandwidth of 0.2 MHz (in accordance with the pulse duration of 5 μs), results with:
On the other hand, we consider the OTDR receiver GaAs APD gain to range between 10 and 40 dB [
13], and choose to adopt the pessimistic value of
GOTDR = 10 dB.
Furthermore, substituting the above exemplar values into Equations (23) and (24) provides the predicted dynamic range extension value of ΔDR ≈ 996 and ΔDR ≈ 30 dB, respectively.
Finally, substituting the latter value into Equation (25), and adopting α = 0.2 dB/km for the fiber attenuation at 1550 nm, we estimate the distance range extension of 75 km.
4. Preliminary Test Results
4.1. Test System
We used the HP 8147A optical time-domain reflectometer, designed for fiber characterization that network operators conduct during installation and field maintenance of their optical transmission systems,
Figure 7.
The OTDR contained the plug-in optical interface module for both 1310 nm and 1550 nm optical windows, and was connected in the test configuration cascade with OC and OA according to
Figure 6.
After selecting fiber type (single-mode in our case), wavelength, and index of refraction, the main parameters to set up were: maximal distance range (i.e., fiber length), pulse width, and acquisition time.
As our distance span extension model is centered around the dynamic range, according to the considerations in
Section 2.2. that longer pulses reach farther along the fiber, we selected 5 μs as quite sufficient for the fiber that we tested.
Having set the pulse width, the OTDR automatically selected the coupled distance range and standard acquisition time values, optimized for the particular fiber under test.
Distance accuracy can be enhanced by proper calibration of the entire OA-OTDR test system, but this requires cost demanding additional equipment [
23,
24]. Unfortunately, it is not available at this point of our research, so our preliminary test results are aimed to just verify the proposed concept, rather than present any firm reference value with this regard.
The follow-up high-accuracy measurements can be repeated as many times as needed for various tests of this kind. So, for example, the OA transmission characteristics ripple, if significant, must be taken into account, as considering transfer function a Fourier series, any sinusoidal ripple in the frequency/wavelength domain, is equivalent to a pulse in the time domain (whose delay is determined by the frequency of the corresponding sinusoid) [
25]. Consequently, a “wavy” OA transfer characteristics could introduce ghost pulses (i.e., events) into the OTDR trace.
4.2. Results
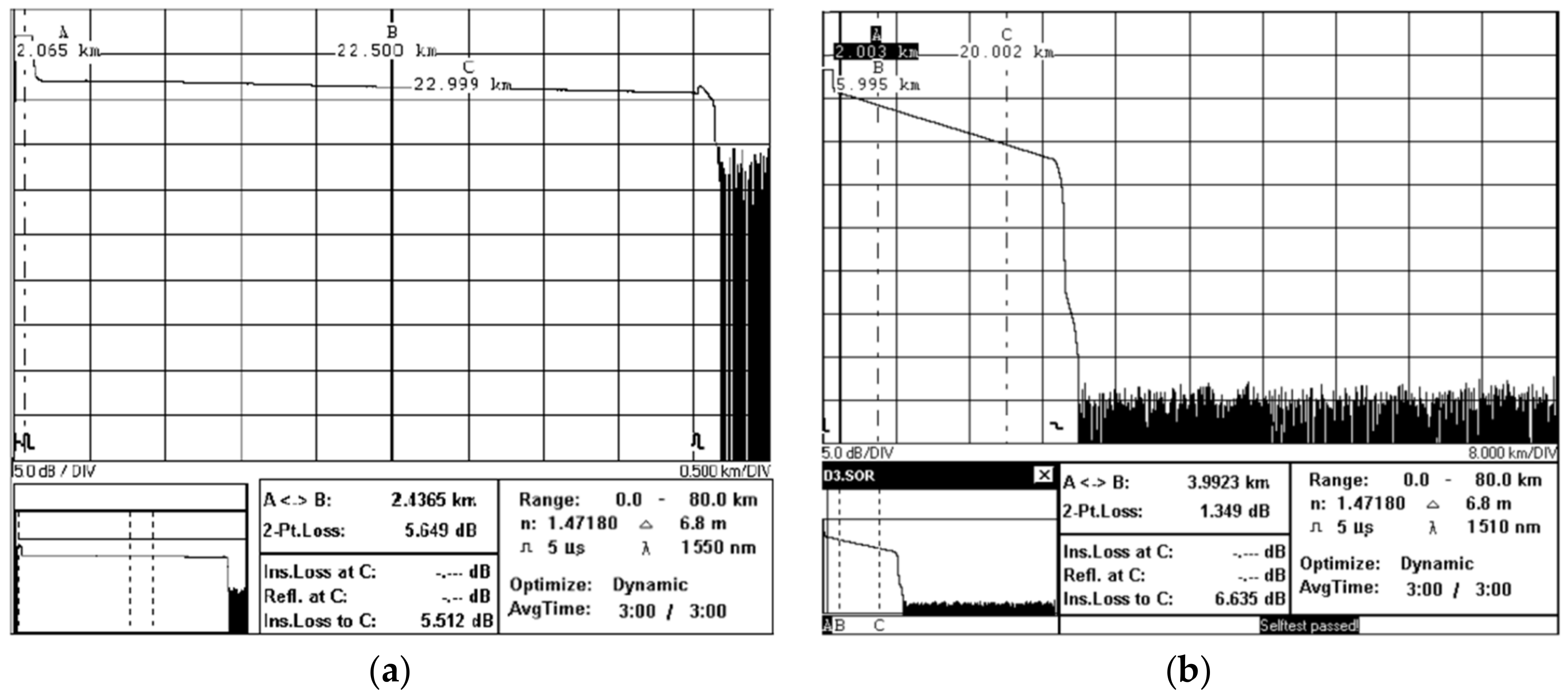
The exemplar preliminary test traces of the OTDR alone, and of the OTDR with the front-end OA, are presented in
Figure 8a,b, respectively.
As it can be seen, the significant difference is evident between the noise floor values in these cases, with the dynamic range enhancement of about 30 dB, which conforms to the predicted value obtained from Equation (24), and consequently verifies the distance span extension of 75 km estimated by Equation (25) as well.
Testing in other optical windows will not be any different, except requiring a more expensive PDFA preamplifier at 1310 nm, thus questioning the profitability of the solution.
We believe that the preliminary results reported here could serve as a hint and a framework for a more comprehensive test strategy in terms of both test diversification (with more fiber links with various events), and repeating rate, which can be implemented in a network operator environment or professional lab.
4.3. Discussion and Potential Model Enhancements
The initial motivation for the proposed model is now planned to stretch beyond just reactivating the older-generation OTDR units, to include other potential enhancements, such as coding, advanced signal processing, trace post-processing, interaction with existing active devices of the fiber optic link, as well as in-service testing.
More specifically, as the here proposed OTDR enhancement targets only distance span extension, the far-end events which (this way) have become visible by introducing the OA front-end, will preserve the resolution of the former OTDR-only far-end ones, whereas, for the shorter distances, no preamplifier should be used.
However, systematic mitigating the impact of OTDR attenuation and event dead zones, specifically once having extended the distance range by the optical preamplifier, deserves to be considered, too. For given receiver bandwidth, a possible solution is to reduce the OTDR noise floor by using simplex codes (scs) [
26], which can be extended to the general noise model in the coded OTDR combining the scs with the complementary correlation codes to achieve higher gains [
27].
Furthermore, the OTDR dynamic range can be extended by some more advanced signal processing techniques to lower the noise floor of backscattering-based systems in general, such as translation-invariant wavelet thresholding (TIWT), and lifting wavelet transform-modified particle swarm optimization (LWT-MPSO) [
28].
Moreover, advanced OTDR trace postprocessing algorithms such as vector indexing, are also of interest for event detection, location, and spatial resolution [
29].
Finally, in an OTDR based sensor system, using EDFA has created an experimental knowledge base regarding gain, insertion loss, and pumping configurations, which would be worth merging with the analytical model derived here [
30,
31,
32,
33,
34].
As the proposed dynamic range (and thereby distance span) extension is done by the very “ground-floor” physical layer action - introduction of the front-end OA, the above-mentioned enhancements could be added “on top of” the proposed model, rather than replace it.
5. Conclusions
Many older-generation OTDR units have insufficient dynamic range to test the far-end of longer fibers. A simple and cost-effective solution for re-activation of these useful and costly devices in installation and maintenance of state-of-the-art fiber-optic links, is shown here to be the introduction of a low-noise high-gain optical preamplifier in front of the OTDR, to effectively reduce its noise floor, as, by this way, the noise figure of the cascade becomes dominantly determined by the front-end optical amplifier.
According to our preliminary tests, this enabled the OTDR to significantly enhance its dynamic range and consequently distance span, by almost 30 dB and 75 km, respectively.
This work was aimed to discover, model, verify and quantify the potential of the proposed OTDR distance span extension, and thereby pave the way to according R&D and field tests taking into account design and deployment issues as well, and using sophisticated hardware and industry-standard software simulation tools.
We believe that the preliminary results reported here could be a hint for a more comprehensive test strategy in terms of both diversification and repeating rate.
Author Contributions
Conceptualization, A.L. and V.L.; methodology, A.L.; software, A.L. and M.H.; validation, A.L., V.L. and M.H.; formal analysis, A.L and V.L.; investigation, A.L.; resources, A.L. and M.H.; data curation, A.L. and M.H.; writing—original draft preparation, A.L.; writing—review and editing, V.L.; visualization, M.H.; supervision, V.B.; project administration, V.B.; funding acquisition, V.L. and V.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research leading to the published results was supported by the Ministry of Civil Affairs of Bosnia and Herzegovina, under Grant No. 02-7142/20.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lipovac, A. Practical Enhancement of Fiber Installation and Maintenance Test Tools-Example of Extending OTDR Distance Range by Optical Preamplifier. In Proceedings of the European Lasers, Photonics and Optics Technologies Summit, Paris, France, 22 September 2020. [Google Scholar]
- Winzer, P.J.; Neilson, D.T.; Chraplyvy, A.R. Fiber-optic transmission and networking: The previous 20 and the next 20 years. Opt. Express 2018, 26, 24190–24239. [Google Scholar] [CrossRef] [PubMed]
- Hui, R. Passive optical components. In Introduction to Fiber-Optic Communications, 1st ed.; Academic Press: Cambridge, MA, USA, 2020; pp. 209–297. [Google Scholar]
- Hui, R.; O’Sullivan, M. Characterization of Optical Devices. In Fiber Optic Measurement Techniques, 1st ed.; Academic Press: Cambridge, MA, USA, 2009; pp. 259–363. [Google Scholar]
- Lu, X.; Soto, M.A.; Thévenaz, L. Temperature-strain discrimination in distributed optical fiber sensing using phase-sensitive optical time-domain reflectometry. Opt. Express 2017, 25, 16059–16071. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alekseev, A.E.; Vdovenko, V.S.; Gorshkov, B.G.; Potapov, V.T.; Simikin, D.E. Fading reduction in a phase optical time-domain reflectometer with multimode sensitive fiber. Laser Phys. 2016, 26, 95–101. [Google Scholar] [CrossRef]
- Hartog, A.H. Frequency-Scanned Optical Time Domain Reflectometry. US Patent 7859654B2, 17 July 2008. [Google Scholar]
- Lu, X.; Soto, M.A.; Thévenaz, L. Optimal detection bandwidth for phase-sensitive optical time-domain reflectometry. In Proceedings of the Sixth European Workshop on Optical Fibre Sensors EWOFS’2016, Limerick, Ireland, 31 May 2016; pp. 374–377. [Google Scholar]
- Agilent Technologies. Optical Time Domain Reflectometers; Pocket Guide. 2001. Available online: http://literature.cdn.keysight.com/litweb/pdf/E6000-91017.pdf (accessed on 1 May 2021).
- Mackowiak, V.; Peupelmann, J.; Ma, Y.; Gorges, A. NEP–Noise Equivalent Power; Thorlabs, Inc.: Dachau, Germany, 2015; pp. 1–5. [Google Scholar]
- Memis, O.G.; Katsnelson, A.; Kong, S.C.; Mohseni, H.; Yan, M.; Zhang, S.; Hossain, T.; Jin, N.; Adesida, I. Sub-Poissonian shot noise of a high internal gain injection photon detector. Opt. Express 2008, 16, 12701–12706. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lau, K.S.; Tan, C.H.; Ng, B.K.; Li, K.F.; Tozer, R.C.; David, J.P.; Rees, G.J. Excess noise measurement in avalanche photodiodes using a transimpedance amplifier front-end. Meas. Sci. Technol. 2006, 17, 1941–1945. [Google Scholar] [CrossRef]
- Huntington, A. Sensitivity Analysis of APD Photoreceivers; VoxtelOpto, Voxtel Inc.: Beaverton, OR, USA, 2016; pp. 1–39. [Google Scholar]
- Olshansky, R. Noise figure for erbium-doped optical fiber amplifiers. Electron. Lett. 1988, 24, 1363–1365. [Google Scholar] [CrossRef]
- Haus, H.A. The noise figure of optical amplifiers. IEEE Photonics Technol. Lett. 1998, 10, 1602–1604. [Google Scholar] [CrossRef]
- Desurvire, E. Comments on ‘The Noise Figure of Optical Amplifiers’. IEEE Photonics Technol. Lett. 1999, 11, 620–621. [Google Scholar] [CrossRef]
- Abedin, K.S.; Taunay, T.F.; Fishteyn, M.; Yan, M.F.; Zhu, B.; Fini, J.M.; Monberg, E.M.; Dimarcello, F.V.; Wisk, P.W. Amplification and noise properties of an erbium-doped multicore fiber amplifier. Opt. Express 2011, 19, 16715–16721. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Jin, C.; Huang, B.; Fontaine, N.K.; Ryf, R.; Shang, K.; Grégoire, N.; Morency, S.; Essiambre, R.J.; Li, G.; et al. Integrated cladding-pumped multicore few-mode erbium-doped fiber amplifier for space-division-multiplexed communications. Nat. Photonics 2016, 10, 529–533. [Google Scholar] [CrossRef] [Green Version]
- Desurvire, E. Erbium-Doped Fiber Amplifiers: Principles and Applications, 1st ed.; John Wiley & Sons: New York, NY, USA, 1994; p. 770. [Google Scholar]
- Pedersen, B.; Dakss, M.L.; Thompson, B.A.; Miniscalco, W.J.; Wei, T.; Andrews, L.J. Experimental and theoretical analysis of efficient erbium-doped fiber power amplifiers. IEEE Photonics Technol. Lett. 1991, 3, 1085–1087. [Google Scholar] [CrossRef]
- Giles, C.R.; Desurvire, E. Modeling erbium-doped fiber amplifiers. J. Lightwave Technol. 1991, 9, 271–283. [Google Scholar] [CrossRef] [Green Version]
- Available online: https://nuphoton.com/product-category/fiber-amplifiers/erbium-doped-fiber-amplifiers/ (accessed on 1 May 2021).
- Larson, D.R.; Paulter, N.G.; Blaney, K.C. Characterization and Calibration of an Optical Time Domain Reflectometer Calibrator. In Proceedings of the National Conference of Standards Laboratories International Workshop and Symposium, Nashville, TN, USA, 7 August 2006. [Google Scholar]
- Larson, D.R.; Paulter, N.G.; Blaney, K.C. Calibration of Optical Time-Domain Reflectometers (OTDR’s); Technical Report Number: NIST Technical Note 1475. 2006. Available online: https://nvlpubs.nist.gov/nistpubs/Legacy/TN/nbstechnicalnote1475.pdf. (accessed on 1 May 2021).
- Sunde, E.D. Theoretical fundamentals of pulse transmission—II. Bell Syst. Tech. J. 1954, 33, 987–1010. [Google Scholar] [CrossRef]
- Lee, D.; Yoon, H.; Kim, P.; Park, J.; Park, N. Optimization of SNR Improvement in the Noncoherent OTDR Based on Simplex Codes. J. Lightwave Technol. 2006, 24, 322–328. [Google Scholar]
- Naseem, A.; Mehmood, H.; Muhammad, S.S.; Abbas, S.A. Composite Coding Scheme for OTDR SNR Enhancement. In Proceedings of the Con TEL, Graz, Austria, 2 June 2011. [Google Scholar]
- Tangudu, R.; Sahu, P.K. Dynamic Range Improvement of Backscattered Optical Signals using Signal Processing Techniques. In Proceedings of the IEEE Applied Signal Processing Conference (ASPCON), Kolkata, India, 7–9 October 2020. [Google Scholar]
- Usama, M.; Muhammad, S.S. Vector Indexing Algorithm for Post Processing of OTDR Data. In Proceedings of the 2013 18th European Conference on Network and Optical Communications & 2013 8th Conference on Optical Cabling and Infrastructure (NOC-OC&I), Graz, Austria, 10–12 July 2013. [Google Scholar]
- Lee, H.H.; Nam, Y.H.; Lee, D.; Chung, H.S.; Kim, K. Demonstration of a Low-Cost 1625-nm OTDR Monitoring for 350-km WDM Networks With Semiconductor Optical Amplifiers. IEEE Photonics Technol. Lett. 2005, 17, 852–854. [Google Scholar] [CrossRef]
- Nascimento, J.F.; Cipriano, E.A.; Martins-Filho, J.F.; Guimarães, J.; da Silva, M.J. Characterization of an Amplified OTDR Fiber-optic Multipoint Sensor System. In Proceedings of the International Microwave and Optoelectronics Conference (IMOC 2011), Natal, Brazil, 8 October 2011. [Google Scholar]
- Pljonkin, A. Vulnerability of the Synchronization Process in the Quantum Key Distribution System. Int. J. Cloud Appl. Comput. 2019, 9, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Pljonkin, A.; Rumyantsev, K. Quantum-cryptographic network. In Proceedings of the IEEE East-West Design & Test Symposium (EWDTS), Yerevan, Armenia, 14 October 2016; pp. 1–4. [Google Scholar]
- Pljonkin, A.; Petrov, D.; Sabantina, L.; Dakhkilgova, K. Nonclassical Attack on a Quantum Key Distribution System. Entropy 2021, 23, 509. [Google Scholar] [CrossRef] [PubMed]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).