A Comparative Performance Analysis of Zero Voltage Switching Class E and Selected Enhanced Class E Inverters

Abstract

This paper presents a comparative analysis of the class E and selected enhanced class E inverters, namely, the second and third harmonic group of class EF_n, E/F_n and the class E Flat Top inverter. The inverters are designed under identical specifications and evaluated against the variation of switching frequency (f), duty ratio (D), capacitance ratio (k), and the load resistance (R_L). To offer a comparative understanding, the performance parameters, namely, the power output capability, efficiency, peak switch voltage and current, peak resonant capacitor voltages, and the peak current in the lumped network, are determined quantitatively. It is found that the class EF₂ and E/F₃ inverters, in general, have higher efficiency and comparable power output capability with respect to the class E inverter. More specifically, the class EF2 (parallel LC and in series to the load network) and E/F3 (parallel LC and in series to the load network) maintain 90% efficiency compared to 80% for class E inverter at the optimum operating condition. Furthermore, the peak switch voltage and current in these inverters are on average 20–30% lower than the class E and other versions for k > 1. The analysis also shows that the class EF₂ and E/F₃ inverters should be operated in the stretch of 1 < k < 5 and D = 0.3–0.6 at the optimum load to sustain the high-performance standard.

1. Introduction

The class E inverter has found numerous applications in radio transmission, induction heating, industrial ultrasonic, renewable energy systems, or the commercial electronics industry [1,2,3,4,5,6,7,8,9,10,11]. The widespread adoption of this inverter is mainly due to the compact structure with low component count and high-power driving capability. On top of that, if coupled with the zero-voltage switching (ZVS) or zero derivative voltage switching (ZVDS) techniques, it can operate with high efficiency even at very high switching frequency. The analytical modeling and design of the ZVS/ZVDS class E inverters are well reported in the literature [1,2,8,9,10,11,12,13,14]. However, the class E has one big disadvantage. The high peak switch voltage (3.5 to 5 times depending simultaneously on the duty ratio, input inductance, and switching frequency) is of significant concern [15]. Henceforth, among other reasons, including improved stability and voltage regulation, the enhanced class E configurations are proposed to counter this issue. These inverters are classified as EF_n or E/F_n inverters where n defines the harmonic tuning component and realized by adding tuned LC networks at the nth harmonic of the switching frequency [16,17,18,19,20]. Traditionally, the class EF_n inverters are a combination of class E and class F inverters where n is even, while the class E/F_n is the combination of class E and class 1/F inverters where n is odd. In addition to that, the flat top-class E is another alternative configuration that offers a flat top switch voltage with lowered peak [21,22,23]. Technically, the flat top feature is achieved by tuning an LC resonant network to the nearest even harmonic and emphasizing the odd harmonics into the fundamental voltage waveform.

The analytical models to correctly describe the characteristic behavior of enhanced class E inverters have been investigated in [11,15,17,18,19,22,23,24,25,26,27,28,29,30,31,32]. Based on the analysis technique, these models can be classified into the waveform equation [11,17,22,24], state-space [15], or frequency domain [25] methods. These models either provide a closed-form analytical expression for describing the circuit behavior or present a numerical solution with design-oriented curves [11].

Despite the attractive features these inverters might offer, the literature on this topic has not grown so far. Currently, only a handful of journals can be found dedicated to developing a comparative performance analysis. For example, a discussion of the class E, EF₂, and E/F₃ inverters can be found in [15,17]. In [15], the inverters are primarily designed to maximize the power output capability at soft switching conditions. The peak switch voltage and current are measured by varying the duty ratio. The paper also concludes that the class EF₂ and E/F₃ inverters outperform class E in terms of efficiency and power output capability. Nevertheless, it does not demonstrate the state of the efficiency, auxiliary peak capacitor voltage and current in the lumped network and against the variation of other important parameters, such as the switching frequency, resonant components, and load. Additionally, instead of considering the diverse configurations for the lumped network, the performance evaluation is restricted to the ‘series LC in parallel to the load network’ only. In [17], the authors mainly concentrate on evaluating the class E/F₃ inverter, which is designed to operate at optimum operating point with a constant 50% duty ratio. It concludes that the third harmonic tuning (i.e., class E/F₃) provides higher efficiency and lower peak switch voltage compared to the class E. However, similar to [15], the performance is not justified with the variation of other important parameters, such as the switching frequency, resonant components, and load. Furthermore, as in [15], only the lumped ‘series LC in parallel to the load network’ configuration is considered. Henceforth, the comparative evaluation is incomplete unless the aforementioned issues are addressed considerably.

Based on these facts, this paper mainly intends to understand the comparative performances of the class E and selected enhanced class E inverters in various configurations designed under identical specifications by adopting the classical analytical models. However, to reduce the workload, a unified design approach is followed. The latter would allow for building a ‘base’ class E prototype circuit and transforming it into the enhanced versions by simply adding the lumped auxiliary networks. The performance parameters are then measured and compared quantitatively.

2. The Circuit Operation of Class E and Enhanced Class E Inverters

2.1. The Circuit Configurations

The generalized class E and enhanced class E inverter topology is shown in Figure 1. The inductance L_s and the capacitance C_s resonate at a resonant frequency (f_r) according to a chosen quality factor (Q). The input inductance (L_f) is designed to provide a constant dc current, a very low ripple current. The input current ripple is inversely proportional to L_f. The input capacitance C_in facilitates the ZVS and absorbs the drain to source non-linear capacitance (C_ds) of the switch. The auxiliary resonant branch in EF_n and E/F_n inverters consists of the auxiliary resonant inductance (L₁) and capacitance (C₁) arranged in a series or parallel formation. They resonate at a frequency of nf_s where f_s is the optimum switching frequency and chosen to be greater than f_r. The multiplier n is an integer and determined by L₁, C₁, and f_s. The switch S₁ is operated at an optimum duty ratio D_opt to achieve the ZVS operation. The switching pattern is given as follows.

$$\mathrm{Switch}=\left\{\begin{array}{l}\mathrm{Turned} \mathrm{ON}, 0\le \theta <2\pi D\\ \mathrm{Turned} \mathrm{OFF}, 2\pi D\le \theta <2\pi \end{array}\right.$$

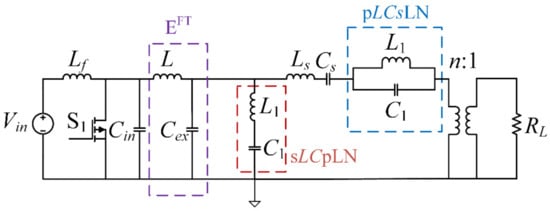
Figure 1. The class E and enhanced class E topologies with auxiliary resonant networks.

Depending on the auxiliary resonant branch configuration, the EF_n and E/F_n inverters can be classified as demonstrated in Table 1. This classification is accompanied by a convenient ‘short-form’ representation. Throughout this document, these short-forms are used to refer to the corresponding inverter. The class EF₂ (pLCsLN) and E/F₃ (pLCsLN) inverters are also known as ‘second harmonic’ and ‘third harmonic’ class E inverters, respectively.

Table 1. Inverter nomenclature.

Inverter Configuration	Short-Form
Class EF2 with series LC in parallel to the load network	EF2 (sLCpLN)
Class EF2 with parallel LC in series to the load network	EF2 (pLCsLN)
Class E/F3 with series LC in parallel to the load network	E/F3 (sLCpLN)
Class E/F3 with parallel LC in series to the load network	E/F3 (pLCsLN)
Class E Flat Top	EFT

2.2. Modes of Operation and Input Impedance (Z_in)

In Figure 2, the impedance distribution and the currents are shown. The class E and class E based inverters operate in two modes. In mode 1, the switch S₁ is turned ON and the voltage across the capacitor C_in falls to zero. The input current (I_in) flows through the switch S₁ and the L_f stores energy. In the resonant tank, resonant current flows through the switch exchanging stored energy from C_s to L_s and completing half of the resonance cycle. By the end of this cycle, this current decreases, and the energy transfer is completed. In mode 2 as soon as S₁ is closed at θ = 2πD, I_in diverts to charge the input capacitor C_in, which eventually reaches the peak voltage before it discharges through the resonant tank. The peak voltage can also be signified as the peak switch voltage (V_S1,peak) of the inverter. Due to the inductive nature of the load network, the output current (I_out) lags the input voltage to the resonant tank (V_S1). To achieve ZVS or ZVDS, the following conditions must be satisfied.

$$V_{S1}(2\pi )=0$$

$$\mathrm{and} \frac{d}{d\theta }{V}_{S1}(2\pi )=0$$

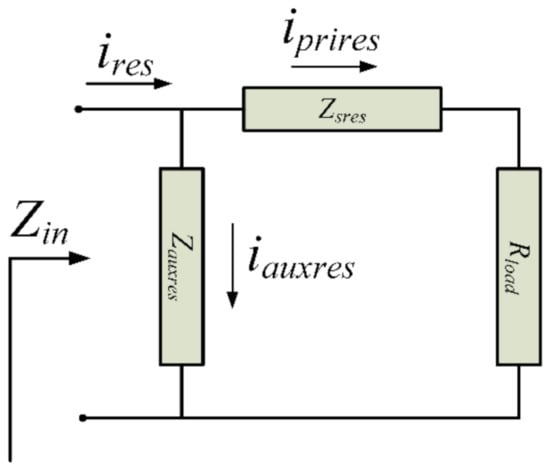
Figure 2. Impedance and current distribution (ideal) for class E and enhanced topologies with auxiliary resonant network.

The class E inverter demonstrates two resonant frequencies: f_r1 (S₁ is ON) and f_r2 (S₁ is OFF). These frequencies can be determined as follows.

$$f_{r1}=\frac{1}{2\pi \sqrt{L_s{C}_s}} \mathrm{and} f_{r2}=\frac{1}{2\pi \sqrt{L_s{C}_{s\_eq}}}$$

$$\mathrm{where} C_{s\_eq}=\frac{C_s{C}_{in}}{C_s+C_{in}}$$

Additionally, the quality factor (Q) of the circuit is defined as:

$$Q_1=\frac{{\omega }_{S1}{L}_s}{R_{L,opt}}=\frac{{\omega }_{S1}}{R_{L,opt}{C}_s}({\mathrm{S}}_1 \mathrm{is} \mathrm{ON}) \mathrm{and} Q_2=\frac{{\omega }_{S2}{L}_s}{R_{L,opt}}=\frac{{\omega }_{S2}}{R_{L,opt}{C}_{s\_eq}}({\mathrm{S}}_1 \mathrm{is} \mathrm{OFF})$$

Throughout this document, wherever f_r is mentioned, it is meant to be the series resonant frequency f_r1. The input impedance of the resonant tank at the switch ON and OFF states are stated in Equations (1) and (2), respectively.

$$\left|Z_{in,ON}\right|=\sqrt{R^2{}_L+{\left(2\pi f_s{L}_s-\frac{1}{2\pi f_s{C}_s}\right)}^2}$$

(1)

$$\left|Z_{in,OFF}\right|=\frac{\sqrt{\frac{\frac{1}{16}+C_s{}^2{L}_s{}^2{\pi }^4{f}_s{}^4+\frac{1}{4}{\pi }^2{C}_s{f}_s{}^2\left(C_s{R}^2{}_L-2L_s\right)}{\left(C_s{}^2{C}_{in}{}^2{L}_s{}^2{\pi }^4{f}_s{}^4+\frac{1}{4}{\pi }^2{C}_s{C}_{in}{f}_s{}^2\left(\left(C_s{R}_L{}^2-2L_s\right)C_{in}-2C_s{L}_s\right)+\frac{1}{16}{\left(C_s+C_{in}\right)}^2\right)f_s{}^2}}}{2\pi }$$

(2)

The class EF_n and E/F_n inverters incorporate an auxiliary resonant branch tuned to multiple n of the optimum switching frequency f_s. The primary series resonant frequency is identical to that of class E and determined by the resonant inductance L_s and resonant capacitance C_s. The secondary resonant frequency f_r2 in the class E and EF_n (sLCpLN) can be characterized by parallel resonance and determined by the primary and auxiliary resonant components (L₁, C₁) and their configurations. The input impedances for sLCpLN and pLCsLN configurations are stated in Equations (3) and (4) respectively. A representative diagram in Figure 2 shows the impedances and currents in the primary and auxiliary resonant networks. The primary and nth harmonic current is defined by i_prires and i_auxres, respectively. The definitions for variables A, B, C, D, and E are stated in Equations (10)–(14).

$$\left|Z_{in,OFF}\right|=\frac{1}{2\pi }\sqrt{\frac{A}{\left(B+C-D\right)f_s{}^2}}$$

(3)

$$\left|Z_{in,OFF}\right|=\frac{\sqrt{{\left(\pi f_s{L}_1-\frac{1}{4\pi f_s{C}_1}\right)}^2+{\left(E-\frac{R_L}{2}\right)}^2}}{\sqrt{{\left(\pi f_s{C}_{in}{R}_L\right)}^2+{\left(E+2\pi f_s{L}_1-\frac{1}{2\pi f_s{C}_1}-\frac{1}{2\pi f_s{C}_{in}}\right)}^2}}$$

(4)

To exemplify the behavior pattern, the impedances are plotted in Figure 3 against ɷ for mode 2 according to the specifications described in Table 2. The primary series resonant frequency f_r1 and the second parallel resonant frequency f_r2 are identical for class E, EF₂ (sLCpLN), and E/F₃ (sLCpLN) configurations. This is shown in Figure 3a,b where ω_fr1/ω_s ≈ 0.85 and ω_fr2/ω_s ≈ 1. However, due to the series configuration of the L₁C₁ to the load network, the primary resonance frequency (f_r1) is altered in EF₂ (pLCsLN) and E/F₂ (pLCsLN) configurations. This is shown in Figure 3c, where ω_fr1/ω_s ≈ 2 and ω_fr1/ω_s ≈ 3 for EF₂ and E/F₃, respectively. In addition to that, a third series resonance close to ω/ω_s ≈ 1 (i.e., at f_r3) occurs in EF₂ (sLCpLN) and E/F₃ (sLCpLN) configurations. This can be observed in Figure 3b, where ω_fr3/ω_s ≈ 2 and ω_fr3/ω_s ≈ 3 for EF₂ and E/F₃, respectively. This feature, particularly, enables these inverters to transfer more power at identical input voltage (V_in), duty ratio (D), and switching frequency (f) compared to class E. Additionally, a lower impedance for class EF_n and E/F_n, in general, induces lower loss and higher efficiency. A fourth parallel resonance can be found for both class EF₂ (sLCpLN, pLCsLN) and E/F₃ (sLCpLN, pLCsLN) inverters at much higher frequency, where ω_fr4/ω_s > 4. Again, f_r4 is characterized by parallel resonance and largely determined by the auxiliary branch components.

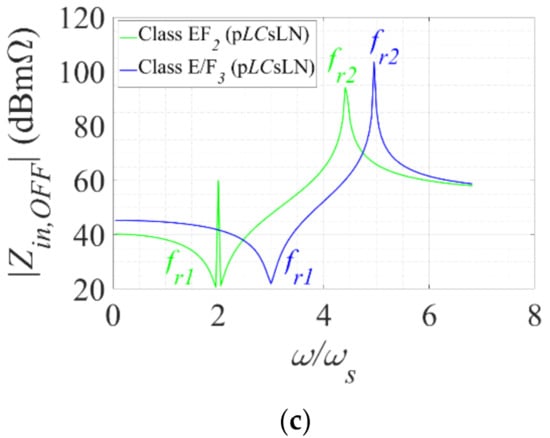
Figure 3. Input impedance (Z_in) of (a) class E at switch ON and OFF conditions (b) class EF₂ and EF₃ at switch OFF condition (c) class E/F₂ and E/F₃ at switch OFF condition at V_in = 50 V, D_opt = 0.5, f_s = 220 kHz, R_L = R_L,opt, k ≈ 0.30 (EF₂) and 0.67 (E/F₃).

Table 2. Converter specifications at the optimum operating point.

Parameter Description	Symbol	Value
Input voltage	Vin	50 V
Output voltage	Vout	5 V
Rated output power	Pout	25 W
Nominal optimum switching frequency	fs	220 kHz
Primary resonant frequency	fr	190 kHz
Loaded quality factor	QL	≈7

2.3. The Peak Switch Voltage (V_S1,peak)

The capacitor current (i_Cin) in class E inverter can be expressed in terms of the input current (I_in) and the sinusoidal resonant current as:

$$i_{Cin}\left(\omega t\right)=I_{in}-I_m\sin \left(\omega t+\phi \right)$$

(5)

where, I_m is the maximum resonant current. By integrating Equation (5) and applying the ZVS conditions [1,2], the switch voltage (V_S1) and the peak switch voltage (V_S1,peak) can be derived as:

$$V_{S1}=\frac{-2I_{in}\pi D+I_{in}\theta n-I_{in}\cos \left(2\pi D+\phi \right)+I_{in}\theta +I_m\cos \left(\theta +\phi \right)}{\omega C_{in}}$$

(6)

$$V_{S1,peak}=\frac{\sqrt{\frac{2P_{out}}{R_L}}\left(\left(D-1\right)\sqrt{\frac{4{\pi }^2{\left(D-1\right)}^2-1}{{\left(D-1\right)}^2}}+{{\displaystyle \sin }}^{-1}\left(\frac{1}{2\pi \left(D-1\right)}\right)+\phi \right)}{2\pi \omega C_{in}\left(D-1\right)}$$

(7)

where symbols carry their usual meaning. As can be noted, V_S1,peak is a function of duty cycle (D), switching frequency (f), and input capacitance (C_in). As for class E^FT, V_S1,peak can be approximated using Equation (9).

$$i_{Cin}\left(\omega t\right)=I_{in}+I_n\sin \left(n\omega t\right)+I_m\sin \left(\omega t+\phi \right)$$

(8)

$$V_{S1}=\frac{-2I_{in}n\pi D+I_{in}\theta n+n{I}_m\cos \left(2\pi D+\phi \right)-n{I}_m\cos \left(\theta +\phi \right)+I_n\cos \left(2n\pi D\right)-I_n\cos \left(nD\right)}{\omega n{C}_{in}}$$

(9)

As opposed to class E and E^FT, i_Cin and V_S1,peak in class EF_n and E/F_n inverters are also a function of n [9,15]. The expression for i_Cin and V_S1 are shown in Equations (8) and (9), respectively. From Equation (9), V_S1,peak is solved numerically and plotted in Figure 4 against ɷ, D, and C_in at the optimum operating condition described in Table 2. In general, it decreases with increasing f and D. Additionally, at any given f and D, V_S1,peak decreases with increasing C_in. It is also to be noted that V_S1,peak for the given case (i.e., k < 1) is higher for EF₂ inverters than class E and EF₃ counterparts. Furthermore, as the odd (particularly, 3rd) harmonic currents are emphasized (second harmonic being bypassed through the auxiliary branch), EF₂ switch voltage peak would have a flattening effect. This is observable in a later section (see Figure 5c).

$$A={\left(C_1{L}_1\pi f_s-\frac{1}{4}\right)}^2\left(\frac{1}{6}+C_s{}^2{L}_s{}^2{\pi }^4{f}_s{}^2+\frac{1}{4}{\pi }^2{C}_s{f}_s{}^2\left(C_s{R}_L{}^2-2L_s\right)\right)$$

(10)

$$B=C_1{}^2{C}_s{}^2{C}_{in}{}^2{L}_1{}^2{L}_s{}^2{\pi }^8{f}_s{}^8+\frac{L_1{\pi }^6{C}_s\left(\left(\left(C_{in}{L}_1{R}_L{}^2-2L_s\left(L_1+L_s\right)\right)C_1-2C_{in}{L}_s{}^2\right)C_s-2C_{in}{C}_1{L}_1{L}_s\right)C_1{C}_{\mathrm{in}}{f}_s{}^6}{4}$$

(11)

$$C=\frac{{\pi }^4}{16}\left(\left(\left(-2C_{in}{L}_1{R}_L{}^2+{\left(L_1+L_s\right)}^2\right)C_1{}^2-2C_{in}\left(C_{in}{L}_1{R}_L{}^2-2L_1{L}_s-L_s{}^2\right)C_1+C_{in}{}^2{L}_s{}^2\right)C_s{}^2+4L_1\left(\left(\frac{L_1}{2}+L_s\right)C_1+C_{in}{L}_s\right)C_1{C}_{in}{C}_s+C_{in}{}^2{C}_1{}^2{L}_1{}^2\right)f_s{}^4$$

(12)

$$D=\frac{{\left(C_{in}+C_1+C_s\right)}^2}{256}-\frac{{\pi }^2{f}_s{}^2\left(\left(-\frac{C_1{}^2{R}_L{}^2}{2}+\left(-C_{in}{R}_L{}^2+L_1+L_s\right)C_1-\frac{C_{in}{}^2{R}_L{}^2}{2}+C_{in}{L}_s\right)C_s{}^2+\left(\left(L_1+L_s\right)C_1{}^2+2C_{in}{C}_1\left(L_1+L_s\right)+C_{in}{}^2{L}_s\right)C_s+C_{in}{C}_1{L}_1\left(C_{in}+C_1\right)\right)}{32}$$

(13)

$$E=\frac{{\left(\frac{1}{2\pi f_s{C}_1}\right)}^3\left(\frac{2L_1}{C_1}-8{\pi }^2{f}_s{}^2{L}_1{}^2\right)}{4{\left(2\pi f_s{L}_1-\frac{1}{2\pi f_s{C}_1}\right)}^2}$$

(14)

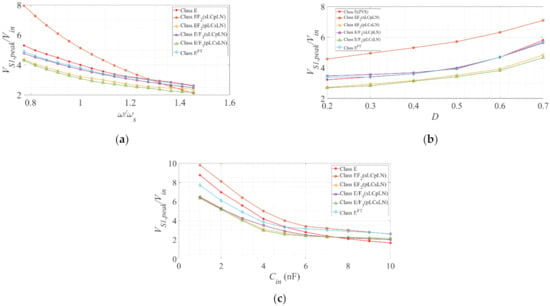
Figure 4. Peak switch voltage (V_S1,peak) of class E, EF₂, and EF₃ against (a) normalized switching frequency (ω/ω_s), (b) duty ratio (D), (c) the input capacitance (C_in) at V_in = 50 V, D_opt = 0.50 (E) or 0.40 (EF₂, E/F₃), f_s ≈ 220 kHz, R_L = R_L,opt, k ≈ 0.30 (EF₂) and 0.67 (E/F₃).

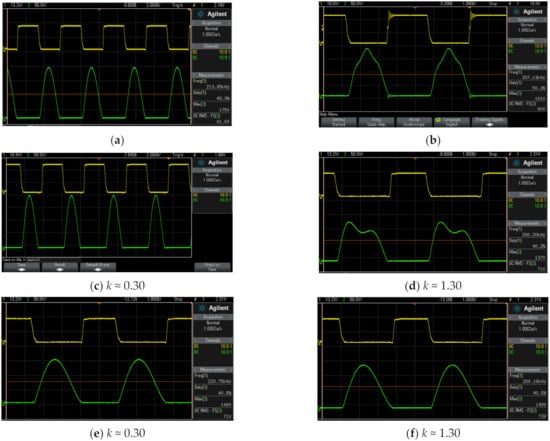
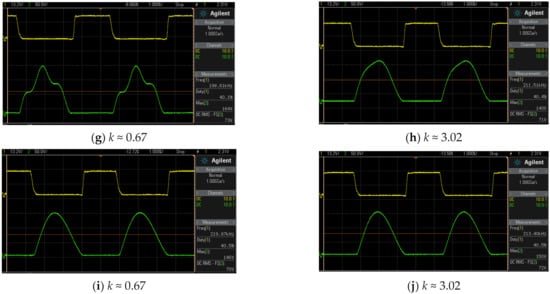
Figure 5. Class E: (a) V_S1; Class E^FT: (b) V_S1; Class EF₂: (c) V_S1 (sLCpLN), (d) V_S1 (sLCpLN), (e) V_S1 (pLCsLN), (f) V_S1 (pLCsLN); Class EF₃: (g) V_S1 (sLCpLN), (h) V_S1 (sLCpLN), (i) V_S1 (pLCsLN), (j) V_S1 (pLCsLN) at f_s ≈ 220 kHz, k ≈ 0.30,1.30 (EF₂) and 0.67,3.02 (E/F₃).

3. Design of the Class E and Enhanced Class E Inverters

In this section, based on the analytical models described elsewhere [1,2,9,15,19,25,26,27], the class E and enhanced class E inverters are designed. The inverters are designed to fulfill an identical requirement, specified in Table 2, to help formulate a fair comparison. The inverters share a common ‘base’ structure of class E with identical input inductance (L_f), resonant components (L_s and C_s), and input capacitance (C_in) [2,28]. In this process, the following assumptions are involved:

• All the components are ideal and do not possess any parasitic resistance, inductance, or capacitances.
• The switch is ideal. The switch on-resistance is zero and off-resistance is infinite. The switching time is negligible.

The design methodology is summarized in Table 3.

Table 3. The design methodology of the class E, EFn, and E/Fn inverters [3,11,26,27,28].

	Class EFnand E/Fn	Class E and EFT
Step 1	Choose Vin, RL, and Pout	Choose Vin and Pout
Step 2	Choose Q, n, and k	Calculate RL,opt
Step 3	Calculate D	Choose n and D
Step 4	Select fs	Calculate phase shift, φ
Step 5	Calculate Cin	Find input capacitance, Cin
Step 6	Calculate L1 and C1	Compute Lf
Step 7	Calculate Lx	Choose fr1 and Q
Step 8	Calculate Cs	Choose fs > fr1
Step 9	Calculate L (Ls + Lx)	Calculate Ls, Cs
Step 10	Calculate RDC	Cex selected for desired VS1,peak and IS1,peak
Step 11	Compute Lf	L is selected to maintain a switch flat top voltage

3.1. The Optimum Load Resistance (R_L,opt)

Class E

To start with the design process, the optimum load resistance for class E has to be determined for the rated output power P_out. Hence, in a transformer less configuration, the optimum load resistance (R_i) is defined as

$$R_i=\frac{8}{{\pi }^2+4}\times \frac{V_{in}{}^2}{P_{out}}$$

(15)

Now, replacing V_in = 50 V and P_out = 25 W in Equation (14) and considering the transformer ratio: n,

$$R_{L,opt}=\frac{8}{{\pi }^2+4}\times \frac{{\left(50\right)}^2}{25}\times \frac{1}{n^2}=\frac{57.68}{n^2}\Omega$$

(16)

The voltage (V_pri) at the primary side of the transformer is a function of V_in and D as defined by the following:

$$V_{pri}=-\frac{4\sin \left(\pi D\right)\sin \left(\pi D+\phi \right)}{{\pi }^2\left(1-D\right)}\times V_{in}$$

(17)

where φ = phase of the resonant tank current and is defined as

$$\varphi =\pi +\arctan \left(\frac{\cos \left(2\pi D\right)-1}{2\pi \left(1-D\right)+\sin \left(2\pi D\right)}\right)$$

(18)

Now, replacing D = D_opt in Equation (18):

$$\varphi =2.574(rad)$$

(19)

Replacing V_in in Equation (17), we obtain:

$$V_{pri}=34.17 \mathrm{V}$$

(20)

However, considering the specified output voltage V_out = 5 V, the required transformer ratio is:

$$n=\frac{34.17}{5}\approx 7$$

(21)

Accordingly, R_L,opt has to be updated as:

$$R_{L,opt}=\frac{57.68}{7^2}\approx 1.17$$

(22)

The load resistance R_L,opt for EF₂ (sLCpLN), EF₃ (sLCpLN), E/F₂ (pLCsLN), and E/F₃ (pLCsLN) is [11,28] selected as 4, 10, 3, and 2 Ω, respectively, to provide specified V_out, P_out and ZVS by varying switching frequency (f).

3.2. The Optimum Duty Ratio (D_opt)

$$D_{opt\left(k\right)}=\frac{0.39275k-0.26593}{k-0.62755}$$

(23)

The optimum duty ratio for class E and EF^FT inverter is 0.50 [2,19,25,26]. The optimum duty ratio for class EF_n and E/F_n inverters (n = 2) can be calculated from Equation (23) as ≈0.40. If n = 3, the concept described in [28] is used to determine the optimum duty ratio.

3.3. The Input Capacitance (C_in,opt)

3.3.1. Class E

The input capacitance (C_in,opt) of the converter is given by:

$$C_{in,opt}=\frac{2\sin \left(\pi D\right)\cos \left(\pi D+\phi \right)\sin \left(\pi D+\phi \right)\left[\left(1-D\right)\pi \cos \left(\pi D\right)+\sin \left(\pi D\right)\right]}{{\pi }^2\omega R_i\left(1-D\right)}$$

(24)

Replacing parametric values in Equation (23) gives us:

$$\begin{array}{c}{C}_{in,opt}\approx \frac{2\sin \left(\pi \times 0.5\right)\cos \left(\pi \times 0.5+2.57\right)\sin \left(\pi \times 0.5+2.57\right)\left[\left(1-0.5\right)\pi \cos \left(\pi \times 0.5\right)+\sin \left(\pi \times 0.5\right)\right]}{{\pi }^2\times 2\pi \times 200k\times 57.68\times \left(1-0.5\right)}\mathrm{F}\\ \approx 2.53 \mathrm{nF}\end{array}$$

(25)

3.3.2. Class EF_n and E/F_n

$$\omega R_{L,opt}{C}_{in}=\frac{0.14069k+0.08613}{k+0.1315}$$

(26)

Using the design curves presented in [11], the C_in for EF₃ (sLCpLN) and E/F₃ (pLCsLN) can be calculated using Equation (26) to achieve ZVS for any given R_L. However, [28] gives us more freedom to select any convenient C_in (and rather vary f) to achieve the ZVS condition. The latter technique is followed in this paper.

3.4. The Input Inductor (L_f)

The input inductance (L_f) of the converter is given by:

$$L_f=2\left(\frac{{\pi }^2}{4}+1\right)\frac{R_i}{f_s}$$

(27)

Replacing parametric values in Equation (27) gives us:

$$L_f=2\left(\frac{{\pi }^2}{4}+1\right)\frac{1.17}{200k}\approx 37 \mu \mathrm{H}$$

(28)

3.5. The Resonant Inductance (L_s)

The resonant inductance can be determined as follows:

$$L_s=\frac{Q_L{R}_{L,opt}}{{\omega }_s}$$

(29)

Replacing the parametric values in (29) and assuming Q_L = 7 and replacing f_s gives us:

$$L_s=\frac{7\times 57.68}{2\pi \times 200000}\approx 321.3 \mu \mathrm{H}$$

(30)

3.6. The Resonant Capacitance (C_s)

Using f_s and L_s as determined in Equation (30) gives us,

$$C_s=\frac{1}{{\omega }_s{}^2{L}_s}$$

(31)

Replacing the parametric values in Equation (31) gives us:

$$C_s=\frac{1}{\left(2\pi \times 200k\right)\times 321 \mu } \mathrm{F}$$

(32)

The design of L_s and C_s are applicable for class E, E^FT, EF_n, and E/F_n inverters [2,9,27].

3.7. The Auxiliary Resonant Inductance (L₁) and Capacitance (C₁)

By choosing k in Equation (33), C₁ is determined. The auxiliary resonant inductance (L₁) is then calculated from Equation (34). Similarly, this design of L₁ and C₁ is applicable for class E, EF_n, and E/F_n inverters [2,9,19,27].

$$k=\frac{C_{in}}{C_1} \mathrm{and} n=\frac{1}{{\omega }_s\sqrt{L_1{C}_1}}$$

(33)

$$L_1=\frac{1}{n^2{\omega }_s{}^2{C}_1}$$

(34)

3.8. The Capacitance (C_ex) and the Shifting Inductance (L)

$$m=\frac{1}{{\omega }_s\sqrt{L{C}_{ex}}} \left(m\approx 5.9\right)$$

(35)

The capacitance (C_ex) and L have to be selected to maintain a flat top switch voltage, as well as for desired peak switch voltage and current. From Equation (35) as in [3], C_ex and L can be determined. Here, m is selected to maintain a flat top switch voltage [3]. Accordingly, C_ex = 2.5 nF and L = 6 µH are selected.

4. Simulation and Experimental Analysis

As mentioned earlier, the inverters are designed to satisfy an identical criterion described in Table 1 for objective comparison. Based on the analytical models, the circuit components for the corresponding inverters are designed. Accordingly, the inverters are tested in LTspice simulation environment, and the prototypes are built to support and verify the simulation data. The list of components used to build and test the prototypes are demonstrated in Table 4. In the next section, the experimental results are presented. In Figure 5a–c, the switch voltage waveforms of class E and EF_n and E/F_n prototype inverters at the optimum operating point are shown. In Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, the performance parameters measured against f, D, k, and R_L are demonstrated. A comparison at the optimum operating point is presented in Figure 6.

Table 4. List of components and measurement devices used in the prototype inverter testing.

Description	Model	Rating/Nominal Values
Mosfet	IRFP460LCPBF	500 V (Vds,br), 20 A (Ids,max), 0.27 Ω (Rds(ON))
Mosfet driver	TC4432CPA	30 V (Vmax), 1.5 A (max. drive current)
Differential probe	-	1/20: 0–60 V1/200: 0–600 V
Current probe	-	100 mV/A,10 mV/A
Lf	-	40 µH
Cin	-	2.60 nF
Ls	-	330 µH
Cs	-	2.40 nF
L1	-	10 µH (kEF2 ≈ 0.30, kE/F3 ≈ 0.67)
		45 µH (kEF2 ≈ 1.30, kE/F3 ≈ 3.02)
C1	-	13 nF (kEF2 ≈ 0.30), 6 nF (kE/F3 ≈ 0.67), 3 nF (kEF2 ≈ 1.30), 1 nF (kE/F3 ≈ 3.02)
RL	-	1Ω
L	-	6 µH
Cex	-	2.5 nF

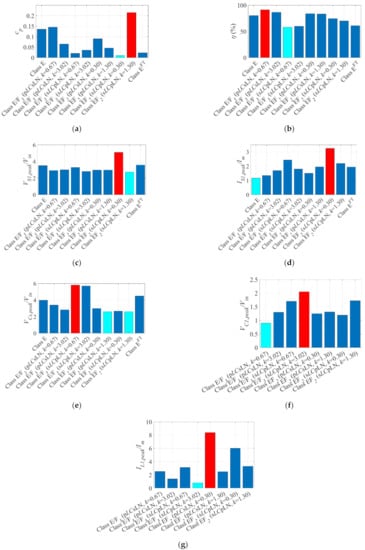
Figure 6. The normalized parameters recorded at the optimum condition (D_opt = 0.50 or 0.40, R_L = R_L,opt, low and high k) (a) power output capability, c_p; (b) Efficiency, η (%); (c) normalized peak switch voltage, V_S1,peak/V_in; (d) normalized peak switch current, I_S1,peak/I_m; (e) normalized peak auxiliary resonant capacitor voltage, V_C1,peak/V_in; (f) normalized peak resonant capacitor voltage, V_Cs,peak/V_in; (g) normalized peak auxiliary resonant current, I_Lc,peak/I_m.

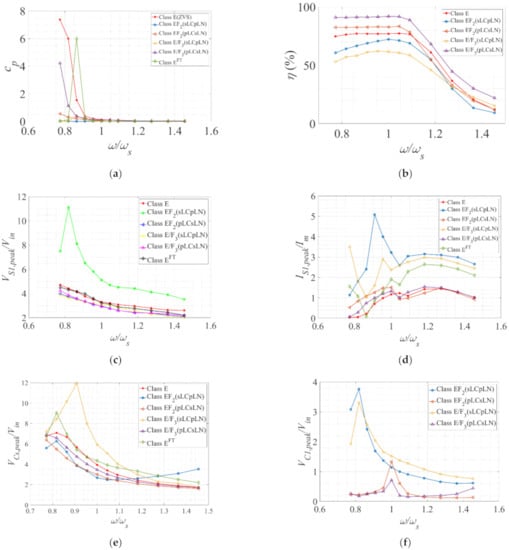
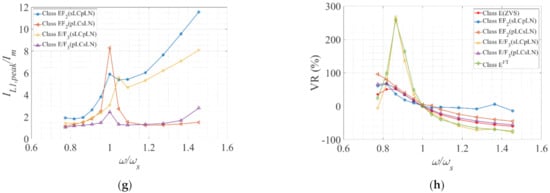
Figure 7. (a) The power output capability (c_p); (b) efficiency (η); (c) the normalized peak switch voltage (V_S1,peak/V_in); (d) the normalized peak switch current (I_S1,peak/I_m); (e) the normalized peak resonant capacitor voltage (V_cs,peak/V_in); (f) the normalized peak auxiliary resonant capacitor voltage (V_C1,peak/V_in); (g) the normalized peak auxiliary resonant current (I_L1,peak/I_m); (h) voltage regulation in percentage against normalized switching frequency (ω/ω_s) at f_s = 220 kHz, D = 0.50 (E), 0.40 (EF₂,E/F₃) k ≈ 0.30 (EF₂) and 0.67 (E/F₃).

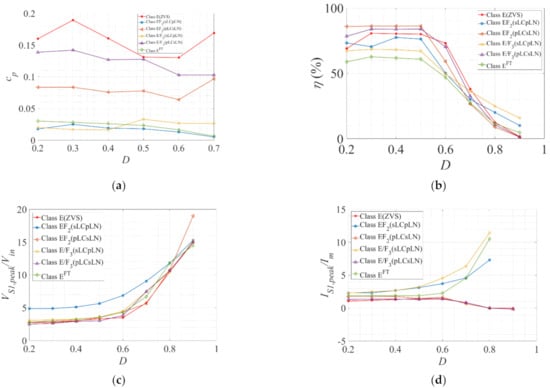
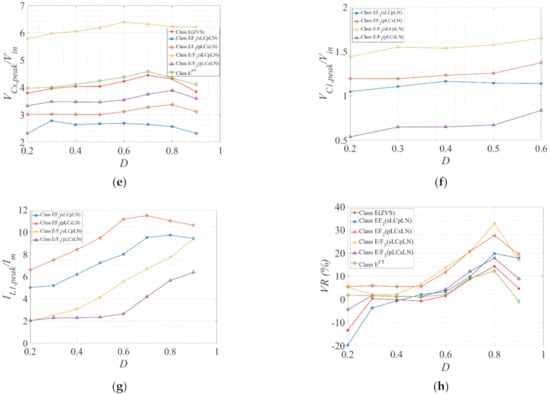
Figure 8. (a) The power output capability (c_p); (b) efficiency (η); (c) the normalized peak switch voltage (V_S1,peak/V_in); (d) the normalized peak switch current (I_S1,peak/I_m); (e) the normalized peak resonant capacitor voltage (V_cs,peak/V_in); (f) the normalized peak auxiliary resonant capacitor voltage (V_C1,peak/V_in); (g) the normalized peak auxiliary resonant current (I_L1,peak/I_m); (h) voltage regulation in percentage against duty ratio (D) at f_s ≈ 220 kHz, k ≈ 0.30 (EF₂) and 0.67 (E/F₃).

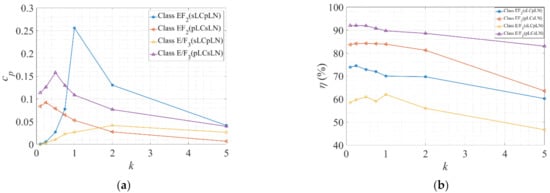
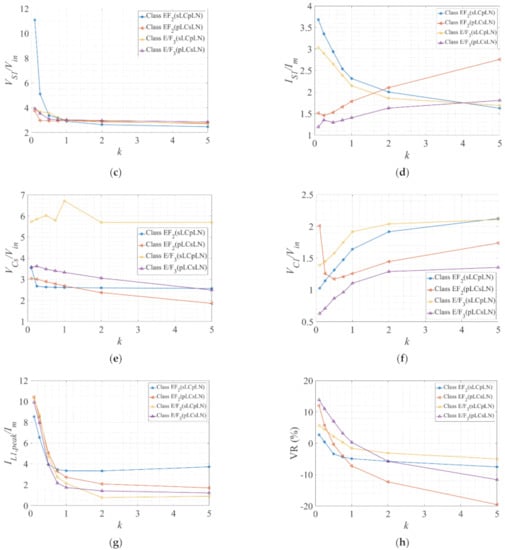
Figure 9. (a) The power output capability (c_p); (b) efficiency (η); (c) the normalized peak switch voltage (V_S1,peak/V_in); (d) the normalized peak switch current (I_S1,peak/I_m); (e) the normalized peak resonant capacitor voltage (V_cs,peak/V_in); (f) the normalized peak auxiliary resonant capacitor voltage (V_C1,peak/V_in); (g) the normalized peak auxiliary resonant current (I_L1,peak/I_m) (h) voltage regulation in percentage against capacitance ratio (k) at f_s ≈ 220 kHz, D = 0.50 (E) or 0.40 (EF₂, E/F₃).

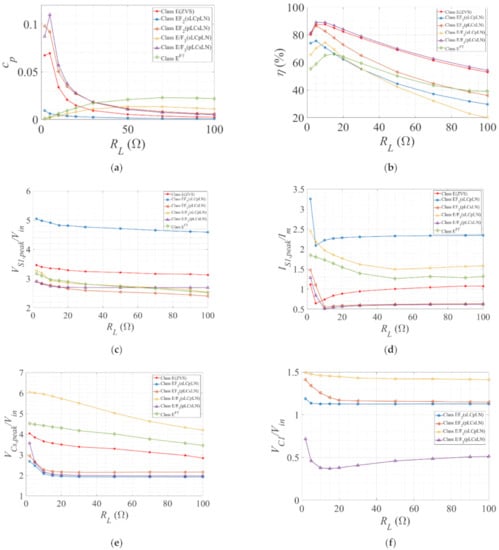
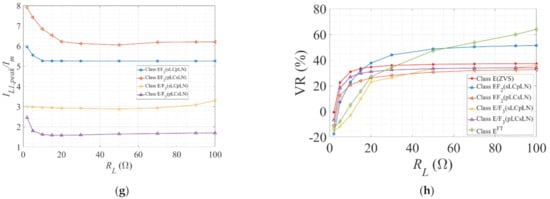
Figure 10. (a) The power output capability (c_p); (b) efficiency (η); (c) the normalized peak switch voltage (V_S1,peak/V_in); (d) the normalized peak switch current (I_S1,peak/I_m); (e) the normalized peak resonant capacitor voltage (V_cs,peak/V_in); (f) the normalized peak auxiliary resonant capacitor voltage (V_C1,peak/V_in); (g) the normalized peak auxiliary resonant current (I_L1,peak/I_m); (h) the voltage regulation (VR) in percentage against load resistance (R_L) at f_s = 220 kHz, D = 0.50 or 0.40, k ≈ 0.30 (EF₂) and 0.67 (E/F₃).

5. Results and Discussion

The inverters were experimentally tested by varying the switching frequency (f), duty cycle ratio (D), capacitance ratio (k), and the load resistance (R_L). The primary objective was to evaluate the voltage and current at different points of interest. These parameters would help define the component ratings, the size of the inverter, and relative complexity in control. Eventually, a qualitative comparison can be formulated. The results are accumulated in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. The voltage regulation is defined as follows:

$$VR\left(\%\right)=\frac{V_{out,rms}-V_{out,rated}}{V_{out,rated}}\times 100$$

(36)

In addition, the efficiency is measured as follows:

$$\eta =\frac{P_{out}}{P_{in}}\times 100=\frac{V_{rms}{I}_{rms}}{V_{dc}{I}_{dc}}\times 100$$

(37)

Table 5 demonstrates a comparative cost difference of the class E and enhanced class E inverters. As low power inverters, the components are small in size. Hence, the induced cost for a single inverter is low. However, in general, the cost of building enhanced class E inverters could be more than 20% than that of the class E inverter. In addition, the cost would increase nonlinearly with the power rating of the inverter.

Table 5. Cost Comparison Chart.

Class E			Class EFn (n = 2)			Class E/Fn (n = 3)
Components	Unit	Price	Components	Unit	Price	Components	Unit	Price
Input inductor	01	x	Input inductor	01	x	Input inductor	01	x
Input capacitor	01	y	Input capacitor	01	y	Input capacitor	01	y
Resonant inductor	01	x	Resonant inductor	02	2x	Resonant inductor	02	2x
Resonant capacitor	01	y	Resonant capacitor	02	2y	Resonant capacitor	02	2y
Switch	01	z	Switch	01	z	Switch	01	z
Total cost		2x + 2y + z	Total cost		3x + 3y + z	Total cost		3x + 3y + z

x = unit price of the input inductor for class E, y = unit price of the input capacitor for class E, z = unit price of the switch.

The resonant tank of the inverters is designed to resonate at f_r with a predefined quality factor Q. By varying the switching frequency f, the inverter rms output voltage, output power, peak switch voltage and current, and peak voltage across the resonant capacitors are measured. It was observed that the optimum operability (i.e., ZVS) sustained at the vicinity or close proximity of the resonant frequency f_r. The power output capability was maximum in this region. As f increased, the resonant tank, which behaves like a bandpass filter, blocked the higher harmonics. Resultantly, the power flow was curtailed. Because of the higher input impedance (Z_in), the efficiency also dropped. In general, the peak switch voltage (V_S1,peak) and the peak resonant capacitor voltage (V_C1,peak) dropped with increasing frequency. This is due to the capacitor current (i_Cin), which also reduces with increasing f. The lowest V_C1,peak were recorded for the pLCsLN configurations for k < 1. However, as more current was being diverted through the switch (S₁) from the auxiliary networks, there was an apparent rise in the peak switch current (I_S1,peak) for sLCpLN configurations. These results are demonstrated in Figure 7a–h.

The optimum duty ratio (D_opt) of class E inverter was 0.50, while for class EF_n and E/F_n inverters, it was approximately 0.40. Any deviation from these values would incur higher switching losses in the respective inverter type due to the loss of soft switching operation. In Figure 8a–h, the inverters were evaluated by varying the duty ratio (D) while operating at the corresponding optimum load (R_L,opt) and f_s. It was observed that at extreme D (≥0.7), the energy delivered to the resonant tank deteriorated due to longer switch ON time. The energy stored in the input inductor (L_f) increased with D but mostly diverted through the switch S₁. Hence, the switch voltage and current increases gave rise to switch conduction losses. Subsequently, the efficiency, while remaining fairly constant, dropped at extreme D. The highest efficiency was recorded for class E and the pLCsLN configurations at around 80–90% in the proximity of D_opt. The peak resonant capacitor voltages were relatively unaffected by D. The peak switch current (I_S1,peak) was significantly higher (2–3 times) for sLCpLN configurations at k < 1. However, this could be lowered significantly by operating the inverters at higher k (>1). This fact is demonstrated in Figure 8c. The peak auxiliary resonant current (I_L1,peak) in the sLCpLN configurations became significantly higher at extreme D however, this could be avoided by increasing k.

The ratio k is defined by the ratio of the input capacitance to the auxiliary resonant capacitance (C_in/C₁). The variation k can be translated as the variation of the auxiliary resonant components (L₁ and C₁) while keeping n constant. Hence, by definition, increasing k means decreasing C₁ and increasing L₁ and vice versa. In general, with increasing k, the rms output voltage and power output capability (c_p) drops. The efficiency (η) also drops with higher k. This is shown in Figure 9a–h. k < 1, V_S1,peak, and I_S1,peak for sLCpLN configurations were significantly higher (2–3 times) than class E and pLCsLN configurations, as mentioned earlier. This was mainly due to the excessive energy that was stored in the large resonant capacitor C₁ and subsequently dissipated through the switch at the turn ON instant. As k increased, the resonant inductance L₁ became bigger and diverted almost a constant current through S₁. Hence, V_S1,peak and I_S1,peak remained fairly constant at higher k. However, because of smaller C₁ at higher k, a relatively larger voltage was induced across C₁ (i.e., V_C1,peak).

On the other hand, the increasing load resistance (R_L) drove the inverter operating from continuous conduction mode (CCM) to the discontinuous conduction mode (DCM). Hence, V_out,rms and c_p decreased, with increasing R_L being maximum at R_L,opt. The peak switch voltage and current (V_S1,peak and I_S1,peak) remained fairly constant over the entire load range. V_C1,peak and I_L1,peak were relatively higher (2–4 times) for sLCpLN configurations. The voltage regulation (VR) was higher at lower loads. The results are demonstrated in Figure 10.

In Figure 6, the performance parameters recorded at the optimum operating point (D_opt = 0.50 or 0.40, R_L = R_L,opt) are demonstrated. The maximum and minimum quantities are marked in ‘red’ and ‘sky blue’, respectively. As obvious from Figure 6a, c_p is maximum for class E and EF₂ (sLCsLN) configuration at k > 1, recorded as 0.1356 and 0.215, respectively. The lowest is 0.01 for EF₂ (sLCsLN) configuration at k < 1. Again, as shown in Figure 6b, the class E and pLCsLN configurations demonstrated higher efficiency compared to the sLCpLNs. The maximum and minimum efficiency were recorded for class E/F₃ (pLCsLN) (k < 1) and E/F₃ (sLCpLN) (k < 1) as 91% and 58%, respectively. However, η did not vary largely with k. The peak switch voltage in Figure 6c was generally lower for higher k. The maximum and minimum are recorded for class EF₂ (sLCpLN) at 5.1 and 2.74 for k < 1 and k > 1, respectively. However, a further reduction of V_S1,peak was possible by increasing k, as demonstrated in Figure 9c. The peak switch current (I_S1,peak) was generally higher in sLCpLN compared to the pLCsLN configurations. The highest and lowest I_S1,peak were recorded at 3.25 and 1.17 for class EF₂ (sLCpLN) (k < 1) and class E, respectively, as demonstrated in Figure 6d. From Figure 9d, it can be deduced that selecting k > 1 and k < 1 for sLCpLN and pLCsLN can minimize I_S1,peak further. The peak voltage across the resonant capacitor (V_C1,peak) was lower for pLCsLN configurations (2–3 times than sLCpLN in general), as can be observed in Figure 6f. This is expected as the voltage across the load network is shared across the capacitors Cs and C1 for pLCsLN configurations. On the other hand, the peak current in the auxiliary resonant network (I_L1,peak) is notably higher for k < 1 (See Figure 9g). The summary of these findings and optimum operating conditions for enhanced inverters are accumulated in Table 6.

Table 6. Summary.

Efficiency (η)
1	Class EFn and E/Fn inverters operate more efficiently at optimum load at: low Q (low Ls) low k D = 0.2 − 0.6
2	Efficiency wise, class EF2 (pLCsLN) and E/F3 (pLCsLN) inverters outperform class E and others with maximum efficiency recorded as 86 and 94%, respectively, at the optimum operating point.
The power output capability (cp)
1	The power output capability (high output power at lower switch stress) of class EF2 (pLCsLN) and E/F3 (pLCsLN) inverters is on par with class E at the optimum load: For D = 0.4 − 0.7 For k < 5
2	Highest power output capability at the optimum operating point is recorded for class EF3 (pLCsLN) as ≈0.10.
The output voltage and power (Vout and Pout)
1	The average output power of class E is higher than the class EFn and E/Fn inverters across the switching frequency (fs), duty cycle ratio (D), capacitance ratio (k), and the load resistance (RL).
2	The output voltage and output power of class EF2 (sLCpLN) are not severely affected by k.
The peak switch voltage (VS1,peak)
1	The peak switch voltage for class EF2 (pLCsLN) and E/F3 (pLCsLN) inverters are 20–30% lower than class E, particularly: at D = 0.2 − 0.7 for any load condition for any k at the optimum load
2	The peak switch voltage of class EF2 (sLCpLN) and E/F3 (sLCpLN) are 40–50% higher than the other inverters at the optimum operating point. However, they are considerably higher, particularly: at ω/ωs << 1 at k < 0.50
3	Comparatively, the peak switch voltage is not affected considerably by the load change.
The peak switch current (IS1,peak)
1	The peak switch current for class EF2 (pLCsLN) and E/F3 (pLCsLN) inverters is lower than class E for any D and load condition.
2	The peak switch current of class EF2 (sLCpLN) is comparatively higher than class E and other variations of EFn and E/Fn at the optimum load and: for D > 0.65 and k < 1
The peak resonant capacitor voltage (Vcs,peak)
1	The peak resonant capacitor voltage is approximately 50% lower in class EFn and E/Fninverters than that in class E for any D, k and load condition
The peak capacitor voltage (VC1,peak) in the lumped network
1	The peak capacitor voltage in the auxiliary network is 2 to 5 times lower in class EF2 (pLCsLN) and E/F3 (pLCsLN) inverters than in class EF2 (sLCpLN).
2	The peak auxiliary resonant capacitor voltage of class EF2 (sLCpLN) is, particularly, very high: at k >> 5 at D ≥ 0.65
The peak current (IL1,peak) in the lumped network
1	The peak auxiliary resonant current in class EFn and E/Fn inverters is on average 2–3 times higher for k < 1.
2	This current is particularly higher for class EF2 (sLCpLN) inverter

In addition to the comparison presented in Figure 7, Figure 8, Figure 9 and Figure 10, the switching losses and THD are demonstrated in Figure 11 and Figure 12 respectively. As can be observed, the switching loss is minimized due to application of ZVS and ZVDS. The percentage loss is maximum for class EF₂ (sLCpLN) at approximately 3.6%. The loss is minimum for class E/F₃ (pLCsLN) inverters at 3.08%. The THD can be greatly improved by adding extra filter at the output of the inverter.

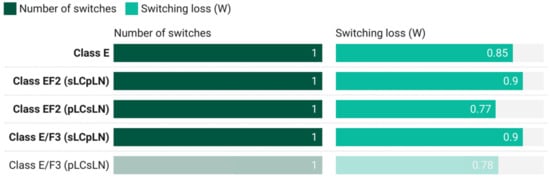
Figure 11. The switching loss in the class E and enhanced class E inverters.

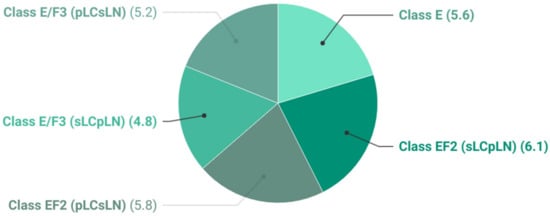
Figure 12. The THD_v of class E and enhanced class E inverters at optimum condition.

6. Conclusions

In this paper, the class E and enhanced class E inverters are investigated for comparative performance analysis. Extensive simulation and experimental testing are performed in this regard. It is observed that the enhanced class E inverters excel beyond the conventional ZVS class E inverters in terms of efficiency and power output capability. This is also in line with the research published elsewhere. To be specific, the class EF₂ (pLCsLN) and E/F₃ (pLCsLN) inverters demonstrate higher efficiency (8–10% higher) compared to other configurations. This is mainly due to the lowered switch conduction losses. In addition, the peak switch voltage and current are significantly lower (≈20–30%) in these inverters at the optimum operating condition while k > 1, and k = C_in/C₁. On the other hand, the peak capacitor voltages in all enhanced versions are lowered by 2–3 times on average. However, the peak current in the lumped auxiliary network of these inverters are 2–3 times higher. Based on the simulation and experimental results, it is recommended that class EF_n and E/F_n inverters are operated at 1 < k < 5 and D = 0.3–0.6 for sustained higher efficiency, power output capability, and lower switch stress.