Abstract
In the development of artificial intelligence (AI), games have often served as benchmarks to promote remarkable breakthroughs in models and algorithms. No-limit Texas Hold’em (NLTH) is one of the most popular and challenging poker games. Despite numerous studies having been conducted on this subject, there are still some important problems that remain to be solved, such as opponent exploitation, which means to adaptively and effectively exploit specific opponent strategies; this is acknowledged as a vital issue especially in NLTH and many real-world scenarios. Previous researchers tried to use an off-policy reinforcement learning (RL) method to train agents that directly learn from historical strategy interactions but suffered from challenges of sparse rewards. Other researchers instead adopted neuroevolutionary (NE) method to replace RL for policy parameter updates but suffered from high sample complexity due to the large-scale problem of NLTH. In this work, we propose NE_RL, a novel method combing NE with RL for opponent exploitation in NLTH. Our method contains a hybrid framework that uses NE’s advantage of evolutionary computation with a long-term fitness metric to address the sparse rewards feedback in NLTH and retains RL’s gradient-based method for higher learning efficiency. Experimental results against multiple baseline opponents have proved the feasibility of our method with significant improvement compared to previous methods. We hope this paper provides an effective new approach for opponent exploitation in NLTH and other large-scale imperfect information games.
1. Introduction
Poker is often regarded as a representative problem for the branch of imperfect information games in game theory. It naturally and elegantly captures the challenges of hidden information for each private player [1]. The complexity of its solving method is much higher compared with perfect information games, such as Go [2]. As the most strategic and popular variation of poker, Texas Hold’em poker has been widely studied for years. AI researchers are working to find its solving method just as in AlphaGo or AlphaZero. However, Texas Hold’em poker contains additional challenges of imperfect information, dynamic decision-making, and misleading deceptions, as well as multistage chip and risk management, etc., which restrict it from being solved perfectly by AI. Most researchers are firmly convinced that the related technology behind the Texas Hold’em Poker’s solution can be extended to multiple real-word applications, such as strategic portfolio, auction, finance, cybersecurity, and military applications [3], and the promising application prospect motivates continuous study until now.
Texas Hold ’em is an interactive decision poker game consisting of four stages: preflop, flop, turn, and river. At each stage players can bet different amounts of money based on private hands and public cards. They can only obtain rewards after taking a series of sequential actions until there is only one player remaining or the end of the last river stage. According to the limitation of betting amount, Texas Hold’em poker can be divided into either a limited game or a no-limit game. The number of their information sets are about and , respectively [4]. It is obvious that solving no-limit Texas Hold’em (NLTH) is much more complex and resource-consuming, which makes NLTH an important benchmark in the domain of large-scale imperfect information games. The most recent and advanced progress of NLTH was achieved by two research teams from the University of Alberta (UoA), and Carnegie Mellon University (CMU). They have almost simultaneously put forward AI programs—Libratus (from CMU) [5] and DeepStack (from UoA) [6]—to solve two-player NLTH in 2017, as well as a Superhuman AI—Pluribus (from CMU) for multiplayer NLTH in 2019 [1].
Despite the above equilibrium-based solutions achieving highlight performances, their lack of adaptability to opponents seems to be a problem. That is, no matter what kind of opponents are there, these AIs always play the same way in order to ensure equilibrium. This is usually not the exact solution we want.
Another approach to deal with this problem is opponent exploitation. Simply put, opponent exploitation is a class of methods that specially design agents to target specific opponents. Sometimes, this approach can achieve greater rewards from the opponents than the equilibrium-based solutions, as it pursues the maximum individual utility against current opponent strategy rather than equalize all possible opponent strategies indiscriminately. Related research for opponent exploitation in NLTH can be seen in several previously published studies [7,8,9,10,11,12], using advanced techniques including deep reinforcement learning, neuroevolution, etc. While methods in these works show practical effectiveness, there still exist some disadvantages that need to be improved. For example, due to the multi-stage sequential decision process and high dimensional action/state space in NLTH, the reinforcement learning (RL) method typically confronts the challenge of sparse rewards that only obtain non-zero values at the final steps [9,10], whereas the neuroevolution (NE) method typically suffers from high sample complexity and struggles to optimize a large number of parameters [11,12]. Generally speaking, these problems can be summed up as ineffective and inefficient learning. For opponent exploitation in a large-scale problem such as NLTH, what we most want to achieve is not merely learning to exploit our opponents as much as possible (effectiveness). We also want to make the learning process as fast as possible (efficiency), which can greatly reduce the consumption of computing resources and time. Thus, developing an effective as well as efficient learning method for opponent exploitation in NLTH is the main motivation of our work.
In this paper, we propose a novel method combining neuroevolution (NE) with reinforcement learning (RL) for opponent exploitation in NLTH. The key insight of our method (NE_RL) is to incorporate NE’s ability to address the challenge of sparse action reward in the RL framework by evaluating returns of entire game episodes (the amount of chips you win/lose) to form a fitness metric. Additionally, RL’s ability to leverage powerful gradient descent methods can in turn help improve the learning efficiency in NE, which will greatly benefit the training process. In addition, NE_RL extends NE’s population-based approach to build two separate populations that evolved by NE and RL seperately. Synchronous interactions within and between the populations can make the learning process more stable and robust. These improvements together make NE_RL a more effective and efficient opponent exploitation method compared to the previous NE- or RL-only methods. It should be noted that the NE method in this work refers to using evolutionary computation to optimize the weights of neural networks with fixed network topologies. The topologies or architectures are manually designed and improved, as discussed in Section 3.2.
2. Background
How AI can solve Texas Hold ’em poker has been a major challenge in recent years. One popular approach to achieve this goal is equilibrium-based solutions, which include the most part of state-of-the-art algorithms [2,5,6,13]. However, these leading “game-solving” paradigms still have some deficiencies in some aspects. For example, they need a large amount of computing resources to obtain so-called equilibrium solutions, and these equilibrium solutions do not take into account any advantage of opponents’ weakness that can be exploited, which corresponds to poor dynamic adaptiveness [14]. More importantly, the theoretical guarantees of the equilibrium no longer stand in multiplayer settings [15].
Basically speaking, the equilibrium solutions work under the assumption that the opponent is perfectly rational and then conduct a no-regret search or fictitious self-play along the entire (or compressed) game tree so as not to lose in expectation, no matter what the opponent does [16]. However, the assumption is makes it difficult to win often against specific opponents (either weak or skilled). Alternatively, we can consider one’s goal as learning to play and maximizing one’s rewards against some specific opponent groups through repeated strategic interactions (which is exactly the core of NLTH). In such a case, an equilibrium strategy is perhaps not so optimal and this is the problem that opponent exploitation mainly deals with. To illustrate at a high level, opponent exploitation means to win over one’s opponents as much as possible [17]. One possible approach to achieve this goal is to explicitly identify opponents’ hand beliefs [8] or strategy styles [18] and then make decisions accordingly. Similar methods can be collectively called “explicit exploitation” and are quite easy to understand. However, these types of methods rely very much on the accuracy of identification, which is as difficult (if not more) as solving the game itself and requires either sufficient domain knowledge or a mass of labeled data. Another possible approach called “implicit exploitation” seems to be more feasible [19]. Its main idea is to improve the rewards directly against the opponents through repeated interactions and a policy optimization function, which is similar to the idea of reinforcement learning. The biggest difference compared to “explicit exploitation” is that it does not explicitly reason about exploitable information about the opponents but instead implicitly learns to win through end-to-end training. Generally speaking, “implicit exploitation” is a more effective and straightforward class of opponent exploitation methods. The opponent exploitation methods mainly discussed in this paper all fall into this class.
In 2009, Nicolai and Hilderman first put forward the idea to use a neuroevolutionary (NE) method in NLTH [12]. Their NE agent was composed of 35-20-5 feed-forward neural networks, with a sigmoidal function applied at each level. However, their experimental results showed that the skill level of the evolved agents is limited, even though evolutionary heuristics such as co-evolution and halls of fame were used. In 2017’s AAAI conference, Xun Li presents a NE method to evolve adaptive LSTM (Long Short Term Memory Network) poker players featuring effective opponent exploitation [11]. His main contribution lies in the introduction of the LSTM to extract useful features and learn adaptive behaviors in NLTH. However, the use of the NE method needs a huge number of training episodes and a large amount of computing resources to update generation by generation, mainly due to high sample complexity facing a large-scale problem such as NLTH. Some researchers instead tried to use more sample-efficient reinforcement learning (RL) methods to train NLTH agents [9,10]. However, the multi-stage sequential decision process in NLTH with sparse rewards imposes restrictions on the policy gradients optimization function in many RL methods. As a result, efficient opponent exploitation in NLTH still remained a problem to be solved in recent years. Combining the NE method with the RL method is a general idea to complement each method’s flaws and use the strengths of both. In 1991, Ackley and Littman first showed the combination of evolutionary and gradient operators to be significantly more effective for agent survival in an uncertain environment [20]. In 1997, Chowdhury and Li used “messy genetic algorithms” to overcome the disadvantages of traditional RL techniques for fuzzy controllers [21]. In 2007, Lin et al. proposed R-HELA, a “reinforcement hybrid evolutionary learning algorithm”, for solving various control problems with uncertainty [22]. Later, in 2011, Koppejan and Whiteson presented the “neuroevolutionary reinforcement learning” method for generalized control of simulated helicopters and demonstrated that neuroevolution can be an effective tool for complex, online RL tasks [23]. More recently, similar ideas have been applied to some small-scale video games [24,25]. Nevertheless, applying such ideas in large-scale games such as NLTH has not been studied yet to the best of our knowledge.
In this work, we focus on the two-player and no-limit version of Texas Hold’em Poker, i.e., Heads-Up No-Limit Hold’em (HUNL). In HUNL, two players compete for money or chips contributed by both of them, i.e., the pot. At the beginning of each game, both players are forced to post a bet into the pot, i.e., the blinds. Then each player is dealt two cards, i.e., the hole cards, from a standard 52-card poker deck. The hole cards are private for the receiver, thus making the states of the game partially observable. The game is divided into four betting rounds: preflop, flop, turn, and river. The players act alternately in each betting round. Players must choose one of the following actions when it is their turn to act: call, check, raise, or fold. If a player chooses to call, that player will need to increase his/her bet until both players have the same number of chips. If one player raises, that player must first make up the chip difference and then place an additional bet. Check means that a player does not choose any action on the round but can only check if both players have the same chips. If a player chooses to fold, the game ends, and the other player wins the game. When all players have equal chips for the round, the game moves on to the next round. As the game proceeds, five cards are dealt face up on the table. Each of them is a community card, and the set of community cards is called the board. Specifically, the board is empty in preflop; three community cards are dealt at the beginning of the flop, a fourth community card is dealt at the beginning of the turn, and the last community card is dealt at the beginning of the river. The board is observable to both players throughout the game. If neither player has folded by the end of the river, the game goes into a showdown. In addition, at any point of the game, if a player who has moved all-in contributes no more chips to the pot than the other, the game also goes into a showdown. In this case, unfinished betting rounds are skipped, and the board is completed immediately. In a showdown, each player combines the hole cards with the board and chooses five out of the seven cards (two hole cards plus five community cards) to form the best possible hand. The player with the better hand wins the pot. If the two hands are equally strong, the players split the pot.
3. Methods
This paper introduces a new method, NE_RL, for opponent exploitation in NLTH. It incorporates NE’s indifference to the sparsity of reward distribution and RL’s gradient-based method to improve learning efficiency. Figure 1 illustrates the hybrid framework of NE_RL. It is divided into two parts by a dotted line. The left part shows a standard off-policy RL agents’ training process and the right part is a standard neuroevolutionary agents’ training process. The opponent pool contains a set of baseline opponent strategies for training. At the beginning, two populations of agents are initialized with different parameter distributions. Then, the individuals from the populations play full NLTH games against one (or more) specific opponent(s) sampled from the opponent pool separately. The populations are continuously updated by NE and RL respectively. The interactions between these two parts are arranged in the following ways (as shown by the red arrow): On the one hand, the trajectories generated by the NE agents can provide diverse experiences for the replay buffer to train the RL agents. On the other hand, we periodically use the RL agents to replace the worst performing NE agents to inject gradient information into the NE population (this process is abbreviated as transfer). There are several advantages to these interactions. First, the recycling of the NE agents’ training data makes full use of information from each agent’s experiences. Most samples can be used for further training rather than simply being discarded. As a result, the learning efficiency is improved with less game samples. Second, the gradient information provided by the RL agents can help guide the evolving directions for the NE population, which leads to faster learning compared to the NE-only method. Additionally, both the NE agents and the RL agents conduct population-based training, which aims to produce moderate diversity and redundancy. With diversity and redundancy, our method can explore the strategy space on a larger scale during the learning process. We argue that these two properties respond well in practice to the challenges of large-scale and high-complexity problems such as NLTH. Experimental results against multiple baseline opponents have proven the feasibility of our method with a significant improvement compared to the previous NE and RL methods.
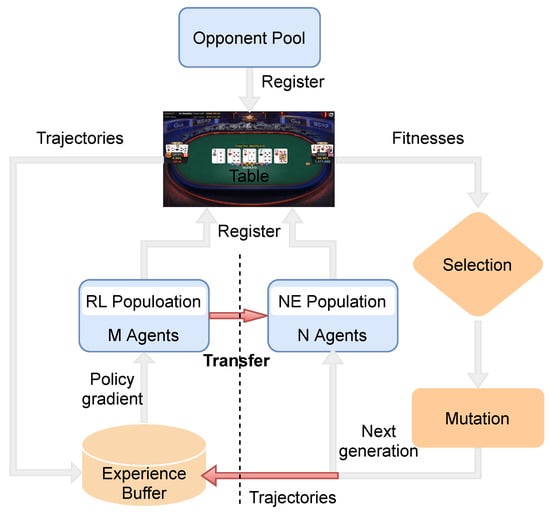
Figure 1.
High-level illustration of the NE_RL method for opponent exploitation in NLTH.
Further details are described in the following subsections on two levels: learning methods and architectures. Section 3.1 separately introduces the learning methods (NE and RL) used in our work. Section 3.2 mainly describes how to organically combine these two learning methods together and then introduce the fundamental network architectures that the learning methods can apply to.
3.1. Introductions of NE and RL
NE is a class of black box optimization algorithms typically used for neural network (NN)-based modules [26]. Inspired by natural evolution, the general flow of NE is as follows: At every iteration, a population of NN’s parameter vectors is perturbed by mutation or a crossover operator and their objective function values (“fitness”) are evaluated. The highest scoring parameter vectors are then recombined to form the population for the next iteration. There are various implementations of NE depending on the specific problem and context. In our method, in order to incorporate with RL we adopted a standard NE algorithm that proceeds as follows: A population of NE agents is initialized with random weights. They are then evaluated in interactions with the same opponent concurrently and independently. Each agent’s cumulative rewards in the current generation are averaged to serve as its fitness. A selection operator then selects a portion of the population for survival with a probability commensurate with their relative fitness scores. The agents in the population are then probabilistically perturbed through mutation and crossover operations to create the next generation of agents. A select portion of agents with the highest relative fitness are preserved as elites and are shielded from the mutation step.
The RL population composed of multiple agents is initialized with different parameter distributions and updated independently by the same RL method. The RL method in this work typically refers to any off-policy reinforcement learner that utilizes a cyclic replay buffer R maintained by both the RL agents and the NE agents. Trajectories in R come from separate game episodes that contain a tuple (,,,), which refers to the current state, action, observed reward, and the next state, respectively. Here we take a Deep Q-learning Network (DQN) method as example to illustrate a representative learning process of RL. First, compute the current state’s estimated Q-value via ( refers to the parameters of the Q-networks). The corresponding loss function is:
where:
Then, use an optimizer such as Adam to minimize the loss function and perform a gradient descent update. Usually the policy of the DQN agent during training is a noisy version of the learned policy: , where is a greedy policy over the estimated Q-value at time step t and the value of decays with t. The additional noise is for the purpose of exploration in the RL agents’ action space.
3.2. Combination of NE and RL
The main idea of our method, NE_RL, is using the advantages of the combination of NE and RL. Algorithm 1 provides a detailed pseudocode as well as the complete procedure of NE_RL. The size of the NE population (N), the size of the RL population (M), and the size of the replay buffer R are important hyperparameters of the algorithm. refers to the max generations of algorithm updates. and are computed as each agent’s fitness value via a Tournament function, which conducts full game episodes and returns averaged game results. The action–reward tuples of are extracted from the game episodes and restored in the replay buffer so that the RL agents can continually learn from them. The RL agents use DQN to update their action-value function Q with weights and represent the q-target value, which is then used along with the predicted q-eval value to compute the mean square loss function . At first sight, one may find it similar to a standard NE method. Compared to NE, which just uses episodes to compute a fitness score, NE_RL also looks into the episodes to extract experience to learn. It stores both the NE agents’ and the RL agents’ experiences in its replay buffer R rather than disregard them immediately. The RL agent can then sample a small batch from R and use it to update its parameters by gradient descent. It is obvious that with this mechanism we can extract maximal information from each individual experience and improve the method’s sample efficiency.
As the fitness score captures an individual’s episode-wide return, the selection operator imposes strong pressure in favor of individuals with higher episode-wide returns. Since the replay buffer consists of the experiences gathered by these individuals, this process skews the state distribution towards regions with higher episode-wide returns. This is a form of implicit prioritization that favors an experience with a higher long-term return, and is effective for NLTH with long time horizons and sparse rewards. RL agents using this state distribution tend to learn strategies to achieve higher episode-wide returns. In addition, a noisy version of the RL agent is used to generate an additional experience for the replay buffer. In contrast to the population of agents that explore by noise in their parameter space (neural weights), the RL agents explore through noise in their action space. These two processes complement each other and form an effective exploration strategy to better explore the policy space.
The final procedure of NE_RL involves contributions from RL agents to NE population. Periodically, the RL agents’ parameters are duplicated into the NE population; we define this process as transfer. It is the key process in which the NE population can directly receive the information learned through gradient descent. If the information from the RL agents is good, it will survive the selection operator and pass on to the NE population via the crossover operator. Otherwise, it will simply be discarded. Such a mechanism only allows constructive information to flow from the RL agents to the NE population.
| Algorithm 1 Main procedure of NE_RL |
|
Up to now, we have provided a complete introduction of our NE_RL method. However, these introductions are all about the agents’ learning method, that is, how to combine NE with RL at the method design level. In order to make such a hybrid learning method possible to implement, the fundamental network architecture of the RL agents and the NE agents should be the same. As shown in Figure 2 and Figure 3, we introduce two architectures that are used in our work.
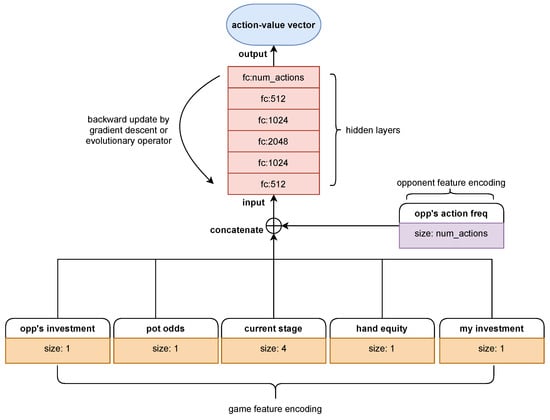
Figure 2.
Arc_pro, a prototype architecture for the NE and RL agents. It receives domain-specific inputs and transfers to output action values with several layers of full-connected (fc) neural networks.
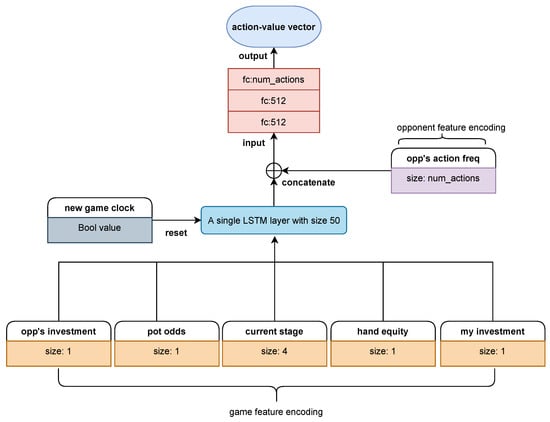
Figure 3.
Arc_lstm, an improved architecture compared to Arc_pro. The biggest difference is the addition of an LSTM layer, which helps to extract useful temporal features and learning adaptive behaviors.
Figure 2 is a prototype architecture mainly designed for early experiments on the combination of the NE and RL methods (henceforth referred to Arc_pro). As seen in Arc_pro, it receives inputs containing two sets of domain-specific features. One (game feature encoding) is made up of detailed information about the current game in which the agent is playing, and the other (opponent feature encoding) is a global vector that tracks the overall performance (simply represented by frequency of actions) of the opponent against which the agent is playing. They are concatenated to form the input tensor and then transferred into hidden layers that consist of fully connected neural networks with the size 512-1024-2048-1024-512. Additionally, the output tensor is mapped to the size of the action space and transformed into an action-value vector. The action space is continuous and infinite in NLTH; however, we observed that it could encourage more exploration by discretizing the actions. This forced the actions to be non-smooth with respect to input observations and parameter perturbations, and thereby encouraged a wide variety of behaviors to be played out. Similar conclusions can be found in Salimans’s work [27]. This architecture is quite straightforward and easily compatible with both the NE and RL methods. It is mainly used to carry out preliminary experiments to verify the feasibility of our method. In the next section we will show the experimental results obtained with Arc_pro to effectively train NLTH agents to exploit weak opponents, such a random agents (RA). Further introductions of game feature encoding rules are as follows:
- Current stage: The current street (preflop, flop, turn, or river) as a one-hot encoding. It costs four features. It has to be a one-hot encoding as there is no continuity between the streets and each has to be considered separately.
- Hand equity: The equity is the probability of winning the hand if all active players went to the showdown. It is the only information about the cards that the player gets. It is calculated by Monte-Carlo simulations. In each simulation a random hand is given to the opponent, and random community cards are added to have a full board. The winner of the hand is then determined. These results are then averaged to estimate the equity. The simulations are repeated until a satisfying standard deviation on the estimated equity is achieved. The tolerance is set to 0.1%. Note that the hand range of the opponent is not explicitly modeled here, as random cards are distributed to him. The equity calculation is the most time-consuming operation in the agent’s decision making, and thus also the generation of game data is time-consuming. In the implementation used it took approximately 10 ms. The repeated estimation and comparison of hand strength is the reason for this relatively long computation.
- My investment: The investment of the player in the hand, normalized by the initial stack.
- Opp’s investment: The investment of the opponent in the hand, normalized by the initial stack. The investments summarize the importance of the current hand and may describe the strength of the hand the opponent is representing.
- Pot odds: The pot odds are the amount of chips necessary to call divided by the total pot. It is an important measure often used by professional players.
Figure 3 shows an improved architecture compared to Arc_pro. The biggest difference is the addition of an LSTM layer, a special class of recurrent neural networks that has been proven to be effective for dealing with sequential decision problems like NLTH. Since strategies in NLTH are essentially based on sequences of actions from different players, LSTM is directly applicable to extracting useful temporal features and learning adaptive behaviors. When we use this architecture (henceforth referred to as Arc_lstm) to train agents, the input features should be managed into episodic sequences. That means that the game trajectories are no longer considered independent but as interrelated within each episode. If an input feature implies the beginning of a game, the LSTM layer will reset to the initialization state in preparation for processing new episodic sequences. Therefore, the main advantage of Arc_lstm is that it captures the sequential nature of NLTH and makes decisions depending on the context of the current game stage as well as the opponent’s overall performance (see the opponent feature set introduced above). It should be noted that in order to generate episodic continuous experiences, the replay buffer must be managed in sequence and the random minibatch sampled from it must contain full episodes rather than independent trajectories. This is another aspect that differs from Arc_pro. Experimental results show that these additional settings can help Arc_lstm achieve better performance against opponents whose strategy is relatively strong and harder to exploit.
4. Experiments
In this section, we present experiments conducted to evaluate the proposed NE_RL method for NLTH. We first compared the performance of NE_RL with the NE- or RL-only methods when training NLTH agents against weak opponents, such as random agents. More specifically, these NLTH agents share the same architecture as Arc_pro but differ in their learning methods (respectively including an evolutionary method, a policy gradient, and the combination of both). With the feasibility of NE_RL validated, we stepped forward to train agents to exploit relatively strong opponents but encountered the problem that the NE method fails to learn anything after tens of thousands of episodes played, which also leads to a poor learning process for NE_RL. Then we used an improved architecture, Arc_lstm, leading to a significant performance boost, thus further validating the role of the additional LSTM in Arc_lstm. We then evaluated the performance of NE_RL with Arc_lstm under a constrained situation in which training episodes were limited to 40,000. Such a limitation is necessary to evaluate the efficiency of all of the learning methods from a practical point of view, because the computational resource consumption grows linearly with the total training episodes. Finally, we conducted ablation experiments to demonstrate the effectiveness of the transfer process, which is the core mechanism within NE_RL for incorporating evolutionary methods and policy gradient methods to achieve the best of both methods.
In all experiments, we chose the two-player NLTH setting in order to focus more on the method itself and leave the extension to multiplayer settings for future research. In addition, we used an open-source toolkit—Rlcard [4]—to carry out all experiments, so as to ensure reproduction of our results. All of the algorithms are based on PyTorch [28] and run through a cloud server with 80 CPUs. The duration of the experiments ranged from hours to tens of hours with multiple threads. The hyper-parameters of each algorithm and related experimental details are as follows:
- NE population size N = 8
- RL population size M = 4
- Size of replay buffer R =
- Learning rate in DQN =
- Discount rate in DQN =
- Training batch size in DQN = 32
- Elite fraction in NE = 0.25
- Mutation rate in NE = 0.3–0.05, mutation strength in NE = 0.5–0.1The mutation rate is set to linearly decrease from 0.3 to 0.05 while the mutation strength linearly is set to decrease from 0.5 to 0.1.
- Number of game episodes in tournament function = 2000Since NLTH is a stochastic game with much uncertainty, 2000 independent full episodes were tested to compute an averaged fitness score.
4.1. Preliminary Evaluation of NE_RL
The first experiment is a motivating example that validates the effectiveness of our method. In it we used a chump opponent random agent (RA) to train NLTH agents with the same architecture (Arc_pro) but different learning methods, and their performances were evaluated periodically after a certain number of episodes played. Figure 4 (Left) shows the comparative performances of methods in previous works (DQN, NE) and our proposed method, NE_RL, which combines the mechanisms within DQN and NE. The rewards of the agents were measured by the average winning big blinds per hand (bb/h for short, each player was initialized with 50 bb for the beginning of each hand). Higher rewards represent higher exploitation of the opponent. Specifically, the evaluation process ran every 100 training episodes for DQN and every evolutionary generation for NE and NE_RL. During the evaluation process, another 2000 episodes were played against the RA for each agent to compute an average reward, which was necessary in order to reduce the impact of luck and uncertainty in NLTH. This experiment was conducted fivr times to compute averaged performance with the standard error band. From the experimental result we can see that the DQN agent learned faster with much less episodes and converged at an exploitation level of about 8.5 bb/h, while the NE population typically needed many more interactions against their opponent but could converge to the exploitability bound computed by the local best response [29], owing to the population-based exploration. We were also excited to see that the NE_RL agents inherited the advantages from both methods and achieved better overall performance on sample efficiency as well as maximum exploitation. Maximum exploitation means the largest amount of money one can win from the opponent and sample efficiency means that the lowest number of training episodes needed to achieve converged performance. These together constitute the goal of our work and the motivation to propose the NE_RL method.
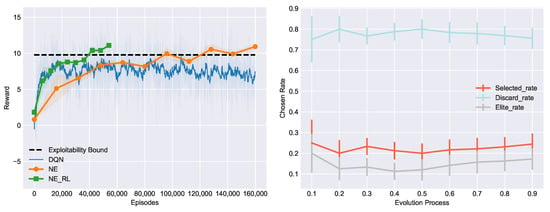
Figure 4.
(Left) Comparative performance of NE_RL, NE, and DQN in training against the RA opponent. (Right) Average selection rate of the transferred RL agents changes during the course of evolution and plot with error bars.
This result validates the feasibility of NE_RL. It outperformed NE and RL by combining the advantages of both methods. The interactions between NE and RL include two types: the training episodes of the NE population are reused to provide diverse experience for the RL agents to train, while the trained RL agents periodically transfer to the NE population to inject gradient information into the NE agents. In order to examine whether such interactions truly help achieve improved performance, we ran additional experiments logging how the transferred RL agents performed among the NE population. Three evaluation indexes were used to log the frequency of these agents chosen as elites, selected, or discarded during selection: elite_rate, selected_rate, and discard_rate, respectively. As shown in Figure 4 (Right), during the course of evolution, the chosen rate of the transferred RL agents remained stable. elite_rate and selected_rate indicate that the gradient information played a role among the NE population and contributes to the evolutionary direction. In other words, the NE population may spend fewer generations to find its way to evolve with the help of gradient information, and the performance of the population continually improves though the discard_rate of transferred RL agents is high. This is due to built-in redundancies and diversities of population-based exploration and exploitation.
In conclusion, the first experiment successfully validated our NE_RL method’s effectiveness for opponent exploitation in NLTH and achieved significant improved performance compared to previous NE- or RL-only methods. However, in this phase we only chose a weak opponent that plays randomly for testing purposes. Further experiments against stronger opponents will be introduced in the following subsection.
4.2. Learning to Exploit Baseline Opponents
The goal of our work is proposing a general method for opponent exploitation in NLTH. The first experiment proved our method’s feasibility in NLTH games against a weak opponent. In the next experiment, we introduced four stronger agents adopted from an open-source NLTH platform [30]. They were designed according to specific rules and characterized by human-like styles, namely Tight Aggressive (TA), Tight Passive (TP), Loose Aggressive (LA), and Loose Passive (LP). Unlike the RA opponent that plays randomly, these baseline opponents take actions based on their hand-strength whose strategies are relatively strong. “Tight” means an opponent only plays a small range of strong hands and “Loose” means the opposite. “Aggressive” means an offensive play style while “Passive” means a defensive play style. Moreover, the TA opponent’s decision-making mechanism also mimics human bluffing behavior and probabilistically takes deceptive actions, which makes it even harder to exploit. When we tried to do the same thing to train agents against these baseline opponents as before, problems began to arise. We observed that the NE method seems to make no progress even after tens of thousands of training episodes. This led us to reflect on what went wrong, such as whether the network architecture Arc_pro needs improvements to adapt to stronger opponents. The main reason may be that the prototype structure of the neural network originally designed in Arc_pro is not available for generating strategies against more complex opponents.
Inspired by previous works that highlighted a special class of recurrent neural networks, LSTM (Long Short Term Memory), as an effective and scalable model for NLTH, we modified Arc_pro by adding a single LSTM layer between the input game feature set and the hidden layers. The main purpose was to extract the temporal features from opponents’ actions, which were simply neglected in the first experiment, since the RA opponent just plays randomly and there is no temporal feature to extract at all. However, if we want to exploit more experienced opponents, these extra features seem to become critical. Figure 5 shows the comparative performance when we replace Arc_pro with the improved architecture Arc_lstm and use the same NE method to train agents against the baseline opponents (take TP for example). From the results we can see that the NE method recovered to optimize its performance once equipped with Arc_lstm. We can now conclude that Arc_lstm is a more suitable architecture to train NLTH agents. This is a crucial improvement not only for the NE method itself but also for our NE_RL method, since the NE method is the most important component of our NE_RL method. In the following experiments we continued testing the feasibility of our NE_RL method with Arc_lstm.
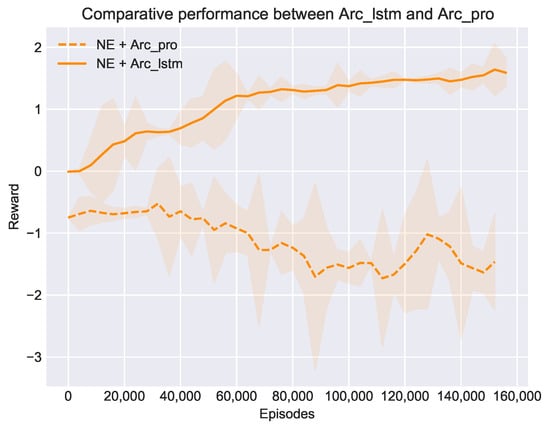
Figure 5.
Comparative performance between Arc_pro and Arc_lstm with the same NE method in training against the TP opponent.
As we have emphasized in this work and validated in the first experiment, the NE_RL method is supposed to be superior to the previous NE- and RL-only methods for opponent exploitation in NLTH. With Arc_lstm we can now compare the performance between these methods against the four baseline opponents to show more evidence of the superiority of our method. As shown in Figure 6, we conducted four independent experiments against each of the baseline opponents (TA, TP, LA, LP) to evaluate the performance of opponent exploitation under different methods. Additionally, we set the maximum number of training episodes to 40,000 to reflect both the sample efficiency and the exploitation performance for each method. Together, these results suggest that our NE_RL method can achieve maximum exploitation of the baseline opponents under limited training episodes. By contrast, the NE method suffered from a lack of samples and the RL method could only converge to a sub-optimal performance under the same conditions. Similarly to the first experiment, we further studied the role of interactions between the RL and NE methods by tracking the elite_rate, selected_rate, and discard_rate of the transferred RL agents within the NE population. Table 1 shows the averaged selection rate during the training process for each baseline opponent. A high level of average discard_rate means that the transferred RL agents were mostly discarded and the NE population is still the mainstream of the NE_RL. The contributions of transferred RL agents are represented by elite_rate and selected_rate. Though it was only a small fraction, it indeed made a big difference for NE_RL, which outperformed both the NE and RL methods.
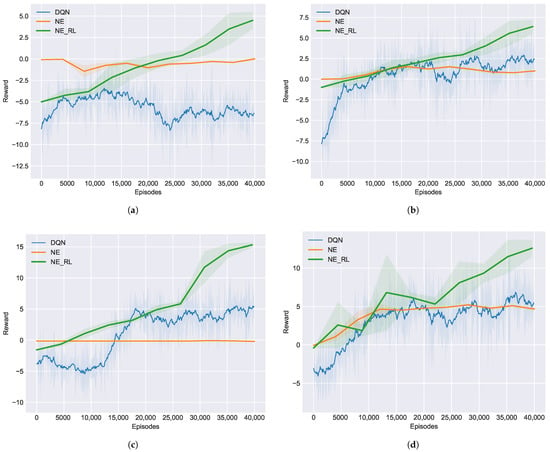
Figure 6.
Learning curves of different methods in training against the four baseline opponents: (a) TA, (b) TP, (c) LA, (d) LP.

Table 1.
Selection rate for transferred RL agents within the NE population.
4.3. Ablation Experiments
Next, we used an ablation experiment to test how the strength of the transfer process affects NE_RL’s performance. During the transfer process, the RL agents reinsert into the NE population to provide learned gradient information. We define the strength of this process as m, which represents the number of RL agents relative to the size of the NE population. Suppose the size of the NE population is fixed; then, a higher m means a stronger impact imposed on the NE population by the RL agents. Here we represented m as a fraction of the size of the NE population and conducted contrast experiments with different m values. Figure 7 shows the experimental results in training against all four baseline opponents, with m ranging from 0 to 0.5, which means the the strength of the transfer process changes from weak to strong. Typically, represents the original NE method and represents a rather strong NE_RL method, which was commonly used in the previous experiments. From those results, we can conclude that in general, different m values may lead to visible performance differences, which indicates that the value of m may be one of the most important hyper-parameters for NE_RL. In this experiment, it seems that a higher value of m achieved better converging performance after a limited number of 40,000 training episodes. However, this may not be true in all cases. It depends on the specific experimental settings and we cannot draw a definite conclusion in this paper. It may be a good topic to study further in future work.
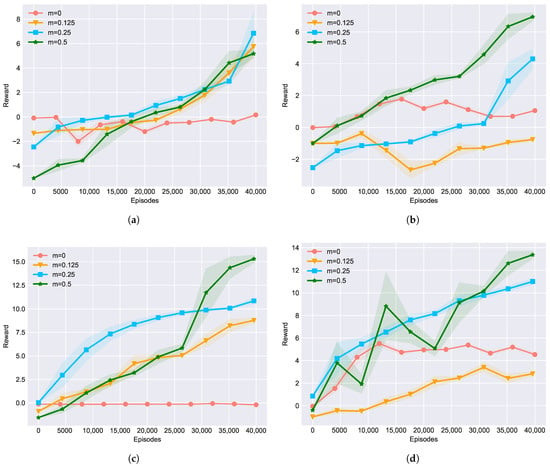
Figure 7.
Ablation experiments on different RL population sizes, m, in training against the four baseline opponents: (a) TA, (b) TP, (c) LA, (d) LP.
5. Discussion
In this paper, we proposed a novel method for opponent exploitation in imperfect information games such as NLTH. Since a NLTH-like game typically contains challenges of sparse rewards and high complexity, the previous RL- or NE-only methods for opponent exploitation struggle with poor optimal performance or low sample efficiency. Our NE_RL method uses NE’s advantage of evolutionary computation with a long-term fitness metric to address the sparse rewards feedback in NLTH and retains RL’s gradient-based method for higher learning efficiency. Additionally, NE_RL recycles data generated by both NE and RL populations and uses an experience replay mechanism for the off-policy RL method to learn from them more than once, which can greatly help improve sample efficiency. Experimental results against various opponents show that NE_RL outperforms the previous NE- and RL-only methods with advantages of maximum exploitation and sample-efficient learning.
Apart from NLTH, we believe that our method can also be extended to other domain problems with challenges of adversarial sequential decision-making processes and imperfect information. Future work based on this paper includes incorporating more complex evolutionary sub-mechanisms to improve the standard NE operators used in NE_RL, or incorporating more advanced off-policy reinforcement learning methods and techniques to replace the currently used DQN in NE_RL. In addition, extending NE_RL to multiplayer NLTH will be another exciting thread of research leading to wider application prospects.
Author Contributions
Conceptualization, J.X.; methodology, J.X. and S.C.; validation, J.X. and S.C.; resources, J.C.; data curation, J.X.; writing—original draft preparation, J.X.; writing—review and editing, S.C.; supervision, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Our code will be available at https://github.com/jiahui-x/NE_RL (accessed on 14 July 2021).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brown, N.; Sandholm, T. Superhuman AI for multiplayer poker. Science 2019, 365, eaay2400. [Google Scholar] [CrossRef] [PubMed]
- Bowling, M.; Burch, N.; Johanson, M.; Tammelin, O. Heads-up limit hold’em poker is solved. Science 2015, 347, 145–149. [Google Scholar] [CrossRef] [PubMed]
- Sandholm, T. The state of solving large incomplete-information games, and application to poker. Ai Mag. 2010, 31, 13–32. [Google Scholar] [CrossRef]
- Zha, D.; Lai, K.H.; Huang, S.; Cao, Y.; Hu, X. RLCard: A Platform for Reinforcement Learning in Card Games. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence and Seventeenth Pacific Rim International Conference on Artificial Intelligence IJCAI-PRICAI-20, Yokohama, Japan, 11–17 July 2020. [Google Scholar]
- Brown, N.; Sandholm, T. Superhuman AI for heads-up no-limit poker: Libratus beats top professionals. Science 2018, 359, 418–424. [Google Scholar] [CrossRef] [PubMed]
- Moravík, M.; Schmid, M.; Burch, N.; Lis, V.; Bowling, M. DeepStack: Expert-Level Artificial Intelligence in No-Limit Poker. Science 2017, 356, 508. [Google Scholar] [CrossRef] [PubMed]
- Maîtrepierre, R.; Mary, J.; Munos, R. Adaptive play in texas hold’em poker. In ECAI 2008: 18th European Conference on Artificial Intelligence, Patras, Greece, 21–25 July 2008: Including Prestigious Applications of Intelligent Systems (PAIS 2008); IOS Press: Amsterdam, The Netherlands, 2008; Volume 178, p. 458. [Google Scholar]
- Southey, F.; Bowling, M.P.; Larson, B.; Piccione, C.; Burch, N.; Billings, D.; Rayner, C. Bayes’ bluff: Opponent modelling in poker. arXiv 2012, arXiv:1207.1411. [Google Scholar]
- Pricope, T.V. A View on Deep Reinforcement Learning in Imperfect Information Games. Stud. Univ. Babeș-Bolyai Inform. 2020, 65, 31. [Google Scholar] [CrossRef]
- Brown, N.; Sandholm, T. Safe and nested endgame solving for imperfect-information games. In Proceedings of the Workshops at the thirty-first AAAI conference on artificial intelligence, San Francisco, CA, USA, 4–5 February 2017. [Google Scholar]
- Li, X.; Miikkulainen, R. Evolving adaptive poker players for effective opponent exploitation. In Proceedings of the AAAI Workshops, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Nicolai, G.; Hilderman, R.J. No-Limit Texas Hold’em Poker agents created with evolutionary neural networks. In Proceedings of the International Conference on Computational Intelligence & Games, Milan, Italy, 7–10 September 2009. [Google Scholar]
- Li, H.; Wang, X.; Jia, F.; Li, Y.; Chen, Q. A Survey of Nash Equilibrium Strategy Solving Based on CFR. Arch. Comput. Methods Eng. 2020, 28, 2749–2760. [Google Scholar] [CrossRef]
- Lu, S. Online Enhancement of Existing Nash Equilibrium Poker Agents. Master’s Thesis, Knowledge Engineering Group, Darmstadt, Germany, 2016. [Google Scholar]
- Ganzfried, S.; Sandholm, T. Game theory-based opponent modeling in large imperfect-information games. In Proceedings of the 10th International Conference on Autonomous Agents and Multiagent Systems, Taipei, Taiwan, 2–6 May 2011; Volume 2, pp. 533–540. [Google Scholar]
- Gilpin, A.; Sandholm, T. Finding Equilibria in Large Extensive form Games of Imperfect Information; Technical Report; Mimeo: New York, NY, USA, 2005. [Google Scholar]
- Ganzfried, S.; Sandholm, T. Safe Opponent Exploitation. ACM Trans. Econ. Comput. 2012, 3, 587–604. [Google Scholar]
- Teófilo, L.; Reis, L.P. Identifying Player’s Strategies in No Limit Texas Hold’em Poker through the Analysis of Individual Moves. arXiv 2013, arXiv:1301.5943. [Google Scholar]
- Bard, N.; Johanson, M.; Burch, N.; Bowling, M. Online implicit agent modelling. In Proceedings of the 2013 International Conference on Autonomous Agents and Multi-Agent Systems, St. Paul, MN, USA, 6–10 May 2013; pp. 255–262. [Google Scholar]
- Ackley, D. Interactions between learning and evolution. Artif. Life II 1991, 11, 487–509. [Google Scholar]
- Munir-ul, M.C.; Yun, L. Evolutionary reinforcement learning for neurofuzzy control. In Proceedings of the International Fuzzy Systems Association World Congress, Prague, Czech Republic, 25–29 June 1997. [Google Scholar]
- Lin, C.J.; Hsu, Y.C. Reinforcement hybrid evolutionary learning for recurrent wavelet-based neurofuzzy systems. IEEE Trans. Fuzzy Syst. 2007, 15, 729–745. [Google Scholar] [CrossRef]
- Koppejan, R.; Whiteson, S. Neuroevolutionary reinforcement learning for generalized control of simulated helicopters. Evol. Intell. 2011, 4, 219–241. [Google Scholar] [CrossRef][Green Version]
- Drugan, M.M. Reinforcement learning versus evolutionary computation: A survey on hybrid algorithms. Swarm Evol. Comput. 2018, 44, 228–246. [Google Scholar] [CrossRef]
- Khadka, S.; Tumer, K. Evolution-Guided Policy Gradient in Reinforcement Learning. arXiv 2018, arXiv:1805.07917. [Google Scholar]
- Floreano, D.; Dürr, P.; Mattiussi, C. Neuroevolution: From architectures to learning. Evol. Intell. 2008, 1, 47–62. [Google Scholar] [CrossRef]
- Salimans, T.; Ho, J.; Chen, X.; Sidor, S.; Sutskever, I. Evolution Strategies as a Scalable Alternative to Reinforcement Learning. arXiv 2017, arXiv:1703.03864. [Google Scholar]
- Ketkar, N. Introduction to PyTorch. In Deep Learning with Python; Apress: Berkeley, CA, USA, 2017. [Google Scholar]
- Lisy, V.; Bowling, M. Equilibrium Approximation Quality of Current No-Limit Poker Bots. arXiv 2016, arXiv:1612.07547. [Google Scholar]
- Li, K.; Xu, H.; Zhang, M.; Zhao, E.; Wu, Z.; Xing, J.; Huang, K. OpenHoldem: An Open Toolkit for Large-Scale Imperfect-Information Game Research. arXiv 2020, arXiv:2012.06168. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).