Parallel Tiled Code for Computing General Linear Recurrence Equations

Abstract

In this article, we present a technique that allows us to generate parallel tiled code to calculate general linear recursion equations (GLRE). That code deals with multidimensional data and it is computing-intensive. We demonstrate that data dependencies available in an original code computing GLREs do not allow us to generate any parallel code because there is only one solution to the time partition constraints built for that program. We show how to transform the original code to another one that exposes dependencies such that there are two linear distinct solutions to the time partition restrictions derived from these dependencies. This allows us to generate parallel 2D tiled code computing GLREs. The wavefront technique is used to achieve parallelism, and the generated code conforms to the OpenMP C/C++ standard. The experiments that we conducted with the resulting parallel 2D tiled code show that this code is much more efficient than the original serial code computing GLREs. Code performance improvement is achieved by allowing parallelism and better locality of the target code.

1. Introduction

The purpose of this document is to show a way to produce a parallel program for computing general linear recurrence equations (GLREs). This code can also be tiled.

A recurrence equation expresses each element of a sequence or multidimensional array of values as a function of the preceding ones. Recurrence equations have a broad spectrum of applications, for example: population dynamics, spatial ecology, analysis of algorithms, binary search, digital signal processing, time series analysis, and theoretical and empirical economics. Such applications deal with multidimensional data and are computing-intensive. To reduce their execution time, those applications should be parallelized and run on modern multicore machines.

Many sequential GLRE solutions have been implemented in a variety of development environments. The main problems of these programs are the long time spent in loops and the low cache performance for a large input data sizes that may make them unapplicable.

Loop parallelization and tiling (blocking) can be used to enhance the efficiency of a sequential program. Blocking is a commonly used technique to improve code performance. It allows us to generate a parallel program with greater granularity of code and data locality that will be executed in a multithreaded environment with both distributed and shared memory.

A classic way to automatically parallelize and tile a loop nest is based on affine transformations and includes the following steps: extracting dependencies available in that nest, forming time partition constraints using the obtained dependencies, finding the maximum number of linear independent solutions to those constraints, and finally generating target code [1,2]. If the number of linear independent solutions to those constraints is two or more, then tiled parallel code can be generated [1,2].

In this paper, we examine the loop nest in the C language presented in Listing 1, which computes GLREs. That code is taken from https://www.netlib.org/benchmark/livermorec (accessed on 24 August 2021).

Listing 1: Original loop nest computing GLREs.

Listing 1: Original loop nest computing GLREs.

In Section 2, we demonstrate that there exists a single solution to the time partition constraints for the program in Listing 1; hence, direct parallelization and tiling of the program is not feasible using affine transformations.

Our proposal is to modify the code in Listing 1 to another one whose dependencies allow us to form time partition constraints for which there exist two linear independent solutions that allow us to generate parallel 2D tiled code.

The main contributions of the article are as follows.

• Proposal to convert the code from Listing 1 to another sequential code allowing the generation of parallel 2D tiled code computing GLREs.
• Demonstration of GLRE computation with parallel 2D tiled code.
• Comparison of the target code performance with that of the original one presented in Listing 1.

The rest of this article is organized as follows. In Section 2, we provide background on dependency analysis and parallel code generation. In Section 3, we show how to generate GLREs with the parallel 2D tiled program. In Section 4, we analyze similar work of parallel code generation for comparable cases. In Section 5, we discuss the results of the experiments performed. Conclusions of the work are presented in Section 6.

2. Background

Generating serial tiled code allows for significant improvements in data locality that results in improved program performance. Generating parallel tiled code lets on additional increasing code performance due to running such a code by means of multiple threads on many cores.

To our best knowledge, there is no technique allowing us to generate any tiled code examined in this paper and presented in Listing 1. All known techniques based on affine transformations and/or transitive closure of dependence graphs [1,2] are unable to generate any tiled code (serial and/or parallel) for the code in Listing 1. Those techniques are within the class of reordering transformations. They do not introduce any additional computations to generated target code in comparison with an original code; they only reorder iterations of the original code allowing for tiling and/or parallelism.

The other known techniques, for example, [3,4], that are not within reordering transformations allow us to parallelize and tile code similar to some extent to the code in Listing 1 but not exactly the same. All of those techniques introduce additional computations to generated target code in comparison with those in an original one. That prevents achieving the maximal target code performance.

Thus, there is the need to develop techniques belonging to the class of reordering transformations to tile and/or parallelize the code presented in Listing 1, allowing for generating code that does not include any additional computations in comparison with those of an original one. In this paper, we present an approach to resolving this challenge, allowing for generation of parallel tiled code.

In the loop nest, we can find dependencies between instruction instances in the iteration space of that loop nest—the collection of all statements executed inside that loop nest. A dependence is a situation when two instruction instances access the same location in memory and at least one of those accesses is a write. Each dependence is represented with its source and destination but only if the source is executed before the destination. Most commonly, dependencies are expressed by relations that map dependency sources to dependency destinations. Dependence sources and destinations are represented with iteration vectors. The notation of such a relation is the following.

$$R:=\left[PARAMS\right]\to \left\{\right[inputtuple]\to [outputtuple]\mid constraints\},$$

where $\left[PARAMS\right]$ is the list of relation parameters, $\left[inputtuple\right]$ represents dependence sources, $\left[outputtuple\right]$ represents dependence destinations, and $constraints$ are the constraints—a system of affine equalities and inequalities on parameters and tuple variables.

In the case of dependencies when the dimensions of the left and right tuples of the relation are the same, the distance vector is the difference between the iteration vector of a dependence target and the iteration vector of the corresponding dependence source.

A dependence vector is uniform if all its elements are constants.

To extract dependencies present in the loop nest, we use the polyhedral model, which is returned by PET [5], and we use the iscc calculator [6], which performs calculations on polyhedral sets and relations [7]. The iscc is an interactive interface to the PET library and barvinok library that will let you count points in polytopes. Barvinok is available online at https://repo.or.cz/barvinok.git (accessed on 24 August 2021). We also used the iscc calculator to calculate distance vectors and generate target code.

To parallelize and tile the loop nest, a time partitioning constraint should be created [1] that states that if iteration I of statement $S1$ depends on iteration J of statement $S2$, then I must be assigned to a time partition that is executed no earlier than the partition containing J, i.e., schedule(I) ≤ schedule(J), where schedule(I) and schedule(J) denote the discrete execution time of iterations I and J, respectively.

Linear independent solutions to time partition constraints are needed to create schedules for each occurence of a single instruction of the loop nest allowing for parallelization and tiling of code. The schedule defines a strict partial order, i.e., an irreflexive and transitive relation on the statement instances that determines the order in which they are or should be executed. Details of use of linear independent schedules for generating parallel tiled code can be found in a number of articles, for example, in article [2].

We should extract as many linear independent solutions to time partition constraints as possible. The degrees of parallelism of the target code and the dimension of the tile are higher when more independent solutions are extracted [1]. When there is a single solution to the time partition constraints, parallelization and tiling of the corresponding loop nest using affine transformations is not possible [1].

3. Methods. Parallel Tiled Code Generation

Using PET and the iscc calculator, we extract dependencies available in the code in Listing 1; they are presented with the following relation.

$$\begin{gathered} R:=(loop,n)\to \{(l,i,k)\to (l^{\prime },i,k^{\prime })\mid l>0\wedge i<n\wedge 0\le k<i\wedge l<l^{\prime }\le loop\wedge 0\le k^{\prime }<i\} \\ \cup (loop,n)\to \{(l,i,k)\to (l^{\prime },-1+i-k,k^{\prime })\mid l>0\wedge i<n\wedge k\ge 0\wedge l<l^{\prime }\le loop\wedge 0\le k^{\prime }\le -2+i-k\} \\ \cup (loop,n)\to \{(l,i,k)\to (l^{\prime },i^{\prime },-1-i+i^{\prime })\mid l>0\wedge 0\le k<i\wedge l\le l^{\prime }\le loop\wedge i<i^{\prime }<n\}\cup (loop,n)\to \\ \{(l,i,k)\to (l,i,k^{\prime })\mid 0<l\le loop\wedge i<n\wedge k\ge 0\wedge k<k^{\prime }<i\}, \end{gathered}$$ where R is the relation name; $loop$ and n are parameters; ∪ is the union operation of sets (relation R is composed as the set union of simpler relations); the tuple before the sign → of each simpler relation is the left tuple of this relation, for example, for the first simpler relation, the left tuple is presented with variables $(l,i,k)$; the tuple after the sign → of each simpler relation is the right tuple of this relation, for example, for the first simpler relation, the right tuple is presented with variables $(l^{\prime },i,k^{\prime })$; the expressions after the sign ∣ are the constraints of each simpler relation, each constraint is represented with the conjunctions of inequalities built on tuple variables and parameters; and ∧ is the logical AND operator.

The left tuple of each simpler relation represents dependence sources, whereas the right represents dependence destinations.

Applying the deltas operator of the iscc calculator to relation R, we obtain the three distance vectors presented with set D below.

$$\begin{gathered} D:=(loop,n)\to \left\{\right(l,i,k)\mid 0\le l<loop\wedge ((l>0\wedge i<0\wedge i<k<n+2i)\vee \\ (i>0\wedge -n+2i<k<i)\left)\right\}\cup \\ (loop,n)\to \left\{\right(0,0,k)\mid loop>0\wedge 0<k\le -2+n\}\cup \\ (loop,n)\to \left\{\right(l,0,k)\mid 0<l<loop\wedge 2-n\le k\le -2+n\}. \end{gathered}$$

where the notations used are the same as for relation R above except from the set is represented with a single tuple.

Each conjunct in the set above represents a particular distance vector.

Taking into account the constraints of those distance vectors, we simplify them to the following form.

$D:=\{(a_1,a_2,a_3)\mid a_1\ge 0\wedge -\infty \le a_2\le \infty \wedge -\infty \le a_3\le \infty ;(0,0,b_3)\mid b_3>0;(c_1,0,c_3)\mid c_1>0\wedge -\infty \le c_3\le \infty \}.$

The time partition constraints created from the resulting distance vectors according to article [1] are as follows.

$$h_1\ast a_1+h_2\ast a_2+h_3\ast a_3\ge 0,$$

(1)

$$h_3\ast b_3\ge 0,$$

(2)

$$h_1\ast c_1+h_3\ast c_3\ge 0,$$

(3)

where $h_1,h_2,h_3$ are the unknowns.

Taking into consideration that $-\infty \le a_2\le \infty$, $-\infty \le a_3\le \infty$, $-\infty \le c_3\le \infty$, we can suppose that to satisfy all the above constraints, $h_2$ and $h_3$ should be 0, i.e., $h_2=h_3=0$. Thus, the above constraints can be rewritten as follows.

$$h_1\ast a_1\ge 0,$$

(4)

$$h_1\ast c_1\ge 0.$$

(5)

Hence, we may cease that there exists a single solution to constraints (1), (2), and (3), namely ${(1,0,0)}^T$. This means that all the three loops in the code in Listing 1 cannot be parallelized and tiled by means of affine transformations.

Next, we try to parallelize and tile only two inner loops i and k in the loop nest in Listing 1. For this purpose, we make the outermost loop l to be serial and extract dependencies for inner loops i and k described with the relation below.

$R:=\left(n\right)\to \{(i,k)\to (i,k^{\prime })\mid i<n\wedge k\ge 0\wedge k<k^{\prime }<i\}\cup n\to \{(i,k)\to (i^{\prime },-1-i+i^{\prime })\mid 0\le k<i\wedge i<i^{\prime }<n\}.$

Applying the deltas operator of the iscc calculator to relation R, we obtain the two distance vectors presented with set D below.

$D:=\left(n\right)\to \left\{\right(i,k)\mid i>0\wedge -n+2i<k<i\}\cup \left(n\right)\to \left\{\right(0,k)\mid 0<k\le -2+n\}.$

Next, we simplify the representation of the distance vectors above to the form.

$D:=\{(a_1,a_2)\mid a_1>0\wedge -\infty \le a_2\le \infty ;(0,b_2)\mid b_2>0\}$.

The time partition constraints formed on the basis of the distance vectors above are the following.

$$h_1\ast a_1+h_2\ast a_2\ge 0,$$

(6)

$$h_2\ast b_2\ge 0,$$

(7)

where $h_1,h_2$ are the unknowns.

Taking into consideration that $-\infty \le a_2\le \infty$, we can deduce that to satisfy constraints (6) and (7), $h_2$ should be 0, i.e., $h_2=0$.

So, there exists a single solution to constraints (6) and (7), namely ${(1,0)}^T$, and we conclude that provided the outermost loop l is serial, the two inner loops i and k cannot be parallelized and tiled by means of affine transformations.

To cope with that problem, we transform the code in Listing 1 to improve dependence properties. With this goal, we apply the following schedule to each iteration of the code in Listing 1:

${(l,i,k)}^T\to {(l,t=i-k)}^T$.

This schedule implies that each iteration of the code in Listing 1, represented with iteration vector ${(l,i,k)}^T$, is mapped to the two-dimensional time ${(l,t=i-k)}^T$. It means that iterations of loop l should be executed serially, while for a given value of iterator l, iteration ${(i,k)}^T$ should be executed at time $t=i-k$. This time guarantees that each iteration ${(i,k)}^T$ is executed when all its operands are ready. To justify that fact, let us noting that for iteration ${(i,k)}^T$, operand $b\left[k\right]\left[i\right]$ is input data; hence, its value is ready at time 0, and operand $w\left[\right(i-k)-1]$ is ready at time $(i-k)-1$ when an actual value of this operand is already calculated and written in memory. Thus, iteration ${(i,k)}^T$ can be executed at time $t=i-k$, i.e., at time, which is one more than the time when operand $w\left[\right(i-k)-1]$ is ready.

In other words, the schedule above is based on data flow software paradigm [8].

To generate target serial code, we form the following relation, which maps each statement instance within the iteration space of the code in Listing 1 to the two-dimensional schedule below.

$CODE:=(loop,n)\to \left\{\right(l,i,k)\to (l,t=i-k)\mid loop>0\wedge 0<l\le loop\wedge 0<i<n\wedge 0\le k<i\},$ where the constraints

$loop>0\wedge 0<l\le loop\wedge 0<i<n\wedge 0\le k<i$

define the iteration space of the code in Listing 1. Applying the iscc codegen operator to the relation above, we get the pseudocode shown in Listing 2.

Listing 2: Target serial pseudocode.

Listing 2: Target serial pseudocode.

We transform the pseudocode code in Listing 2 to C code, taking into account that in that pseudocode, variables $counter,var1$, and $var2$ correspond to variables $l,t$, and i, respectively, in the tuple of set $CODE$; the second variable $var2$ in the pseudostatement relates to variable i, while the third expression $-var1+var2$ corresponds to variable k in the tuple of set $CODE$. Thus, we replace the pseudostatement in the code in Listing 2 with the statement

w[i] + = b[k][i] ∗ w[(i − k) − 1];

from Listing 1 changing variables i and k with variable $var2$ and the expression $-var1+var2$, respectively. As a result, we obtain the compilable program fragment presented in Listing 3.

Listing 3: Target sequential compilable program fragment.

Listing 3: Target sequential compilable program fragment.

The target serial code in Listing 3 is in the scope of reordered transformations. It performs the same computations as those performed with the initial code in Listing 1 but in a different order. It is well-known that a reordered transformation of a code is correct if it executes the same computations as those executed with the initial one (1) and respects all the dependencies that appear in that code (2) [1]. The transformed code is correct as it performs the same computations as those executed with the initial one (1) and it respects all the dependencies available in the initial one as explained below (2).

There exist three kinds of dependencies in the code presented in Listing 3: data flow dependencies (some statement instance first generates a result, then that result is used with another statement instance, those instances belong to different time units represented with the value of iterator counter), antidependencies (some statement instance first reads a result, then that result is updated with another statement instance, and output dependencies (two statement instances write their results to the same memory location).

Data flow dependencies are respected due to the fact that in the target code, the execution of a statement instance being the target of each data dependence starts only when all the arguments (data) of this operation are prepared, i.e., the processing of all the instruction instances generating these arguments has already finished, and the operand values are stored in the shared part of memory. This is guaranteed because the source of each data dependence is executed at a time unit defined with the value of iterator counter that is less than the one when the corresponding target is executed.

Anti- and output dependencies are honored due to the lexicographical order of the execution of dependent statement instances within each time partition represented with the value of iterator var1.

We also experimentally confirmed that the both loop nests presented in Listing 1 and Listing 3 generate correct results. The experiments used for input data prepared deterministically and randomly.

Dependencies available in the code in Listing 3 are represented with the following relation.

$$\begin{gathered} R:=(loop,n)\to \{(counter,var1,var2)\to (counte{r}^{\prime },1+var2,var{2}^{\prime })\mid counter>0\wedge var1>0\wedge var2 \\ \ge var1\wedge counter\le counte{r}^{\prime }\le loop\wedge var2<var{2}^{\prime }<n\}\cup (loop,n)\to \{(counter,var1,var2)\to \\ (counte{r}^{\prime },var{1}^{\prime },var2)\mid counter>0\wedge var1>0\wedge var1\le var2<n\wedge counter<counte{r}^{\prime }\le loop\wedge 0<var{1}^{\prime } \\ \le var2\}\cup (loop,n)\to \{(counter,var1,var2)\to (counte{r}^{\prime },var{1}^{\prime },-1+var1)\mid counter>0\wedge var1\le var2<n \\ \wedge counter<counte{r}^{\prime }\le loop\wedge 0<var{1}^{\prime }<var1\}\cup (loop,n)\to \{(counter,var1,var2)\to \\ (counter,var{1}^{\prime },var2)\mid 0<counter\le loop\wedge var1>0\wedge var2<n\wedge var1<var{1}^{\prime }\le var2\}, \end{gathered}$$ where $loop$ and n are parameters.

Applying the deltas operator of the iscc calculator to relation R, we obtain the three distance vectors presented below.

$$\begin{gathered} D:=(loop,n)\to \left\{\right(counter,var1,var2)\mid 0\le counter<loop\wedge ((var1>0\wedge 0< \\ var2<n-var1)\vee \\ (counter>0\wedge var1<0\wedge -n-var1<var2<0)\left)\right\}\cup \\ (loop,n)\to \left\{\right(0,var1,0)\mid loop>0\wedge 0<var1\le -2+n\}\cup \\ (loop,n)\to \left\{\right(counter,var1,0)\mid 0<counter<loop\wedge 2-n\le var1\le -2+n\}. \end{gathered}$$

Taking into account the constraints of those distance vectors, we simplify their representation to the following form.

$$\begin{gathered} D:=\{(a_1,a_2,a_3)\mid a_1\ge 0\wedge -\infty \le a_2\le \infty \wedge -\infty \le a_3\le \infty ; \\ (0,b_2,0)\mid b_2>0; \\ (c_1,c_2,0)\mid c_1>0\wedge -\infty \le c_2\le \infty \}. \end{gathered}$$

The time partition constraints constructed according to article [1] are as follows.

$$h_1\ast a_1+h_2\ast a_2+h_3\ast a_3\ge 0,$$

(8)

$$h_2\ast b_2\ge 0,$$

(9)

$$h_1\ast c_1+h_2\ast c_2\ge 0,$$

(10)

where $h_1,h_2,h_3$ are the unknowns.

Taking into account that $-\infty \le a_2\le \infty$, $-\infty \le a_3\le \infty$, $-\infty \le c_2\le \infty$, we can deduce that $h_2$ and $h_3$ should be 0, i.e., $h_2=h_3=0$ for the constraints (8), (9), and (10) to be compatible. Therefore, these constraints can be written with the following formulas.

$$h_1\ast a_1\ge 0,$$

(11)

$$h_1\ast c_1\ge 0.$$

(12)

Thus, we may conclude that there exists a single solution to constraints (8), (9), and (10), namely ${(1,0,0)}^T$. This means that all thee loops in the code in Listing 3 cannot be parallelized and tiled by means of affine transformations.

Next, we try to parallelize and tile only two inner loops $var1$ and $var2$ in the loop nest presented in Listing 3. For this purpose, we make the outermost loop $counter$ to be serial and extract dependencies for inner loops $var1$ and $var2$. They are expressed with the relation below.

$$\begin{gathered} R:=\left(n\right)\to \{(var1,var2)\to (1+var2,var{2}^{\prime })\mid var1>0\wedge var2\ge var1\wedge var2< \\ var{2}^{\prime }<n\}\cup n\to \{(var1,var2)\to (var{1}^{\prime },var2)\mid var1>0\wedge var2<n\wedge var1<var{1}^{\prime }\le var2\}. \end{gathered}$$

Applying the deltas operator of the iscc calculator to relation R, we obtain the two distance vectors presented below.

$D:=\left(n\right)\to \left\{\right(var1,var2)\mid var1>0\wedge 0<var2<n-var1\}\cup n\to \left\{\right(var1,0)\mid 0<var1\le -2+n\}.$

After the simplification of the representation of the distance vector above, we obtain the following vectors.

$D:=\{(a_1,a_2)\mid a_1>0\wedge a_2>0;(b1,0)\mid b_1>0\}$

The time partition constraints created from the distance vectors above are the following:

$$h_1\ast a_1+h_2\ast a_2\ge 0,$$

(13)

$$h_1\ast b_1\ge 0,$$

(14)

where $h_1,h_2$ are the unknowns. There are two linear independent solutions to the constraints above: ${(1,0)}^T$ and ${(0,1)}^T$. Applying those solutions, we are able to parallelize and tile the two inner loops of the code in Listing 3 using the technique presented in paper [2].

The target parallel tiled code presented by means of the OpenMP C/C++ API is shown in Listing 4. It is generated for the best tile size equal to 24 × 54; choosing the best tile size is explained in Section 5.

Listing 4: Transformed parallel loop nest.

Listing 4: Transformed parallel loop nest.

In that code, outermost loop $i0$ is serial nontiled, and loops $w0$ and $h0$ enumerate tile identifiers, while loops $i1$ and $i2$ enumerate iterations within each tile. Parallelism is extracted with the wavefront technique [2] and presented with the OpenMP directive $\#pragmaompparallelfor$ inserted before loop $h0$ that means that this loop is parallel.

4. Related Work

Related techniques can be divided into the following two classes: the class of reordering transformations and the one of nonreordering transformations. There are numerous publications concerned with both of the classes. Approaches based on affine transformations [1,2,9,10,11] and those based on the transitive closure of dependence graphs [12,13,14,15,16] belong to reordering transformations. Reordering techniques are code-independent and are used in optimizing compilers, for example [17,18,19], which automatically generate optimized target code for source code.

Nonreordering transformations are code-dependent, i.e., for a given code, a transformation is fulfilled manually. The following publications within nonreordering transformations concern the problem similar to that implemented with the code in Listing 1 but not exactly the same problem [3,4,8,20,21,22,23,24,25,26].

Both classes allow for generating the target program that is semantically identical to the original one. However, there are the following differences in target code generated using techniques of those classes.

Reordering transformations do not introduce any additional computations to generated target code in comparison with those of original code; they only reorder loop nest iterations of the original code allowing for tiling and/or parallelism. They are code-independent and are aimed at automatic code generation.

Nonreordering transformations allow us to parallelize and tile code similar to some extent to the code in Listing 1 but not exactly the same. All of those techniques introduce additional computations to generated target code in comparison with those in the original code. That increases the computational complexity of the algorithm and prevents achieving the maximal target code performance, and it is the main drawback in comparison with reordering transformations.

Each technique is manually created for the code that should be optimized. Adapting such a technique even to a slightly different problem can require additional work that can be time-consuming and not always possible.

After an extensive analysis of many nonreordering techniques mentioned above, we did not find any one that exactly implements the problem presented with the code in Listing 1. Without extensive research, it is not clear how any of those techniques can be adapted to implement exactly the same problem that implements the code in Listing 1.

In the class of reordering transformations, we examined the PLUTO [17] and TRACO compilers [15]. PLUTO is based on affine transformations and automatically generates tiled and/or parallel code. TRACO uses the transitive closure of dependence graphs to tile and/or parallelize input code. For the code in Listing 1, both PLUTO and TRACO are unable to generate any tiled and/or parallel code. In Section 3, we presented the reason why affine transformations fail to generate any parallel and/or tiled code for the serial code in Listing 1.

Below, we discuss some nonreordering transformations, which allow for generation of code implementing algorithms similar to that realizing with the code in Listing 1 but not exactly the same. Without extensive research, it is not clear how to adapt any of those techniques to generate target code fulfilling the same calculations as those performed with the code in Listing 1.

Karp et al. [20] discussed parallelism in recurrence equations. They proposed a decomposition algorithm that decides if a system of uniform recurrence equations (SURE) is computable or not. If so, multidimensional schedules can be derived and applied to extract parallelism.

Papers [3,4] introduced a recursive doubling strategy to compute recurrence equations in parallel. Recursive doubling envisages the splitting of the computation of a function into two subfunctions whose evaluation can be performed simultaneously in two separate processors. Successive splitting of each of these subfunctions allows for the computation over more processors.

Maleki and Burtscher [21] introduced two phase approach to compute recurrence equations. The first phase iteratively merges pairs of adjacent chunks by correcting the values in the second chunk of each pair. The second phase produces the resulting chunks in a pipelined mode to compute the final solution.

Sung et al. [22,23] proposed the idea to divide the input into blocks and decompose the computation over each block. Interblock parallelism is exploited to enhance code performance.

Nehab et al. [24] also suggested splitting the input data into blocks that are processed in parallel by modern GPU architectures and overlapped the causal, anticausal, row, and column filter processing.

Marongiu and Palazzari [25] addressed the parallelization of a class of iterative algorithms described as the system of affine recurrence equations (SARE). It introduces an affine timing function and an affine allocation function that perform a space-time transformation of the loop nest iteration space. It considers algorithms dealing with only uniform dependence vectors, while the approach presented in this paper deals with nonuniform vectors.

Ben-Asher and Haber [26] defined recurrence equations called “simple indexed recurrences” (SIR). In this type of equation, for extending capabilities, ordinary recurrences are generalized to $X\left[g\left(i\right)\right]=o{p}_i(X\left[f\left(i\right)\right],X\left[g\left(i\right)\right])$, where f and g are affine functions $o{p}_i(x,y)$ is a binary associative operator. In that paper, the authors proposed a parallel solution to the SIR problem. This case of recurrences is simpler than that considered in our paper and any tiled code is not considered.

Summing up, we may conclude that in the class of reordering transformations, there does not exist any technique allowing for parallelizing and/or tiling the code in Listing 1. In the class of nonordering transformations, to our best knowledge, no technique has been published to generate parallel tiled code implementing the problem addressed in this paper.

The main contribution of our paper is presenting a novel technique, which for the first time allows us to parallelize and tile the examined loop nest implementing computing general linear recurrence equations by means of reordering transformations. The novelty consists in adding an additional phase to classical reordering transformations: to source code, we first apply a reordering schedule that respects all data dependencies; then, we apply classical affine transformations to the serial code obtained in the first phase. This increases target code generation time but does not introduce any additional computations to the source code. Generated target code is still within the class of reordering transformations.

5. Results

The primary reason for writing a parallel program is speed. We strive that the parallel program execution should be completed at a shorter time in comparison with that of the serial one. We need to know what is the benefit from tiling and parallelism. For this purpose, we need to compute the parallel program speedup.

The speedup of a parallel program over a corresponding sequential program is the ratio of the compute time for the sequential program to the time for the parallel program. The value of speedup shows how efficient is a parallel program.

Perfect linear speedup occurs when the value of speedup is the same as the number of threads used for running a parallel program. In practice, perfect linear speedup seldom occurs because of parallel program overhead and the fact that all computations of an original program cannot be parallelized.

According to Amdahl’s law, the parallel code speedup, S, is limited to $S<=1/s$, where s is the serial fraction of code, i.e., the fraction of code that cannot be parallelized. For example, if $s=0.2$, the maximal speedup is 5 regardless of the number of threads used for running a parallel program.

To evaluate the performance of the parallel tiled code presented in Listing 4, we carried out experiments aimed at measuring the execution time of the original program and parallel one (for the different number of threads) and next calculated the speedup of the parallel program.

Below, we present the results of experiments carried out with the codes shown in Listing 1 (serial code) and Listing 4 (parallel code). As we mentioned in the previous section, we cannot find any related parallel code that fulfills exactly the same computations as those executed with the code in Listing 1. Thus, we limited our experiments to the codes mentioned above.

To carry out experiments, we used a processor Intel Xeon X5570, 2.93 GHz, 2 physical units, 8 (2 × 4) cores, 16 hyper-threads, and an 8 MB cache. Executable parallel tiled code was generated by means of the g++ compiler with the -O3 flag of optimization.

Experiments were carried out for ten different lengths of the problem defined with parameter N from 1000 to 5000 for the codes presented in Listing 1 (serial code) and Listing 4 (parallel code).

All of the source code to perform the experiments and the program to run the tested codes can be found at https://github.com/piotrbla/livc (accessed on 24 August 2021).

We carried our experiments to choose the optimal size of a tile. The size of a tile is optimal if (i) all data associated with that tile can be held in cache, (ii) those data occupy almost the entire capacity of cache, and (iii) tiled code execution time is minimal provided that the conditions (i) and (ii) above are satisfied.

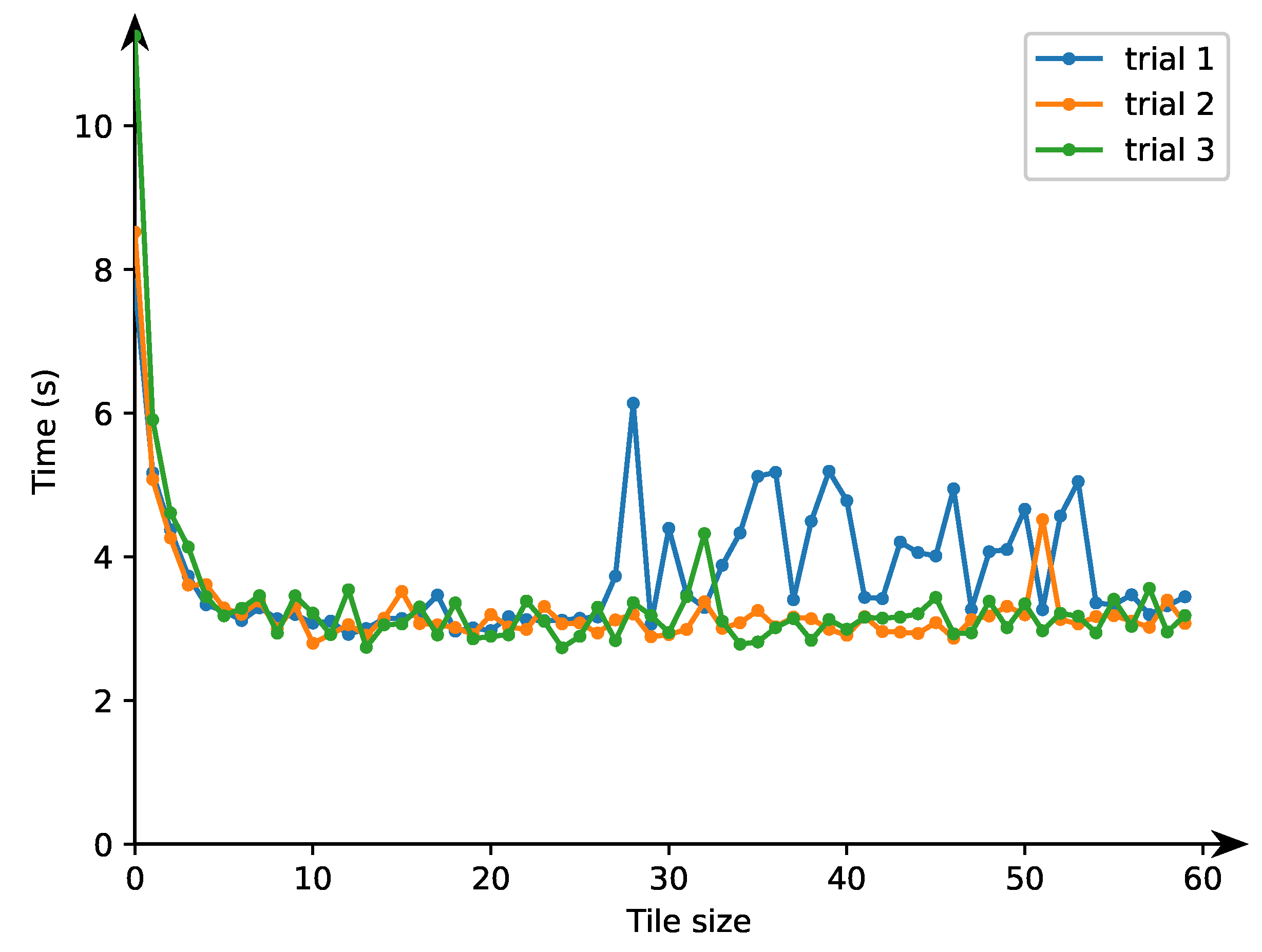
For this purpose, we fulfilled three trials whose results are shown in Figure 1. The curve “trial1” represents how the time of tiled program execution depends on the block size along axis $h0$ when the block size along axis $w0$ is fixed equal to 16. After first trial 1, we chose the best size along the $h0$ axis equal to 32.

The curve “trial2” demonstrates how the time of tiled program execution depends on the block size along axis $w0$ when the block size along axis $h0$ is equal to 32 (the result of trial 1). After trial 2, we chose the best size along axis $w0$ equal to 24.

The curve “trial3” shows how the time of tiled program execution depends on the block size along axis $h0$ when the block size along axis $w0$ is equal to 24 (the result of trial 2). After trial 3, we chose the best tile size along axis $h0$ equal to 54. Finaly, as the best size of a 2D tile in the parallel tiled code, we chose 24 × 54.

For the best tile size,

Table 1. Time in seconds and speedup for Intel Xeon X5570 and 32 OpenMP threads.

N	Serial	Parallel	Speedup
1000	0.27	0.13	2.08
1500	0.75	0.21	3.57
2000	1.46	0.32	4.56
2500	2.38	0.49	4.86
3000	4.14	0.70	5.91
3500	6.22	0.89	6.99
4000	8.22	1.12	7.34
4500	10.6	1.33	7.97
5000	12.0	1.52	7.89

presents execution times and speedup of the serial program in Listing 1 and the parallel tiled one presented in Listing 4 for 32 OpenMP threads used. Figure 2 depicts the data presented in Table 1 in a graphical way. As presented, the execution time of parallel tiled program grows practically in a linear manner exposing considerable speedup (the ratio of the serial program execution time to that of the corresponding parallel one) presented in Figure 3.

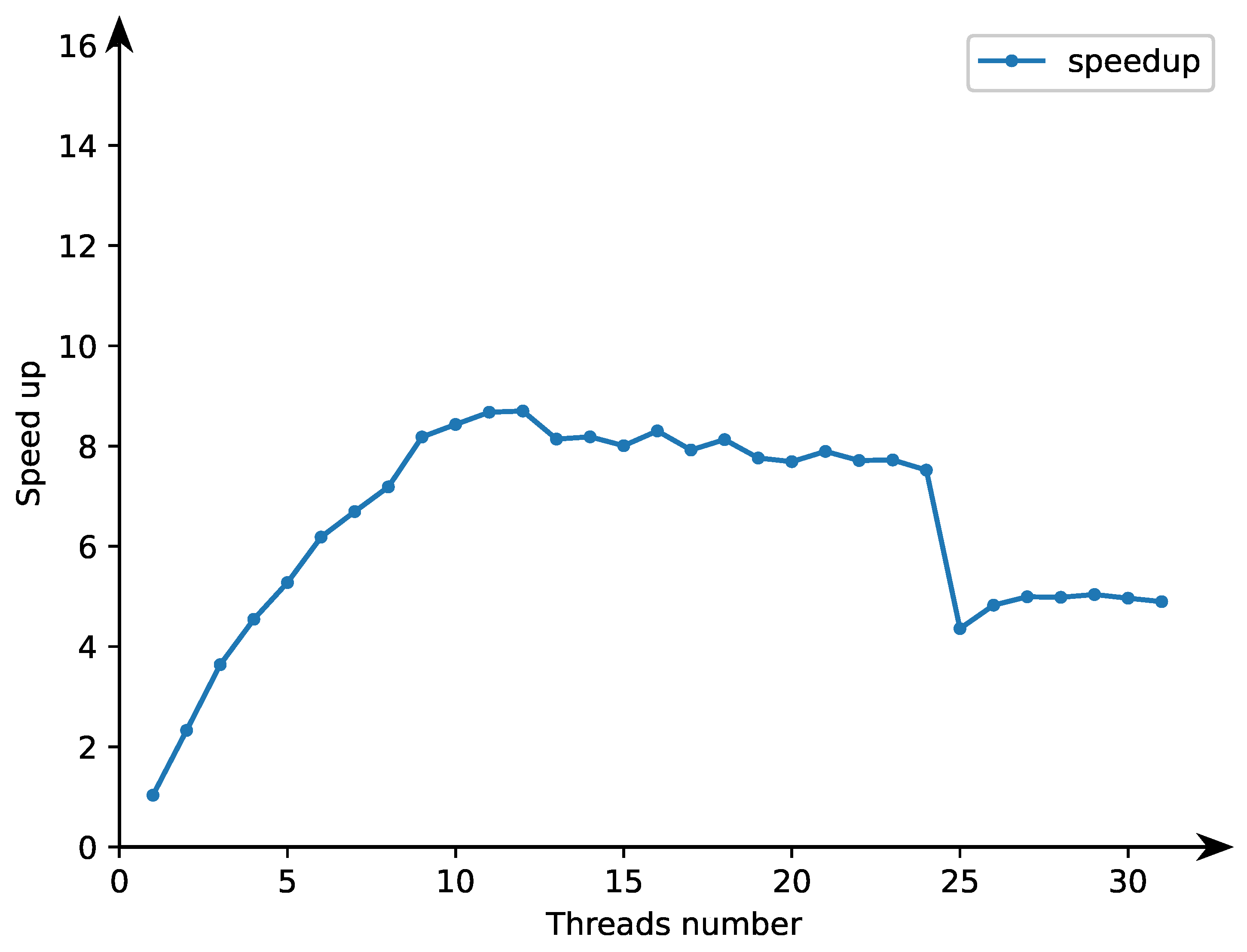
Figure 4 presents how parallel tiled code speedup depends on the thread number for the maximal problem size used for experiments, i.e., for $N=5000$. The parallel tiled code speedup grows practically linear for the number of threads 1 to 12. Linear speedup for the number of threads $\ge 12$ is prevented with the serial fraction of code (Amdahl’s law)—parallel loop initialization fulfilled with a single thread and serial input–output operations. Speedup is also limited with parallel program overhead—there is thread synchronization in the examined parallel code, after each wavefront, barrier synchronization is inserted because the following wavefront can be executed after completing the calculations of the previous wavefront.

We may conclude that the generated parallel tiled code implementing computing-intensive general linear recurrence equations and presented in Listing 4 can be successfully run on modern multicore machines with a large number of cores.

6. Conclusions

We presented an approach to generate parallel tiled code for computing general linear recurrence equations (GLREs) presented in Listing 1. That code is computing-intensive and must be run on modern multicore computers to reduce execution time. We demonstrated how to transform that code to obtain the modified code shown in Listing 3, which exposes dependencies such that there exist two linear independent solutions to the time partition constraints formed on the basis of those dependencies. This allows us to apply the affine transformation framework and generate parallel 2D tiled code computing GLREs presented in Listing 4. The parallelism is achieved using the wavefront technique and presented with the code that conforms to the OpenMP standard. To our best knowledge, the target parallel tiled code generated by us and presented in Listing 4 is the first to allow for enumerating 2D tiles and the first that does not require any additional computations in comparison with those of the original serial code. This code is derived by means of tiling the loop nest iteration space. Our experiments with the resulting parallel tiled code show that the code significantly outperforms the original GLREs computing serial code. The code performance improvement is achieved due to the parallelism and better locality of the target code.