Dual Image Deblurring Using Deep Image Prior
Abstract
:1. Introduction
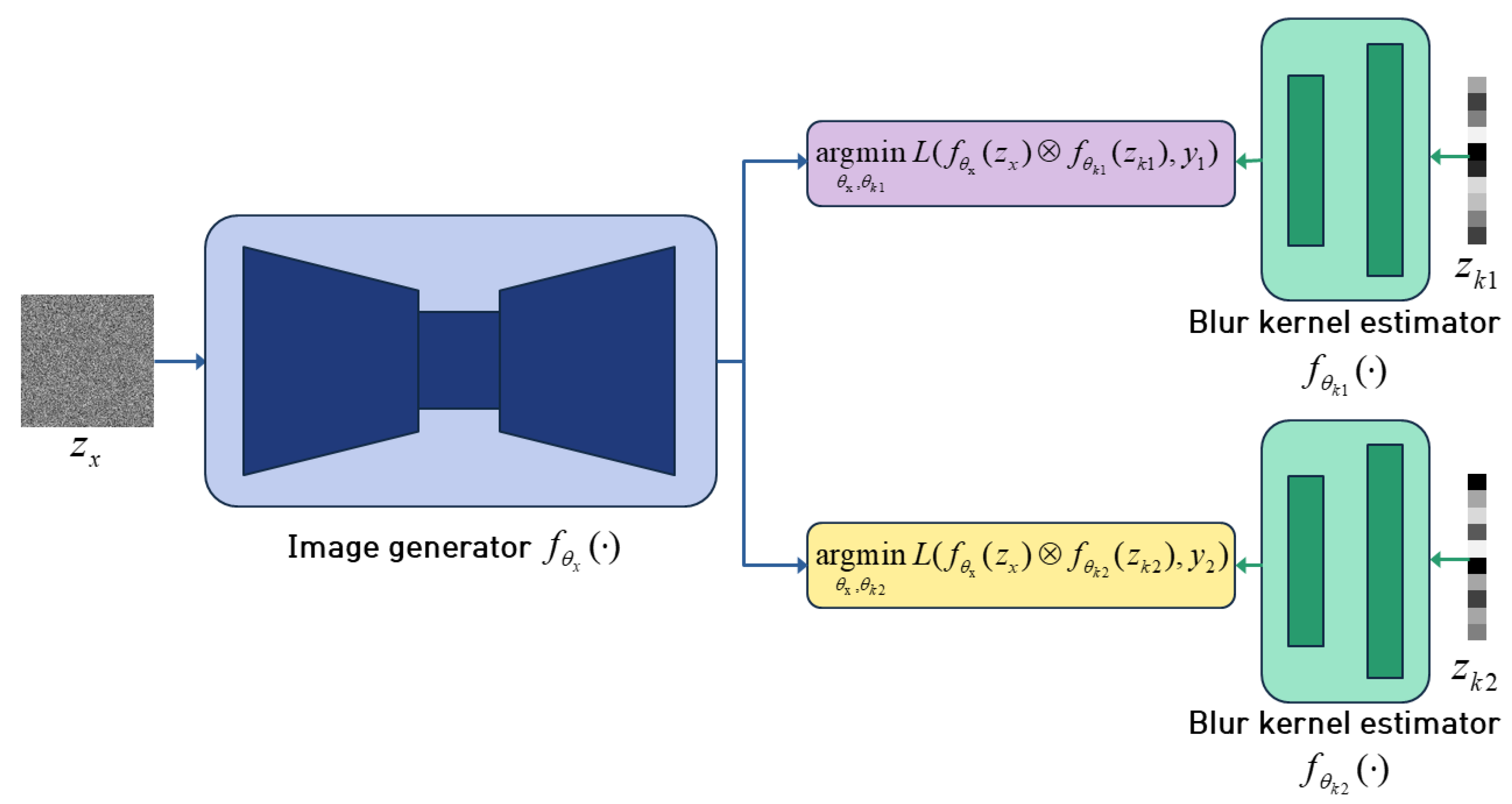
- We propose a DIP-based deblurring method called DualDeblur using two blurry images of the same scene. Multiple images are used to jointly optimize complementary information.
- We propose an adaptive SSIM loss that adjusts the weights of both and SSIM for each optimization step. From this, we ensure both pixel-wise accuracy and structural properties in the deblurred image.
- The experimental results show that our method is quantitatively and qualitatively superior to previous methods.
2. Related Works
2.1. Optimization-Based Image Deblurring
2.2. DL-Based Image Deblurring
3. Proposed Method
3.1. DualDeblur
3.2. Adaptive SSIM Loss
| Algorithm 1 DualDeblur optimization process |
Input: blurry images and T iterations Output: restored image , estimated blur kernels and
|
4. Experimental Results
4.1. Dataset
- 1
- Levin test set [33]: In their seminal work, Levin et al. [33] provided 8 blur kernels with size of , where and 4 sharp images, resulting in 32 blurry gray-scale images with size of . To evaluate our method, we divided the soft and hard pairs on the basis of difference in blur kernel size. If the difference was less than 5 pixels, we classified such an image pair as a soft pair, and vice versa as a hard pair. Following this pipeline, we randomly selected 7 soft pairs and 7 hard pairs, totaling to 14 blurry pairs per image. In short, we prepared a total of 56 pairs of blurry images for evaluation. The composition of the Levin test set [33] is described in detail in Table 3. Specifically, the soft pairs comprised , and . Here, each number represents the blur kernel size of k. For example, [11, 13] means that the blur kernel sizes 13 × 13 and 15 × 15 are paired. Because the Levin test set contains two blur kernels with a size of 23 × 23, we denote each as and . The hard pairs contained , and .
- 2
- Lai test set [45]: We further compared our method using the Lai test set [45], which contains RGB images of various sizes. The Lai test set comprises 4 blur kernels and 25 sharp images, resulting in 100 blurry images. It is divided into five categories: and , with 20 images for each category. The sizes of the 4 blur kernels are and . Thus, we prepared a soft pair (i.e., ), and 4 hard pairs (i.e., , and ). As described in Table 3, there are 25 sharp images and 5 blur kernel pairs; a total of 125 pairs of blur images are used for evaluation.
4.2. Implementation Details
4.3. Comparison on the Levin Test Set
4.4. Comparison on Lai Test Set
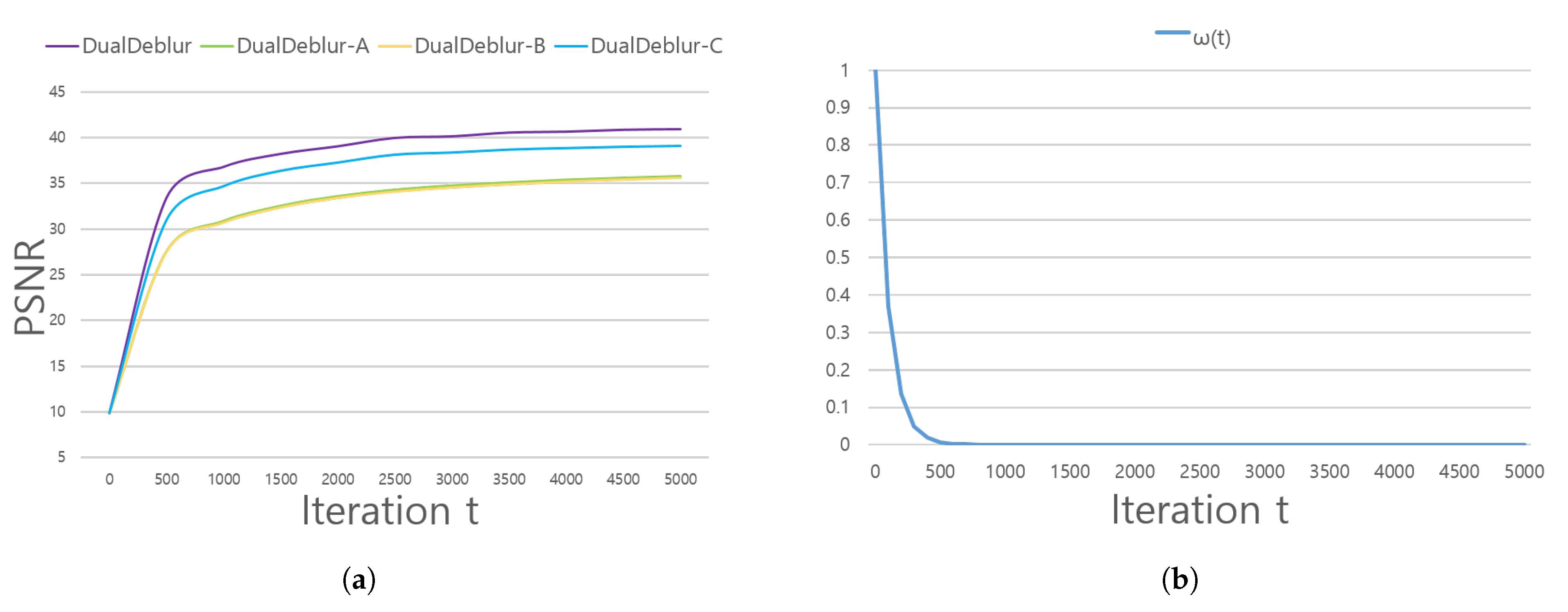
4.5. Ablation Study
4.5.1. Effects of Dual Architecture
4.5.2. Effects of Adaptive _SSIM Loss
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–16 December 2015; pp. 1440–1448. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nah, S.; Hyun Kim, T.; Mu Lee, K. Deep multi-scale convolutional neural network for dynamic scene deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3883–3891. [Google Scholar]
- Su, S.; Delbracio, M.; Wang, J.; Sapiro, G.; Heidrich, W.; Wang, O. Deep video deblurring for hand-held cameras. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1279–1288. [Google Scholar]
- Tao, X.; Gao, H.; Shen, X.; Wang, J.; Jia, J. Scale-recurrent network for deep image deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8174–8182. [Google Scholar]
- Zhang, J.; Pan, J.; Ren, J.; Song, Y.; Bao, L.; Lau, R.W.; Yang, M.H. Dynamic scene deblurring using spatially variant recurrent neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2521–2529. [Google Scholar]
- Zhang, H.; Dai, Y.; Li, H.; Koniusz, P. Deep stacked hierarchical multi-patch network for image deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 5978–5986. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H.; Shao, L. Multi-stage progressive image restoration. arXiv 2021, arXiv:2102.02808. [Google Scholar]
- Quan, Y.; Chen, M.; Pang, T.; Ji, H. Self2self with dropout: Learning self-supervised denoising from single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1890–1898. [Google Scholar]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep image prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 9446–9454. [Google Scholar]
- Ren, D.; Zhang, K.; Wang, Q.; Hu, Q.; Zuo, W. Neural blind deconvolution using deep priors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 3341–3350. [Google Scholar]
- Zhang, H.; Wipf, D.; Zhang, Y. Multi-image blind deblurring using a coupled adaptive sparse prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–27 June 2013; pp. 1051–1058. [Google Scholar]
- Rav-Acha, A.; Peleg, S. Two motion-blurred images are better than one. Pattern Recognit. Lett. 2005, 26, 311–317. [Google Scholar] [CrossRef]
- Xu, L.; Jia, J. Two-phase kernel estimation for robust motion deblurring. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010; pp. 157–170. [Google Scholar]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale structural similarity for image quality assessment. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; 2003; Volume 2, pp. 1398–1402. [Google Scholar]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, H.; Yue, Z.; Zhao, Q.; Meng, D. A Deep Variational Bayesian Framework for Blind Image Deblurring. arXiv 2021, arXiv:2106.02884. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Chan, T.F.; Wong, C.K. Total variation blind deconvolution. IEEE Trans. Image Process. 1998, 7, 370–375. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perrone, D.; Favaro, P. Total variation blind deconvolution: The devil is in the details. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2909–2916. [Google Scholar]
- Fergus, R.; Singh, B.; Hertzmann, A.; Roweis, S.T.; Freeman, W.T. Removing camera shake from a single photograph. In ACM SIGGRAPH 2006 Papers; Association for Computing Machinery: New York, NY, USA, 2006; pp. 787–794. [Google Scholar]
- Zuo, W.; Ren, D.; Zhang, D.; Gu, S.; Zhang, L. Learning iteration-wise generalized shrinkage–thresholding operators for blind deconvolution. IEEE Trans. Image Process. 2016, 25, 1751–1764. [Google Scholar] [CrossRef]
- Cho, S.; Lee, S. Fast motion deblurring. In ACM SIGGRAPH Asia 2009 Papers; Association for Computing Machinery: New York, NY, USA, 2009; pp. 1–8. [Google Scholar]
- Krishnan, D.; Fergus, R. Fast image deconvolution using hyper-Laplacian priors. Adv. Neural Inf. Process. Syst. 2009, 22, 1033–1041. [Google Scholar]
- Krishnan, D.; Tay, T.; Fergus, R. Blind deconvolution using a normalized sparsity measure. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 233–240. [Google Scholar]
- Levin, A.; Weiss, Y.; Durand, F.; Freeman, W.T. Understanding and evaluating blind deconvolution algorithms. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1964–1971. [Google Scholar]
- Levin, A.; Weiss, Y.; Durand, F.; Freeman, W.T. Efficient marginal likelihood optimization in blind deconvolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 2657–2664. [Google Scholar]
- Xu, L.; Zheng, S.; Jia, J. Unnatural l0 sparse representation for natural image deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1107–1114. [Google Scholar]
- Pan, J.; Hu, Z.; Su, Z.; Yang, M.H. l_0-regularized intensity and gradient prior for deblurring text images and beyond. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 342–355. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Cho, S.; Wang, J.; Hays, J. Edge-based blur kernel estimation using patch priors. In Proceedings of the IEEE International Conference on Computational Photography, Cambridge, MA, USA, 19–21 April 2013; pp. 1–8. [Google Scholar]
- Michaeli, T.; Irani, M. Blind deblurring using internal patch recurrence. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2014; pp. 783–798. [Google Scholar]
- Pan, J.; Sun, D.; Pfister, H.; Yang, M.H. Deblurring images via dark channel prior. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 2315–2328. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Cao, W.; Xu, Z.; Ponce, J. Learning a convolutional neural network for non-uniform motion blur removal. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 7–9 May 2015; pp. 769–777. [Google Scholar]
- Chakrabarti, A. A neural approach to blind motion deblurring. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016; pp. 221–235. [Google Scholar]
- Sajjadi, M.S.; Scholkopf, B.; Hirsch, M. Enhancenet: Single image super-resolution through automated texture synthesis. In Proceedings of the IEEE International Conference on Computer Vision, Honolulu, HI, USA, 21–26 July 2017; pp. 4491–4500. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 586–595. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Lai, W.S.; Huang, J.B.; Hu, Z.; Ahuja, N.; Yang, M.H. A comparative study for single image blind deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1701–1709. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. Adv. Neural Inf. Process. Syst. 2019, 32, 8026–8037. [Google Scholar]
- Whyte, O.; Sivic, J.; Zisserman, A. Deblurring shaken and partially saturated images. Int. J. Comput. Vis. 2014, 110, 185–201. [Google Scholar] [CrossRef]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Loss functions for image restoration with neural networks. IEEE Trans. Comput. Imaging 2016, 3, 47–57. [Google Scholar] [CrossRef]






| Input: ( of a uniform distribution | ||||||||
| Output: latent image | ||||||||
| Encoder | Operation | Kernel | In→Out | Decoder | Operation | Kernel | In→Out | |
| Encoder 1 | Conv2d, lReLU | 128, 3 × 3, 1 | Decoder 1 | Conv2d, lReLU | 128, 3 × 3, 1 | |||
| Conv2d, lReLU | 16, 3 × 3, 1 | |||||||
| Encoder 2 | Conv2d, lReLU | 128, 3 × 3, 1 | Decoder 2 | Conv2d, lReLU | 128, 3 × 3, 1 | |||
| Skip 2 | Conv2d, lReLU | 16, 3 × 3, 1 | ||||||
| Encoder 3 | Conv2d, lReLU | 128, 3 × 3, 1 | Decoder 3 | Conv2d, lReLU | 128, 3 × 3, 1 | |||
| Skip 3 | Conv2d, lReLU | 16, 3 × 3, 1 | ||||||
| Encoder 4 | Conv2d, lReLU | 128, 3 × 3, 1 | Decoder 4 | Conv2d, lReLU | 128, 3 × 3, 1 | |||
| Skip 4 | Conv2d, lReLU | 16, 3 × 3, 1 | ||||||
| Encoder 5 | Conv2d, lReLU | 128, 3 × 3, 1 | Decoder 5 | Conv2d, lReLU | 128, 3 × 3, 1 | |||
| Skip 5 | Conv2d, lReLU | 16, 3 × 3, 1 | ||||||
| Output layer | Conv2d, | C, 1 × 1, 0 | ||||||
| Input: (200) of uniform distributions, blur kernel size of | |
| Output: blur kernel | |
| FCN | Operation |
| Layer 1 | Linear (200, 1000), |
| Layer 2 | Linear (1000, ), |
| Test Set | # GT Images | # Blur Kernel | # Blur Images | # Soft Pair | # Hard Pair | # Total Pair |
|---|---|---|---|---|---|---|
| Levin test set [33] | 4 | 8 | 32 | 28 | 28 | 56 |
| Lai test set [45] | 25 | 4 | 100 | 25 | 100 | 125 |
| Method | Blur Kernel | PSNR ↑ | SSIM ↑ | Error Ratio ↓ | FSIM↑ | LPIPS ↓ | Method | Blur Kernel | PSNR ↑ | SSIM ↑ | Error Ratio↓ | FSIM ↑ | LPIPS ↓ |
| known k * | 13 | 36.53 | 0.9659 | 1.0000 | 0.8868 | 0.0530 | known k * | 15 | 35.33 | 0.9525 | 1.0000 | 0.8167 | 0.0919 |
| Krishnan et al. * [32] | 13 | 34.88 | 0.9575 | 1.1715 | 0.9116 | 0.0604 | Krishnan et al. * [32] | 15 | 34.87 | 0.9481 | 1.0563 | 0.7862 | 0.1201 |
| Cho & Lee * [30] | 13 | 33.93 | 0.9532 | 1.2536 | 0.8578 | 0.0925 | Cho & Lee * [30] | 15 | 33.88 | 0.9429 | 1.3191 | 0.7891 | 0.1226 |
| Levin et al. * [34] | 13 | 34.29 | 0.9533 | 1.3454 | 0.8213 | 0.0922 | Levin et al. * [34] | 15 | 30.94 | 0.8950 | 2.5613 | 0.8003 | 0.1199 |
| Xu & Jia * [21] | 13 | 34.10 | 0.9532 | 1.2846 | 0.8612 | 0.0939 | Xu & Jia * [21] | 15 | 33.04 | 0.9355 | 1.4272 | 0.7763 | 0.1417 |
| Sun et al. * [37] | 13 | 36.24 | 0.9659 | 0.9933 | 0.8639 | 0.0685 | Sun et al. * [37] | 15 | 34.96 | 0.9497 | 1.1277 | 0.7887 | 0.1073 |
| Zuo et al. * [29] | 13 | 35.28 | 0.9598 | 1.0686 | 0.8449 | 0.0892 | Zuo et al. * [29] | 15 | 34.31 | 0.9442 | 1.1660 | 0.7717 | 0.1281 |
| Pan-DCP * [39] | 13 | 35.47 | 0.9591 | 1.0690 | 0.8359 | 0.0887 | Pan-DCP * [39] | 15 | 34.19 | 0.9415 | 1.1244 | 0.7495 | 0.1259 |
| SelfDeblur [18] | 13 | 33.03 | 0.9388 | 1.5078 | 0.8731 | 0.0938 | SelfDeblur [18] | 15 | 33.80 | 0.9409 | 1.3533 | 0.8000 | 0.1030 |
| Ours (soft) | 13, 15 | 39.93 | 0.9863 | 0.5942 | 0.9424 | 0.0283 | Ours (soft) | 15, 17 | 40.41 | 0.9857 | 0.4562 | 0.8770 | 0.0448 |
| Ours (hard) | 13, 27 | 41.17 | 0.9879 | 0.3475 | 0.9018 | 0.0307 | Ours (hard) | 15, 27 | 40.90 | 0.9862 | 0.3757 | 0.8177 | 0.0578 |
| Method | Blur Kernel | PSNR↑ | SSIM↑ | Error Ratio↓ | FSIM↑ | LPIPS↓ | Method | Blur Kernel | PSNR↑ | SSIM↑ | Error Ratio↓ | FSIM↑ | LPIPS↓ |
| known k * | 17 | 33.17 | 0.9386 | 1.0000 | 0.7491 | 0.1176 | known k * | 19 | 34.04 | 0.9424 | 1.0000 | 0.8607 | 0.0719 |
| Krishnan et al. * [32] | 17 | 31.69 | 0.9160 | 1.2328 | 0.7605 | 0.1317 | Krishnan et al. * [32] | 19 | 32.87 | 0.9325 | 1.1749 | 0.8257 | 0.0939 |
| Cho & Lee * [30] | 17 | 31.71 | 0.9203 | 1.1958 | 0.7760 | 0.1334 | Cho & Lee * [30] | 19 | 32.20 | 0.9231 | 1.2596 | 0.8552 | 0.1027 |
| Levin et al. * [34] | 17 | 29.61 | 0.8892 | 1.6049 | 0.7122 | 0.1613 | Levin et al. * [34] | 19 | 31.03 | 0.9106 | 1.6047 | 0.8101 | 0.1146 |
| Xu & Jia * [21] | 17 | 30.54 | 0.9028 | 1.4637 | 0.7443 | 0.1528 | Xu & Jia * [21] | 19 | 32.58 | 0.9294 | 1.1322 | 0.8732 | 0.0999 |
| Sun et al. * [37] | 17 | 32.67 | 0.9318 | 1.1492 | 0.7584 | 0.1229 | Sun et al. * [37] | 19 | 32.97 | 0.9312 | 1.2007 | 0.8810 | 0.0747 |
| Zuo et al. * [29] | 17 | 32.31 | 0.9278 | 1.1495 | 0.7471 | 0.1406 | Zuo et al. * [29] | 19 | 33.28 | 0.9355 | 0.9873 | 0.8750 | 0.9515 |
| Pan-DCP * [39] | 17 | 31.82 | 0.9215 | 1.2084 | 0.7405 | 0.1397 | Pan-DCP * [39] | 19 | 32.50 | 0.9250 | 1.1536 | 0.8613 | 0.1031 |
| SelfDeblur [18] | 17 | 33.12 | 0.9275 | 0.9403 | 0.7721 | 0.1251 | SelfDeblur [18] | 19 | 33.11 | 0.9232 | 1.1142 | 0.8292 | 0.1182 |
| Ours (soft) | 17, 19 | 40.99 | 0.9876 | 0.3630 | 0.8157 | 0.0565 | Ours (soft) | 19, 21 | 41.82 | 0.9893 | 0.4726 | 0.7233 | 0.0955 |
| Ours (hard) | 17, 27 | 40.53 | 0.9864 | 0.2984 | 0.8506 | 0.0454 | Ours (hard) | 19, 27 | 40.73 | 0.9874 | 0.3351 | 0.7937 | 0.0703 |
| Method | Blur Kernel | PSNR↑ | SSIM↑ | Error Ratio↓ | FSIM↑ | LPIPS↓ | Method | Blur Kernel | PSNR↑ | SSIM↑ | Error Ratio↓ | FSIM↑ | LPIPS↓ |
| known k * | 21 | 36.41 | 0.9672 | 1.0000 | 0.7725 | 0.1441 | known k * | 23a | 35.21 | 0.9573 | 1.0000 | 0.8222 | 0.1169 |
| Krishnan et al. * [32] | 21 | 30.59 | 0.9249 | 2.9369 | 0.7725 | 0.1021 | Krishnan et al. * [32] | 23a | 23.75 | 0.7700 | 4.6599 | 0.8657 | 0.1497 |
| Cho & Lee * [30] | 21 | 30.46 | 0.9143 | 2.5131 | 0.7926 | 0.1106 | Cho & Lee * [30] | 23a | 28.67 | 0.8856 | 2.3186 | 0.8403 | 0.1276 |
| Levin et al. * [34] | 21 | 32.26 | 0.9376 | 2.0328 | 0.7239 | 0.1287 | Levin et al. * [34] | 23a | 30.05 | 0.9126 | 2.0796 | 0.7516 | 0.1419 |
| Xu & Jia * [21] | 21 | 33.82 | 0.9509 | 1.4399 | 0.8084 | 0.1029 | Xu & Jia * [21] | 23a | 29.48 | 0.8651 | 2.4357 | 0.8494 | 0.1428 |
| Sun et al. * [37] | 21 | 33.29 | 0.9402 | 1.7488 | 0.8279 | 0.0774 | Sun et al. * [37] | 23a | 32.48 | 0.9379 | 1.3988 | 0.8690 | 0.0858 |
| Zuo et al. * [29] | 21 | 33.65 | 0.9515 | 1.5416 | 0.8067 | 0.0942 | Zuo et al. * [29] | 23a | 31.99 | 0.9344 | 1.5303 | 0.8944 | 0.0972 |
| Pan-DCP * [39] | 21 | 34.49 | 0.9518 | 1.3103 | 0.8008 | 0.0997 | Pan-DCP * [39] | 23a | 32.69 | 0.9361 | 1.2969 | 0.8705 | 0.0949 |
| SelfDeblur [18] | 21 | 32.52 | 0.9402 | 1.9913 | 0.8058 | 0.0946 | SelfDeblur [18] | 23a | 34.29 | 0.9478 | 0.9519 | 0.8524 | 0.0757 |
| Ours (soft) | 21, 23a | 40.39 | 0.9879 | 0.5244 | 0.8751 | 0.0374 | Ours (soft) | 21, 23b | 40.73 | 0.9880 | 0.4385 | 0.8843 | 0.0365 |
| Ours (hard) | 21, 27 | 41.94 | 0.9895 | 0.3482 | 0.8702 | 0.0456 | Ours (hard) | 23b, 27 | 40.80 | 0.9867 | 0.2285 | 0.9167 | 0.0267 |
| Method | Blur Kernel | PSNR↑ | SSIM↑ | Error Ratio↓ | FSIM↑ | LPIPS↓ | Method | Blur Kernel | PSNR↑ | SSIM↑ | Error Ratio↓ | FSIM↑ | LPIPS↓ |
| known k * | 23b | 33.58 | 0.9493 | 1.0000 | 0.7483 | 0.1153 | known k * | Avg. | 34.53 | 0.9492 | 1.0000 | 0.7754 | 0.1058 |
| Krishnan et al. * [32] | 23b | 26.67 | 0.7924 | 2.5681 | 0.8195 | 0.1429 | Krishnan et al. * [32] | Avg. | 29.88 | 0.8666 | 2.4523 | 0.8046 | 0.1282 |
| Cho & Lee * [30] | 23b | 27.84 | 0.8510 | 1.6925 | 0.7802 | 0.1529 | Cho & Lee * [30] | Avg. | 30.57 | 0.8966 | 1.7113 | 0.8051 | 0.1280 |
| Levin et al. * [34] | 23b | 29.58 | 0.9012 | 1.4543 | 0.7785 | 0.1379 | Levin et al. * [34] | Avg. | 30.80 | 0.9092 | 1.7724 | 0.7708 | 0.1301 |
| Xu & Jia * [21] | 23b | 30.35 | 0.9096 | 1.2175 | 0.8744 | 0.1142 | Xu & Jia * [21] | Avg. | 31.67 | 0.9163 | 1.4898 | 0.8253 | 0.1232 |
| Sun et al. * [37] | 23b | 31.98 | 0.9331 | 1.1005 | 0.8653 | 0.0882 | Sun et al. * [37] | Avg. | 32.99 | 0.9330 | 1.2847 | 0.8349 | 0.0935 |
| Zuo et al. * [29] | 23b | 31.35 | 0.9306 | 1.1356 | 0.8845 | 0.1009 | Zuo et al. * [29] | Avg. | 32.66 | 0.9332 | 1.2500 | 0.8361 | 0.1084 |
| Pan-DCP * [39] | 23b | 31.43 | 0.9267 | 1.2614 | 0.8605 | 0.0935 | Pan-DCP * [39] | Avg. | 32.69 | 0.9284 | 1.2555 | 0.8161 | 0.1114 |
| SelfDeblur [18] | 23b | 33.05 | 0.9304 | 0.9651 | 0.7986 | 0.1091 | SelfDeblur [18] | Avg. | 33.07 | 0.9313 | 1.1968 | 0.8086 | 0.1082 |
| Ours (soft) | 23a, 23b | 40.74 | 0.9851 | 0.2646 | 0.9092 | 0.0339 | Ours (soft) | Avg. | 40.72 | 0.9871 | 0.4448 | 0.8610 | 0.0476 |
| Ours (hard) | 23a, 27 | 41.40 | 0.9877 | 0.2700 | 0.8996 | 0.0357 | Ours (hard) | Avg. | 41.07 | 0.9874 | 0.3148 | 0.8643 | 0.0446 |
| Method | Time (s) | Parameters (M) |
|---|---|---|
| Krishnan et al. * [32] | 8.9400 | - |
| Cho & Lee * [30] | 1.3951 | - |
| Levin et al. * [34] | 78.263 | - |
| Xu & Jia * [21] | 1.1840 | - |
| Sun et al. * [37] | 191.03 | - |
| Zuo et al. * [29] | 10.998 | - |
| Pan-DCP * [39] | 295.23 | - |
| SelfDeblur [18] | 368.57 | 29.1 |
| Ours | 423.49 | 35.9 |
| Method | Blur Kernel | PSNR ↑ | SSIM ↑ | FSIM ↑ | LPIPS ↓ | Method | Blur Kernel | PSNR ↑ | SSIM ↑ | FSIM ↑ | LPIPS ↓ |
| Cho & Lee * [30] | 31 | 19.60 | 0.6664 | 0.7182 | 0.3855 | Cho & Lee * [30] | 51 | 16.74 | 0.4342 | 0.6394 | 0.4996 |
| Xu & Jia * [21] | 31 | 23.70 | 0.8534 | 0.8069 | 0.3099 | Xu & Jia * [21] | 51 | 19.69 | 0.6821 | 0.6773 | 0.3982 |
| Xu et al. * [35] | 31 | 22.90 | 0.8077 | 0.7928 | 0.3151 | Xu et al. * [35] | 51 | 19.18 | 0.6603 | 0.6703 | 0.4073 |
| Michaeli et al. * [38] | 31 | 22.02 | 0.7499 | 07668 | 0.3492 | Michaeli et al. * [38] | 51 | 18.07 | 0.4995 | 0.6562 | 0.4791 |
| Perrone et al. * [27] | 31 | 22.12 | 0.8279 | 0.7562 | 0.3501 | Perrone et al. * [27] | 51 | 16.21 | 0.4471 | 0.6358 | 0.5002 |
| Pan-L0 * [36] | 31 | 22.58 | 0.8405 | 0.7886 | 0.3267 | Pan-L0 * [36] | 51 | 18.08 | 0.6233 | 0.6637 | 0.4271 |
| Pan-DCP * [39] | 31 | 23.38 | 0.8478 | 0.8029 | 0.3580 | Pan-DCP * [39] | 51 | 19.69 | 0.6961 | 0.6736 | 0.4475 |
| SelfDeblur [18] | 31 | 22.40 | 0.8345 | 0.8005 | 0.4205 | SelfDeblur [18] | 51 | 21.27 | 0.7748 | 0.7928 | 0.4708 |
| Ours (hard) | 31, 51 | 28.57 | 0.9711 | 0.8056 | 0.1959 | Ours (soft) | 51, 55 | 28.32 | 0.9598 | 0.8034 | 0.2131 |
| Ours (hard) | 31, 75 | 29.09 | 0.9751 | 0.8276 | 0.1691 | Ours (hard) | 51, 75 | 28.78 | 0.9613 | 0.8252 | 0.1781 |
| Method | Blur Kernel | PSNR↑ | SSIM↑ | FSIM↑ | LPIPS↓ | Method | Blur Kernel | PSNR↑ | SSIM↑ | FSIM↑ | LPIPS↓ |
| Cho & Lee * [30] | 55 | 16.99 | 0.4857 | 0.6581 | 0.4863 | Cho & Lee * [30] | Avg. | 17.06 | 0.4801 | 0.6571 | 0.4997 |
| Xu & Jia * [21] | 55 | 18.98 | 0.6454 | 0.6794 | 0.4179 | Xu & Jia * [21] | Avg. | 20.18 | 0.7080 | 0.7123 | 0.4121 |
| Xu et al. * [35] | 55 | 18.12 | 0.5859 | 0.6707 | 0.4386 | Xu et al. * [35] | Avg. | 19.23 | 0.6593 | 0.6971 | 0.4278 |
| Michaeli et al. * [38] | 55 | 17.66 | 0.4945 | 0.6554 | 0.4942 | Michaeli et al. * [38] | Avg. | 18.37 | 0.5181 | 0.6729 | 0.4904 |
| Perrone et al. * [27] | 55 | 17.33 | 0.5607 | 0.6657 | 0.4545 | Perrone et al. * [27] | Avg. | 18.48 | 0.6130 | 0.6887 | 0.4568 |
| Pan-L0 * [36] | 55 | 17.19 | 0.5367 | 0.6542 | 0.4602 | Pan-L0 * [36] | Avg. | 18.54 | 0.6248 | 0.6888 | 0.4454 |
| Pan-DCP * [39] | 55 | 18.71 | 0.6136 | 0.6637 | 0.4520 | Pan-DCP * [39] | Avg. | 19.89 | 0.6656 | 0.6987 | 0.4625 |
| SelfDeblur [18] | 55 | 20.84 | 0.7590 | 0.7017 | 0.5112 | SelfDeblur [18] | Avg. | 20.97 | 0.7524 | 0.7488 | 0.5076 |
| Ours (hard) | 55, 75 | 28.72 | 0.9624 | 0.8337 | 0.1813 | Ours (average) | Avg. | 28.69 | 0.9660 | 0.8191 | 0.1875 |
| Approach | Loss Fn. | PSNR ↑ | SSIM ↑ | Error Ratio ↓ | FSIM ↑ | LPIPS ↓ |
|---|---|---|---|---|---|---|
| (a) SelfDeblur [18] | + TV | 33.07 | 0.9438 | 1.2509 | 0.8086 | 0.1082 |
| (b) DualDeblur-A | + TV | 35.75 | 0.9536 | 0.6921 | 0.8824 | 0.0748 |
| (c) DualDeblur-B | 35.63 | 0.9528 | 0.7087 | 0.8816 | 0.0758 | |
| (d) DualDeblur-C | 39.11 | 0.9661 | 0.6226 | 0.7890 | 0.0819 | |
| (e) DualDeblur | 40.89 | 0.9873 | 0.3798 | 0.8627 | 0.0461 |
| PSNR ↑ | SSIM ↑ | FSIM ↑ | LPIPS | ||
|---|---|---|---|---|---|
| 1 | 10 | 38.85 | 0.9649 | 0.7770 | 0.0870 |
| 1 | 100 | 39.69 | 0.9766 | 0.7904 | 0.0780 |
| 1 | 200 | 40.65 | 0.9858 | 0.8126 | 0.0660 |
| 10 | 10 | 39.77 | 0.9799 | 0.8073 | 0.0684 |
| 10 | 100 | 40.89 | 0.9873 | 0.8627 | 0.0461 |
| 10 | 200 | 40.70 | 0.9872 | 0.8592 | 0.0487 |
| 50 | 10 | 39.33 | 0.9826 | 0.8610 | 0.0514 |
| 50 | 100 | 39.27 | 0.9818 | 0.8756 | 0.0465 |
| 50 | 200 | 38.96 | 0.9805 | 0.8784 | 0.0459 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, C.J.; Lee, T.B.; Heo, Y.S. Dual Image Deblurring Using Deep Image Prior. Electronics 2021, 10, 2045. https://doi.org/10.3390/electronics10172045
Shin CJ, Lee TB, Heo YS. Dual Image Deblurring Using Deep Image Prior. Electronics. 2021; 10(17):2045. https://doi.org/10.3390/electronics10172045
Chicago/Turabian StyleShin, Chang Jong, Tae Bok Lee, and Yong Seok Heo. 2021. "Dual Image Deblurring Using Deep Image Prior" Electronics 10, no. 17: 2045. https://doi.org/10.3390/electronics10172045
APA StyleShin, C. J., Lee, T. B., & Heo, Y. S. (2021). Dual Image Deblurring Using Deep Image Prior. Electronics, 10(17), 2045. https://doi.org/10.3390/electronics10172045






