Abstract
This paper presents a carrier modulation technique to control the three-phase, two-level quasi switched boost inverter. This PWM algorithm uses three carrier waves, the first of which is for the inverter while the others are for the booster. The boost factor depends on the short circuit interval on the DC/DC booster and the inverter. When the short circuit interval on the DC boost is twice that on the inverter, the modulation index can be enlarged. The new algorithm is analyzed, calculated, simulated, and tested. The analysis and calculation results show that the proposed technique can reduce the voltage on the DC link capacitor compared to a conventional approach. It can reach 22.16% when the ratio of the DC source voltage to the effective reference voltage is 0.5. The modulation index can extend to 29% under these conditions and the current ripple in the boost inductor can be reduced by 4.8%. The simulation and experimental results also show similarities, thereby confirming the analysis and calculation.
1. Introduction
Single-stage direct boost inverters are widely used in electrical systems such as wind power, solar cells (PV), UPS, and electric vehicles [1,2,3,4]. There are two types of single-stage direct boost inverters: the Z source inverter (ZSI) [5,6] (Figure 1) and the quasi switched boost inverter (QSBI) [7,8] (Figure 2).
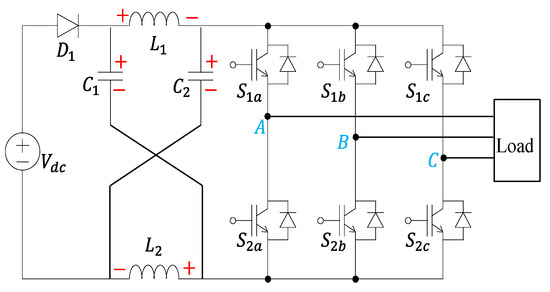
Figure 1.
Schematic of ZSI.
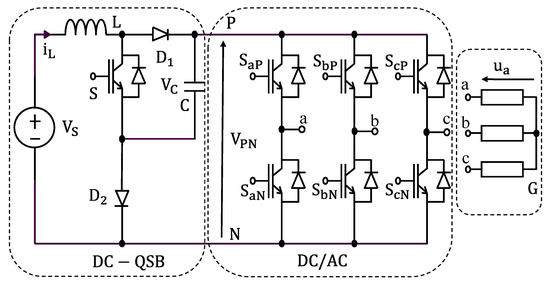
Figure 2.
Schematic of QSBI.
Both inverter configurations overcome the problem of short circuit on the switches [9]. In addition, QSBIs have advantages over ZSIs due to their reduced size, weight, and low power losses [10]. Because the QSBI adds a controllable switch for DC/DC boost, the QSBI uses more IGBT than ZSI [11]. However, the addition of the S switch also gives more control solutions.
The papers [12,13,14,15] presented PWM control strategies to enhance the continuous input current for QSBIs. In [12], a PWM technique applying in single-phase QBSI was employed to obtain a higher modulation index. The PWM method in [13] controls the input inductor current ripple by turning on the additional switch at a different time of the shoot-through state so that a low inductor current ripple and a high modulation index are achieved for a QSBI. A maximum boost PWM control technique is used in [14] with an improved voltage gain of QSBI by modifying the shoot-through (ST) control signal. A PWM with a low modulation index and a large ST duty cycle operation in the buck mode was shown in [15]. As a result of using a low modulation index at a high boost factor for the buck mode operation, the QSBI has a lower efficiency and a higher current distortion. The disadvantage of QSBIs are the low modulation index (m), the high voltage on the DC link capacitor, and the high input current ripple [15]. Therefore, it is necessary to propose an improved PWM technique to increase the modulation index (m), reduce the voltage across the capacitor, and reduce the current ripple. The content of this paper will consist of four main parts: an analysis of QSBI in Section 2; the QSBI control technique will be analyzed to propose a control algorithm to reduce current ripple and reduce the voltage of the DC link in Section 3; Section 4 presents the simulation and experimental results; and Part 5 will generalize the conclusions and discussions.
The improved PWM technique is based on using more than two carriers for reducing the current ripple through the booster inductor and the stress voltage on the DC link.
2. Three-Phase, Two-Level QSBI
The three-phase, two-level quasi switched boost inverter (3P2LQSBI) consists of a booster circuit combined with a voltage source inverter (VSI) in Figure 2. The 3P2LQSBI components include VS source, an inductor (L), a capacitor (C), two diodes (D1, D2), six inverter IGBT switches (denoted SxP, SxN where x is a, b, c), and an IGBT switch S in the boost DC–DC circuit. The output load phase voltage is ua, ub, and uc.
Let be a desired voltage vector in the dq coordinate, with angle α, then is represented through state vectors as shown in Figure 3 and calculated using Formula (1)
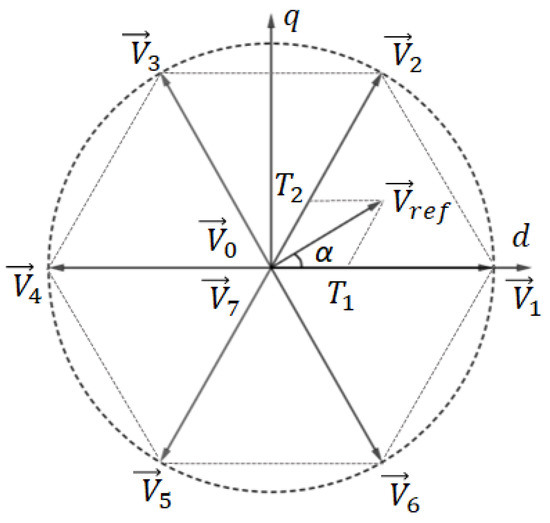
Figure 3.
Space Vector for three-phase, two-level inverter.
In Table 1, the vectors and that are located at the center of the space vector hexagon are zero vectors. In the vector state or , the outputs a, b, and c are connected through N or P [8,9]. Therefore, the VPN voltage does not affect the load at this time, so it is possible to short-circuit P–N to store the energy in the inductor L. There are three main operation modes in the 3P2LQSBI circuit: short-circuit for the booster (SB), non-short circuit (NST), and short-circuit on the inverter side (ST). Figure 4 shows the operation modes of 3P2LQSBI.

Table 1.
State of space vector.
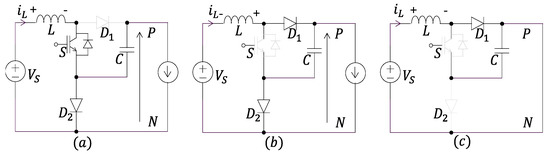
Figure 4.
The operation modes of 3P2LQSBI: (a) short circuit for booster mode, (b) non-short circuit mode, and (c) short circuit in inverter mode (shoot-through mode).
2.1. Short Circuit for Booster Mode
Figure 4a shows the short circuit on the booster mode (SB). In this mode, the switch S turns on, charging the inductor L. The voltage across the inductor is:
Diode D2 turns on, so the VSI operates with a voltage supply to the capacitor C. The state of the six switches on the inverter side is like in a normal VSI, so that:
where m is the modulation index of the inverter and is the peak amplitude of the phase voltage fundamental.
2.2. None Short Circuit Mode (NST)
In this mode (Figure 4), the switch S is off and two diodes (D1, D2) are turned on. The energy from the source (VS) and inductor (L) charges capacitor C and supplies the power to the VSI.
where phase voltage is as Equation (3).
2.3. Short Circuit in Inverter Mode (ST)
This mode corresponds to the moment when zero vectors orc are active. At this time, all six switches of the VSI are on so that P to N is short-circuited and the energy from the source is charged into the inductor.
Combine Equations (3)–(6) to get:
where T is the carrier period, tS is the ON time of switch S, and tST is the short circuit time on the VSI.
2.4. The Two Carrier Technique for QSBI
A QSBI controlled by two carrier techniques is presented in [16,17]. This technique uses two triangle carriers, one for the inverter and the other for the booster. They are 90° phase shift triangle carriers. Because the tS and tST are the same as shown in Figure 5, the duty cycle on the DC–DC boost and the inverter are the same too, and if the offset function is the third harmonic component, they have the same values as in Formula (7):
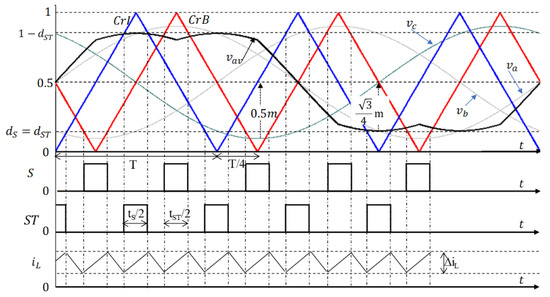
Figure 5.
The principle of the two carrier technique.
So that stress across the DC link is given by:
Then, the ripple of input current is calculated as:
Under this technique, the VSI’s switches have to switch more because, besides the inverter function, they also undertake the boost function. The duty cycle for the inverter boost is large. It equals half of the required short-circuit ratio, so the modulation index leads to a larger DC link voltage.
3. The Proposed Algorithms
Set the duty cycle of the signal control for the switch (S) turn on as ds and for shoot-through in the VSI as dST. The proposed technique reduces the inverter (dST) duty cycle and increases the modulation index, lowering the voltage of the DC-link capacitor (VC). In one cycle, there are two S turn-ons and four short-circuits in the VSI. Per carrier period, there are two S turn-ons and four short-circuits in the VSI. This is the same as when using three triangle carriers, two for the VSI and one for the booster, where each waver is phase shifted by α angle where α = π/3. The inverter carrier is CrI, while the booster carriers are CrB1 and CrB2.
Figure 6 shows that when minimizing the ripple of the input current, the charging time with the S switch closed (tS/4) and charging time with the inverter switches closed (tST/2) should be the same, so that:
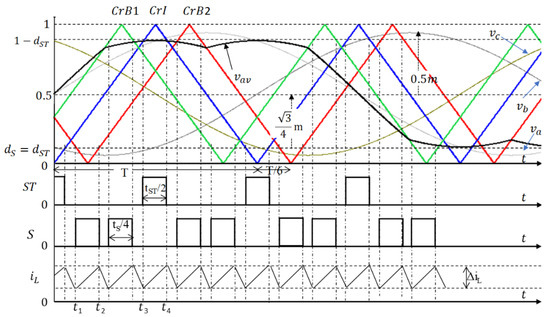
Figure 6.
The principle of the improved technique.
So when the inverter control voltages are :
Additionally, the offset function is the third harmonic component as in (12) [16]:
where x = a, b, c and:
The principle of the improved technique is shown in Figure 6.
Figure 6 shows that in every carrier cycle there are four instances of charging the inductance through switch S and two instances of charging through the VSI switches. Therefore:
Additionally, (6) becomes:
With being the amplitude-phase voltage. So the DC link voltage is:
Applying the offset function in (12) and looking at Figure 6 gives:
We then combine (15)–(17) with (18) to get:
Therefore, the modulation index will change according to the supply voltage VS and reference RMS voltage (urms) as in (19):
Set k as the ratio of DC sources (VS) and reference RMS output voltage, . Compared with conventional techniques [16], the modulation index of the proposed algorithm increases the Δm value, calculated as:
The percentage of the modulation index increases Δm% as in (21):
Figure 7 shows the ability to increase the modulation index (m) with the ratio (k). Figure 7 shows that the effect of increasing the modulation index decreases as the k ratio increases. The efficiency increase in the modulation index of the technique corresponds to the ratio . For example, with power supply VS = 55 V, referent output voltage urms = 110 V, meaning k = 0.5 if the proposed algorithms are used and the modulation index can be reduced by 29% compared with the method used in [16]. Compared to the two carrier technique, the voltage across the capacitor (C) will decrease with :
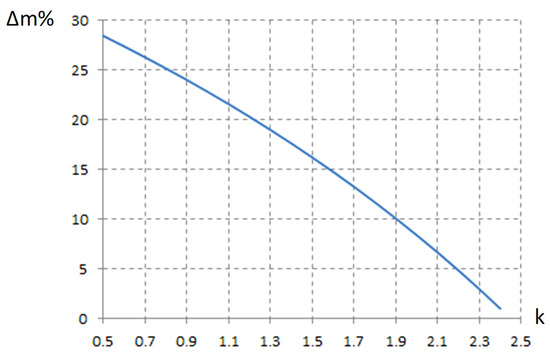
Figure 7.
The relationship between Δm% and k.
The characteristic of reducing the stress voltage percentage, as seen in (23), is shown in Figure 8:
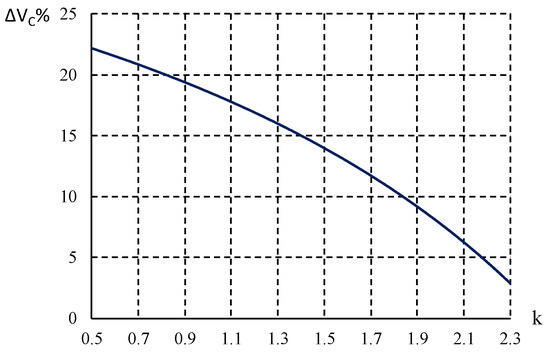
Figure 8.
The relationship between ΔVC% and k.
Figure 8 shows that the reducing effect (of the voltage on the DC link) decreases in the k range from 0.5 to 2.2. When applying the proposed algorithm at k = 0.5, the DC link voltage is less than 22% compared to conventional techniques. With (19) and f = 1/T, the ripple of the input current can be calculated using Formula (24):
From Figure 6, it is easy to see that the input current frequency with the proposed technique is 1.5 times higher than its frequency with the application of conventional technology. Therefore, for the same input current frequency, the carrier frequency of the two-carrier technique must be 1.5 times higher in the proposed method. In this case, the current ripple of the three-carrier technology is smaller than that of conventional technology by the value of . The value is calculated using Formula (25) and represented by the graph in Figure 9.
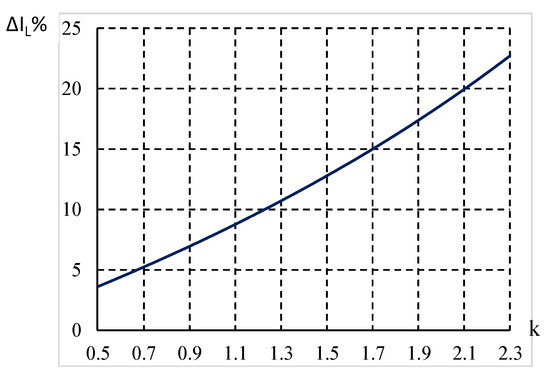
Figure 9.
The relationship between ΔIL% and k.
Figure 9 shows the reduction characteristic of the input current ripple at the same frequency when applying the conventional and proposed technique.
When the reference voltage is 110 Vrms, the DC source voltage (VS) is 55 V, 110 V, and 165 V, respectively. The calculation results of the voltage across the capacitor, the percentage reduction in the capacitor voltage, and the current ripple compared with the conventional technique are presented in Table 2.

Table 2.
The calculation results of the voltage across the capacitor, the percentage reduction in the capacitor voltage, and the current ripple.
It is easy to see that when the output voltage is greater than the DC supply voltage, the capacitor voltage reduction effect is higher and can reach 22.16%. On the contrary, the reducing effect of the current ripple is more effective when the ratio of the DC source voltage and the reference voltage is large.
The proposed algorithm uses the flowchart in Figure 10.
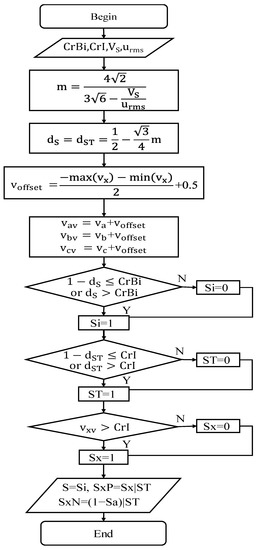
Figure 10.
Proposed algorithm flowchart.
4. Simulation and Experimental Results
The algorithm is simulated in PSIM software with parameters as shown in Table 3. To verify the proposed technique, a simulation was performed with DC power voltages of 55 V, 110 V, and 165 V. The desired output voltage is 110 Vrms and 50 Hz with a carrier frequency of 5.1 kHz with two carriers and 3.4 kHz with the proposed technique.

Table 3.
Component parameters.
Figure 11 shows the simulation results with VS = 55 V. From the top to the bottom of Figure 11, the first graph (Figure 11a) is the voltage of the capacitor, the second is the current in the boost inductor (Figure 11b), and the third is the inverter output voltage (Figure 11c). Red lines are with two carriers, and the blues are with the proposed algorithm. It is easy to see that the capacitor voltage reduces from 483 V down to 376 V. ΔVC is 107 V, a 22.15% reduction, and the input current ripple reduces from 0.569 A down to 0.550 A, a 3.5% reduction. Moreover, the average input current also decreased from 4.99 A to 3.87 A, equivalent to a 22.4% reduction. These values are presented in Table 2.
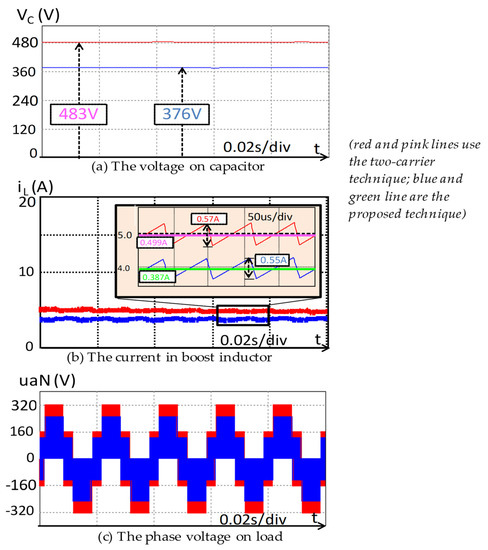
Figure 11.
The simulation results with Vs = 55 V.
The same can be seen in Figure 12 and Figure 13, with Vs being 110 V and 165 V, respectively. When VS is 110 V, the voltage of the capacitor reduces to 348 V with ΔVC being 81 V (an 18.9% reduction) (Figure 12a) and the input current ripple reduces from 0.963 A down to 0.891 A (a 7.47% reduction) (Figure 12b).
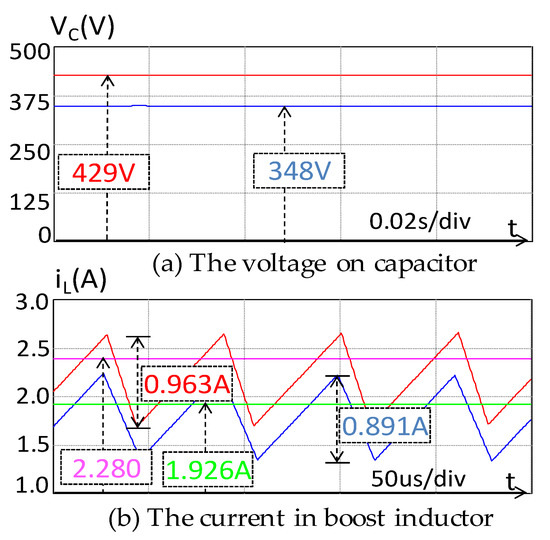
Figure 12.
The simulation results with Vs = 110 V.
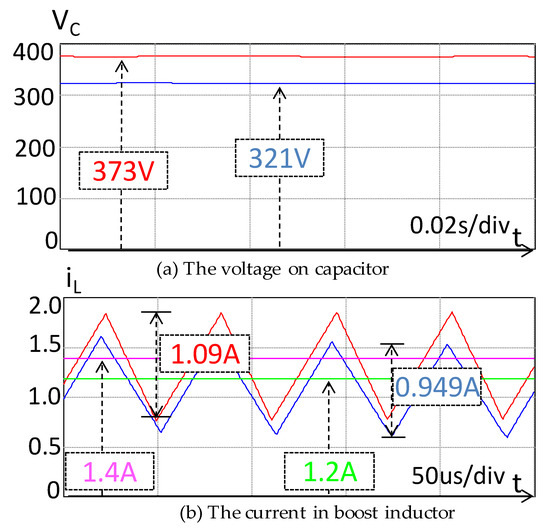
Figure 13.
The simulation results with Vs = 165 V.
With VS = 165 V, the ΔVC is 52 V (a 13% reduction) and the input current ripple reduces from 1.09 A down to 0.949 A (a 12.9% reduction) (Figure 13a,b).
The FFT of the phase voltage is shown in Figure 14, with the red graph being the two-carrier and the blue graph being the proposed algorithm. It is easy to see that at a frequency of 2fc, the amplitude of the harmonics with the two-carrier technique is higher than it is in the proposed algorithm. This is not a problem because the proposed method has a higher modulation index.
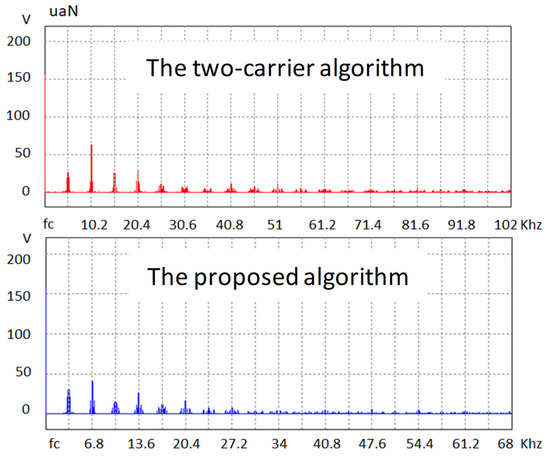
Figure 14.
FFT of phase voltage with Vs = 165 V.
The experiment applied the same model as the simulation conditions for easy comparison. The devices used were a TMS320 F28335, a GWINSTEK GDS 1072A-U, and a GDS 1104B oscilloscope with an inductance (L) of 4.2 mH, variable 55 V, 110 V, and 165 V DC power supplies, and a filter with LS = 2.3 mH and CS = 11.2 µF (Figure 15).

Figure 15.
Experimental devices.
Figure 16 shows the experimental results with a DC supply of 55 V with the proposed algorithm. The top to bottom graphs are phase voltage, load current, capacitor voltage, and the current in the boost inductor, respectively. The experimental results are the same as the simulation (Figure 11), once again confirming the validity of the proposed technique.
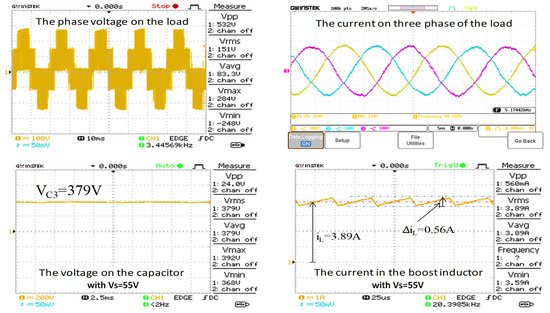
Figure 16.
The experiment results with VS = 55 V.
The experimental results with a DC supply of 165 V, including the phase voltage, load currents, capacitor voltage, and the boost inductor (Figure 17) show a similar trend.
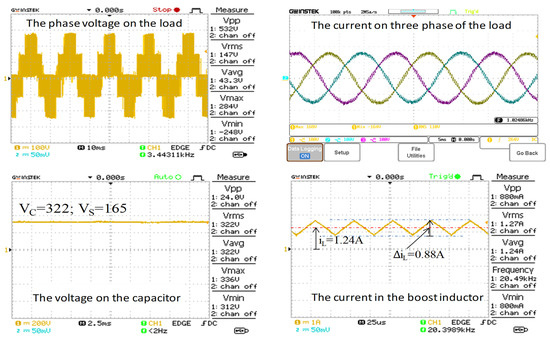
Figure 17.
The experimental results with VS = 165 V.
5. Conclusions
This paper presents a carrier modulation technique with three carriers to control the three-phase, two-level quasi switched boost inverter.
The three-carrier QSBI control technique has been analyzed, calculated, simulated, and tested. The results show that the analysis and new technical recommendations are appropriate. In addition, the calculation, simulation, and experimental results show that the technique is especially effective when a large voltage boost ratio is required.
Specifically, at the ratio of the DC source (VS) and reference RMS output voltage (k) is equal to 0.5. Compared with the two-carrier technique, the proposed method reduces the voltage on the capacitor by 22.16%, but at k = 1.5 this figure is only 13.97%.
Compared with the two-carrier technique, the proposed technique helps to extend the modulation index so that it is possible to reduce the capacitor voltage. For example, it shows that when the reference voltage is double the DC supply voltage, the modulation index (m) can be expanded by 29%, thus reducing the voltage of the DC link by 22.16% if we apply the three-carrier PWM technique. It also shows the ability to reduce the current ripple in the boost inductor with the same switching frequency.
Experimentally, the reduced current ripple effect will increase if the boost coefficient reduces. For example, with a 165VDC supply and 110 V reference phase voltage, compared with the two-carrier technique, the current ripple with the proposed method can be reduced by 12.9%. However, it is only 3.65% at a DC supply voltage of 55 V.
Besides, this technique also has other advantages that needs to be studied, e.g., reducing the amplitude at the first harmonic of the carrier frequency.
The simulation and experiment results also show that the proposed technique can help increase the performance of QSBI (because the average input current also decreased from 4.99 A to 3.87 A, a reduction of 22.4%). Future research in this area is encouraged.
Author Contributions
Conceptualization, T.-H.Q.; Data curation, X.-V.L.; Resources, V.-A.T.; Writing—original draft, T.-H.Q.; Writing—review & editing, V.-A.T. All authors have read and agreed to the published version of the manuscript.
Funding
This study was carried out by the support of laboratories C201 and C406 of Ho Chi Minh City University of Technology and Education.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| VS | DC power supply | (V) |
| VL | Voltage on the inductor | (V) |
| IL | Current in the inductor | (A) |
| ΔIL | Ripple of the current in the inductor | (A) |
| VPN | DC link voltage | (V) |
| Amplitude of the phase voltage fundamental | (V) | |
| urms | RMS value of the phase voltage fundamental | (V) |
| m | Modulation index | |
| tS | Short circuit time on the DC–DC boost side | (s) |
| tST | Short circuit time on the VSI side | (s) |
| dS | Duty cycle when switch S is turned on | |
| dST | Duty cycle when the VSI is shot through |
References
- Sreekanth, T.; Lakshminarasamma, N.; Mishra, M.K. A Single-Stage Grid-Connected High Gain Buck–Boost Inverter with Maximum Power Point Tracking. IEEE Trans. Energy Convers. 2016, 32, 330–339. [Google Scholar] [CrossRef]
- Pal, A.; Basu, K. A Unidirectional Single-Stage Three-Phase Soft-Switched Isolated DC–AC Converter. IEEE Trans. Power Electron. 2018, 34, 1142–1158. [Google Scholar] [CrossRef]
- Serrano, D.; Ramos, R.; Alou, P.; Oliver, J.A.; Cobos, J.A. Multimode Modulation with ZVS for a Single-Phase Sin-gle-Stage Inverter. IEEE Trans. Power Electron. 2020, 35, 5319–5330. [Google Scholar] [CrossRef]
- Sriramalakshmi, P.; Sreedevi, V.T. Design and Implementation of a Dual DC Source-based Quasi-Switched Boost Inverter for Renewable Energy Applications. IETE J. Res. 2020. [Google Scholar] [CrossRef]
- Ahmad, A.; Bussa, V.K.; Singh, R.K.; Mahanty, R. Switched-Boost-Modified Z-Source Inverter Topologies With Improved Voltage Gain Capability. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 2227–2244. [Google Scholar] [CrossRef]
- Noroozi, N.; Zolghadri, M.R. Three-Phase Quasi-Z-Source Inverter with Constant Common-Mode Voltage for Photo-voltaic Application. IEEE Trans. Ind. Electron. 2018, 65, 4790–4798. [Google Scholar] [CrossRef]
- Nandi, P.; Adda, R. Reduction of Capacitance in Four-Switch quasi-Switched Boost Inverter using Low-frequency Ripple Damping Scheme. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 6285–6292. [Google Scholar]
- Barath, J.G.N.; Soundarrajan, A.; Stepenko, S.; Prystupa, A.; Bondarenko, O.; Padmanaban, S. Interleaved Single-Phase Quasi-Switched Boost and Active Quasi-Z-Source Inverter. In Proceedings of the 2020 IEEE 40th International Conference on Electronics and Nanotechnology (ELNANO), Kyiv, Ukraine, 22–24 April 2020; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2020; pp. 874–878. [Google Scholar]
- Kumar, A.; Bao, D.; Beig, A.R. Comparative Analysis of Extended SC-qSBI with EB-QZSI and EB/ASN-QZSI. IEEE Access 2021, 9, 61539–61547. [Google Scholar] [CrossRef]
- Nguyen, M.-K.; Le, T.-V.; Park, S.-J.; Lim, Y.C. A Class of Quasi-Switched Boost Inverters. IEEE Trans. Ind. Electron. 2015, 62, 1526–1536. [Google Scholar] [CrossRef]
- Nguyen, M.-K.; Choi, Y.-O. PWM Control Scheme for Quasi-Switched-Boost Inverter to Improve Modulation Index. IEEE Trans. Power Electron. 2018, 33, 4037–4044. [Google Scholar] [CrossRef]
- Gambhir, A.; Mishra, S.K.; Joshi, A. A modified PWM scheme to improve performance of a single-phase ac-tive-front-end impedance source inverter. IEEE Trans. Ind. Appl. 2019, 55, 928–942. [Google Scholar] [CrossRef]
- Nguyen, M.-K.; Tran, T.-T.; Lim, Y.-C. A family of PWM control strategies for single-phase quasi-switched-boost in-verter. IEEE Trans. Power Electron. 2019, 34, 1458–1469. [Google Scholar] [CrossRef]
- Nguyen, M.-K.; Choi, Y.-O. Maximum Boost Control Method for Single-Phase Quasi-Switched-Boost and Quasi-Z-Source Inverters. Energies 2017, 10, 553. [Google Scholar] [CrossRef]
- Nag, S.S.; Mishra, S. Current-Fed Switched Inverter. IEEE Trans. Ind. Electron. 2014, 61, 4680–4690. [Google Scholar] [CrossRef]
- Le, X.-V.; Nguyen, D.-M.; Truong, V.-A.; Quach, T.-H. Algorithm to control output voltage and reduce the ripple of input current in quasi switched boost inverter. Sci. Technol. Dev. J. Eng. Technol. 2021, 4, 999–1008. [Google Scholar] [CrossRef]
- Do, D.-T.; Nguyen, M.-K.; Quach, T.-H.; Tran, V.-T.; Blaabjerg, F.; Vilathgamuwa, D.M. A PWM Scheme for a Fault-Tolerant Three-Level Quasi-Switched Boost T-Type Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 3029–3040. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).