Trajectory Tracking and Stabilization of Nonholonomic Wheeled Mobile Robot Using Recursive Integral Backstepping Control
Abstract
:1. Introduction
- We have proposed a novel generalized nontriangular normal form by a suitable change of coordinates (diffeomorphism) transformation. During the formulation of generalized nontriangular normal form, the output vector is selected in such a way that the decoupling matrix would be nonsingular, even when the look-ahead distance (coordinates of virtual reference point in front of the mobile robot) or linear velocity is zero, as compared with previous work [5,6,8,16,17,18,19]. The proposed internal dynamics of WMR is one dimension, where nonholonomic constraints of WMR has been sensibly exploited to reduce the complexity of nonlinear internal dynamics, with structural properties that provide ease to the design controller. In contrast to the previous research [16,18], internal dynamics were two-dimension coupling with the derivative of output functions.
- We have proposed a systematic method of ensuring asymptotic stabilization of internal dynamics during trajectory tracking and posture stabilization, unlike the previous research [16,17,18,19]. Furthermore, the proposed method used an exact model of nonlinear internal dynamics rather than a linear approximation of internal dynamics [5].
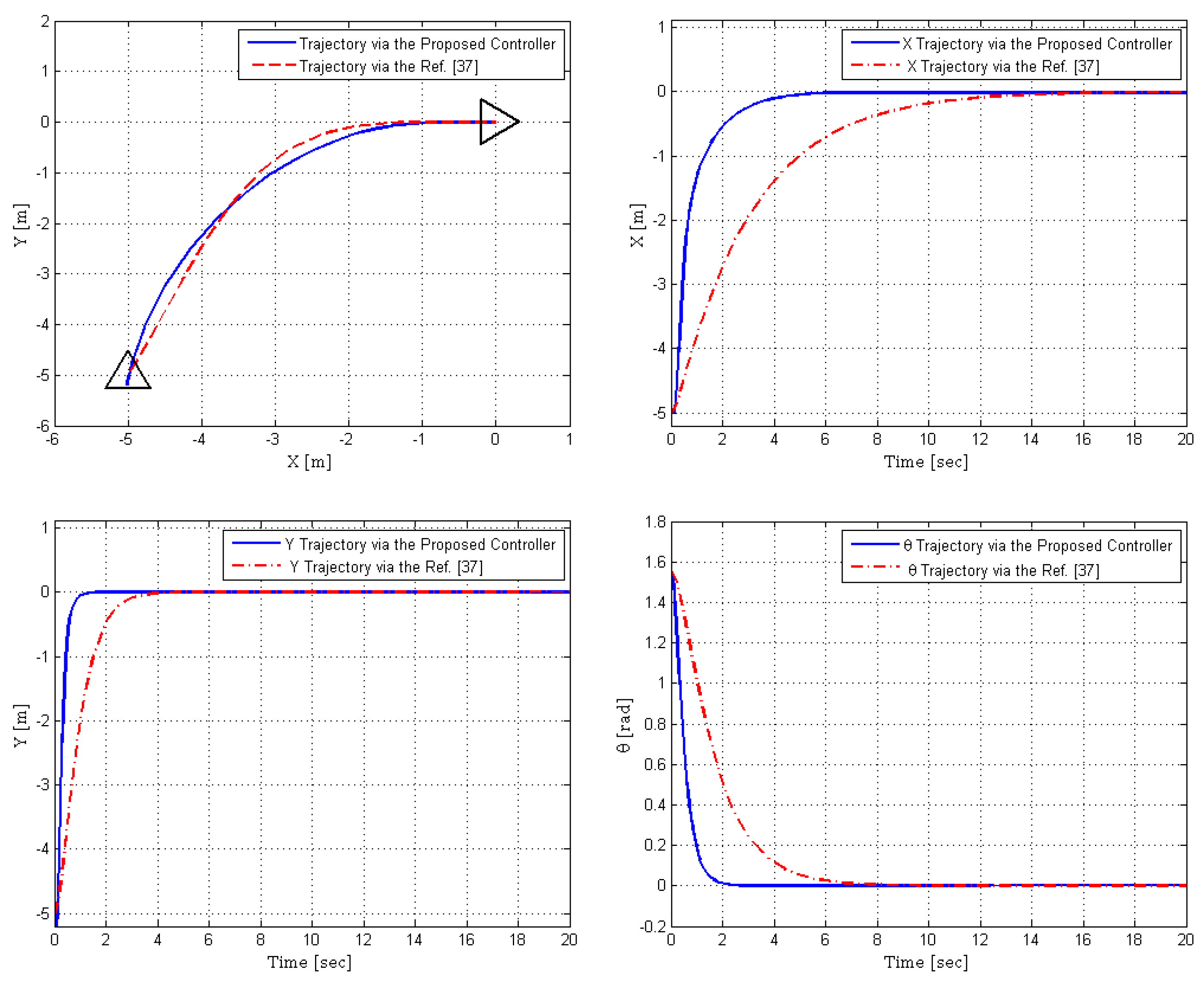
- This paper proposes a novel recursive integral backstepping control based on generalized nontriangular normal form structure for differential drive WMR. The proposed single controller can perform trajectory tracking and posture stabilization better than existing backstepping-based tracking/stabilization controllers [3,22,23,24,25,38]. Using a normal form representation of WMR makes the proposed algorithm simpler because of the features of regular backstepping technique as compared with modified backstepping control [20] and block-backstepping [37]. Moreover, the proposed controller provides a solution for the kinematic model cascaded with the dynamic model of WMR, as compared with previously designed controllers for kinematic and/or dynamics models [6,37,39]. In our approach, the actual robot motion commands are the wheel velocities rather than robot driving and steering velocities, calculated from the motor torques based on a dynamic model. Therefore, it would be more appropriate to represent the robot’s dynamic equations of motion based on wheel velocities to have a modular control structure unlike [37].
2. Modeling of Nonholonomic WMR
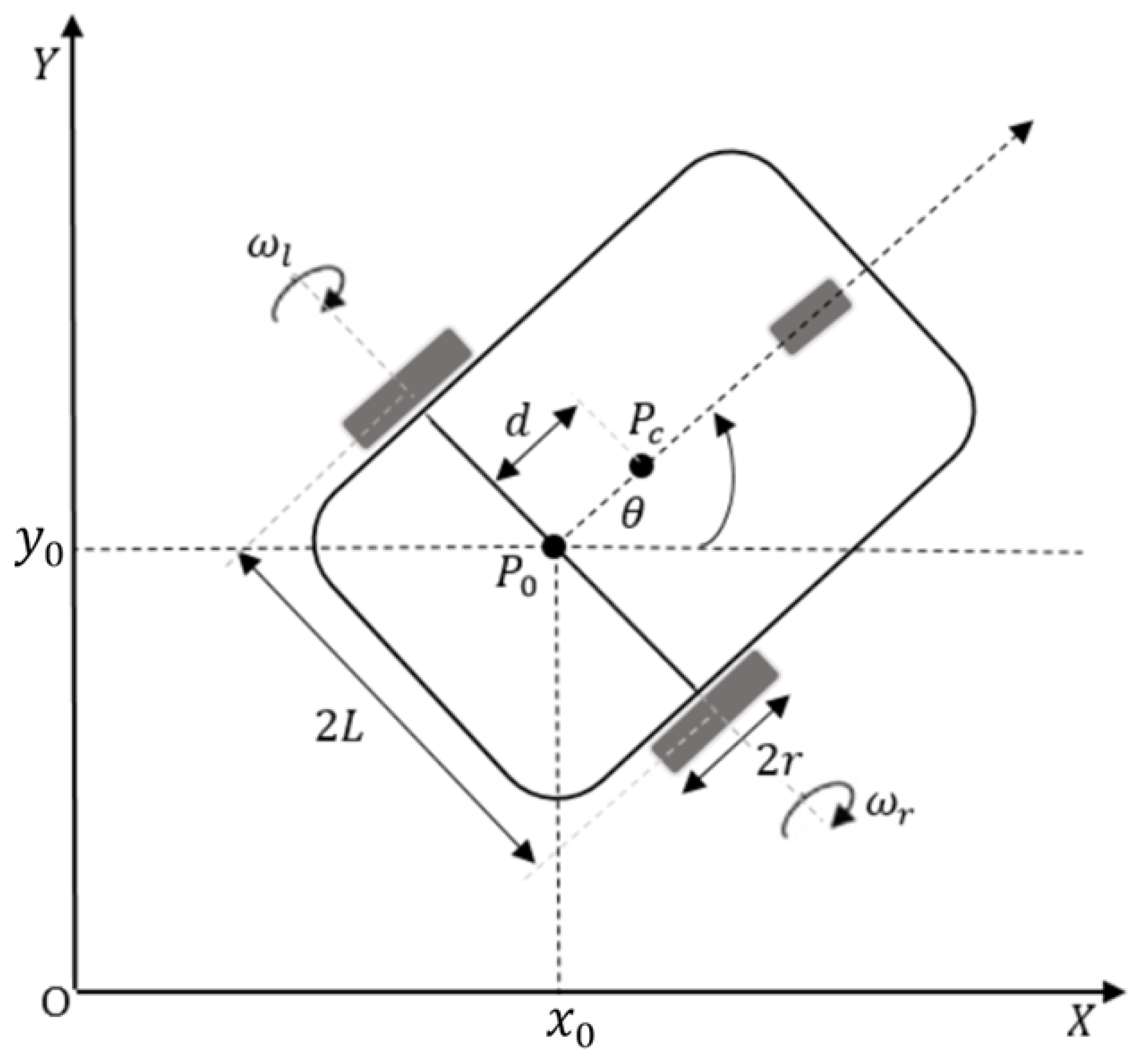
2.1. Kinematic Model of WMR
2.2. Dynamic Model of WMR
2.3. State Space Model of WMR
3. Input-Output Feedback Linearization: Normal form for WMR
4. Backstepping Control Design for Trajectory Tracking
- C1.
- , for all
5. Backstepping Control Design for Posture Stabilization
- C1.
- C2.
- for all
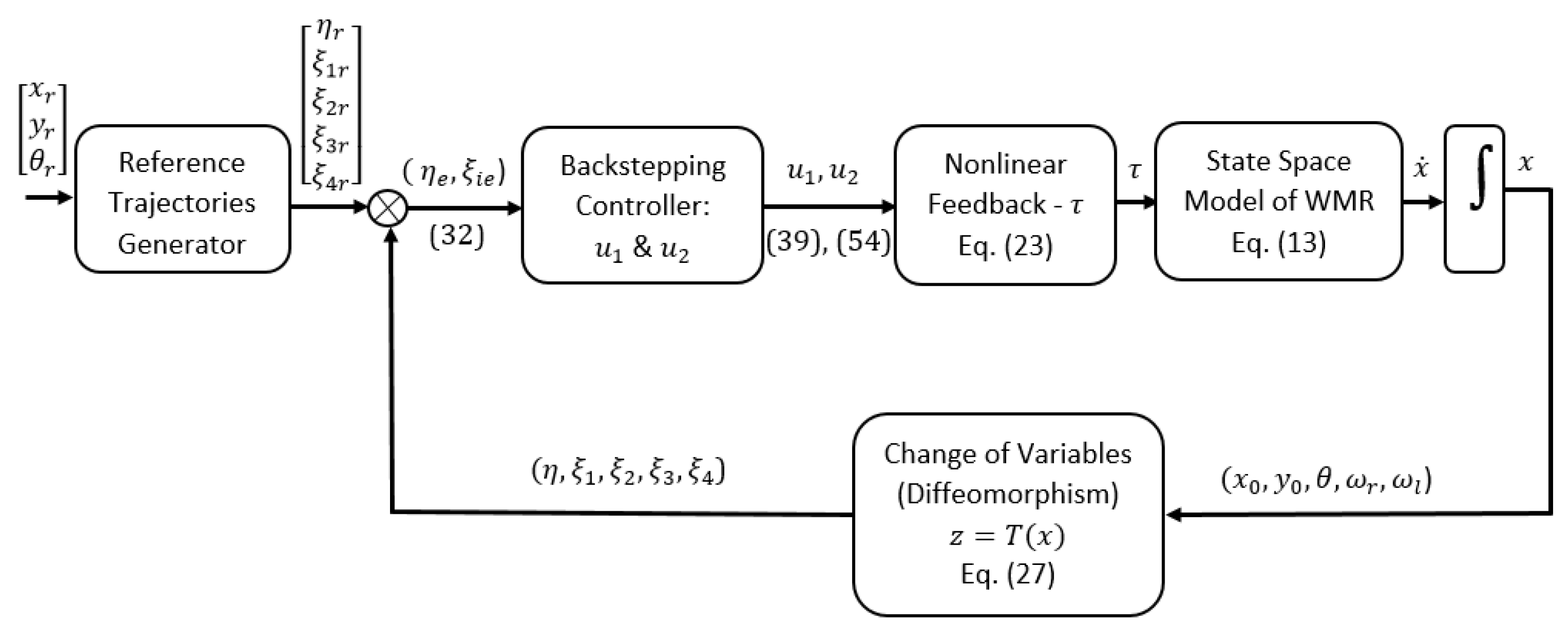
6. Simulation Results
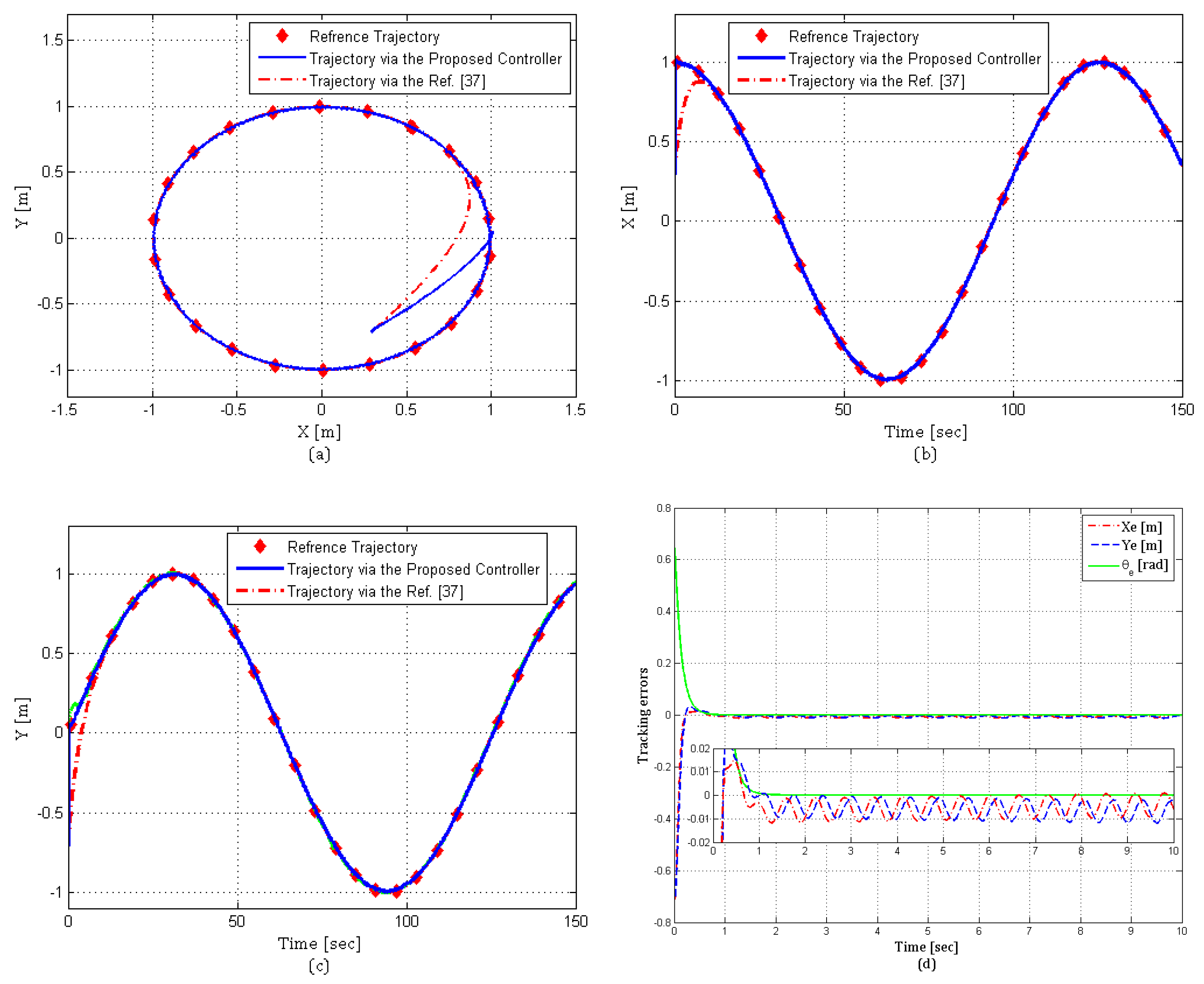
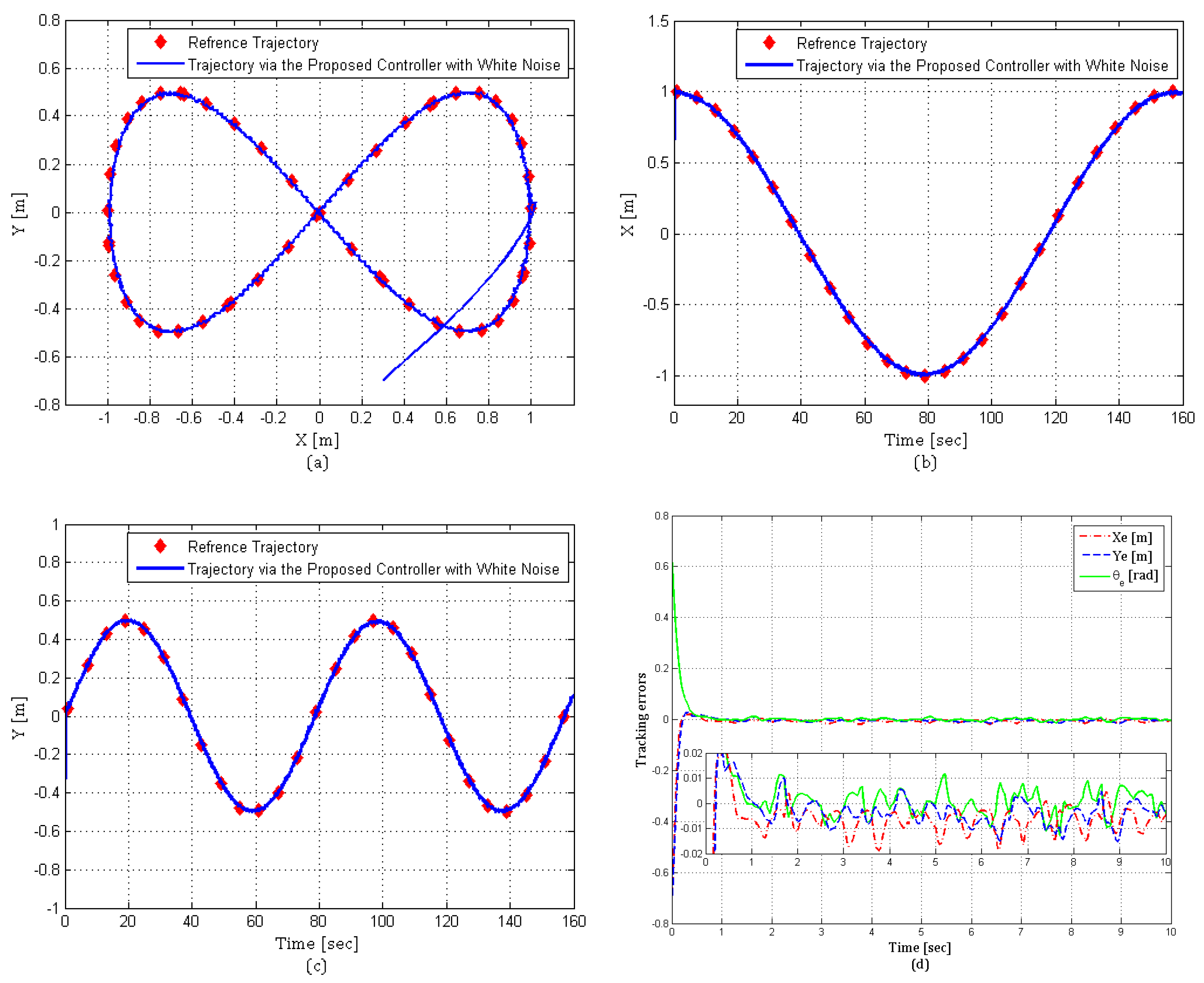
6.1. Simulation Results for Trajectory Tracking
6.2. Simulation Results for Posture Stabilization
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| WMR | Wheeled Mobile Robot |
| MIMO | Multiple Input Multiple Output |
References
- Bloch, A.M.; Reyhanoglu, M.; McClamroch, N.H. Control and stabilization of nonholonomic dynamic systems. IEEE Trans. Autom. Control 1992, 37, 1746–1757. [Google Scholar] [CrossRef]
- Campion, G.; d’Andrea-Novel, B.; Bastin, G. Modelling and state feedback control of nonholonomic mechanical systems. In Proceedings of the 30th IEEE Conference on Decision and Control, Brighton, UK, 11 December 1991; pp. 1184–1189. [Google Scholar]
- Sun, W.; Tang, S.; Gao, H.; Zhao, J. Two time-scale tracking control of nonholonomic wheeled mobile robots. IEEE Trans. Control Syst. Technol. 2016, 24, 2059–2069. [Google Scholar] [CrossRef]
- Xiao, H.; Li, Z.; Yang, C.; Zhang, L.; Yuan, P.; Ding, L.; Wang, T. Robust stabilization of a wheeled mobile robot using model predictive control based on neurodynamics optimization. IEEE Trans. Ind. Electron. 2016, 64, 505–516. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Xu, G. Full-state tracking and internal dynamics of nonholonomic wheeled mobile robots. IEEE/ASME Trans. Mechatron. 2003, 8, 203–214. [Google Scholar] [CrossRef]
- Oriolo, G.; De Luca, A.; Vendittelli, M. WMR control via dynamic feedback linearization: Design, implementation, and experimental validation. IEEE Trans. Control Syst. Technol. 2002, 10, 835–852. [Google Scholar] [CrossRef]
- Brockett, R.W. Asymptotic stability and feedback stabilization. Differ. Geom. Control Theory 1983, 27, 181–191. [Google Scholar]
- Sun, S.; Cui, P. Path tracking and a practical point stabilization of mobile robot. Robot. Comput. Integr. Manuf. 2004, 20, 29–34. [Google Scholar] [CrossRef]
- Chen, H. Robust stabilization for a class of dynamic feedback uncertain nonholonomic mobile robots with input saturation. Int. J. Control Autom. Syst. 2014, 12, 1216–1224. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, C. Robust exponential stabilization of nonholonomic wheeled mobile robots with unknown visual parameters. J. Control Theory Appl. 2011, 9, 295–301. [Google Scholar] [CrossRef]
- Coelho, P.; Nunes, U. Path-following control of mobile robots in presence of uncertainties. IEEE Trans. Robot. 2005, 21, 252–261. [Google Scholar] [CrossRef]
- Montoya-Villegas, L.; Moreno-Valenzuela, J.; Pérez-Alcocer, R. A feedback linearization-based motion controller for a UWMR with experimental evaluations. Robotica 2019, 37, 1073–1089. [Google Scholar] [CrossRef]
- Liang, X.; Wang, H.; Chen, W.; Guo, D.; Liu, T. Adaptive image-based trajectory tracking control of wheeled mobile robots with an uncalibrated fixed camera. IEEE Trans. Control Syst. Technol. 2015, 23, 2266–2282. [Google Scholar] [CrossRef]
- Sarrafan, N.; Shojaei, K. High-Gain Observer-Based Neural Adaptive Feedback Linearizing Control of a Team of Wheeled Mobile Robots. Robotica 2020, 38, 69–87. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Yun, X. Coordinating locomotion and manipulation of a mobile manipulator. In Proceedings of the 31st IEEE Conference on Decision and Control, Tucson, AZ, USA, 16 December 1992; pp. 2643–2648. [Google Scholar]
- Yun, X.; Yamamoto, Y. Stability analysis of the internal dynamics of a wheeled mobile robot. J. Robot. Syst. 1997, 14, 697–709. [Google Scholar] [CrossRef]
- Coelho, P.; Nunes, U. Lie algebra application to mobile robot control: A tutorial. Robotica 2003, 21, 483–493. [Google Scholar] [CrossRef]
- Al-Mutib, K.; Abdessemed, F.; Hedjar, R.; Alsulaiman, M.; Bencherif, M.; Faisal, M.; Algabri, M.; Mekhtiche, M. Mobile robot nonlinear feedback control based on Elman neural network observer. Adv. Mech. Eng. 2015, 7, 1–14. [Google Scholar] [CrossRef]
- Eghtesad, M.; Necsulescu, D.S. Study of the internal dynamics of an autonomous mobile robot. Robot. Auton. Syst. 2006, 54, 342–349. [Google Scholar] [CrossRef]
- Chwa, D. Tracking control of differential-drive wheeled mobile robots using a backstepping-like feedback linearization. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2010, 40, 1285–1295. [Google Scholar] [CrossRef]
- Chwa, D. Robust distance-based tracking control of wheeled mobile robots using vision sensors in the presence of kinematic disturbances. IEEE Trans. Ind. Electron. 2016, 63, 6172–6183. [Google Scholar] [CrossRef]
- Mnif, F. Recursive backstepping stabilization of a wheeled mobile robot. Int. J. Adv. Robot. Syst. 2004, 1, 25. [Google Scholar] [CrossRef] [Green Version]
- Andreev, A.; Peregudova, O. Lyapunov vector function method in the motion stabilisation problem for nonholonomic mobile robot. Int. J. Syst. Sci. 2017, 48, 2003–2012. [Google Scholar] [CrossRef]
- Alshamali, S. A backstepping design approach to a class of mobile robots. In Proceedings of the 11th Asian Control Conference (ASCC), Gold Coast, QLD, Australia, 17–20 December 2017; pp. 1341–1344. [Google Scholar]
- Wu, X.; Jin, P.; Zou, T.; Qi, Z.; Xiao, H.; Lou, P. Backstepping trajectory tracking based on fuzzy sliding mode control for differential mobile robots. J. Intell. Robot. Syst. 2019, 96, 109–121. [Google Scholar] [CrossRef]
- Ascencio, P.; Astolfi, A.; Parisini, T. Backstepping pde design: A convex optimization approach. IEEE Trans. Autom. Control 2017, 63, 1943–1958. [Google Scholar] [CrossRef] [Green Version]
- Asif, M.; Khan, M.J.; Memon, A.Y. Integral terminal sliding mode formation control of non-holonomic robots using leader follower approach. Robotica 2017, 35, 1473–1487. [Google Scholar] [CrossRef]
- Memon, A.Y.; Khalil, H.K. Output regulation of nonlinear systems using conditional servocompensators. Automatica 2010, 46, 1119–1128. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Nonlinear Control of Underactuated Mechanical Systems with Application to Robotics and Aerospace Vehicles. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2001. [Google Scholar]
- Zhang, X.; Wang, R.; Fang, Y.; Li, B.; Ma, B. Acceleration-level pseudo-dynamic visual servoing of mobile robots with backstepping and dynamic surface control. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 2071–2081. [Google Scholar] [CrossRef]
- Sun, K.; Sui, S.; Tong, S. Fuzzy adaptive decentralized optimal control for strict feedback nonlinear large-scale systems. IEEE Trans. Cybern. 2017, 48, 1326–1339. [Google Scholar] [CrossRef]
- Jiang, J.; Astolfi, A. Under-actuated back-stepping: An introduction. In Proceedings of the IEEE Conference on Decision and Control (CDC), Miami Beach, FL, USA, 17–19 December 2018; pp. 5910–5915. [Google Scholar]
- Herzig, N.; Moreau, R.; Redarce, T.; Abry, F.; Brun, X. Nonlinear position and stiffness Backstepping controller for a two Degrees of Freedom pneumatic robot. Control Eng. Pract. 2018, 73, 26–39. [Google Scholar] [CrossRef]
- Moghanni-Bavil-Olyaei, M.R.; Ghanbari, A.; Keighobadi, J. Trajectory Tracking Control of a Class of Underactuated Mechanical Systems with Nontriangular Normal Form Based on Block Backstepping Approach. J. Intell. Robot. Syst. 2019, 96, 209–221. [Google Scholar] [CrossRef]
- Fu, J.; Chai, T.; Su, C.Y.; Jin, Y. Motion/force tracking control of nonholonomic mechanical systems via combining cascaded design and backstepping. Automatica 2013, 49, 3682–3686. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, X.; Zhang, S.; Zong, G. Adaptive neural backstepping control design for a class of nonsmooth nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 1820–1831. [Google Scholar] [CrossRef]
- Rudra, S.; Barai, R.K.; Maitra, M. Design and implementation of a block-backstepping based tracking control for nonholonomic wheeled mobile robot. Int. J. Robust Nonlinear Control 2016, 26, 3018–3035. [Google Scholar] [CrossRef]
- Fu, J.; Tian, F.; Chai, T.; Jing, Y.; Li, Z.; Su, C.Y. Motion tracking control design for a class of nonholonomic mobile robot systems. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 2150–2156. [Google Scholar] [CrossRef]
- Wang, Z.; Li, G.; Chen, X.; Zhang, H.; Chen, Q. Simultaneous stabilization and tracking of nonholonomic WMRs with input constraints: Controller design and experimental validation. IEEE Trans. Ind. Electron. 2018, 66, 5343–5352. [Google Scholar] [CrossRef]
- Byrnes, C.I.; Isidori, A. A frequency domain philosophy for nonlinear systems, with applications to stabilization and to adaptive control. In Proceedings of the 23rd IEEE Conference on Decision and Control, Las Vegas, NV, USA, 12–14 December 1984; pp. 1569–1573. [Google Scholar]
- Rubio Hervas, J. Dynamics and Control of Higher-Order Nonholonomic Systems. Ph.D. Thesis, Embry-Riddle Aeronautical University, Daytona Beach, FL, USA, 2013. [Google Scholar]


| Parameter | Description | Value |
|---|---|---|
| r | Radius of wheels | 0.05 m |
| Distance between two driving wheels | 0.27 m | |
| m | Mass of robot | 4 kg |
| I | Moment of inertia of whole robot | 2.5 kg·m |
| d | Distance from point to point | 0.05 m |
| Parameter | Trajectory Tracking | Posture Stabilization |
|---|---|---|
| 2.5 | 2.5 | |
| 8 | 6 | |
| 6.5 | 6 | |
| 60 | 20 | |
| 9 | 10 | |
| 5 (rad/s) | 0 | |
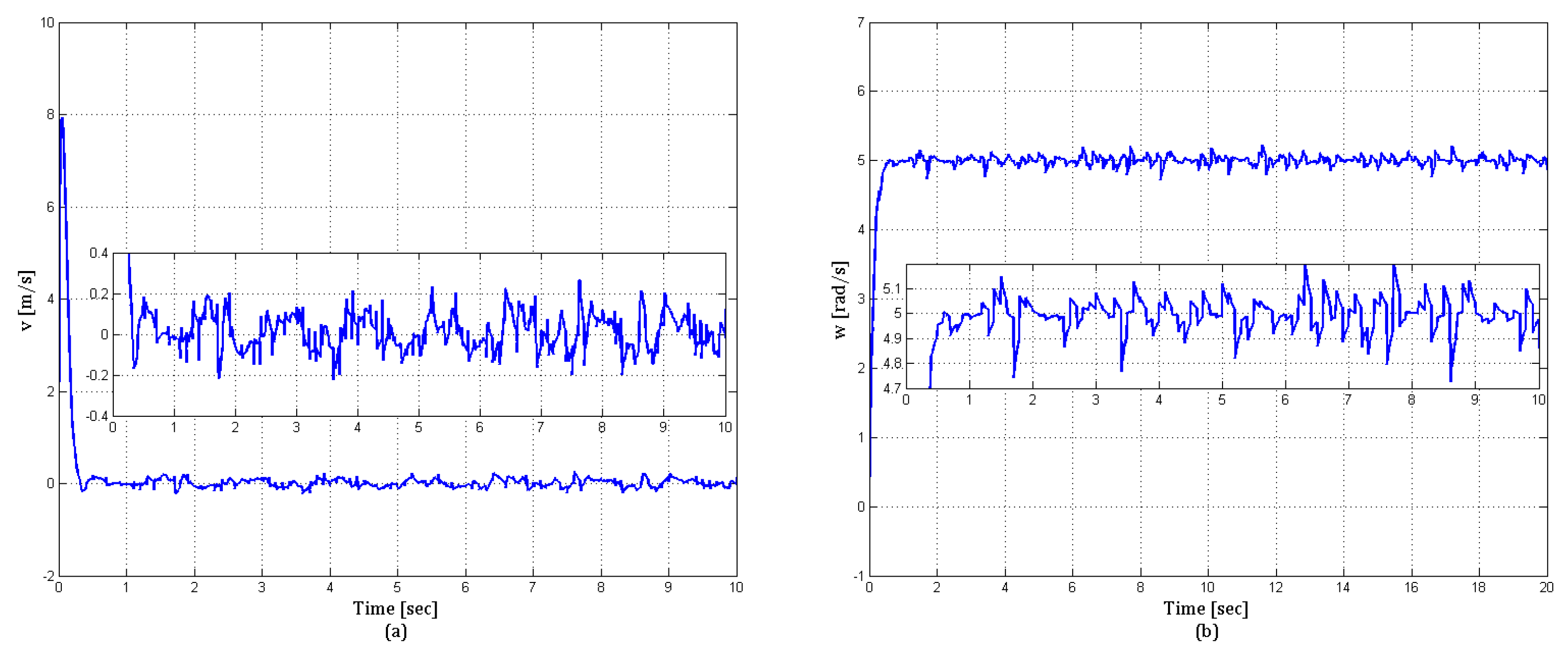
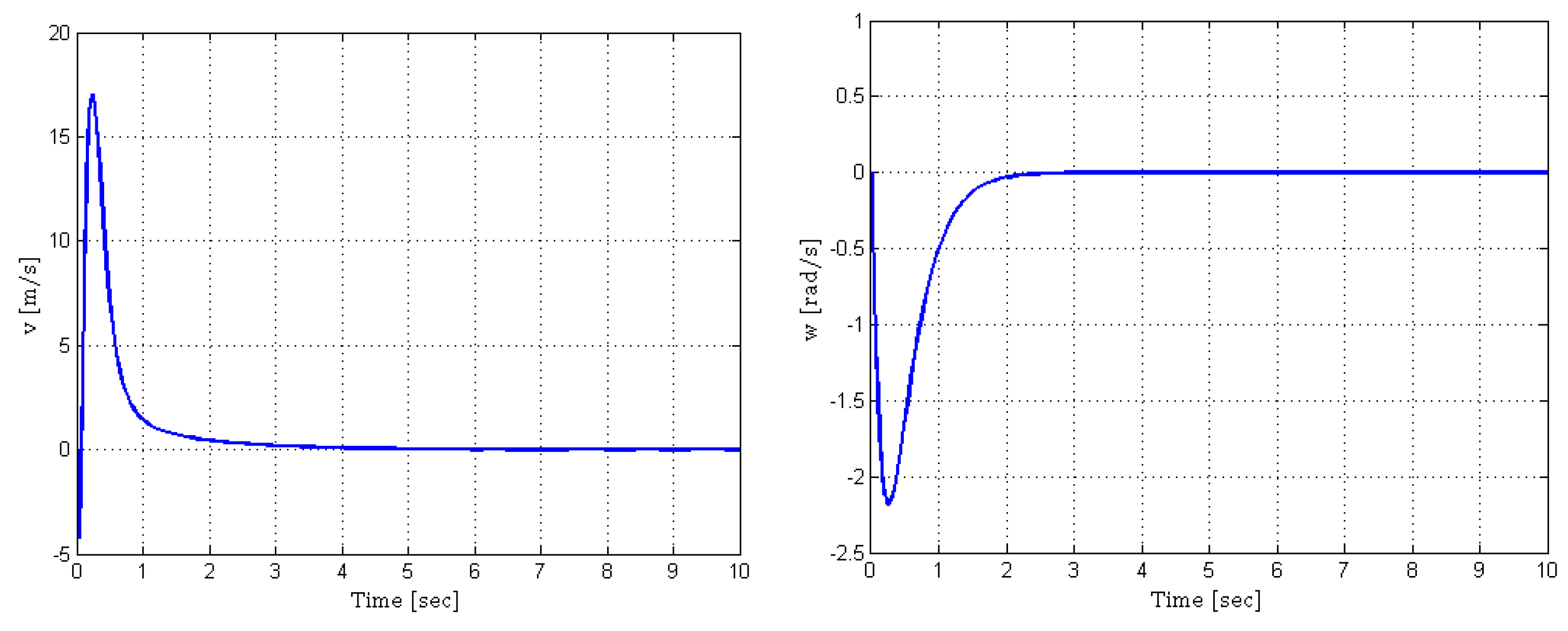
| (0.3, −0.7, ) | (−5, −5, ), Figure 7 and Figure 8 and | |
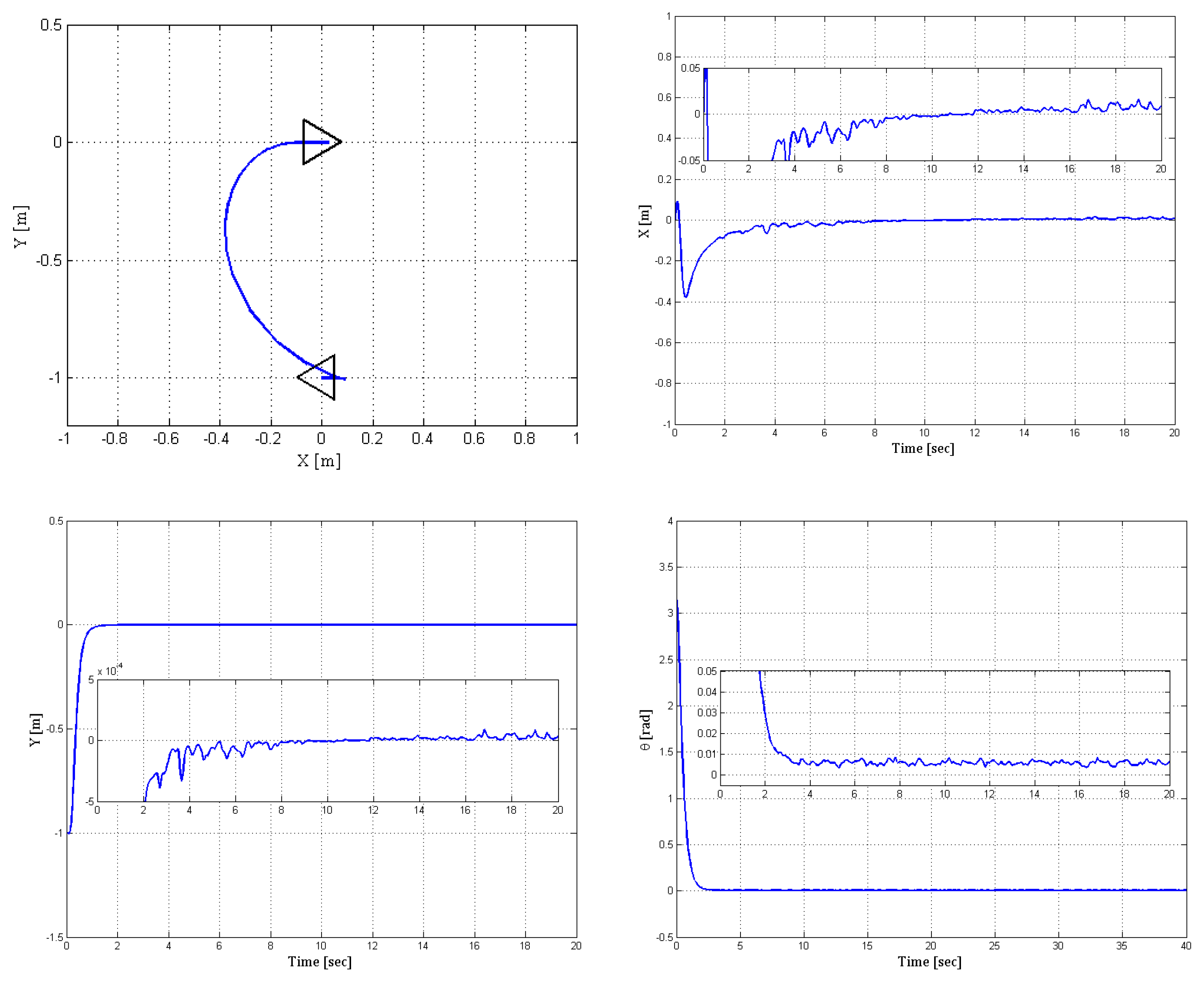
| (0, −1, ), Figure 9 and Figure 10 |
| Parameter | Circular Trajectory | Lamniscate Curve Trajectory |
|---|---|---|
| x (m) | 0.0114 | 0.0123 |
| y (m) | 0.0117 | 0.0123 |
| (rad) | 0.0097 | 0.0109 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rabbani, M.J.; Memon, A.Y. Trajectory Tracking and Stabilization of Nonholonomic Wheeled Mobile Robot Using Recursive Integral Backstepping Control. Electronics 2021, 10, 1992. https://doi.org/10.3390/electronics10161992
Rabbani MJ, Memon AY. Trajectory Tracking and Stabilization of Nonholonomic Wheeled Mobile Robot Using Recursive Integral Backstepping Control. Electronics. 2021; 10(16):1992. https://doi.org/10.3390/electronics10161992
Chicago/Turabian StyleRabbani, Muhammad Junaid, and Attaullah Y. Memon. 2021. "Trajectory Tracking and Stabilization of Nonholonomic Wheeled Mobile Robot Using Recursive Integral Backstepping Control" Electronics 10, no. 16: 1992. https://doi.org/10.3390/electronics10161992
APA StyleRabbani, M. J., & Memon, A. Y. (2021). Trajectory Tracking and Stabilization of Nonholonomic Wheeled Mobile Robot Using Recursive Integral Backstepping Control. Electronics, 10(16), 1992. https://doi.org/10.3390/electronics10161992






