Quadrature Demodulator-Assisted Estimation of Load Voltage and Resistance Based on Primary-Side Information of a Wireless Power Transfer Link

Abstract

This paper proposes an algorithm for the extraction of primary-side first harmonic voltage and current components for inductive wireless power transfer (WPT) links by employing quadrature demodulation. Such information allows for the accurate estimation of corresponding receiver-side components and hence permits the monitoring of the output voltage and resistance necessary for protection and/or control without using either sensors or feedback communication. It is shown that precision estimation is held as long as the parameter values of the system are known and the phasor-domain equivalent circuit is valid (i.e., in continuous conduction mode). On the other hand, upon light load operation (i.e., in discontinuous conduction mode), the proposed technique may still be employed if suitable nonlinear correction is employed. The methodology is applied to a 400 V, 1 kW inductive WPT link operating at a load-independent-voltage-output frequency and is well-verified both by simulations and experiments.

1. Introduction

The WPT system has the potential to become a practical solution for power delivery in the future due to its flexibility, movability, and cordless nature. WPT links are most commonly utilized in electric vehicles, implanted medical devices, portable electronics, etc. [1,2,3,4]. Today, resonant inductive WPT, which utilizes magnetic field for energy transmission, is the most widely employed methodology. Series–series compensation is the simplest yet most popular compensation topology for inductive WPT links [5] and is considered in this paper.

In typical WPT systems, the component values are known, while the coupling coefficient and load may vary significantly [6,7]. Generally, upon load and coupling coefficient variations, output voltage, current, or power must be regulated. Therefore, corresponding sensors and feedback implemented by some kind of additional wireless communication link are required [8,9,10,11,12], increasing system complexity and cost. It was recently proposed in [13] to modulate the transmitted power signal using amplitude or frequency shift keying modulation, thus eliminating the additional communication link. However, this approach was also shown to lead to undesired voltage and current ripples at the WPT output. A promising research direction for controlling the WPT link output without wireless feedback is to identify one or more output variables utilizing primary-side only electrical information [14,15,16,17]. The proposed methods are commonly divided into two main subgroups: time-domain [8,14,18] and phasor-domain [19,20,21,22,23,24] solutions. The former mostly leans on measuring the decaying current envelope during the free resonant reaction to the energy injection. The transfer of energy must be discrete during the energy injection interval to allow for decaying reaction detection and therefore cannot be used for continuous load regulation. Thus, this group of solutions seems to suit initial load identification, mostly necessary for induction heating applications. Moreover, the estimation results of this method demonstrate relatively low accuracy [14].

The phasor-domain solutions subgroup utilizes a first harmonic equivalent circuit of the WPT link, suitable for a wide region of operating frequencies. The WPT link equivalent circuit at the phasor-domain establishes a two-input (transmitter-side voltage and current) two-output (receiver-side voltage and current) linear network. Thus, for known primary-side phasors and system parameters, it is possible to calculate the secondary-side phasors in case the coupling coefficient is known or may be estimated. However, it was pointed out that actual AC-side WPT voltages and currents are not pure sinusoids, containing one or more distorting components [25,26] even if operating in continuous conduction mode (CCM). Therefore, the first harmonic components obtained from RMS-based reconstruction or peak value measurements are often inaccurate due to the non-sinusoidal shape of the instantaneous primary side voltage and current. In order to overcome this issue, the paper suggests utilizing the quadrature demodulation (QD) algorithm [27], typically employed in communication systems engineering. This technique accurately reveals the Cartesian components of first harmonic phasors while taking advantage of the fact that non-sinusoidal periodic signal harmonics are orthogonal. By utilizing QDs, the accuracy of the phasor-domain solutions subgroup is greatly improved. In order to demonstrate the enhanced algorithm performance, it is applied to a series-series compensated inductive WPT link operating at a load-independent-voltage-output frequency [28,29]. Such an operation is suitable for systems operating with a constant and known coupling coefficient [30,31], yielding a DC voltage output that is nearly unaffected by the load. However, it must be emphasized that fundamental harmonic-based approximations are insufficient for a WPT link operating under light loads [32]. This is due to the fact that when the receiving-side diode rectifier operates in discontinuous current mode (DCM), the harmonic content of primary and secondary currents rises significantly [33], and the relation between the secondary-side AC variables of the equivalent phasor-domain circuit and the output WPT link DC variables become nonlinear [34,35,36]. In order to overcome this obstacle, it is proposed to utilize a nonlinear correction function that allows for the adjustment of the output of the QD-assisted phasor-domain solution to yield an accurate estimation of WPT output voltage and load resistance under light loading.

The rest of the paper is organized as follows. The series–series compensated WPT link is analyzed in Section 2 and an equivalent dual-input dual-output linear phasor-domain network is established. Quadrature demodulation essentials are revealed in Section 3. An application of the proposed QD-assisted estimation algorithm to a series–series compensated inductive WPT link operating at load-independent-voltage-output frequency is described in detail in Section 4. The paper is summarized in Section 5.

2. Inductive WPT Link

Consider an inductive series-series compensated WPT link, shown in Figure 1 [34], where $V_I$ and $V_o$ symbolize input and output DC voltages, $L_1$ and $L_2$ are primary and secondary inductances, $C_1$ and $C_2$ represent primary and secondary compensating capacitance, $r_1$ and $r_2$ denote primary and secondary equivalent series resistances, $k$ indicates coupling coefficient, and $C_o$ and $R_o$ signify load filter capacitance and resistance, respectively. The inverter is operated with bipolar switching at a constant frequency of $\omega =2\mathsf{\pi }·f$ with a 50% duty cycle, such that

$$v_1(t)\hspace{0.17em}={\displaystyle \sum _{n=1,odd}^{\infty }{V}_{1n}}\sin \left(n\omega t+{\alpha }_n\right)$$

(1)

is a bipolar square-wave signal. The current of the primary-side is then described as

$$i_1(t)={\displaystyle \sum _{n=1,odd}^{\infty }{I}_{1n}}\sin \left(n\omega t+{\varphi }_n\right).$$

(2)

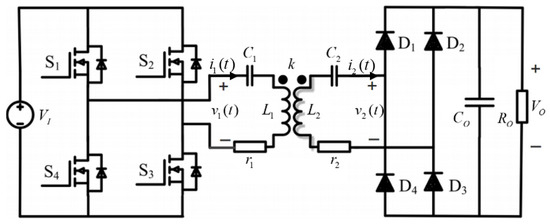
Figure 1. Series-series compensated inductive WPT link.

Similarly, voltage and current signals at the secondary side are given by

$$v_2(t)={\displaystyle \sum _{n=1,odd}^{\infty }{V}_{2n}\sin (n\omega t+{\theta }_n), i_2(t)=}{\displaystyle \sum _{n=1,odd}^{\infty }{I}_{2n}\sin (n\omega t+{\delta }_n)},$$

(3)

respectively.

In case ω is close to the resonant frequency given by

$${\omega }_R=\frac{1}{\sqrt{L_1{C}_1}}=\frac{1}{\sqrt{L_2{C}_2}},$$

(4)

the WPT link may be described by its first harmonic equivalent phasor-domain circuit [8] in Figure 2, where

$$\begin{array}{cccc}{\overrightarrow{v}}_1=V_{11}\angle {\alpha }_1,& {\overrightarrow{i}}_1=I_{11}\angle {\varphi }_1,& {\overrightarrow{v}}_2=V_{21}\angle {\theta }_1,& {\overrightarrow{i}}_2=I_{21}\angle {\delta }_1\end{array}$$

(5)

with [14] $V_{11}=\frac{4}{\pi }{V}_I$ and

$$\begin{array}{cc}{L}_M=k\sqrt{L_1{L}_2},& {\overrightarrow{Z}}_L=R_L+j\omega L_L\end{array}.$$

(6)

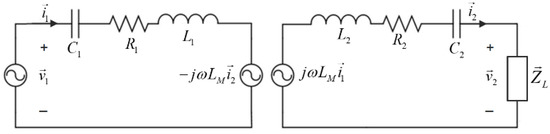
Figure 2. Equivalent phasor-domain circuit.

Denoting

$$\begin{array}{c}\begin{array}{ccc}{X}_1=\omega L_1-\frac{1}{\omega C_1},& X_2=\omega L_2-\frac{1}{\omega C_2},& X_M=\omega L_M\end{array},\hspace{0.17em}{X}_L=\omega L_L,\\ \begin{array}{cc}{\overrightarrow{Z}}_1=r_1+j{X}_1,& {\overrightarrow{Z}}_2=r_2+j{X}_2,\end{array}\end{array}$$

(7)

and letting ${\alpha }_1=0$ as the reference angle. Moreover, the secondary-side variables of the phasor domain equivalent circuit in Figure 2 may be derived from the primary side variables as

$$\left(\begin{array}{c}{\overrightarrow{v}}_2\\ {\overrightarrow{i}}_2\end{array}\right)=\left(\begin{array}{cc}-j\frac{{\overrightarrow{Z}}_2}{X_M}& j\frac{{\overrightarrow{Z}}_1{\overrightarrow{Z}}_2+X_M^2}{X_M}\\ j\frac{1}{X_M}& -j\frac{{\overrightarrow{Z}}_1}{X_M}\end{array}\right)\left(\begin{array}{c}{\overrightarrow{v}}_1\\ {\overrightarrow{i}}_1\end{array}\right).$$

(8)

Representing voltage and current phasors in (5) as

$$\begin{array}{cc}{\overrightarrow{v}}_1=V_{1R}+j{V}_{1I},& {\overrightarrow{v}}_2=\end{array}{V}_{2R}+j{V}_{2I}$$

(9)

and

$$\begin{array}{cc}{\overrightarrow{i}}_1=I_{1R}+j{I}_{1I},& {\overrightarrow{i}}_2=I_{2R}+j{I}_{2I},\end{array}$$

(10)

respectively, and substituting in (8) yields

$$\left(\begin{array}{l}{V}_{2R}\\ V_{2I}\\ I_{2R}\\ I_{2I}\end{array}\right)=\left(\begin{array}{cccc}\frac{X_2}{X_M}& \frac{r_2}{X_M}& -\frac{X_1{r}_2+r_1{X}_2}{X_M}& -\frac{r_1{r}_2-X_1{X}_2-X_M^2}{X_M}\\ \frac{-r_2}{X_M}& \frac{X_2}{X_M}& \frac{r_1{r}_2-X_1{X}_2-X_M^2}{X_M}& -\frac{X_1{r}_2+r_1{X}_2}{X_M}\\ 0& \frac{-1}{X_M}& \frac{X_1}{X_M}& \frac{r_1}{X_M}\\ \frac{1}{X_M}& 0& \frac{-r_1}{X_M}& \frac{X_1}{X_M}\end{array}\right)·\left(\begin{array}{l}{V}_{1R}\\ V_{1I}\\ I_{1R}\\ I_{1I}\end{array}\right).$$

(11)

Moreover (cf. (6))

$${\overrightarrow{Z}}_L=R_L+j{X}_L=\frac{{\overrightarrow{v}}_2}{{\overrightarrow{i}}_2},$$

(12)

hence (cf. (5), (9), and (10))

$$\begin{array}{l}\begin{array}{cc}{V}_{21}=\sqrt{V_{2R}^2+V_{1I}^2},& {\theta }_1=t{g}^{-1}\left(\frac{V_{1I}}{V_{1R}}\right)\end{array},\\ R_L=\frac{V_{2R}{I}_{2R}+V_{2I}{I}_{2I}}{I_{2R}^2+I_{2I}^2}, X_L=\frac{V_{2I}{I}_{2R}+V_{2R}{I}_{2I}}{I_{2R}^2+I_{2I}^2}.\end{array}$$

(13)

To summarize, the estimation of secondary-side first harmonic components may be carried out using the corresponding primary-side variables in case all the WPT link parameters are known.

Furthermore, in case the diode rectifier operates in continuous conduction mode (CCM), the following relations between the rectifier input and output sides hold [14,32]

$$\begin{array}{cc}{V}_O=\frac{\pi }{4}{V}_{21}-2V_d,& R_O=\frac{{\pi }^2}{8}{R}_L\end{array}$$

(14)

where V_d denotes a forward diode voltage drop.

3. Quadrature Demodulation Essentials

Consider a general periodic non-sinusoidal signal given by

$$x(t)={\displaystyle \sum _{n=1}^{\infty }{X}_n}(t)\sin \left(n\omega t+{\psi }_n(t)\right),$$

(15)

fed into a phasor detection performed by QD, shown in Figure 3 [27].

Figure 3. Quadrature demodulator.

The QD consists of two output channels, detecting the in-phase component of x(t) in the first channel and the quadrature component in the second channel. The channel outputs are denoted as $y_1\left(t\right)$ and $y_2$(t), respectively. The signal generating x(t) must be in the same phase as the sync signal to accurately detect ωt and the QD output channels described by

$$\overrightarrow{y}(t)=\{\begin{array}{c}{y}_1(t)\\ y_2(t)\end{array}=\{\begin{array}{c}LP{F}_{{\omega }_C}\left\{2\sin \left(\omega t\right)·x(t)\right\}\\ LP{F}_{{\omega }_C}\left\{2\cos \left(\omega t\right)·x(t)\right\}\end{array}$$

(16)

with $LP{F}_{{\omega }_C}\{·\}$ describing a high-cut filter with a low cut-off frequency such that ${\omega }_c\ll \omega$. Combining (15) with (16) yields

$$\overrightarrow{y}(t)=\{\begin{array}{c}{y}_1(t)\\ y_2(t)\end{array}=\{\begin{array}{c}{X}_1(t)\cos {\psi }_1(t)\\ X_1(t)\sin {\psi }_1(t)\end{array}.$$

(17)

Moreover, $x_1\left(t\right)$ denotes the first harmonic of x(t) by

$$x_1(t)=X_1(t)\sin \left(\omega t+{\psi }_1(t)\right)$$

(18)

or

$${\overrightarrow{x}}_1(t)=\underset{X_{1R}(t)}{\underbrace{X_1(t)\cos {\psi }_1(t)}}+j\underset{X_{1I}(t)}{\underbrace{X_1(t)\sin {\psi }_1(t)}}=X_{1R}(t)+j{X}_{1I}(t)$$

(19)

in the phasor domain. Therefore, the quadrature demodulator output yields

$$\overrightarrow{y}(t)=\{\begin{array}{c}{y}_1(t)=X_{1R}(t)\\ y_2(t)=X_{1I}(t)\end{array}.$$

(20)

Moreover, there is

$$\begin{array}{l}{X}_1(t)=\sqrt{X_{1R}^2(t)+X_{1I}^2(t)}=\sqrt{y_1^2(t)+y_2^2(t)}\\ {\psi }_1=t{g}^{-1}\left(\frac{X_{1I}(t)}{X_{1R}(t)}\right)=t{g}^{-1}\left(\frac{y_2(t)}{y_1(t)}\right)\end{array}$$

(21)

Consequently, feeding v₁(t) and i₁(t) (cf. (1) and (2)) into separate QDs with the sync signal used to drive the inverter switches would detect the real-time values of the primary-side complex phasor components (cf. (9)) required for the calculation of the corresponding secondary-side variables (11) and (13) and then of the output WPT link quantities (14), as shown in Figure 4.

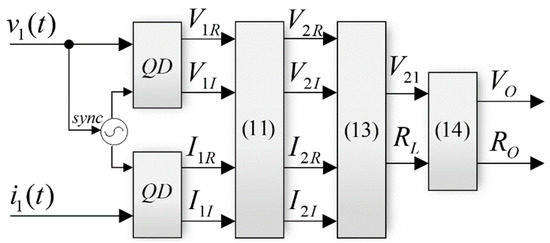
Figure 4. Flow diagram of the QD-based output variables calculation process.

4. Application to WPT Link Operating at Load-Independent-Voltage-Output Frequency

4.1. Attaining Load-Independent Voltage Output

The ratio between the inverter output voltage and rectifier input voltage phasors of the WPT link is derived from Figure 2 (taking (7) into account) as [34]

$$\frac{{\overrightarrow{v}}_2}{{\overrightarrow{v}}_1}=\frac{j{X}_M}{{\overrightarrow{Z}}_1+\frac{{\overrightarrow{Z}}_1{\overrightarrow{Z}}_2+X_M^2}{{\overrightarrow{Z}}_L}}.$$

(22)

The load-independent frequencies are derived by forcing the load-impedance-related component in (22) to zero, i.e.,

$${\overrightarrow{Z}}_1{\overrightarrow{Z}}_2+X_M^2=0.$$

(23)

Neglecting the equivalent series resistances $r_1$ and $r_2$ brings (23) to

$$X_1{X}_2=X_M^2.$$

(24)

The two load-independent frequencies ${\omega }_1$ and ${\omega }_2$ are identified by solving (24) using (4) and (7) as

$${\omega }_1=\frac{{\omega }_R}{\sqrt{1+k}},\hspace{0.17em}{\omega }_2=\frac{{\omega }_R}{\sqrt{1-k}}$$

(25)

with ${\omega }_1$ residing below resonance (the capacitive region) and ${\omega }_2$ belonging to the inductive region above resonance, i.e., ${\omega }_2>{\omega }_R>{\omega }_1$. The higher frequency ${\omega }_2$ is typically employed due to the lower harmonic distortion of the current and the natural zero voltage switching (ZVS) of inverter switches. In case the coupling coefficient is known, setting the operation frequency $\omega$ to ${\omega }_1$ or ${\omega }_2$ would ideally yield the load-independent output voltage [35]

$${\overrightarrow{v}}_2=j{\overrightarrow{v}}_1\sqrt{\frac{L_2}{L_1}}\Rightarrow V_O=\sqrt{\frac{L_2}{L_1}}{V}_I.$$

(26)

However, $r_1$ and $r_2$ are nonzero in practice. Moreover, (14) is only valid in case the diode rectifier operates in CCM, as mentioned above. In DCM, the linear relation between the AC and DC side variables of the secondary no longer holds. As shown in [27], the imaginary part of the diode rectifier input impedance (possessing inductive characteristics [29] yet susceptible to neglect in CCM) rises significantly in DCM. Moreover, the primary and secondary currents contain significant harmonic content and the first harmonic approximation becomes inaccurate. Consequently, ${\omega }_1$ or ${\omega }_2$ are not entirely load-independent in practice. It was shown in [35] that the output voltage is actually given by

$$V_O\approx \{\begin{array}{cc}\sqrt{\frac{L_2}{L_1}}{V}_I-\frac{{\pi }^2}{8V_I}\left(\sqrt{\frac{L_1}{L_2}}{r}_2+\sqrt{\frac{L_2}{L_1}}{r}_1\right)P_O,& P_O\ge P_{O,B}\\ C_1+C_2·P_O^{-0.5},& P_{O,MIN}<P_O\le P_{O,B}\end{array}$$

(27)

with P_O denoting the power absorbed by R_O, P_O,B signifying the power level corresponding to the diode rectifier operation on the bound between CCM and DCM, P_O,MIN indicating the minimum allowed loading of the inductive WPT link [36] and

$$\begin{array}{cc}{C}_1=V_{O,B}-P_{O,B}^{-0.5}{C}_2,& C_2=\frac{V_{O,MAX}-V_{O,B}}{P_{O,MIN}^{-0.5}-P_{O,B}^{-0.5}}\end{array},$$

(28)

where V_O,B and V_O,MAX are output voltage levels corresponding to P_O,B and P_O,MIN, respectively. Obviously, neglecting the equivalent series resistances $r_1$ and $r_2$ reduces the first row of (27) (corresponding to CCM) to (26). In case the diode rectifier operates in DCM (second row of (27)), the relation between the output voltage and the load power becomes highly nonlinear. Nevertheless, the relation between the first and the second rows of (27) is injective (one-to-one) in this region and hence the DCM-related output voltage may be estimated from its corresponding CCM counterpart. The relation between the load resistance value and the load power may be obtained by substituting (27) into

$$R_O[\mathsf{\Omega }]=\frac{1}{P_O}{V}_O^2.$$

(29)

4.2. Example

Consider a 1 kW inductive WPT link shown in Figure 1 with parameter values summarized in Table 1 operating at a load-independent-voltage-output frequency in the inductive region. The resonant and operating frequencies of the WPT link are

$${\omega }_R=2\pi ·67,000\frac{rad}{s},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\omega =2\pi ·124,500\frac{rad}{s},$$

(30)

respectively. The system has been designed for power delivery into an enclosed compartment through a 10 mm thick polyvinyl-chloride plate with near-unity voltage gain, as shown in Figure 5. The transmitter-side inverter was utilized by a modified Transphorm TDINV1000P100-KIT 1-kW Inverter GaN Evaluation Platform [37] utilizing 650 V, 150 mΩ TPH3206PSB gallium-nitride field effect transistors (FET) and driven by silicon labs SI8273AB1 isolated drivers. The switching signal was generated by a Taxes-Instrument F28335 digital signal processor. The receiver-side rectifier was performed by Microsemi APT40DQ120BG ultrafast diodes. The system was fed from an IT61517D ITECH high-voltage DC power supply and loaded by a Maynuo M9715 DC electronic load operated in the constant-power mode. A 20 kΩ resistor was constantly connected at the DC output of the inductive WPT link to realize the minimum allowed loading of P_O,MIN = 9 W [36]. An interested reader may refer to [34,35,36] for further details. Measured static output voltage versus load power curve was derived in [34] and is reproduced in Figure 6.

Table 1. System parameter values.

Parameter	Value	Units
VI	400	V
L1, L2	180	µH
k	0.71	--
r1, r2	1.9	Ω
C1, C2	31.3	nF
CO	660	µF

Figure 5. Experimental setup.

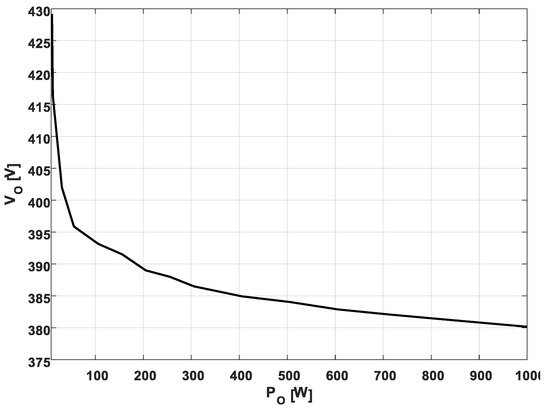
Figure 6. Measured output voltage versus load power [34].

The output voltage versus load power relation of the system is then given by

$$V_O[V]\approx \{\begin{array}{cc}394-0.0165P_O,& P_O\ge 250W\\ 380+145P_O^{-0.5},& 9W<P_O\le 250W\end{array},$$

(31)

corresponding well with the theoretical predictions in (27) with V_O,B = 388 V, V_O,MAX = 428 V, P_O,B = 250 W, and P_O,MIN = 9 W. However, since the algorithm in Figure 4 assumes CCM at all times, its output would be given by the first row of (31) for all of the load levels. In order to include the estimation of V_O in DCM, an additional action is applied on the output of (14) in Figure 4 according to (31) to obtain the final estimate $V_O^{est}$ as

$$V_O^{est}=\{\begin{array}{cc}{V}_O,& V_O\le V_{O,B}=388\\ 380+145{\left(\frac{394-V_O}{0.016}\right)}^{-0.5},& V_O>V_{O,B}=388\end{array}\hspace{0.17em}.$$

(32)

The measured static output voltage versus load power curve was derived in [27] and is reproduced in Figure 7. According to (29) and (31), there is

$$R_O[\mathsf{\Omega }]\approx \{\begin{array}{cc}\frac{1}{P_O}{\left(394-0.0165P_O\right)}^2,& P_O\ge 250W\\ \frac{1}{P_O}{\left(380+145P_O^{-0.5}\right)}^2,& 9W\le P_O<250W\end{array}.$$

(33)

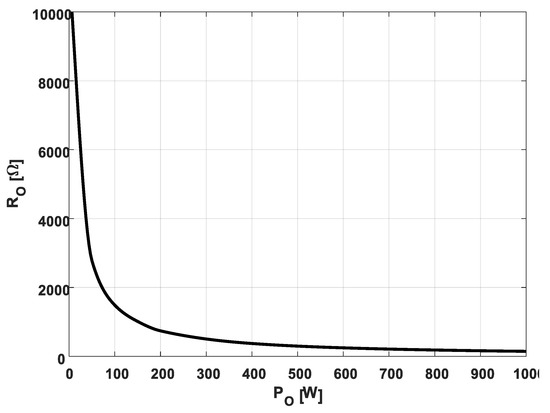
Figure 7. Measured load resistance versus load power [27].

Due to the CCM assumption, the output of the algorithm in Figure 4 would be given by the first row of (32) for all of the load levels. Consequently, in order to estimate the value of R_O in DCM, an additional action is applied on the output of (14) in Figure 4 according to (33) to obtain the final estimate $R_O^{est}$ as

$$R_O^{est}=\{\begin{array}{cc}{R}_O,& R_O\le R_{O,B}=602\\ \frac{{\left(380+145{\left(1237-1.64R_O\right)}^{-0.5}\right)}^2}{1237-1.64R_O},& R_O>R_{O,B}=602\end{array}\hspace{0.17em}$$

(34)

with $R_{O,B}=V_{O,B}^2/P_{O,B}$ signifying load resistance corresponding to the diode rectifier operation on the bound between CCM and DCM.

4.3. Simulations

In order to validate the proposed QD-assisted estimation methodology, the system was simulated with primary-side variables employed as real-time inputs, according to Figure 4 with (32) and (34). The real AC-side variables were compared with the predicted ones (recognized by superscript “est” from now on). The time-domain AC-side waveforms for different load levels are shown in Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, where V1, I1, V2, and I2 denote the primary and secondary AC-side voltages and currents, respectively; V1_h1, I1_h1, V2_h1, and I2_h1 symbolize the corresponding first harmonic components (obtained by band-pass filtering); and V₁₁, I₁₁, V₂₁, and I₂₁ with α₁, ϕ₁, θ₁, and δ₁ signify the QD outputs (estimated phasors) processed using (21). It is evident that QDs accurately estimate the first harmonic components of primary-side variables and that the proposed algorithm correctly determines their secondary-side counterparts for all of the load levels. Table 2 summarizes the overall estimation algorithm performance. It may be concluded that the estimated values of output voltage and resistance are satisfactory to indicate the correct operation of the system, which is the major goal of the proposed process.

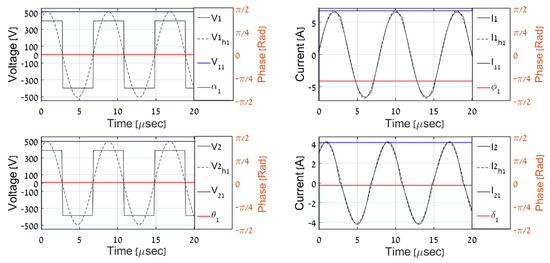
Figure 8. Simulation results, P_O = 1000 W.

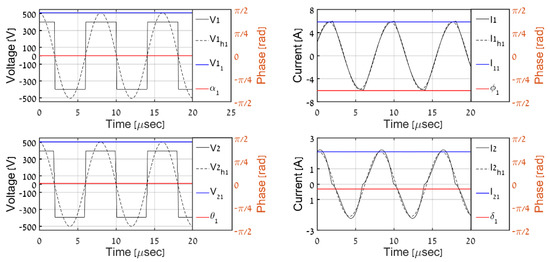
Figure 9. Simulation results, P_O = 500 W.

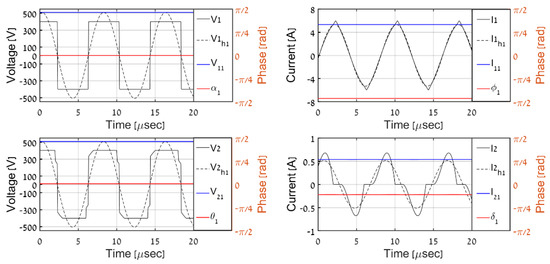
Figure 10. Simulation results, P_O = 200 W.

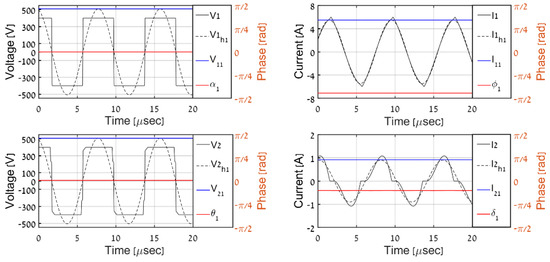
Figure 11. Simulation results, P_O = 100 W.

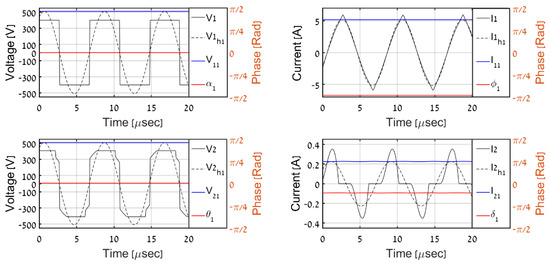
Figure 12. Simulation results, P_O = 50 W.

Table 2. Simulation results summary.

Power	${\mathit{V}}_{\mathit{O}}$	${\mathit{V}}_{\mathit{o}}^{\mathit{e}\mathit{s}\mathit{t}}$	${\mathit{R}}_{\mathit{O}}$	${\mathit{R}}_{\mathit{L}}^{\mathit{e}\mathit{s}\mathit{t}}$
1000	388	387.79	150.5	151.5
500	394.3	394.07	310.9	299.6
200	398.7	399.8	794.8	815
100	402.3	401	1618.4	1620
50	405.2	405.6	3283.7	3272

It should be highlighted that DCM operation (for load levels below 250 W) is well-reflected by the discontinuous nature of secondary current. Moreover, the diode rectifier input voltage shape deviates from the pure-square wave due to conduction ceasing regions.

4.4. Experiments

In order to experimentally validate the proposed methodology, the system in Figure 5 was operated under similar load levels as during simulations. All AC-side and output DC-side variables were acquired during experiments.

Then, the recorded primary-AC-side waveforms were used in an offline manner to perform corresponding estimations. The time-domain AC-side waveforms for the different load levels are shown in Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17. It is evident that the results match well with the simulation outcomes. Table 3 and Figure 18 and Figure 19 summarize the overall estimation algorithm performance.

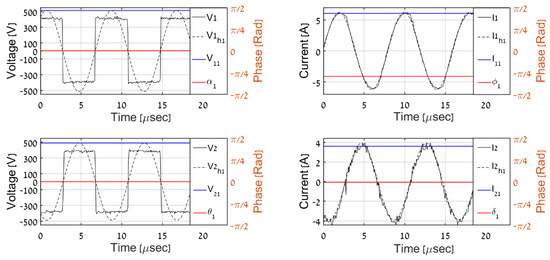
Figure 13. Experimental results, P_O = 1000 W.

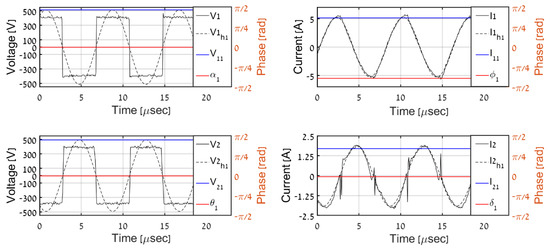
Figure 14. Experimental results, P_O = 500 W.

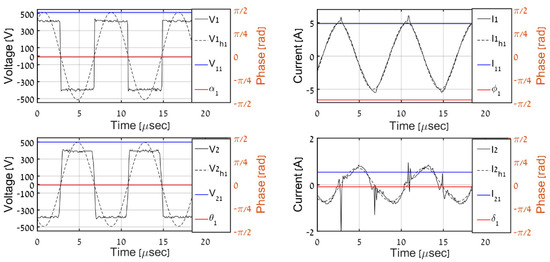
Figure 15. Experimental results, P_O = 200 W.

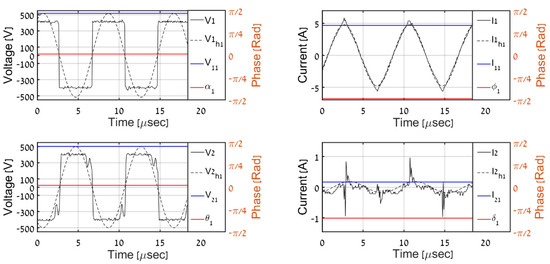
Figure 16. Experimental results, P_O = 100 W.

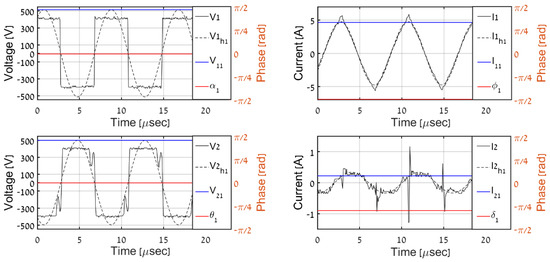
Figure 17. Experimental results, P_O = 50 W.

Table 3. Experimental results summary.

Power	${\mathit{V}}_{\mathit{O}}$	${\mathit{V}}_{\mathit{o}}^{\mathit{e}\mathit{s}\mathit{t}}$	${\mathit{R}}_{\mathit{O}}$	${\mathit{R}}_{\mathit{L}}^{\mathit{e}\mathit{s}\mathit{t}}$
1000	380	379.2	147.4	150
500	384	384.7	294	305
200	389	389.6	786	815
100	393.1	393.6	1546	1475
50	395.9	399	3215	3210

Figure 18. Measured and estimated output voltage versus load power.

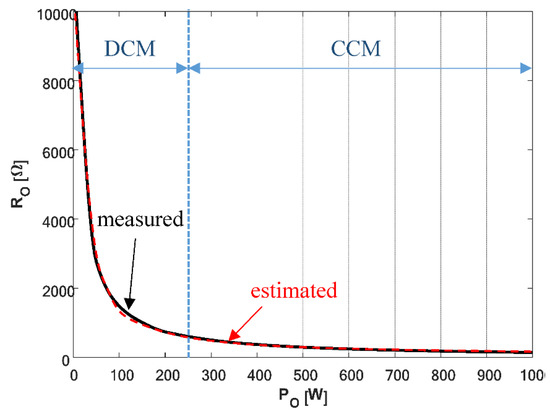
Figure 19. Measured and estimated load resistance versus load power.

It should be emphasized that DCM secondary current waveforms are somewhat different from their simulation counterparts. This is due to the fact that the simulation model does not include the parasitic capacitances of the coil and the diode bridge since they do not affect the first harmonic behavior. When parasitics are brought into the model, the results generally look much more similar—see [36]. Here, the first harmonics are of interest, and it is shown that the first harmonic approximations are similar in simulations and experiments. Moreover, switching instants spikes are present, imposed by parasitic capacitances. Note that the spikes’ magnitudes remain relatively low, hence they do not present any visible hazard. As shown in Figure 5, the receiver components are discrete rather than residing on a single PCB. If these components are brought together, the spikes are reduced significantly.

5. Conclusions

The quadrature demodulation-based extraction of inductive WPT link transmitter-side first harmonic phasor voltage and current components was proposed in this work, with the aim of improving the accuracy of the output voltage and resistance estimation based on only primary-side information. Such an approach allows for the potential elimination of both sensors and the feedback communication link. In order to retain the accuracy under light loading, additional nonlinear correction based on preliminary measurements was employed, while future work may include the derivation of an analytical relation between the load power and output voltage. The proposed methodology was successfully applied to a 400 V, 1 kW inductive WPT link operating at a load-independent-voltage-output frequency and validated by matching simulation and experimental results.