Analytical Winding Power Loss Calculation in Gapped Magnetic Components
Abstract
:1. Introduction
2. Review of 2D Analytical Approaches
2.1. Methods for Calculating the Overall Magnetic Field
2.2. Conduction Loss Calculations in the Presence of a Given Magnetic Field
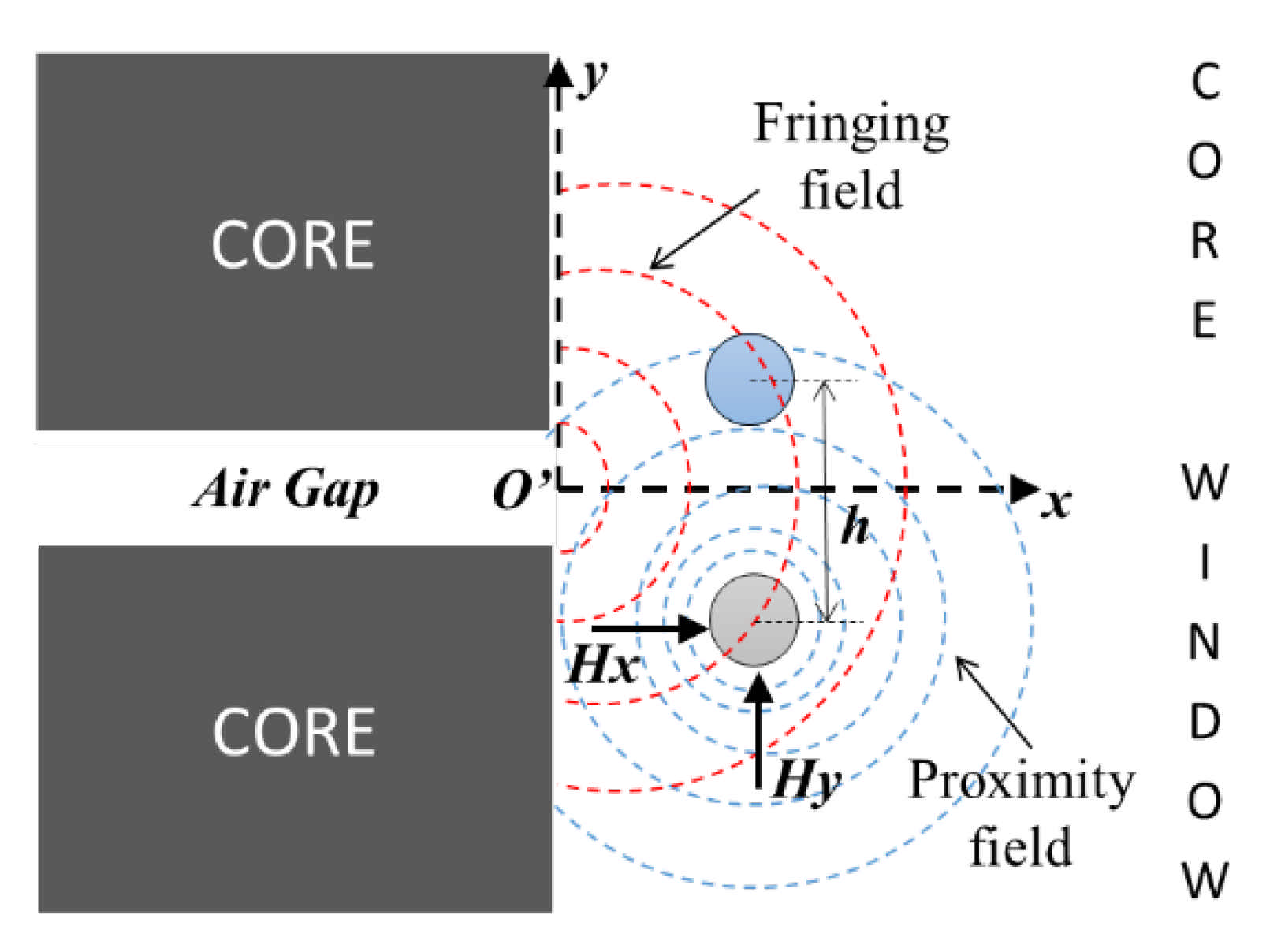
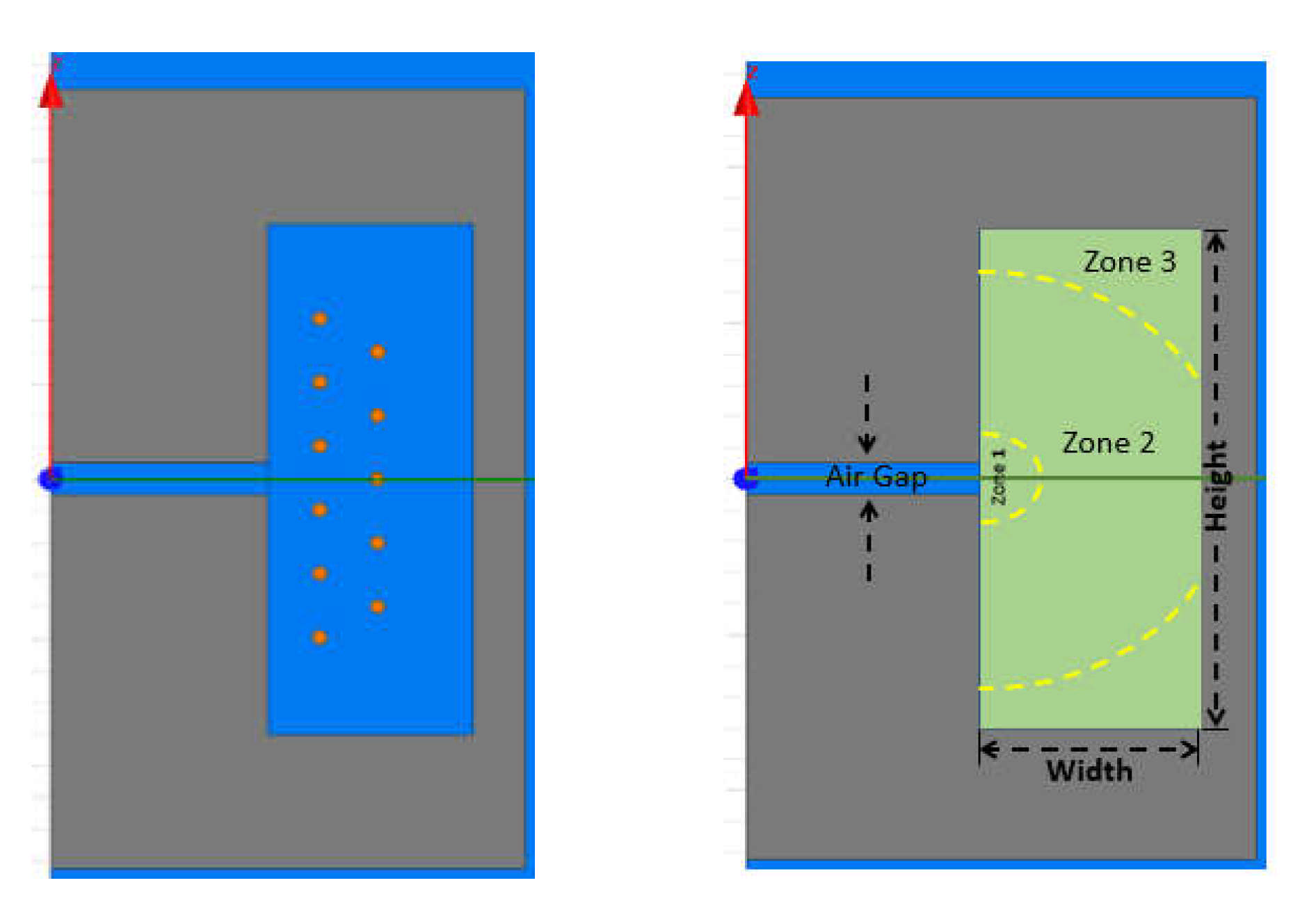
3. Proposed 2D Analytical Model
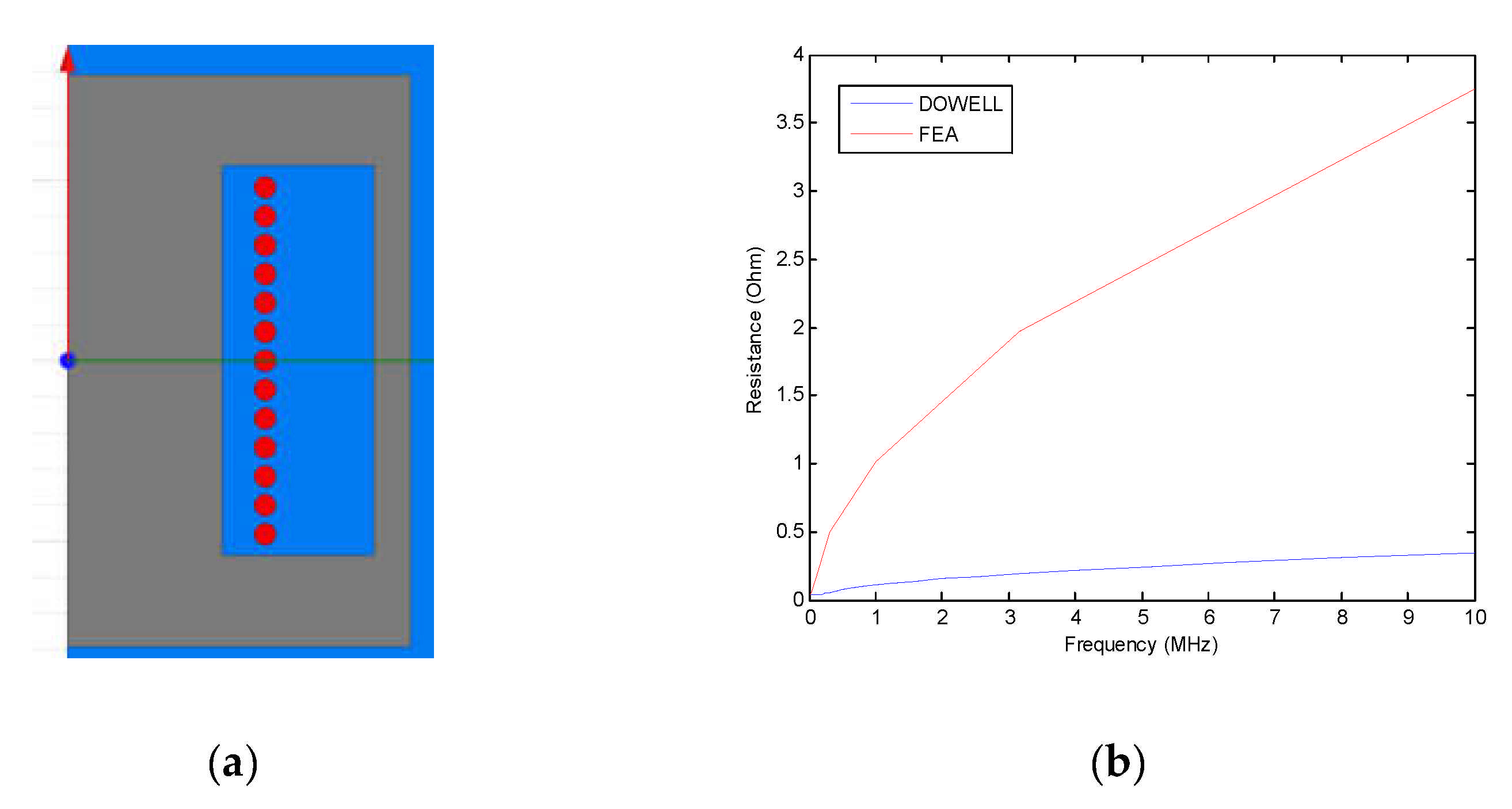
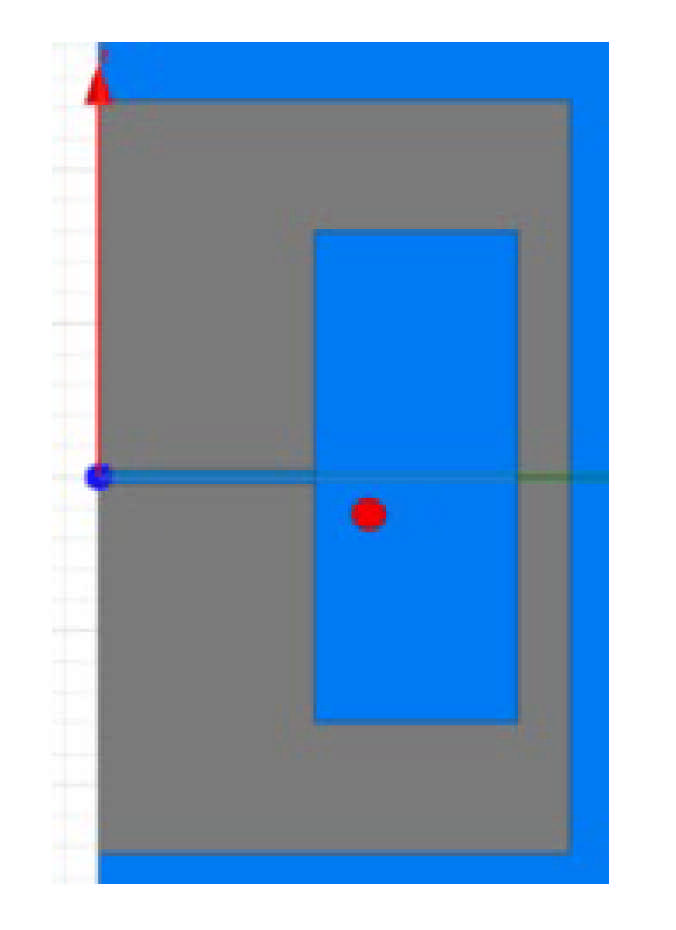
4. Model Validation
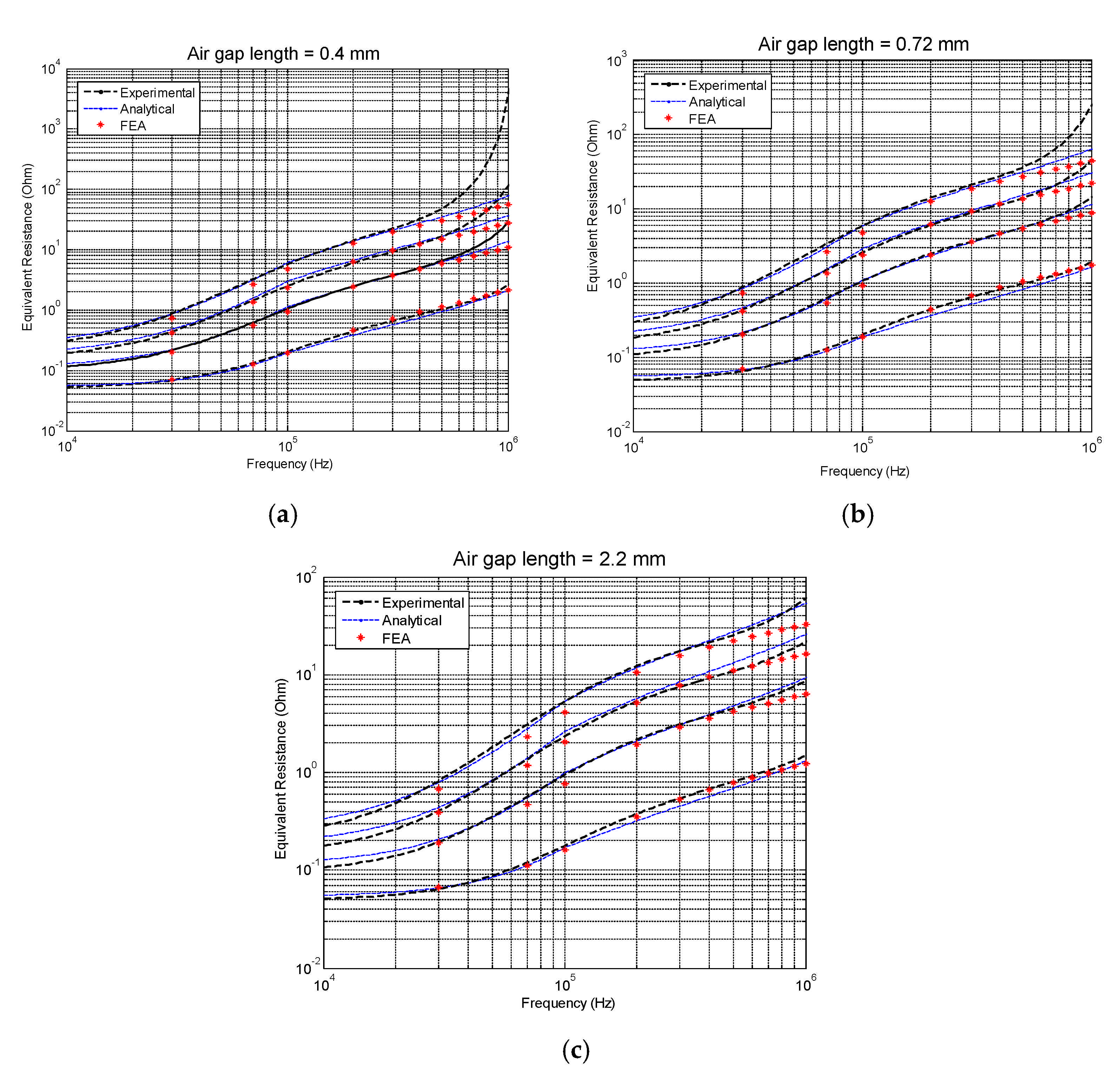
5. Results and Applications
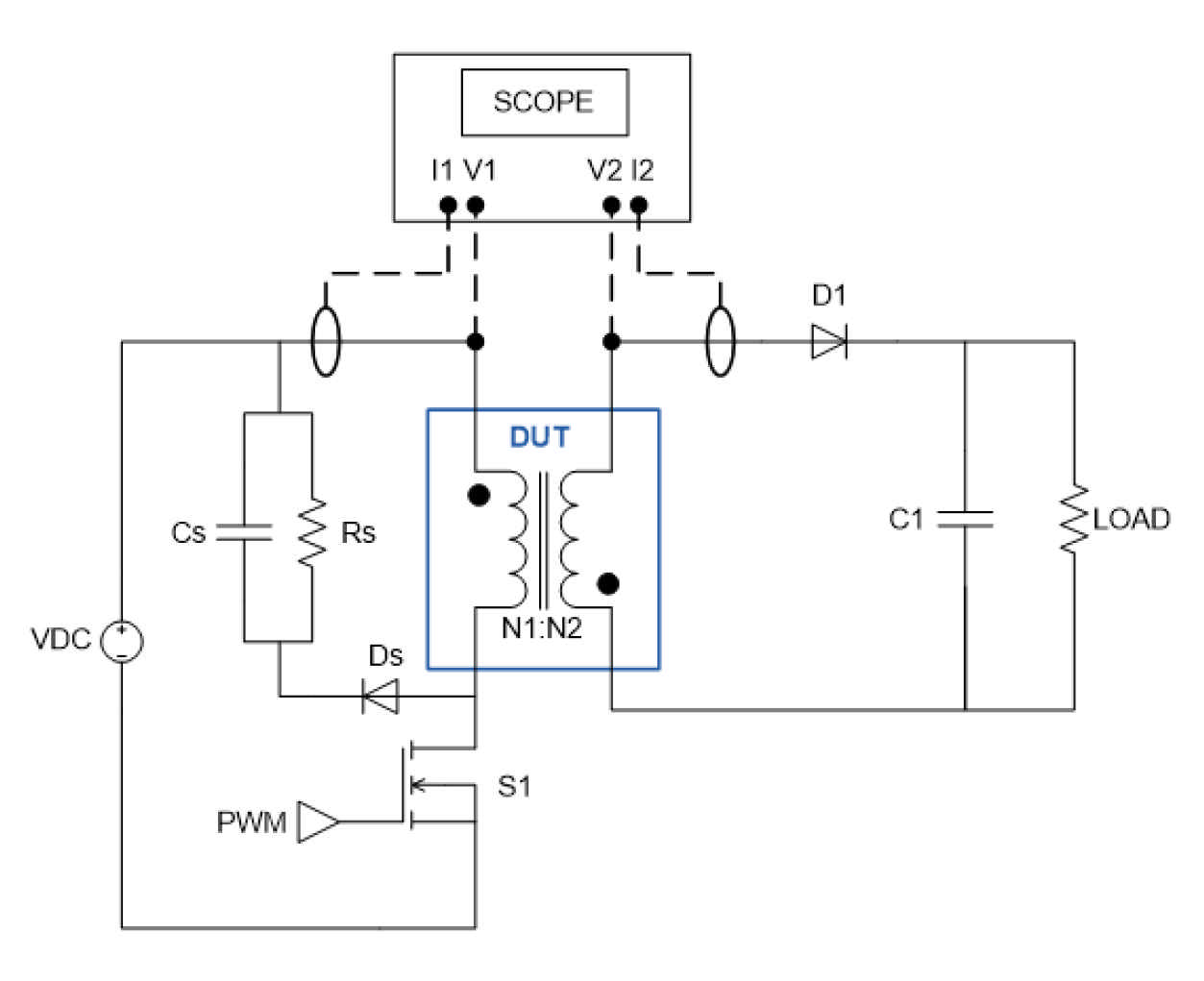
Applying the Proposed Calculation Method to Flyback Transformers
- For a given operating point in the converter, the input and output power were measured using precision meters, while an infrared camera was used to register the temperature of the semiconductors (main switch, the clamping diode, and output diode) and the clamping resistor. The total loss in the converter is the difference between the measured input and output power;
- Since a regulated source was used for the input voltage, no input capacitor was used in order to avoid additional loss due to the corresponding ESR. Furthermore, the required output capacitance, as well as the clamping capacitance were obtained by stacking a big number of parallel capacitors (in order to reduce, and neglect, the power loss due to the corresponding ESR);
- The semiconductors and clamping resistor were later characterized in order to subtract their respective losses from the measured values. To do this, the information taken from the thermal monitor was used to characterize the components by means of the association of a specific power loss with a given temperature (which corresponds to the considered operating point). This was performed by pushing a controlled DC current through the device to make it reach the same temperature that was observed during operation;
- Then, the power loss in the transformer (which includes the core loss) was assumed to be the difference between the total power loss and losses in the semiconductors and clamping circuit;
- The core loss was later taken out from the obtained value by means of the subtraction of an analytically calculated core loss (using the iGSE described in [40]), by means of (16), where k, α, and β are the Steinmetz parameters of the used magnetic materials (from datasheet). The waveform of the flux density was determined according to the measured currents, or voltages, in the transformer;
- Finally, the measured winding loss is the total difference among the input power, output power, losses in the devices, and the calculated core loss of the transformer (18).
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dowell, P. Effects of eddy currents in transformer windings. Proc. Inst. Electr. Eng. 1966, 113, 1387–1394. [Google Scholar] [CrossRef]
- Nan, X.; Sullivan, C.R. An improved calculation of proximity-effect loss in high-frequency windings of round conductors. In Proceedings of the IEEE 34th Annual Conference on Power Electronics Specialist, 2003. PESC ’03, Acapulco, Mexico, 15–19 June 2003; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2003; Volume 2, pp. 853–860. [Google Scholar]
- Nan, X.; Sullivan, C.R. Simplified high-accuracy calculation of eddy-current loss in round-wire windings. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No. 04CH37551), Aachen, Germany, 20–25 June 2004; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2004; Volume 2, pp. 873–879. [Google Scholar]
- Ferreira, J. Improved analytical modeling of conductive losses in magnetic components. IEEE Trans. Power Electron. 1994, 9, 127–131. [Google Scholar] [CrossRef]
- Robert, F.; Mathys, P.; Schauwers, J.-P. A closed-form formula for 2-D ohmic losses calculation in SMPS transformer foils. IEEE Trans. Power Electron. 2001, 16, 437–444. [Google Scholar] [CrossRef]
- Holguin, F.A.; Asensi, R.; Prieto, R.; Cobos, J.A. Simple analytical approach for the calculation of winding resistance in gapped magnetic components. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2014; pp. 2609–2614. [Google Scholar]
- Bahmani, M.A.; Thiringer, T.; Ortega, H. An accurate pseudoempirical model of winding loss calculation in HF foil and round conductors in Switchmode magnetics. IEEE Trans. Power Electron. 2014, 29, 4231–4246. [Google Scholar] [CrossRef]
- Severns, R. Additional losses in high frequency magnetics due to non ideal field distributions. In Proceedings of the APEC ’92 Seventh Annual Applied Power Electronics Conference and Exposition, Boston, MA, USA, 23–27 February 1992; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2003; pp. 333–338. [Google Scholar]
- Mao, X.; Chen, W.; Li, Y. Winding loss mechanism analysis and design for new structure high-frequency gapped inductor. IEEE Trans. Magn. 2005, 41, 4036–4038. [Google Scholar]
- Asensi, R.; Cobos, J.A.; García, O.; Prieto, R.; Uceda, J. A full procedure to model high frequency transformer windings. In Proceedings of the 25th Annual IEEE Power Electronics Specialists Conference, Taipei, Taiwan, 20–25 June 1994; Volume 2, pp. 856–863. [Google Scholar]
- Asensi, R.; Prieto, R.; Cobos, J.A.; Uceda, J. Modelling high-frequency multiwinding magnetic components using fi-nite-element analysis. IEEE Trans. Magn. 2007, 43, 3840–3850. [Google Scholar] [CrossRef]
- Prieto, R.; Asensi, R.; Fernandez, C.; Oliver, J.A.; Cobos, J.A. Bridging the gap between FEA field solution and the magnetic component model. IEEE Trans. Power Electron. 2007, 22, 943–951. [Google Scholar] [CrossRef]
- Prieto, R.; Cobos, J.A.; García, O.; Alou, P.; Uceda, J. Study of 3-D magnetic components by means of double 2-D methodology. IEEE Trans. Ind. Electron. 2003, 50, 183–192. [Google Scholar] [CrossRef]
- Prieto, R.; Oliver, J.; Cobos, J. Study of non-axisymmetric magnetic components by means of 2D FEA solvers. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Recife, Brazil, 12–16 June 2005; pp. 1074–1079. [Google Scholar] [CrossRef]
- Van den Bossche, A.; Valchev, V.C. Taylor and francis. In Inductors and Transformers for Power Electronics; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Snelling, E.C. Soft Ferrites, Properties and Applications, 2nd ed.; Butterworths: London, UK, 1988. [Google Scholar]
- Roshen, W.A. Fringing field formulas and winding loss due to an air gap. IEEE Trans. Magn. 2007, 43, 3387–3394. [Google Scholar] [CrossRef]
- Wei, C.; Xiaosheng, H.; Juanjuan, Z. Improved winding loss theoratical calculation of magnetic component with air gap. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012; Volume 1, pp. 471–475. [Google Scholar]
- Hu, J.; Sullivan, C.R. Optimization of shapes for round-wire high-frequency gapped-inductor windings. In Proceedings of the Conference Record of 1998 IEEE Industry Applications Conference. Thirty-Third IAS Annual Meeting (Cat. No.98CH36242), St. Louis, MO, USA, 12–15 October 1998; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2002; Volume 2, pp. 907–912. [Google Scholar]
- Leuenberger, D.; Biela, J. Semi-numerical method for loss-calculation in foil-windings exposed to an air-gap field. In Proceedings of the 2014 International Power Electronics Conference (IPEC-Hiroshima 2014—ECCE ASIA), Hiroshima, Japan, 18–21 May 2014; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2014; pp. 868–875. [Google Scholar]
- Albach, M.; Rossmanith, H. The influence of air gap size and winding position on the proximity losses in high frequency transformers. In Proceedings of the 2001 IEEE 32nd Annual Power Electronics Specialists Conference (IEEE Cat. No.01CH37230), Vancouver, BC, Canada, 17–21 June 2001; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2002; Volume 3, pp. 1485–1490. [Google Scholar]
- Albach, M. Two-dimensional calculation of winding losses in transformers. In Proceedings of the 2000 IEEE 31st Annual Power Electronics Specialists Conference. Conference Proceedings (Cat. No.00CH37018), Galway, Ireland, 23 June 2000; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2002; Volume 3, pp. 1639–1644. [Google Scholar]
- Sullivan, C.R. Computationally efficient winding loss calculation with multiple windings, arbitrary waveforms, and two-dimensional or three-dimensional field geometry. IEEE Trans. Power Electron. 2001, 16, 142–150. [Google Scholar] [CrossRef] [Green Version]
- Zimmanck, D.R.; Sullivan, C.R. Efficient calculation of winding-loss resistance matrices for magnetic components. In Proceedings of the 2010 IEEE 12th Workshop on Control and Modeling for Power Electronics (COMPEL), Boulder, CO, USA, 28–30 June 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Acero, J.A.; Hernandez, P.; Burdio, J.; Alonso, R.; Barragdan, L. Simple resistance calculation in litz-wire planar windings for induction cooking appliances. IEEE Trans. Magn. 2005, 41, 1280–1288. [Google Scholar] [CrossRef]
- Lope, I.; Acero, J.; Burdío, J.M.; Carretero, C.; Alonzo, R. Design and implementation of PCB inductors with litz-wire structure for conventional-size large-signal domestic induction heating applications. IEEE Trans. Ind. Appl. 2015, 51, 2434–2442. [Google Scholar] [CrossRef]
- Lope, I.; Carretero, C.; Acero, J.A.; Alonso, R.; Burdio, J.M. Frequency-dependent resistance of planar coils in printed circuit board with litz structure. IEEE Trans. Magn. 2014, 50, 1–9. [Google Scholar] [CrossRef]
- Acero, J.A.; Burdio, J.; Barragan, L.; Puyal, D.; Alonso, R. Frequency-dependent resistance in Litz-wire planar windings for all-metal domestic induction heating appliances. In Proceedings of the Twentieth Annual IEEE Applied Power Electronics Conference and Exposition, 2005, APEC 2005, Austin, TX, USA, 6–10 March 2005; Volume 2, p. 1294. [Google Scholar] [CrossRef]
- Wallmeier, P.; Frohleke, N.; Grotstollen, H. Improved analytical modeling of conductive losses in gapped high-frequency inductors. In Proceedings of the Conference Record of 1998 IEEE Industry Applications Conference. Thirty-Third IAS Annual Meeting (Cat. No.98CH36242), The 1998 IEEE Industry Applications Conference, St. Louis, MO, USA, 12–15 October 1998; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2002; Volume 37, pp. 1045–1054. [Google Scholar] [CrossRef]
- Lammeraner, J.; Stalf, M. Eddy Currents; ILIFFE books LTD.: London, UK, 1966. [Google Scholar]
- Albach, M.; Stadler, A.; Spang, M. The influence of ferrite characteristics on the inductance of coils with rod cores. IEEE Trans. Magn. 2007, 43, 2618–2620. [Google Scholar] [CrossRef]
- Deng, Q.; Liu, J.; Czarkowski, D.; Kazimierczuk, M.K.; Bojarski, M.; Zhou, H.; Hu, W. Frequency-dependent resistance of litz-wire square solenoid coils and quality factor optimization for wireless power transfer. IEEE Trans. Ind. Electron. 2016, 63, 2825–2837. [Google Scholar] [CrossRef]
- Podoltsev, A.; Kucheryavaya, I.; Lebedev, B.; Podoltsev, A.; Kucheryavaya, I.; Lebedev, B. Analysis of effective resistance and eddy-current losses in multiturn winding of high-frequency magnetic components. IEEE Trans. Magn. 2003, 39, 539–548. [Google Scholar] [CrossRef]
- Etemadrezaei, M.; Lukic, S.M. Equivalent complex permeability and conductivity of Litz wire in wireless power transfer systems. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 3833–3840. [Google Scholar] [CrossRef]
- Stadler, A.; Huber, R.; Stolzke, T.; Gulden, C. Analytical calculation of copper losses in Litz-Wire windings of gapped inductors. IEEE Trans. Magn. 2014, 50, 81–84. [Google Scholar] [CrossRef]
- Meeker, D.C.; Meeker, D.C. An improved continuum skin and proximity effect model for hexagonally packed wires. J. Comput. Appl. Math. 2012, 236, 4635–4644. [Google Scholar] [CrossRef] [Green Version]
- Stadler, A. The optimization of high frequency inductors with litz-wire windings. In Proceedings of the 2013 International Conference-Workshop Compatibility and Power Electronics, Ljubljana, Slovenia, 5–7 June 2013; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2013; pp. 209–213. [Google Scholar]
- Gyselinck, J.; Dular, P. Frequency-domain homogenization of bundles of wires in 2-D magneto-dynamic FE calculations. IEEE Trans. Magn. 2005, 41, 1416–1419. [Google Scholar] [CrossRef] [Green Version]
- Spreen, J. Electrical terminal representation of conductor loss in transformers. IEEE Trans. Power Electron. 1990, 5, 424–429. [Google Scholar] [CrossRef]
- Venkatachalam, K.; Sullivan, C.R.; Abdallah, T.; Tacca, H. Accurate prediction of ferrite core loss with nonsinusoidal waveforms using only Steinmetz parameters. In Proceedings of the 2002 IEEE Workshop on Computers in Power Electronics, Mayaguez, PR, USA, 3–4 June 2002; pp. 36–41. [Google Scholar]


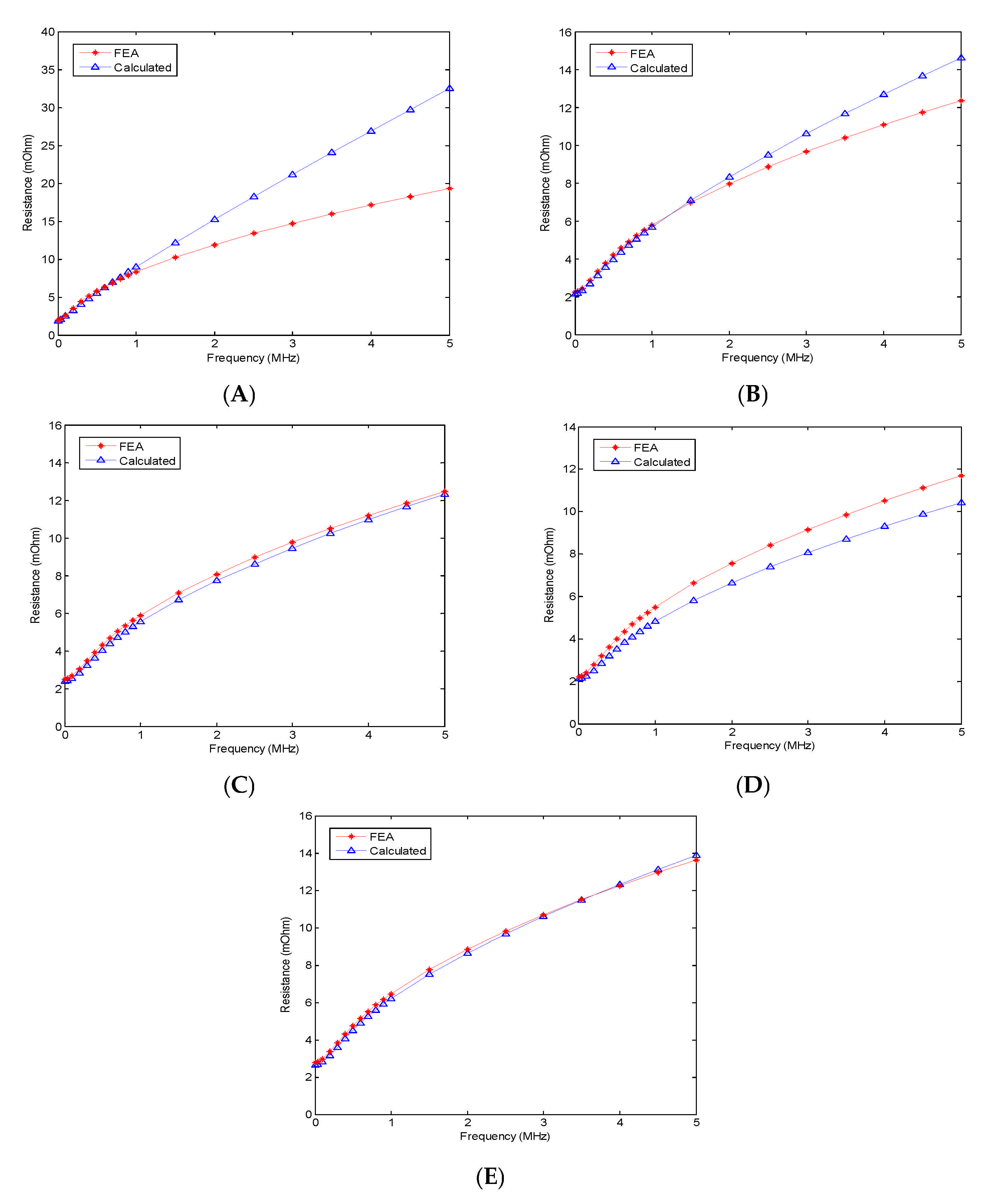
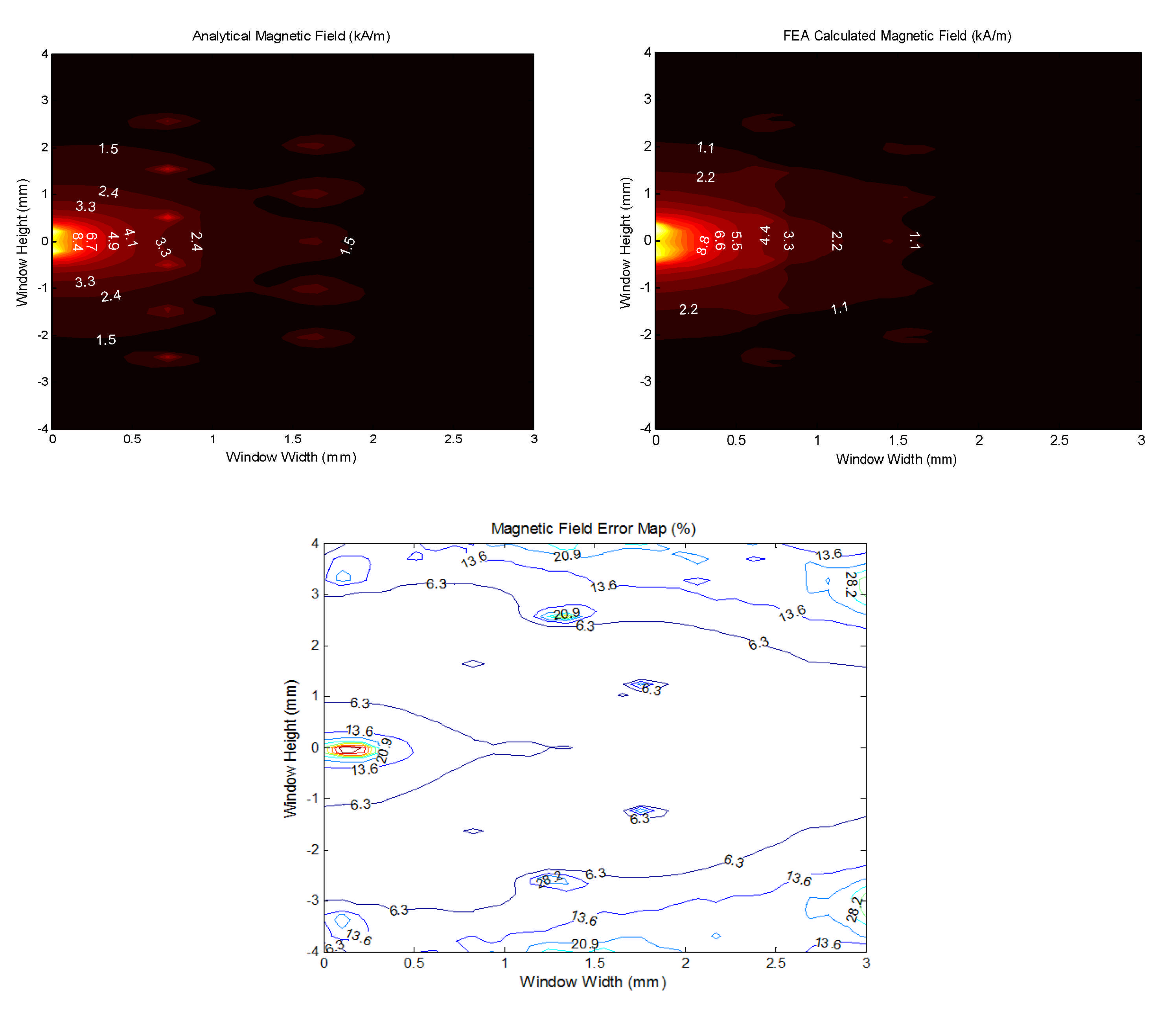




| Case | Conductor Position (mm) | Gap Length (mm) | Calculated Equivalent Resistance (mΩ) | Relative Error at 500 kHz (%) | |
|---|---|---|---|---|---|
| Analytical | FEA | ||||
| A | (0.40, 0) | 0.40 | 5.50 | 5.75 | −4.35 |
| B | (0.80, −0.60) | 0.20 | 3.94 | 4.19 | −5.97 |
| C | (1.30, 1.50) | 0.15 | 4.02 | 4.31 | −6.73 |
| D | (0.80, −2.50) | 0.70 | 3.52 | 4.00 | −12.00 |
| E | (1.80, 0.50) | 0.50 | 4.49 | 4.74 | −5.27 |
| Component | Core Material | Gap Length (mm) | Turns/Parallel | |
|---|---|---|---|---|
| Primary | Secondary | |||
| T1 | RM8/I 3F3 | 0.40 | 20/1 AWG23 | 3/3 AWG23 |
| T2 | RM8/I 3F3 | 0.72 | 26/1 AWG25 | 4/3 AWG25 |
| T3 | RM10 N41 | 0.44 | 12/1 AWG23 | 2/3 AWG19 |
| DUT | Duty Cycle (%) | INPUT | OUTPUT | Temperature (°C) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Voltage (V) | Current (A) | Voltage (V) | Current * (A) | MOSFET | DIODE | R Snubber | D Snubber | ||
| T1 | 50 | 40.45 | 0.80 | 1.75 | 3.09 | 113.2 | 61.0 | 104.4 | 46.8 |
| 50 | 28.30 | 0.60 | 1.26 | 2.23 | 56.5 | 52.8 | 70.7 | 39.4 | |
| 15 | 48.15 | 0.06 | 1.16 | 0.52 | 32.0 | 34.1 | 37.3 | 31.8 | |
| T2 | 50 | 39.20 | 0.79 | 2.20 | 2.86 | 99.0 | 59.0 | 98.8 | 43.9 |
| 50 | 27.11 | 0.58 | 1.56 | 2.03 | 53.7 | 51.0 | 65.4 | 38.6 | |
| 15 | 48.20 | 0.06 | 1.22 | 0.56 | 31.0 | 34.0 | 36.5 | 30.6 | |
| T3 | 50 | 28.00 | 0.78 | 1.10 | 1.95 | 141.8 | 50.2 | 77.7 | 38.2 |
| 15 | 48.13 | 0.11 | 0.86 | 1.02 | 33.8 | 39.2 | 45.2 | 31.5 | |
| DUT | Input Power (W) | Output Power (W) | Clamping Loss (W) | MOSFET Loss (W) | Diode Loss (W) | Calculated Core Loss (W) | Measured Winding Loss (W) | Calculated Winding Loss (W) Proposed Skin Depth | |
|---|---|---|---|---|---|---|---|---|---|
| T1 | 32.36 | 5.41 | 14.77 | 5.88 | 1.29 | 4.40 | 0.62 | 0.60 | 0.18 |
| 16.98 | 2.81 | 7.63 | 1.85 | 0.85 | 3.48 | 0.37 | 0.32 | 0.10 | |
| 2.70 | 0.60 | 1.49 | 0.12 | 0.16 | 0.29 | 0.03 | 0.03 | 0.01 | |
| T2 | 30.97 | 6.29 | 14.64 | 4.89 | 1.18 | 2.92 | 1.04 | 1.03 | 0.32 |
| 15.72 | 3.17 | 7.54 | 1.59 | 0.94 | 1.93 | 0.56 | 0.54 | 0.18 | |
| 2.84 | 0.69 | 1.49 | 0.10 | 0.16 | 0.35 | 0.07 | 0.06 | 0.01 | |
| T3 | 21.84 | 2.15 | 9.53 | 8.03 | 0.83 | 0.71 | 0.59 | 0.56 | 0.09 |
| 5.44 | 0.88 | 2.99 | 0.18 | 0.37 | 0.88 | 0.13 | 0.13 | 0.02 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holguín, F.A.; Prieto, R.; Asensi, R.; Cobos, J.A. Analytical Winding Power Loss Calculation in Gapped Magnetic Components. Electronics 2021, 10, 1683. https://doi.org/10.3390/electronics10141683
Holguín FA, Prieto R, Asensi R, Cobos JA. Analytical Winding Power Loss Calculation in Gapped Magnetic Components. Electronics. 2021; 10(14):1683. https://doi.org/10.3390/electronics10141683
Chicago/Turabian StyleHolguín, Fermín A., Roberto Prieto, Rafael Asensi, and José A. Cobos. 2021. "Analytical Winding Power Loss Calculation in Gapped Magnetic Components" Electronics 10, no. 14: 1683. https://doi.org/10.3390/electronics10141683
APA StyleHolguín, F. A., Prieto, R., Asensi, R., & Cobos, J. A. (2021). Analytical Winding Power Loss Calculation in Gapped Magnetic Components. Electronics, 10(14), 1683. https://doi.org/10.3390/electronics10141683






