Digital Image Watermarking Processor Based on Deep Learning

Abstract

Much research and development have been made to implement deep neural networks for various purposes with hardware. We implement the deep learning algorithm with a dedicated processor. Watermarking technology for ultra-high resolution digital images and videos needs to be implemented in hardware for real-time or high-speed operation. We propose an optimization methodology to implement a deep learning-based watermarking algorithm in hardware. The proposed optimization methodology includes algorithm and memory optimization. Next, we analyze a fixed-point number system suitable for implementing neural networks as hardware for watermarking. Using these, a hardware structure of a dedicated processor for watermarking based on deep learning technology is proposed and implemented as an application-specific integrated circuit (ASIC).

1. Introduction

Until recently, watermark embedding for most 2D images has been algorithmically performed, and watermark extracting has been proposed according to the embedding process or by modifying it [1,2,3,4,5,6,7]. In general, watermarking is subject to non-malicious and malicious attacks. Deliberately damaging or removing watermark information is called a malicious attack, and image processing to store or distribute content is called a non-malicious attack. Watermark embedding can be performed algorithmic or deterministic, but watermark extracting is not. An image signal that has already been attacked may not be a signal predicted when an algorithmic extracting method is devised. Therefore, it may not be possible to extract the embedding watermark by the deterministic extracting method. To overcome such difficulties, techniques for watermarking using machine learning have been studied [8,9,10,11,12,13,14]. These methods are also performed as a network by separating the embedding process and the extracting process.

Research on watermarking techniques using deep learning is still in the beginning stage. Although not many studies exist, it can be seen that the number has been increasing in recent years. Previous studies mainly use convolutional neural network (CNN), autoencoder (AE), and generative adversarial network (GAN), which are widely used in deep learning. We will look at the features of the previous studies in detail in the next Section [8,9,10,11,12,13,14,15]. A lot of research has been conducted to implement a watermarking algorithm in hardware for various purposes [16,17,18,19,20,21,22,23,24]. It is mainly targeting field programmable gate arrays (FPGAs), and recently, studies based on graphic processing units (GPUs) have also been conducted. Looking at previous studies, it is difficult to find a case where a deep learning-based watermarking algorithm is implemented in hardware. Considering the recent trend in which neural processing units (NPUs) are embedded inside various system on chip (SoC), it can be predicted that the hardware implementation of deep learning-based watermarking algorithms will be expanded.

In this study, we design and implement a watermark embedder to the ASIC for embedding a user-selected watermark with high-speed. For this, we propose an optimization methodology for arithmetic and bus after applying the fixed-point simulation for implementing hardware. We propose a new hardware architecture for the efficient operation of watermarking and implement it to hardware. We verify that the implemented hardware can operate with high speed by analyzing the watermarking processor.

This paper consists as follows. Section 2 introduces the related work for the deep learning-based watermarking and the hardware implementation of watermarking. Section 3 explains the deep learning-based watermarking algorithm, which was previously proposed by our team. In Section 4, we propose an optimization methodology for developing hardware and propose a hardware structure. In Section 5, we show the experimental result and conclude the paper in Section 6.

2. Related Work

In this section, we analyze previous studies in the two fields that underlie our research. First, we review watermarking techniques using deep learning [8,9,10,11,12,13,14,15], which includes a study that we previously published, providing a deep learning-based watermarking algorithm in this paper [15]. Next, we review the studies that implemented the watermarking algorithm in hardware. However, when analyzing previous studies, it can be confirmed that there is no case of implementing a deep learning-based watermarking algorithm in hardware [16,17,18,19,20,21,22,23,24].

J. Zhu et al. proposed the steganalysis network and added an adversarial loss between a host image and a watermarking image to the loss function of the watermarking network [9]. M. Ahmadi et al. proposed a watermark embedding and extracting method with the DCT and inverse DCT layer which have the pre-trained and fixed weight in the frequency domain [10]. S. M. Mun et al. used an AE that consisted of the residual block for watermarking [11]. X. Zhong et al. used the invariance layer for removing the effect of attack and proposed a new modeling method for attack simulation using the Frobenius norm in loss function [12]. Bingyang et al. used the same network as J. Zhu’s, but they replaced the fixed attack simulation with the adaptive attack simulation [13]. Y. Liu et al. propose a new two-stage training method that re-trains the extractor with adding attack simulation after training the whole network without attack simulation [14].

The most machine learning-based methods are blind watermarking [9,10,11,12,13,14], use spatial data rather than frequency data [8,9,11,12,13,14], and limitedly use both host and watermark data [9,10,11,12,13,14,15]. In using the specified watermark for training data, new training is inevitable when a new watermark is used. They have a problem that the host image is fixed using a fully-connected layer [9,13,14] or that there is no universality because they did not execute the experiment using various resolutions [10,11,12]. Among them, some methods did not develop a trade-off relationship between invisibility and robustness [8,9,12,13]. Our research team proposed a new universal and practical watermarking algorithm that embeds a watermark without additional training. It proved high invisibility and robustness against various pixel-value and geometric attacks from versatile experiments [15].

Although it might be easier to implement a watermarking algorithm on a software platform, there is a strong motivation for a move toward hardware implementation. The hardware implementation offers several distinct advantages over the software implementation in terms of low power consumption, less area usage, and reliability. It features real time capabilities and compact implementations [16]. In consumer electronic devices, a hardware watermarking solution is often more economical because adding the watermark component only takes up a small dedicated area of silicon. Several hardware implemented watermarking techniques in various domains have been proposed. There are several proposed techniques to implement hardware watermarking, which involve the use of Very Large Scale Integration (VLSI), hash function, or FPGA. Mohanty et al. presented a Field Programmable Gate Array (FPGA) based implementation of an invisible spatial domain watermarking encoder [17]. Another attempt by Mohanty and others is to provide a VLSI implementation of invisible digital watermarking algorithms towards the development of secure JPEG encoder [18]. Several attempts have been made to develop digital cameras with watermarking capabilities. The important research has been done in developing algorithms for watermarking and encryption with the aim of using them in digital cameras by Friedman et al. [19]. Adamoand et al. used VLSI architecture along with FGPA prototype of digital camera for the purpose of image security and authentication [20]. Adamo et al. proposed a chip for the secure digital camera using the DCT-based visible watermarking algorithm [21]. Mathai et al. proposed a real time video watermarking scheme, called Just another Watermarking System (JAWS) [22]. Mohanty at al. in [23] proposed a new generation of GPU architecture with watermarking co-processor to enable the GPU to watermark multimedia elements, like images, efficiently. A hierarchical watermarking scheme is proposed using IC design to independently process multiple abstraction levels present in a design [24]. When observing the results researched until recently, there is still no case of implementing watermarking hardware based on deep learning. We intend to optimize the deep learning-based watermarking we recently developed [15] and implement it in hardware. Therefore, we try to show the first case of watermarking hardware based on deep learning.

3. Deep Learning-Based Watermarking

We studied an algorithm that effectively executes watermarking using deep learning. Based on this algorithm, we propose a new dedicated processor for watermarking. This section introduces the deep learning-based watermarking algorithm [15] and then proposes the optimization methodology in the next section.

3.1. Network Structure

The structure of the digital watermarking network is shown in Figure 1. It consists of four sub-networks; host image pre-processing, watermark pre-processing, embedding, and extraction networks. The attack simulation is also in the network, and this is not a neural network, but a signal processing. The host image pre-processing consists of a convolution layer with 64 filters, which maintains the original resolution of the host image and has 1 stride step.

3.2. Network Operation

The watermark pre-processing network is configured to gradually increase the resolution to match the host image pre-processing network’s resolution. It is to increase the watermark invisibility. Our experiments have confirmed that the case maintaining the resolution of the host image in watermark embedding has high watermark invisibility than the case reducing the resolution to that of the watermark and increasing the resolution to output the watermarked image. This network includes four network blocks: the first three consist of the convolution layer (CL), batch normalization (BN), activation function (AF), and average pooling (AP), but the last block consists of CL and AP. All CLs have a 0.5 stride for up-sampling. The corresponding number of filters is 512, 256, 128, and 1, respectively. AF is the rectified linear unit (ReLU), and AP is a 2 × 2 filter with a stride of 1. The watermark pre-processing network output is multiplied by the strength scaling factor to control the invisibility and robustness of the WM.

The watermark embedding network concatenates the 64 channels of the pre-processed host information and one channel of the pre-processed watermark information and uses them as the input to output the watermarked image information. The network consists of CL-BN-AF (ReLU) for the front four blocks, and the last block consists of CL-AF (tanh). The tanh activation maintains the positive and negative values to meet the data range of [−1, 1] to the input host information. Because we are aiming for invisible watermarking, we use the mean square error (MSE) between the watermarked image ($I_{WMed}$) and the host image ($I_{host}$) as a loss function ($L_1$) of the pre-processing network and the embedded network. This is shown in Equation (1). Here, M × N is the resolution of the host image [15].

$$L_1=\frac{1}{MN}\sum _{i,j}^{MN}{[I_{host}(i,j)-I_{WMed}(i,j)]}^2$$

(1)

The extraction network consists of three CL-BN-AF (ReLU) blocks and one CL-AF (tanh) block, which is the last block. We set the stride of all CLs to 2 for down-sampling. The number of filters used in the CLs is 128, 256, 512, and 1, respectively. This network uses mean absolute error (MAE) between the extracted WM ($W{M}_{ext}$) and the original WM ($W{M}_0$) as a loss function ($L_2$) as shown in Equation (2), where X × Y is the resolution of a watermark [15].

$$L_2=\frac{1}{XY}\sum _{i,j}^{XY}|W{M}_o(i,j)-W{M}_{ext}(i,j)|$$

(2)

The loss function $L_{emb}$ for the watermark embedding consists of $L_1$ for the embedding network and $L_2$ for the extracting in Equation (3). On the other hand, the loss function $L_{ext}$ for the extracting consists of only $L_1$ in Equation (4).

$$L_{emb}={\lambda }_1{L}_1+{\lambda }_2{L}_2$$

(3)

$$L_{ext}={\lambda }_3{L}_2$$

(4)

In Equations (3) and (4), ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$ are hyper-parameter of the neural network which control both invisibility and robustness.

For high robustness, the watermarked image is intentionally suffered from preset attacks in the attack simulation.

Table 1. Attacks used in training.

Attack Type	Attack	Strength	Ratio
No attack	Identity	-	1/12
Pixel-value change attack	Gaussian filtering	3 × 3, 5 × 5, 7 × 7, 9 × 9	2/12
	Average filtering	3 × 3, 5 × 5	2/12
	Median filtering	3 × 3, 5 × 5	1/12
	Salt & Pepper	P = 0.1	0.5/12
	Gaussian noise	Sigma = 0.1	0.5/12
	Sharpening	5-point stencil, 9-point stencil	1/12
	JPEG	Quality factor = 50	1/12
Geometric attack	Rotation	0∼90° (random)	1/12
	Crop	0.5∼0.8 (random)	1/12
	Dropout	0.3∼0.9 (random)	1/12

shows the types, strengths, and the ratio of each attack used in one mini-batch in training [9,10].

In this paper, the deep learning-based watermarking algorithm proposed in our previous study [15] is used. The robustness of this watermarking algorithm is summarized in

Table 2. Performance analysis of the deep learning-based watermarking.

Attack	Strength	Proposed (BER)	Proposed (VIF)
No attack		40.58 [dB]	0.7350
	-	0.7015
Gaussian filtering	radius = 1	7.1429	0.0359
	radius = 1.6	9.7258	0.0462
	radius = 2	12.7232	0.0323
Median filtering	3 × 3	8.4184	0.7680
	5 × 5	10.5548	0.9639
Salt and pepper noise addition	0.02	1.0204	0.1760
	0.6	1.5306	0.1283
	0.1	3.1888	0.0832
Gaussian noise addition	5%	5.9949	0.2136
	15%	27	0.0393
	25%	38.1696	0.0311
Sharpening	radius = 1	0.9885	0.1720
	radius = 5	1.7217	0.0680
	radius = 10	2.0089	0.0666
JPEG	90	0.9566	1.000
	70	4.24	1.000
	50	8.0676	0.7951
Cropout	0.1	2.1365	1.0000
	0.2	5.3253	0.8056
	0.3	8.6735	0.5746

[15]. The result of Table 2 is a case where the quality of the watermark-embedded image is 40.58 dB (BER:0.7015, VIF [25]: 0.7350). The quality of the image was chosen for comparison with the latest similar study, ReDMark [10]. Compared with ReDMark, it showed excellent attack robustness in most cases. Table 2 shows the quality of the watermark extracted from the watermark-embedded image in terms of BER (bit error rate) and VIF (visual information fidelity).

4. Watermarking Processor

In this section, we develop hardware for digital watermarking based on deep learning. Hardware implementation is for high-speed operation or high performance. Since the extracting does not need a high-speed operation, the embedding is only implemented to hardware.

We propose an optimization method to implement a deep learning-based watermarking algorithm in hardware. The optimizations that we propose include computational optimization for batch normalization and memory optimization using shared memory. That is, the optimization step corresponds to the process of reconfiguring the S/W-based algorithm for hardware implementation. When a modified algorithm is obtained through this process, the hardware is designed using this algorithm. These two optimization techniques are at the core of what we are proposing.

We consider the operation information of the hardware and modify the operation method of the algorithm for the software to be suitable for the operation of the hardware. We define this process as an optimization process. Since we use a watermarking algorithm based on deep learning, we optimize the operation method of the neural network for deep learning according to the hardware implementation and operation. Since the deep neural network for our watermarking algorithm is a CNN-based network, we propose an optimization technique for hardware implementation by analyzing the calculation and operation of CNN. CNN operation requires a lot of memory resources and the number of memory accesses. This is not a big problem when it is a software operation, but when implemented in hardware, it greatly affects the operation of the hardware due to a memory bottleneck. Therefore, we propose a memory access optimization technique to alleviate the memory access bottleneck.

4.1. Optimization Methodology

For improving hardware performance, we propose an optimization for deep learning to minimize the amount of calculation and the number of memory access. The convolution arithmetic consists of multiplication of input feature map (IFM) $I_{i,j}$ and the weight $W_{i,j}$ and addition of the multiplication result and the bias B. The convolution formula is defined as Equation (5), where A × B is the resolution of the weight.

$$O_C=\sum _{i,j}^{AB}{I}_{i,j}\times W_{i,j}+b$$

(5)

The batch normalization has four kinds of parameters; data average $\mu$, standard deviation $\sigma$, and trained parameters $\gamma$ and $\beta$. The formular is defined as Equation (6). $O_B$ corresponds the batch normalized result of $O_C$.

$$O_B=\frac{O_C-\mu }{\sigma }\times \gamma +\beta$$

(6)

Since the batch normalization requires a large number of parameters, it has a large number of memory accesses and high calculating cost by division. For optimizing the batch normalization, we try to analyze the arithmetic of the convolution and batch normalization. Equation (7) is the reconfigured version of the combined result of Equations (5) and (6). Through Equation (7), we can find that both convolution and batch normalization are calculated using only the convolution without any other calculation for batch normalization. This method seems to be a kind of efficient optimization because it excessively reduces the number of memory access and the calculation cost. In Equation (7), $W^{\prime }$ is the modified weight and ${\alpha }^{\prime }$ is the modified bias.

$$\begin{array}{cc}\hfill O_B& =\frac{\gamma }{\sigma }\times O_C-\frac{\gamma }{\sigma }\times \mu +\beta \hfill \\ \hfill & =\frac{\gamma }{\sigma }\times \left(\sum _{i,j}^{AB}{I}_{i,j}\times W_{i,j}+b\right)-\frac{\gamma }{\sigma }\times \mu +\beta \hfill \\ \hfill & =\sum _{i,j}^{AB}{I}_{i,j}\times (\frac{\gamma }{\sigma }\times W_{i,j})+\frac{\gamma }{\sigma }\times b-\frac{\gamma }{\sigma }\times \mu +\beta \hfill \\ \hfill & =\sum _{i,j}^{AB}{I}_{i,j}\times W_{i,j}^{\prime }+{\alpha }^{\prime }\hfill \\ \hfill & =O_C^{\prime }+{\alpha }^{\prime }\hfill \end{array}$$

(7)

Table 3. Calculation after and before algorithm optimization.

Arithmetic Unit	Before Optimization	After Optimization
Multiplier (2-input)	2,499,035,136	2,493,775,872
Adder (9-input)	277,086,208	277,086,208
Adder (4-input)	69,271,552	69,271,552
Adder (2-input)	15,777,792	5,259,264
Divider (2-input)	5,259,264	0

shows the comparison result before and after optimization. After optimization, the 2-input adder is reduced to about 30%, and the divider is no longer required.

After the algorithm performs optimization on the number of operations of the operator, we perform optimization on the amount of memory access. We propose a method to reduce the number of memory accesses of repeatedly used weights. Whenever weights are used, they are not fetched from external memory but stored in shared internal memory and reused. We increase the reuse rate and reduced the number of memory accesses by reusing the input feature map for each row of the image. The amount of memory access due to Equation (7) is compared in

Table 4. Memory access after and before algorithm optimization, after memory optimization.

Parameter	Before Optimization	After Algorithm Optimization	After Memory Optimization
W/$W^{\prime }$	2,444,230,656	149,184
B/${\alpha }^{\prime }$	5,259,264	5,259,264	321
$\mu$	5,259,264	0	0
$\sigma$	5,259,264	0	0
$\gamma$	5,259,264	0	0
$\beta$	5,259,264	0	0
IFM	48,976,200	48,976,200	5,441,800
Out	5,259,264	5,259,264	5,259,264
Total Memory Access	2,524,762,440	2,503,725,384	10,850,569

. It can be seen that before and after algorithm optimization, it is decreased by about 21 × ${10}^6$ times, and before and after memory optimization, it is decreased by about 2492 × ${10}^6$ times.

In addition, the maximum and minimum values of IFM before optimization changed from 41.95 and −57.22 to 22.54 and −21.58 after optimization. This fact makes it possible to use less hardware resources in the process of analyzing the number system, which will be explained in the next section.

4.2. Fixed-Point Number System

Unlike other signal processing techniques, some variables to be processed in an equation have very different value ranges such that a variable has almost no fractional part and a large integer part. Still, another variable has almost no integer part and only has many digits of a fractional part. Such calculation dramatically increases the size of the computing element and decreases the calculation efficiency. Therefore, before implementing the hardware, the number range and precision for the intermediate calculations must be analyzed, and the bit-width (size of the bus) adequately adjusted.

For a software implementation, the calculation error seldomly occurs or is trivial if it happens because the calculation is usually carried out with high precision. However, there must be precision limits for hardware implementation due to the limitations in the hardware resources. Let us consider a case in which two operators with both integer part and fraction part are multiplied, but we only need the fractional part of the result to calculate the argument of the cosine function in the CGH calculation. An example of a fixed-point simulation for such a case is shown in Figure 2, in which three partial products are generated. The desired result can be obtained by adding all these partial products. In the fixed-point simulation, the result is checked as increasing the number of bits for the integer and fractional parts in executing. Note that each bit increased for the integer and fractional parts increase the precision twice as before. In our experiment, the number of bits was increased until the fixed-point simulation, and the software execution results are the same.

As the method to check if the two results are the same, we used both numerical analysis and visual analysis for both the calculated digital hologram and the restored object. The peak signal-to-noise ratio (PSNR) value and the error rate are used as the numerical analysis. We divide the data into four types: weight, IFM, partial sum, and tanh.

4.3. Hardware Structure

Figure 3 shows the top structure, including the host and watermark image pre-processing network and the embedding network. The structure is divided into the datapath part and the control part. The datapath part includes the memory buffer, the input interface, the convolution block (CONV), the post-processing block (POST), the output buffer, and the SRAM. The memory buffer receives and sends the data for calculation from and to the external memory. The input interface inputs the data to the internal blocks such as the convolution and the post-processing blocks. The post-processing block calculates the activation function. The control part includes the SRAM controller for the SRAM and the main controller for controlling the operation of the datapath part.

In Figure 3, the solid line represents the flow of the control signal, and the dotted line represents the data flow. The signal from the main controller is used as an input to all blocks except SRAM, which means that all blocks are executed under the control of the main controller. Data input from the external memory is transferred to the memory buffer under the control of the main controller. The input interface transfers data to registers in the convolution block and post-processing block according to the timing of the operation. In convolution and post-processing operations, the input data map and filter data are repeatedly reused. The main controller controls the signal to prioritize the reuse of filter data over the input feature map.

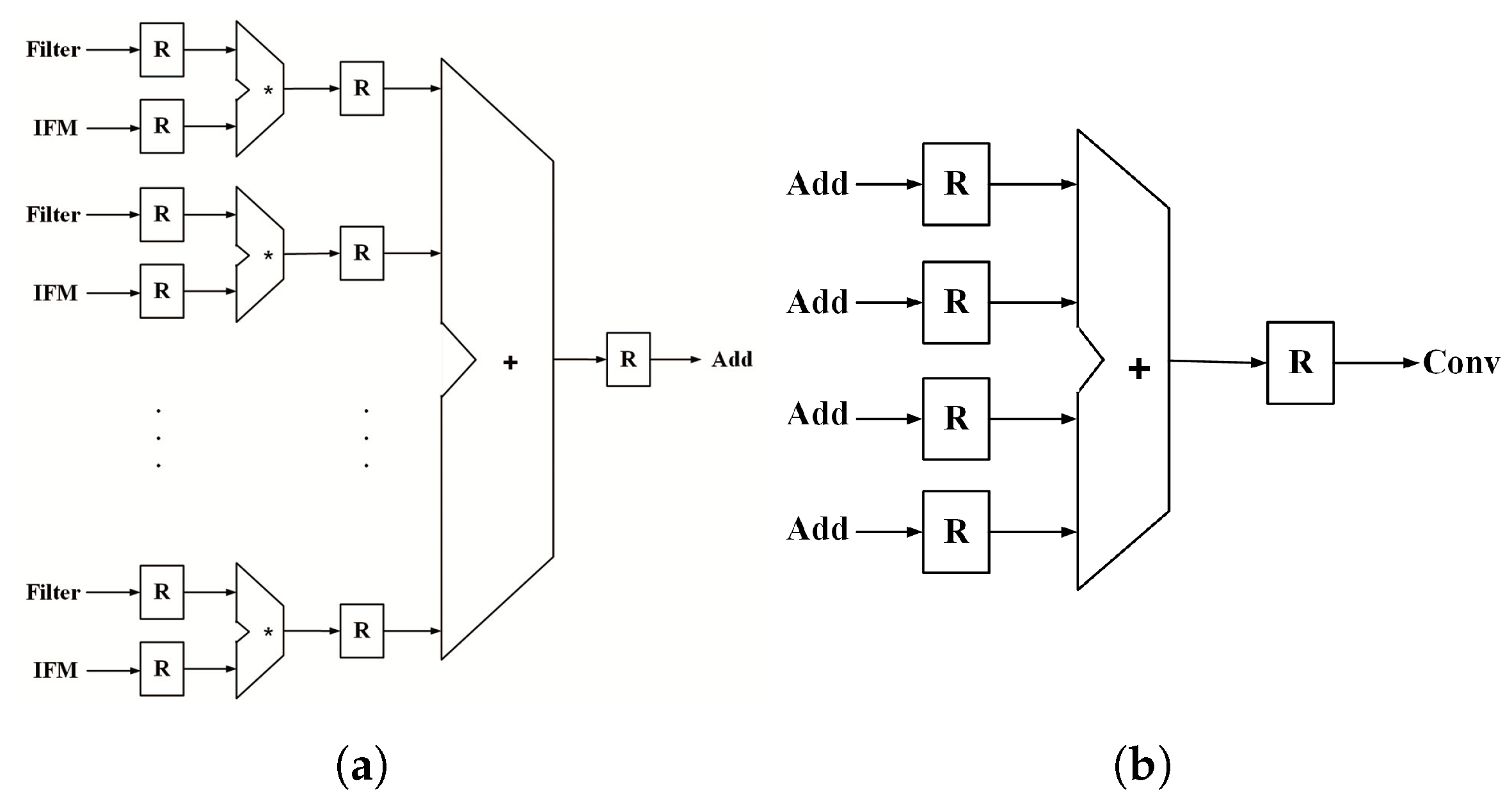
The convolution block is shown in detail in Figure 4. All convolution layers use a 3 × 3 filter, and the number of channels varies according to the convolution block. Considering the amount of hardware, we design the hardware for the 4-channel operation that can be calculated by dividing the number of channels in each block. It has a structure consisting of 4 units of one channel convolution operator (Figure 4a) that performs 3 × 3 multiplication and accumulation. Next, it consists of an adder (Figure 4b) that adds all four outputs (Add). The convolution operation of each block controls the number of operations by using information about the block in the main controller. The result of the convolutional block (Conv) is stored in the SRAM for addition with the additional channel operation or is added with the data output from the SRAM. The data on which all convolution operations have been completed is transferred to the post-processing block.

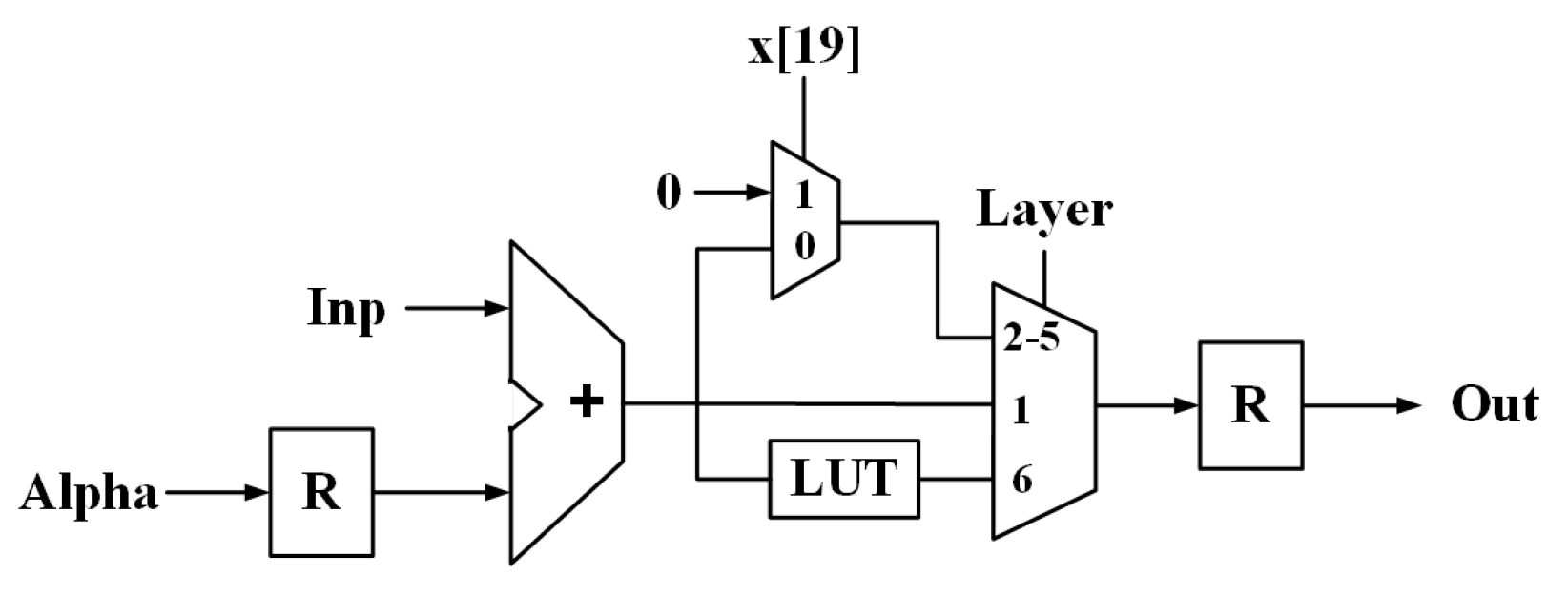
The structure of the post-processing block is shown in Figure 5. The input of this block is added with the modified bias stored in the alpha register. The addition result is output through the activation function (MUX) to the output buffer. The activation function operates in variety according to the operating layer. The first layer does not use the activation function, so the input is directly output without any calculation. The second to fifth layers execute the activation function in which the ReLU is used, and the ReLU is designed as the MUX. If the most significant bit is one, the MUX outputs the input. Otherwise, the MUX outputs the zero value. The sixth layer uses the tanh function as activation. The other calculations are covered with the multiplication and addition, but the tanh activation function requires the complicated exponential function and division operation. The hardware implementation of them needs large hardware resources and calculation amount. Therefore we replace the complex and large logic with the look-up table (LUT). The size of the LUT is 256 because the bitwidth is eight, including the sign bit.

5. Experimental Results

5.1. Experimental Environment

Hyperparameters used in the experiment are shown in

Table 5. The values of the hyper-parameters for the experiment.

Hyper-Parameter	Value
Total number of epochs for training	4000
Number of host images in a mini-batch	100
Optimization technique	Adam
${\lambda }_1$	45
${\lambda }_2$	0.2
${\lambda }_3$	20
Learning rate of the embedding network	0.0001
Learning rate of the extraction network	0.00001
Strength factor s	1
Weight decay rate	0.01

, and these are all values obtained from experimental results. Since each parameter does not independently affect the neural network but is interdependent, it is obtained through hyperparameter optimization. In learning, the unit of mini-batch is 100. After observing the output of the loss function for each epoch, training was performed until this value was saturated. In our experiment, it took about 4000 epochs to train the network. Adam optimization method, including momentum loss [15], was used, and learning rate decay was applied. The value of ${\lambda }_1$ is three times larger than ${\lambda }_3$. This is because $L_1$ is much larger than $L_2$. If $L_2$ has larger value, invisibility become to be superior than robustness. The opposite condition holds as well. If $L_2$ has a one-sided value, the embedding and the extracting network do not be trained. The experimental hyper-parameters are shown in Table 5.

We propose an optimization method to implement a deep learning-based watermarking algorithm in hardware. The optimizations that we propose include computational optimization for batch normalization and memory optimization using shared memory. That is, the optimization step corresponds to the process of reconfiguring the S/W-based algorithm for hardware implementation. When a modified algorithm is obtained through this process, the hardware is designed using this algorithm. These two optimization techniques are at the core of what we are proposing.

5.2. Robustness

The comparison result with the previous networks (HiDDeN [9] and ReDMark [10]) is shown in

Table 6. Comparison with the recent researches for 2D images.

Attack	Strength	[9]	[10]	Proposed (s = 2.75)
PSNR		-	-	33.5
JPEG	50	37	25.4	0.6696
Cropout	0.3	6	7.5	5.8355
Dropout	0.3	7	8	4.7194
Crop	0.035	12	0	44.1327
Gaussian filtering	$\sigma$ = 2	4	50	4.3048

. s is set to 2.75 to adjust the PSNR of the watermarked image to 33.5 dB. As a result, our network has better results except for the cropping attack than [9,10]. The value of 0.035 for the cropping attack means that the ratio of the attacked area is 3.5%. In this result, our network shows good performance, except for the Gaussian noise addition and the high rate cropping.

5.3. Bitwidth Optimization

For weighted fixed-point analysis, IFM, partial sum, and tanh results are set in floating-point format. Since the maximum absolute value of the weight is 12.3842, a maximum of 4 bits is required for an integer part. We performed experiments on 3-bit and 4-bit integer part. The decimal part changes from 1 bit to 27 bits and measures the performance of the PSNR (left) and the BER (right). The results are shown in Figure 6. The x-axis is the total number of bits of the weight and is the sum of the number of sign bit, integer part, and decimal part. The performance changes of both results show the same trend. When the decimal part is 3 bits, it can be seen that the PSNR rapidly decreases to 5 dB, and in most cases, the PSNR increases linearly. When the decimal part is 1 bit and 2 bits, the BER is very large at 57%, and when the decimal part is 3 bits, it decreases rapidly. The BER rises from 4 bits to 6 bits, and saturation starts from 7 bits. Therefore, we selected the weight bit as 16 bits (sign 1 bit, integer 4 bits, decimal 11 bits).

For analyzing the fixed-point number of the IFM, we fixed the weight bit to 4 bits. The partial sum and the tanh result were selected as the floating-point number. Since the maximum absolute value of the IFM is 22.54, the bit width of the integer part is required as the bit width of 5 bits as maximum. Therefore we simulated with 4 and 5 bits as the integer part. The bit width of the decimal number changes from 1 to 27 bits. When the integer part of the IFM is 5 bits, the decimal part ranges from 2 to 27 bits for the weight and from 1 to 26 bits for the IFM. When the integer part of the IFM is 4 bits, the decimal part of them ranges from 1 bit to 26 bits. The experimental results are shown in Figure 7. The graphs have a similar trend of the case of the weight in Figure 6. The PSNR rapidly increases to 6 bits of the decimal number, and saturation starts from 7 bits.

Considering the performance of the network in terms of hardware, the bitwidth of the weight and IFM were decided as the 16 bits (1 sign bit, 4 integer bits, 11 decimal bits). After fixing the bitwidth of the weight and IFM, the fixed-point simulation was performed to decide the bitwidth of the partial sum. Since the maximum value of the tanh is 22.02, the integer part requires 5 bits at least. Having two cases of 4 and 5 bits for the integer part, the analysis was performed while increasing the bitwidth of the decimal part from 1 bit to 27 bits. The result is shown in Figure 8. In the case of the 4 bits of the integer part, the BER is saturated at over 15 bits of the entire bitwidth. It can be seen that the decimal part directly affects the performance of the partial sum. In the case of 20 bits, it can be seen that the PSNR is about 1 dB higher and the BER is about 0.03% lower than the case of 5 bits in the case of 4 bits of the integer part.

The fixed-point simulation of the tanh was performed by fixing the partial sum to 4 bits for the integer part and 15 bits for the decimal point. Since the tanh outputs a result between −1 and 1, the experiment was performed by increasing the decimal bit from 1 to 31 bits without assigning an integer bit. The results are shown in Figure 9. It can be seen that as the decimal part increases, the PSNR increases and is maintained from 13 bits. When the decimal part is 5 bits, the BER shows the best performance. However, compared to the case of the 7-bit decimal point, since the performance difference is about 0.09%, the 7-bit decimal part was selected.

Table 7. Experimental results of fixed point simulation.

Parameter	Sign Bit	Integer Bits	Fractional Bits	Total
Weight	1	4	11	16
IFM	1	4	11	16
Partial Sum	1	4	15	20
Tanh	1	0	7	8

shows the number system determined by the results of the fixed-point simulation. Considering the maximum value of the IFM and partial sum, it is reasonable to select the integer part as 5 bits, but the difference from the 4 bits of the integer part is 0.000001%, so the effect on performance is negligible. Therefore, to bear this performance degradation and reduce the amount of hardware, 4 bits were selected. As a result of measuring the performance using the selected number system, the PSNR of the host image and the watermarked image was 37.6775 dB. The extraction rate of the watermark extracted from the image without attack was 0.6696%.

5.4. Hardware Implementation Result

The design process was carried out according to the design process of Samsung Electronics, and the design result was manufactured with the MPW (multi-project wafer) of Samsung Electronics 65 nm process. The functional verification was performed using the VCS of Synopsys, and the synthesis was performed using the Design Compiler. When writing the constraint, to use the zero delay model, a 40% margin was added to the target frequency of 75 MHz, and a clock was generated and synthesized at 125 MHz. The front-end design was completed by checking whether the result after synthesis matches the design before synthesis through the Equivalence Check, then static timing analysis (Pre-Layout STA) before layout step was performed and confirmed through simulation. The result of the synthesis is shown in Figure 10. Figure 10a is a schematic of the data path, control unit, and input interface, and Figure 10b is an expanded view of all the schematics.

Table 8. Resource usage of the designed H/W.

Module	Number of Gates	Percentage [%]
Control part	1892	0.23
Data path part	61,792	7.59
Input interface	142,491	17.51
Black boxes	607,502	74.67
Total	813,679	100

shows the resource utilization rate of the implemented H/W. Black boxes represent the used SRAM, occupying the largest area with 74.67%. The input interface occupies 17.51%, the datapath part occupies 7.59%, and the control part occupies 0.23%.

In order to verify the watermarking operation of the result implemented by hardware, we performed a simulation of the implemented hardware using Vivado 18.3. Figure 11 shows the simulation results. In Figure 11a, when the control signal (FR_SS) becomes 1, the weights are sequentially input, and after 36 clocks, the weights are placed in all registers. In Figure 11b, when the control signal (FW_valid) becomes 1, it can be seen that the 2-input multiplication and the 9-input addition of the corresponding weight and IFM are output. In Figure 11c, the results of the 4-input addition, the POST addition, and the tanh function are generated.

Next, the pad was placed in the netlist due to synthesis, and floor planning was performed with the IC Compiler. DPRAM (dual-port DRAM) was used as SRAM, and two 20 K Byte DPRAMs were arranged to fit the required capacity (SRAM1 and SRAM2 in Figure 12). The layout completed up to P&R verifies DRC (Design Rule Check) and LVS (Layout Versus Schematic) using Virtuoso. Through this process, the design process for the ASIC chip was completed. The designed ASIC chip has 66 input ports (1 clock, 1 reset, 64 inputs for data) and 16 output ports as outputs for data. The remaining ports were used as ports for power. The chip area is 1,076,147.3750, and it consists of two 20,480 Bytes DPRAMs (40,960 Bytes total) and 2418 Bytes random logic (see Figure 12). The implemented hardware processor watermarks 128 × 128 images with a performance of about 3 fps at a clock frequency of 200 MHz.

Our deep learning-based watermarking algorithm was implemented using CPU and GPU. Watermarking software based on CPU and GPU (Intel Core i7-9700 CPU @3.00 GHz, NVIDIA GeForce RTX 2080Ti) takes 45 ms for watermark insertion and 13 ms for extraction. In the case of the implemented ASIC-based watermarking processor, it is for the insertion of watermarks, and the extraction uses the same GPU-based software. When the implemented hardware operates with a 200 MHz clock, it takes 333 ms to insert a watermark. In the case of the GPU, it was manufactured in a 12 nm process, operates at 1545 MHz, has 4352 cores, and has very high-performance with a memory bandwidth of 616 Gbps, so it is somewhat difficult to directly compare it with hardware implemented in a 65 nm process. As shown in the fixed-point simulation results, the performance of the software method and the hardware method is almost the same.

6. Conclusions

In this paper, we proposed a hardware dedicated to watermarking that can embed watermarks on digital images and videos at high speed and implement them in the form of ASIC. The deep learning-based watermarking algorithm we previously proposed was used as the basis platform and the algorithm optimization and the memory optimization were applied to the algorithm for software. As a result, the computational amount of the algorithm was reduced by 21 × ${10}^6$ times, and the number of memory accesses decreased by about 2492 × ${10}^6$. Through the number system analysis technique, the precision of 64 bits of the software was optimized to 16, 16, 20, and 8 bits for the weight, the IFM, the partial sum, and the tanh, respectively. Finally, the processor implemented as an ASIC used a silicon area of 1,076,147.3750, and watermarking of 1.05 frames per second is possible based on 75 Mhz. If the operating frequency is increased, a real-time watermarking operation will be sufficiently possible.