Fixed-Point Arithmetic Unit with a Scaling Mechanism for FPGA-Based Embedded Systems

Abstract

The work describes the new architecture of a fixed-point arithmetic unit. It is based on the use of integer arithmetic operations for which the information about the scale of the processed numbers is contained in the binary code of the arithmetic instruction being executed. Therefore, this approach is different from the typical way of implementing fixed-point operations on standard processors. The presented solution is also significantly different from the one used in floating-point arithmetic, as the decision to determine the appropriate scale is made at the stage of compiling the code and not during its execution. As a result, the real-time processing of real numbers is simplified and, therefore, faster. The described method provides a better ratio of the processing efficiency to the complexity of the digital system than other methods. In particular, the advantage of using the described method in FPGA-based embedded control systems should be indicated. Experimental tests on an industrial servo-drive confirm the correctness of the described solution.

1. Introduction

Embedded systems are used in devices that represent a huge market area. These systems are found in almost all of the household appliances around us, in industrial machines and robots, in vehicles, in specialized apparatus used by research laboratories, by the military, factories, hospitals, and in a variety of portable devices, including those for wireless communication. Designing embedded systems is a complex issue as it requires many aspects to be considered. One should mention the need to ensure sufficiently high processing performance, reduce electricity consumption, minimize dimensions, ability to work in difficult environmental conditions, and minimize the cost of production.

In many applications of embedded systems for the implementation of control, modeling or identification systems, the processing efficiency requirements are very high. Additionally, it is necessary to ensure time determinism, i.e., guaranteed reaction time to external events. In some cases, a hardware solution is available on the commercial market, e.g., in the form of application-specific integrated circuits (ASICs) dedicated to specific applications. Typically, ASIC-based solutions provide the required parameters due to embedded hardware signal processing mechanisms. However, the basic disadvantage of these solutions is that it is not possible to change the algorithms built into them in any way. As a result, the development of such systems is impossible.

In many other cases, it is possible to use microcontrollers dedicated to a specific area of application. It is well known that microcontrollers are well suited to the efficient execution of control tasks in their assigned application area [1]. In particular, one should mention the very widespread various digital platforms based on microcontrollers with the ARM Cortex-M core. Programmed in the bare-metal model or using the real-time operating system (RTOS), they are currently the most commonly used hardware platforms for the implementation of various types of control systems [2].

In control systems that require higher computing performance, application processors based on ARM Cortex-A cores are often used. Typically, digital platforms based on such processors are equipped with an operational memory of large capacity and managed by one of the many available distributions of the popular Linux operating system. This approach offers several benefits, such as the ability to use available abstraction layers that support a variety of communication interfaces and storage. In addition, operating systems, such as Linux, offer access to many libraries that are useful for data processing. As a result, it is possible to obtain a functional control system relatively quickly, even in the case of designing advanced algorithms, for example for processing images transmitted from a camera in real-time [3] or for controlling an electric motor [4]. However, it should be pointed out that despite their high performance, the application processors and the Linux operating system do not provide a sufficiently short response time for many demanding applications [5]. One solution to this problem may be the use of heterogeneous, system-on-chip (SoC) type platforms, containing both of the above-mentioned types of processors, i.e., application processors and microcontrollers [6].

Similarly, systems with digital signal processors (DSPs) are widely used in home and professional audiovisual equipment [7]. DSPs, in their versions with various specialized peripherals, are also used for many other signal processing tasks. Such dedicated processors are used e.g., in military and commercial radar systems [8], and in modern wired and wireless communication systems [9].

However, there is one important area of the previously analyzed applications where it is not possible to use commercially available ASIC solutions, while solutions based on microcontrollers, application processors, and signal processors are not efficient enough. One of the reasons may be the implementation of novel algorithms [10,11], for which ASICs are not available. The second reason is the necessity to provide a compact device, e.g., integrating most of the elements of a complex system in one silicon structure. The latter reason is justified by many significant advantages of compact systems. For example, when several separate integrated circuits are used (e.g., application processors, signal processors, microcontrollers, complex communication interfaces, large capacity RAMs, etc.) it is necessary to provide a sufficiently efficient and deterministic communication interface between them. For this, a 16-bit, 32-bit, or even 64-bit parallel data bus is usually required. The necessity to use it complicates the design and increases the cost of such a system. Compact systems, combining all the most important elements in one silicon structure, offer greater reliability, lower electricity consumption, lower cost, and, in many cases, higher efficiency than systems built of many separate ASICs connected on a complex printed circuit board.

In all the cases analyzed above, it is necessary to use solutions that offer both very high efficiency and versatility. These features are provided by field-programmable gate array (FPGA) technology. Although FPGAs usually have a slightly lower allowable clock frequency compared to ASICs, the effective performance of FPGA-based solutions may in many practical cases be higher [11,12]. This is because FPGAs offer the ability to flexibly adjust their hardware structure to implement innovative and non-standard algorithms.

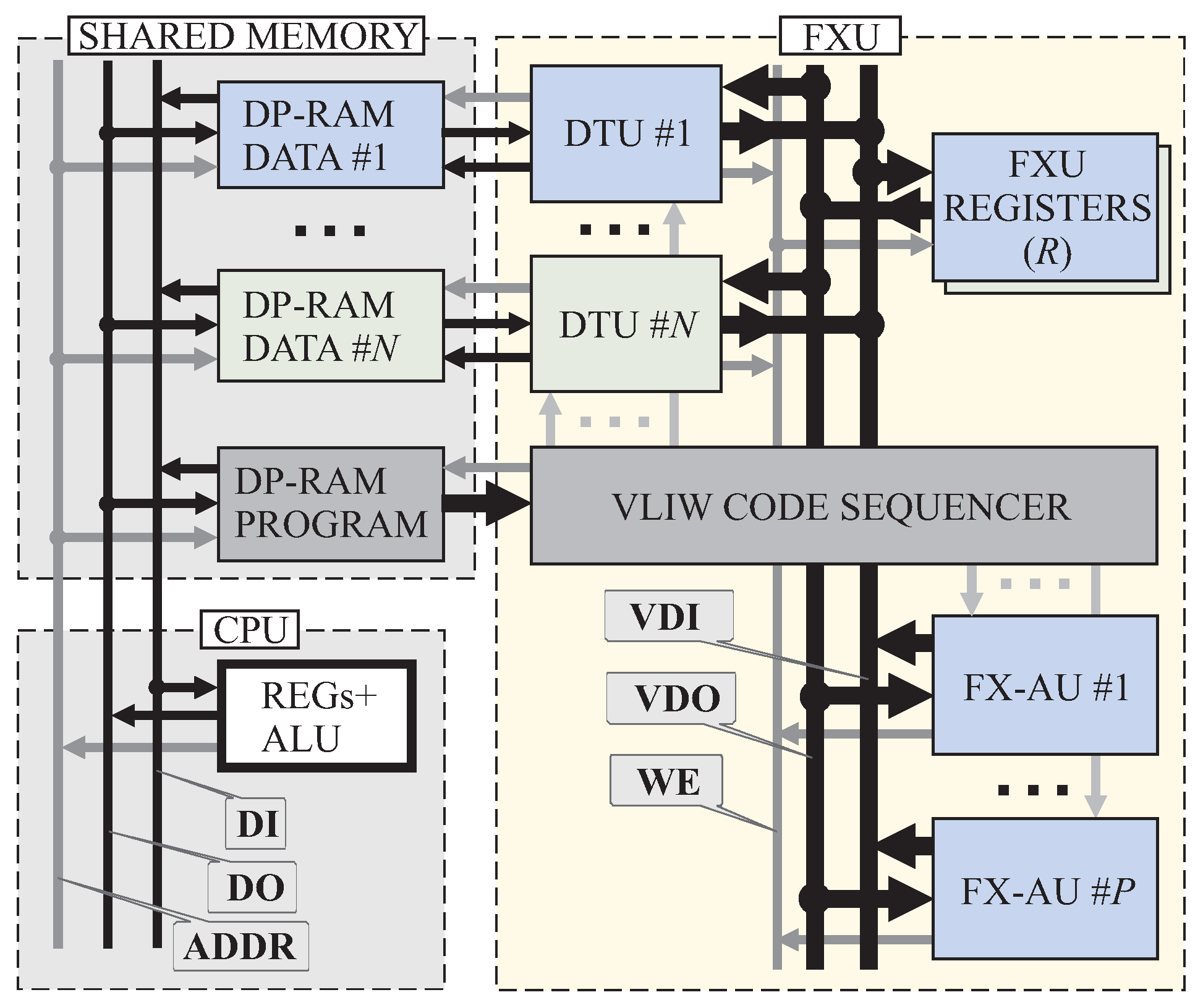
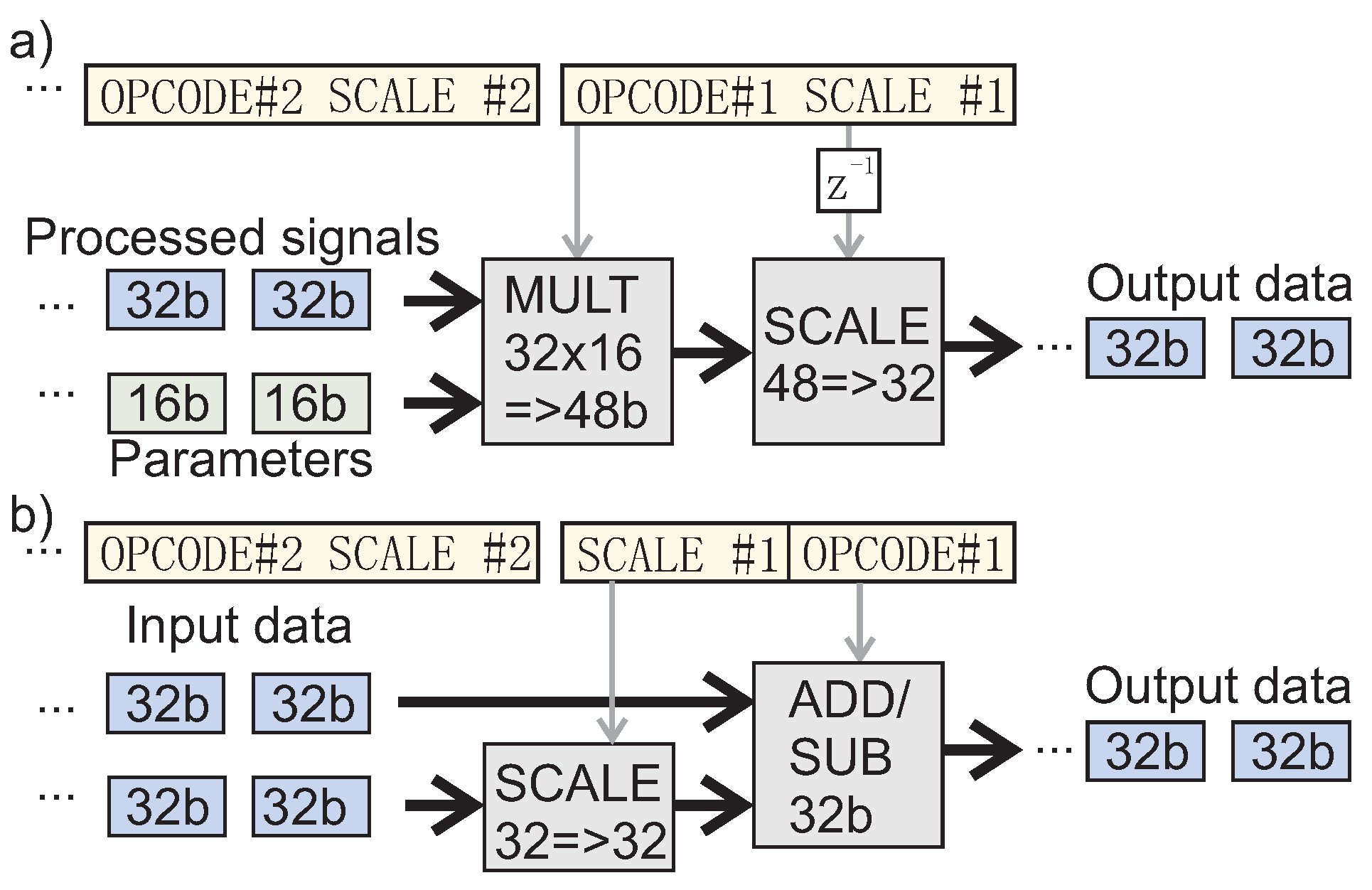
This paper presents the concept of a cooperative superscalar fixed-point processing unit (FXU). Important features of such a unit (which will be described in detail later in this work) are the scalable architecture (Figure 1) and the integrated scaling mechanism for fixed-point operations based on information provided by the software designer (Figure 2). Due to these features, the described solution offers a better ratio of performance to the complexity of the digital system than other similar solutions.

To confirm the correctness of the approach proposed in this paper, the results of the implementation of a certain type of control algorithm on various digital platforms are presented. In particular, these are selected mechanisms of the vector control algorithm for electric drives, which are usually used in high-speed numerical machine tools. It should be noted, however, that the scope of application of the method presented in this paper is much wider and is not limited to this type of algorithms.

The second section of this work presents an analysis of the methods of implementing control algorithms on FPGAs. The third section describes a superscalar coprocessor built based on the fixed-point number processing method proposed in this paper. The experimental research is included in the fourth section, while the conclusions are presented in the fifth section.

2. Different Ways of Algorithms Implementation on FPGA

According to what has been noted in Reference [13], papers involving various techniques for implementations of control algorithms in FPGA may be divided into two groups. The first one applies a conversion from a formal description of a program to a code in a hardware description language (HDL). Much faster execution of hardware-coded programs is the basic advantage of this approach. However, any change of control concept requires a tedious synthesis of the FPGA design. It should be noted that various design environments facilitate the design of the system based on the FHD method. For example, Matlab-Simulink software allows for automatic generation of an HDL code based on the algorithm presented in the form of a [14] block diagram. As a result, the convenience of the design process is much better than in the case of manual HDL code generation. However, the design process remains lengthy as a complete synthesis of the FPGA structure must be performed with each change.

The second approach, according to the classification presented in Reference [13], assumes that some kind of a programmable controller dedicated to a certain area of application is implemented in FPGA. Such a complete controller can be reprogrammed without the necessity to use any HDL tool. For example, Reference [15] presents a solution where a general-purpose FPGA-based micro-PLC executes Ladder Diagram (LD) instructions. A somewhat similar approach is described in Reference [13]. In this case, the so-called hardware function blocks (HFBs) were used to represent the most important parts of algorithms, e.g., PID controllers and IIR/FIR filters. These HFBs are configured directly in HDL, which allows for increased processing speed. While the other fragments of a controller code are implemented as a program for some kind of dedicated soft-core processors.

To understand this issue well, it is necessary to indicate some specificity of control systems. A typical control algorithm requires, in most cases, the shortest possible processing time. This is because this value determines the overall system response time, which is a critical parameter in most control systems. Moreover, in control systems, it is not possible to process consecutive input data until the end of the current control cycle. For this reason, it is typically not possible to apply data-level pipelining. However, it is still possible to apply it at the level of used subordinate components of the implemented algorithm. For this reason, high throughput is not a critical parameter of typical control systems.

In this paper, the classification of methods for the implementation of control algorithms on FPGAs is slightly modified and extended. 

Table 1. Comparison of the properties of various implementation methods of control algorithms on FPGAs.

Features	FHD	SC-HFB	SC-SS	SC-CPU
Processing performance	+++	++	+	-
Design comfort	-	+	++	+++
Economical use	-	-	++	+++

shows the proposed new classification. The symbols + placed in the table indicate a positive assessment of a given method (presented in the column of the table) in relation to the compliance with the feature presented in a given row of the table. The greater the number of such symbols, the higher the rating. Similarly, the symbols denote a negative grade.

A typical and historically first method is fully hardware design (FHD), i.e., a complete project description in one of the hardware description languages, such as VHDL or Verilog. Thus, this method complies with the first of the categories presented in Reference [13] and is used in many practical solutions [11,16]. As mentioned before, this method provides the highest possible performance for various algorithms implemented on FPGAs [17], but the design process is tedious and lengthy. Additionally, it should be pointed out that in the case of some control algorithms their implementation based on this method does not make sense from an economic point of view. Thus, the universality of such a solution is low.

The SS-CPU method presented in the last column of Table 1 has completely different properties. It is based on the implementation of a universal soft-core processor in the FPGA structure and the implementation of the required control algorithm by this processor. The main advantages of this method are the economical use of hardware resources and the convenience of the design process resulting from the possibility of using standard programming languages (typically C or C ++). However, the main disadvantage of the SC-CPU method is the lowest performance among all the methods presented.

On the other hand, the SC-HFB (soft-core—hardware function blocks) method is based on the cooperation of a standard soft-core CPU with HFB blocks dedicated to performing specific functions in the implemented control algorithm. Thus, it is partially consistent with the second category presented in Reference [13], and in particular, with the HFB-based solution described there. It should be noted that HFBs are called hardware accelerators in some publications [18].

According to the data in Table 1, the SC-HFB solution offers high performance for algorithms that are supported by the HFBs. This is because the HFBs, designed with the use of HDL, offer the possibility to match the configuration of the hardware resources the best to the implementation of specific functions. Unfortunately, the consequence of this is very limited versatility. In a situation where any of the HFBs need modification, the only way is to carry out the tedious design process using the hardware description language. Therefore, both the versatility and the convenience of using this method are not very high.

The last method presented in Table 1 is SC-SS (soft-core super-scalar). This method is not strictly dedicated to specific types of implemented algorithms. It is equipped with mechanisms dedicated to digital signal processing, similar to those used in digital signal processors. These mechanisms can of course be equipped with some dedicated functionalities supporting the efficient execution of typical algorithms in the field of control, approximation, or modeling. At the same time, these additional functions are so universal (as opposed to the functions performed by HFB blocks) that they can be successfully used to accelerate algorithms from a very wide range of applications.

The most important feature of the SC-SS method is that the superscalar architecture used in it enables the parallel execution of many simple arithmetic operations, controlled by the very-long instruction word (VLIW). Examples of solutions that can be classified to the SC-SS method are presented, for example, in References [19,20,21]. Dedicated signal processors are also designed based on the super-scalar VLIW architecture, e.g., Refs. [7,22]. To ensure a sufficiently efficient data flow between many computing units of a superscalar architecture, the parallel operation of several memory blocks is typically used. Thus, it is again possible to refer to the similarity to the mechanisms used in signal processors, namely the Harvard architecture.

A somewhat similar architecture is also used in a modern and very efficient, heterogeneous computing unit called Xilinx Adaptive Compute Acceleration Platform (ACAP) [23,24]. This solution uses many scalar arithmetic units called AI engine tiles, arranged in a matrix structure. Each of the elements of such a matrix is equipped not only with an arithmetic unit but also with a local, multiport block of RAM. AI engine tiles arranged in this way have direct access to the multiport memories of their immediate neighbors. So, they can efficiently exchange processed data with each other.

The main advantage of the SC-SS method presented in Table 1 is that it is possible to change the implemented algorithm without the need to carry out the tedious and time-consuming process of FPGA structure synthesis. This change requires only the modification of the machine code instructions executed by the unit with the VLIW architecture. Thus, the SC-SS method is partially consistent with the second category of classification presented in Reference [13], and in particular, with the description in Reference [15]. However, as mentioned earlier, the computing unit designed based on the SC-SS method is much more universal. It does not assume the execution of a specific code (e.g., ladder diagrams instructions, as proposed in Reference [15]) but enables the efficient implementation of a whole range of different algorithms.

The SC-SS method provides slightly more economical management of the FPGA hardware resources than the FHD and SC-HFB methods. This is because these resources (e.g., arithmetic units and registers) in the SC-SS method are not statically assigned to perform specific functions in the implemented algorithm. However, they are dynamically configured to perform various computational functions at the subsequent stages of the implemented algorithm, similar to the standard CPU. This configuration is performed based on information contained in the very long binary code of the currently executed VLIW instruction. For example, at a given moment, some multiplier acts as a proportional gain of the error in the controller, and a few cycles later it is used to determine the current value of the summed terms used in the FIR algorithm or to expand the nonlinear function into a Taylor series. Similarly, the hardware adder/subtractor module in a given step may be used to calculate the value of the control error, the input signal of the IIR filters, or the sum term in the process of accumulation of the neuron activation signal in artificial neural networks.

If both the number of configurable, possibly the simplest, computational units was quite large, and additionally their interconnectivity relatively flexible, then this method could be called very-low level programming, according to the concept presented by the author of the blog [25]. However, in the case of using, at most, a few complex arithmetic units, the SC-SS method can be compared to the architecture of super-scalar signal processors [7].

Therefore, it should be said that the SC-SS method is highly scalable, as the number of arithmetic units working in parallel and the manner of their interactions (e.g., communication using shared registers or separate RAM blocks) can be selected from a wide range. The choice of the implementation method of the SC-SS unit depends on the specificity of the envisaged application area.

Summing up, according to the data contained in Table 1, the SC-SS method is slightly less efficient than the FDH and SC-HFB methods. However, it is more universal than them, much more convenient to use, and it uses the hardware resources of the FPGA chip more economically. Therefore, the choice of one of the methods presented in Table 1 depends on the specifics of a particular application. Therefore, such a choice should be the result of a compromise between the expected efficiency and economy of a given solution and the convenience of the design process.

This paper proposes a method of implementing a hardware computing unit based on the SC-SS method and an innovative real number processing mechanism. This mechanism allows for high processing efficiency with the low demand for hardware resources. Details of this solution will be presented in the next sections.

3. Fixed-Point Coprocessor Based on a Scaling Schedule

As already written in the introduction, this paper presents the concept of a superscalar fixed-point unit (FXU). Important features of such a unit are the integrated scaling mechanism for fixed-point operations (Figure 2) and scalable architecture (Figure 1).

The proposed solution can be used to support some arithmetic operations on real numbers in digital systems built based on FPGAs very efficiently. In such cases, FXU acts as a cooperating processor, supporting the operation of a universal soft-core processor implemented in the same FPGA unit.

The characteristic feature of the FXU unit presented in this section is that it is equipped with a scaling mechanism for fixed-point arithmetic operations. This mechanism is based on a definition of a fixed-point data format provided by the software designer. Due to this mechanism, such a unit offers much higher processing performance than a typical soft-core processor equipped with standard integer multiplication and bit shifting instructions, as will be shown later in this paper.

The FXU unit is intended to be implemented in the FPGA system as a unit cooperating with a standard, universal soft-core CPU. As part of such cooperation, the role of the CPU is to control the startup and configuration process of the system, its management and supervision, and the operation of the user interface. On the other hand, the role of the FXU is to implement a certain class of control, modeling, planning, or identification algorithms efficiently.

As mentioned before, the FXU shown in Figure 1 is highly scalable. Both the N value defining the number of dual-port memory blocks, the R value representing the number of working registers, and the P value representing the number of arithmetic processing units are selected by the system designer. The greater the number of such units working in parallel, the greater the performance, but, unfortunately, the greater the demand for hardware resources of such a computing system. Adjusting these system parameters to the requirements of a specific application allows for reaching a compromise between the obtained performance and the demand for FPGA hardware resources.

The general idea presented in Figure 1 ensures that all fixed-point arithmetic-units (FX-AUs) and data transfer units (DTUs) have unlimited and simultaneous access to all FXU registers (R0,1, …). However, this approach has the limitation that the complexity of such a system increases significantly as $P+N+R$ increases. The high complexity of the digital circuit implemented in the FPGA structure results in a noticeable limitation of its maximum operating frequency. Experience shows that it is reasonable to use the parameters of such a system in the following range: $R\in 〈16\dots 32〉$, $P\in 〈1\dots 8〉$ and $N\in 〈1\dots 4〉$.

Somewhat similar solutions for the possibility of simultaneous access to two memory blocks ($N=2$) are used, for example, in signal processors with the Harvard architecture [7]. In the case of the described FXU, the DTUs are primarily used to manage the data flow between the working registers of the FXU and the dual-port memories, which are found in typical FPGAs [26]. However, it should be remembered that the use of more than one block of RAM requires appropriate (i.e., following the algorithm being executed) assigning the locations of the processed signals and/or parameters, i.e., placing them in selected memory blocks. This causes some complication in the process of designing the program code for such a system, but at the same time allows for greater processing efficiency.

In all the experiments presented in this publication, the work of a super-scalar FXU is controlled by a low-level human-written code. Most operations are performed in one or, at most, two clock cycles.

To ensure a low level of complexity of the entire system, the use of an architecture based on MIPS was proposed [27]. In this architecture, the low-level code must be written in such a way that executed instructions do not take the result of processing a particular arithmetic unit until it is ready. This requirement must be taken into account by a dedicated compiler or programmer who designs the low-level code.

It should be mentioned here that the “manual” code creation for the VLIW type computing unit (Figure 1), which is presented in this paper, is a much more difficult task than programming a typical computer system in C or C ++. VLIW code development, on the other hand, is much easier than the hardware design process in HDL. Therefore, the solution described in this paper should be considered as a compromise. It facilitates the process of implementation of algorithms requiring high processing efficiency. Besides, this solution allows for reasonable management of hardware resources of an FPGA chip.

Based on the cooperation of DTU and FX-AU units, it is possible to efficiently implement many practical algorithms. For example, it is possible to implement an algorithm for determining the values of complex nonlinear functions based on a local Taylor series approximation in combination with a look-up table (LUT) method. This method (LUT-Taylor series expansion, LTSE) is based on the approximation mechanism described in Reference [28].

In the LTSE method, the domain of the approximated function $y=f\left(x\right)$ must be scaled to a range $\left.〈-1\cdots 1\right)$. Then, based on the highest few bits of the input digital word, a single segment, i.e., an appropriate fragment of this domain, is identified. In such a segment, the local approximation is performed using the Taylor series expansion method. In the identified segment, the value of the following polynomial is then determined:

$$y\left(x\right)=y_0+C_1·z^1+C_2·z^2+C_3·z^3+\cdots ,$$

(1)

where: $y_0=y\left(x_0\right)$ and $z=x-x_0$, while $x_0$ is the middle of a given segment, and $C_1,C_2,\dots$ are the parameters of the approximation in this segment.

According to Reference [28], “the evaluation of the function on the reduced argument is less expensive than on the original input. This is due to the higher-order terms in the evaluation of the series being shifted out to lower weights than the target precision, thus they do not need to be computed”. In many practical applications, domains of the approximated functions are easily predictable; therefore, the LTSE method can be easily applied and is very effective at the same time. Namely, it is usually possible to obtain the required accuracy by dividing the domain of the approximated function into just a few segments.

Based on the LTSE method, the following nonlinear functions are implemented in the experiments described later in the paper: sine, cosine, and the arithmetic reciprocal operation. In the same way, other nonlinear functions, such as square root, sigmoid, or gaussoid, can also be approximated. The last two nonlinear functions are used in various types of computational intelligence algorithms, such as artificial neural networks, radial function networks, or fuzzy structures [29,30,31]. Based on the LTSE solution, the approximation time for such functions (assuming a similar level of precision) is usually a dozen or so clock cycles. For example, when dividing the domain of the sine function into eight segments and applying the 5th-order Taylor expansion in each of them, the approximation precision at the level of $1.1·{10}^{-3}\%$ is obtained. This precision is fully sufficient for applications in typical control systems. Of course, the precision of the approximation can be improved by increasing the expansion order or by dividing the domain into a larger number of segments.

In the algorithm presented later in this paper, each segment requires one 32-bit and six 16-bit parameters describing the approximation. As a result, the implemented LTSE method requires only 128 bytes of data. Moreover, such an LTSE process takes only twelve clock cycles, which in the following experiment gives a computation time of 0.15 μs.

The code fragment for a super-scalar FXU implementing the LTSE algorithm is presented below. In the analyzed experiment, an FXU with two DTU units ($N=2$), five FX-AU units ($P=5$), and sixteen working registers ($R=16$) are used. The first two FX-AUs perform fixed-point multiplications (Figure 2a) and two more perform arithmetic addition/subtraction operations (Figure 2b). The last one, FX-AU, performs basic, universal arithmetic operations useful in signal processing algorithms [7]. These are operations, such as MIN, MAX, NEG, and a few simple operations of testing and modifying bit-fields in a binary word.

In the code fragment shown in Listing 1, it can be seen that in most work cycles three arithmetic operations (two multiplications and one addition) and one or two memory access operations are performed. However, in other algorithms (e.g., in the case of the implementation of two PI controllers working in parallel), it is possible to arrange the code for the VLIW unit in such a way that in most work cycles all AU and DTU units are used simultaneously.

Listing 1: Fragment of FXU code for LTS algorithm.

In the above code, the numbers given in parentheses are example values of the i-parameters describing, respectively, the format of the result and components for fixed-point operations, following the Fxi_n notation. In this notation, the ‘i’ parameter describes the position of the binary point counting to the right, starting from the left side of the binary word. In the research described in this publication, 32-bit words ($n=32$) were used to represent the values of the processed signals. It is easy to check that the range of real numbers encoded in this way is $\left.〈-2^{i-1}\cdots 2^{i-1}\right)$, and the resolution is $2^{i-n}$.

In the example code presented above, memory access operations are represented by instructions M1 and M2 relating to one of the two dual-port memories (dual-port RAM, DP-RAM) with associated DTUs, respectively. The syntax of individual instructions is not important and will not be discussed in detail.

This fragment of the code shows the essence of the proposed algorithm for scaling the processed fixed-point real numbers. This algorithm assumes that there is a pre-planned (by the system designer) scaling schedule for successive numbers processed by the fixed-point unit. This scaling schedule is created by the compiler based on information provided by the designer. This information is provided in the form of i-parameter values for each arithmetic instruction (which will be explained later in the paper) according to the example code shown in Listing 1. Based on the appropriate hardware mechanisms, such a schedule is used for the ongoing configuration of individual FX-AUs. Thus, this approach significantly simplifies the calculations that have to be performed online. As a result, it is possible to obtain higher processing efficiency and lower consumption of hardware resources compared to the implementation of analogous calculations in floating-point arithmetic. Floating-point arithmetic assumes that the scale of the processed numbers is determined on an ongoing basis, i.e., during each arithmetic operation. As a consequence, not only the computation time is extended, but also the consumption of hardware resources of the FPGA, on which floating-point algorithms are implemented, is higher.

In the above-mentioned example, the scale of numbers processed in subsequent steps of the algorithm was selected by the designer to obtain the highest processing precision. However, it is also possible to automate this process to some extent. This is possible, for example, by using the profiling mechanism described in Reference [32]. The description of the possibility of automatic implementation of such a method is beyond the scope of this paper.

The inclusion of information about the scale of the processed fixed-point numbers in the binary code of the instructions of the executed program is, as mentioned above, one of the most important features of the real number processing mechanism described here. Based on this concept, Figure 2 shows a method for multiplication and addition/subtraction of fixed-point numbers.

Based on the analysis of the requirements of typical algorithms used in control systems (i.e., PID controllers, IIR/FIR filters, Taylor series expansion) it has been observed that it is possible to use a relatively low 16-bit precision of the parameters used in such algorithms, without any noticeable negative impact on the final work result. These parameters are coefficients of the above-mentioned algorithms. Consequently, it is possible to significantly optimize the processing unit by using a non-symmetrical structure. Half of the registers (i.e., R0-R7) are realized as 32-bit words and are used to store signal values with a full resolution. Such registers are marked in blue in Listing 1. While the other half of the registers (i.e., R8-R15) are realized as 16-bit words and are used to store the above-mentioned parameters. One of the registers belonging to this group, i.e., R8 is used in the algorithm presented in Listing 1. This register is marked in green. The asymmetric structure of processing unit working registers is a novelty proposed in this paper. It allows for a significant simplification of the hardware structure of the processing unit while maintaining the requirements of typical control algorithms.

As mentioned earlier, in the method presented in Figure 2a, each fixed-point multiplication operation requires the knowledge of the value of the parameter i for both components and for the result. Following the idea already presented in Listing 1, such information may be included in an instruction using the following syntax: $Ro=Ra*Rb\left(i_o,i_a,i_b\right)$, where $o,a,b$ are indexes of FXU registers, while $i_o,i_a,i_b$ are values of parameters i that define their format (scale). On this basis, the compiler will determine the correct scaling result of multiplying a 32-bit integer by a 16-bit integer. In order to obtain the expected output format, a 48-bit integer multiplication result will be shifted to the right by the number of positions expressed by formula (2).

$$s_M=(32-i_a)+(16-i_b)-(32-i_o).$$

(2)

The value of $s_M$ is placed in the ’SCALE’ field of the binary code of the FXU instruction.

For example, the multiplication instruction for two registers written in the following form R0 = R1 * R8(6,2,4) means that the result is represented in the format Fx6_32 (i.e., $i_o=6$), the first argument is represented in the format Fx2_32 (i.e., $i_a=2$) and the second argument in the format Fx4_16 (i.e., $i_b=4$). In this case, the compiler will automatically calculate a scale factor of $S_M=16$ based on the formula (2).

For the sake of clarity, let us consider a numerical example. Suppose the real number contained in register R1 has the value 0.5. According to the well-known method of a fixed-point encoding of real numbers, it will be represented by an integer with the value $0.5·2^{32-2}$, written in hexadecimal notation as $0\times 20,000,000$. Similarly, assume that the real number contained in register R8 has the value 1.25; therefore, it is represented by an integer with the value $1.25·2^{16-4}=$ 0 × 1400. The result of the multiplication of both integers is the number $0\times 28,000,000,000$, which after scaling by the factor $S_M=16$ (i.e., after shifting to the right by 16 binary positions) will give the result $0\times 2,800,000$. According to the expected format of the result (i.e., Fx6_32), this integer represents a valid real number of $0\times 2,800,000·2^{-(32-6)}=0.625$.

In the case of an arithmetic addition or subtraction operation (according to Figure 2b) any scaling applies only to the second component. With pre-defined requirements ($i_a\ge i_b$) for this instruction, the format of the result is determined by the format of the first component, i.e., $i_o=i_a$. Thus, for example, the addition instruction has the following syntax Ro = Ra + Rb $(i_a,i_b)$. The ’SCALE’ field contained in the binary code of the arithmetic instruction (Figure 2b) describing, in this case, the number of binary offset positions of the second component is:

$$s_A=i_a-i_b.$$

(3)

For instance, the instruction for adding two registers written in the following form R0 = R1 + R2 (6,4) means that both the result and the first component of addition are represented in the form Fx6_32 (i.e., $i_a=6$), while the second component is represented in the format Fx4_32 (i.e., $i_b=4$). In this case, the compiler will automatically calculate a scale factor of $S_A=2$ based on the formula (3).

As before, let us analyze the numerical example. Suppose the number in register R1 has a real value of 0.5. According to the fixed-point encoding method for real numbers, it will be represented by an integer with value $0.5·2^{32-6}=0\times 2,000,000$. Similarly, suppose the real number contained in register R2 has the value 1.25, so it is represented by an integer value of $1.25·2^{32-4}=0\times 14,000,000$. The latter argument will be scaled by the scale factor $S_A=2$, i.e., shifted two binary positions to the right, before performing the addition operation. In consequence, integers $0\times 2,000,000$ and $0\times 5,000,000$ will be fed to the ADD/SUB unit inputs. The result of the integer addition is $0\times 7,000,000$ which represents, according to the Fx6_32 format, a valid real number of $0\times 7,000,000·2^{-(32-6)}=1.75$

A similar analysis could also be performed for other elementary fixed-point arithmetic operations, such as division or reciprocal. However, according to the idea presented in this publication, the fixed point arithmetic unit (Figure 2) performs only two types of arithmetic operations, i.e., multiplication and addition/subtraction. All other operations are performed through the LTSE mechanism presented in Listing 1. This approach allows for a significant simplification of the arithmetic units implemented in FPGAs.

It is worth mentioning that in practical applications it is reasonable to significantly limit the allowed values for the parameters $i_a$, $i_b$, and $i_o$. In this way, it is possible to simplify the design of the digital circuit implemented in FPGAs. In the experiment described later in this publication, it was assumed that these parameters can only be set to one of sixteen values, i.e., $i\in \{-8,-6,\cdots ,+22\}$. In this way, it was possible to process numbers from a wide range, with a resolution that is sufficient for the implementation of typical control systems.

4. Experimental Results

The experiment described in this section concerns the implementation of selected fragments of the vector control algorithm of permanent-magnet synchronous-motor (PMSM) on the FPGA system [14,33,34]. The experiment shows the benefits of using the proposed method in practical applications. The test was carried out on a compact servo-drive controller built based on an FPGA chip (Figure 3). Such controllers are used, inter alia, in high-speed numerical machine tools [35].

Due to the need to achieve the highest possible precision of such machines, the requirements for servo-drives are very high. For example, in a typical case, it is required to process the full control algorithm in no more than 50 μs, which allows power electronic actuators to work with their maximum allowable switching frequency of 20 kHz [33]. Operation with a lower commutation frequency is possible but results in a lower precision of such a control system. Moreover, by reducing the above-mentioned processing time by half, the precision of such a control system can be significantly improved. This is because it is possible to modify the parameters of the generated impulse control signals in the middle of their cycle, which results in the reduction of the response time of such a control system.

It should be noted here that the use of FPGAs for the implementation of servo-drives is a very attractive solution. This is because such controllers very often have to handle fast pulse signals. Such pulse signals are used, inter alia, in non-standard communication protocols, such as a real-time Ethernet [36], synchronous and asynchronous serial protocols for communication with incremental or absolute position sensors (e.g., a digital quadrature or a BISS interface), or in specialized analog-to-digital converters. The FPGA chip can easily handle very fast impulse signals; therefore, its use allows the implementation of a complete algorithm in one integrated circuit and keeps the design of the device compact. Other solutions that could provide similar functionality must be based on the cooperation of several separate ASIC-type integrated circuits. Nevertheless, such a solution would not allow the designed device to be compacted. As already presented in the Introduction, compact devices have several significant advantages over devices built from separate integrated circuits.

As part of the experimental research, the mentioned control algorithm was implemented on the controller shown in Figure 3. For comparison purposes, this implementation was made based on two different methods, i.e., SC-CPU and SC-SS as described in Table 1. In the first case, the above-mentioned algorithm was implemented in a standard way, in the C language. The resulting code was then executed by a 32-bit soft-core CPU unit (TSK3000A) implemented in the FPGA programmable logic. In the second case (based on the SC-SS method), the same FPGA also includes the super-scalar fixed-point cooperating unit (FXU) proposed in this paper and shown in Figure 1. The FXU is equipped with a scaling mechanism for fixed-point operations shown in Figure 2. Then, a low-level code was designed for this unit, implementing the same control algorithm as in the first case, i.e., based on the SC-CPU method. The obtained results made it possible to compare the processing efficiency and the demand for hardware resources for both implementation methods.

The digital platform used in the experiment was equipped with an FPGA system from a low-end family of Xilinx Spartan-6 [26], i.e., XC6SLX45-3 produced with 45nm technology (Figure 3). The chip has 27,288 6-input combination look-up tables (LUTs), 58 integer arithmetic units (DSP48E1s), and 116 blocks of 16-bit dual-port RAM (RAMB16WERs). FPGAs from the low-end series are characterized by relatively low efficiency, but also low cost and low electricity consumption.

For the SC-CPU method, the maximum allowable operating frequency was slightly over 50MHz. While the FPGA hardware resource consumption was: 3065 LUTs (11%), 2 DSP48Es (3%), and 20 RAMB16WERs (17%).

When the SC-SS method was used, the maximum allowable frequency of the FXU operation was over 80MHz and the total consumption of resources (i.e., soft-core CPU + FXU) was: 3943 LUTs (14%), 7 DSP48E1s (12%), and 22 RAMB16WERs (19%).

For comparison purposes, an analogous experiment (with the implementation of the FXU unit) was also carried out on a slightly more modern hardware platform, i.e., the Xilinx Artix-7 XC7A200T-3 FPGA chip made in 28 nm technology. In this case, the maximum allowable operating frequency was just over 110 MHz.

The project was implemented in the Altium Designer v.14.3 and Xilinx ISE 14.3 design environments. As mentioned earlier, a universal 32-bit processor called TSK3000A was used as the soft-core CPU. The CPU was used as the only unit processing the complete algorithm in the case of implementation using the SC-CPU method. However, in the second case, i.e., with an implementation based on the SC-SS method, the CPU only managed and supervised the work of the main computing unit (FXU).

Table 2. Obtained performance and memory consumption for the implementation of selected algorithms on soft-core CPU and soft-core super-scalar FXU.

Servo Code Functional Block	SC-CPU	SC-SS	Speed-Up
Sine&Cosine calculation	1.16 s, 8192 B	0.30 s, 128 B	3.87
Clarke & Park	2.30 s	0.18 s	12.8
Inverse Park & SVM	5.54 s, 0 B	0.61 s, 128 B	9.1
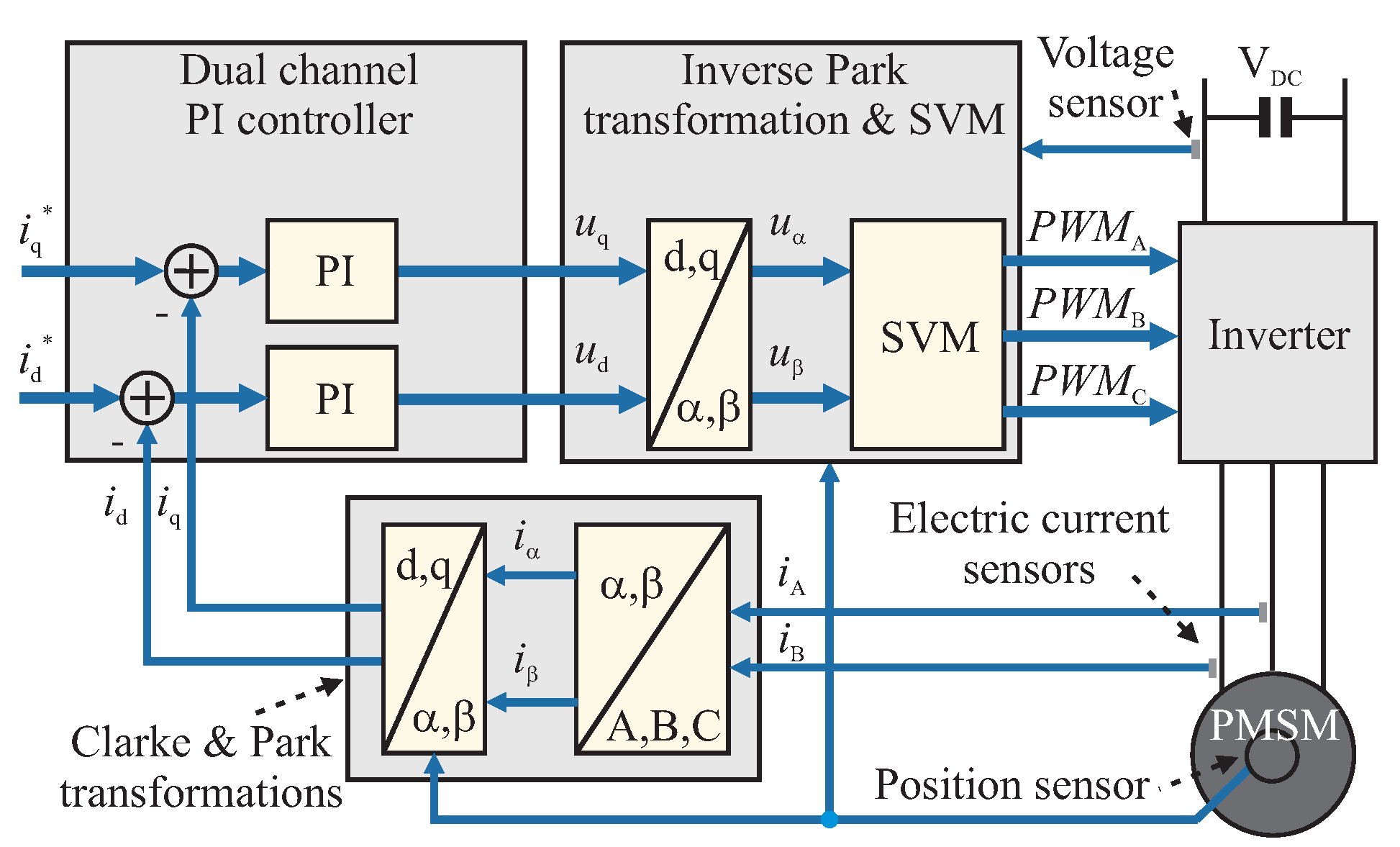
DC-PI	4.72 s	0.48 s	9.8

contains the results of experimental research on the implementation of the most important modules of the vector control algorithm (Figure 4) of an electric servo drive with a PMSM motor [14,33,34].

In the experiment with the use of the algorithm implemented by the soft-core CPU, 16-bit fixed-point arithmetic was used. With carefully selected ranges for the numbers processed by the CPU, it was possible to obtain an acceptable quality of work of the implemented algorithm. Nevertheless, managing such software was very troublesome. Each modification of the program code required detailed analysis to avoid exceeding the range of processed numbers, and at the same time to ensure the required precision of calculations. The use of 32-bit arithmetic (floating-point or fixed-point) would greatly facilitate the design of such software. But its use would entail a significant extension of the computation time and the required work cycle would not be achieved. However, in the second case (i.e., with the algorithm implementation on the FXU unit), it was possible to apply precise 32-bit fixed-point arithmetic to the processed digital signals. This is because the FXU provides a much higher signal processing performance than the CPU.

The first row of Table 2 shows the results (i.e., the obtained performance and memory consumption) for the implementation of the algorithm that determines the value of the sine and cosine functions. These functions are necessary for the operation of the PMSM vector control algorithm. In the case of implementation on a soft-core CPU, the look-up table (LUT) method was used. An array of 4096 digital words with a width of 16 bits was used to store the values of the sine function from the first quadrant. Values for the remaining quarters of this function were determined based on the first quadrant with appropriate consideration of symmetry.

It is well known that the LUT method is quite often used in embedded systems software to store the values of functions whose determination is time-consuming. This is because, as mentioned earlier, the execution time of the algorithm is a critical parameter for most embedded systems. Unfortunately, embedded systems (both those based on microcontrollers and FPGAs) are characterized by a relatively small amount of memory in which data arrays can be stored. For example, the FPGA XC6SLX45 has only 232 kB of RAM. For this reason, the LUT method must be used with caution, as too much memory demand leads to the need to use a chip with more hardware resources. As a consequence, it increases the cost and energy consumption of the designed solution.

As mentioned in the previous section of this paper, in the solution based on the FXU the LTSE method was used to determine the values of the sine and cosine functions. As can be seen, the time of Sine&Cosine evaluation is much shorter than for the implementation on a standard CPU. In addition, this method only requires 128 bytes of data compared to the 8192 bytes required by the LUT algorithm implemented on the CPU.

The second row of the table contains the results of implementing the Clarke and Park transforms. These transforms are used in the PMSM vector drive control algorithms. The next row of the table contains the results of the implementation of the inverse Park transformation and space vector modulation (SVM) algorithms. The last row of the table shows the results for the dual-channel PI-controller (DC-PI), i.e., the controller of the two spatial vector components of the electric current flowing through the stator winding of the PMSM motor.

Based on the analysis of the results presented in Table 2, it can be concluded that the presented algorithm implemented on the soft-core FXU works almost ten times faster than the same algorithm implemented on the soft-core CPU.

It should be noted that the data presented in the table represent the results obtained only for the most important parts of the complex servo control system with the PMSM motor. The remaining blocks are omitted from this list. Tests previously carried out by the author showed that the processing time of the complete, complex PMSM position control algorithm by the soft-core CPU was over 65 μs. Therefore, in such a case, it was not possible to fully use the possibilities offered by power electronic devices. On the other hand, the use of the soft-core FXU unit presented in this publication enables the implementation of such an algorithm in less than 20 μs. Consequently, it allows to obtain a higher quality of work of the analyzed control system and to meet all the other requirements mentioned earlier.

5. Conclusions

The paper presents a new architecture of a computational unit based on fixed-point arithmetic. The characteristic feature of this unit that distinguishes it from other solutions is primarily the built-in scaling mechanism for fixed-point arithmetic operations. Other distinctive features of the proposed method are universal superscalar architecture and asymmetric structure of working registers. Thanks to such solutions, the designed unit performs arithmetic operations efficiently.

As part of the experimental research, the described solution was implemented on an FPGA chip and the consumption of hardware resources was determined in comparison to the solution based on a standard soft-core CPU. Experimental research was preceded by an analysis of the existing methods of implementing control algorithms in programmable FPGA structures. The result of this analysis is the proposed modified and extended classification of such methods.

As part of the experimental research, the processing efficiency of an exemplary control algorithm, implemented based on the solution proposed in this publication, was also determined. From the obtained results, it can be concluded that the proposed method allows for an almost tenfold increase in the processing efficiency of typical control algorithms compared to solutions based on standard soft-core processors. Such a significant reduction of the processing time allows improving the quality of control systems, as their response time is shortened.

The relatively low demand for hardware resources, as demonstrated in the case of the implementation of the described solution, enables the implementation of a complete controller in a compact form and based on an FPGA chip from the economical low-end series.

The main contributions of this work can be summarized as follows:

• comparison and classification of various methods for the implementation of control algorithms on FPGAs,
• the concept of a high-performance, fixed-point arithmetic unit with the integrated scaling mechanism and the asymmetric structure of working registers, and
• implementation of experimental studies that confirm the usefulness of the developed method for industrial systems requiring a short response time.

The presented solutions can be used in many different areas, i.e., not only in the implementation of algorithms known from classical control theory, but also in the implementation of adaptive fuzzy control systems [37], real-time emulation of objects based on the HIL methodology [38], or for the implementation of real-time reference trajectory planning algorithms for machines and robots [39]. The developed solution can also be useful for many other applications that require a short response time, for example, to detect visual objects in images delivered in real-time from the camera of mobile or industrial robots [40].

The implementation of the above-mentioned algorithms in the manner presented in this paper causes that the ratio of the obtained performance to the hardware complexity is much better than in the case of using other implementation methods. Therefore, the proposed solution leads, in many cases, to a significant optimization of control systems, and, consequently, its application is justified.