A One-Step Leapfrog ADI Procedure with Improved Absorption for Fine Geometric Details
Abstract
1. Introduction
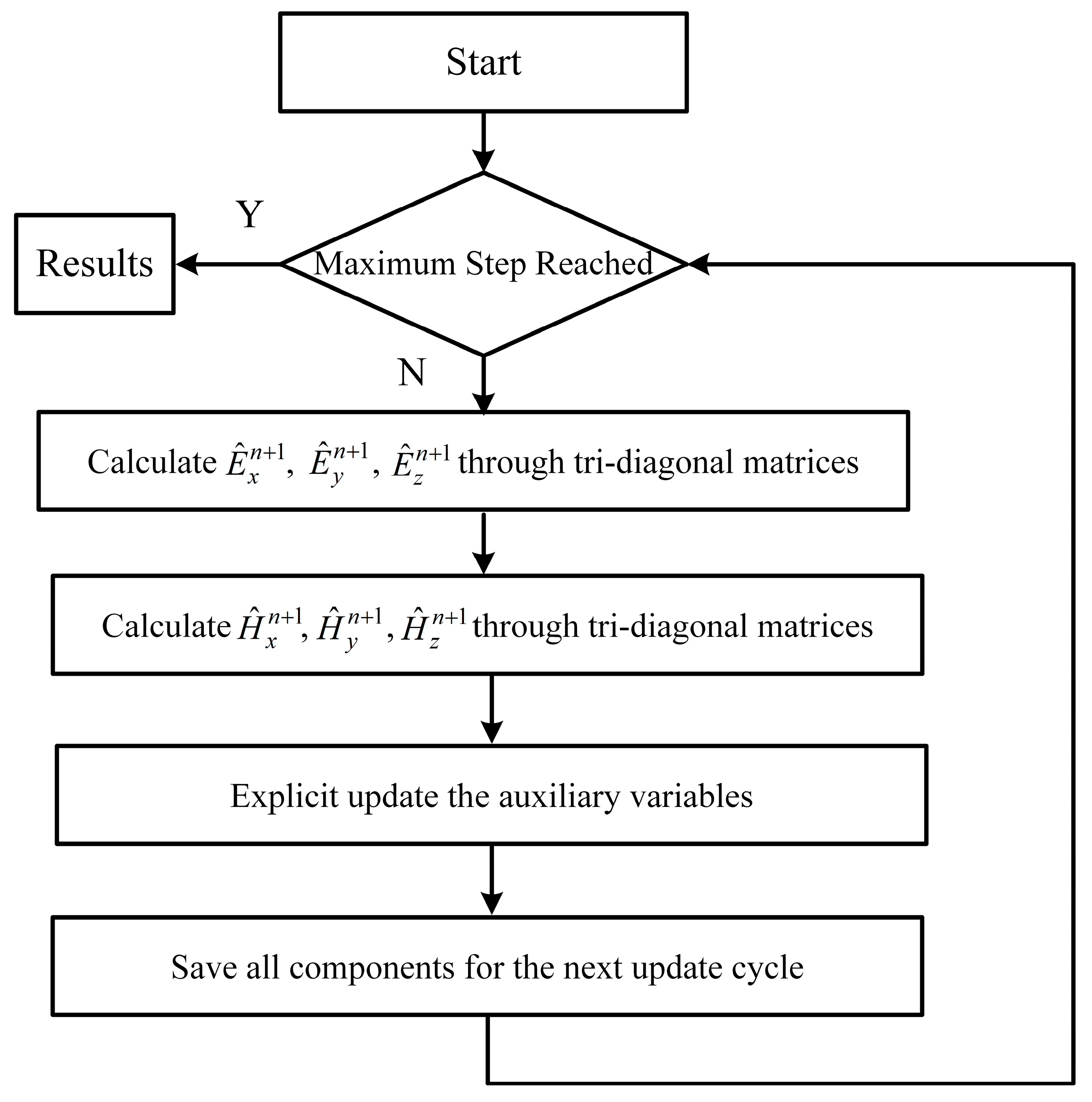
2. Formulation
3. Numerical Simulation and Results
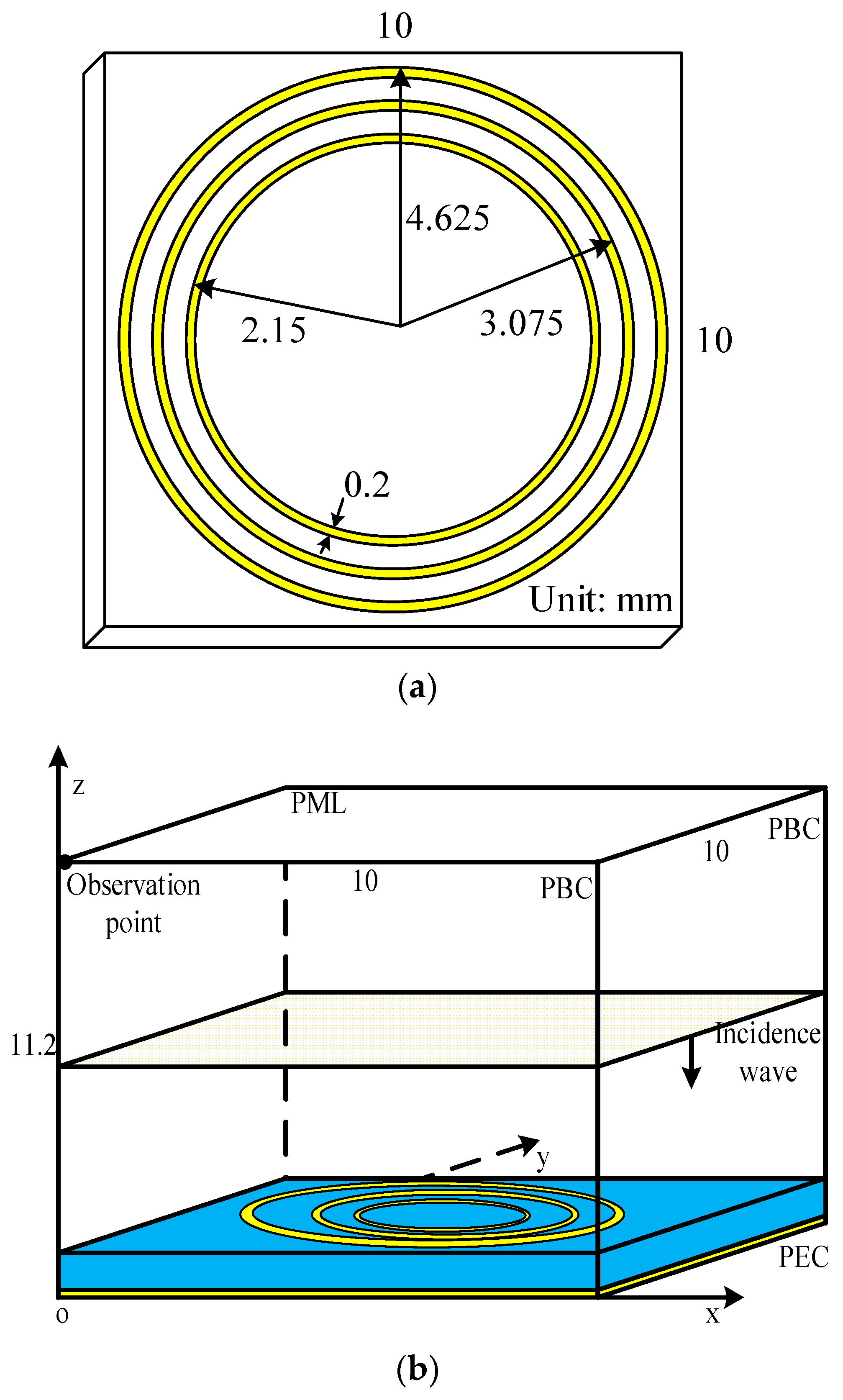
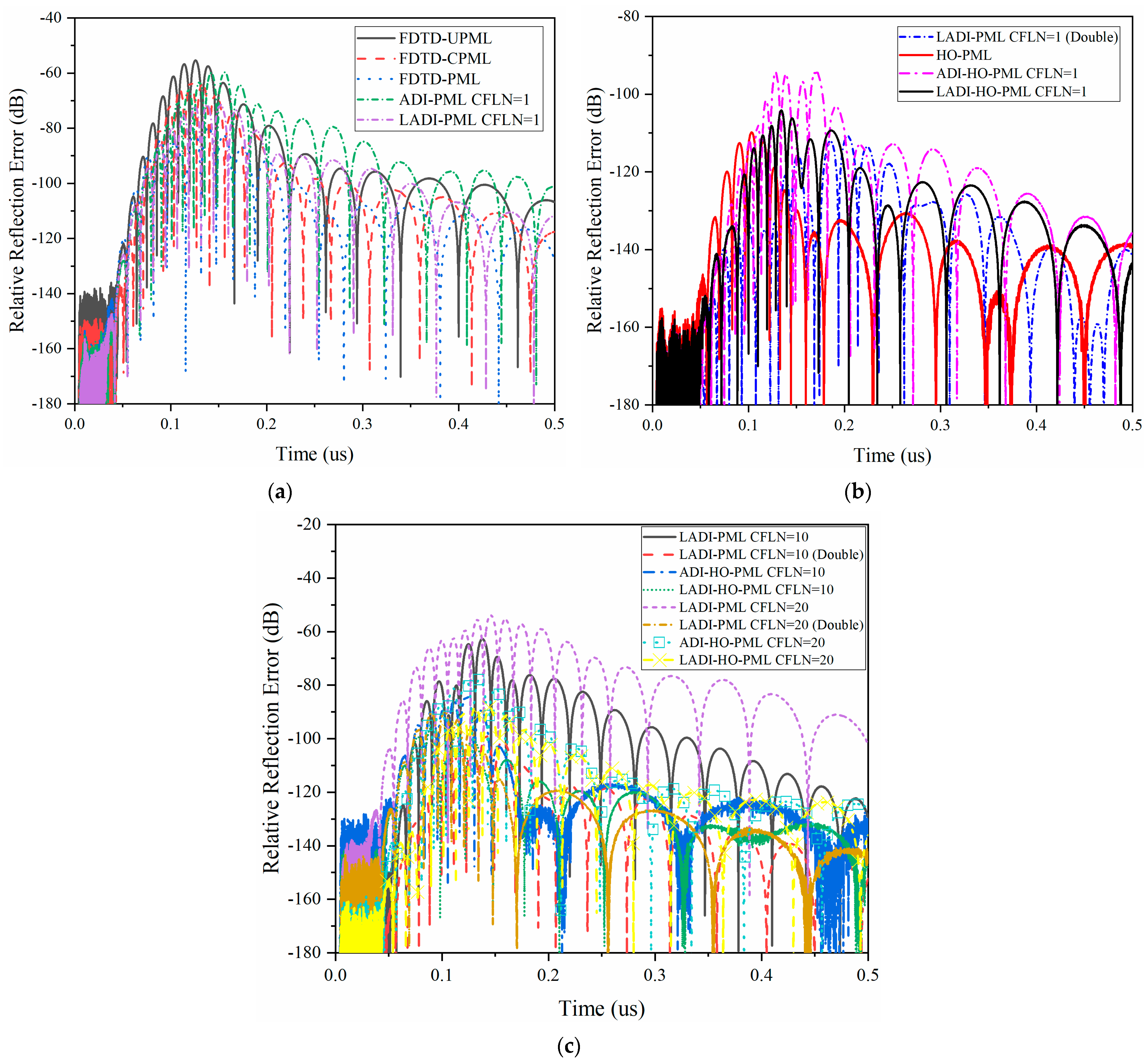
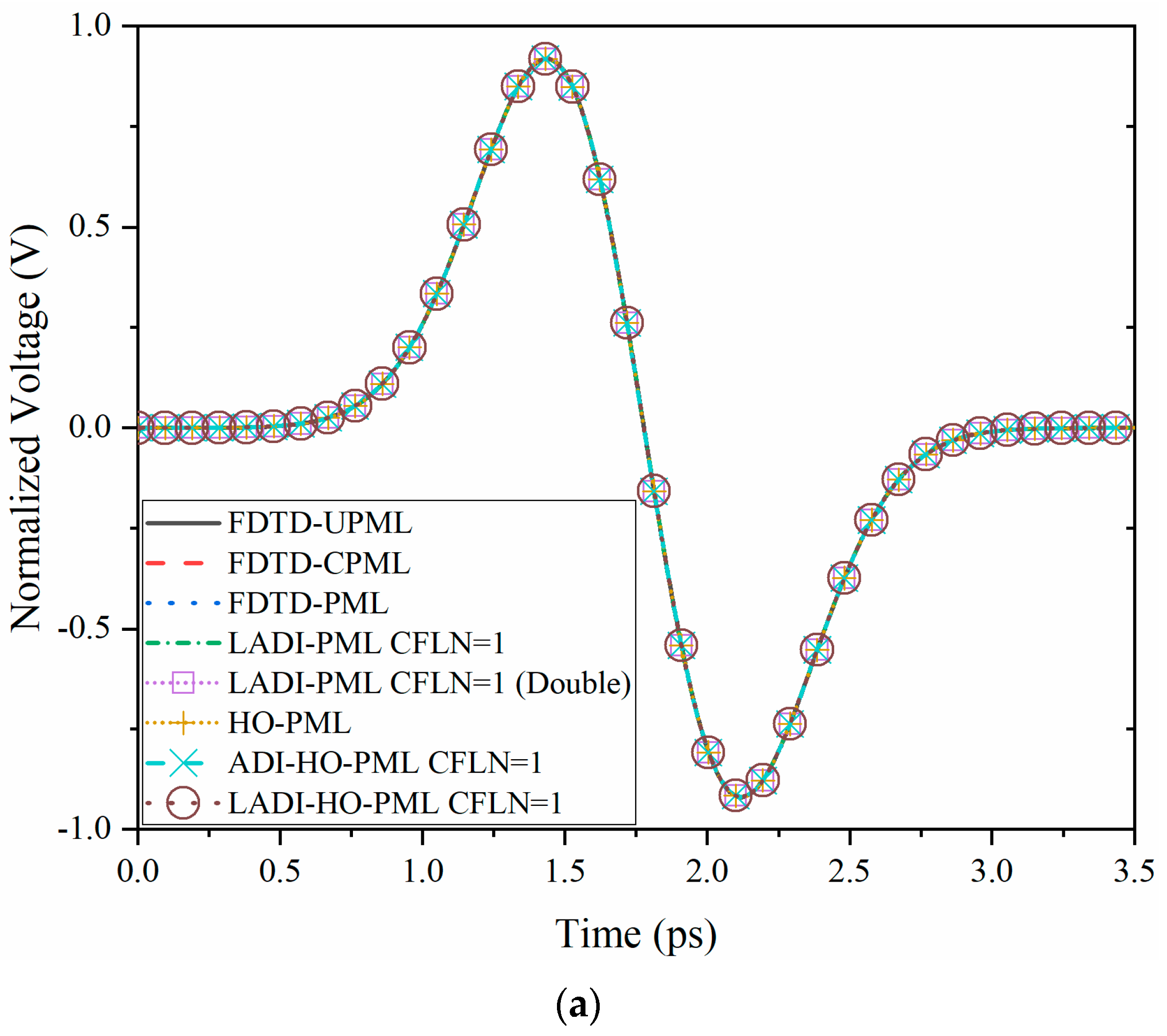
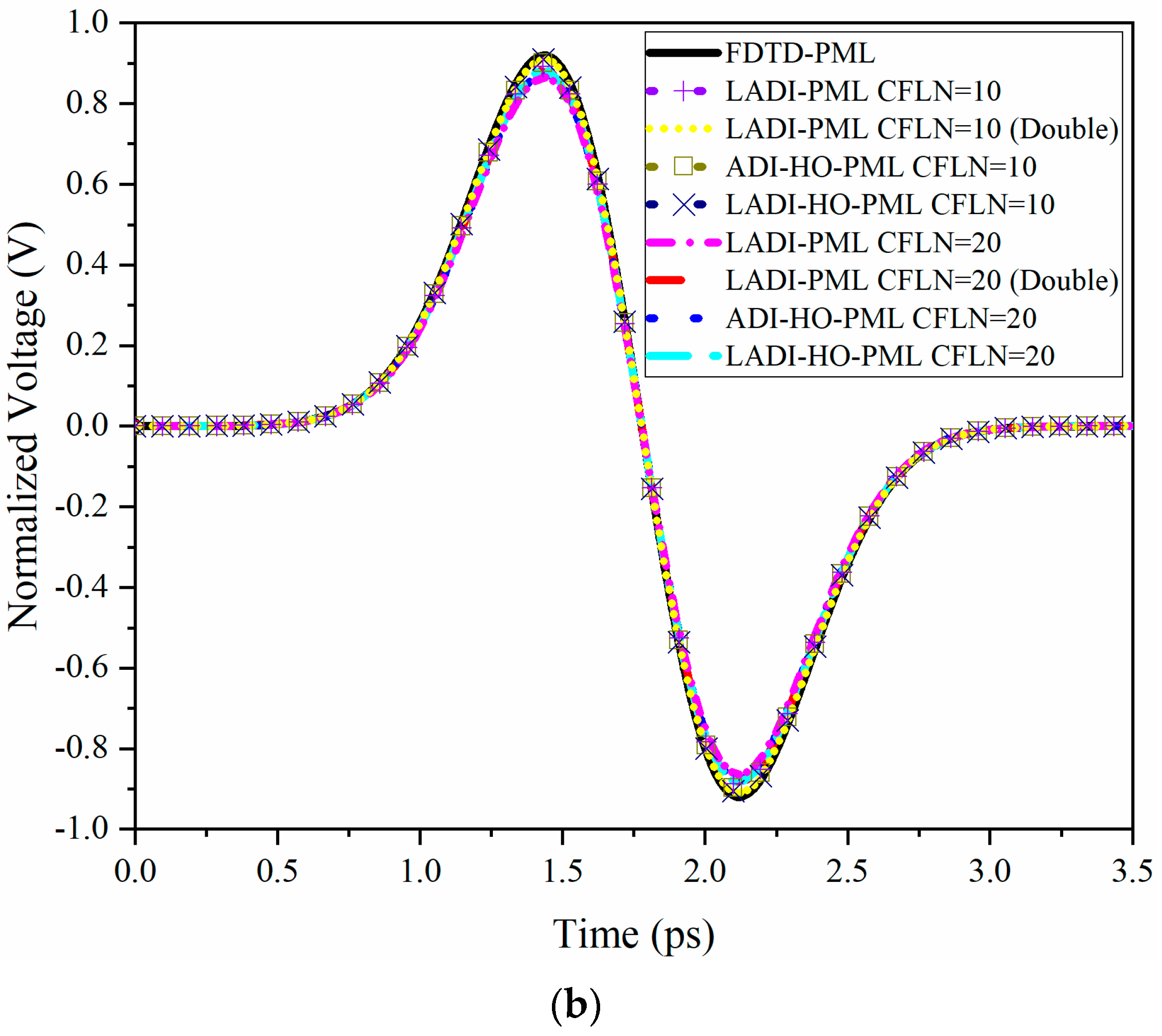
3.1. Wave Radiation Problem in a Metamaterial Structure
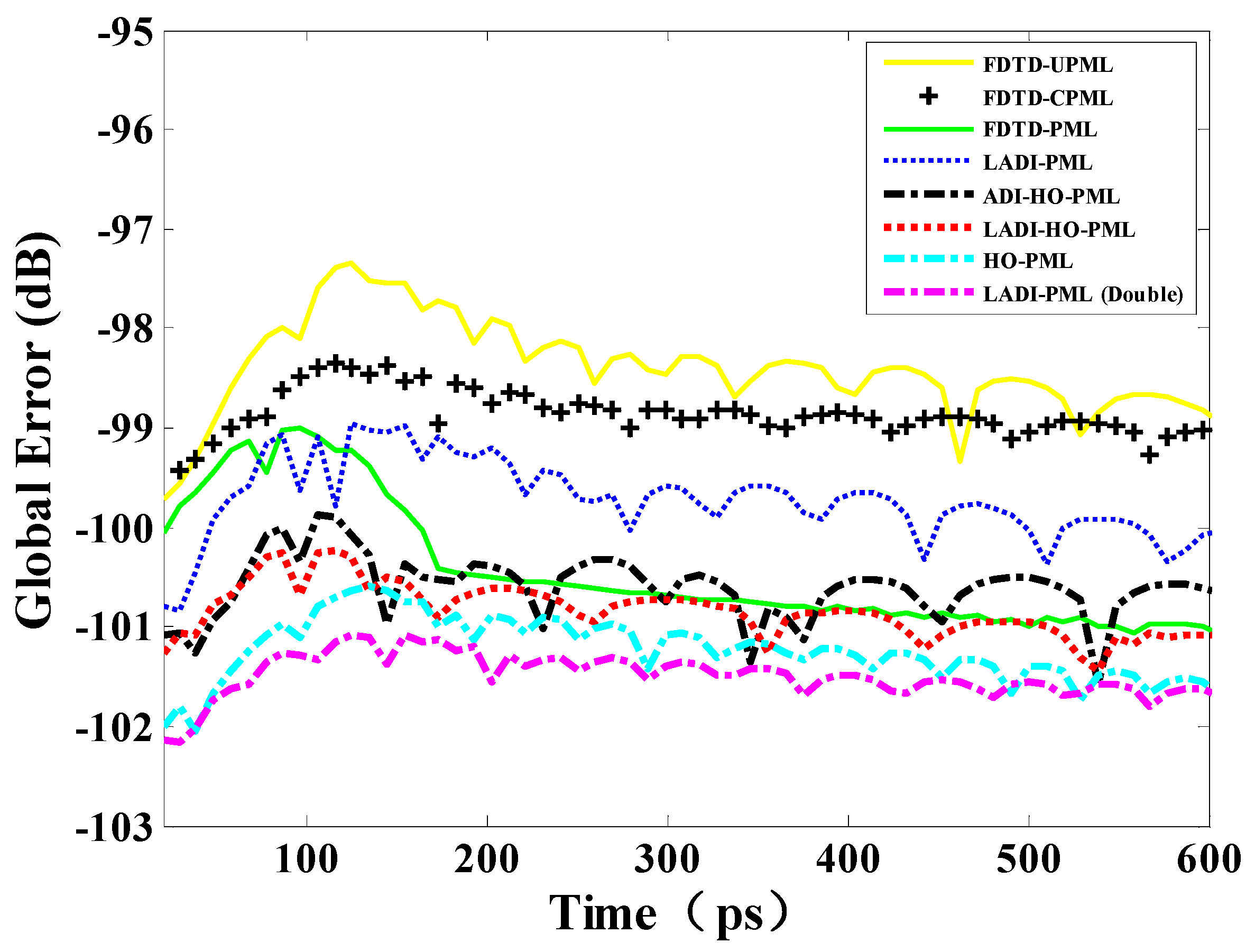
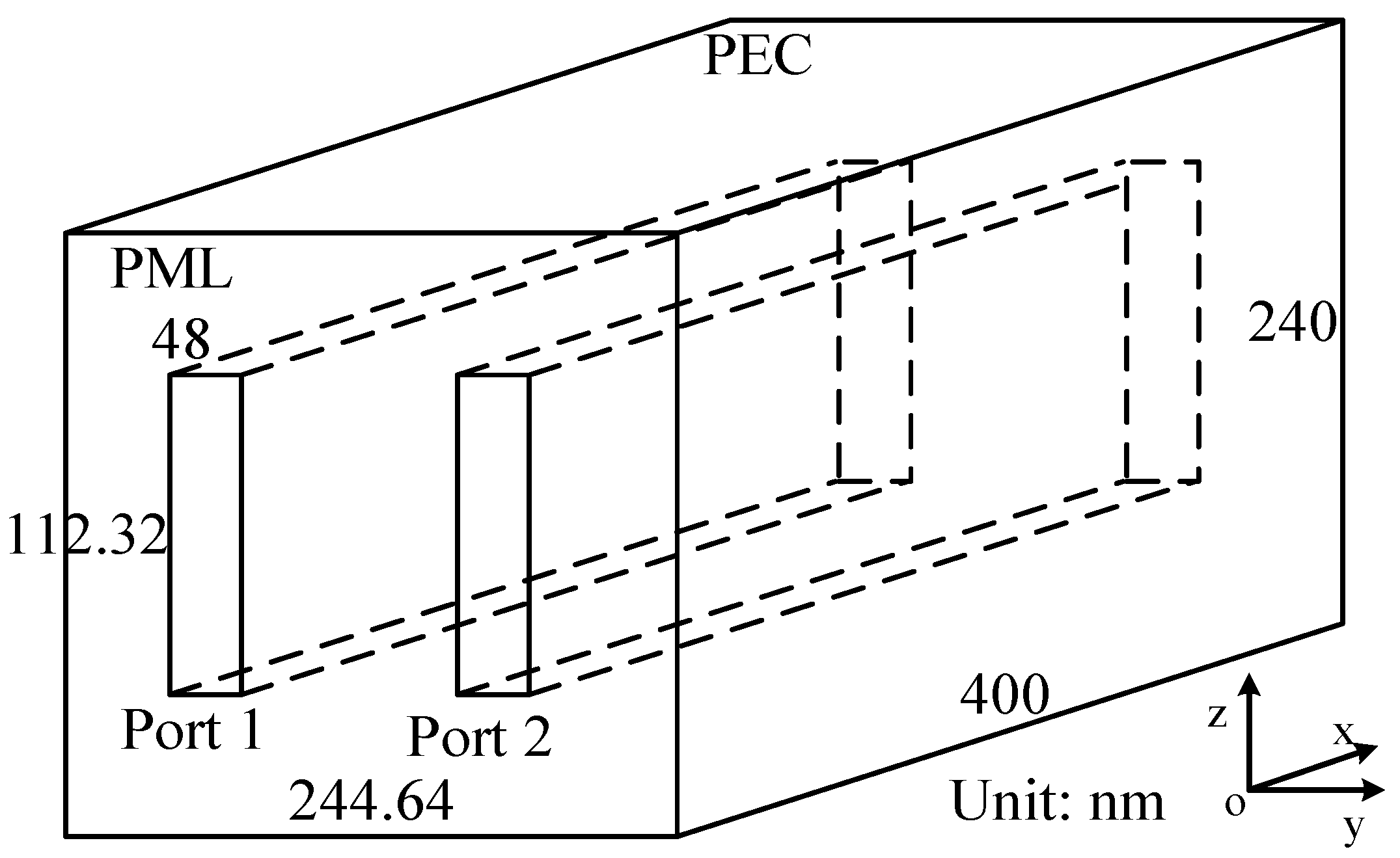
3.2. Wave Propagation Problem—Very Large Scale Integration (VLSI) Interconnect Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yee, K. Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Namiki, T. 3-D ADI-FDTD method unconditionally stable time- domain algorithm for solving full vector Maxwell’s equations. IEEE Trans. Microw. Theory Tech. 2000, 48, 1743–1748. [Google Scholar] [CrossRef]
- Yang, S.-C.; Chen, Z.D.; Yu, Y.-Q.; Yin, W.-Y. The Unconditionally Stable One-Step Leapfrog ADI-FDTD Method and Its Comparisons with Other FDTD Methods. IEEE Microw. Wirel. Compon. Lett. 2011, 21, 640–642. [Google Scholar] [CrossRef]
- Yang, S.-C.; Chen, Z.; Yu, Y.; Yin, W.-Y. An Unconditionally Stable One-Step Arbitrary-Order Leapfrog ADI-FDTD Method and Its Numerical Properties. IEEE Trans. Antennas Propag. 2012, 60, 1995–2003. [Google Scholar] [CrossRef]
- Kong, Y.; Chu, Q.; Li, R. Efficient unconditionally stable one-step leapfrog ADI-FDTD method with low numerical dispersion. IET Microw. Antennas Propag. 2014, 8, 337–345. [Google Scholar] [CrossRef]
- Berenger, J.P. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Chew, W.C.; Weedon, W.H. A 3D perfectly matched medium from modified Maxwells equations with stretched coordinates. Microw. Opt. Technol. Lett. 1994, 7, 599–604. [Google Scholar] [CrossRef]
- Kuzuoglu, M.; Mittra, R. Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers. IEEE Microw. Guid. Wave Lett. 1996, 6, 447–449. [Google Scholar] [CrossRef]
- Bérenger, J.-P. Perfectly Matched Layer (PML) for Computational Electromagnetics. Synth. Lect. Comput. Electromagn. 2007, 2, 1–117. [Google Scholar] [CrossRef]
- Wagner, C.L.; Young, J.L. FDTD Numerical Tests of the Convolutional? PML at Extremely Low Frequencies. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 1398–1401. [Google Scholar] [CrossRef]
- Correia, D.; Jin, J.-M. Performance of regular PML, CFS-PML, and second-order PML for waveguide problems. Microw. Opt. Technol. Lett. 2006, 48, 2121–2126. [Google Scholar] [CrossRef]
- Feng, N.; Yue, Y.; Zhu, C.; Wan, L.; Liu, Q.H. Second-order PML: Optimal choice of nth-order PML for truncating FDTD domains. J. Comput. Phys. 2015, 285, 71–83. [Google Scholar] [CrossRef]
- Wei, X.-K.; Shao, W.; Shi, S.-B.; Cheng, Y.-F.; Wang, B.-Z. An Optimized Higher Order PML in Domain Decomposition WLP-FDTD Method for Time Reversal Analysis. IEEE Trans. Antennas Propag. 2016, 64, 4374–4383. [Google Scholar] [CrossRef]
- Hwang, J.-N.; Chen, F.-C. A Rigorous Stability Analysis of Instability in ADI-FDTD Method with PML Absorber. 2006 IEEE Antennas Propag. Soc. Int. Symp. 2006, 1739–1742. [Google Scholar] [CrossRef]
- Sun, S.-H.; Choi, C. Performance of the improved PML for the envelope ADI-FDTD method in two-dimensional domain. IEEE Microw. Wirel. Compon. Lett. 2005, 15, 820–822. [Google Scholar]
- Wang, X.-H.; Yin, W.-Y.; Yu, Y.-Q.; Chen, Z.; Wang, J.; Guo, Y. A Convolutional Perfect Matched Layer (CPML) for One-Step Leapfrog ADI-FDTD Method and Its Applications to EMC Problems. IEEE Trans. Electromagn. Compat. 2012, 54, 1066–1076. [Google Scholar] [CrossRef]
- Wu, P.Y.; Jiang, H.L.; Xie, Y.J.; Niu, L.Q. Three-Dimensional Higher Order PML Based on Alternating Direction Implicit Algorithm. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2592–2596. [Google Scholar] [CrossRef]
- Sauer, T. Numerical Analysis, 2nd ed.; Pearson Education: London, UK, 2012. [Google Scholar]
- Appannagarri, N.; Bardi, I.; Edlinger, R.; Manges, J.; Vogel, M.; Cendes, Z.; Hadden, J. Modeling phased array antennas in Ansoft HFSS. In Proceedings of the 2000 IEEE International Conference on Phased Array Systems and Technology (Cat. No.00TH8510), Dana Point, CA, USA, 21–25 May 2000; pp. 323–326. [Google Scholar]
- Shin, Y.-M.; Barnett, L.R.; Baig, A.; Luhmann, N.C.; Pasour, J.; Larsen, P. Numerical modeling analysis of 0.22 THz sheet beam TWT circuit. In Proceedings of the 2011 IEEE International Vacuum Electronics Conference (IVEC), Bangalore, India, 21–24 February 2011; pp. 139–140. [Google Scholar]
- Wu, P.Y.; Xie, Y.J.; Niu, L.Q.; Jiang, H.L. Hybrid domain multipactor prediction algorithm and its CUDA parallel implementation. J. Syst. Eng. Electron. 2020, 31, 1097–1104. [Google Scholar]
- Bhattacharyya, S.; Ghosh, S.; Srivastava, K.V. Equivalent circuit model of an ultra-thin polarization-independent triple band metamaterial absorber. AIP Adv. 2014, 4, 097127. [Google Scholar] [CrossRef]
- You, J.W.; Zhang, J.F.; Jiang, W.X.; Ma, H.F.; Cui, W.Z.; Cui, T.J. Accurate Analysis of Finite-Volume Lumped Elements in Metamaterial Absorber Design. IEEE Trans. Microw. Theory Tech. 2016, 64, 1966–1975. [Google Scholar] [CrossRef]
- Cui, T.J.; Smith, D.R.; Liu, R. Metamaterials; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Niu, L.Q.; Xie, Y.J.; Jiang, H.L.; Wu, P. Exponential time differencing based efficient SC-PML for RCS simulation. J. Syst. Eng. Electron. 2020, 31, 703–711. [Google Scholar]
- Li, J.; Dai, J. Efficient implementation of the stretched co-ordinate perfectly matched layer based on the Z-transform method. IET Microw. Antennas Propag. 2007, 1, 645–650. [Google Scholar] [CrossRef]
- Li, J.; Wu, P.; Jiang, H. The implementation of unconditionally stable higher order PML based on the implicit CNAD-FDTD algorithm. J. Electromagn. Waves Appl. 2018, 33, 151–164. [Google Scholar] [CrossRef]
- Gan, T.H.; Tan, E.L. Analysis of the Divergence Properties for the Three-Dimensional Leapfrog ADI-FDTD Method. IEEE Trans. Antennas Propag. 2012, 60, 5801–5808. [Google Scholar] [CrossRef]
- Su, M.; Liu, P.-G. A global optimized parameter to reduce the numerical dispersion of the LOD-FDTD method. 2016 Asia-Pac. Int. Symp. Electromagn. Compat. 2016, 1, 742–744. [Google Scholar]
- Wang, S.; Teixeira, F. An efficient PML implementation for the ADI-FDTD method. IEEE Microw. Wirel. Compon. Lett. 2003, 13, 72–74. [Google Scholar] [CrossRef]
- Hong, W.; Sun, W.-K.; Zhu, Z.-H.; Ji, H.; Song, B.; Dai, W.-M. A novel dimension-reduction technique for the capacitance extraction of 3-D VLSI interconnects. IEEE Trans. Microw. Theory Tech. 1998, 46, 1037–1044. [Google Scholar] [CrossRef]
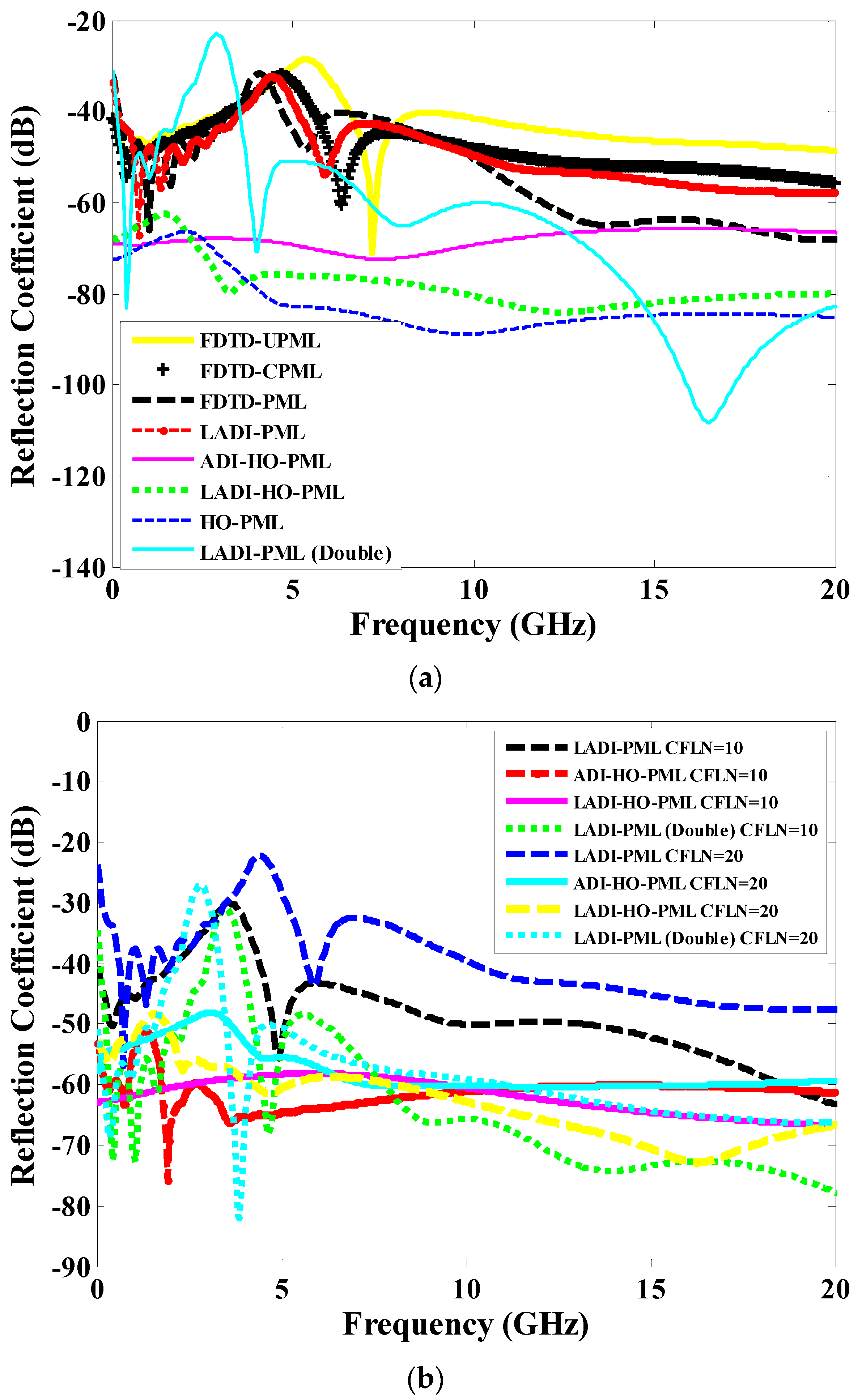
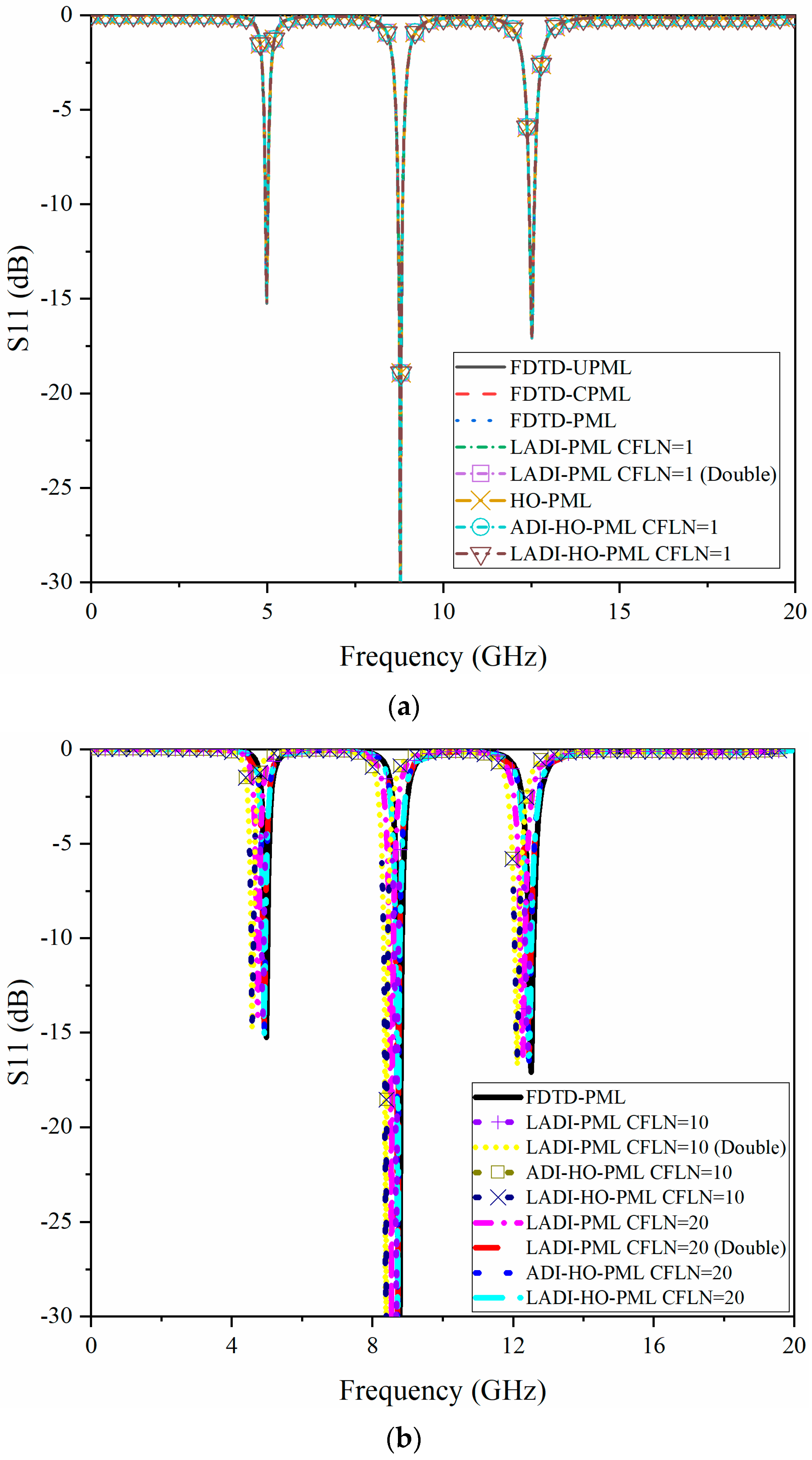
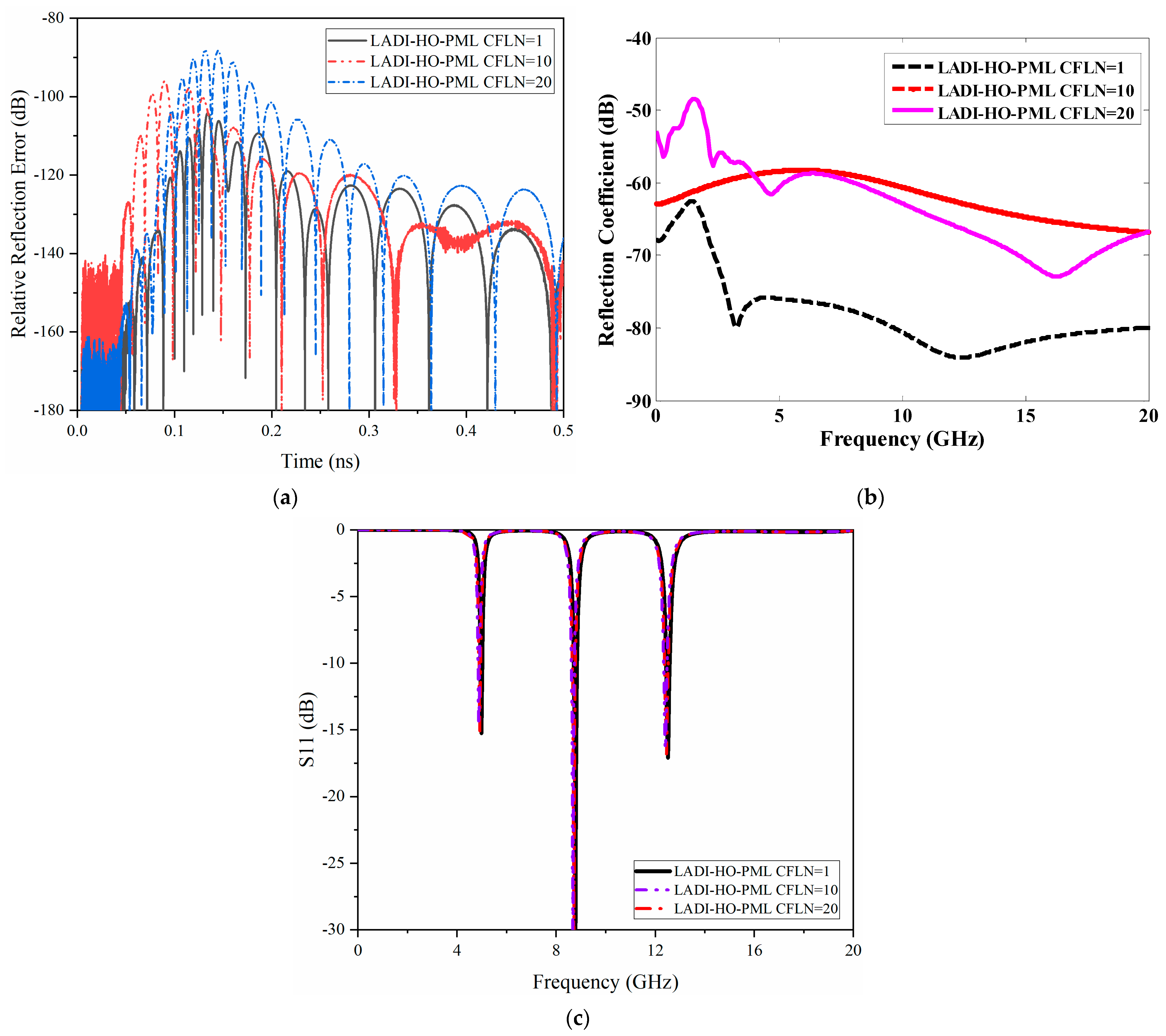
| PML Algorithm | Tri-Diagonal Matrices | M/D | A/S | Total | ||
|---|---|---|---|---|---|---|
| I | E | I | E | |||
| LADI-PML | 6 | 32 | 28 | 10 | 48 | 124 |
| ADI-HO-PML | 6 | 48 | 66 | 24 | 72 | 210 |
| LADI-HO-PML | 6 | 42 | 36 | 18 | 60 | 156 |
| PML Algorithm | CFLN | Time (min) | Memory (GB) | Reduction (%) | MRRE (dB) |
|---|---|---|---|---|---|
| FDTD-PML | 1 | 49.2 | 2.2 | - | −79.5 |
| FDTD-UPML | 1 | 45.4 | 2.0 | 7.7 | −57.3 |
| FDTD-CPML | 1 | 48.1 | 2.2 | 2.2 | −62.2 |
| LADI-PML | 1 | 396.8 | 3.3 | −706.5 | −71.3 |
| LADI-PML | 10 | 43.7 | 3.3 | 11.2 | −62.7 |
| LADI-PML | 20 | 17.2 | 3.3 | 54.5 | −53.8 |
| LADI-PML (D) | 1 | 1077.3 | 5.1 | −2089.6 | −118.6 |
| LADI-PML (D) | 10 | 129.0 | 5.1 | −161.2 | −98.6 |
| LADI-PML (D) | 20 | 41.1 | 5.1 | 16.5 | −92.9 |
| HO-PML | 1 | 104.4 | 3.2 | −112.2 | −109.7 |
| ADI-HO-PML | 1 | 851.8 | 5.0 | −1631.3 | −95.9 |
| ADI-HO-PML | 10 | 90.2 | 5.0 | −83.3 | −83.8 |
| ADI-HO-PML | 20 | 38.2 | 5.0 | 22.4 | −77.9 |
| LADI-HO-PML | 1 | 749.6 | 4.7 | −1423.6 | −104.1 |
| LADI-HO-PML | 10 | 72.7 | 4.7 | −47.8 | −96.0 |
| LADI-HO-PML | 20 | 30.4 | 4.7 | 38.2 | −88.1 |
| PML Algorithm | CFLN | Time (min) | Memory (GB) | Reduction (%) |
|---|---|---|---|---|
| FDTD-PML | 1 | 32.9 | 1.7 | - |
| FDTD-UPML | 1 | 30.8 | 1.5 | 6.4 |
| FDTD-CPML | 1 | 31.6 | 1.7 | 4.0 |
| LADI-PML | 1 | 283.0 | 2.6 | –88.4 |
| LADI-PML | 10 | 31.1 | 2.6 | 5.5 |
| LADI-PML | 20 | 13.8 | 2.6 | 58.1 |
| LADI-PML (D) | 1 | 403.9 | 4.2 | –1127.7 |
| LADI-PML (D) | 10 | 44.2 | 4.2 | –35.3 |
| LADI-PML (D) | 20 | 23.3 | 4.2 | 29.2 |
| HO-PML | 1 | 86.9 | 2.6 | –164.1 |
| ADI-HO-PML | 1 | 536.6 | 4.1 | –1531.0 |
| ADI-HO-PML | 10 | 50.1 | 4.1 | –52.3 |
| ADI-HO-PML | 20 | 26.2 | 4.1 | 20.4 |
| LADI-HO-PML | 1 | 379.0 | 3.8 | –1052.0 |
| LADI-HO-PML | 10 | 35.2 | 3.8 | 7.0 |
| LADI-HO-PML | 20 | 19.6 | 3.8 | 40.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, P.; Yu, H.; Xie, Y.; Jiang, H.; Natsuki, T. A One-Step Leapfrog ADI Procedure with Improved Absorption for Fine Geometric Details. Electronics 2021, 10, 1135. https://doi.org/10.3390/electronics10101135
Wu P, Yu H, Xie Y, Jiang H, Natsuki T. A One-Step Leapfrog ADI Procedure with Improved Absorption for Fine Geometric Details. Electronics. 2021; 10(10):1135. https://doi.org/10.3390/electronics10101135
Chicago/Turabian StyleWu, Peiyu, Han Yu, Yongjun Xie, Haolin Jiang, and Toshiaki Natsuki. 2021. "A One-Step Leapfrog ADI Procedure with Improved Absorption for Fine Geometric Details" Electronics 10, no. 10: 1135. https://doi.org/10.3390/electronics10101135
APA StyleWu, P., Yu, H., Xie, Y., Jiang, H., & Natsuki, T. (2021). A One-Step Leapfrog ADI Procedure with Improved Absorption for Fine Geometric Details. Electronics, 10(10), 1135. https://doi.org/10.3390/electronics10101135








