A Period-Aware Routing Method for IEEE 802.1Qbv TSN Networks
Abstract
1. Introduction
- We first analyze the combinability among various periods of flows and show the ability of different periods of flows to utilize the decentralized bandwidth.
- We introduce a new metric to measure the bottleneck of scheduling. Moreover, we propose a period-aware routing algorithm for time-triggered flows and improve their schedulability.
- Finally, we evaluate the proposed algorithm from three dimensions: load, topology and flow type. The experiment results demonstrate that our method can achieve higher schedulability compared to the shortest path algorithm and the load balanced algorithm.
2. Related Work
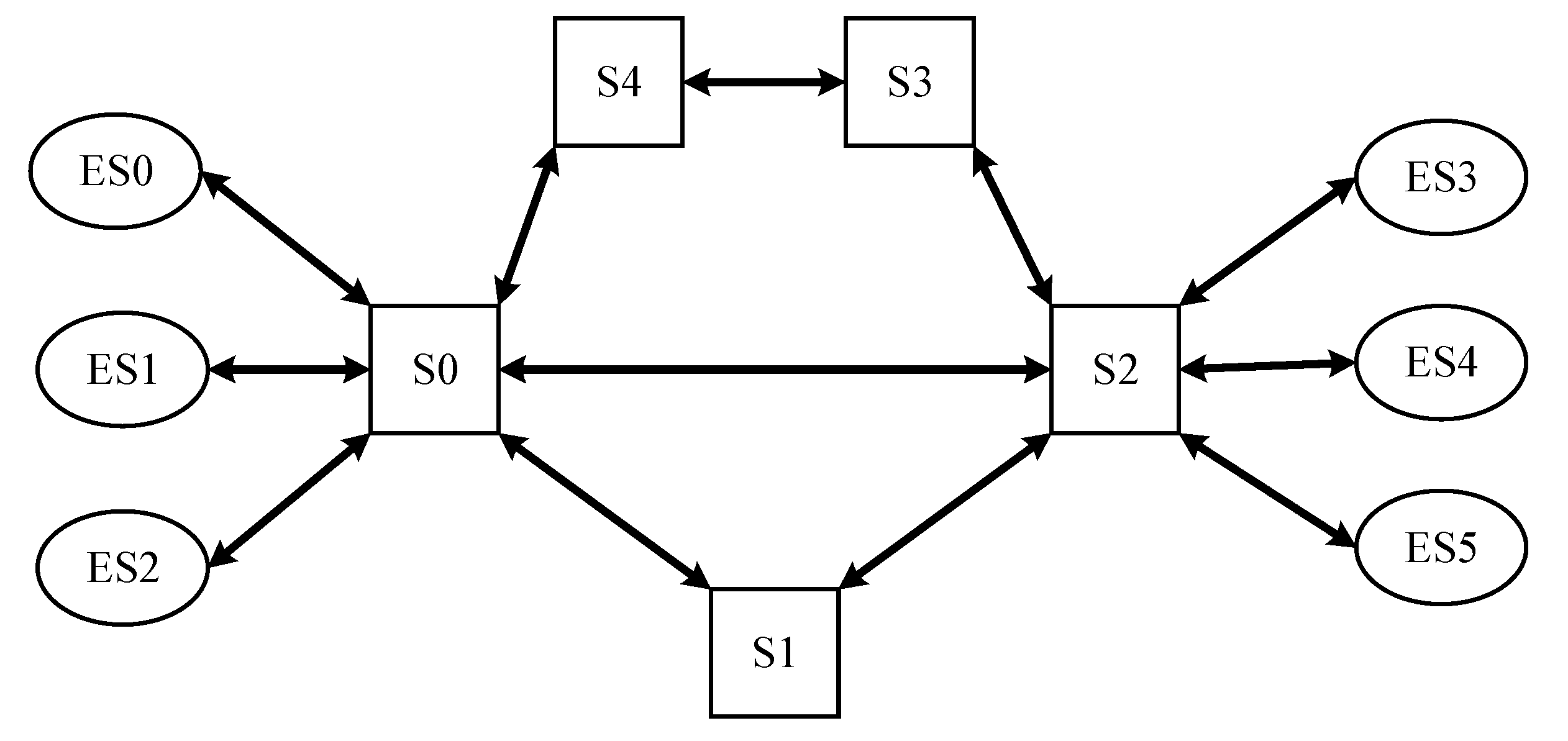
3. System Model and Problem Definition
3.1. System Model
3.2. Problem Definition
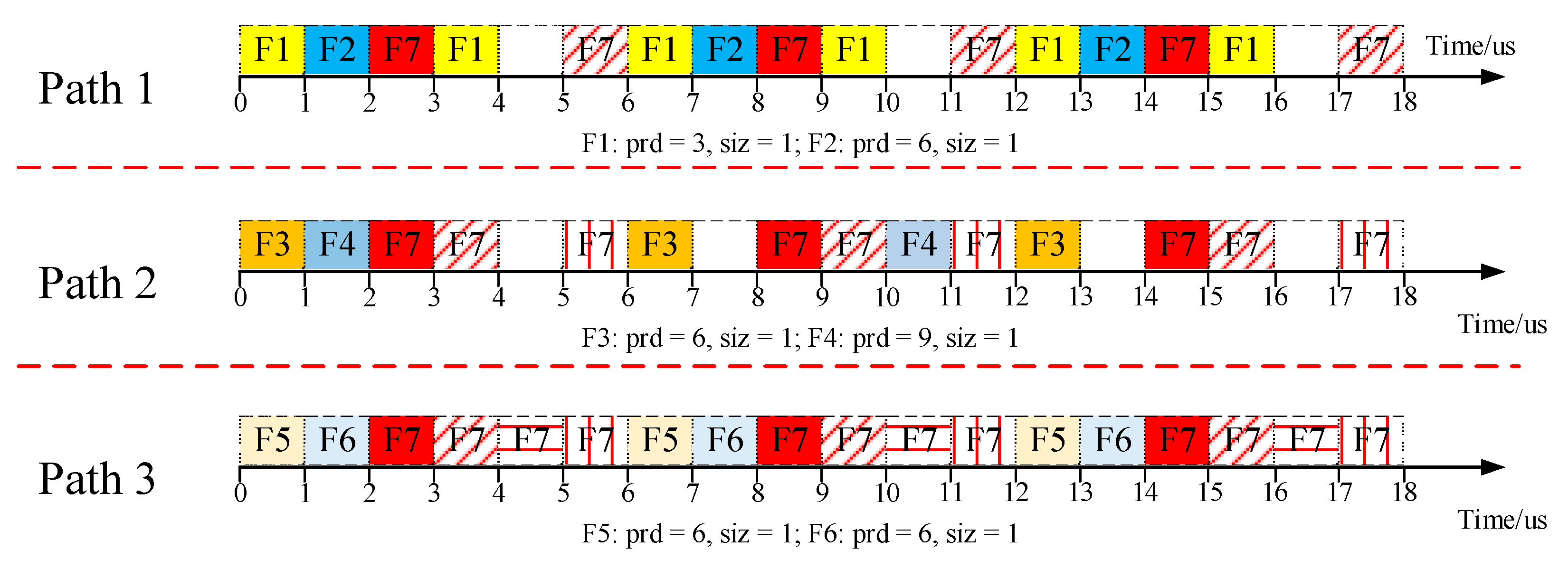
4. Motivation Example
5. Proposed Solution
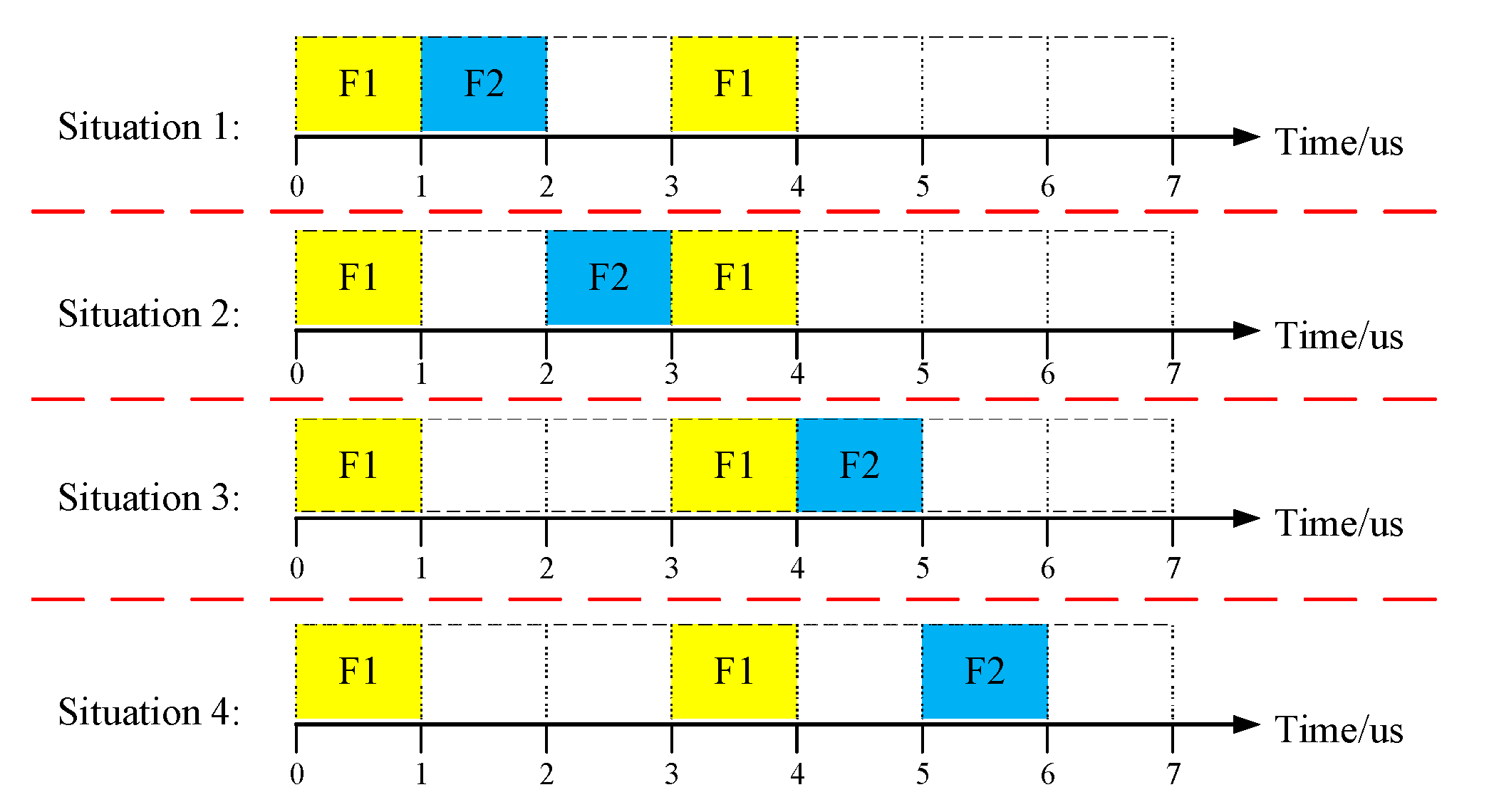
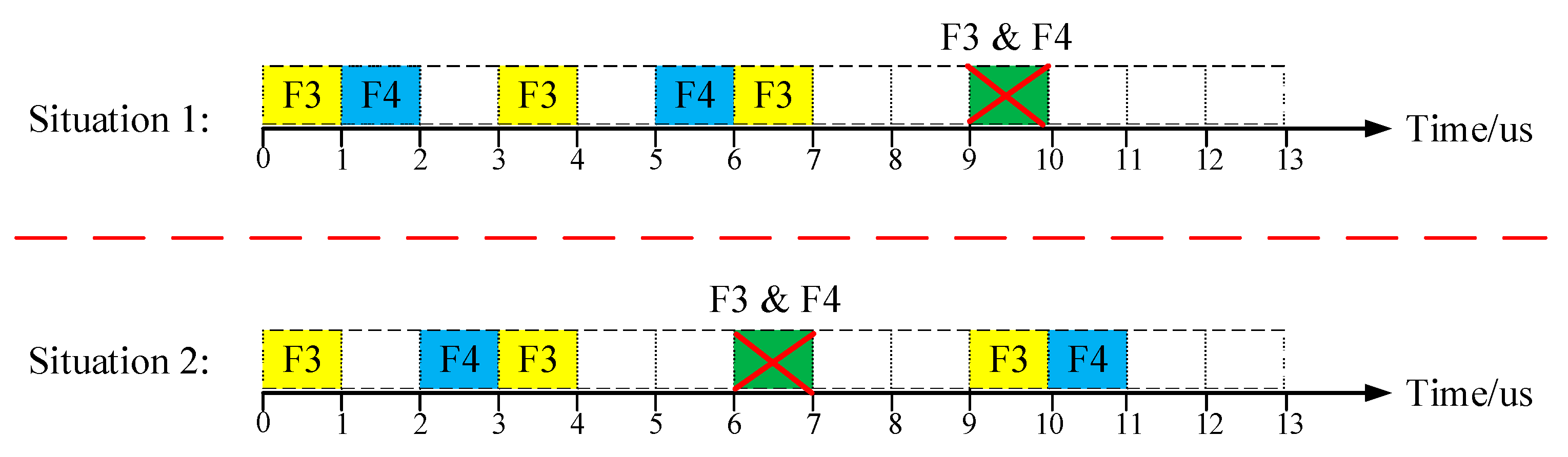
5.1. The Combinability of Different Periods of Flows
5.1.1. Examples for Different Combinability
5.1.2. Analysis of the Combinability between Two Flows
“For nonzero integers a and b, let d be the greatest common divisor d = gcd(a,b). Then, there exist integers x and y such that: ax + by = d.”
5.1.3. Combinability among Multiple Flows
5.2. The Proposed Routing Algorithm
5.2.1. Period-Aware Routing Algorithm
| Algorithm 1 Period-aware routing algorithm (PAR) |
| Input: Network topology G; Flows set F; Constant K |
| Output: Best path for each flow Path_set 1: Path_set ← {} 2: Fs ← Sorting_the_flows(F); 3: foreach fi ∈ Fs do 4: paths = all_simple_paths (G, flow.src, flow.dst); 5: path* ← Find_best_path (G, fi, paths, K); 6: Path_set.append(path*); 7: end 8: return Path_set |
5.2.2. Sorting the Flows
- Class 0: The flows whose GCD with every other flow is 1;
- Class 1: The flows do not affect LCM of the flows set after removal;
- Class 2: Other flows.
| Algorithm 2 Sorting the flows |
| Input: Initial flows set F |
| Output: Flows set after sorted Fs 1: lcm_old = least_common_multiple(F.prd); 2: foreach fi ∈ F do 3: Remove fi from F; 4: lcm_new = least_common_multiple(F.prd); 5: if (lcm_new == lcm_old/fi.prd) then 6: fi.class = 0; 7: else if (lcm_new == lcm_old) 8: fi.class = 1; 9: else 10: fi.class = 2; 11: end 12: Append fi to F; 13: end 14: Fs ← sort F by f.class and f.prd from small to large 15: return Fs |
5.2.3. Find Best Path
| Algorithm 3 Find best path |
| Input: Network topology G; Flow f; Paths set Paths; Constant K |
| Output: Best path for flow f 1: foreach path ∈ paths do 2: hops = len(path) − 1; 3: MSOW = 0; 4: foreach edge ∈ path do 5: edge.prd_list.append (f.prd); 6: wgt ← Calculate wgt (edge, f); 7: edge.SOW += wgt; 8: if (SOW > MSOW) then 9: MSOW = SOW; 10: end 11: end 12: cost = MSOW + K × hops; 13: foreach edge ∈ path do 14: wgt ← Calculate wgt (edge, f); 15: edge.prd_list.remove (f.prd); 16: edge.SOW = edge.SOW − wgt; 17: end 18: end 19: path* ← arg min cost(path*, K); 20: foreach edge ∈ path* do 21: wgt ← Calculate wgt (edge, f); 22: edge.prd_list.remove (f.prd); 23: edge.SOW += wgt; 24: end 25: return path* |
| Algorithm 4 Calculate wgt |
| Input: Edge edge, Flow f |
| Output: Wgt for the f on the edge 1: if (len(edge.prd_list) == 1)) then 2: edge.gcd = fi.prd; 3: else 4: new_gcd = greatest_common_divisor (edge.prd_list); 5: if (new_gcd != edge.gcd) then 6: edge.gcd = new_gcd; 7: Recalculate the edge.SOW for all the previous flows on the edge; 8: end 9: end 10: if (edge.gcd == 1) then 11: wgt = D; (D is a large enough integer.) 12: else 13: wgt = get_wgt (f); 14: end 15: return wgt |
6. Experiments and Evaluation
6.1. Experiment Setup
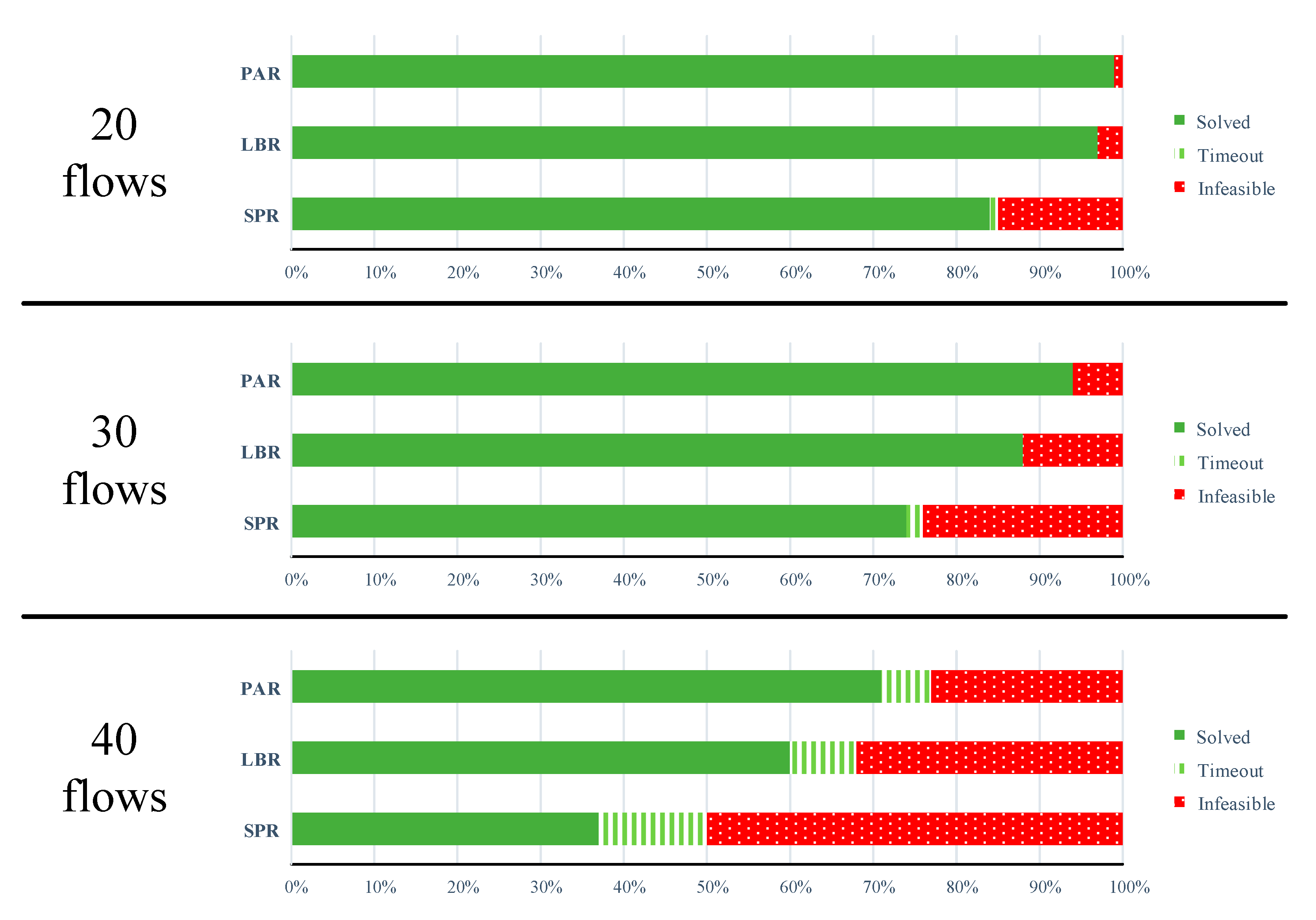
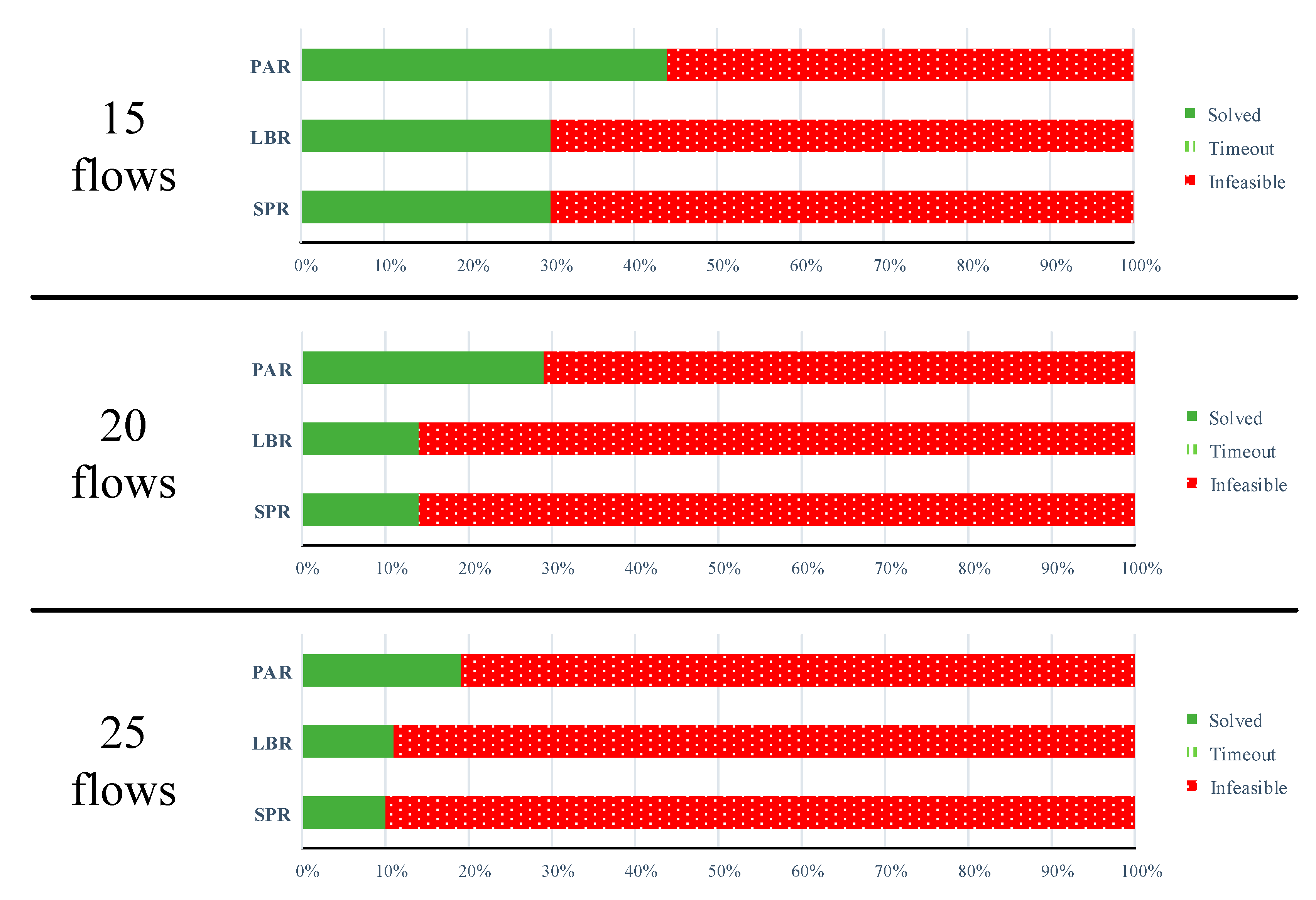
6.2. Evaluation Results
- Solved: One sub-optimal schedule found (optimal solution is not pursued in this paper).
- Timeout: Time limit reached without a feasible schedule.
- Infeasible: Cannot be scheduled with the given flows and routes.
6.2.1. Load Dependency
6.2.2. Topology Dependency
6.2.3. Flow Type Dependency
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bello, L.L.; Steiner, W. A perspective on IEEE time-sensitive networking for industrial communication and automation systems. Proc. IEEE 2019, 107, 1094–1120. [Google Scholar] [CrossRef]
- Craciunas, S.S.; Oliver, R.S.; Chmelík, M.; Steiner, W. Scheduling real-time communication in IEEE 802.1 Qbv time sensitive networks. In Proceedings of the 24th International Conference on Real-Time Networks and Systems, Brest, France, 19–21 October 2016; pp. 183–192. [Google Scholar]
- Ojewale, M.A.; Yomsi, P.M. Routing heuristics for load-balanced transmission in TSN-based networks. ACM Sigbed Rev. 2020, 16, 20–25. [Google Scholar] [CrossRef]
- Singh, S. Routing Algorithms for Time Sensitive Networks. Master’s Thesis, University of Stuttgart, Stuttgart, Germany, 2017. [Google Scholar]
- Nayak, N.G.; Duerr, F.; Rothermel, K. Routing Algorithms for IEEE 802.1Qbv Networks. ACM SIGBED Rev. 2018, 15, 13–18. [Google Scholar] [CrossRef]
- Atallah, A.A.; Hamad, G.B.; Mohamed, O.A. Routing and Scheduling of Time-Triggered Traffic in Time-Sensitive Networks. IEEE Trans. Ind. Inf. 2019, 16, 4525–4534. [Google Scholar] [CrossRef]
- Messenger, J.L. Time-sensitive networking: An introduction. IEEE Commun. Stand. Mag. 2018, 2, 29–33. [Google Scholar] [CrossRef]
- Schweissguth, E.; Danielis, P.; Timmermann, D.; Parzyjegla, H.; Mühl, G. ILP-based joint routing and scheduling for time-triggered networks. In Proceedings of the 25th International Conference on Real-Time Networks and Systems, Grenoble, France, 4–6 October 2017; pp. 8–17. [Google Scholar]
- Dürr, F.; Nayak, N.G. No-wait packet scheduling for IEEE time-sensitive networks (TSN). In Proceedings of the 24th International Conference on Real-Time Networks and Systems, Brest, France, 19–21 October 2016; pp. 203–212. [Google Scholar]
- Steiner, W.; Peón, P.G.; Gutiérrez, M.; Mehmed, A.; Rodriguez-Navas, G.; Lisova, E.; Pozo, F. Next generation real-time networks based on IT technologies. In Proceedings of the 2016 IEEE 21st International Conference on Emerging Technologies and Factory Automation (ETFA), Berlin, Germany, 6–9 September 2016; pp. 1–8. [Google Scholar]
- Guck, J.W.; Van Bemten, A.; Kellerer, W. DetServ: Network models for real-time QoS provisioning in SDN-based industrial environments. IEEE Trans. Netw. Serv. Manag. 2017, 14, 1003–1017. [Google Scholar] [CrossRef]
- Nasrallah, A.; Thyagaturu, A.S.; Alharbi, Z.; Wang, C.; Shao, X.; Reisslein, M.; ElBakoury, H. Ultra-low latency (ULL) networks: The IEEE TSN and IETF DetNet standards and related 5G ULL research. IEEE Commun. Surv. Tutor. 2018, 21, 88–145. [Google Scholar] [CrossRef]
- Avni, G.; Guha, S.; Rodriguez-Navas, G. Synthesizing time-triggered schedules for switched networks with faulty links. In Proceedings of the 13th International Conference on Embedded Software, Chengdu, China, 13–14 August 2016. [Google Scholar]
- Bingqian, L.; Yong, W. Hybrid-GA based static schedule generation for time-triggered ethernet. In Proceedings of the 2016 8th IEEE International Conference on Communication Software and Networks (ICCSN), Beijing, China, 4–6 June 2016; pp. 423–427. [Google Scholar]
- Tindell, K.W.; Burns, A.; Wellings, A.J. Allocating hard real-time tasks: An NP-hard problem made easy. Real Time Syst. 1992, 4, 145–165. [Google Scholar] [CrossRef]
- Pozo, F.; Rodriguez-Navas, G.; Hansson, H. Schedule reparability: Enhancing time-triggered network recovery upon link failures. In Proceedings of the 2018 IEEE 24th International Conference on Embedded and Real-Time Computing Systems and Applications (RTCSA), Hakodate, Japan, 28–31 August 2018; pp. 147–156. [Google Scholar]
- Zhang, D.G.; Zhang, T.; Dong, Y.; Liu, X.H.; Cui, Y.Y.; Zhao, D.X. Novel optimized link state routing protocol based on quantum genetic strategy for mobile learning. J. Netw. Comput. Appl. 2018, 122, 37–49. [Google Scholar] [CrossRef]
- Al-Turjman, F. Cognitive routing protocol for disaster-inspired internet of things. Future Gener. Comput. Syst. 2019, 92, 1103–1115. [Google Scholar] [CrossRef]
- Pop, P.; Raagaard, M.L.; Craciunas, S.S.; Steiner, W. Design optimisation of cyber-physical distributed systems using IEEE time-sensitive networks. IET Cyber Phys. Syst. Theory Appl. 2016, 1, 86–94. [Google Scholar] [CrossRef]
- IEEE. IEEE Standard for Local and Metropolitan Area Networks—Bridges and Bridged Networks—Amendment 24; IEEE: New York, NY, USA, 2016. [Google Scholar]
- Steiner, W.; Craciunas, S.S.; Oliver, R.S. Traffic planning for time-sensitive communication. IEEE Commun. Stand. Mag. 2018, 2, 42–47. [Google Scholar] [CrossRef]
- Atallah, A.A.; Hamad, G.B.; Mohamed, O.A. Fault-resilient topology planning and traffic configuration for IEEE 802.1 Qbv TSN networks. In Proceedings of the 2018 IEEE 24th International Symposium on On-Line Testing and Robust System Design (IOLTS), Platja D’Aro, Spain, 2–4 July 2018; pp. 151–156. [Google Scholar]
- Gavrilut, V.; Zarrin, B.; Pop, P.; Samii, S. Fault-tolerant topology and routing synthesis for IEEE time-sensitive networking. In Proceedings of the 25th International Conference on Real-Time Networks and Systems, Grenoble, France, 4–6 October 2017; pp. 267–276. [Google Scholar]
- Falk, J.; Dürr, F.; Rothermel, K. Exploring practical limitations of joint routing and scheduling for TSN with ILP. In Proceedings of the 2018 IEEE 24th International Conference on Embedded and Real-Time Computing Systems and Applications (RTCSA), Hakodate, Japan, 28–31 August 2018; pp. 136–146. [Google Scholar]
- Yu, Q.; Gu, M. Adaptive Group Routing and Scheduling in Multicast Time-Sensitive Networks. IEEE Access 2020, 8, 37855–37865. [Google Scholar] [CrossRef]
- Hofmann, R.; Nikolić, B.; Ernst, R. Slack-based Traffic Shaping for Real-time Ethernet Networks. In Proceedings of the 2019 IEEE 25th International Conference on Embedded and Real-Time Computing Systems and Applications (RTCSA), Hangzhou, China, 18–21 August 2019; pp. 1–11. [Google Scholar]
- Falk, J.; Dürr, F.; Rothermel, K. Time-Triggered Traffic Planning for Data Networks with Conflict Graphs. In Proceedings of the 2020 IEEE Real-Time and Embedded Technology and Applications Symposium (RTAS), Sydney, Australia, 21–24 April 2020; pp. 124–136. [Google Scholar]
- Arif, F.A.R.; Atia, T.S. Load balancing routing in time-sensitive networks. In Proceedings of the 2016 Third International Scientific-Practical Conference Problems of Infocommunications Science and Technology (PIC S&T), Kharkiv, Ukraine, 4–6 October 2016; pp. 207–208. [Google Scholar]
- Bullynck, M. Modular arithmetic before CF Gauss: Systematizations and discussions on remainder problems in 18th-century Germany. Hist. Math. 2009, 36, 48–72. [Google Scholar] [CrossRef]
- Platt, E.L. Network Science with Python and NetworkX Quick Start Guide: Explore and Visualize Network Data Effectively; Packt Publishing Ltd.: Birmingham, UK, 2019. [Google Scholar]

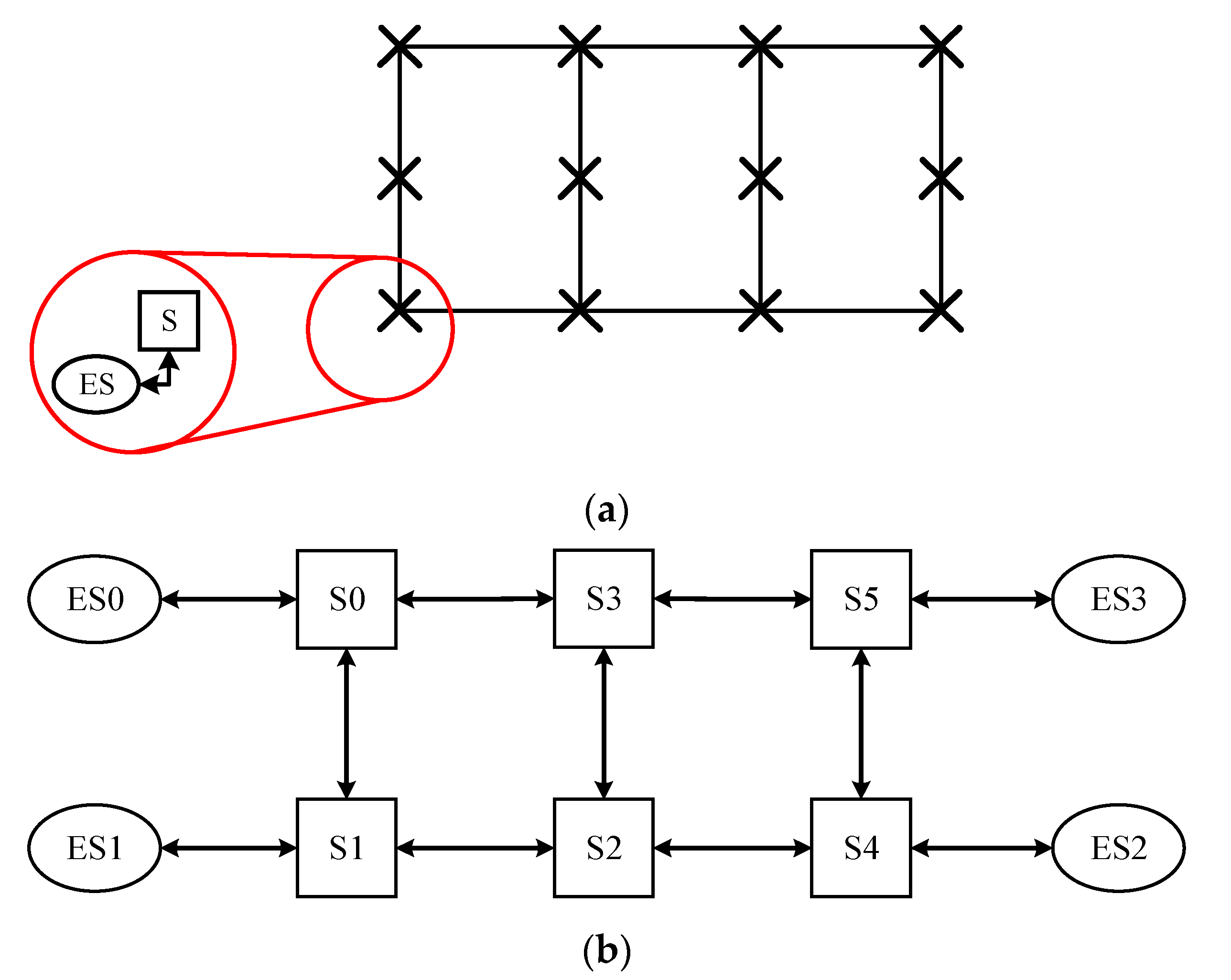

| Notation | Explanation |
|---|---|
| src | The source node of a flow. |
| dst | The destination node of a flow. |
| siz | The size of a flow measured by the length of time consumed during propagation. |
| prd | The cycle period of a flow. |
| MSTL | The maximum scheduled traffic load. |
| LCM | The least common multiple of the periods of all flows. |
| GCD | The greatest common divisor of the periods of all flows. |
| BWu | The used bandwidth. |
| BWt | The total bandwidth, |
| BWr | The residual bandwidth. |
| num | The number of flows that can be accommodated. |
| wgt | The specific weight of a flow. |
| SOW | Sum of wgt. |
| MSOW | The maximum sum of wgt. |
| hops | The number of edge/link in a path. |
| PATH | SOW | TSL | NOF |
|---|---|---|---|
| Path 1 | 1 | 12 | 1 |
| Path 2 | 2/3 | 8 | 2 |
| Path 3 | 3/5 | 9 | 3 |
| Flow ID | Prd | Siz | Pro.1 |
|---|---|---|---|
| F1 | 10 | 1 | 1/6 |
| F2 | 20 | 1 | 1/6 |
| F3 | 30 | 2 | 1/6 |
| F4 | 40 | 2 | 1/6 |
| F5 | 50 | 3 | 1/6 |
| F6 | 60 | 3 | 1/6 |
| Flow ID | Prd | Siz | Pro. |
|---|---|---|---|
| F1 | 9 | 1 | 1/10 |
| F2 | 10 | 1 | 3/10 |
| F3 | 20 | 1 | 3/10 |
| F4 | 30 | 2 | 3/10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, K.; Wu, J.; Jiang, X.; Xiong, D.; Huang, K.; Yao, H.; Xu, W.; Peng, Y.; Liu, Z. A Period-Aware Routing Method for IEEE 802.1Qbv TSN Networks. Electronics 2021, 10, 58. https://doi.org/10.3390/electronics10010058
Huang K, Wu J, Jiang X, Xiong D, Huang K, Yao H, Xu W, Peng Y, Liu Z. A Period-Aware Routing Method for IEEE 802.1Qbv TSN Networks. Electronics. 2021; 10(1):58. https://doi.org/10.3390/electronics10010058
Chicago/Turabian StyleHuang, Kai, Jingkang Wu, Xiaowen Jiang, Dongliang Xiong, Kaitian Huang, Hao Yao, Wenyuan Xu, Yonggang Peng, and Zhili Liu. 2021. "A Period-Aware Routing Method for IEEE 802.1Qbv TSN Networks" Electronics 10, no. 1: 58. https://doi.org/10.3390/electronics10010058
APA StyleHuang, K., Wu, J., Jiang, X., Xiong, D., Huang, K., Yao, H., Xu, W., Peng, Y., & Liu, Z. (2021). A Period-Aware Routing Method for IEEE 802.1Qbv TSN Networks. Electronics, 10(1), 58. https://doi.org/10.3390/electronics10010058





