Regression Model to Predict the Higher Heating Value of Poultry Waste from Proximate Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection, Selection and Nomalization
2.2. Proposed Regression Models
2.3. Evalation and Validation of New Regression Models
3. Results and Discussion
3.1. Effects of Proximate Analysis Composition on HHV
3.2. Derivation of the New Regression Models
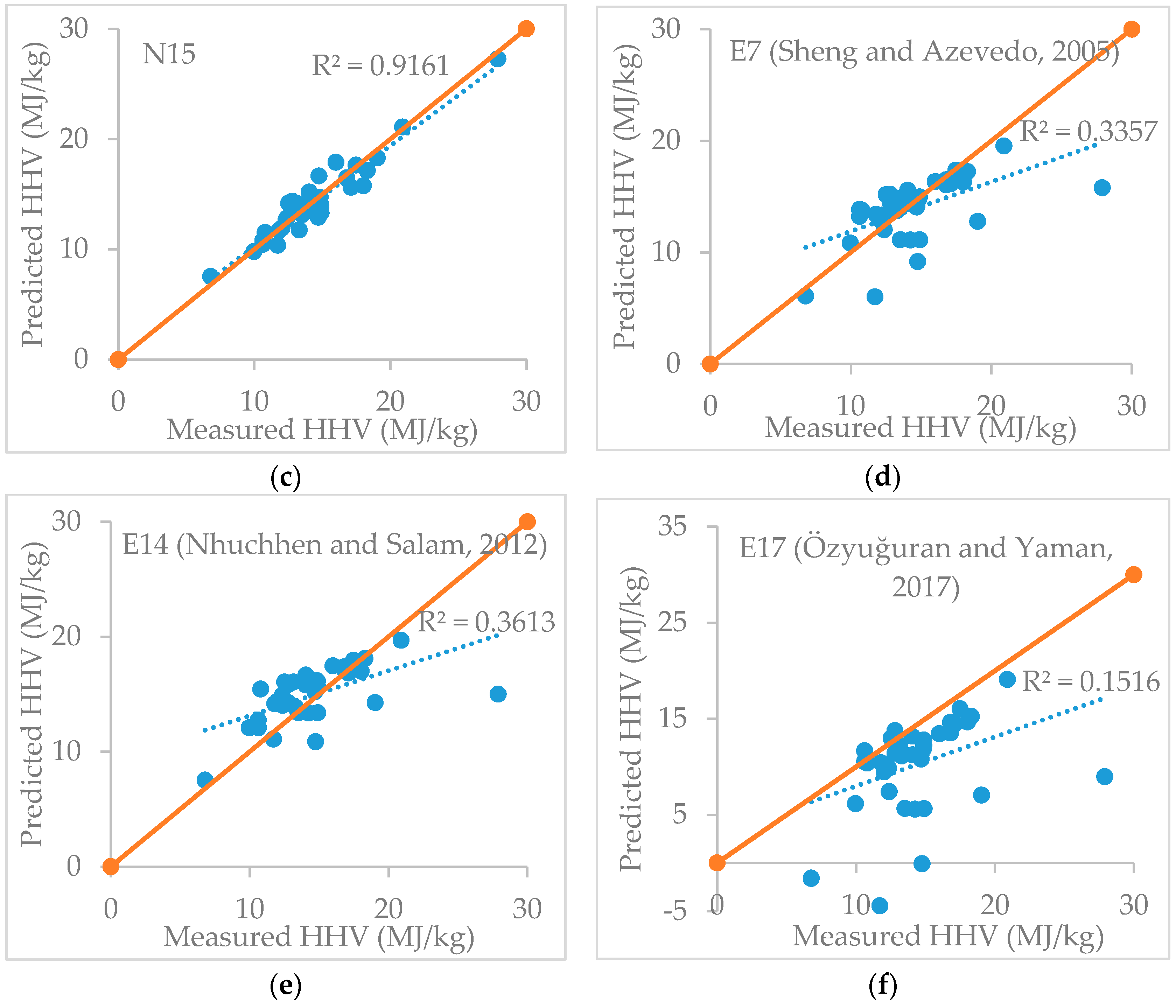
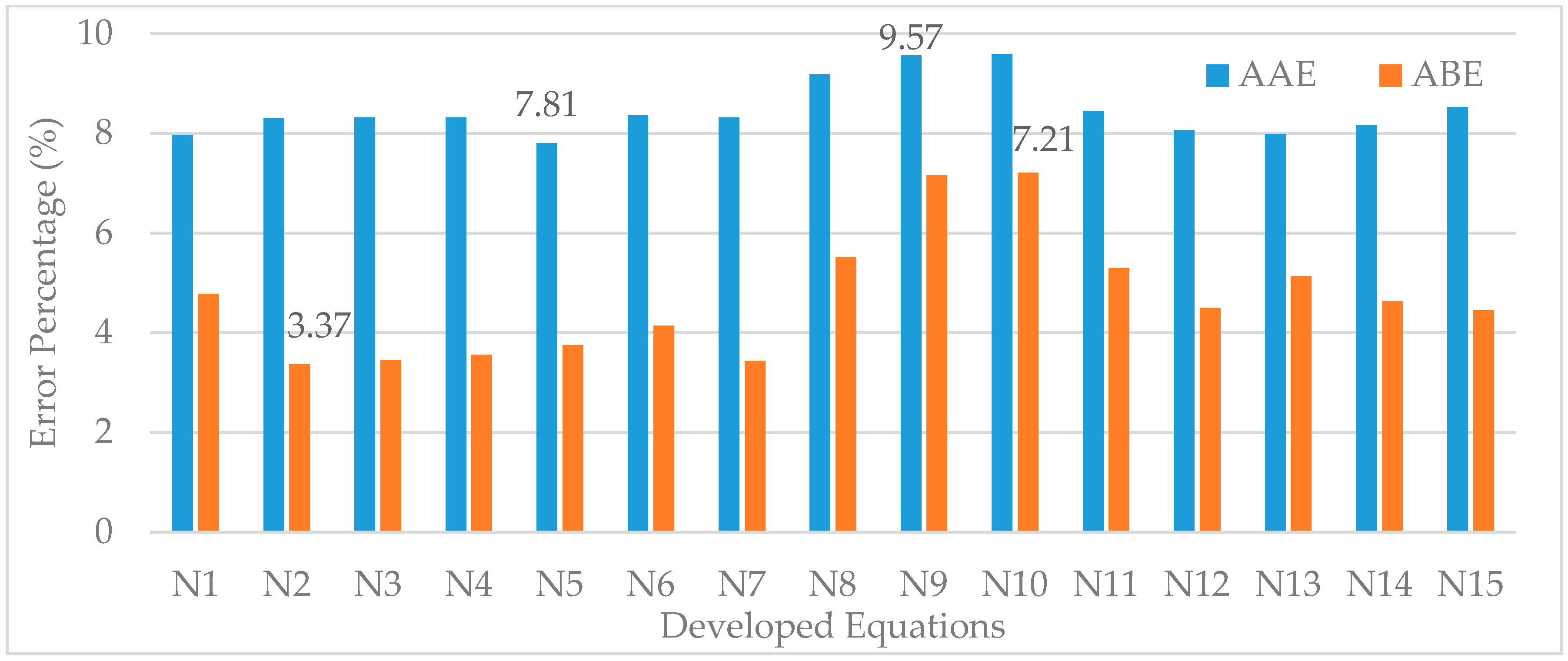
3.3. Validation and Comparative Studies
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lynch, D.; Henihan, A.M.; Bowen, B.; Lynch, D.; McDonnell, K.; Kwapinski, W.; Leahy, J.J. Utilisation of poultry litter as an energy feedstock. Biomass Bioenergy 2013, 49, 197–204. [Google Scholar] [CrossRef]
- Kelleher, B.P.; Leahy, J.J.; Henihan, A.M.; O’dwyer, T.F.; Sutton, D.; Leahy, M.J. Advances in poultry litter disposal technology—A review. Bioresour. Technol. 2002, 83, 27–36. [Google Scholar] [CrossRef]
- Abelha, P.; Gulyurtlu, I.; Boavida, D.; Barros, J.S.; Cabrita, I.; Leahy, J.; Kelleher, B.; Leahy, M. Combustion of poultry litter in a fluidised bed combustor. Fuel 2003, 82, 687–692. [Google Scholar] [CrossRef]
- Li, S.; Wu, A.; Deng, S.; Pan, W.P. Effect of co-combustion of chicken litter and coal on emissions in a laboratory-scale fluidized bed combustor. Fuel Process. Technol. 2008, 89, 7–12. [Google Scholar] [CrossRef]
- Dalólio, F.S.; da Silva, J.N.; de Oliveira, A.C.C.; Tinôco, I.D.F.F.; Barbosa, R.C.; de Oliveira Resende, M.; Albino, L.F.T.; Coelho, S.T. Poultry litter as biomass energy: A review and future perspectives. Renew. Sustain. Energy Rev. 2017, 76, 941–949. [Google Scholar] [CrossRef]
- Sheng, C.; Azevedo, J.L.T. Estimating the higher heating value of biomass fuels from basic analysis data. Biomass Bioenergy 2005, 28, 499–507. [Google Scholar] [CrossRef]
- Yin, C.Y. Prediction of higher heating values of biomass from proximate and ultimate analyses. Fuel 2011, 90, 1128–1132. [Google Scholar] [CrossRef]
- Nhuchhen, D.R.; Salam, P.A. Estimation of higher heating value of biomass from proximate analysis: A new approach. Fuel 2012, 99, 55–63. [Google Scholar] [CrossRef]
- Ghugare, S.B.; Tiwary, S.; Elangovan, V.; Tambe, S.S. Prediction of higher heating value of solid biomass fuels using artificial intelligence formalisms. Bioenergy Res. 2014, 7, 681–692. [Google Scholar] [CrossRef]
- Vargas-Moreno, J.M.; Callejón-Ferre, A.J.; Pérez-Alonso, J.; Velázquez-Martí, B. A review of the mathematical models for predicting the heating value of biomass materials. Renew. Sustain. Energy Rev. 2012, 16, 3065–3083. [Google Scholar] [CrossRef]
- Cordero, T.; Marquez, F.; Rodriguez-Mirasol, J.; Rodriguez, J.J. Predicting heating values of lignocellulosics and carbonaceous materials from proximate analysis. Fuel 2001, 80, 1567–1571. [Google Scholar] [CrossRef]
- Quiroga, G.; Castrillón, L.; Fernández-Nava, Y.; Marañón, E. Physico-chemical analysis and calorific values of poultry manure. Waste Manag. 2010, 30, 880–884. [Google Scholar] [CrossRef] [PubMed]
- Cotana, F.; Coccia, V.; Petrozzi, A.; Cavalaglio, G.; Gelosia, M.; Merico, M.C. Energy valorization of poultry manure in a thermal power plant: Experimental campaign. Energy Procedia 2014, 45, 315–322. [Google Scholar] [CrossRef]
- Majumder, A.K.; Jain, R.; Banerjee, P.; Barnwal, J.P. Development of a new proximate analysis based correlation to predict calorific value of coal. Fuel 2008, 87, 3077–3081. [Google Scholar] [CrossRef]
- Özyuğuran, A.; Yaman, S. Prediction of Calorific Value of Biomass from Proximate Analysis. Energy Procedia 2017, 107, 130–136. [Google Scholar] [CrossRef]
- Huang, C.; Han, L.; Liu, X.; Yang, Z. Models predicting calorific value of straw from the ash content. Int. J. Green Energy 2008, 5, 533–539. [Google Scholar] [CrossRef]
- Küçükbayrak, S.; Dürüs, B.; Meríçboyu, A.E.; Kadioġlu, E. Estimation of calorific values of Turkish lignites. Fuel 1991, 70, 979–981. [Google Scholar] [CrossRef]
- Basu, P. Biomass Gasification and Pyrolysis: Practical Design and Theory, 1st ed.; Elsevier: Oxford, UK, 2010; ISBN 9780123749888. [Google Scholar]
- Demirbas, A. Prediction of higher heating values for vegetable oils and animal fats from proximate analysis data. Energy Source Part A 2009, 31, 1264–1270. [Google Scholar] [CrossRef]
- Parikh, J.; Channiwala, S.A.; Ghosal, G.K. A correlation for calculating HHV from proximate analysis of solid fuels. Fuel 2005, 84, 487–494. [Google Scholar] [CrossRef]
- Jiménez, L.; González, F. Study of the physical and chemical properties of lignocellulosic residues with a view to the production of fuels. Fuel 1991, 70, 947–950. [Google Scholar] [CrossRef]
- Demirbaş, A. Calculation of higher heating values of biomass fuels. Fuel 1997, 76, 431–434. [Google Scholar] [CrossRef]
- Demirbaş, A. Relationships between heating value and lignin, fixed carbon, and volatile material contents of shells from biomass products. Energy Source 2003, 25, 629–635. [Google Scholar] [CrossRef]
- Kathiravale, S.; Yunus, M.N.M.; Sopian, K.; Samsuddin, A.H.; Rahman, R.A. Modeling the heating value of Municipal Solid Waste. Fuel 2003, 82, 1119–1125. [Google Scholar] [CrossRef]
- Thipkhunthod, P.; Meeyoo, V.; Rangsunvigit, P.; Kitiyanan, B.; Siemanond, K.; Rirksomboon, T. Predicting the heating value of sewage sludges in Thailand from proximate and ultimate analyses. Fuel 2005, 84, 849–857. [Google Scholar] [CrossRef]
- Callejón-Ferre, A.J.; Velázquez-Martí, B.; López-Martínez, J.A.; Manzano-Agugliaro, F. Greenhouse crop residues: Energy potential and models for the prediction of their higher heating value. Renew. Sustain. Energy Rev. 2011, 15, 948–955. [Google Scholar] [CrossRef]
- García, R.; Pizarro, C.; Lavín, A.G.; Bueno, J.L. Spanish biofuels heating value estimation. Part II: Proximate analysis data. Fuel 2014, 117, 1139–1147. [Google Scholar] [CrossRef]
- Nhuchhen, D.R.; Afzal, M.T. HHV Predicting Correlations for Torrefied Biomass Using Proximate and Ultimate Analyses. Bioengineering 2017, 4, 7. [Google Scholar] [CrossRef] [PubMed]
- Whitely, N.; Ozao, R.; Artiaga, R.; Cao, Y.; Pan, W.P. Multi-utilization of chicken litter as biomass source. Part I. Combustion. Energy Fuel 2006, 20, 2660–2665. [Google Scholar] [CrossRef]
- Topal, H.; Amirabedin, E. Determination of some important emissions of poultry waste co-combustion. Sci. J. Riga Tech. Univ. Environ. Clim. Technol. 2012, 8, 12–17. [Google Scholar] [CrossRef]
- Reardon, J.P.; Lilley, A.; Wimberly, J.; Browne, K.; Beard, K.; Avens, J. Demonstration of a Small Modular Biopower System Using Poultry Litter; DOE SBIR Phase-I Final Report; Community Power Corporation: Englewood, CO, USA, 2001. Available online: https://www.osti.gov/servlets/purl/794292/ (accessed on 2 May 2018).
- Bock, B.R. Poultry litter to energy: Technical and economic feasibility. Available online: brbock.com/RefFiles/PoultryLitter_Energy.doc (accessed on 2 May 2018).
- Henihan, A.M.; Leahy, M.J.; Leahy, J.J.; Cummins, E.; Kelleher, B.P. Emissions modeling of fluidised bed co-combustion of poultry litter and peat. Bioresour. Technol. 2003, 87, 289–294. [Google Scholar] [CrossRef]
- Ghanim, B.M.; Kwapinski, W.; Leahy, J.J. Hydrothermal carbonisation of poultry litter: Effects of initial pH on yields and chemical properties of hydrochars. Bioresour. Technol. 2017, 238, 78–85. [Google Scholar] [CrossRef] [PubMed]
- Patel, B.; McQuigg, K.; Toerne, R. Integration of poultry Litter Gasification with Conventional Pulverized Coal Fired Power Plant. Available online: http://infohouse.p2ric.org/ref/35/34198.pdf (accessed on 2 May 2018).
- Ekpo, U.; Ross, A.B.; Camargo-Valero, M.A.; Williams, P.T. A comparison of product yields and inorganic content in process streams following thermal hydrolysis and hydrothermal processing of microalgae, manure and digestate. Bioresour. Technol. 2016, 200, 951–960. [Google Scholar] [CrossRef] [PubMed]
- Kantarli, I.C.; Kabadayi, A.; Ucar, S.; Yanik, J. Conversion of poultry wastes into energy feedstocks. Waste Manag. 2016, 56, 530–539. [Google Scholar] [CrossRef] [PubMed]
- Florin, N.H.; Maddocks, A.R.; Wood, S.; Harris, A.T. High-temperature thermal destruction of poultry derived wastes for energy recovery in Australia. Waste Manag. 2009, 29, 1399–1408. [Google Scholar] [CrossRef] [PubMed]
- Priyadarsan, S.; Annamalai, K.; Sweeten, J.M.; Holtzapple, M.T.; Mukhtar, S. Co-gasification of blended coal with feedlot and chicken litter biomass. Proc. Combust. Inst. 2005, 30, 2973–2980. [Google Scholar] [CrossRef]
- Miller, S.F.; Miller, B.G. The occurrence of inorganic elements in various biofuels and its effect on ash chemistry and behavior and use in combustion products. Fuel Process. Technol. 2007, 88, 1155–1164. [Google Scholar] [CrossRef]
- Cantrell, K.B.; Hunt, P.G.; Uchimiya, M.; Novak, J.M.; Ro, K.S. Impact of pyrolysis temperature and manure source on physicochemical characteristics of biochar. Bioresour. Technol. 2012, 107, 419–428. [Google Scholar] [CrossRef] [PubMed]
- Striūgas, N.; Zakarauskas, K.; Džiugys, A.; Navakas, R.; Paulauskas, R. An evaluation of performance of automatically operated multi-fuel downdraft gasifier for energy production. Appl. Therm. Eng. 2014, 73, 1151–1159. [Google Scholar] [CrossRef]
- Giuntoli, J.; De Jong, W.; Arvelakis, S.; Spliethoff, H.; Verkooijen, A.H.M. Quantitative and kinetic TG-FTIR study of biomass residue pyrolysis: Dry distiller’s grains with solubles (DDGS) and chicken manure. J. Anal. Appl. Pyrolysis 2009, 85, 301–312. [Google Scholar] [CrossRef]
- Burra, K.G.; Hussein, M.S.; Amano, R.S.; Gupta, A.K. Syngas evolutionary behavior during chicken manure pyrolysis and air gasification. Appl. Energy 2016, 181, 408–415. [Google Scholar] [CrossRef]
- Mehmood, S.; Reddy, B.V.; Rosen, M.A. Energy analysis of a biomass co-firing based pulverized coal power generation system. Sustainability 2012, 4, 462–490. [Google Scholar] [CrossRef]
- Leahy, M.J.; Henihan, A.M.; Kelleher, B.P.; Leahy, J.J.; O’Connor, J. Mitigation of Large-Scale Organic Waste Damage Incorporating a Demonstration of a Closed Loop Conversion of Poultry Waste to Energy at the Point of Source, (2000-LS-1-M2) Final Report. 2007. Available online: https://ulir.ul.ie/handle/10344/4053 (accessed on 2 May 2018).
- Ghani, W.A.W.A.K. Co-Combustion of Biomass Fuels with Coal in a Fluidised Bed Combustor. Ph.D. Thesis, University of Sheffield, Sheffield, UK, May 2005. [Google Scholar]
- Vamvuka, D.; Sfakiotakis, S.; Panopoulos, K. An experimental study on the thermal valorization of municipal and animal wastes. Int. J. Energy Environ. Econ. 2013, 4, 191–198. [Google Scholar]
- Taupe, N.; Jeahy, J.J.; Kwapinski, W. Gasification and Pyrolysis of Poultry Litter—An Opportunity to Produce Bioenergy and Nutrient Rich Biochar; Joint Scientific Workshop: Erfurt, Germany, 2015. [Google Scholar]
- Jia, L.; Anthony, E.J. Combustion of poultry-derived fuel in a coal-fired pilot-scale circulating fluidized bed combustor. Fuel Process. Technol. 2011, 92, 2138–2144. [Google Scholar] [CrossRef]
- Dayananda, B.S.; Sreepathi, L.K. An experimental study on gasification of chicken litter. Int. Res. J. Environ. Sci. 2013, 2, 63–67. [Google Scholar]
- Di Gregorio, F.; Santoro, D.; Arena, U. The effect of ash composition on gasification of poultry wastes in a fluidized bed reactor. Waste Manag. Res. 2014, 32, 323–330. [Google Scholar] [CrossRef] [PubMed]
- Manure to Energy Feasibility Study for Duncannon Borough. Available online: http://www.gabi-software.com/uploads/media/Manure_to_Energy_Feasibility_Study_03.pdf (accessed on 2 May 2018).
- Acharya, B.; Dutta, A.; Mahmud, S.; Tushar, M.; Leon, M. Ash analysis of poultry litter, willow and oats for combustion in boilers. J. Biomass Biofuel 2014, 1, 16–26. [Google Scholar] [CrossRef]
- Akkaya, A.V. Proximate analysis based multiple regression models for higher heating value estimation of low rank coals. Fuel Process. Technol. 2009, 90, 165–170. [Google Scholar] [CrossRef]
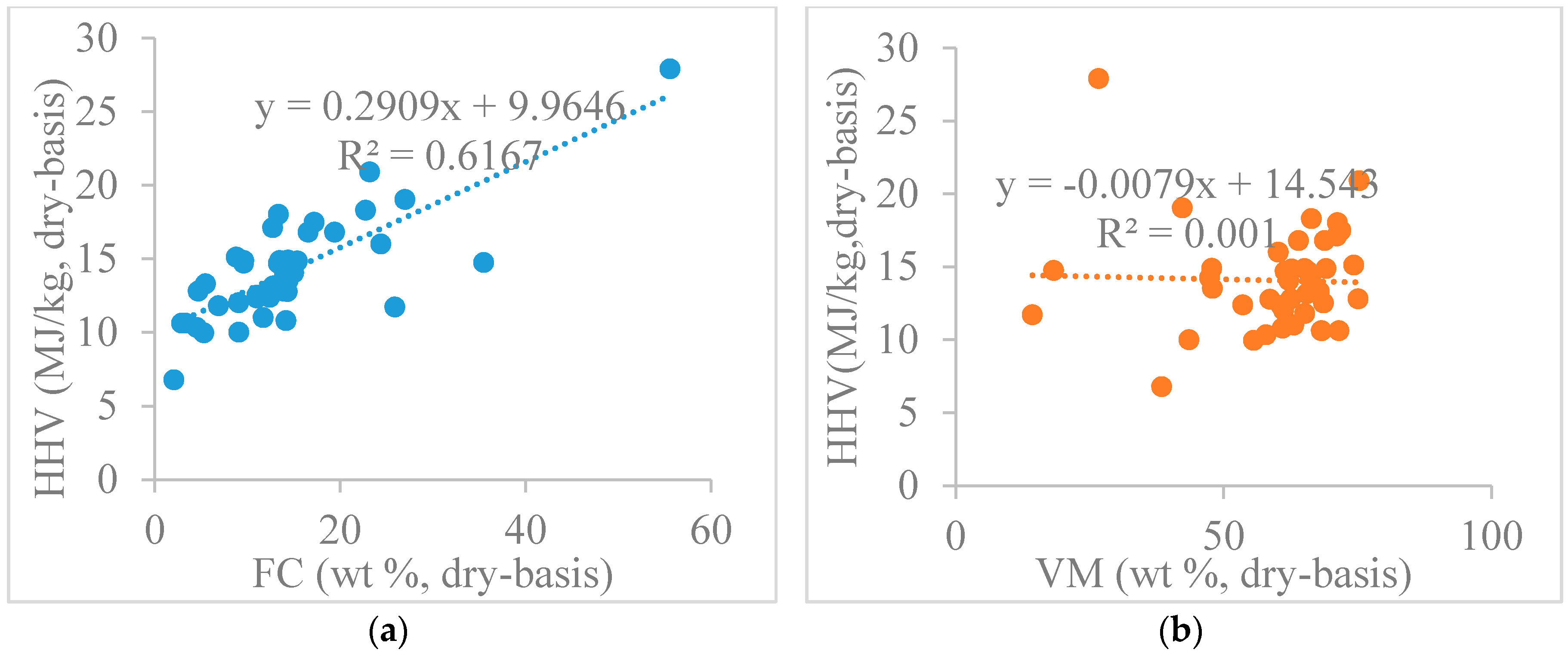
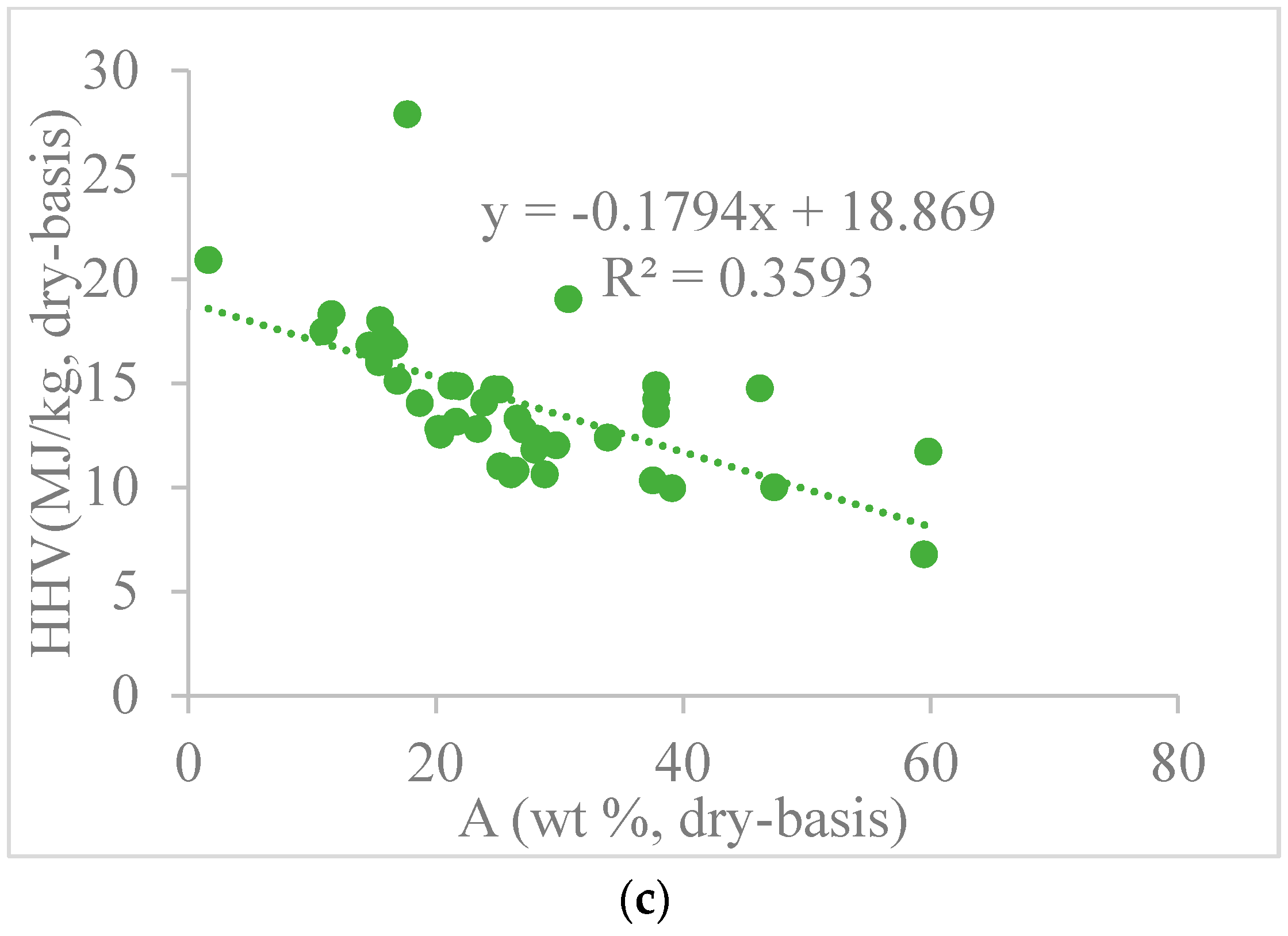
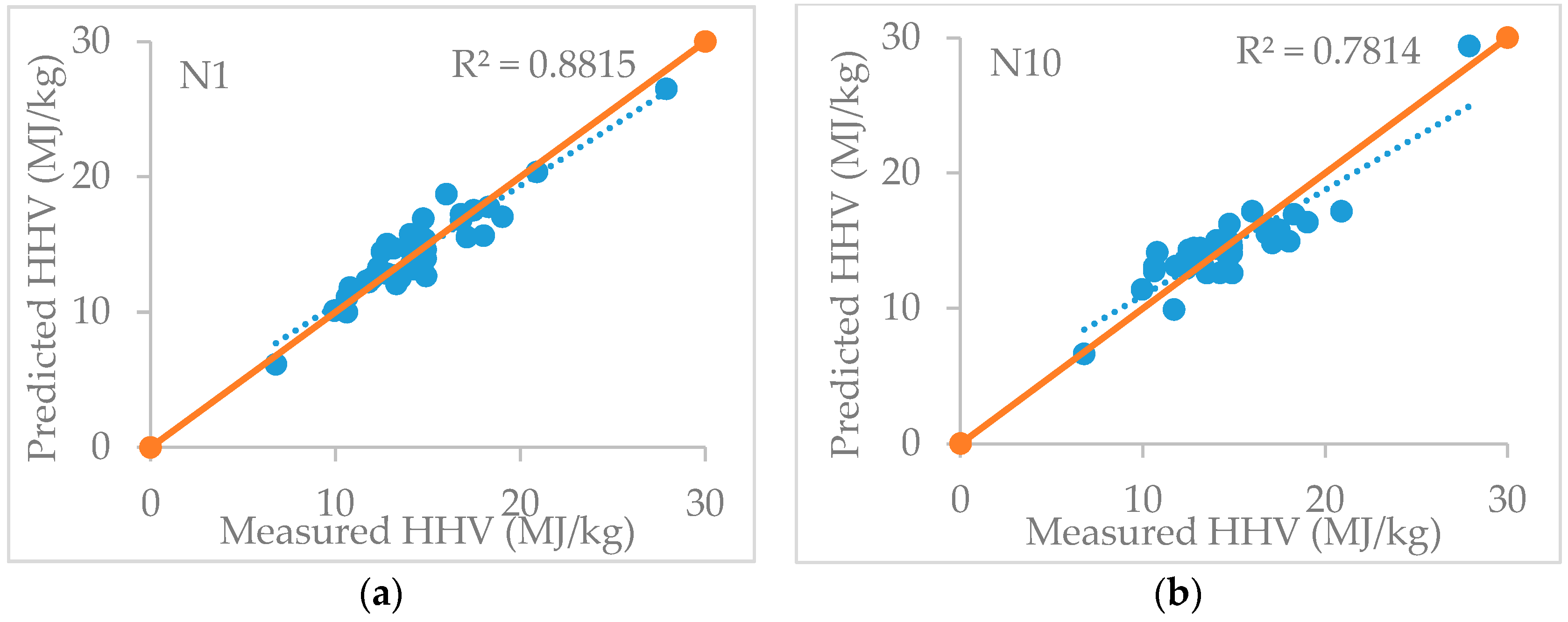

| Existing Models | HHV (MJ/kg) * | Raw Materials | Ref. |
|---|---|---|---|
| E1 | HHV = −10.81408 + 0.3133 (VM + FC) | Lignocellulosic Residues | [21] |
| E2 | HHV = 76.56 − 1.3 (VM + A) + 7.3 × 10−3 (VM + A)2 | Coal | [17] |
| E3 | HHV = 0.196 (FC) + 14.119 | Biomass | [22] |
| E4 | HHV = 0.3543 FC + 0.1708 VM | Lignocellulosics & Charcoals | [11] |
| E5 | HHV = −0.066 (FC)2 + 0.5866 (FC) + 8.752 | Shell of biomass | [23] |
| E6 | HHV = 0.356047 VM − 0.118035 FC − 5.600613 | Municipal solid waste | [24] |
| E7 | HHV = 19.914 − 0.2324 A | Biomass fuels | [6] |
| E8 | HHV = 0.3536 (FC) + 0.1559 (VM) − 0.0078 A | Solid fuels | [20] |
| E9 | HHV = 0.25575 VM + 0.28388 FC − 2.38638 | Sewage sludge | [25] |
| E10 | HHV = 18.96016 − 0.22527 A | Straw | [16] |
| E11 | HHV = −0.1882 (VM) + 32.94 | Vegetable oil and tallow | [19] |
| E12 | HHV = 0.1905 VM + 0.2521 FC | Biomass | [7] |
| E13 | HHV = −2.057 − 0.092 A + 0.279 VM | Greenhouse crop residues | [26] |
| E14 | HHV = 20.7999 − 0.3214 VM/FC + 0.0051 (VM/FC)2 − 11.2277 A/VM + 4.4953 (A/VM)2 − 0.7223 (A/VM)3 + 0.038 (A/VM)4 + 0.0076 FC/A | Biomass | [8] |
| E15 | HHV = 1.83 × 104 − 3.98 A2 − 112.10 A | Spanish biofuels | [27] |
| E16 | HHV = 0.1846 VM + 0.3525 FC | Torrefied biomass | [28] |
| E17 | HHV = 10.982 + 0.1136 VM − 0.2848 A | Biomass | [15] |
| No. | FC 1 | VM 2 | ASH 3 | HHV 4 | Ref. |
|---|---|---|---|---|---|
| 1 | 2.98 | 68.25 | 28.77 | 10.62 | [3] |
| 2 | 6.88 | 65.16 | 27.96 | 11.8 | [4] |
| 3 | 9.07 | 61.2 | 29.73 | 12.02 | [29] |
| 4 | 11.02 | 60.77 | 28.21 | 12.33 | [29] |
| 5 | 5.31 | 55.61 | 39.09 | 9.96 | [29] |
| 6 | 2.08 | 38.46 | 59.46 | 6.78 | [29] |
| 7 | 13.36 | 71.26 | 15.49 | 18.02 | [1] |
| 8 | 14.4 | 47.93 | 37.79 | 13.52 | [1] |
| 9 | 14.4 | 47.82 | 37.79 | 14.9 | [1] |
| 10 | 11.05 | 68.63 | 20.33 | 12.52 | [30] |
| 11 | 12.4 | 53.6 | 33.9 | 12.38 | [31] |
| 12 | 15.4 | 62.7 | 21.9 | 14.84 | [31] |
| 13 | 15 | 66.3 | 18.7 | 14.05 | [31] |
| 14 | 17.2 | 71.9 | 10.9 | 17.48 | [31] |
| 15 | 14 | 62.2 | 23.9 | 14.07 | [31] |
| 16 | 13.49 | 65.1 | 21.61 | 14.87 | [32] |
| 17 | 2.91 | 68.28 | 28.81 | 10.62 | [33] |
| 18 | 12.74 | 71.11 | 16.16 | 17.11 | [34] |
| 19 | 13.36 | 61.49 | 25.15 | 14.69 | [35] |
| 20 | 22.77 | 66.39 | 11.54 | 18.3 | [36] |
| 21 | 24.4 | 60.2 | 15.4 | 16 | [37] |
| 22 | 23.2 | 75.3 | 1.6 | 20.9 | [38] |
| 23 | 19.42 | 63.97 | 16.61 | 16.8 | [39] |
| 24 | 9.63 | 69.13 | 21.25 | 14.87 | [40] |
| 25 | 27 | 42.3 | 30.7 | 19.03 | [41] |
| 26 | 35.5 | 18.3 | 46.2 | 14.75 | [41] |
| 27 | 16.56 | 68.83 | 14.61 | 16.8 | [42] |
| 28 | 5.5 | 67.9 | 26.6 | 13.3 | [43] |
| 29 | 9.6 | 65.7 | 24.7 | 14.7 | [43] |
| 30 | 12.8 | 65.56 | 21.65 | 13.15 | [44] |
| 31 | 14.45 | 47.42 | 37.83 | 14.24 | [45] |
| 32 | 14.17 | 60.99 | 26.42 | 10.79 | [46] |
| 33 | 13.88 | 62.55 | 23.39 | 12.8 | [46] |
| 34 | 25.9 | 14.3 | 59.8 | 11.71 | [20] |
| 35 | 3.37 | 71.54 | 26.09 | 10.62 | [47] |
| 36 | 55.6 | 26.7 | 17.7 | 27.9 | [48] |
| 37 | 4.7 | 75.1 | 20.2 | 12.8 | [49] |
| 38 | 14.3 | 58.64 | 27.06 | 12.77 | [50] |
| 39 | 11.7 | 63.1 | 25.2 | 11 | [38] |
| 40 | 9.08 | 43.57 | 47.35 | 10 | [39] |
| 41 | 8.8 | 74.3 | 16.9 | 15.11 | [41] |
| 42 | 4.53 | 57.93 | 37.54 | 10.33 | [51] |
| 43 | - | - | 17.2 | 14.59 | [52] |
| 44 | - | - | 25.1 | 13.67 | [52] |
| 45 | - | - | 22.9 | 15.28 | [53] |
| 46 | - | 26.56 | 10.6 | 14.587 | [13] |
| 47 | - | 64.43 | 15.41 | 11.552 | [13] |
| 48 | 3.3 | 54.3 | - | 10.1 | [54] |
| 49 | 11.98 | 63.96 | 24.06 | 14.34 |
| No. | Proposed New Models * | Note |
|---|---|---|
| 1 | HHV = a + bFC + cVM + dA | Linear (FC, VM, A) |
| 2 | HHV = a + bFC + cVM | Linear (FC, VM) |
| 3 | HHV = a + bFC + cASH | Linear (FC, A) |
| 4 | HHV = a + bVM + cASH | Linear (VM, A) |
| 5 | HHV = a + bFC2 + cVM + dA | Quadratic (FC), Linear (VM, A) |
| 6 | HHV = a + bFC + cVM2 + dA | Quadratic (VM), Linear (FC, A) |
| 7 | HHV = a + bFC + cVM + dA2 | Quadratic (A), Linear (FC, VM) |
| 8 | HHV = a + bFC2 + cVM2 + dA | Quadratic (FC, VM), Linear (A) |
| 9 | HHV = a + bFC2 + cVM + dA2 | Quadratic (FC, A), Linear (VM) |
| 10 | HHV = a + bFC2 + cVM2 + dA2 | Quadratic (FC, VM, A) |
| 11 | HHV = a + bFC + cVM + dA + eVM2 + fVM3 | Linear (FC, VM, A), Quadratic & Cubic (VM) |
| 12 | HHV = a + bFC + cVM + dA + eFC × VM | Linear (FC, VM, A), Interaction (FC&VM) |
| 13 | HHV = a + bFC + cVM + dA + eFC × A | Linear (FC, VM, A), Interaction (FC&A) |
| 14 | HHV = a + bFC + cVM + dA + eVM × A | Linear (FC, VM, A), Interaction (VM&A) |
| 15 | HHV = a + bFC + cVM + dA + eVM2 + fVM3 + gFC × A | Linear (FC, VM, A), Quadratic & Cubic (VM), Interaction (FC&A) |
| No. | Developed New Regression Model * | Percentage (%) | |||
|---|---|---|---|---|---|
| R2 | R2(adj) | AAE | ABE | ||
| N1 | HHV = 174.3 − 1.335 FC − 1.596 VM − 1.749 A | 88.15 | 87.08 | 7.02 | 0.68 |
| N2 | HHV = −0.33 + 0.4109 FC + 0.1461 VM | 85.72 | 84.88 | 7.50 | 0.70 |
| N3 | HHV = 14.355 + 0.2642 FC − 0.1480 A | 86.11 | 85.29 | 7.42 | 0.69 |
| N4 | HHV = 40.89 − 0.2651 VM − 0.4138 A | 86.73 | 85.95 | 7.25 | 0.61 |
| N5 | HHV = 36.27 + 0.00104 FC2 − 0.2140 VM − 0.3651 A | 87.03 | 85.85 | 7.23 | 0.75 |
| N6 | HHV = 20.60 + 0.1900 FC − 0.000823 VM2 − 0.2281 A | 86.43 | 85.20 | 7.28 | 0.66 |
| N7 | HHV = −0.02 + 0.4077 FC + 0.1426 VM − 0.00006 A2 | 85.72 | 84.42 | 7.53 | 0.73 |
| N8 | HHV = 28.46 + 0.002104 FC2 − 0.001712 VM2 − 0.3205 A | 86.38 | 85.14 | 7.73 | 0.90 |
| N9 | HHV = 18.16 + 0.00425 FC2 − 0.0463 VM − 0.00288 A2 | 78.37 | 76.40 | 10.36 | 1.47 |
| N10 | HHV = 15.41 + 0.004800 FC2 − 0.000145 VM2 − 0.002430 A2 | 78.14 | 76.15 | 10.31 | 1.53 |
| N11 | HHV = 143.7 − 1.161 FC − 0.364 VM − 1.562 A − 0.02458 VM2 + 0.000173 VM3 | 91.54 | 90.18 | 6.05 | 0.47 |
| N12 | HHV = 174.3 − 1.331 FC − 1.595 VM − 1.751 A − 0.00012 FC × VM | 88.16 | 86.68 | 7.01 | 0.46 |
| N13 | HHV = 172.2 − 1.262 FC − 1.587 VM − 1.698 A − 0.00237 FC × A | 88.91 | 87.53 | 6.74 | 0.57 |
| N14 | HHV = 175.2 − 1.332 FC − 1.615 VM − 1.780 A + 0.000652 VM × A | 88.32 | 86.86 | 7.05 | 0.20 |
| N15 | HHV = 140.2 − 1.167 FC − 0.210 VM − 1.558 A − 0.02739 VM2 + 0.000191 VM3 + 0.00104 FC × A | 91.62 | 89.94 | 5.98 | −0.35 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, X.; Lee, S.; Soto, A.-m.; Chen, G. Regression Model to Predict the Higher Heating Value of Poultry Waste from Proximate Analysis. Resources 2018, 7, 39. https://doi.org/10.3390/resources7030039
Qian X, Lee S, Soto A-m, Chen G. Regression Model to Predict the Higher Heating Value of Poultry Waste from Proximate Analysis. Resources. 2018; 7(3):39. https://doi.org/10.3390/resources7030039
Chicago/Turabian StyleQian, Xuejun, Seong Lee, Ana-maria Soto, and Guangming Chen. 2018. "Regression Model to Predict the Higher Heating Value of Poultry Waste from Proximate Analysis" Resources 7, no. 3: 39. https://doi.org/10.3390/resources7030039
APA StyleQian, X., Lee, S., Soto, A.-m., & Chen, G. (2018). Regression Model to Predict the Higher Heating Value of Poultry Waste from Proximate Analysis. Resources, 7(3), 39. https://doi.org/10.3390/resources7030039







