Damage Effects and Fractal Characteristics of Coal Pore Structure during Liquid CO2 Injection into a Coal Bed for E-CBM
Abstract
:1. Introduction
2. Coal Samples and Methods
2.1. Coal Samples Re-Preparation
- (1)
- Three specimens were infiltrated in LqCO2 at −50 °C for 4 h with self-developed equipment. A previous study indicated that the cooling radius of LqCO2 injected into coal seam was approximately 10 m, meanwhile the coal around the injection hole was fully infiltrated after 4 h of LqCO2 injection [25,26].
- (2)
- After the infiltration process, raw and treated coal samples were added into a vacuum oven at 65 °C for 12 h until the mass changes in the initial and treated coal samples did not exceed 0.2% [5].
- (3)
- All the coal samples were desorbed in a vacuum chamber for 48 h to remove the mixed gases adsorbed on the surface of the coal samples.
2.2. Fractal Dimension from LP-N2-Ad Isotherms
2.3. Fractal Dimension from MIP
2.4. Grey System Theory
3. Results and Discussion
3.1. Evolution and Fractal Characteristics of Adsorbed Pores
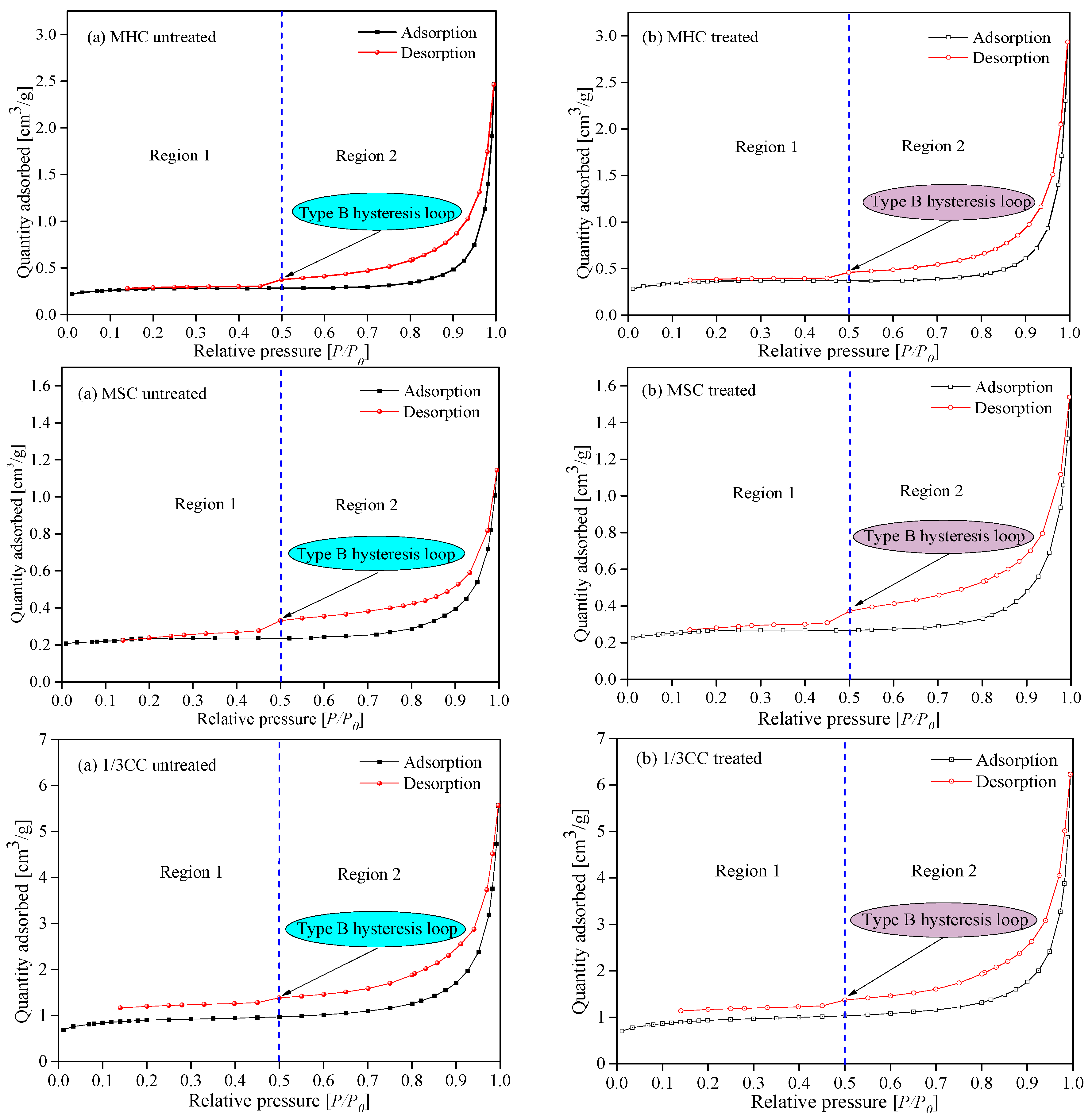
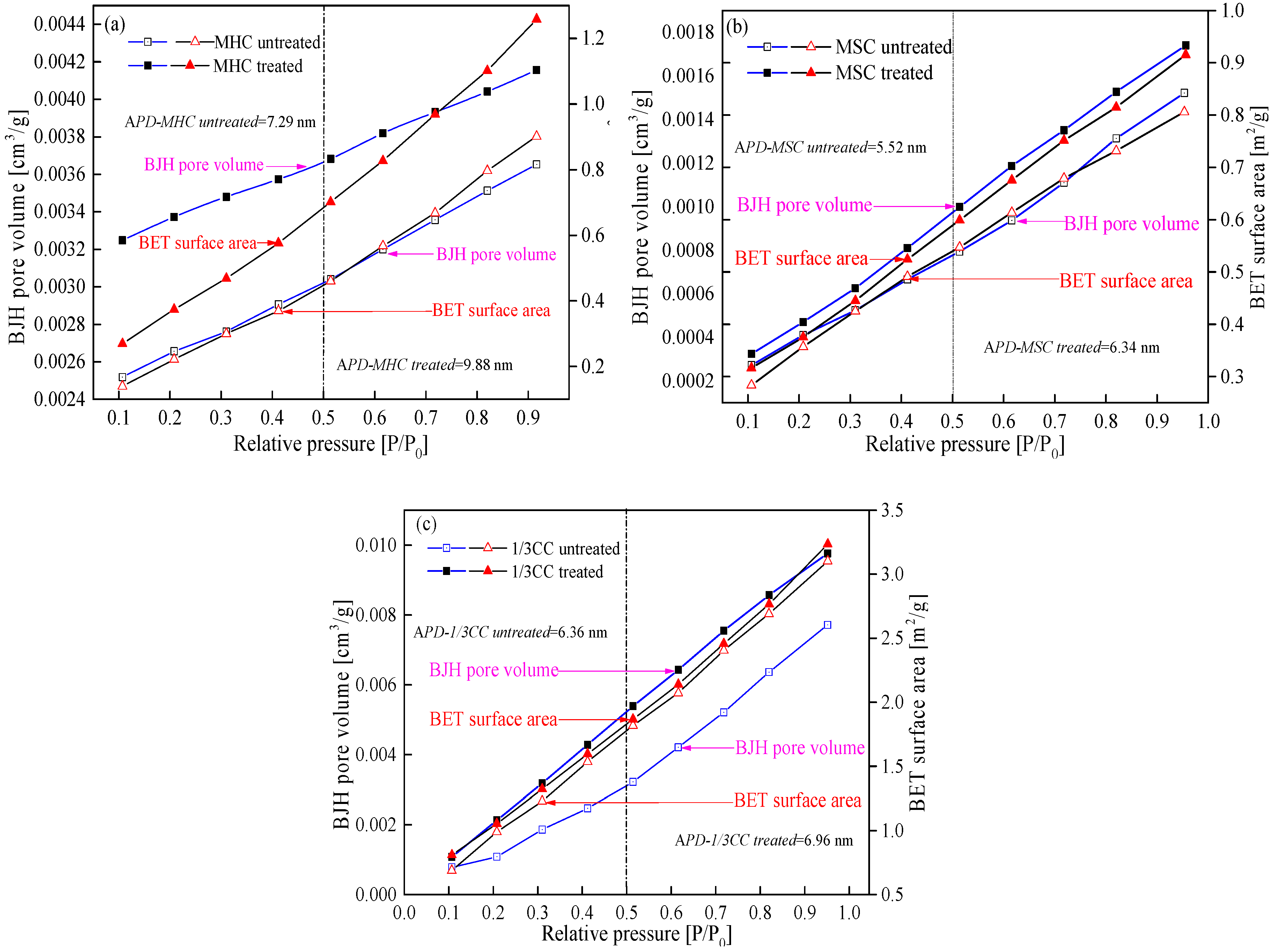
3.1.1. LP-N2-Ad Isotherms and Pore Structure Parameters Analysis of Adsorbed Pores
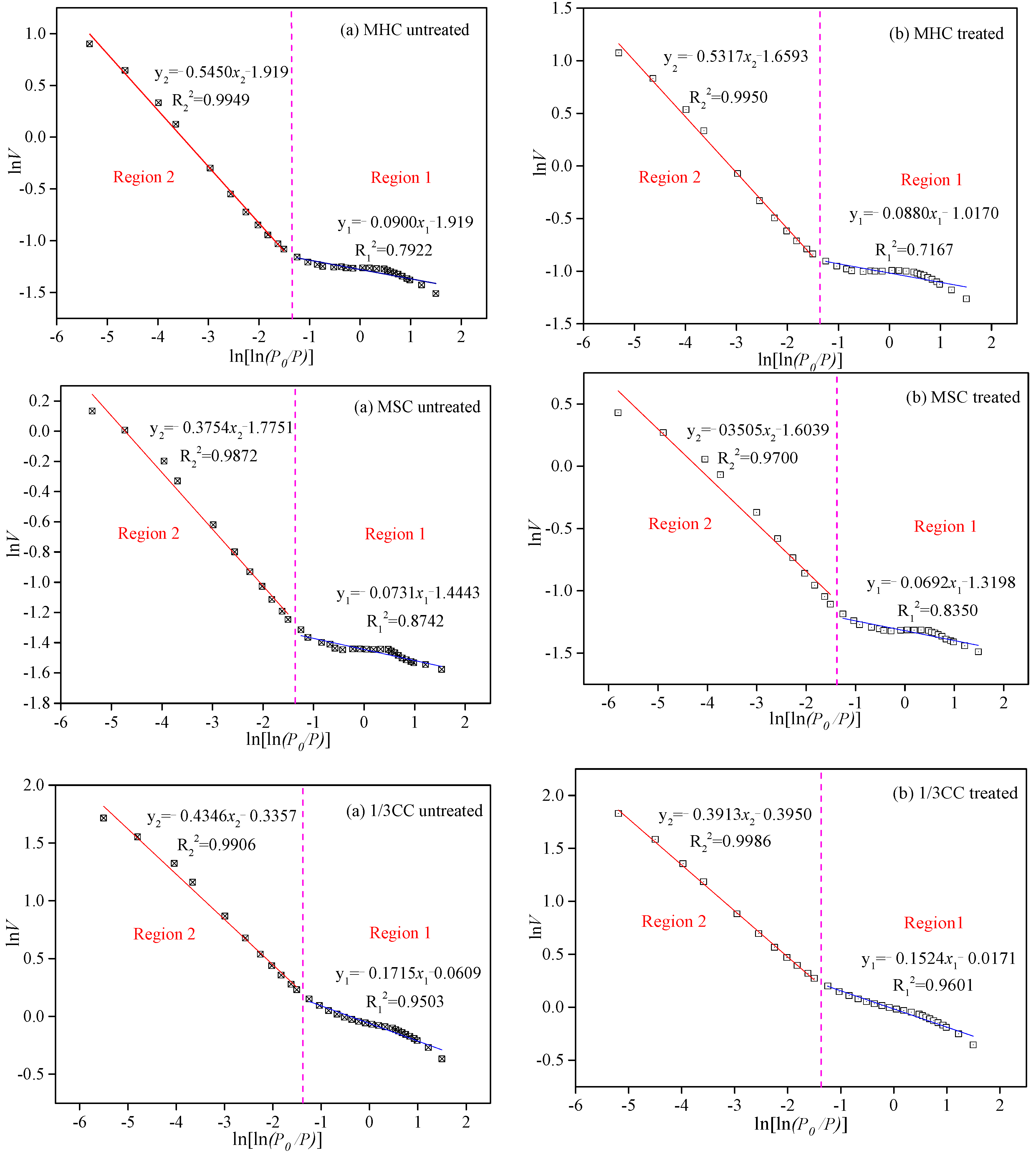
3.1.2. Fractal Characteristics of the Adsorbed Pores from Raw and LqCO2-Treated Coal Samples
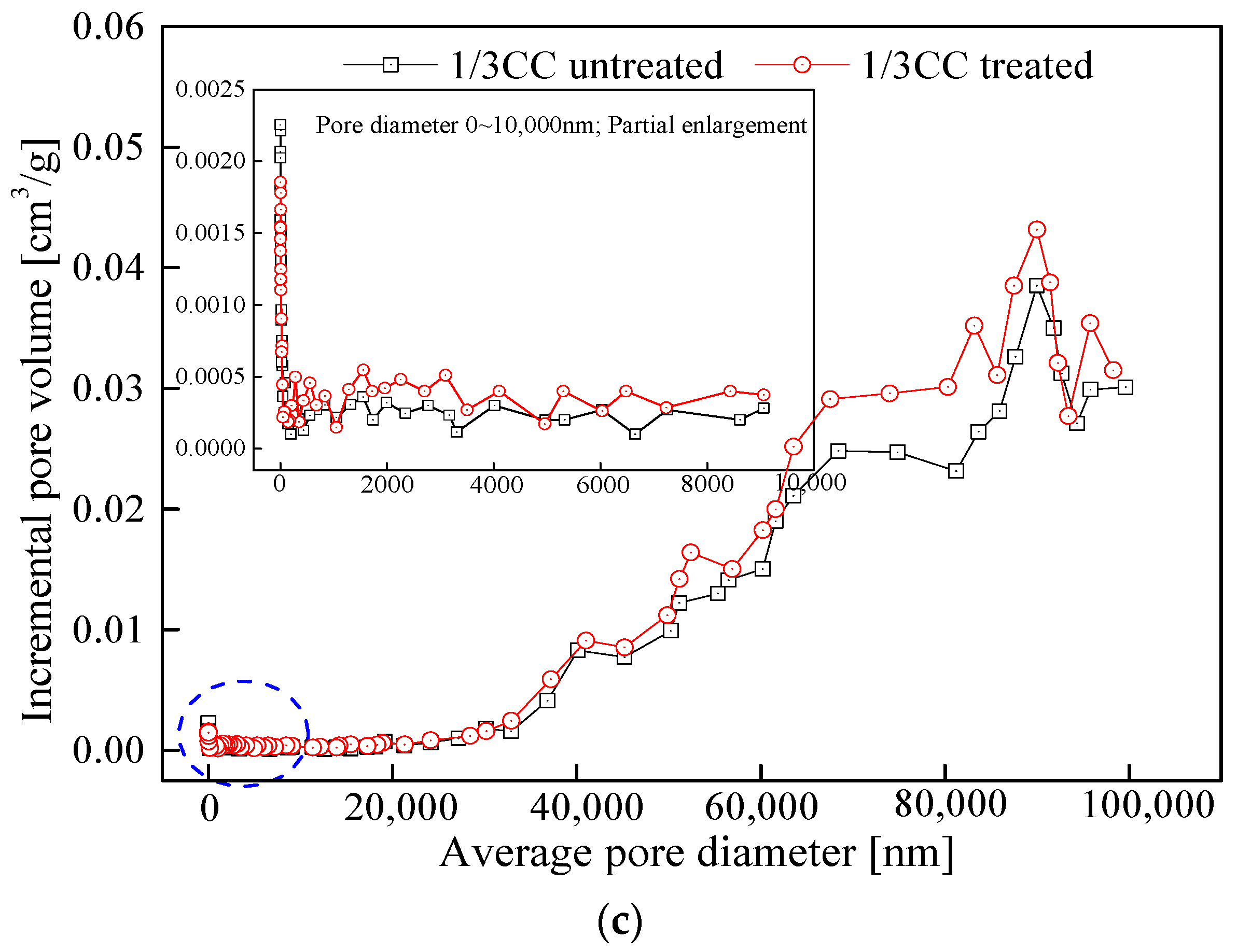
3.2. Variations and Fractal Characteristics of Seepage Pores
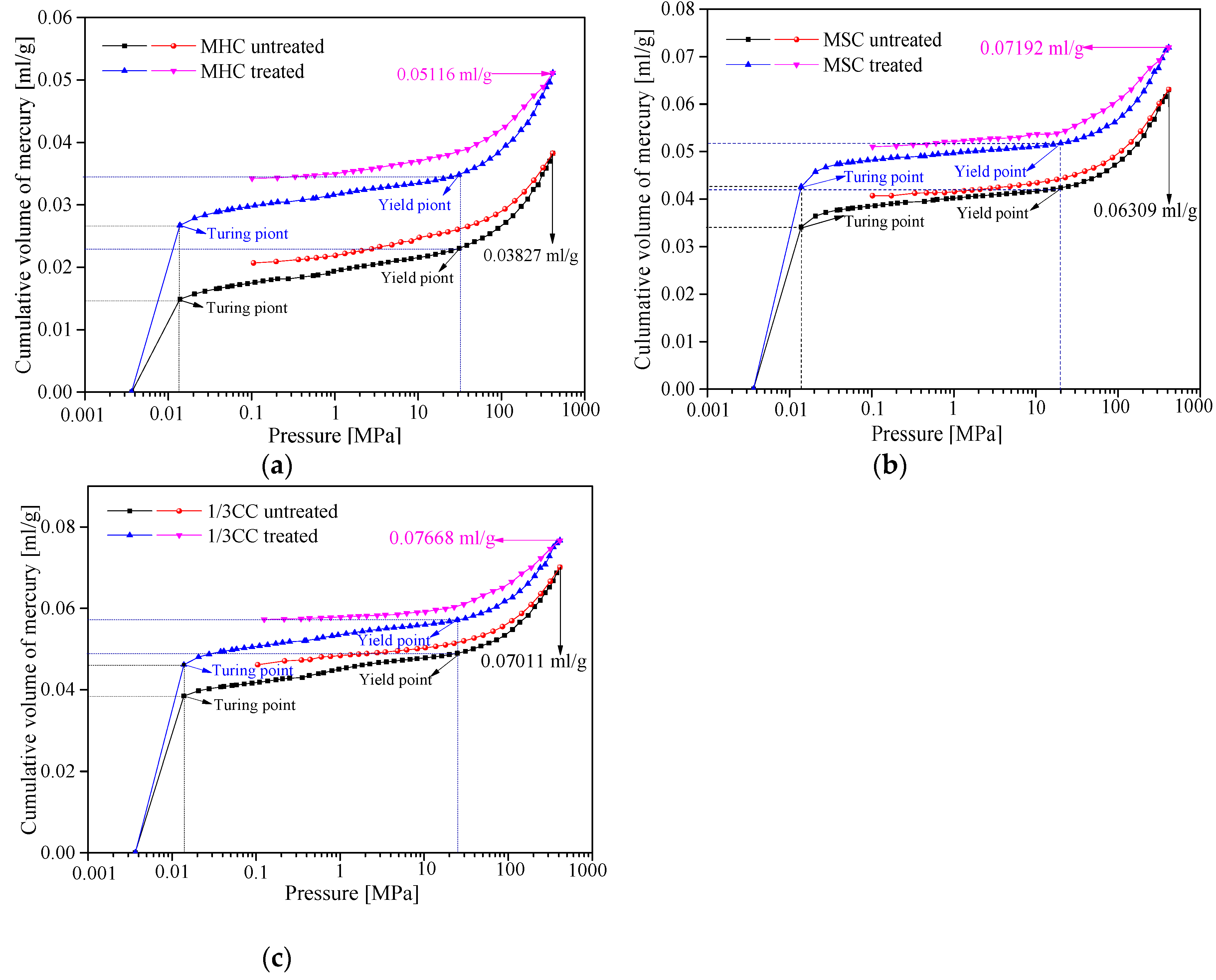
3.2.1. MIP Curves
3.2.2. Pore Structure Parameters Analysis of Seepage Pores
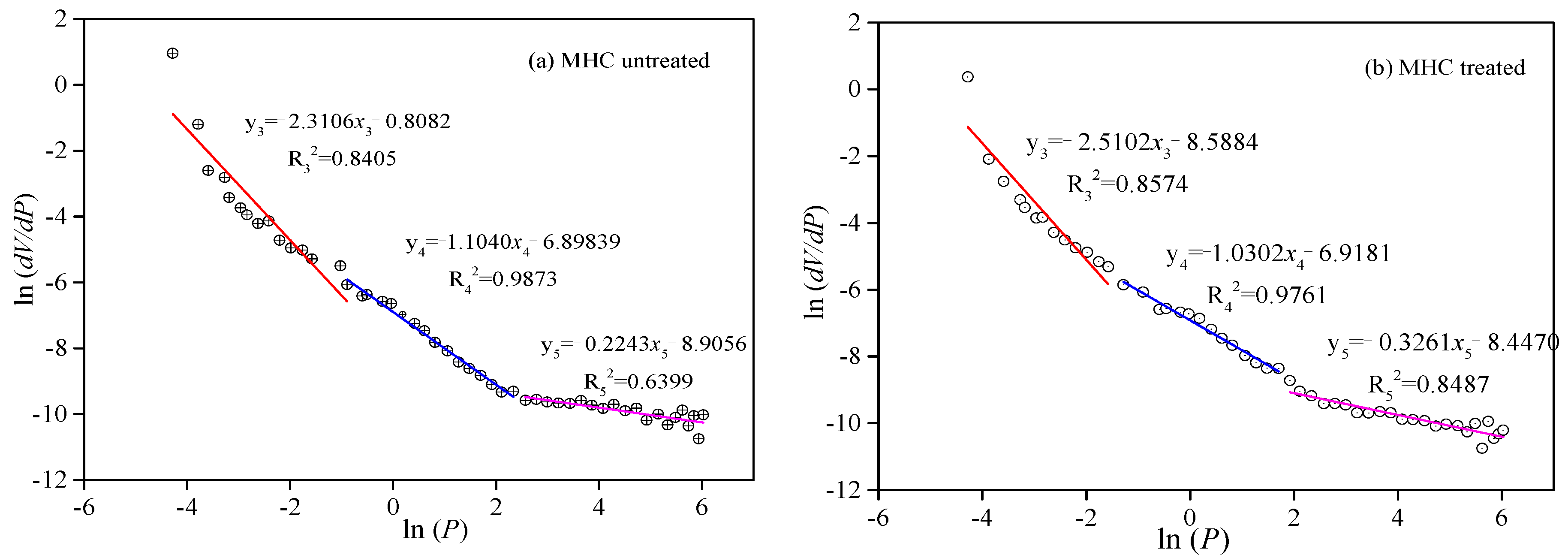
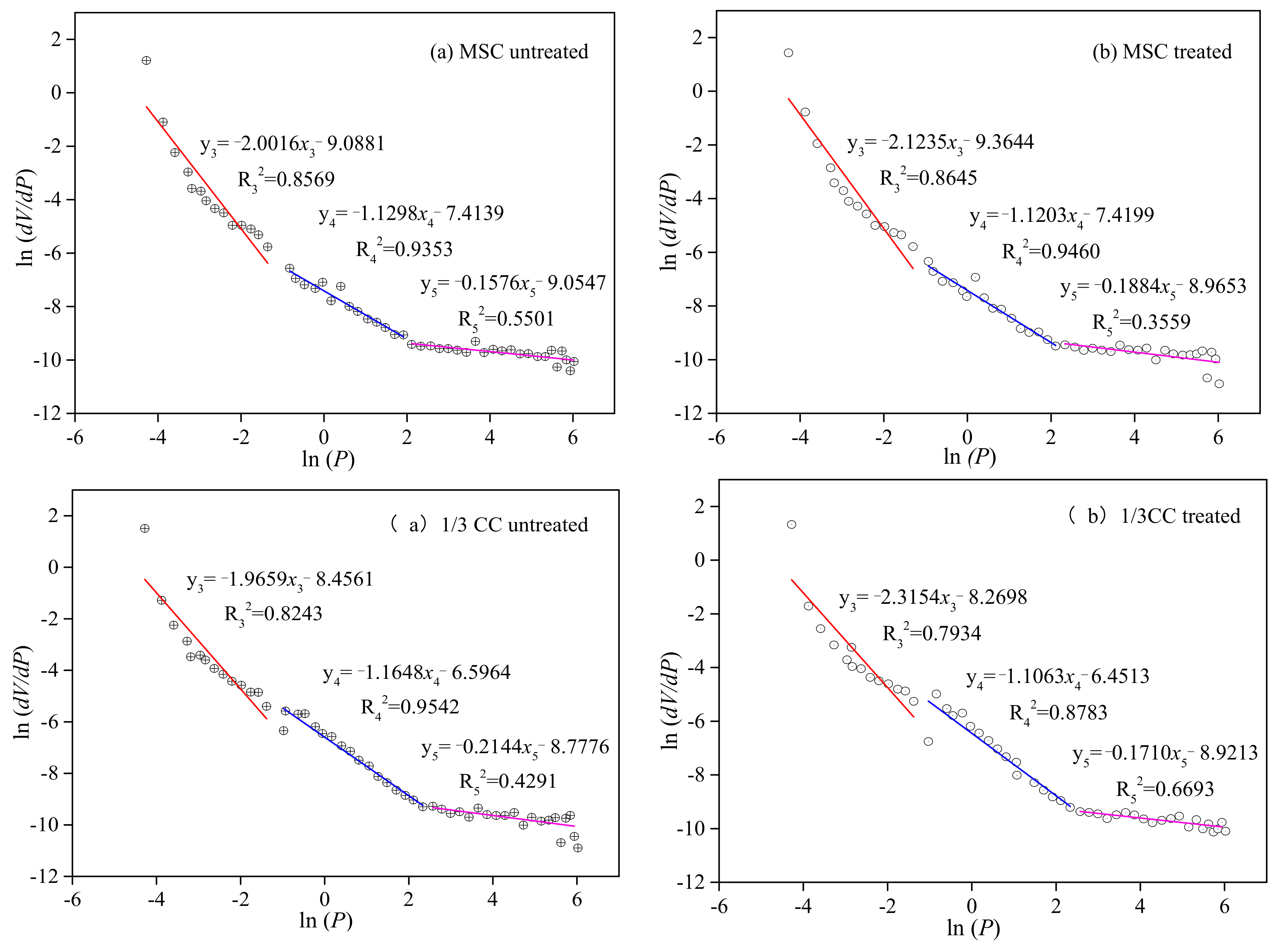
3.2.3. Fractal Features of Seepage Pores between the Initial and LqCO2-Treated Coal Samples
3.3. Grey Relational Application and Discussion
3.3.1. Calculated Degrees of Correlation
3.3.2. Characterization of the Fractal Dimension and Coal Pore Structure Parameters by the Grey Correlation Degree
4. Conclusions
- (1)
- The adsorption isotherms of three coal specimens were of type B, which illustrates that the coal samples contained numerous cylindrical shaped-pores with one closed side and slit-shaped and bottle-shaped pores. From the LP-N2-Ad and MIP tests, the APD (average growth rate of 18.20%), SSA (average growth rate of 7.38%), and TPV (average growth rate of 18.26%) were higher after the coal specimens were infiltrated by liquid CO2. This is because of the large number of new pores generated and plenty of micropores and transition pores transferred into mesopores and macropores. Therefore, the adsorption ability was lower while the seepage capacity was higher, which is suitable for CBM recovery.
- (2)
- Fractal dimensions D1 (average of 2.58), D2 (average of 2.90), and D4 (average of 2.91) exhibited the same tendencies for the treated coal samples, which were typically higher than those of the original specimens (D1, average of 2.55, D2, average of 2.87, and D4, average of 2.86), indicating that the coal surfaces are rougher and the internal pore structures are more complex after the coal samples were treated by LCO2.
- (3)
- The grey relational theory was applied to analyze the relationship between fractal dimension and coal pore structure parameters. The correlation degree was higher than , indicating that the fractal features of the treated coal specimens are more evident. The degree of correlation between the fractal dimension and pore structure parameters show that the SSA of the raw and treated coal samples was largest, followed by APD, porosity, TPV, and permeability. The SSA, APD, and porosity positively influence the fractal characteristics of coal samples, but TPV and permeability exert negative influences.
Author Contributions
Funding
Conflicts of Interest
References
- Fu, F.; Liu, H.; Polenske, K.R.; Li, Z. Measuring the energy consumption of China’s domestic investment from 1992 to 2007. Appl. Energy 2013, 102, 1267–1274. [Google Scholar] [CrossRef]
- Chandran Govindaraju, V.G.R.C.; Tang, C.F. The dynamic links between CO2 emissions, economic growth and coal consumption in China and India. Appl. Energy 2013, 104, 310–318. [Google Scholar] [CrossRef]
- Wang, K.; Wei, Y.; Zhang, X. Energy and emissions efficiency patterns of Chinese regions: A multi-directional efficiency analysis. Appl. Energy 2013, 104, 105–116. [Google Scholar] [CrossRef]
- Zhao, L.; Dong, H.; Tang, J.; Cai, J. Cold energy utilization of liquefied natural gas for capturing carbon dioxide in the flue gas from the magnesite processing industry. Energy 2016, 105, 45–56. [Google Scholar] [CrossRef]
- Wen, H.; Li, Z.; Deng, J.; Shu, C.; Lai, W.; Wang, Q. Influence on coal pore structure during liquid CO2-ECBM process for CO2 utilization. J. CO2 Util. 2017, 21, 543–552. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, L.; Zhang, X. Environmental impact of coal mine methane emissions and responding strategies in China. Int. J. Greenh. Gas Control. 2011, 5, 157–166. [Google Scholar] [CrossRef]
- Wang, H.; Cheng, Y.; Wang, W.; Xu, R. Research on comprehensive CBM extraction technology and its applications in China’s coal mines. J. Nat. Gas Sci. Eng. 2014, 20, 200–207. [Google Scholar] [CrossRef]
- Green, U.; Aizenstat, Z.; Gieldmeister, F.; Cohen, H. CO2 adsorption inside the pore structure of different rank coals during low temperature oxidation of open air coal stockpiles. Energy Fuels 2011, 25, 4211–4215. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Z.; Chen, X.; Wang, L. Increasing permeability of coal seams using the phase energy of liquid carbon dioxide. J. CO2 Util. 2017, 19, 112–119. [Google Scholar] [CrossRef]
- Wang, H.; Ran, Q.; Liao, X.; Zhao, X.; Xu, M.; Fang, P. Study of the CO2 ECBM and sequestration in coalbed methane reservoirs with SRV. J. Nat. Gas Sci. Eng. 2016, 33, 678–686. [Google Scholar] [CrossRef]
- Ranathunga, A.S.; Perera, M.S.A.; Ranjith, P.G.; Zhang, X.; Wu, B. Super-critical carbon dioxide flow behavior in low rank coal: A meso-scale experimental study. J. CO2 Util. 2017, 20, 1–3. [Google Scholar] [CrossRef]
- IUPAC. Reporting physisorption of naturally fractured reservoirs. Trans. Soc. Petrol. Eng. AIME 1963, 228, 245–255. [Google Scholar]
- Hodot, B.B. Outburst of Coal and Coalbed Gas; China Industry Press: Beijing, China, 1966; pp. 23–25. [Google Scholar]
- Clarkson, C.R.; Wood, J.; Burgis, S.; Aquino, S.; Freeman, M. Nanopore-structure analysis and permeability predictions for a tight gas siltstone reservoir by use of low-pressure adsorption and mercury-intrusion techniques. SPE Reserv. Eval. Eng. 2012, 15, 648–661. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, D.; Tang, S.; Huang, W.; Liu, Z.; Che, Y. Fractal characterization of seepage-pores of coals from China: An investigation on permeability of coals. Comput. Geosci. 2009, 35, 1159–1166. [Google Scholar] [CrossRef]
- Fu, H.; Tang, D.; Xu, T.; Xu, H.; Tao, S.; Li, S. Characteristics of pore structure and fractal dimension of low rank coal: A case study of lower jurassic Xishanyao coal in the southern Junggar basin, NW China. Fuel 2017, 193, 254–264. [Google Scholar] [CrossRef]
- Pan, J.; Peng, C.; Wan, X.; Zheng, D.; Lv, R.; Wang, K. Pore structure characteristics of coal-bearing organic shale in Yuzhou coalfield, China using low temperature N2 adsorption and FESEM methods. J. Pet. Sci. Eng. 2017, 153, 234–243. [Google Scholar] [CrossRef]
- Okolo, G.N.; Everson, R.C.; Neomagus, H.W.J.P.; Roberts, M.J.; Sakurovs, R. Comparing the porosity and surface areas of coal as measured by gas adsorption, mercury intrusion and SAXS techniques. Fuel 2015, 141, 293–304. [Google Scholar] [CrossRef]
- Zou, M.; Wei, C.; Zhang, M.; Shen, J.; Chen, Y. Classifying coal pores and estimating reservoir parameters by nuclear magnetic resonance and mercury intrusion porosimetry. Energy Fuels 2013, 27, 3699–3708. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, S.; Elsworth, D.; Jiang, J.; Zhu, J. Pore structure characterization of coal by synchrotron small-angle X-ray scattering and transmission electron microscopy. Energy Fuels 2014, 28, 3704–3711. [Google Scholar] [CrossRef]
- Xu, J.; Zhai, C.; Liu, S.; Qin, L.; Wu, S. Pore variation of three different metamorphic coals by multiple freezing-thawing cycles of liquid CO2 injection for coalbed methane recovery. Fuel 2017, 208, 41–51. [Google Scholar] [CrossRef]
- Vishal, V. In-situ disposal of CO2: Liquid and supercritical CO2 permeability in coal at multiple down-hole stress conditions. J. CO2 Util. 2017, 17, 235–242. [Google Scholar] [CrossRef]
- Zhang, Y.; Lebedev, M.; Sarmadivaleh, M.; Barifcani, A. Swelling-induced changes in coal microstructure due to supercritical CO2 injection. Geophys. Res. Lett. 2016, 43, 9077–9083. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Sarmadivaleh, M.; Lebedev, M.; Barifcani, A.; Yu, H. Micro-scale fracturing mechanisms in coal induced by adsorption of supercritical CO2. Int. J. Coal Geol. 2017, 175, 40–50. [Google Scholar] [CrossRef]
- Wen, H.; Li, Z.; Wang, Z.; Ma, L.; Guo, Y.; Wang, X. Experiment on the liquid CO2 fracturing process for increasing permeability and the characteristics of crack propagation in coal seam. J. China Coal Soc. 2016, 41, 2793–2799. (In Chinese) [Google Scholar]
- Ma, L.; Wei, G.; Wang, S.; Li, Z.; Liu, X. Experimental study of displacing and replacing methane in low permeability coal seam by liquid CO2 injection. J. Chongqing Univ. 2018, 31, 251–277. (In Chinese) [Google Scholar]
- Tsakiroglou, C.D.; Payatakers, A.C. Characterization of the pore structure of reservoir rocks with the aid of serial auctioning analysis, mercury porosimetry and network simulation. Adv. Water Resour. 2000, 23, 773–789. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Les Objects Fractals: Forme, Hazard et Dimension; Flammarion: Paris, France, 1975. (In French) [Google Scholar]
- Yang, F.; Ning, Z.; Liu, H. Fractal characteristics of shales from a shale gas reservoir in the Sichuan Basin, China. Fuel 2014, 115, 378–384. [Google Scholar] [CrossRef]
- Pfeifer, P.; Wu, Y.; Cole, M.W.; Krim, J. Multilayer adsorption on a fractally rough surface. Phys. Rev. Lett. 1989, 62, 1977–2000. [Google Scholar] [CrossRef] [PubMed]
- Mahamud, M.M. Textural characterization of active carbons using fractal analysis. Fuel Process. Technol. 2006, 87, 907–917. [Google Scholar] [CrossRef]
- Cai, Y.; Liu, D.; Yao, Y.; Li, J.; Liu, J. Fractal characteristics of coal pores based on classic geometry and thermodynamics models. Acta Geol. Sin. 2011, 85, 1150–1162. [Google Scholar] [CrossRef]
- Frisen, W.I.; Mikula, R.J. Fractal dimensions of coal particles. J. Colloid Interface Sci. 1987, 120, 263–271. [Google Scholar] [CrossRef]
- Deng, J.L. Grey Theory; Huazhong University of science and Technology Press: Wuhan, China, 2002; pp. 218–227. (In Chinese) [Google Scholar]
- Chiang, Y.M.; Hsieh, H.H. The use of the Taguchi method with grey relation analysis to optimize the thin-film sputtering process with multiple quality characteristic in color filter manufacturing. Comput. Ind. Eng. 2009, 56, 648–661. [Google Scholar] [CrossRef]
- Rao, R.; Yadava, V. Multi-objective optimization of Nd: YAG laser cutting of thin superalloy sheet using grey relational analysis with entropy measurement. Opt. Laser Technol. 2009, 41, 922–930. [Google Scholar]
- Khanna, R.; Kumar, A.; Garg, M.P.; Singh, A.; Sharma, N. Multiple performance characteristics optimization for Al 7075 on electric discharge drilling by Taguchi grey relational theory. J. Ind. Eng. Int. 2015, 11, 459–472. [Google Scholar] [CrossRef]
- Takara, E.A.; Quiroga, E.; Matozfernandez, D.A.; Ochoa, N.A.; Ramirezpastor, A.J. Fractional statistical theory of finite multilayer adsorption. Appl. Surf. Sci. 2016, 360, 14–19. [Google Scholar] [CrossRef]
- Zhu, J.F.; Liu, J.Z.; Yang, Y.M.; Cheng, J.; Zhou, J.H.; Cen, K.F. Fractal characteristics of pore structures in 13 coal specimens: Relationship among fractal dimension, pore structure parameter, and slurry ability of coal. Fuel Process. Technol. 2016, 149, 256–267. [Google Scholar] [CrossRef]
- Everett, D.H.; Stone, F.S. The Structure and Properties of Porous Materials; Butterworths: London, UK, 1958; pp. 68–94. [Google Scholar]
- Nie, B.; Liu, X.; Yang, L.; Meng, J.; Li, X. Pore structure characterization of different rank coals using gas adsorption and scanning electron microscopy. Fuel 2015, 158, 908–917. [Google Scholar] [CrossRef]
- Sun, X.; Wang, Z.; Sun, B.; Wang, W. Research on hydrate formation rules in the formations for liquid CO2 fracturing. Fuel 2016, 33, 1390–1401. [Google Scholar]
- Tang, J.; Feng, L.; Li, Y.; Liu, J.; Liu, X. Fractal and pore structure analysis of Shengli lignite during drying process. Powder Technol. 2016, 303, 251–259. [Google Scholar] [CrossRef]
- Wang, G.; Wang, K.; Ren, T. Improved analytic methods for coal surface area and pore size distribution determination using 77 K nitrogen adsorption experiment. Int. J. Min. Sci. Technol. 2014, 24, 329–334. [Google Scholar] [CrossRef]
- Liu, C.; Wang, G.; Sang, S.; Gilani, W.; Rudolph, V. Fractal analysis in pore structure of coal under condition of CO2 sequestration process. Fuel 2015, 139, 125–132. [Google Scholar] [CrossRef]

| Sample No. | R0 (%) | Coal Macerals (%) | Proximate and Ultimate (wt %) | Coal Species | |||||
|---|---|---|---|---|---|---|---|---|---|
| V | I | E | M,ad | A,d | V,daf | FC,ad | |||
| MHC | 2.20 | 62.06 | 26.90 | 1.70 | 1.53 | 21.95 | 12.50 | 65.14 | Meager coal |
| MSC | 1.90 | 63.38 | 29.15 | 2.10 | 1.67 | 22.47 | 12.46 | 65.43 | Meager coal |
| 1/3CC | 0.99 | 52.60 | 31.60 | 15.80 | 1.67 | 25.71 | 38.87 | 33.75 | 1/3 cocking coal |
| Sample No. | SBET,Ad (m2/g) | Smi+tra (m2/g) | VBJH,Ad (cm3/g) | Vmi+tra (cm3/g) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Smi | Proportion/% | Stra | Proportion/% | Vmi | Proportion/% | Vtra | Proportion/% | |||
| MHC untreated | 0.96 | 0.32 | 32.7 | 0.66 | 67.0 | 0.0035 | 0.00039 | 11.0 | 0.0032 | 89.0 |
| MHC treated | 1.26 | 0.42 | 33.5 | 0.84 | 66.5 | 0.0042 | 0.00013 | 3.1 | 0.0040 | 96.9 |
| MSC untreated | 0.81 | 0.36 | 49.1 | 0.41 | 50.9 | 0.0015 | 0.00038 | 25.0 | 0.0011 | 75.0 |
| MSC treated | 0.92 | 0.40 | 43.8 | 0.51 | 56.2 | 0.0017 | 0.00024 | 13.8 | 0.0015 | 86.2 |
| 1/3CC untreated | 3.10 | 1.57 | 50.4 | 1.54 | 49.6 | 0.0077 | 0.00023 | 29.4 | 0.0055 | 70.6 |
| 1/3CC treated | 3.24 | 1.58 | 48.7 | 1.66 | 51.3 | 0.0088 | 0.00021 | 23.9 | 0.0067 | 76.1 |
| Coal Sample | D = 3 + A | |||||
|---|---|---|---|---|---|---|
| Relative Pressure (P/P0): 0.0–0.5 | Relative Pressure (P/P0): 0.5–1.0 | |||||
| A2 | D2 | R22 | A1 | D1 | R12 | |
| MHC untreated | −0.090 | 2.90 | 0.792 | −0.545 | 2.45 | 0.995 |
| MHC treated | −0.088 | 2.91 | 0.717 | −0.532 | 2.47 | 0.995 |
| MSC untreated | −0.073 | 2.92 | 0.874 | −0.375 | 2.63 | 0.987 |
| MSC treated | −0.069 | 2.94 | 0.835 | −0.351 | 2.65 | 0.970 |
| 1/3CC untreated | −0.171 | 2.82 | 0.950 | −0.435 | 2.56 | 0.991 |
| 1/3CC treated | −0.152 | 2.85 | 0.960 | −0.391 | 2.61 | 0.999 |
| Sample No. | Φ (%) | K (mD) | APD (nm) | St (m2/g) | Sme+ma (cm2/g) | Vt (cm3/g) | Vme+ma (cm3/g) | ||
|---|---|---|---|---|---|---|---|---|---|
| Sme | Sma | Vme | Vma | ||||||
| MHC-untreated | 5.47 | 19.6 | 15.1 | 10.14 | 0.044 | 0.013 | 0.038 | 0.0033 | 0.011 |
| MHC-treated | 7.02 | 21.5 | 18.9 | 10.82 | 0.026 | 0.027 | 0.051 | 0.0028 | 0.028 |
| MSC-untreated | 7.63 | 28.1 | 19.2 | 12.58 | 0.030 | 0.028 | 0.063 | 0.0041 | 0.018 |
| MSC-treated | 8.59 | 30.2 | 22.9 | 13.16 | 0.012 | 0.035 | 0.072 | 0.0018 | 0.038 |
| 1/3 CC-untreated | 8.77 | 18.8 | 20.7 | 12.22 | 0.046 | 0.038 | 0.070 | 0.0051 | 0.016 |
| 1/3 CC-treated | 9.44 | 20.0 | 25.4 | 13.79 | 0.021 | 0.046 | 0.077 | 0.0035 | 0.040 |
| Coal Samples | APD (100–1000 nm) | APD (1000–20,000 nm) | APD (>20,000 nm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R32 | A3 | D3 | R42 | A4 | D4 | R52 | A5 | D5 | |
| MHC untreated | 0.841 | −2.310 | 1.69 | 0.987 | −1.104 | 2.89 | 0.640 | −0.224 | 3.78 |
| MHC treated | 0.857 | −2.510 | 1.49 | 0.976 | −1.030 | 2.97 | 0.849 | −0.326 | 3.67 |
| MSC untreated | 0.857 | −2.002 | 1.99 | 0.935 | −1.129 | 2.87 | 0.550 | −0.158 | 3.84 |
| MSC treated | 0.865 | −2.124 | 1.88 | 0.946 | −1.120 | 2.88 | 0.356 | −0.118 | 3.88 |
| 1/3CC untreated | 0.824 | −1.965 | 2.03 | 0.954 | −1.165 | 2.83 | 0.429 | −0.214 | 3.79 |
| 1/3CC treated | 0.793 | −2.315 | 1.68 | 0.878 | −1.106 | 2.89 | 0.669 | −0.171 | 3.83 |
| Sample No. | for Raw Coal Samples | for LCO2 Frozen Treated Coal Samples | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MHC | 0.260 | 0.124 | 0.186 | 0.139 | 0.338 | 0.172 | 0.086 | 0.175 | 0.143 | 0.255 |
| MSC | 0.046 | 0.267 | 0.046 | 0.079 | 0.106 | 0.035 | 0.235 | 0.034 | 0.017 | 0.055 |
| 1/3CC | 0.214 | 0.143 | 0.140 | 0.060 | 0.241 | 0.108 | 0.148 | 0.032 | 0.032 | 0.132 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Wei, G.; Li, Z.; Wang, Q.; Wang, W. Damage Effects and Fractal Characteristics of Coal Pore Structure during Liquid CO2 Injection into a Coal Bed for E-CBM. Resources 2018, 7, 30. https://doi.org/10.3390/resources7020030
Ma L, Wei G, Li Z, Wang Q, Wang W. Damage Effects and Fractal Characteristics of Coal Pore Structure during Liquid CO2 Injection into a Coal Bed for E-CBM. Resources. 2018; 7(2):30. https://doi.org/10.3390/resources7020030
Chicago/Turabian StyleMa, Li, Gaoming Wei, Zhenbao Li, Qiuhong Wang, and Weifeng Wang. 2018. "Damage Effects and Fractal Characteristics of Coal Pore Structure during Liquid CO2 Injection into a Coal Bed for E-CBM" Resources 7, no. 2: 30. https://doi.org/10.3390/resources7020030
APA StyleMa, L., Wei, G., Li, Z., Wang, Q., & Wang, W. (2018). Damage Effects and Fractal Characteristics of Coal Pore Structure during Liquid CO2 Injection into a Coal Bed for E-CBM. Resources, 7(2), 30. https://doi.org/10.3390/resources7020030




