Understanding Human Actions and Institutional Change: What Are the Impacts of Power Asymmetries on Efficiency in Pasture Use?

Abstract

The paper investigates actions and decisions of agricultural resource users and explores their implications for institutional change and natural resource management in the post-socialist context of Central Asia. More specifically, the authors propose a novel methodological approach for the aforementioned context to support policy-relevant research that explicitly addresses behavioral responses of pastoralists in Kyrgyzstan. The paper builds on distributive and economic theories of institutional change and combines findings from lab and field framed economic experiments with complementary qualitative methods (questionnaires, group discussions and semi-structured interviews). By these means the authors test the impact of a specific variable on institutional change in pasture use: the role of power and specifically the difference in the ability of players to “survive” in a bargaining game without an agreement. The impact of power asymmetries and its implications for cooperation and the efficiency of bargaining outcomes are discussed and analyzed. Experimental results largely confirm findings reported in the literature: as players learn about the game and the behavior of others, they adjust their decisions accordingly; the subjects also exhibit other-regarding preferences, resulting to the prevalence of relatively equally distributed gains as an outcome. Furthermore, the findings of the study suggest that under the condition of incomplete information about the preferences of other players, the experimental subjects internalize the game as a group. The authors propose that an explanatory variable for such situations might be that actual shared beliefs of pasture users assist players to economize on information processing and coordinate the bargaining in an effective way. From this perspective, the paper raises a series of questions regarding the proposition that power asymmetry leads to inefficient bargaining outcomes, and provides some first insights for further investigation.

1. Introduction

Intended institutional change, implies the deliberate replacement of existing, formal or informal institutions, or the creation of new institutions with the aim of changing de facto institutions by regularizing actors’ interactions [1]. Changes in institutions following institutional design can emerge as an outcome of changed perceptions about roles, identities, normative values, cognitive frames and rules in a particular context. It has been argued however that outcomes of institutional design can be essentially unpredictable, largely depending on the specificities of the problem situation and the way in which experience, expert knowledge or intuition are applied [1]. A variety of theories of institutional change have been proposed, but wishing to keep our account short, we focus on distributive and economic theories of institutional change that offer alternative, yet complementary in our view, interpretations of the main drivers for such change.

Economic theory views institutional change primarily as the result of contracting between economic actors, whereas distributive bargaining theory perceives institutions to be equilibriums achieved through bargaining outcomes. The “naive” version of such an economic approach assumes that institutional change is the result of opportunities for Pareto improvements which arise because of price changes or new production and monitoring technologies [2]. The advanced version, however, includes transaction costs in the analysis and assumes that bargaining and transaction costs may block the establishment of efficient institutions [3]. In this respect, power and efficiency considerations of actors are suggested as alternative determinants of institutional change. However, due to the complexity of institutional change, actors—who intentionally make decisions concerning new institutions based on their beliefs about the potential benefits offered by different institutional forms—may be disappointed by its unintended consequences. This might contribute to difficulties in distinguishing the predictions of economic and distributional theories. Jack Knight and Douglass North [4] underline that economic and distributional theories share common assumptions about the motivations of actors but are different in their claims about the context in which they make their choices. They argue that both theories can be complementary, depending on the set of conditions within which interactions and institutional change are occurring.

The aim of this paper is to explore how power asymmetry as a vital condition in the context of rural Kyrgyzstan, can affect the outcomes of interactions (efficiency). In order to investigate this relationship we conducted framed laboratory and field bargaining experiments based on Rubinstein’s bargaining game [5]. Our motivation is to advance the understanding of the individual preferences and bargaining strategies of pasture users. Our findings contribute to the rich literature comparing decisions between students and resource users in experimental games [6,7,8,9]. Although, this is a well explored field, no such comparison has been made for the Rubinstein’s game, at least to our knowledge. The experimental results have been complemented by additional qualitative findings (from questionnaires, group discussions and interviews) to advance our understanding and enhance the analysis of the given socio-ecological pastoral context in which bargaining takes place.

The paper is structured as follows: First, we briefly introduce the institutional context in pasture management in Kyrgyzstan and provide an illustrative bargaining situation (Section 2). In the following we present Knight’s and Oliver Williamson’s positions on the role of power and efficiency in social interactions according to bargaining theory (Section 3). Here we also describe the design of the pasture experiment and we outline the complementary methods used in the study. In the following Section 4, we present the findings from laboratory and field experiments carried out in Kyrgyzstan. In this section, we use the Kolmogorov-Smirnov and contingency coefficient tests in order to measure the deviation between two sets of sample values in the symmetric and asymmetric treatments. In Section 5 we discuss the relation between the demands of players and the bargaining outcomes. The qualitative data acquired complement the analysis by explaining the difference between laboratory and field experimental results. Finally, in the concluding Section 6 we reflect on our findings concerning the role of power, efficiency and shared actor beliefs during bargaining interactions related to pasture use in Kyrgyzstan.

2. Institutional Context in Pasture Management in Kyrgyzstan

Since the early 1990s, Kyrgyzstan has undergone a change from a centralized state-managed economy to a decentralized market-oriented economy and, in the process, gained valuable experience in designing new institutions in pasture management.

This period of change in Kyrgyzstan and other former Soviet states triggered the emergence of an academic discourse on how the post-socialist transition, transformation and institutional change should be conceptualized. There has been a shift in the understanding of the nature of the transition process: from support of “blueprint” top-down approaches to designing a post-socialist transition to a critical analysis of bottom-up transformation and institutional change. The transformation context has been perceived as an experimental laboratory, where actors develop and try out new organizational forms and institutional arrangements [10,11]. In many cases, path dependence and institutional complementarities with informal institutions have played key roles in the transformation process [12,13,14].

Seen in this light, post-socialist institutional change has been characterized by: (i) the livelihood, institutional and ecological uncertainties that have resulted from radical agricultural reforms; (ii) path dependence and persistence of traditional and Soviet institutions; and (iii) discrepancy and complex interplay between law and social organization, informal and formal institutions. It is also assumed that (iv) conflicts, bargaining and power relationships among actors shape institutional change.

In pasture management, there is great consensus among scholars today that sustainable pasture use and management in Central Asia depends largely on pastoral migration [15,16,17,18]. However, the early post-Soviet pasture management reforms in Kyrgyzstan did not recognize the importance of institutions coordinating pastoral migration and did not take into account the economic and political dynamics related to mobile herding [19,20]. These early reforms resulted in a massive reduction in pastoral mobility leading to the overgrazing of pastures, decreasing livestock productivity and increasing conflicts between pasture users over access to the resource. The consequences of such change could be grave for a country where the economy is primary agricultural and 65% of its population lives in rural areas.

Furthermore, under the conditions of uncertainty and legal pluralism marking this period—with many institutional levels coexisting in an uneasy and often contradictory state—pasture users began referring to different old and new rules, both formal and informal, to pursue their interests, relying on their power in different situations to advance them [13]. As a result of this transformation, traditional institutions and practices started adapting to the new realities and many new informal institutional arrangements were developed [13,21]. In the following we provide an illustrative example that the authors observed and largely informed consecutive research phases.

Illustrative Bargaining Situation between Community Herders and Livestock Owners Leading to Creation of a New Informal Institution

In this illustrative action situation, a livestock owner (actor A) and a community herder (actor B) bargain over the price, place, and terms and conditions of herding (Figure 1). Similar to Rubinstein’s [5] bargaining model, this is a dynamic form of bargaining interaction, with sequential exchange of offers and counteroffers:

The livestock owner approaches the community herder, making a payment offer for his herding service. The community herder may accept this offer, or refuses and makes a counteroffer instead.

If there is no agreement reached, it is assumed that the livestock owner must take care of the livestock himself, as another suitable price or another herder is not found.

If the community herder accepts the price offer of the livestock owner, they then begin to negotiate the herding plan (when and to which pastures the community herder will move livestock this year) and other conditions of the cooperation (e.g., advance payments and in-kind help during labor-intensive periods).

An experienced herder may obtain a better price even if he stays on spring and autumn pastures whereas an inexperienced herder may agree to move to remote summer pastures, despite a lower price offer.

There are two possible equilibrium outcomes for the second part of their negotiations, when they decide to cooperate: (i) the community herder moves with the collected livestock to distant spring, summer and autumn pastures or (ii) the herder stays on spring and autumn pastures close to the village and market, without moving to distant summer pastures. We assume that the main goal of the pasture users is to achieve a distributional advantage, which depends on the specific outcome equilibrium that is attained and the implications for either party. The livestock owner gains a distributional advantage if the community herder moves to spring, summer and autumn pastures. In this case, his livestock is likely to gain more weight as more feed will be available, and the livestock will consequently have a higher value. In contrast, the strategy of staying on spring and autumn pastures close to village and market, without moving to summer pasture, has a distributional advantage for the herder, as he can sell livestock products at the local market and have smaller transportation costs. In a case of non-cooperation, herder and livestock owner need to take care of their livestock themselves, but in this bargaining situation payoffs (breakdown values) are lower than payoffs for cases of cooperation.

The social dilemma we are concerned with emerges when the community herder selects the strategy of staying on pastures without seasonal rotation, leading to overgrazing, degradation and decrease of pasture productivity. Here, community herders would be in a stronger bargaining position than livestock owners.

This bargaining outcome was observed in both communities investigated empirically at an early stage of this study: winter pastures and most accessible spring and autumn pastures are overgrazed, as herders use them throughout the whole year without rotation; meanwhile, the most distant summer pastures are underused. This outcome is essentially a new informal institution, created through the way actors have bargained in this action situation.

Bargaining positions in this action situation depend, to a large degree, on how credible livestock owners find the commitment of community herders. This is the key to the relative bargaining power community herders have in this bargaining situation. The credibility of the commitment of community herders depends on their professional reputations. The commitment of inexperienced young herders without their own livestock may not be credible to livestock owners, as the risks associated with herding require a certain amount of knowledge and experience, which are key assets in pasture use. In making their decisions, herders take into account many ecological factors of the pastoral system and must know quite a bit about the complex dynamics between vegetation cover, stocking densities and other environmental aspects [13,22] (p. 69). This interaction between herders and owners is repeated every year, and livestock owners will hardly entrust their livestock to the community herders who have not cared well for their livestock in a previous year. These observations motivated the authors to investigate the role of power in the bargaining situations regarding pasture use as a vital condition affecting the efficiency of the outcomes of such interactions.

3. Materials and Methods

3.1. Power or Efficiency?

Knight [23,24] suggests that economic contract and distributive bargaining approaches to interpreting institutional change, model basic social interactions differently. Thereby Knight offers alternative explanations of change by referring to different sets of conditions. The mainstream economic approaches are based on examining interaction situations where cooperation payoffs are higher than breakdown values, where breakdown values are equal. The bargaining approach on the other hand, emphasizes the differences in both player payoff structures and breakdown values. Knight argues that, unlike the efficiency concept, the distributive theory of institutional change seeks to explain rational self-interested behavior in a broader range of conditions in which social interaction takes place.

Williamson [25] insists however, that efficiency is also an important explanatory variable under conditions of asymmetric interaction: “power has little to contribute to the study of contract and organization in circumstances where parties to an exchange can and do contract in a relatively farsighted way” [25] (p. 23). He argues that asymmetric interaction may have an efficient constructional arrangement, and underlines an important condition: the actors involved in such interaction tend to look toward the future, recognizing potential hazards and transaction costs prior to their agreement. Thus, in order to protect their interests, the actors choose what appear to be the most efficient agreements, which include safeguards.

In order to explore the relationship between sets of conditions (related to power asymmetry) and the outcomes of interactions (explicitly referring to efficiency) we have conducted a study of bargaining interactions based on Rubinstein’s bargaining game [5]. In what follows, we present the bargaining game model and we position it in relation to the experimental literature regarding the interplay between power and efficiency.

3.2. Rubinstein’s Bargaining Game and Experimental Evidence

Rubinstein [5] (p. 97) defines the bargaining problem by setting the following situation and question: “Two individuals have before them several possible contractual agreements. Both have interests in reaching agreement, but their interests are not entirely identical. What will be the agreed contract, assuming that both parties behave rationally?” He proposes a formal solution to the bargaining problem: The higher a player’s bargaining power, the larger the share he or she will obtain in the outcome. Under the necessary condition of complete information, Rubinstein predicts that an agreement can be reached in the most efficient way if:

• The first offer is accepted and
• There are no inefficiency-inducing delays, no matter how much power players have.

In line with this bargaining-game theory prediction, experimental evidence has indicated a high percentage of efficient agreements in bargaining experiments. However, the literature reports that a non-negligible amount of offers have not been accepted immediately, leading to decreases in bargaining efficiency [26,27,28].

The implications of power asymmetry for equity and efficiency are further explored in the public good and common pool games in Kyrgyzstan [29] and elsewhere [30,31] it has been found that player payoffs significantly decrease when one of the players has asymmetric power and “there is a fundamental balance between inequality and efficiency” [31] (p. 1596). Experimental literature offers some possible explanations for this observation:

• Subjects learn about the game and the behavior of other players, adjusting their behavior accordingly. Bargainers are not only concerned about their own payoffs but for the earning of their fellow co-players. Consequently there is a prevalence of equal divisions in experiments [27] (p. 327).
• The differences of players between the expectations about the terms of a potential agreement and a failure to reach one influence their behavior [26].
• Power asymmetry does not exclude cooperation, however it might hinder it. This occurrence is related to the degree of “inequality” disadvantaged players are willing to tolerate [31].

In order to explore how power asymmetry can affect the efficiency of bargaining outcomes, we conducted framed laboratory and field experiments dealing with the use of pasture in Kyrgyzstan. The selection of the particular case allowed us to explore the relationship between power asymmetry and efficiency in a setting where users regularly face bargaining dilemmas related to the use of this vital resource. The laboratory experiments were carried out in Naryn State University in Naryn and the initial intention of the authors was to test the game, recruit and train field assistants and to use students as control group. However, as it will be later discussed the experimental findings from the students offered further insights. The field experiments were conducted in Jergetal and Tosh Bulak communities (Jergetal Ayil Okrugu, Naryn rayon, Naryn Oblast) and Tosh Bulak (Tosh Bulak Ayil Okrugu, Sokuluk rayon, Chui oblast) (see Figure 2), representative cases of the different environmental and socio-economic characteristics of two typical regions of Kyrgyzstan. While Jergetal is located in a remote mountain region with harsh climate conditions, with a traditional specialization in livestock and limited economic alternatives, Tosh Bulak has characteristics of a peri-urban area with a mild climate, good access to market and developed infrastructure. Compared with Tosh Bulak, Jergetal has a larger total area of pastures for climatic and topographic reasons. Due to the scarcity of pasture areas, the pressures on the resources are much higher in the Tosh Bulak. Despite their different characteristics, the selected communities face similar problems of pasture use, for instance, livestock has increased significantly in recent years in both communities affecting pasture conditions.

We further complemented our findings and triangulated our results with other qualitative methods, such as a post-experimental survey, group discussions and semi-structured interviews with experiment participants. In the following we describe the design of the game and the applied complementary methods.

3.3. Experimental Design

Rubinstein’s bargaining game [5] was chosen as the basis for our experiment. According to bargaining game theory, the credibility of commitment is key to relative bargaining power, as the logic of institutionalization is to constrain the choices of others through one’s own credible commitments. Awareness of differences of social actors in their payoffs for non-coordination (breakdown values) can influence the credibility of strategies. The mechanism of bargaining is illustrated with the following example: Let us assume that player A communicates to player B that he will choose strategy (R), which provides greater benefit to him, regardless of the choice of player B; we can expect that, if he finds the commitment of player A to be credible, player B will select strategy (L), even if it is less beneficial for him. The credibility of commitment depends on the difference of the breakdown values of players, and the availability of exit costs, exit opportunities of non-coordination and time preferences (favoring early rather than delayed coordination) which can all affect actor’s choices. Player B accepts the credibility of commitment of player A, if she knows that player A is likely to suffer less in a case of non-cooperation. In Rubinstein’s bargaining game bargaining power is the ability of a player to survive without an agreement; thus, bargaining power time preference (or patience of the players involved) is modeled using discount factors. For example, there are two players bargaining over the partition of a pie of size L. Each makes a proposal regarding how the pie should be divided between them. Each player has a discount factor $d_1$ or $d_2$. The discount factor ($d_i$) has to be less than 1 and at least one of them has to be positive (0 < $d_i$ > 1). If $d_2$ = 0, that means that pie has no worth for Player 2 after the first round, and Player 1 can exploit this to get all the pie. If $d_1$ = 0, Player 1 gains 1 − $d_2$, which is the proportion of the pie that Player 2 loses, if he refuses an offer from Player 1 in the first round.

In cases where offers are rejected, the pie decreases for each player differently, according to her or his discount factor. The stronger a player is, the higher their share will be. Bargaining game theory predicts that

• In the first round, player 1 offers (1 − $d_2$)/(1 − $d_1{d}_2$) for himself and 1 − (1 − $d_2$)/(1 − $d_1{d}_2$) for player 2.
• Player 2 will immediately accept this offer.

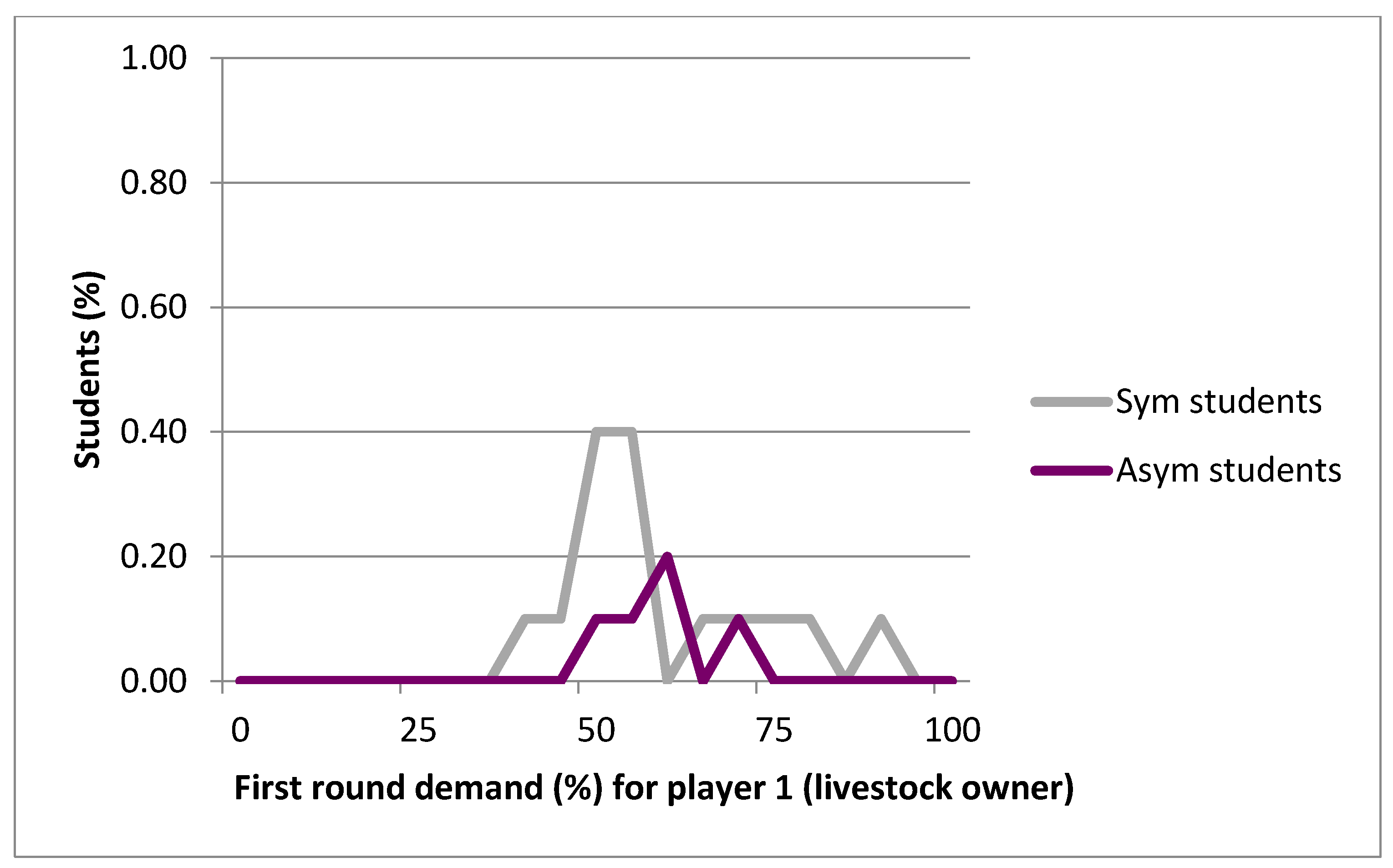
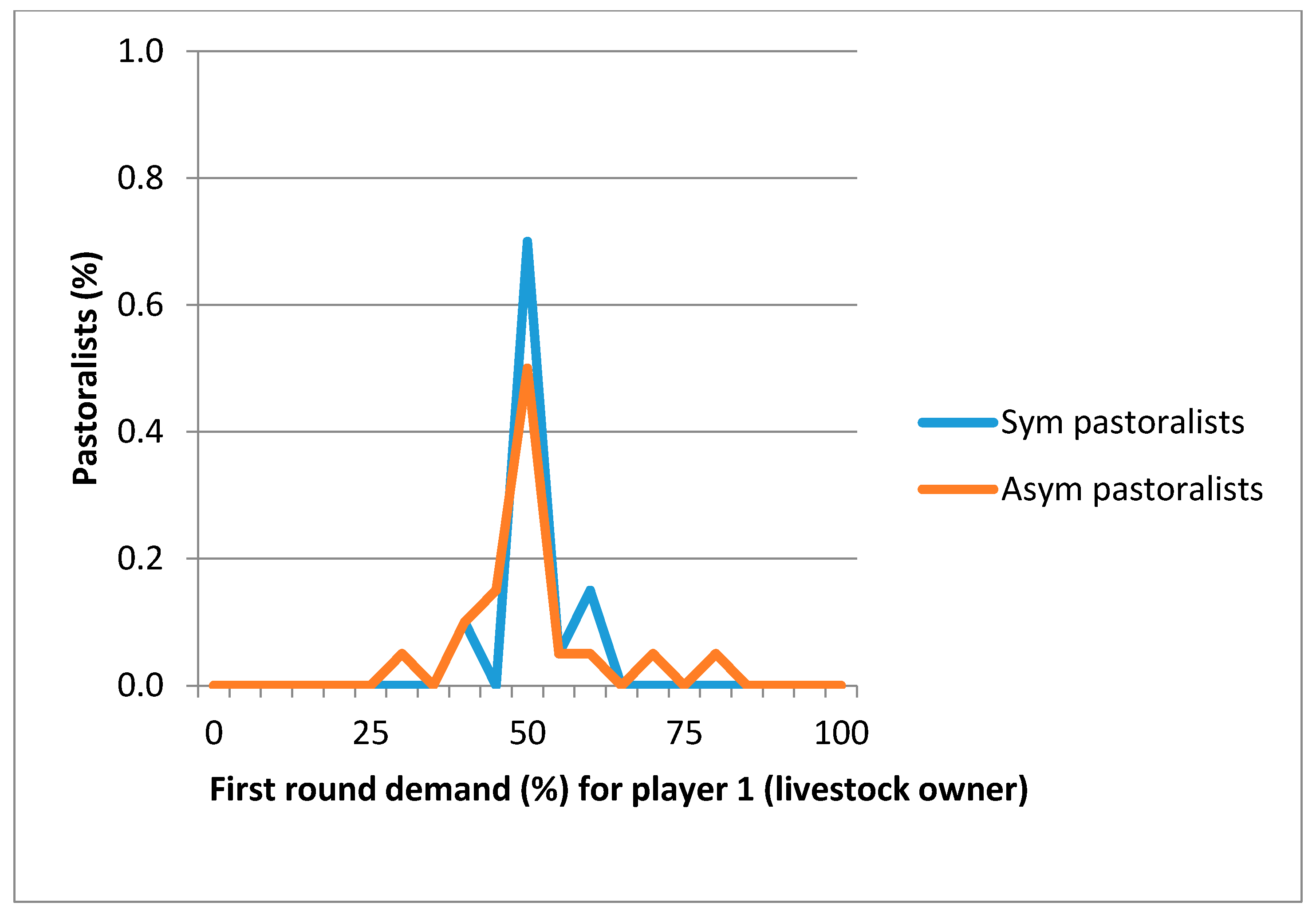
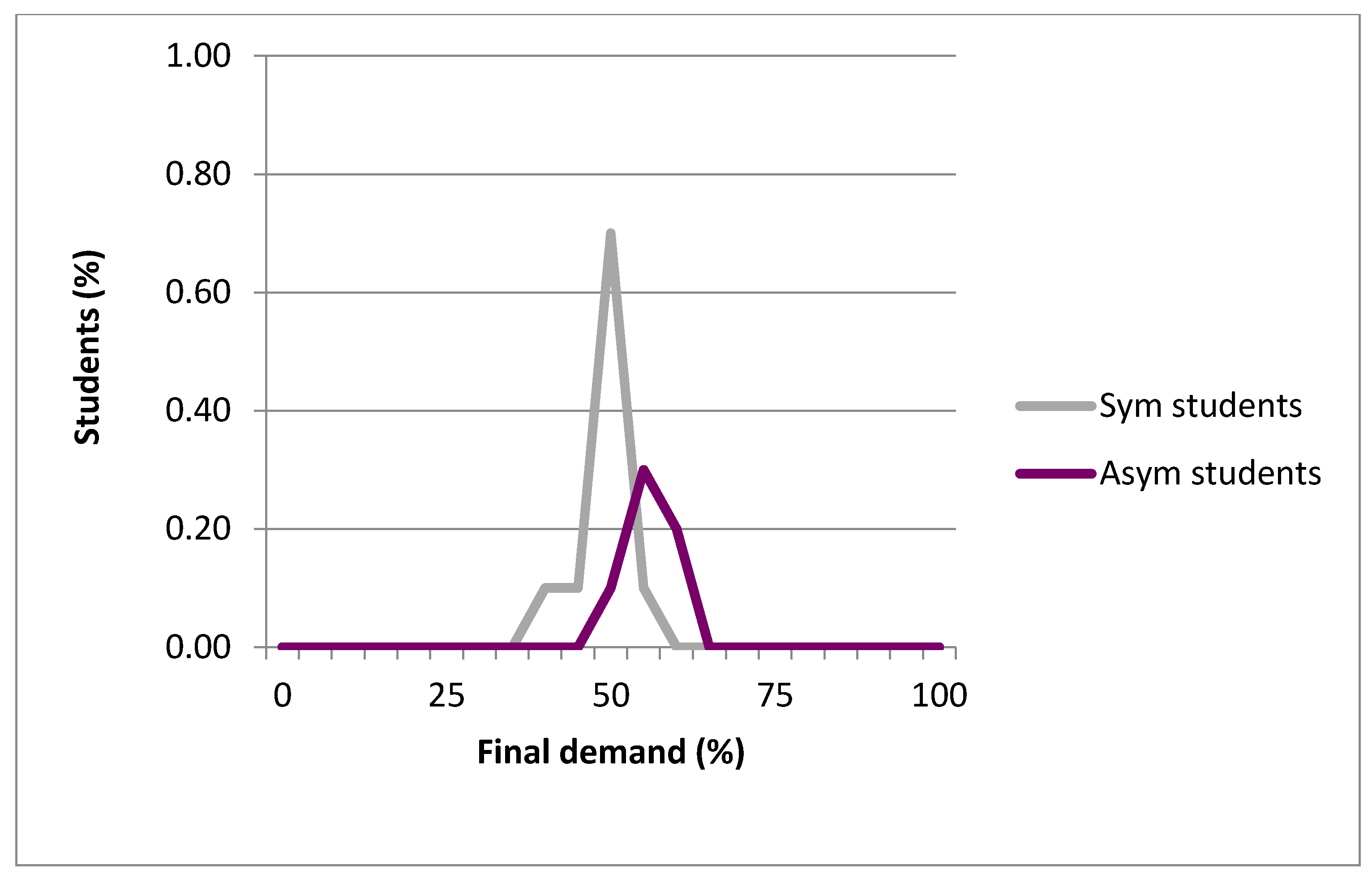
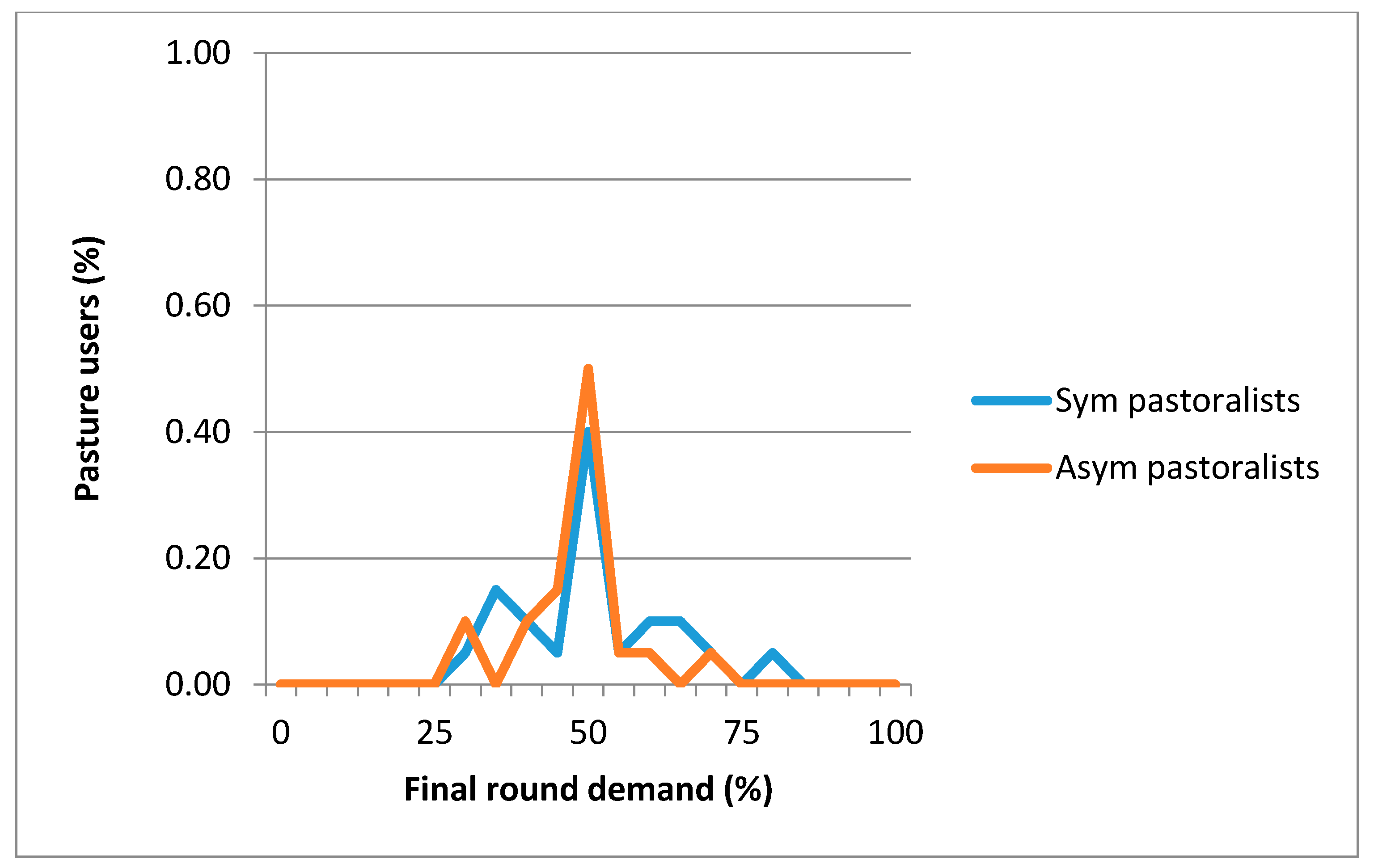
For each run of the experiment, each of the players was randomly selected to be either the young community herder or livestock owner. In this game, the livestock owner and young community herder are to share 100 KGS (Exchange rates are based on http://www.nbkr.kg, on 1 August 2013, the exchange rate was 48.90 KGS to the USD; on 1 May 2014, it was 53.90 KGS to the USD). In first round, the livestock owner starts and writes on a piece of paper an offer to share this amount in (%) to the herder. The young community herder may accept or reject the offer. If the herder accepts, the game is over and the agreed amount is shared between the players. But, if the herder rejects the offer, then the next round begins. The new amount to share however is decreased and now differentiates for each player (see

Table 1. Symmetric and asymmetric treatments.

Treatment	“Livestock Owner’s” Discount Factor	“Young Community Herder” Player’s Discount Factor	Subgame Perfect Equilibrium
Symmetric	0.60	0.70	(0.52; 0.48) 1 round
Asymmetric	0.95	0.70	(0.90; 0.10) 1 round

Source: Adapted from Vollstädt [28].

). The higher a player’s discount factor is, the higher her bargaining power. The participant who plays first (in this game the livestock owner) has an additional positional advantage as well.

In the symmetric treatment, the amount to share decreases by 40% for the livestock owner (first mover) and by 30% for the young community herder (second mover). The discount factor is higher for the livestock owner. This difference illustrates the fact that the first mover has more bargaining power than the second mover. Meanwhile, in the asymmetric treatment, the amount to share decreases by 5% for the livestock owner and by 30% for the community herder (Table 1). The chosen discount factors were selected following Vollstädt [28] in order to keep calculations simple while differentiating enough between players and treatment types. We tried to adjust the discount factors of livestock owners and herders in order to reflect their power relation in practice. This adjustment was informed by qualitative research preceding the experiment, which was more of an informed assumption or a vague estimation rather than an actual measurement.

The laboratory experiment was conducted at the Naryn State University in Naryn, Kyrgyzstan in May 2013. Twenty undergraduate students from the economics and environmental departments were invited to participate in the game. Subsequently, the field experiments were conducted with forty pasture users in the Jergetal and Tosh Bulak communities in June–July 2013 and in May 2014 respectively. Undergraduate students (50% female) from the economics and environmental departments were invited to participate in the game, of which 20 students with an average age of 21 participated in both symmetric and asymmetric treatments. About 30% of participants were from households living in a rural area. The field experiments were conducted in the Jergetal and Tosh Bulak communities with 40 pastoralists with an average age of 37 taking part in both symmetric and asymmetric treatments. About 40% of the participants were female and 82% had at least a secondary education. Half of the participants were medium livestock owners and 30% were community herders. In both experiments, the majority of participants reported that they understood the game (93% in field and 70% in the laboratory) and were satisfied with the money they earned (87% in field and 95% in the laboratory).

3.3.1. Experimental Procedure

The authors, together with local research assistants visited the university and rural communities before the actual experiment in order to discuss the selection criteria for the players, a realistic number of participants, acquires some background data, find a venue and deal with organizational issues. We opted not to invite subjects with previous experience on economic experiments, ruling out possible learning effects and biases from other ongoing or past similar activities [29]. Participants for the experiment were finally recruited via local partners: members of the Pasture Committees within the selected communities and staff from the Department of Ecology at Naryn State University.

Before the game, the participants signed consent letters and randomly selected their ID numbers. In the following, they assumed the role of either livestock owner or young herder and 30 bargaining pairs were formed in total (10 pairs of students and 20 of pasture users). Instructions in the local language were distributed and players had time to read them and to ask questions. During the introductory sessions (asymmetric and symmetric) the participants were informed about the discount rates of the bargaining pair. Please note that prior to and during the experiment we did not explain power and why bargaining pairs have different discount rates. During the focus group discussion after the experiment though, we discussed extensively what discount rates means for the power of pasture users and how the bargaining outcome of the game relates to real-life situations. During the experiment, players were not allowed to communicate; bargaining pairs were placed in separate rooms or places so as to ensure sufficient privacy. The players’ decisions were written on a previously prepared paper distributed to the players just before the beginning of the game. After the experiment, each participant filled out a questionnaire. At the end of all games, a focus group discussion followed and in depth interviews with all players were conducted. As a very last step, participants were paid according to their earnings from the game in cash and in private, receiving also a show-up fee. On average, each player earned the equivalent of one day’s wages for their local area for his or her participation in a 2.5 to 3 h session. The moderators did not limit the time for the bargaining in each round, but the experiments lasted a minimum of 1 and a maximum of 4 rounds. Each of the 60 individuals that took part in the experiment received an average of 285 KGS (6 USD), including their earnings and the show-up fee.

3.3.2. Complementary Methods

Before and after the field experiments, in total 40 qualitative semi-structured interviews were conducted with pasture users in the studied communities within a framework of qualitative case study. Two communities, were chosen for the case study, identified as administrative units (Aiyl Okrugu). The units of analysis were core bargaining situations in which actors make decisions that tend to have strong impacts on shaping the outcome of social dilemmas in pasture use and management. The case study was undertaken as a means to investigate formal as well as informal mostly undocumented institutions for regulating pasture use. The acquired knowledge was deemed necessary in order to analyze the causes and reasons for actors’ decisions as well as to better understand and explain ongoing change of pastoral institutions.

Inputs from these in-depth interviews provided important information for framing the experiment and also for equipping the researchers with qualitative information that would prepare them for the games and enable them to understand possible reasons and motivations for decisions made by the pasture users. The post-experimental survey acquired some additional information on players’ demographics, current pasture practices and reasoning behind personal decisions made in the different treatments of the bargaining game. The focus group discussions reflected upon the game bargaining situations and real-life interactions seeking to explore similarities and differences between the bargaining process and outcomes.

There are many methodological challenges in the operationalization of theories of institutional change. A difficult one to operationalize is the concept of power. Power is dynamic and changes over time; it might be offset by another resource; and it is very difficult to measure [33]. In order to address these challenges, the bargaining power here was conceptualized as an ability to survive longer without a cooperative agreement, in other words an ability to exhibit considerable patience in bargaining. Three analytical steps were taken to triangulate the methods (case study and bargaining experiments) and analysis of the collected qualitative and quantitative data (

Table 2. Methodological triangulation to explain and understand pasture use power relationships in Kyrgyzstan.

Analytical Steps	Qualitative Case Study	Bargaining Experiment
First step:	Core bargaining situations and power resources in pasture use are identified; Qualitative evaluation of power and its dynamics
Second step:		An example of bargaining situation and power resource are modeled in experiment
		Power—the time preference is quantitatively measured in experiment using a discount factor; Causal relation between power and efficiency tested
Third step:	Reasons for decision making and their implications for bargaining outcome in pasture use investigated using statistical and qualitative content analysis methods

Source: Authors.

).

Scientific investigation always starts with a qualitative step. Before scientists can study quantitatively, they must first figure out what exactly they want to study and then need to define the scale and/or levels of measurement of the phenomena in question [34]. Thus, here core action situations in pasture use and key power resources involved in bargaining and their dynamics were first identified and evaluated within the framework of the qualitative case study.

A quantitative analysis then follows in order to learn more about the selected empirical phenomena. Knowledge gained about core bargaining situations and the main power of actors in step one was later used to frame the experimental game. In line with the Rubinstein’s bargaining game, power was measured in terms of the time preference of players, and quantitative data collected from the bargaining experiments was statistically analyzed to learn about the causal relationships between power asymmetry and the efficiency of bargaining outcomes.

The results of a quantitative analysis then were interpreted, again qualitatively. For the present study, the experimental results were interrelated by referring to the findings from the case studies in order to understand the reasons behind the decision-making processes of pasture users and their implications for bargaining outcomes in pasture use.

4. Experimental Results

The efficiency of the bargaining that took place during the game, based on the mean final round needed to achieve an agreement, is shown in

Table 3. Mean final round and equilibrium for each treatment.

Treatment	Mean Final Round and Equilibrium (Students)	Mean Final Round and Equilibrium (Pasture Users)
Symmetric	2.00 rounds (44.80; 55.20)	1.90 rounds (45.77; 54.33)
Asymmetric	2.30 rounds (52.00; 48.00)	1.25 rounds (51.67; 48.33)

Source: Authors.

, which shows that the students needed fewer rounds to reach an agreement in the symmetric treatment (2.00) compared to the asymmetric treatment (2.30). The pasture users, however, needed a relatively similar number of rounds to reach an agreement in the symmetric treatment (1.90) but fewer rounds in the asymmetric treatment (1.25). We can also see that the equilibrium achieved in the laboratory and field experiments by students and pasture users were close to each other for both treatments.

For analysis of the experimental results, we compared the players’ bargaining demands in the symmetric and asymmetric treatments in order to test the assumption that they will differ due to being affected by power asymmetry. To do this, we conducted a Kolmagorov-Smirnov two-sample (one-tailed) test, which measures the significance of deviation between two sample sets [35] (p. 127). Following Vollstädt [28], we assume that first round demands made by player 1 may influence the bargaining process. Therefore, we tested their cumulative distribution function.

Table 4. Difference in cumulative frequency distributions of first round demands in field and laboratory experiments.

Field:	30–34	35–39	40–44	45–49	50–54	55–59	60–64	65–69	70–74	75–79	80–84
$S_{{20}_1}$(X)	0	0	2/20	0.00	13/20	2/20	3/20	0	0	0	0
$S_{{20}_2}$(X)	1/20	0	2/20	3/20	10/20	1/20	1/20	0	1/20	0	1/20
$S_{{20}_1}$(X)$–S_{{20}_2}$(X)	1/20	0	0	3/20	3/20	1/20	2/20	0	1/20	0	1/20
Lab:	40–44	45–49	50–54	55–59	60–64	65–69	70–74	75–79	80–84	85–89	90–94
$S_{{10}_1}$(X)	1/10	2/10	3/10	1/10	0	1/10	1/10	0	1/10	0	1/10
$S_{{10}_2}$(X)	0	0	1/10	4/10	2/10	1/10	1/10	0	0	0	0
$S_{{10}_1}$(X)$–S_{{10}_2}$(X)	1/10	1/10	2/10	3/10	2/10	0	0	0	1/10	0	1/10

Source: Authors.

and Figure 3 and Figure 4 reveal that pastoralists and students offered more equal shares in the first round in the symmetric than in the asymmetric treatments.

However, the results of the test also show that the deviation between the different treatments is not significant in either the field or the laboratory:

• In the laboratory experiment, 10 pairs of students (N = 10) had the largest discrepancy between two series of demands $K_D$ = 4, which is not significant at the $\alpha$ = 0.05 level.
• In the field experiment, 20 pairs of pastoralists (N = 20) had the largest discrepancy between two series of first round demands $K_D$ = 3, which is not significant at the $\alpha$ = 0.05 level.

Consequently, we then tested the cumulative distribution function of the final round demands (

Table 5. Difference in cumulative frequency distributions of final round demands in field and laboratory experiments.

Field:	30–34	35–39	40–44	45–49	50–54	55–59	60–64	65–69	70–74	75–79	80–84
$S_{{20}_1}$(X)	1/20	3/20	2/20	1/20	7/20	1/20	2/20	2/20	0	0	1/20
$S_{{20}_2}$(X)	2/20	0	2/20	3/20	9/20	1/20	1/20	0	0	0	0
$S_{{20}_1}$(X)$–S_{{20}_2}$(X)	1/20	3/20	0	2/20	2/20	0	1/20	2/20	0	0	1/20
Lab:	30–34	35–39	40–44	45–49	50–54	55–59	60–64	65–69	70–74	75–79	80–84
$S_{{10}_1}$(X)	0	0	1/10	1/10	7/10	1/10	0	0	0	0	0
$S_{{10}_2}$(X)	0	0	0	0	1/10	3/10	0	0	0	0	0
$S_{{10}_1}$(X)$–S_{{10}_2}$(X)	0	0	1/10	1/10	6/10	2/10	2/10	0	0	0	10

Source: Authors.

and Figure 5 and Figure 6) and found that the cumulative distribution function there is significant for the students but not for the pastoralists:

• In the laboratory experiment, 10 pairs of students (N = 10) had the largest discrepancy between two series of demands $K_D$ = 6, which is significant at the $\alpha$ = 0.05 level.
• In the field experiment, 20 pairs of pastoralists (N = 20) had the largest discrepancy between two series of demands $K_D$ = 3, which is not significant at the $\alpha$ = 0.05 level.

The test results show that in the final round of the symmetric treatment significantly higher numbers of students made equal share offers, which were then accepted. This was not the case in the field experiment, where we found no significant difference between the final demands in the symmetric and asymmetric treatments.

5. Discussion

The laboratory and field experiments demonstrate that power asymmetry may lead to significant decrease in the efficiency of bargaining among students but not among pasture users. Although this experiment has been conceived as a first exploratory step towards the investigation of how power asymmetry affects efficiency in bargaining and was not intended to distinguish between different settings (students versus resource users), we will analyze the findings here, going beyond typical interpretations offered in the experimental literature on the well investigated differences between lab and field experiments. Instead we will make an attempt to examine players’ decisions through the lenses of shared beliefs.

The basic structure of the game may not contain sufficient information for the players, who thus feel the need to search for additional information [36]. Therefore, incomplete information about the preferences of players [5] and shared beliefs [37] may play an important role in their interaction. In seeking to understand this, we first assumed that incomplete information in the asymmetric treatment may lead to longer bargaining times and inefficient outcomes and, thus, tested this assumption by measuring the degree of relation between the frequencies of the demands of students in the first and second rounds with the bargaining outcomes in the symmetric and asymmetric treatments. In the next step, we introduced an additional assumption—shared beliefs—as an explanation for why pasture users in the field experiment were more efficient in the asymmetric treatment. In order to test this, we analyzed the qualitative data collected by the complementary methods applied in the study, as described in Section 3.3.2.

5.1. Why Does Power Asymmetry Reduce the Efficiency of Bargaining among Students?

A critical assumption of Rubinstein’s bargaining model is that bargainers have complete information about each other’s preferences. But what happens if we assume that players do not have such complete information? Rubinstein [5] (p. 99) suggests that in this situation new aspects will appear: ($a_1$) player 1 may try to figure out what the actual bargaining costs for player 2 are and ($b_1$) player 2 may cheat player 1 into thinking that he is stronger than he actually is. Bargaining under these conditions can result in inefficient outcomes.

In order to test Rubinstein’s assumptions, we measured the degree of relation between the frequencies of the demands of player 1 in first rounds and player 2 in second rounds with the bargaining outcomes in the symmetric and asymmetric treatments by calculating contingency coefficient C. This test is widely applied to measure the degree of relation between two sets of data in small samples and has a certain freedom from assumptions and requirements. For example, it requires only nominal measurements and does not require assumptions about the shape of population data and continuity in the variables under analysis [35] (p. 201).

To do this test, we took the following analytical steps:

• We arranged the observed frequencies of demands of players ($O_{ij}$) and bargaining outcomes into a 2 × 2 (r × k) contingency table and determined the expected frequencies ($E_{ij}$) under null hypothesis ($H_0$) for each cell by multiplying the two marginal totals common to that cell and dividing by total number of cases (

  Table 6. Frequency of student demands related to outcomes.

  Player	Inefficient (Asym)	Efficient (Sym)	Total
  Player 1 “livestock owner” (1st round)	65	53	118
  	62	56
  Player 2 “young community herder” (2nd round)	68	56	124
  	71	53
  Total	133	109	242

  Source: Authors.

  ).
• We then measured the significance of the difference between player demands in two the treatments $x^2$ and determined the correlation expressed by contingency coefficient C by using the following formulas [35] (p. 197):

  $$x^2={\sum }_{i=1}^r{\displaystyle \sum }_{j=1}^k\frac{{(O_{ij}-E_{ij})}^2}{E_{ij}}$$

  (1)

  $$C=\sqrt{\frac{x^2}{N+x^2}}$$

  (2)

We tested whether the measured value C indicates a relation between player demands and the outcomes of the treatments (Sym and Asym).

The test demonstrates that

3.

The relation between the frequency of player demands in first and second rounds with bargaining outcomes has the contingency coefficient C = 0.04.

4.

The significance of the difference between the player demands in the two treatments $x^2$ = 0.6, which means that $x^2$ > 0.6 with degrees of freedom (df) = (k ‒ 1)(r − 1) = (2 − 1)(2 − 1) = 1 and has a probability of occurrence under $H_0$ of less than 0.90.

Thus, we conclude that there is a relation between the demands of player 1 (livestock owner) in the first round and player 2 (herder) in the second round for the outcomes of treatments in which participants of the lab experiment were students and that contingency coefficient C = 0.04 is different from zero.

5.2. Why Does Power Asymmetry not Reduce Bargaining Efficiency among Pasture Users?

Another important question now arises: why were the pastoralists more efficient than students in the asymmetric treatment of the bargaining game? The framed field experiment was conducted in a more complex environment compared with the laboratory experiment, which was simpler and set in an artificial setting. Therefore, we assume that some added factor was present during bargaining in the more natural environment. The bargaining experiments were conducted on the summer pastures in Jergetal and in the municipality office in Tosh Bulak. The field experiment allowed us to gain important insights about the bargaining process and to formulate certain hypotheses to explain the experimental results, which were then further explored using the complementary methods mentioned above. During this stage of the research, we analyzed information from the interviews and focus groups about how real-life negotiations take place among pasture users and about their views on bargaining power. In this subsection, we explore whether the results of the field experiment can be explained via the additional explanatory variable of shared beliefs [37,38] by presenting the shared beliefs of pastures users regarding actual bargaining costs and the credibility of commitments and discussing their role in bargaining among pasture users.

In line with Aoki [37,38] we assume that (1) pastoralists form individual beliefs and expectations concerning how others will play and what expectations they have as well as about the potential equilibrium of the played game; (2) even under the condition of complete information about the setting of the game, boundedly rational players have incomplete information about the preferences of others and credibility of their commitments; and (3) based on this information and common experience, their shared beliefs evolve concerning the way in which the game should be played. These beliefs are either supported and confirmed by players’ choices during the game, or they are undermined and must be abandoned. From the field experiment we can see that, in the asymmetric interaction, where relative bargaining power (their breakdown values) differs, players may not have complete information and face a challenge to answer two important questions:

(i)

What are the actual bargaining costs the players have?

(ii)

How credible are the commitments of other players?

Here we describe the beliefs pasture users have about real-life bargaining interactions, which may help them to economize on information and answer the questions posed above, which they may have faced during the field experiment. During real-life interactions community herders and livestock owners pool their livestock and cooperate in the use of common pastures. Their interaction is repeated every year and represents a mixed-motive cooperative game, where both players oppose non-cooperation and prefer cooperation though they may disagree about alternative cooperation outcomes.

Regarding the shared beliefs of pasture users about actual bargaining costs, it must be kept in mind that these actors are strongly interdependent in their real-life bargaining interactions. They have different cooperation payoffs, but the non-cooperation costs are also high for both sides. Pasture users have experienced dynamic changes in their power relations due to changing economic conditions. Initially, increased livestock value and numbers raised the demand for herder’s services, which has consequently stimulated an increase of community herders offering such services. Thus, community herders first increased their bargaining power, as they had lower exit costs compared to the livestock owners who were dependent on herder’s services. The situation has changed recently however, as the greater amount of herders offering their services has resulted in livestock owners becoming stronger during bargaining.

Shared beliefs concerning the credibility of commitment of community herders in real-life bargaining interactions depend very much on their reputation. Their interaction with livestock owners is repeated every year, and the latter would not usually entrust their animals to a community herder who had not taken good care of his livestock in the previous year. A herder’s credibility is also dependent on experience and knowledge about the pastoral system and livestock management, which can increase herder bargaining power in negotiations with livestock owners. Thus, experienced herders may get better payment offers compared to their inexperienced colleagues.

Based on the above considerations, we suggest the following interpretation of the experimental results from the bargaining experiment (

Table 7. Shared beliefs help to economize on information.

1. Incomplete Information	2. Important Questions the Players Face	3. Shared Beliefs Help to Economize on Information
($a_1$) Player 1 (livestock owner) may try to figure out what the actual bargaining costs for player 2 are;	($a_2$) What are the actual bargaining costs the community herder and livestock owner actually have?	($a_3$) High interdependence between the livestock owner and community herder, as bargaining costs are high for both actors involved
($b_1$) Player 2 (herder) may cheat player 1 into believing that he is stronger than he actually is;	($b_2$) How credible is the commitment of the herder?	($b_3$) The credibility of commitment, which is the main bargaining power, depends very much on the reputation and experience of community herders.

Source: Authors.

): First, incomplete information in the asymmetric treatment may have caused longer bargaining (inefficient outcome) because $(a_1)$ player 1 (livestock owner) may have tried to figure out what the actual bargaining costs for player 2 (herder) are and $\left(b_1\right)$ player 2 may have tried to cheat player 1 into thinking that she was stronger than she actually was. Second, as a result, the players were confronted during the game with questions regarding issues such as ($a_2$) what the actual bargaining costs of the other players were and ($b_2$) how credible the commitments of the other players were. Third, the pasture users had shared beliefs about expectations they already had in real-life interactions. These shared beliefs have been gradually developed on the basis of their interaction history and experiences and as observed, ultimately influenced their decisions during the experiment. Thus, ($a_3$) there was a strong interdependence between pasture users, as bargaining costs are high for both actors, and ($b_3$) the credibility of commitment, which is the main bargaining power, depended very much on the reputation and experience of the community herder. The pasture users internalized the game because their shared beliefs helped them to economize on information and be more efficient in their bargaining.

6. Conclusions

In this paper, we have examined the role of power and efficiency in institutional change in pasture use in Kyrgyzstan by exploring how the set of the conditions (here, power asymmetry), in which bargaining takes place, affects the outcomes of interaction (efficiency). To explore these issues, we conducted laboratory and framed field bargaining experiments based on Rubinstein’s [5] bargaining game, complemented by additional qualitative methods (questionnaires, group discussions and interviews) in order to enhance the analysis of the broader socio-ecological context. The experimental results confirm the findings reported in the literature that as players in bargaining experiments learn about the game they are playing and the behavior of others, they adjust their behavior accordingly; they are also concerned not only about their own payoffs but those of others too, so there is a prevalence of equal division as an outcome [27].

The paper has sought to explore whether power asymmetry leads to inefficient bargaining outcomes. While students had difficulties in coordinating their cooperation in the asymmetric game, pasture users were generally more efficient. The study formulates certain hypotheses to explain the experimental results by suggesting that, even under the condition of complete information about the setting of the game, the boundedly rational players have nevertheless incomplete information about the preferences and the commitments’ credibility of other players, and tend to internalize the game as a group. In such a case, the shared beliefs of pasture users might have helped them to economize on information processing and coordinate their bargaining.

Incomplete information about the preferences of others in the asymmetric treatment may lead to longer bargaining (inefficient outcomes) because $(a_1)$ player 1 may try to figure out what the actual bargaining costs for player 2 are and $\left(b_1\right)$ player 2 may try to cheat player 1 into thinking that he is stronger than he actually is. As a result, the players will search for additional information about ($a_2$), the actual bargaining costs the players have, and ($b_2$), the credibility of the commitments of other players. The pasture users who were taking part in the field experiment had shared beliefs about expectations they already held in real-life interactions about ($a_3$) the high interdependence between pasture users and ($b_3$) the importance of a herder’s reputation. They thus internalized these beliefs into the experimental game, which actually allowed them to economize on information and be more efficient in their bargaining.

This interpretation of the experimental findings supports both the arguments of Knight and Williamson about the impact of sets of conditions in social interactions. In the asymmetric interactions, where breakdown values are different, power may play a greater role, leading to an inefficient outcome. On the other hand, actors involved in an asymmetric interaction may also achieve an efficient outcome under the condition that they can negotiate it “in a relatively farsighted way”—in the sense that they can look toward the future and recognize potential hazards and transaction costs ex ante their agreement [25] (p. 23).

The study contributes to the literature comparing students and resource users in experimental games by providing valuable insights about the dynamics of the bargaining process and the role of power and efficiency therein, but some limitations of the study should be recognized as well. Similarly to observations made by Cárdenas and Ostrom [36], bringing the experimental laboratory into the field proved to be a challenging task. The research we have presented here has a largely exploratory character, with planned initially small research steps to test the impact of power on the efficiency in bargaining in symmetric and asymmetric sets of conditions. The explanatory variable shared beliefs was not included in the initial design of the experiment nor tested experimentally. Moreover, we did not analyze individual beliefs of the players with additional methods. For future studies, this suggests the need to specifically address the formation and changing character of players’ individual and shared beliefs in bargaining and experimentally test these important variables by including them in an experimental design.

The paper offers some methodological insights concerning the use of experiments in the study of power concepts in dynamic contexts of changing power balances over time. The qualitative methods employed, admittedly underplayed in this paper, enabled the authors to understand the institutional context and the reasons actors may have to change institutions. That understanding was later tested in the laboratory and framed field experiments, revealing their value but also their limitations. In experimentally studying power relations in pasture use, critical dimensions of core bargaining situations regarding power (for example credibility of commitment, exit costs and time preferences) are revealed and can increase the explanatory power of qualitative findings.

Last but not least, and in a wider policy relevant effort, the paper seeks to contribute to the discourse among practitioners about designing and implementing agricultural reforms and especially introducing pastoral institutions. Therefore, the paper explores the process of institutional change in relation to change of bargaining power and distributional consequences, followed by a first attempt to acknowledge the role of the beliefs of actors in the learning process which Kyrgyz policy makers and pasture users go through due to recent reforms in the legislation. Although such an analysis goes beyond the scope of the present paper, the investigated core action situations in Jergetal and Tosh Bulak communities where pasture users negotiate and interact in pasture use demonstrates the high interdependence amongst actors. It further highlights that herder and livestock owners are involved in a continuous dynamic process of bargaining. Although this process engages different actors at local, regional and national level, in this paper we focused on the bargaining process between herders and owners, comparing their decisions with those of students. We have observed a change of power asymmetries strongly influenced by dynamics of economic conditions and enforcement of new formal institutions and governance structures, but we have also explored the role of time dimension in shaping power relations. The latter was manifested through the time preferences actors have, and in the development of shared beliefs in dealing with power asymmetries and the effectiveness of bargaining outcomes. Such lessons can be further picked up by Pasture Committees and policy makers, in an attempt to better understand actors’ interactions, commit to a better-informed process of institutional design and advocate the need for intended institutional change taking into consideration local specificities.