An Approach to the Integrated Design of PCM-Air Heat Exchangers Based on Numerical Simulation: A Solar Cooling Case Study
Abstract
:1. Introduction
1.1. DOE Approach
1.2. Numerical Simulations Based On DOE
- The overall frame is the DOE approach which includes the response surface technique for multi-objective optimization purposes. One important point of the response surface is that once an optimal solution is calculated, the optimization plot is obtained. The optimal solution serves as the starting point for this plot and then the settings can be modified interactively to see how different settings affect responses. No additional simulation runs are required to achieve any other design allowing to modify factors and getting new responses.
- This approach is easier and more intuitive to use for “non-expert” designers and decision-makers. The main idea is to provide a more attractive, though rigorous, tool for designers. Traditional optimization techniques usually require a medium-high level of mathematics. Although not trivial, it is much easier to understand and interpret design criteria, as well as the main parameters that define the analysis (such as the weight and the importance).
- Numerical simulations are not supposed to suffer from variability; however, it is well known that uncertainties in the model input variables/parameters can lead to completely different results in the simulations. In fact, in the type of systems studied here, this occurs with the uncertainty in the inlet temperature (among others). Although not considered in this article, the DOE approach can deal with such uncertainties.
1.3. Design and Optimization of TES Systems for Solar Cooling
2. Methodology
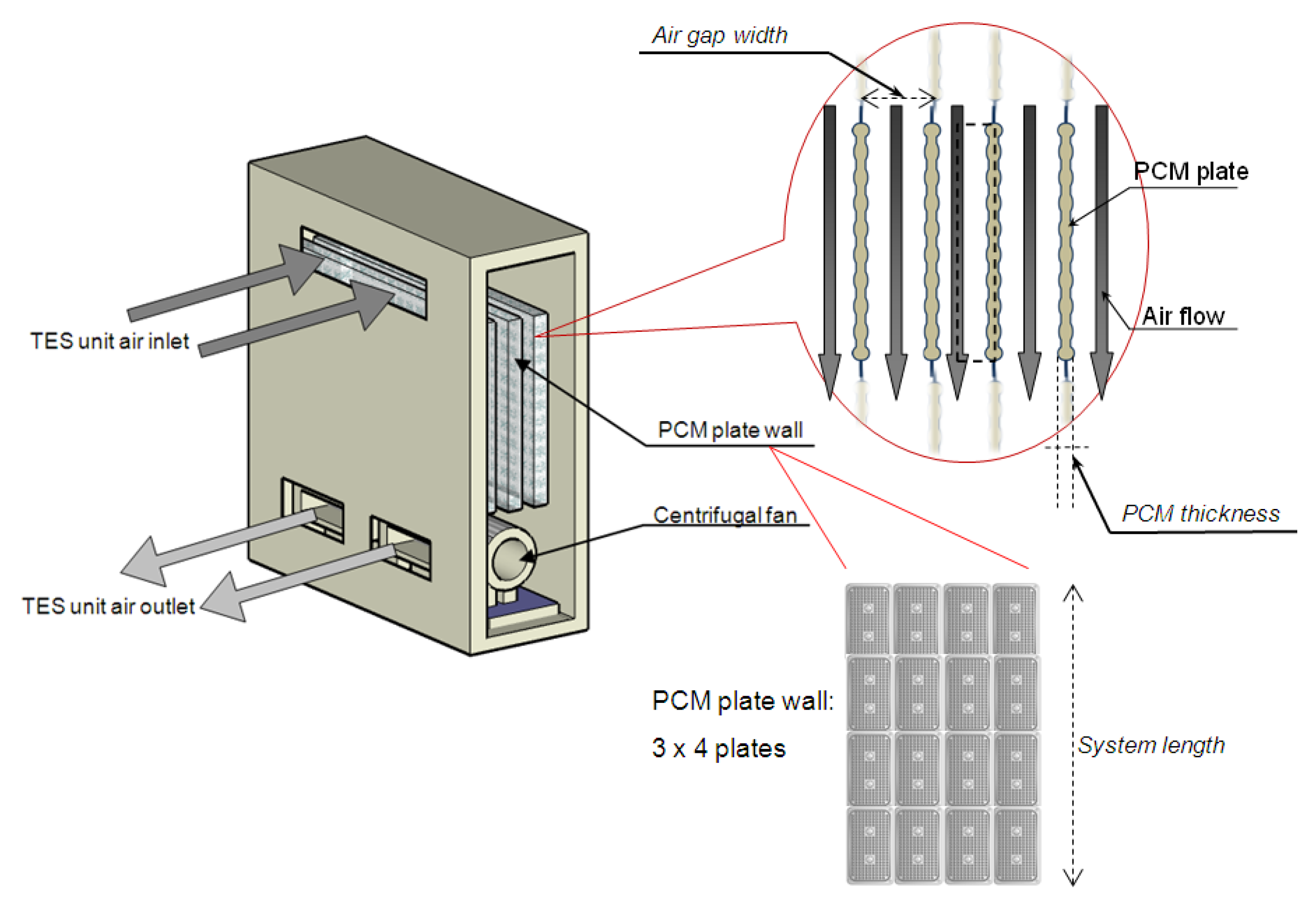
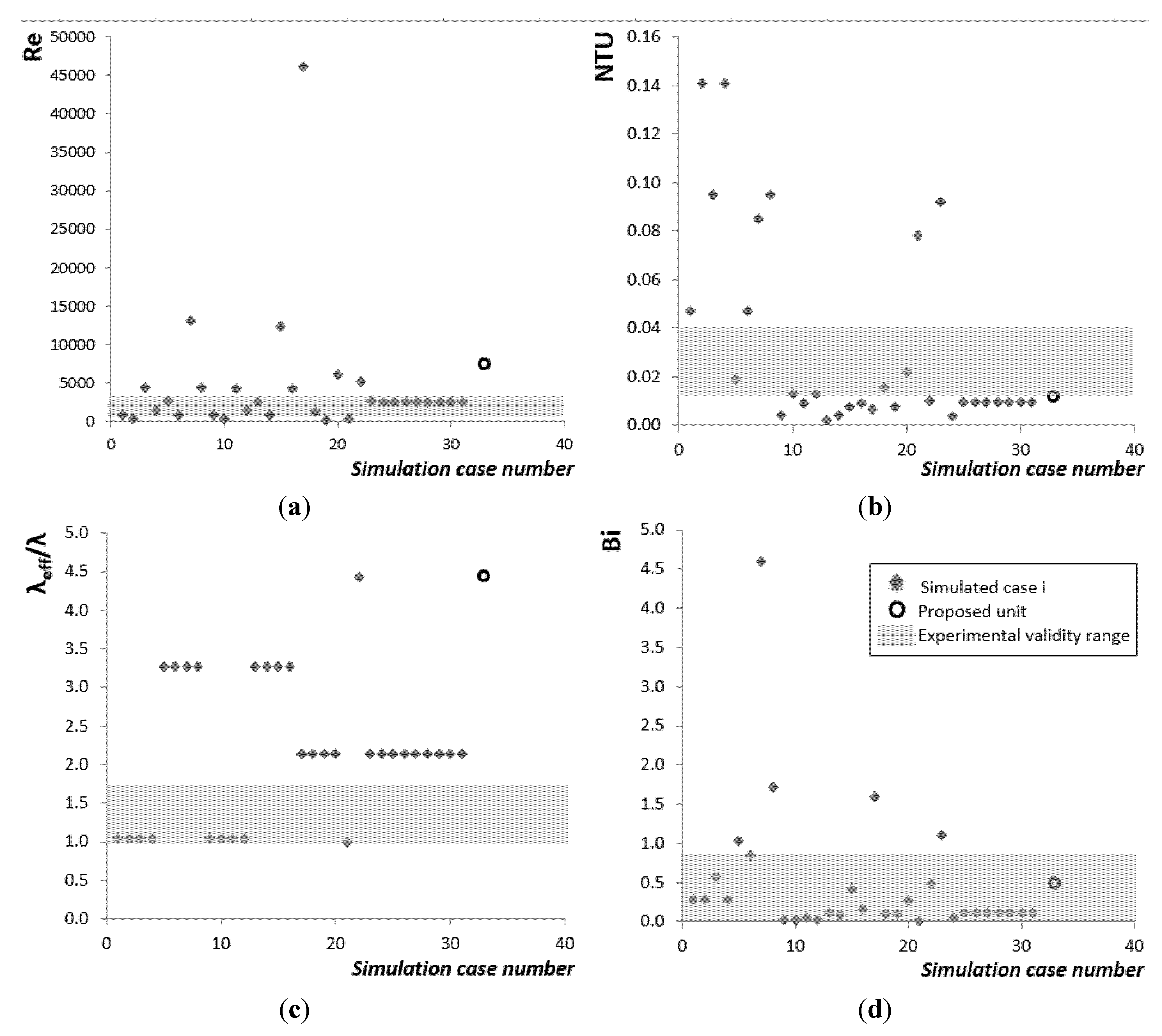
2.1. Similarity Analysis: Scaling the Model
2.2. Validity Range
- Re is the Reynolds number defined as Re = ρ·v·Dh/µ, where Dh = 4·A/P;
- NTU is the number of transfer units defined as NTU = (h·Δx·w)/Cair
- Bi is the Biot number defined as Bi = h·e/λencapsulation
- λeff/λ is the thermal conductivities ratio that quantifies the effect of natural convection within the PCM inside the plate. As this relation goes beyond one, the effect of natural convection is more substantial.
| Re | NTU | Bi | λeff/λ | Ramp (°C/min) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Min | Max | Min | Max | Min | Max |
| 917 | 2577 | 0.013 | 0.039 | 0.088 | 0.875 | 1.00 | 1.74 | 0.05 | 0.25 |
3. Calculation
3.1. Potential Application: Case Study of Absorption Cycles for Solar Cooling
3.2. A Real Case of an Absorption Cycle and a Proposed Combi-System with a PCM Storage Unit
3.3. Design
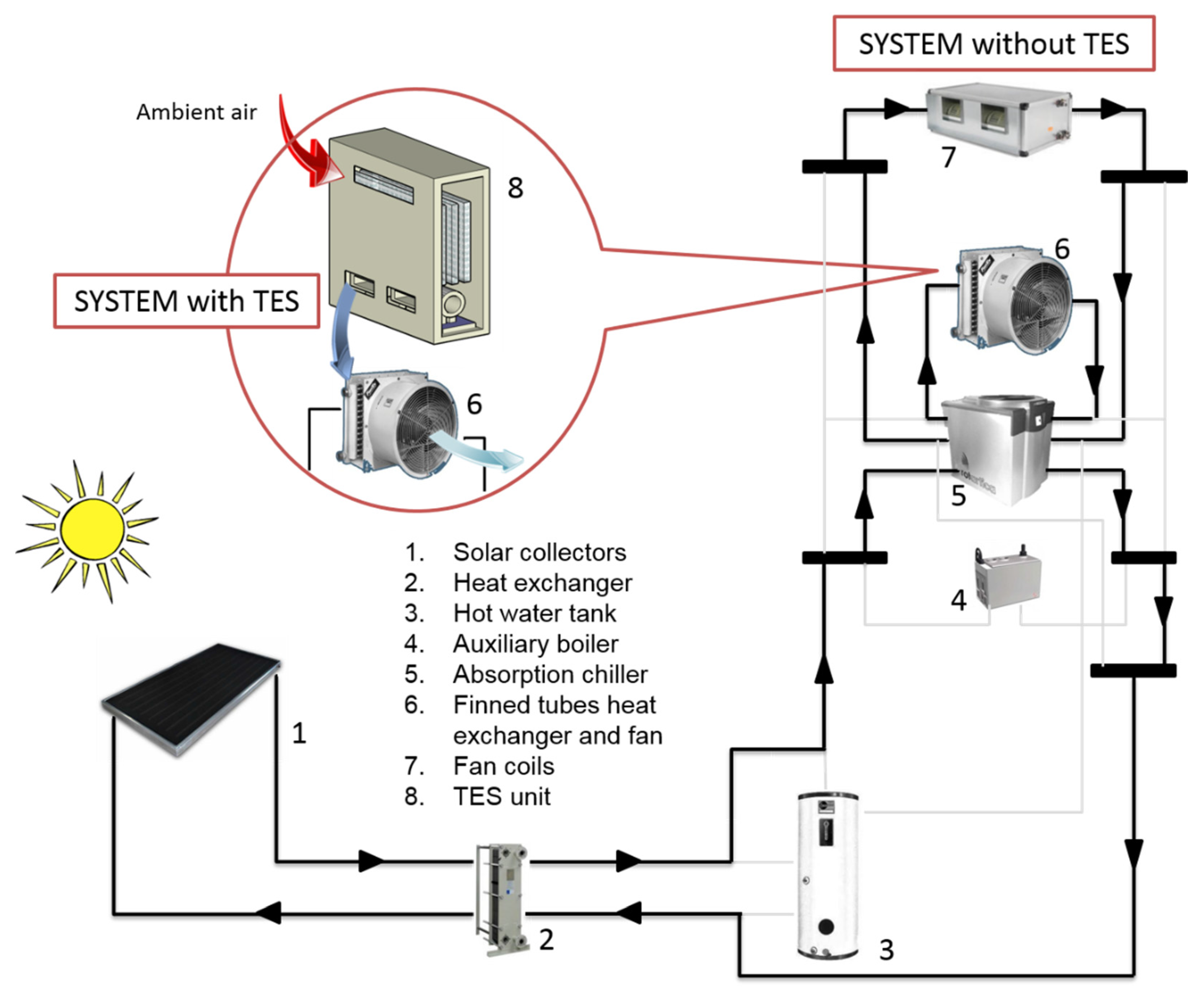
- Reducing the maximum temperature of air flowing through the condensing unit.
- Smoothing the air temperature curve at the outlet of the condenser.
- Reducing the pressure drop in order to achieve a low electrical consumption of the fan.
- Improving the melting degree (i.e., efficiency: Ratio between the energy exchanged and the theoretical energy available of the PCM).
- Volumetric airflow is determined by the condensing unit and is set at 5500 m3/h.
- Number of plate walls is set at 18 (the same number as in the experimental prototype).
- The only PCM considered was the commercial one used in the experimental prototype: RT27 (Rubitherm [29]).
- Finishing of the simulated plates is the same as the plates in the prototype (round bulges).
- Heat generation of the fan is considered constant and equal to 300 W.
- Air maximum temperature, Tmax.
- Pressure drop (necessary to determine which fan to use, electrical consumption, and noise), Δp.
- PCM melting degree for design conditions, ° Melt.
- Width of the TES unit (along with the length and depth allowing the floor space and the volume occupied by the unit to be calculated).
- Maximum heat transfer rate supplied by the TES unit,.
- The amount of PCM has to be theoretically sufficient for the stored energy to cover the needs of the average heat rate (13 kW);
- Demand: 13 kW during eight hours 374,400 kJ;
- Mass of RT27 required to cover the demand: hsl = 179 kJ/kg (which corresponds to the PCM latent heat in the thermal window of 20 to 32 °C) 2092 kg.
| Factors | Domain | |
|---|---|---|
| Level (−) | Level (+) | |
| PCM mass (kg) | 1000 | 3000 |
| Length of the plate system (m) | 1 | 5 |
| Thickness of the PCM plate (mm) | 5 | 15 |
| Thickness of air duct gap (mm) | 5 | 55 |
- The length of the plate system is one of the two dimensions that will determine the unit’s floor space. Depending on the location of the unit (on the roof or inside ducts), this value will depend on the available space. In this case, for the factor length, we have selected a lower level of 1 m and a higher level of 5 m (that allows the placement on the roof with sufficient room).
- The plate thickness is set at a lower level of 5 mm and a higher level of 15 mm. This value of maximum thickness should always obey the relation L/e > 10 in order to assume one-dimensional conduction (in this specific case 1000/15 = 66.6 >> 10).
- The air gap has a lower level of 5 mm and a higher level of 55 mm. The idea behind this is to leave ample room to find a trade-off between compactness on the one hand and a small pressure drop on the other.
4. Results and Discussion
4.1. Response Optimization
- Minimizing the maximum temperature reached by the air (32 °C is the objective, the upper limit being 33.5 °C, which is 3 °C below the maximum outdoors temperature).
- Maximizing the melting degree (i.e., efficiency) with the objective of minimizing the amount of PCM, but accepting as a minimum an efficiency of 50%.
- Minimizing the pressure drop reducing the electrical consumption, accepting values close to 25 Pa, but not beyond 50 Pa.
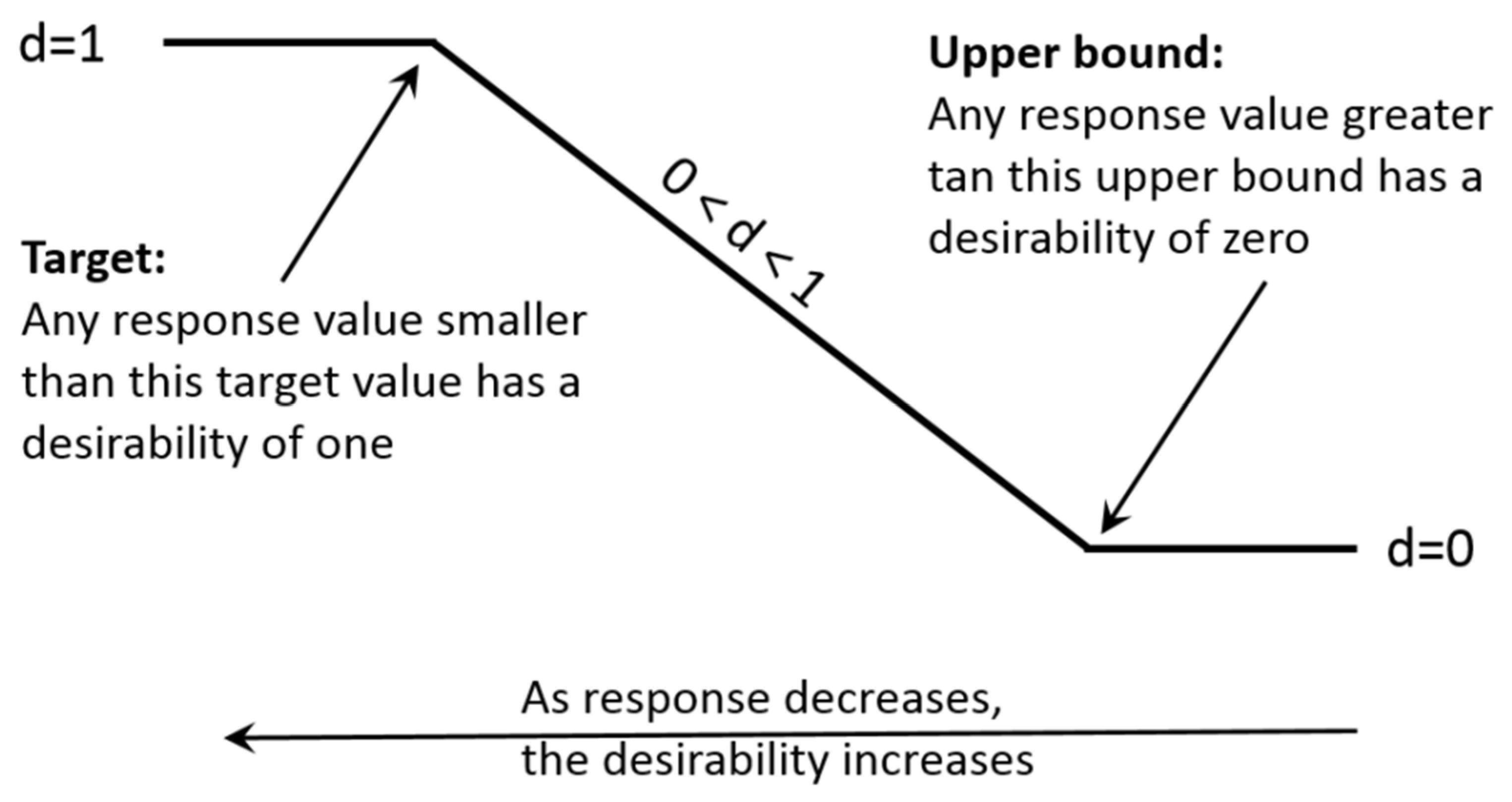
| Response | Goal | Lower | Target | Upper | Weight | Importance |
|---|---|---|---|---|---|---|
| Tmax (°C) | Maximum | 20 | 32 | 33.5 | 1 | 5 |
| °Melt (%) | Maximum | 50 | 100 | 100 | 1 | 10 |
| Δp (Pa) | Minimum | 1 | 25 | 50 | 1 | 1 |
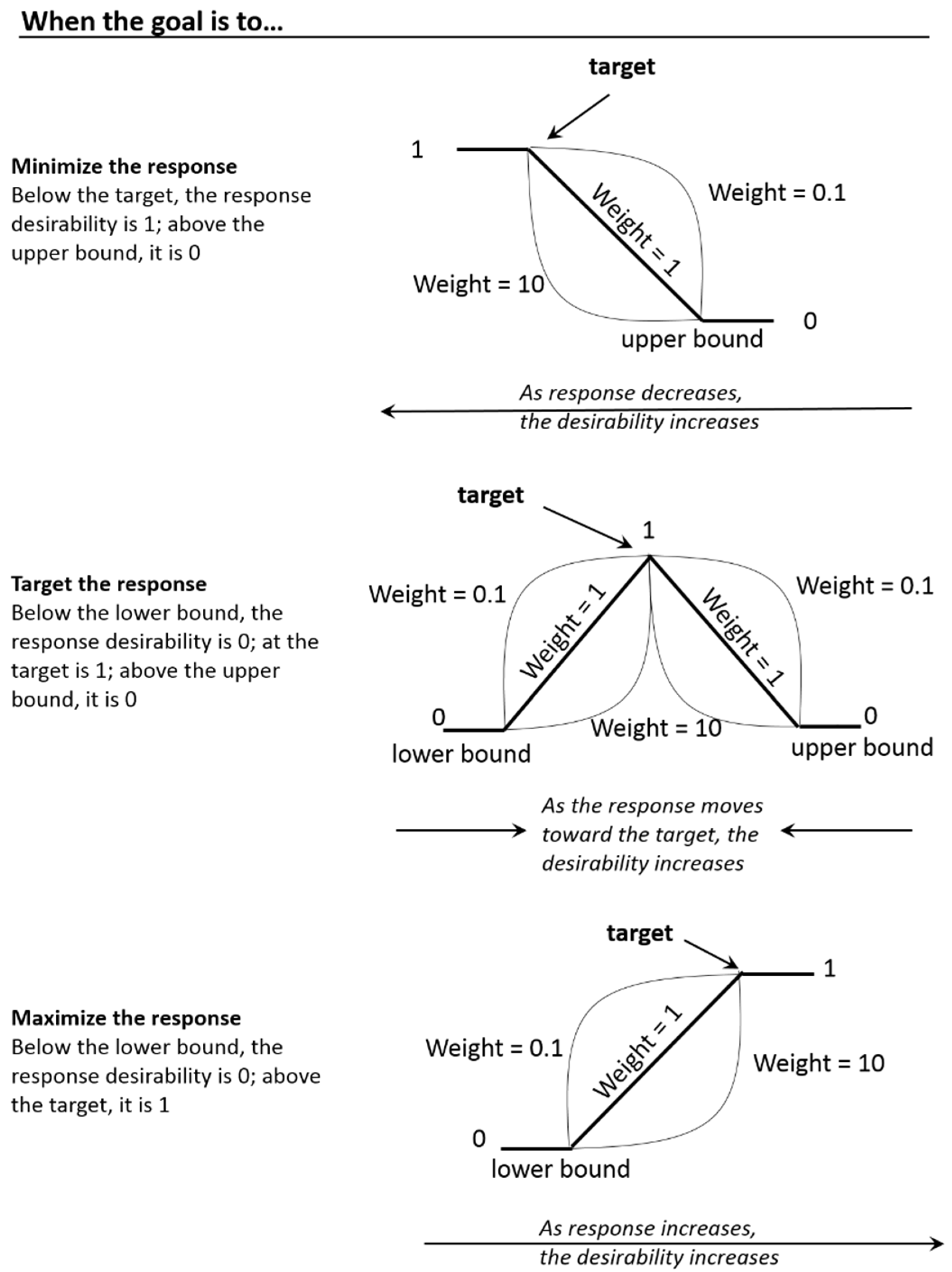
- minimize the response,
- target the response,
- maximize the response.
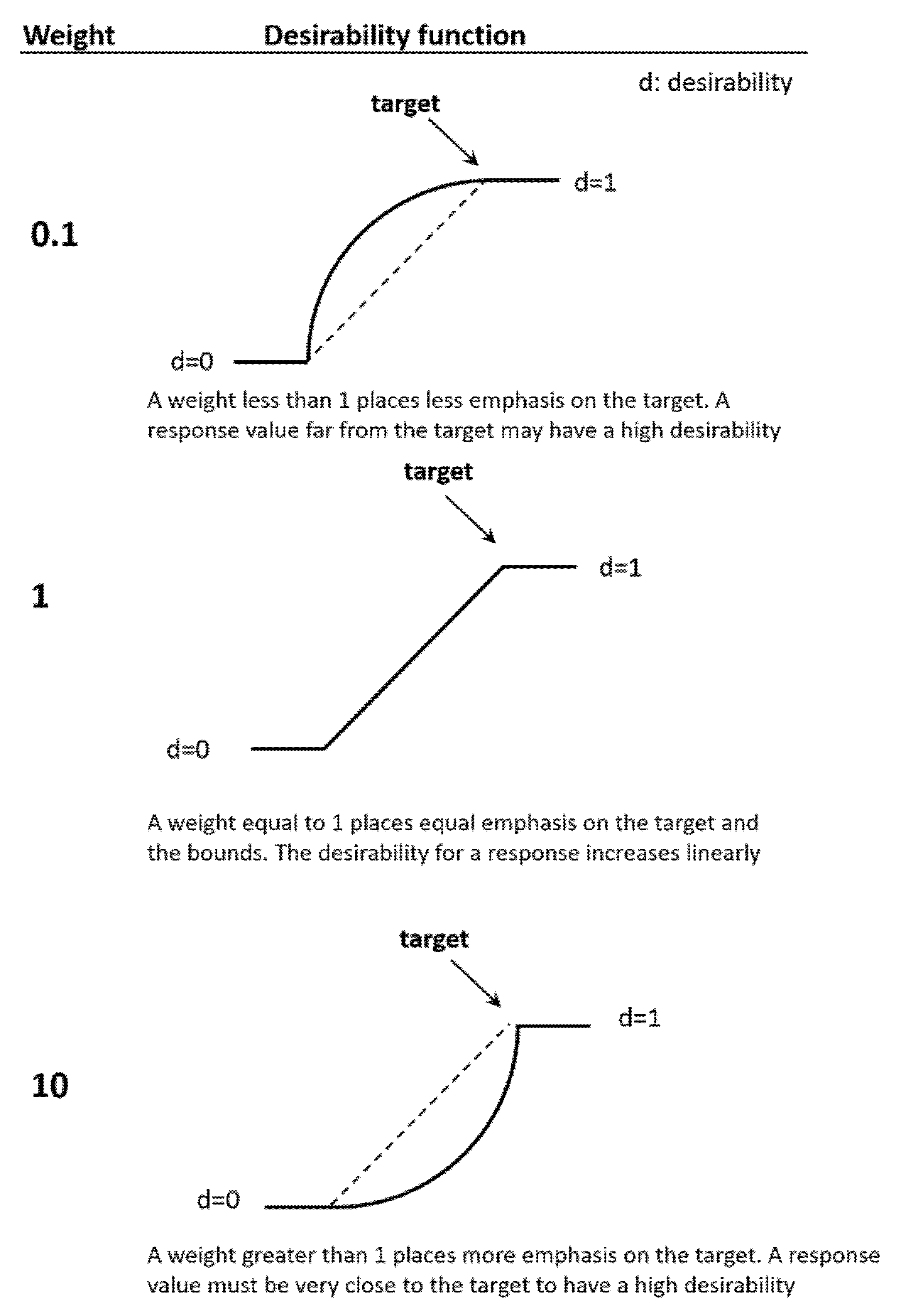
- less than 1 (minimum is 0.1) places less emphasis on the target,
- equal to 1 places equal importance on the target and the bounds,
- greater than 1 (maximum is 10) places more emphasis on the target.

4.2. Suggested TES Unit
| MPCM (kg) | Lsist (m) | eplate (mm) | eair (mm) | (W) | Tmax (°C) | vair (m/s) | w (m) | °Melt. (%) | Δp (Pa) |
|---|---|---|---|---|---|---|---|---|---|
| 2200 | 4.9 | 20 | 40 | 10257 | 32.9 | 1.43 | 1.48 | 66.07 | 63 |
4.3. Dimensional Analysis and Similarity
| # | Simulation plan | Responses | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MPCM (kg) | Lsist (m) | eplate (mm) | eaire (mm) | (W) | Tmax (°C) | vair (m/s) | Width (m) | °Melt (%) | Δp (Pa) | |
| 1 | 1000 | 1 | 5 | 5 | 8227 | 36.2 | 1.33 | 12.77 | 74.09 | 117 |
| 2 | 3000 | 1 | 5 | 5 | 15,500 | 34.5 | 0.44 | 38.31 | 65.34 | 56 |
| 3 | 1000 | 5 | 5 | 5 | 11,935 | 36.3 | 6.65 | 2.55 | 100 | 170 |
| 4 | 3000 | 5 | 5 | 5 | 15,501 | 34.5 | 2.22 | 7.66 | 65.34 | 150 |
| 5 | 1000 | 5 | 15 | 55 | 7385 | 36.3 | 3.99 | 4.26 | 71.75 | 120 |
| 6 | 3000 | 5 | 15 | 55 | 12,673 | 31.8 | 1.33 | 12.77 | 51.83 | 115 |
| 7 | 100 | 3 | 10 | 30 | 7621 | 36.3 | 19.94 | 0.85 | 73.02 | 250 |
| 8 | 4000 | 3 | 10 | 30 | 16,085 | 32.3 | 6.65 | 2.55 | 67.65 | 180 |
| 9 | 2000 | 0.25 | 10 | 30 | 3912 | 34.2 | 0.12 | 12.77 | 47.00 | 25 |
| 10 | 2000 | 7 | 10 | 30 | 9310 | 31.2 | 0.04 | 38.31 | 38.63 | 25 |
| 11 | 2000 | 3 | 1 | 30 | 7543 | 36.2 | 0.60 | 2.55 | 72.91 | 27 |
| 12 | 2000 | 3 | 20 | 30 | 9334 | 31.1 | 0.20 | 7.66 | 38.72 | 26 |
| 13 | 2000 | 3 | 10 | 3 | 4284 | 34.2 | 0.36 | 4.26 | 50.29 | 25 |
| 14 | 2000 | 3 | 10 | 80 | 4830 | 33.5 | 0.12 | 12.77 | 20.13 | 25 |
| 15 | 2000 | 3 | 10 | 30 | 4844 | 34.2 | 1.81 | 0.85 | 55.99 | 53 |
| 16 | 2000 | 3 | 10 | 30 | 11,543 | 31.2 | 0.60 | 2.55 | 47.20 | 27 |
| 17 | 2000 | 3 | 10 | 30 | 1077 | 36.3 | 13.29 | 0.21 | 61.59 | 185 |
| 18 | 2000 | 3 | 10 | 30 | 10,608 | 30.4 | 0.33 | 8.52 | 33.16 | 27 |
| 19 | 2000 | 3 | 10 | 30 | 6400 | 32.7 | 0.06 | 51.08 | 39.24 | 30 |
| 20 | 2000 | 3 | 10 | 30 | 12,222 | 35.4 | 1.55 | 1.82 | 70.69 | 76 |
| 21 | 2000 | 3 | 10 | 30 | 13,967 | 35.1 | 0.07 | 42.57 | 87.99 | 31 |
| 22 | 1000 | 5 | 15 | 55 | 9553 | 33.1 | 1.33 | 2.13 | 56.54 | 37 |
| 23 | 3000 | 5 | 15 | 55 | 14,791 | 35.5 | 6.65 | 4.26 | 90.19 | 230 |
| 24 | 100 | 3 | 10 | 30 | 7865 | 32.3 | 0.25 | 4.26 | 47.49 | 25 |
| 25 | 4000 | 3 | 10 | 30 | 10,592 | 34.2 | 0.66 | 4.26 | 62.61 | 28 |
| 26 | 2000 | 0.25 | 10 | 30 | 10,592 | 34.2 | 0.66 | 4.26 | 62.61 | 28 |
| 27 | 2000 | 7 | 10 | 30 | 10,592 | 34.2 | 0.66 | 4.26 | 62.61 | 28 |
| 28 | 2000 | 3 | 1 | 30 | 10,592 | 34.2 | 0.66 | 4.26 | 62.61 | 28 |
| 29 | 2000 | 3 | 20 | 30 | 10,592 | 34.2 | 0.66 | 4.26 | 62.61 | 28 |
| 30 | 2000 | 3 | 10 | 3 | 10,592 | 34.2 | 0.66 | 4.26 | 62.61 | 28 |
| 31 | 2000 | 3 | 10 | 80 | 10,592 | 34.2 | 0.66 | 4.26 | 62.61 | 28 |
4.4. Evaluation of the System Performance During the Operation Period (Cooling)
| System setup | Average COP | Hours working with T > 27 °C |
|---|---|---|
| without TES | 0.51 | 456 |
| with TES | 0.583 | 399.3 |
4.5. Initial Investment Evaluation
| Volume (m3) | Cost (€) |
|---|---|
| 0.5 | 174 |
| 1.3 | 376 |
| 2.0 | 658 |
| Flow (m3/h) | Type | Consumption (W) | Cost (€) |
|---|---|---|---|
| 2000 | RER10 11-315 | 290 | 547 |
| 5000 | RER10 11-384 | 450 | 591 |
| 8000 | RER10 11-577 | 720 | 837 |
5. Conclusions
- Reducing the number of simulation runs and the time invested. In the case study described in this paper, each numerical simulation corresponds to one single cycle at most (with a duration of two to six minutes per run on an average desktop computer), and only the behavior of the TES unit is simulated. Simulations of buildings are usually for one-year periods and include a complete system: an annual simulation with a simple system, a building and incorporating the TES unit can last 12 h with the numerical model.
- Provided you have a PCM-TES numerical model empirically validated, the methodology can:
- -
- Adapt the design of the TES unit depending on the final requirements (responses) and in accordance to a series of variables or parameters (factors) influencing the system.
- -
- Find optimal points of operation based on multi-response functions criteria. These functions can be shape-defined by the designer depending on their goal (maximization of the function, minimization, or target objective), their weight, and their importance. This is done through desirability functions. In the approach to optimization, each of the response values are transformed using a specific desirability function. The weight determines how the desirability is distributed on the interval between the lower (or upper) bound and the target. It determines the shape of the desirability function that is used to translate the response scale to the zero-to-one desirability scale to determine the individual desirability of a response. In addition, the individual desirabilities are weighted according to the importance that we assign each response.
- -
- A key feature is that without having to run more numerical simulations, a designer can identify the factor settings that enable any other requirements to be fulfilled.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature, Acronyms and Definitions
| A [m2] | area |
| cp [J/(kg·K)] | specific heat capacity at constant pressure |
| d | desirability parameter (ranges from 0 to 1) |
| Dh [m] | hydraulic diameter |
| eair [m] | thickness of the air gap between two PCM plates |
| eenc [m] | thickness of the plate encapsulation material |
| eplate [m] | thickness of the PCM plate |
| h [W/(m2·K)] | air convection coefficient |
| Lsist [m] | Length of the PCM system in the TES unit |
| [kg/s] | mass flow |
| MPCM [kg] | PCM mass |
| N | number of PCM plate walls (inside the TES unit) |
| P [m] | wet perimeter |
| [W] | heat transfer rate |
| T [°C] | temperature |
| Tamb [°C] | outdoors air temperature |
| v [m/s] | velocity |
| V [m3] | volume |
| w [m] | width |
| °Melt | ratio of PCM melted, percentage |
| Δp [Pa] | pressure difference |
| λ [W/(m·K)] | thermal conductivity |
| λeff [W/(m·K)] | effective thermal conductivity |
| ρ [kg/m3] | density |
| µ [Pa·s] | dynamic viscosity |
| Bi = h·e/λenc | Biot number |
heat capacity [J/(s·K)] | |
| Re, = ρ·v·Dh/μ | Reynolds number |
| NTU = (h·Δx·w)/Cair | number of transfer units |
| COP | Coefficient of Performance |
| CSM | Compact Storage Module |
| DOE | Design of Experiments |
| PCM | Phase Change Material |
| TES | Thermal Energy Storage |
References
- Pérez Vergara, I.G.; Díaz Batista, J.A.; Díaz Mijares, E. Experimentos de simulación utilizando superficies de respuesta para su optimización (Simulation experiments using response surfaces for optimization). Cent. Azúcar 2001, 2, 68–74. [Google Scholar]
- Del Coz Díaz, J.J.; García Nieto, P.J.; Lozano Martínez-Luengas, A.; Suárez Sierra, J.L. A study of the collapse of a WWII communications antenna using numerical simulations based on design of experiments by FEM. Eng. Struct. 2010, 32, 1792–1800. [Google Scholar]
- Gunasegaram, D.R.; Farnsworth, D.J.; Nguyen, T.T. Identification of critical factors affecting shrinkage porosity in permanent mold casting using numerical simulations based on design of experiments. J. Mater. Process. Technol. 2009, 209, 1209–1219. [Google Scholar]
- Antony, J. Training for design of experiments using a catapult. Qual. Reliab. Eng. Inter. 2002, 18, 29–35. [Google Scholar] [CrossRef]
- Dolado, P.; Lázaro, A.; Marín, J.M.; Zalba, B. Characterization of melting and solidification in a real scale PCM-air heat exchanger: Numerical model and experimental validation. Energy Convers. Manag. 2011, 52, 1890–1907. [Google Scholar] [CrossRef]
- Doehlert, D.H. Uniform shell designs. J. R. Stat. Soc. Ser. C 1970, 19, 231–239. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Beyer, H.; Sendhoff, B. Robust optimization—A comprehensive survey. Comput. Methods Appl. Mech. Eng. 2007, 196, 3190–3218. [Google Scholar] [CrossRef]
- Dellino, G.; Kleijnen, J.P.C.; Meloni, C. Robust optimization in simulation: Taguchi and response surface methodology. Inter. J. Prod. Econ. 2010, 125, 52–59. [Google Scholar] [CrossRef]
- Dessouky, Y.M.; Bayer, A. A simulation and design of experiments modeling approach to minimize building maintenance costs. Comput. Ind. Eng. 2002, 43, 423–436. [Google Scholar] [CrossRef]
- Ramakrishnan, S.; Tsai, P.F.; Srihari, K.; Foltz, C. Using Design of Experiments and Simulation Modeling to Study the Facility Layout for a Server Assembly Process. In Proceedings of the 17th Annual Industrial Engineering Research Conference, Vancouver, B.C., Canada, 17–21 May 2008; pp. 601–606.
- Zalba, B. Thermal Energy Storage with Phase Change: Experimental Procedure. Ph.D. Thesis, University of Zaragoza, Zaragoza, Spain, 10 April 2002. [Google Scholar]
- Zalba, B.; Sánchez Valverde, B.; Marín, J.M. An experimental study of thermal energy storage with phase change materials by design of experiments. J. Appl. Stat. 2005, 32, 321–332. [Google Scholar]
- Gunasegaram, D.R.; Smith, B.J. MAGMASOFT helps assure quality in a progressive Australian iron foundry. In Proceedings of the 32nd National Convention of the Australian Foundry Institute, Fremantle, Australia, 20–23 October 2001; pp. 99–104.
- Calise, F.; Palombo, A.; Vanoli, L. Maximization of primary energy savings of solar heating and cooling systems by transient simulations and computer design of experiments. Appl. Energy 2010, 87, 524–540. [Google Scholar]
- Gupta, A.; Ding, Y.; Xu, L.; Reinikainen, T. Optimal parameter selection for electronic packaging using sequential computer simulations. J. Manuf. Sci. Eng. 2006, 128, 705–715. [Google Scholar] [CrossRef] [Green Version]
- Whitt, W. Analysis for the Design of Simulation Experiments; Columbia University: New York, NY, USA, 2005. [Google Scholar]
- Salazar, J.C.; Baena Zapata, A. Analysis and design of experiments applied to simulation studies. Dyna Bilbao 2009, 76, 249–257. [Google Scholar]
- Vanderplaats, G.N. Numerical Optimization Techniques for Engineering Design: With Applications; McGraw-Hill: New York, NY, USA, 1984. [Google Scholar]
- Jaluria, Y. Design and Optimization of Thermal Systems, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer Science: New York, NY, USA, 2006. [Google Scholar]
- Dolado, P.; Lázaro, A.; Marín, J.M.; Zalba, B. Characterization of melting and solidification in a real-scale PCM-air heat exchanger: Experimental results and empirical model. Renew. Energy 2011, 36, 2906–2917. [Google Scholar] [CrossRef]
- Lázaro, A.; Dolado, P.; Marín, J.M.; Zalba, B. PCM-air heat exchangers for free-cooling applications in buildings: Experimental results of two real-scale prototypes. Energy Convers. Manag. 2009, 50, 439–443. [Google Scholar] [CrossRef]
- Lázaro, A.; Dolado, P.; Marín, J.M.; Zalba, B. PCM-air heat exchangers for free-cooling applications in buildings: Empirical model and application to design. Energy Convers. Manag. 2009, 50, 444–449. [Google Scholar] [CrossRef]
- Dolado, P.; Mazo, J.; Lázaro, A.; Marín, J.M.; Zalba, B. Experimental validation of a theoretical model: Uncertainty propagation analysis to a PCM-air thermal energy storage unit. Energy Build. 2012, 45, 124–131. [Google Scholar] [CrossRef]
- Dolado, P. Thermal Energy Storage with Phase Change. Design and Modeling of Storage Equipment to Exchange Heat with Air. Ph. D. Thesis, University of Zaragoza, Zaragoza, Spain, 2011. [Google Scholar]
- Lebini, G. Solar cooling for small residential applications: Setup of “casetta di Cimiano” (laboratory) in Milan—The ISSA system. In Innovative solutions for building conditioning focus on solar cooling; Report of the ProEcoPolyNet Network project: Bergamo, Italy, 2008. [Google Scholar]
- Monne, C.; Alonso, S.; Palacin, F.; Guallar, J. Stationary analysis of a solar LiBr-H2O absorption refrigeration system. Inter. J. Refrig. 2011, 34, 518–526. [Google Scholar] [CrossRef]
- Rubitherm GmbH. Available online: http://www.rubitherm.com/ (accessed on 26 October 2015).
- Minitab. Downloads. Available online: http://www.minitab.com/en-us/downloads/ (accessed on 26 October 2015).
- Minitab User’s Guide 2: Data Analysis and Quality Tools, Release 13 for Windows; Minitab Inc.: State College, PA, USA, 2000.
- Trnsys. Available online: http://www.trnsys.com/ (accessed on 26 October 2015).
- Monne, C.; Alonso, S.; Palacin, F.; Serra, L. Monitoring and simulation of an existing solar powered absorption cooling system in Zaragoza (Spain). Appl. Therm. Eng. 2011, 31, 28–35. [Google Scholar] [CrossRef]
- Nicotra-Gebhardt. Pro-Selecta fan configurator. Available online: http://www.nicotra-gebhardt.com/en/infocenter/proselecta-ii.html (accessed on 26 October 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dolado, P.; Lazaro, A.; Delgado, M.; Peñalosa, C.; Mazo, J.; Marin, J.M.; Zalba, B. An Approach to the Integrated Design of PCM-Air Heat Exchangers Based on Numerical Simulation: A Solar Cooling Case Study. Resources 2015, 4, 796-818. https://doi.org/10.3390/resources4040796
Dolado P, Lazaro A, Delgado M, Peñalosa C, Mazo J, Marin JM, Zalba B. An Approach to the Integrated Design of PCM-Air Heat Exchangers Based on Numerical Simulation: A Solar Cooling Case Study. Resources. 2015; 4(4):796-818. https://doi.org/10.3390/resources4040796
Chicago/Turabian StyleDolado, Pablo, Ana Lazaro, Monica Delgado, Conchita Peñalosa, Javier Mazo, Jose M. Marin, and Belen Zalba. 2015. "An Approach to the Integrated Design of PCM-Air Heat Exchangers Based on Numerical Simulation: A Solar Cooling Case Study" Resources 4, no. 4: 796-818. https://doi.org/10.3390/resources4040796
APA StyleDolado, P., Lazaro, A., Delgado, M., Peñalosa, C., Mazo, J., Marin, J. M., & Zalba, B. (2015). An Approach to the Integrated Design of PCM-Air Heat Exchangers Based on Numerical Simulation: A Solar Cooling Case Study. Resources, 4(4), 796-818. https://doi.org/10.3390/resources4040796





