Taylor Law in Wind Energy Data
Abstract
:1. Introduction
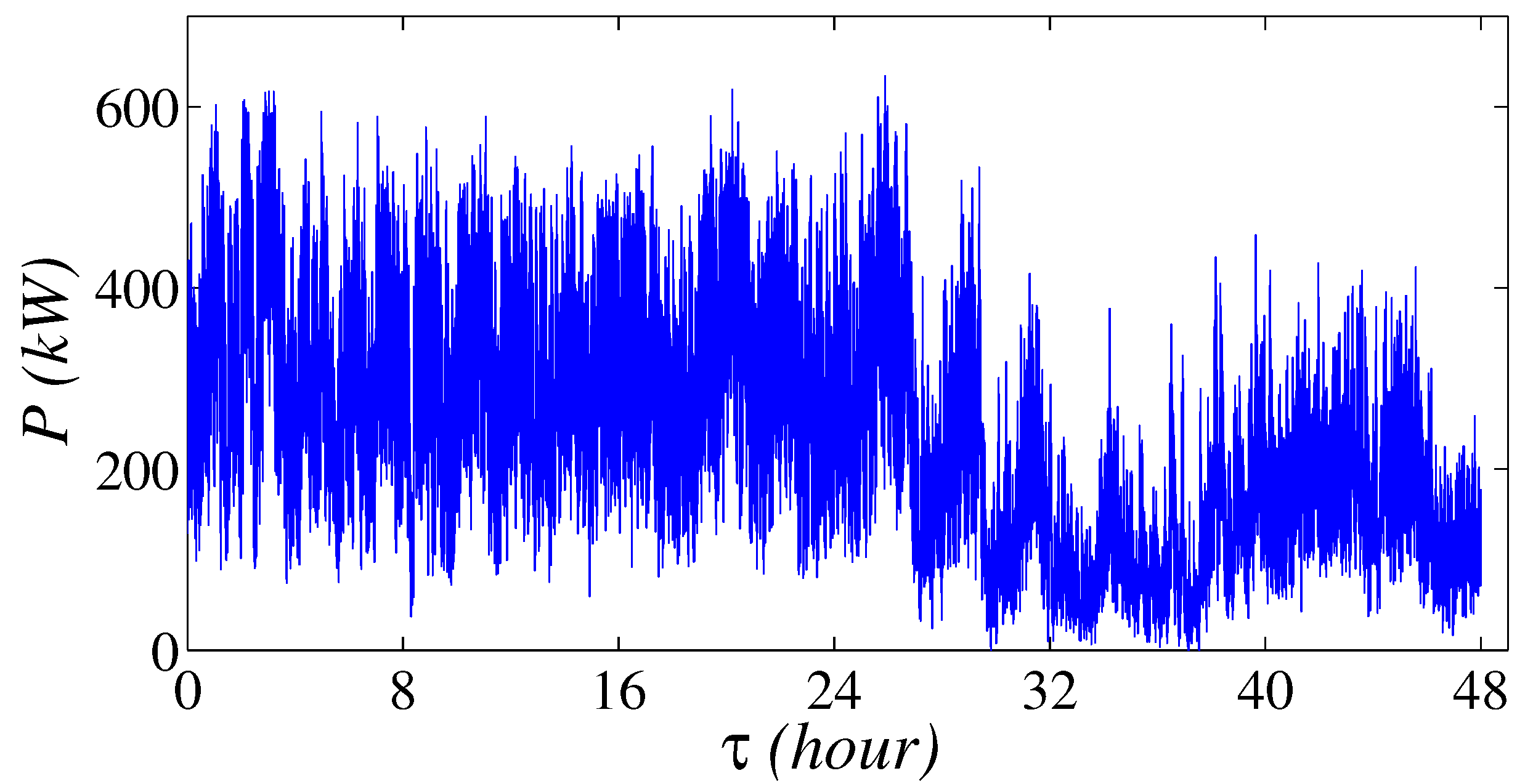
2. Wind Power Output Data
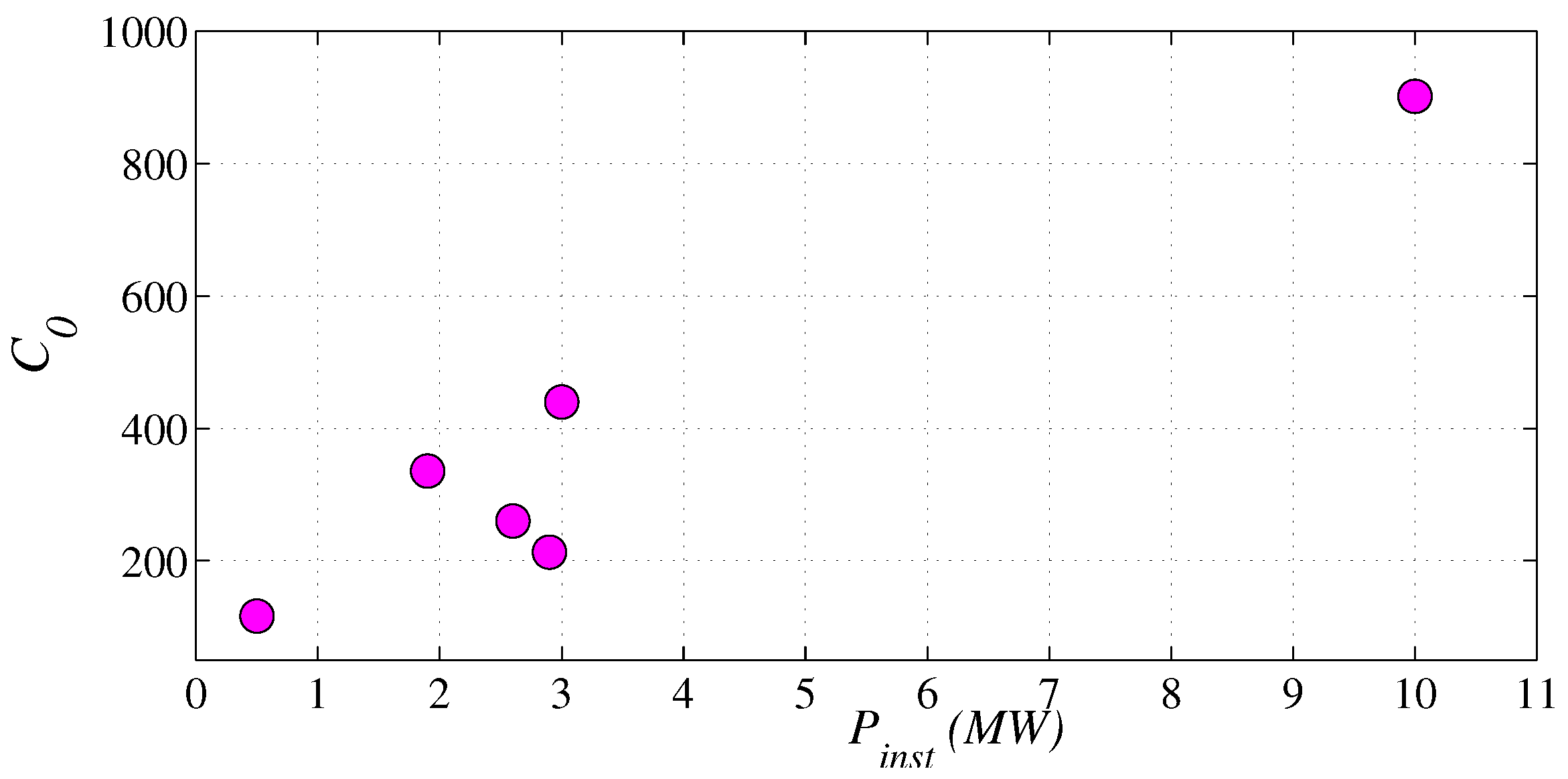
| Dataset | Sampling Frequency (Hz) | Number of Data Points | Implementation Site | Installed Capacity |
|---|---|---|---|---|
| Wind farm1 | plateau | 2.6 MW | ||
| Wind farm2 | plain | 2.9 MW | ||
| Wind farm3 | plateau | 1.9 MW | ||
| Wind farm4 | plain | 3 MW | ||
| Wind farm5 | 1 | cliff | 10 MW | |
| Single wind turbine | 1 | plain | 500 kW |
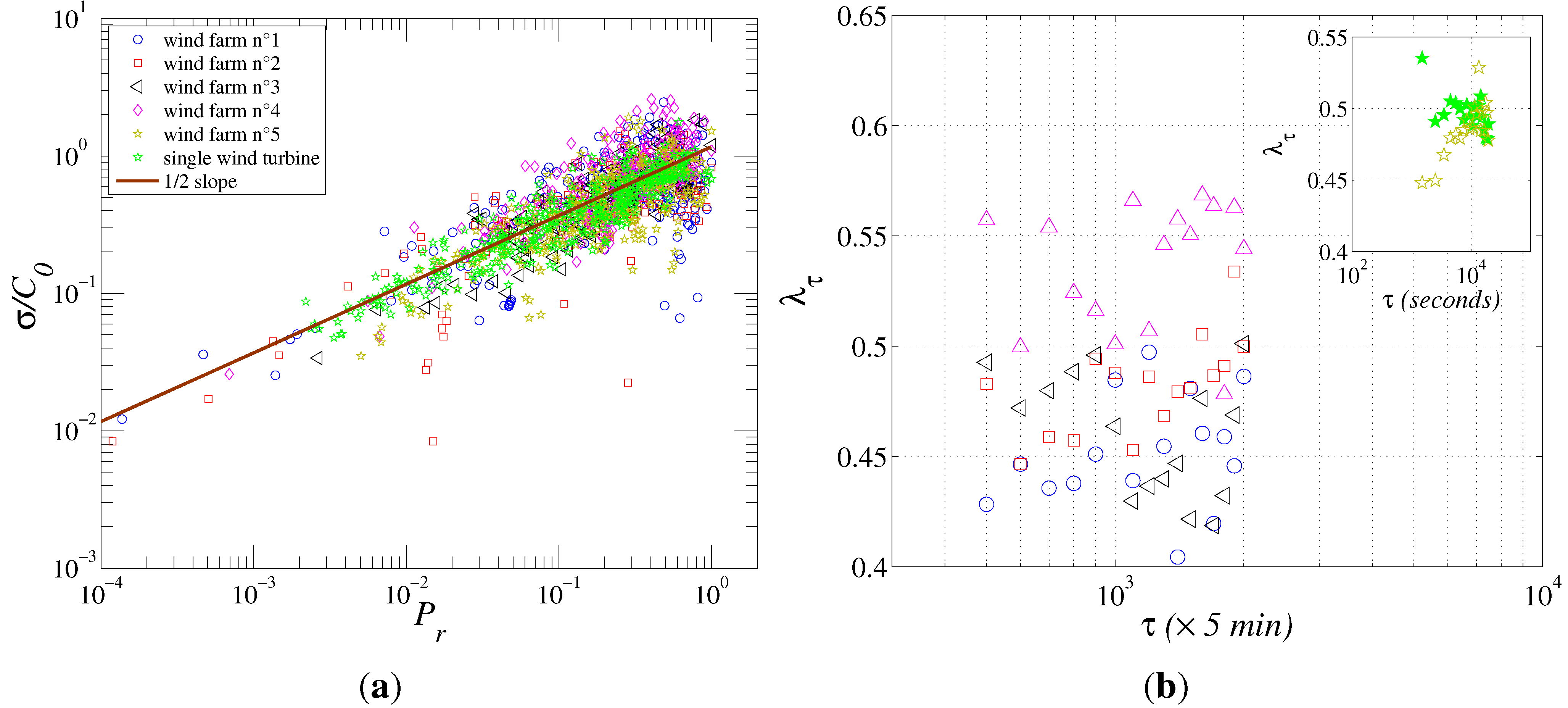
3. Taylor Law, a Scaling Relationship between the Mean Value and the Standard Deviation
3.1. Definition of the Taylor Power Law
3.2. Taylor Power Law in Wind Energy Data
| Data | ||
|---|---|---|
| Wind farm1 | ||
| Wind farm2 | ||
| Wind farm3 | ||
| Wind farm4 | ||
| Wind farm5 | ||
| Single wind turbine |
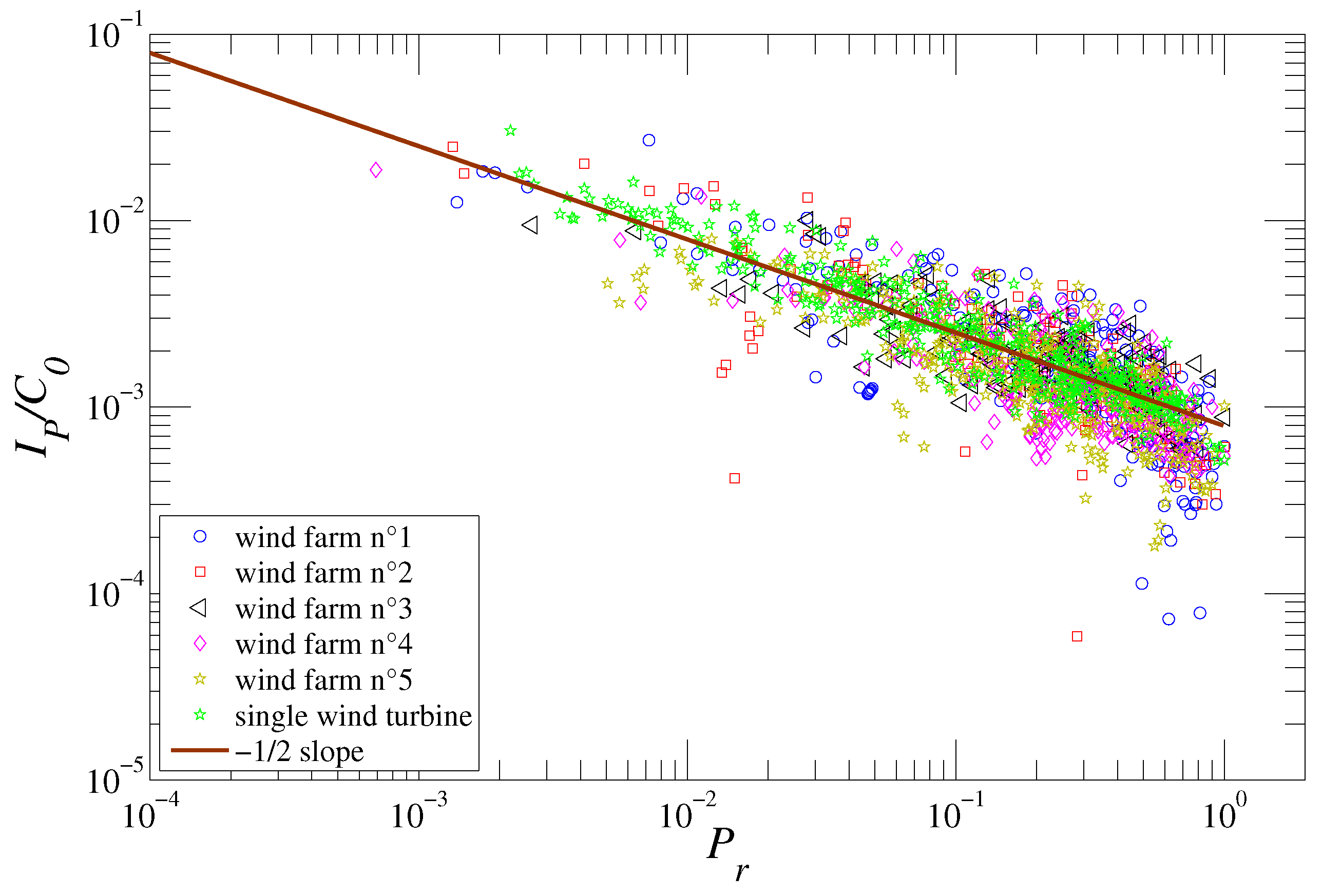
3.3. Turbulent Production Intensity
| Data | α |
|---|---|
| Wind farm1 | |
| Wind farm2 | |
| Wind farm3 | |
| Wind farm4 | |
| Wind farm5 | |
| Single wind turbine |
4. Conclusions and Discussions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Taylor, L.R. Aggregation, variance and the mean. Nature 1961, 189, 732–735. [Google Scholar] [CrossRef]
- Smith, H.F. An empirical law describing heterogeneity in the yields of agricultural crops. J. Agric. Sci. 1938, 28, 1–23. [Google Scholar] [CrossRef]
- Keitt, T.H.; Stanley, H.E. Dynamics of North American breeding bird populations. Nature 1998, 393, 257–260. [Google Scholar] [CrossRef]
- Kerkhoff, A.J.; Ballantyne, F. The scaling of reproductive variability in trees. Ecol. Lett. 2003, 6, 850–856. [Google Scholar] [CrossRef]
- Xu, M.; Schuster, W.S.; Cohen, J.E. Robustness of Taylor’s law under spatial hierarchical groupings of forest tree samples. Popul. Ecol. 2015, 103, 1–11. [Google Scholar] [CrossRef]
- De Menezes, M.; Barabási, A.L. Fluctuations in Networks Dynamics. Phys. Rev. Lett. 2004, 92, 028701. [Google Scholar] [CrossRef] [PubMed]
- De Menezes, M.; Barabási, A.L. Separating Internal and External Dynamics of Complex Systems. Phys. Rev. Lett. 2004, 93, 068701. [Google Scholar] [CrossRef]
- Eisler, Z.; Kertész, J.; Yook, S.G.M.; Barabási, A.L. Multiscaling and non-universality in fluctuations of driven complex systems. Europhys. Lett. 2005, 69, 664–670. [Google Scholar] [CrossRef]
- Eisler, Z.; Kerész, J. Random walks on complex networks with inhomogeneous impact. Phys. Rev. E 2005, 71, 057104. [Google Scholar] [CrossRef]
- Eisler, Z.; Kertész, J. Scaling theory of temporal correlations and size-dependent fluctuations in the traded value of stocks. Phys. Rev. E 2006, 73, 040109. [Google Scholar] [CrossRef]
- Šuvakov, M.; Tadić, B. Transport processes on homogeneous planar graphs with scale-free loops. Phys. A 2006, 372, 354–361. [Google Scholar] [CrossRef]
- Eisler, Z.; Bartos, I.; Kertész, J. Fluctuation scaling in complex systems: Taylor’s law and beyond. Adv. Phys. 2008, 57, 89–142. [Google Scholar] [CrossRef]
- Lee, Y.; Amaral, L.A.N.; Canning, D.; Meyer, M.; Stanley, H.E. Universal features in the growth dynamics of complex organizations. Phys. Rev. Lett. 1998, 81, 3275–3278. [Google Scholar] [CrossRef]
- Jiang, Z.Q.; Guo, L.; Zhou, W.X. Endogenous and exogenous dynamics in the fluctuations of capital fluxes: An empirical analysis of the Chinese stock market. Eur. Phys. J. B 2007, 57, 347–355. [Google Scholar] [CrossRef]
- Jánosi, I.M.; Gallas, J.A. Growth of companies and water-level fluctuations of the river Danube. Phys. A 1999, 271, 448–457. [Google Scholar] [CrossRef]
- Dahlstedt, K.; Jensen, H.J. Fluctuation spectrum and size scaling of river flow and level. Phys. A 2005, 348, 596–610. [Google Scholar] [CrossRef]
- Azevedo, R.B.; Leroi, A.M. A power law for cells. Proc. Natl. Acad. Sci. 2001, 98, 5699–5704. [Google Scholar] [CrossRef] [PubMed]
- Nacher, J.C.; Ochiai, T.; Akutsu, T. On the relation between fluctuation and scaling-law in gene expression time series from yeast to human. Mod. Phys. Lett. B 2005, 19, 1169–1177. [Google Scholar] [CrossRef]
- Kendal, W.S. An exponential dispersion model for the distribution of human single nucleotide polymorphisms. Mol. Biol. Evol. 2003, 20, 579–590. [Google Scholar] [CrossRef] [PubMed]
- Calif, R.; Schmitt, F.G. Analyse de séries temporelles de production éolienne: Loi de Taylor et propriétés multifractales. In Compte Rendu de la 15e Rencontre du Non-Linéaire; Falcon, E., Josserand, C., Lefranc, M., Letellier, C., Eds.; Non-Linéaire Publications: Paris, France, 2012; pp. 61–66. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000; p. 792. [Google Scholar]
- Petersen, E.K.; Mortensen, N.G.; Landberg, L.; Højstrup, J.; Frank, H.P. Wind power meteorology. Wind Energy 1999, 1, 25–45. [Google Scholar] [CrossRef]
- Calif, R.; Emilion, R.; Soubdhan, T. Classification of wind speed distributions using a mixture of Dirichlet distributions. Renew. Energ. 2011, 36, 3091–3097. [Google Scholar] [CrossRef]
- Fronczak, A.; Fronczak, P. Origins of Taylor’s power law for fluctuation scaling in complex systems. Phys. Rev. E 2010, 81, 066112. [Google Scholar] [CrossRef]
- Kendal, W.S.; Jørgensen, B. Tweedie convergence: A mathematical basis for Taylor’s power law, 1/f noise, and multifractality. Phys. Rev. E 2011, 84, 066120. [Google Scholar] [CrossRef]
- Apt, J. The spectrum of power from wind turbines. J. Power Sources 2007, 169, 369–374. [Google Scholar] [CrossRef]
- Calif, R.; Schmitt, F.G.; Huang, Y. The multifractal description of wind power fluctuations using arbitrary order Hilbert spectral analysis. Phys. A 2013, 392, 4106–4120. [Google Scholar] [CrossRef]
- Milan, P.; Wächter, M.; Peinke, J. Turbulent character of wind energy. Phys. Rev. Lett. 2013, 110, 138701. [Google Scholar] [CrossRef] [PubMed]
- Calif, R.; Schmitt, F.G. Multiscaling and joint multiscaling description of the atmospheric wind speed and the aggregate power output from a wind farm. Nonlinear Proc. Geophys. 2014, 21, 379–392. [Google Scholar] [CrossRef] [Green Version]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calif, R.; Schmitt, F.G. Taylor Law in Wind Energy Data. Resources 2015, 4, 787-795. https://doi.org/10.3390/resources4040787
Calif R, Schmitt FG. Taylor Law in Wind Energy Data. Resources. 2015; 4(4):787-795. https://doi.org/10.3390/resources4040787
Chicago/Turabian StyleCalif, Rudy, and François G. Schmitt. 2015. "Taylor Law in Wind Energy Data" Resources 4, no. 4: 787-795. https://doi.org/10.3390/resources4040787
APA StyleCalif, R., & Schmitt, F. G. (2015). Taylor Law in Wind Energy Data. Resources, 4(4), 787-795. https://doi.org/10.3390/resources4040787






